A Generative Model for Brain Tumor Segmentation in Multi-Modal Images

Abstract

We introduce a generative probabilistic model for segmentation of tumors in multi-dimensional images. The model allows for different tumor boundaries in each channel, reflecting difference in tumor appearance across modalities. We augment a probabilistic atlas of healthy tissue priors with a latent atlas of the lesion and derive the estimation algorithm to extract tumor boundaries and the latent atlas from the image data. We present experiments on 25 glioma patient data sets, demonstrating significant improvement over the traditional multivariate tumor segmentation.

1 Introduction

Limited therapy options require a careful diagnostic for patients with brain tumors. A multitude of available brain imaging sequences gives rise to patient data sets that include multi-parametric, multi-modal, and multi-temporal volumes even in standard clinical settings. Quantitative analysis of a lesion in these data poses a challenging computational problem. In this paper, we present a fully automated method for channel-specific tumor segmentation in such multidimensional images.

Generative probabilistic models of spatial tissue distribution and appearance have enjoyed popularity for tissue classification as they exhibit good generalization to unseen images [1,2,3]. Encoding spatial prior knowledge for a lesion, however, is difficult. Tumors may be modeled as outliers relative to the expected shape [4,5] or image signal of healthy tissues [2,6]. In [2], for example, a criterion for detecting outliers is used to generate a tumor prior in a subsequent EM segmentation which is treating tumor as an additional tissue class. Alternatively, the spatial prior for the tumor can be derived from the appearance of tumor-specific bio-markers [7,8]. The tumor classification methods can be augmented with spatial regularization using a Markov Random Field prior [9] or a boundary finding step [2,10] to ensure spatial contiguity of the segmentation results.

Discriminative approaches directly learn the difference between the appearance of the lesion and other tissues and do not rely on spatial priors [11,12,13,14,15,16]. They do, however, often require substantial amounts of training data and typically come at the cost of manual interaction for initialization and postprocessing. Most require the imaging protocol to be exactly the same in the training set and in the novel images to be segmented. Discriminative approaches proposed for tumor segmentation may use specific anatomical [13], but also generic image features (e.g., wavelets [11]) as input to the classifier. A spatial regularization via boundary modeling [11,12,13] or Markov Random Fields [14,15,16] has proved useful when used with discriminative methods as well.

Both generative and discriminative models face significant challenges when applied to multi-modal data. Automatic discriminative approaches are limited to the image modalities of the training set and are sensitive to missing data. Generative models may generalize straightforwardly to multi-channel observations [8,7], but do not allow for modeling differences between the biological processes observed in different modalities. By assuming the same shape and extend of pathology in all modalities, the standard multi-channel segmentation may ignore much of the information potentially available in images. Examples include differences in tissue water (T₂, Flair-MRI), enhancement of contrast agents (post-Gadolinium T₁-MRI), diffusion (DTI, DCE-MRI), or relative concentrations of selected metabolites (MRSI). Delineating the tumor area in each of these modalities individually is highly preferred for subsequent quantitative analysis of tumor shape and evolution.

We present a tumor appearance model for such multi-dimensional sequences and derive an algorithm for a channel-specific segmentation of the tumor. The method shares information about the spatial location of the lesion among channels while making full use of the highly specific multi-modal signal of the healthy tissue classes for segmenting normal tissues in the brain. In addition to tissue types, the model includes a latent variable for each voxel encoding the probability of observing tumor at that voxel. We derive an estimation algorithm for this model that generalizes the standard atlas-based EM segmentation. In our experiment with 25 multi-modal image volumes, the proposed approach performs significantly better than the traditional multivariate tissue classification method that assumes a single tumor segmentation that is shared by all channels.

2 Generative Tumor Model

We use a generative modeling approach, in which we first build an explicit statistical model of image formation and subsequently use this model to derive a fully automatic segmentation algorithm. Fig. 1 illustrates our generative model.

Fig. 1.

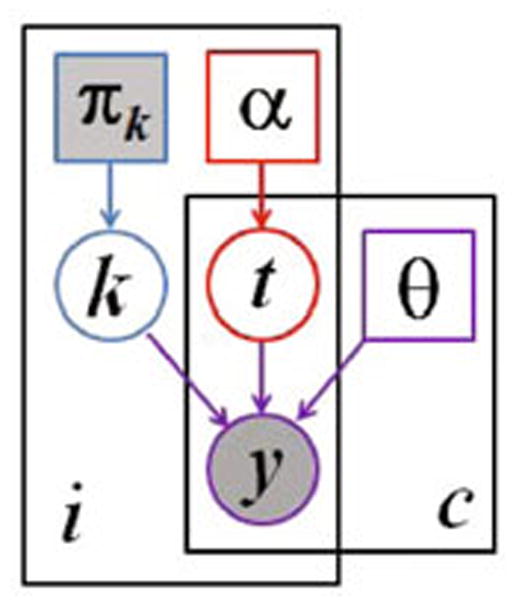
Graphical model for the proposed segmentation approach. Voxels are indexed with i, the channels are indexed with c. The known prior π_k determines the label k of the normal, healthy tissue. The latent atlas α determines the channel-specific presence of tumor t. Normal state k, tumor state t, and intensity distribution parameters θ jointly determine the multi-modal image observations y. Observed (known) quantities are shaded. The tumor segmentation aims to estimate $p(t_i^c\mid \mathit{y})$, along with the segmentation of healthy tissue p(k_i|y).

We model the normal state of the healthy brain using a spatially varying probabilistic prior π_k for each of the K tissue classes (Fig. 1, blue). This prior (atlas) is estimated from prior examples and is assumed to be known. At each voxel i, the atlas defines a multinomial distribution for the tissue label k_i:

$$p(k_i=k)={\pi }_{ki}.$$ (1)

The normal state k_i is shared among all C channels at voxel i. In our experiments we assume K = 3, representing gray matter, white matter and cerebrospinal fluid (CSF).

We model the tumor state using a spatially varying “latent” probabilistic atlas α, similar to [10] (Fig. 1, red). At each voxel i, this atlas provides a scalar parameter α_i that defines the probability of observing tumor at that voxel. Parameter α_i is unknown and is estimated as part of the segmentation process. We define a latent tumor state $t_i^c\in \{0,1\}$ that indicates the presence of tumor in channel c at voxel i and model it as a Bernoulli random variable with parameter α_i. We form a binary tumor state vector ${\mathit{t}}_i={[t_i^1,\dots ,t_i^C]}^T$ indicating the tumor presence for all c observations at voxel i, with probability

$$p({\mathit{t}}_i;{\alpha }_i)=\prod _{c}p(t_i^c;{\alpha }_i)=\prod _c{\alpha }_i^{t_i^c}·{(1-{\alpha }_i)}^{1-t_i^c}.$$ (2)

Image observations $y_i^c$ are generated by Gaussian intensity distributions for each of the K tissue classes and the C channels, with mean ${\mu }_k^c$ and variance $v_k^c$, respectively (Fig. 1, purple). In tumor tissue (i.e., if $t_i^c=1$) the normal observations are replaced by intensities from another set of channel-specific Gaussian distributions with mean ${\mu }_{K+1}^c$ and variance $v_{K+1}^c$, representing the tumor class. Letting θ denote the set of all mean and variance parameters, and ${\mathit{y}}_i={[y_i^1,\dots ,y_i^C]}^T$ denote the vector of the intensity observations at voxel i, we define the data likelihood:

$$\begin{array}{l}p({\mathit{y}}_i\mid {\mathit{t}}_i,k_i;\mathit{\theta })=\prod _{c}p(y_i^c\mid t_i^c,k_i;\mathit{\theta })\\ =\prod _c\left[\mathcal{N}{(y_i^c;{\mu }_{k_i}^c,v_{k_i}^c)}^{1-t_i^c}·\mathcal{N}{(y_i^c;{\mu }_{K+1}^c,v_{K+1}^c)}^{t_i^c}\right],\end{array}$$ (3)

where 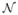(·; μ, v) is the Gaussian distribution with mean μ and variance v.

Finally, the joint probability of the the latent atlas and the observed variables

$$p({\mathit{y}}_i,{\mathit{t}}_i,k_i;\mathit{\theta },{\alpha }_i)=p({\mathit{y}}_i\mid {\mathit{t}}_i,k_i;\mathit{\theta })·p({\mathit{t}}_i;{\alpha }_i)·p(k_i)$$ (4)

is the product of the components defined in Eqs. (1–3).

3 Maximum Likelihood Parameter Estimation

We seek Maximum Likelihood estimates of the model parameters {θ, α}:

$$\langle \widehat{\mathit{\theta }},\widehat{\mathit{\alpha }}\rangle =arg\underset{\langle \mathit{\theta },\mathit{\alpha }\rangle }{max}p({\mathit{y}}_1,\dots ,{\mathit{y}}_N;\mathit{\theta },\mathit{\alpha })=arg\underset{\langle \mathit{\theta },\mathit{\alpha }\rangle }{max}\prod _{i=1}^{N}p({\mathit{y}}_i;\mathit{\theta },\mathit{\alpha }),$$

where N is the number of voxels in the volume and

$$p({\mathit{y}}_i;\mathit{\theta },\mathit{\alpha })=\sum _{{\mathit{t}}_i}\sum _{k_i}p({\mathit{y}}_i,{\mathit{t}}_i,k_i;\mathit{\theta },\mathit{\alpha }).$$

Observing that evaluating the objective function involves summing over values of t_i and k_i in Eq. (4), we use Jensen’s inequality to perform the optimization using an iterative, EM-style minorization technique [17]. Letting {θ̃, α̃} denote the current parameter estimates, we can compute the posterior probability of any of the 2^C tumor state vectors t_i, writing out the components of Eq. (4):

$$q_i({\mathit{t}}_i)\triangleq p({\mathit{t}}_i\mid k_i,{\mathit{y}}_i;\stackrel{\sim }{\mathit{\theta }},\stackrel{\sim }{\mathit{\alpha }})\propto \sum _{k_i}p({\mathit{y}}_i\mid {\mathit{t}}_i,k_i;\stackrel{\sim }{\theta })p({\mathit{t}}_i;{\stackrel{\sim }{\alpha }}_i)p(k_i),$$ (5)

and Σ_tiq_i(t_i) = 1. Based only on the intensity channels that do not show tumor ( $t_i^c=0$), we also compute the posterior probability of tissue k at voxel i:

$$w_{ik}({\mathit{t}}_i)\triangleq p(k_i\mid {\mathit{t}}_i,{\mathit{y}}_i;\stackrel{\sim }{\mathit{\theta }},\stackrel{\sim }{\mathit{\alpha }})\propto {\pi }_{ki}\prod _c\mathcal{N}{(y_i^c;{\stackrel{\sim }{\mu }}_k^c,{\stackrel{\sim }{v}}_k^c)}^{1-t_i^c},$$

and Σ_k w_ik (t_i) = 1 for all t_i. Using q_i(·) and w_ik(·), we arrive at closed-form update expressions that guarantee increasingly better estimates of the model parameters. The updates are intuitive: the latent tumor prior is an average of the corresponding posterior estimates

$${\stackrel{\sim }{\alpha }}_i\leftarrow \sum _{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)\left(\frac{1}{C}\sum _c{t}_i^c\right)$$

and the intensity parameters are updated with the weighted statistics of the data for the healthy tissues (k = 1, …, K)

$${\stackrel{\sim }{\mu }}_k^c\leftarrow \frac{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)w_{ik}({\mathit{t}}_i)(1-t_i^c)y_i^c}{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)w_{ik}({\mathit{t}}_i)(1-t_i^c)},{\stackrel{\sim }{v}}_k^c\leftarrow \frac{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)w_{ik}({\mathit{t}}_i)(1-t_i^c){(y_i^c-{\stackrel{\sim }{\mu }}_k^c)}^2}{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)w_{ik}({\mathit{t}}_i)(1-t_i^c)}$$

and for the tumor class:

$${\stackrel{\sim }{\mu }}_{K+1}^c\leftarrow \frac{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)t_i^c{y}_i^c}{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)t_i^c},{\stackrel{\sim }{v}}_{K+1}^c\leftarrow \frac{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)t_i^c{(y_i^c-{\stackrel{\sim }{\mu }}_{K+1}^c)}^2}{{\sum }_i{\sum }_{{\mathit{t}}_i}{q}_i({\mathit{t}}_i)t_i^c}.$$

We iterate the estimation of the parameters {θ̃, α̃} and the computation of the posterior probabilities {q_i(·), w_ik (·)} until convergence.

4 Tumor Segmentation

Once we have an estimate of the model parameters {θ̂, α̂}, we can evaluate the probability that tumor is visible in channel c of voxel i by summing over all the configurations t_i for which $t_i^c=1$:

$$p(t_i^c=1\mid {\mathit{y}}_i;\widehat{\mathit{\theta }},\widehat{\mathit{\alpha }})=\sum _{{\mathit{t}}_i}{t}_i^{c}p({\mathit{t}}_i\mid {\mathit{y}}_i;\widehat{\mathit{\theta }},\widehat{\mathit{\alpha }})=\sum _{{\mathit{t}}_i}{t}_i^c{q}_i({\mathit{t}}_i).$$ (6)

We then assign channel c of voxel i to tumor if $p(t_i^c=1\mid {\mathit{y}}_i;\widehat{\mathit{\theta }},\widehat{\mathit{\alpha }})>0.5$.

5 Extensions

To augment the generative model outlined above with further physiological knowledge, we derive and implement extensions considering the expected shape, multivariate signal and structural appearance of the tumor.

Little spatial context is used in the basic model, as we assume the tumor state t_i in each voxel to be independent from the state of other voxels (Eq. 6 and Eq. 3). It is only the atlas π_k that encourages smooth classification for the healthy tissue classes by imposing similar priors in neighboring voxels. To encourage a similar smoothness of the tumor labels, we extend the latent atlas α to include a Markov Random Field (MRF) prior:

$$p({\mathbf{t}}_1,\dots ,{\mathbf{t}}_N;\beta ,\mathit{\alpha })\propto \prod _c\prod _i{\alpha }_i^{t_i^c}{(1-{\alpha }_i)}^{1-t_i^c}exp\left[-\frac{\beta }{2}\sum _{j\in {\mathcal{N}}_i}{t}_i^c(1-t_j^c)+t_j^c(1-t_i^c)\right].$$

Here, 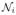denotes the set of the six nearest neighbors of voxel i, and β is a parameter governing how similar the tumor states tend to be in neighboring voxels. When β = 0, there is no interaction between voxels and the model reduces to the one described in Section 2. For β ≠ 0, the posteriors q_i(t_i) are no longer given by Eq. (5), and their exact computation becomes infeasible. However, relaxing the MRF to a mean-field approximation [18] we derive an efficient approximate algorithm. We let

$$n_i^c=\sum _{j\in {\mathcal{N}}_i}\sum _{{\mathit{t}}_j}{t}_j^c{q}_j({\mathit{t}}_j)$$

denote the currently estimated “soft” count of neighbors that show tumor in channel c. The mean-field approximation implies

$$p({\mathit{t}}_i\mid {\alpha }_i)\simeq \prod _c{\gamma }_i^{t_i^c}{(1-{\gamma }_i)}^{(1-t_i^c)},\text{where}{\gamma }_i=\frac{{\alpha }_i}{{\alpha }_i+(1-{\alpha }_i)exp[-\beta (2n_i^c-6)]}$$

to replace the previously defined p(t_i|α_i) in Eq. (4), leading to smoothed estimates of the tumor segmentations.

Moreover, we want to account for the non-homogeneity in the appearance of the tumor class, as gliomas show characteristic substructures such as active and necrotic areas and edema. We model this via a straightforward extensions of the tissue classes to include more than one class for tumor in a second modification to our approach. Finally, to consider higher-order interactions in the multivariate biological signal y_i of healthy tissue, we can relax the conditional independence of observations across channels by using multivariate Gaussians in the data likelihood in Eq. (3). We report tests of these three extensions in the next section.

6 Experiments

We evaluate our approach on a data set of 25 patients with glioma. The data set comprises T₁, T₂, FLAIR-, and post-Gadolinium T₁ MR images. Tumors were outlined by a rater in three planes intersecting with the tumor center. We register all images of a patient to the FLAIR volume by using affine registration and segment the volume into the three healthy and an outlier class using a freely available implementation of the EM segmentation with bias correction [1]. Outliers are defined as being more than three standard deviations away from the centroid of any of the three normal tissue classes.

We apply our algorithm to the bias field corrected volumes and initialize intensity parameters with values estimated in the initial segmentation. When using multivariate distributions 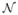(·; μ; V), we initialize off-diagonal element in V to zero. When modeling the tumor class with multiple Gaussian densities we initialize the means of additional subclasses to random values. We use outliers in the initial segmentation to initialize the latent atlas α, setting α_i for pixels of the outlier class to 0.7 and otherwise to 0.3. We typically observe convergence after 10 to 15 steps. For comparison, we also implement an EM segmentation treating tumor as one of the tissue classes, with a weak MRF prior for spatial regularization, similar to [2]. We use the same data and initializations as above, but augment the atlas by a tumor prior obtained by smoothing the outlier class of the initial segmentation with a 3cm kernel. This alternative segmentation is applied to every single image volume individually in a first experiment, and to the multivariate features of the whole multi-modal volume in a second experiment. To evaluate the classification maps we calculate Dice scores for both methods [19].

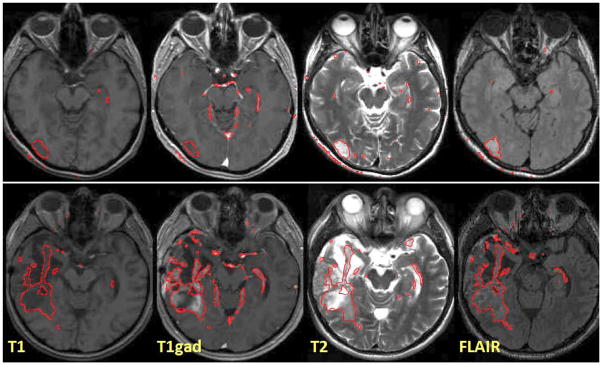
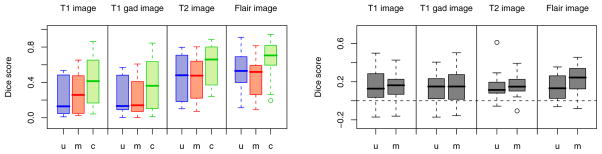
Fig. 2 illustrates results for two different subjects. We note that the tumor boundaries change across different modalities and the proposed method captures this variation well, even in post-therapeutic images. The method produces few false positives which can be easily eliminated in a post-processing step. We evaluate the robustness and accuracy of our method in a series of experiments. First, we test the sensitivity of the performance to the MRF parameter β that governs the smoothness of the resulting segmentations. It is the only parameter to be adjusted in our model. We find the performance of the algorithm to be relatively stable for a wide range of β values (Fig. 3), irrespective of size, location or shape of the tumor (i.e., β ∈ [1; 50]). For simplicity, we set β = 1 in all further experiments. In the second experiment, we test different model options for normal tissue and tumor classes. We find little differences between approaches that use non-zero off-diagonal elements in the covariance matrix of the intensity likelihood and those that do not. Modeling tumor by three Gaussians improves the result for some cases, but leads to a somewhat lower performance on average. In a third experiment, we compare our approach to the two alternative EM segmentation methods (Fig. 4). Here, we find the proposed channel-specific segmentation to always perform significantly better (p < 5 · 10⁻⁴, paired Cox-Wilcoxon test); it improves the absolute value of the Dice score over all four modalities for nearly all data sets by 0.1 to 0.2 (Fig. 4, right).

Fig. 2.

Examples of channel-specific segmentation results for four different modalities, in two patients. The outlines of regions with $p(t_i^c=1\mid {\mathit{y}}_i;\widehat{\mathit{\theta }},\widehat{\mathit{\alpha }})>0.5$ are shown in red. The proposed method localizes the tumor reliably in post-therapeutic images (below), where surgery has led to significant deviations from normalcy for healthy tissues.

Fig. 3.

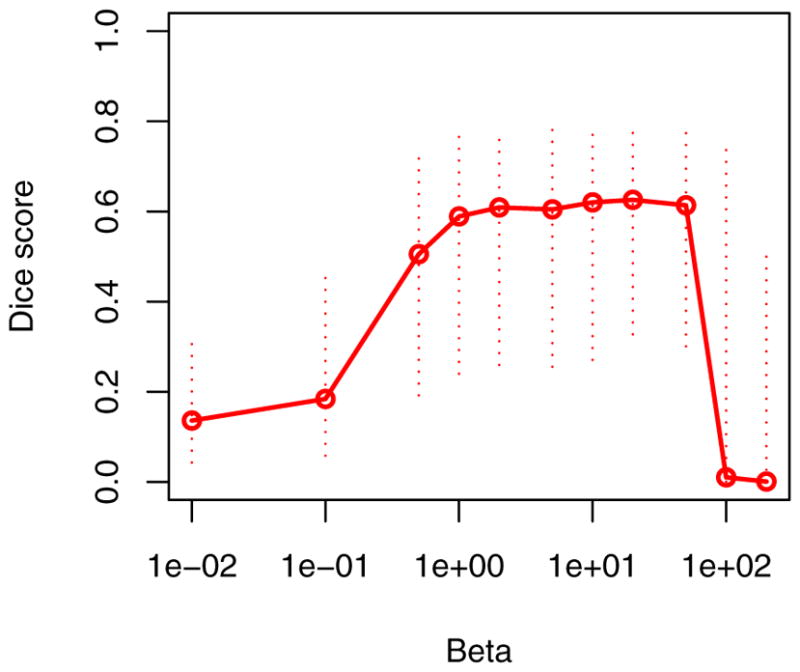
Sensitivity to the MRF parameter β. Indicated are the median (solid line) and the interquartile ranges of the average Dice scores of all 25 data set. While some regularization is beneficial, the segmentation performance is relatively insensitive to the choice of the only model parameter β.

Fig. 4.

Benefits of the channel-specific segmentation. Boxplots show median, quartiles and outliers for the Dice scores of all 25 subjects, for all four modalities. Our channel-wise segmentation (c, green) improves over both multiple univariate (u, blue) and multivariate (m, red) segmentation, both in the absolute terms (left) and with respect to patient-specific differences (right). The right figure shows c–u and c–m.

7 Conclusions

We present a generative model for tumor appearance in multi-modal image volumes of the brain that provides channel-specific segmentations. We derive an estimation algorithm and demonstrate superior performance over standard multivariate EM segmentation. Unlike discriminative tumor segmentation methods, our model is applicable to any set of multi-modal image volumes, and is fully automatic. Further extensions of the model may consider structure of the tumor, or temporal evolution in longitudinal data sets.