Abstract
Humans learn how to behave directly through environmental experience and indirectly through rules and instructions. Behavior analytic research has shown that instructions can control behavior, even when such behavior leads to sub-optimal outcomes (Hayes, S. (Ed.). 1989. Rule-governed behavior: cognition, contingencies, and instructional control. Plenum Press.). Here we examine the control of behavior through instructions in a reinforcement learning task known to depend on striatal dopaminergic function. Participants selected between probabilistically reinforced stimuli, and were (incorrectly) told that a specific stimulus had the highest (or lowest) reinforcement probability. Despite experience to the contrary, instructions drove choice behavior. We present neural network simulations that capture the interactions between instruction-driven and reinforcement-driven behavior via two potential neural circuits: one in which the striatum is inaccurately trained by instruction representations coming from prefrontal cortex/hippocampus (PFC/HC), and another in which the striatum learns the environmentally based reinforcement contingencies, but is “overridden” at decision output. Both models capture the core behavioral phenomena but, because they differ fundamentally on what is learned, make distinct predictions for subsequent behavioral and neuroimaging experiments. Finally, we attempt to distinguish between the proposed computational mechanisms governing instructed behavior by fitting a series of abstract “Q-learning” and Bayesian models to subject data. The best-fitting model supports one of the neural models, suggesting the existence of a “confirmation bias” in which the PFC/HC system trains the reinforcement system by amplifying outcomes that are consistent with instructions while diminishing inconsistent outcomes.
Keywords: Reward, Dopamine, Basal ganglia, Reinforcement learning, Rule-governance
1. Introduction
Functionally, reinforcement increases the probability of the behavior that precedes it. Conversely, punishment decreases the probability of the behavior that precedes it. A rich literature catalogs this trial-and-error learning of environmental contingencies (Thorndike, 1911; Skinner, 1938; Baum, 2004). Trial-and-error learning is, however, less than ideal. Testing possible contingencies is a costly, and sometimes dangerous, strategy. Humans have other options. By using rules1 and instructions, we can reap the benefits of others' trial-and-error learning without personally investing the time or enduring the perils associated with such an exercise. We can learn not to smoke, to save for retirement, and to obey traffic laws without experiencing the negative outcomes that result from violating these rules personally.
Nevertheless, individuals also learn when rules do not apply. Various dual process models posit separable decision-making systems that contribute to rule-based/descriptive choices versus those based on experience/procedural-learning (Sloman, 1996; Ashby et al., 1998; Hertwig et al., 2004; Kahneman, 2003). Here, we examine rule-following in a reinforcement learning task with well-studied neural correlates, and explore plausible neurocomputational interactions between rule-based and reinforcement-based systems that may produce this pattern of behavior.
Rule-following is typically adaptive, and people may be biased to follow instructions even when they are inaccurate (Galizio, 1979; Hayes et al., 1986, Hayes, 1993). An early study on the effect known to behavior analysts as “rule-governance” is illustrative. Kaufman et al. (1966) placed subjects on a variable-interval (VI) schedule for monetary reward. The experimenters accurately described the underlying schedule to one group of individuals and inaccurately described the schedule to two others: telling one of the latter groups they would experience a variable-ratio (VR) schedule, and the other they would experience a fixed-interval (FI) schedule. Despite the identical (VI) contingencies shared among groups, the participants in each group exhibited response patterns characteristic of the instructed schedule over a 3 hour period: those in the VR group responded at high rates, those in the FI group responded at low rates, and those in the VI group responded at the expected moderate rates.
Experiments investigating category learning in humans show the opposite effect, such that useful categorization rules are sometimes abandoned in favor of categorization by similarity (Allen and Brooks, 1991; Neal et al., 1995). In one such experiment (Nosofsky et al., 1989), subjects classified objects into one of two groups based on a number of attributes. After each categorization trial, subjects received feedback about the accuracy of their choice. One group received instructions permitting them to categorize stimuli accurately; the other learned to categorize by trial and error. Following a training period, subjects categorized novel stimuli. Though instructed subjects received and practiced a rule that could facilitate accurate categorization of these test stimuli, they did not always follow this rule, instead they reverted to categorization by similarity. Uninstructed subjects showed a greater tendency to group by similarity, leading the investigators to conclude that inductive learning about similarity had interfered with the use of instructions.
Noelle has developed a connectionist model of instructed learning that produces the effects found in category learning experiments (Noelle and Cottrell, 1995, 1996, 2000). This model learns both to follow instructions (modeled by setting the initial attractor states of the network), and from trial and error. When following instructions, the model behaves like human subjects, sometimes making categorization errors based on similarity when instruction-following would produce a more accurate outcome.
We build on this work by developing a biologically anchored model of the mechanisms that may underlie instruction-following even when experience indicates that the instructions are incorrect. To this end, we replicate the basic behavioral rule-governance effect using a task with well-studied neural correlates (Frank et al., 2004, 2005, 2007a; Klein et al., 2007). We then modify a neural network model of the reinforcement learning processes thought to govern performance in this task (Frank, 2005) to accommodate instruction-following. The modified model generates two concrete hypotheses for the neural underpinnings of rule-following, and produces a number of testable predictions for future empirical work. We then develop analytical mathematical models that attempt to capture the essence of the two proposed neurobiological mechanisms of instruction-following in abstract form. Qualitative fits of these models to subject data allow us to test between the computational accounts produced by the network simulations. Finally, we fit Bayesian models to subject data, in order to test alternative accounts for instruction-following behavior and individual differences therein.
2. Behavioral results and discussion
As expected, misleading instructions in the probabilistic selection task (Fig. 1, see experimental proceedures for details) produced sub-optimal choice behavior on the instructed stimulus alone. This effect occurred during both the training and test phases.
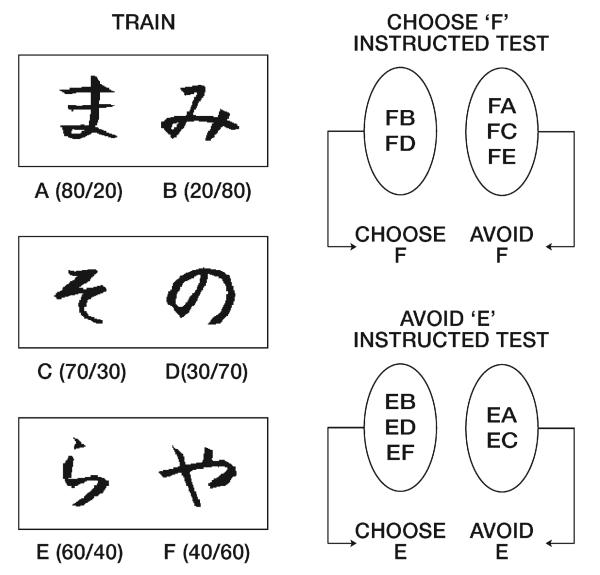
Fig. 1.
Probabilistic selection task. Example stimulus pairs, which minimize explicit verbal encoding by using Japanese Hiragana characters. Each pair is presented separately in different trials. The three different pairs are presented in random order to create blocks of 60 trials (20 per stimulus pair). Instructed subjects were misinformed either that F would have the highest probability of being correct or that E would have the lowest probability of being correct. Correct choices are determined probabilistically, with percent positive/negative feedback shown in parentheses for each stimulus. When reward was programmed for a given stimulus, a punishment was programmed for its paired alternative. A test (transfer) phase follows in which all possible stimulus pairs are presented and no feedback is given after choices are made. The effect of instructions on learning is measured by performance on all pairs featuring the instructed stimulus. “Choose F” refers to test pairs in which choice of stimulus F is optimal according to reinforcement probabilities, whereas “avoid F” refers to pairs in which the optimal choice is to select the alternative stimulus. Deviations from the accurate response (e.g. choose F, avoid F) indicate instructional control.
2.1. Training
Consistent with previous data, subjects matched the proportion of their responses to the proportion of positive feedback outcomes associated with that stimulus choice during the training phase (Estes, 1950; Frank et al., 2004).2 This pattern occurred on all but the instructed stimulus pair, in which choice was in accordance with the instructions rather than the true probabilities.
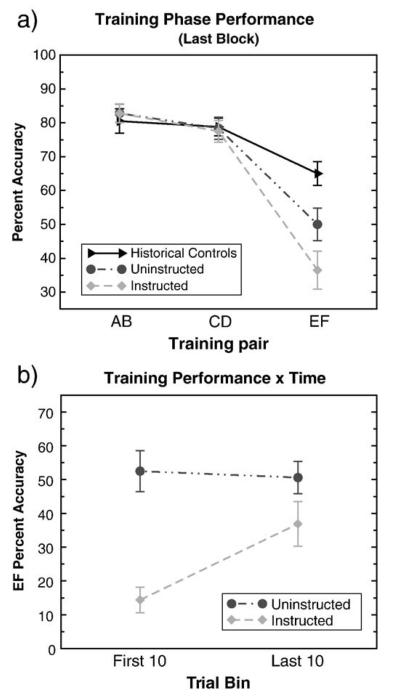
Choice in the EF pair by instructed subjects was suboptimal. Despite experiencing negative feedback on 60% of trials, these subjects continued to show a preference for the instructed F stimulus throughout the training phase (Fig. 2a). In the last block of instructed pair trials, these subjects chose the optimal stimulus E only 36.5% (standard deviation (sd): 22.4%) of the time, whereas uninstructed subjects chose it 53% (sd: 19%) of the time. Across training, a mixed-model ANOVA revealed an effect of instructions (F(1,30)= 8.84, p = 0.0058) and of stimulus type (F(2,30)= 38.91, p < 0.0001), but no significant interaction between instructions and stimulus type (F(2,30) = 2.81, p = 0.076). Planned comparisons revealed that the instructed subjects selected the incorrect stimulus F significantly more often than the uninstructed subjects (uninstructed accuracy: 51%, sd: 16.9%, instructed accuracy: 34.1%, sd: 17.6%, t(30) = 2.78, p = 0.005).
Fig. 2.
(a) Instructed subjects frequently chose stimulus F in the last block of the training phase, despite the repeated negative feedback that resulted from doing so. These subjects were told that either that the F stimulus (40% correct) would have the highest probability of being correct, or that the E stimulus (60% correct) would have the lowest probability of being correct. In actual fact, the E stimulus was more likely to be correct. The instructions did not affect learning of the uninstructed pairs, AB and CD. Performance in the last 20 trials of each stimulus pair is shown here. Historical controls (Frank et al., 2007c) plotted here show rough probability matching on all stimulus pairs. (b) Experience with the true contingencies reduced the influence of instructions on choice. However, by the end of training, subjects continued to choose more in accordance with the instructions than with the true probabilistic contingencies.
These results might occur if subjects followed the instructions early in training then switched their behavior after experiencing the true reinforcement contingencies. Because some subjects completed the training phase in one block (experiencing a total of 20 EF trials), we assessed learning of the EF pair by comparing performance in the first 10 trials to that of the last 10 trials across all subjects. For instructed subjects, EF performance was more inaccurate during the first ten trials (14.4%, sd: 15.5%) than during the final 10 trials (36.9%, sd: 26.3%), (t(15) = −2.94, p = 0.01). Despite this improvement in performance over blocks, EF accuracy for instructed subjects remained below that for uninstructed subjects during the final ten trials (instructed accuracy: 36.8%, sd: 26.2%; uninstructed accuracy: 52.5%, sd: 24.6%; t(30) = −1.73, p < 0.05. one-tailed) (Fig. 2b). This pattern of data suggests that, although instructed subjects learned from experience (given their increased accuracy over blocks), they did so at slower rate than expected. Subjects in previous studies exhibited rough probability matching on all pairs in a comparable number of trials (e.g., Frank et al., 2007c).
Because the number of training trials depends on subjects accuracy in the AB and CD pairs (see Experimental procedures for details), it is possible that those reaching performance criteria after relatively few trials may not have been exposed to sufficient instances of reinforcement feedback to be able to determine that the E stimulus had a higher probability of being correct than the F stimulus. To address this possibility, we fit a Bayesian learning model (see below for details) to subject data.
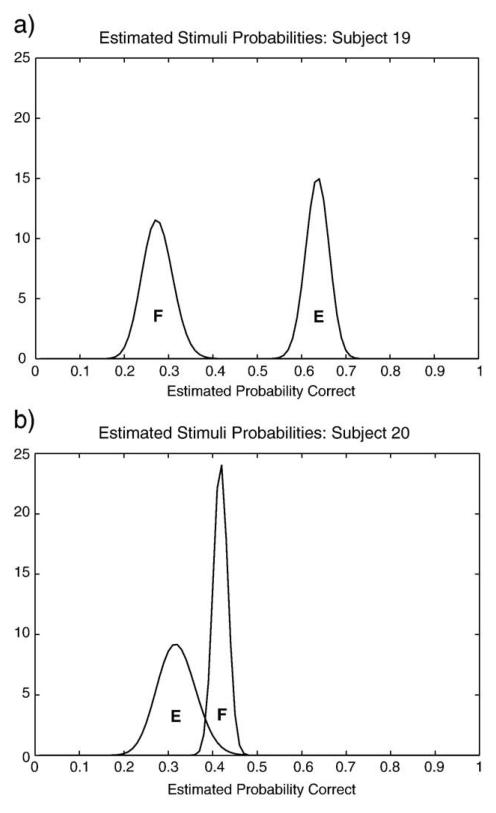
We compared posterior distributions produced by this model for the E and F stimuli at the end of the training phase. We then considered whether the above effects hold after filtering out participants who were judged not to have sufficient feedback to discriminate between E and F. Because the threshold for determining whether there was sufficient feedback is arbitrary, we used a liberal and more conservative threshold. In the liberal case we simply eliminated the 4 subjects (2 in each group) whose final F modes were not actually lower than those of E (which could occur due to spurious probabilistic feedback). In the conservative case we eliminated 12 subjects (6 in each group) whose final F modes were not at least one standard deviation below those of stimulus E (see Fig. 10 in Appendix for representative posterior distributions at the end of the training phase). Neither of these filtering measures changed the pattern of effects described above (Liberal: instructed subjects first ten trials (16.4%, sd: 15.5%) compared to last ten (40%, sd: 25%) t(14)= −2.73, p=0.02; last ten instructed subject trials (40%, sd: 25%) compared to last ten uninstructed subject trials (58.6%, sd:19.2%) t(26)=−2.15, p=0.04. Conservative: instructed subjects first ten trials (18%, sd:14.8%) compared to last ten (37%, sd:27%) t(9)= −2.08, p=0.067; last ten instructed subject trials (37%, sd:27%) compared to last ten uninstructed subject trials (66%, sd:17%) t(18)=−2.86, p=0.01)).
Fig. 10.
Plots of representative posterior estimated distributions for E and F stimuli. The basic Bayesian model computes optimally inferred probability distributions based on individual subject data. This model revealed that 4 subjects did not receive sufficient evidence to discriminate between the E and F stimuli. (a) Typical subject discriminated the relationship of the EF stimulus pair, E being more reliably correct than F. (b) One of four subjects who were unable to infer the correct relationship of E and F based on the probabilistic feedback received.
2.2. Test phase
Performance during the test (transfer) phase provides a measure of the extent to which subjects learned about the task contingencies. The experimenter told the subjects they would see both new and old pairings of the stimuli from the training phase,andtogowiththeir “gut” on these novel pairs. Therefore, the test phase provides a measure of the degree to which subjects integrated reinforcement values during the training phase. Performance during the test phase also provides a way to determine if subjects would follow instructions or rely on established reinforcement values in a novel context, particularly given that instructed subjects' training performance approached that of uninstructed subjects toward the end of training.
The subjects told that F would be good should be impaired at avoiding F when it is paired with relatively more positive stimuli A, C, and E (80%, 70%, and 60% probabilities respectively). Subjects told that E would be bad should be impaired at picking E when it is paired with relatively less positive stimuli B and D (20% and 30% probabilities respectively) (Fig. 1).
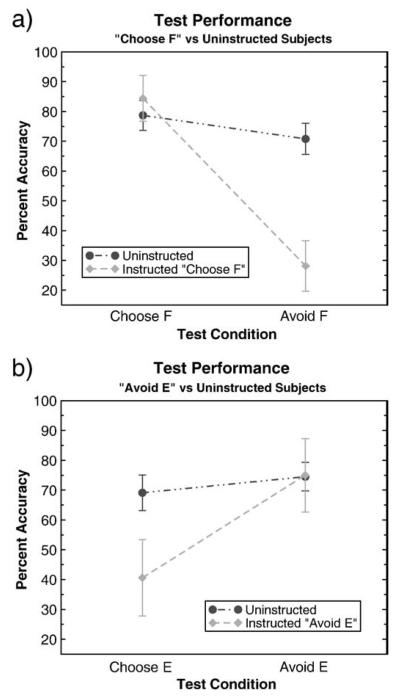
A mixed-model ANOVA revealed a main effect of type of instruction (choose F, avoid E, and uninstructed) between subjects (F(2,29)= 4.58, p = 0.0030), no within subjects effect of test measure (avoiding F or picking E) (F(1,29) = 0.8, n.s.) but a significant interaction between instructions and test measure (F(2,29) = 11.45, p = 0.0002).
These effects were driven by group differences in avoiding F when it was the less optimal stimulus (and should have been avoided) (F(2, 29) = 10.9, p = 0.0003). Group differences in choosing E when it was the best choice (and should have been chosen), approached but did not quite reach statistical significance, perhaps due to lack of power (F(2,29) = 3.2, p = 0.0556). Subjects did not differ in choosing F when it should have been chosen (F(2,29) = 0.84, p = 0.4419) or in avoiding E when it should not have been avoided (F(2,29)= 2.54, p = 0.0961) (Fig. 3). Removal of the subjects with posterior modes for E less than one standard deviation above F did not alter these results (subjects instructed to pick F were impaired at avoiding it: F(2,17) = 5.66, p = 0.0131, while impairments in subjects instructed to avoid E did not reach significance F(2,17) = 1.79, p = 0.197).
Fig. 3.
(a) Subjects instructed that F had the highest probability of being correct were more likely to choose F in the test phase when it was statistically suboptimal according to reinforcement probabilities (avoid F condition), and were just as likely as uninstructed subjects to select F when it was optimal. (b) Subjects instructed that E had the lowest probability of being correct were marginally more likely to avoid E when it was actually the more optimal response in the test phase (choose E condition), and were just as likely as uninstructed subjects to avoid E when it was suboptimal.
Given that all of the subjects correctly learned the reward probabilities associated with the uninstructed stimuli, these results are striking. During the training phase, choice of A and C produced greater reward (roughly twice as often) than choice of F. Subjects told that F had a high probability of reward, however, consistently chose it over statistically superior stimuli. Similarly, choice of B and D produced fewer rewards than choice of E. Nevertheless, subjects instructed to avoid E tended to, even when avoidance resulted in selection of statistically inferior stimuli. We found no differences in reaction times between groups in the training or test phases.
2.3. Individual differences
In the analysis above, we looked for effects at the group level. An inspection of individual subject data, however, revealed interesting within-group differences for those receiving misleading instructions. In this group, five of the sixteen subjects chose correctly on the EF pair on at least 50% of the last 10 training trials. These subjects appeared to be responding according to the experienced contingencies rather than instructions. Although all subjects initially followed the instructions, they were not equally likely to continue to do so throughout the learning trials.
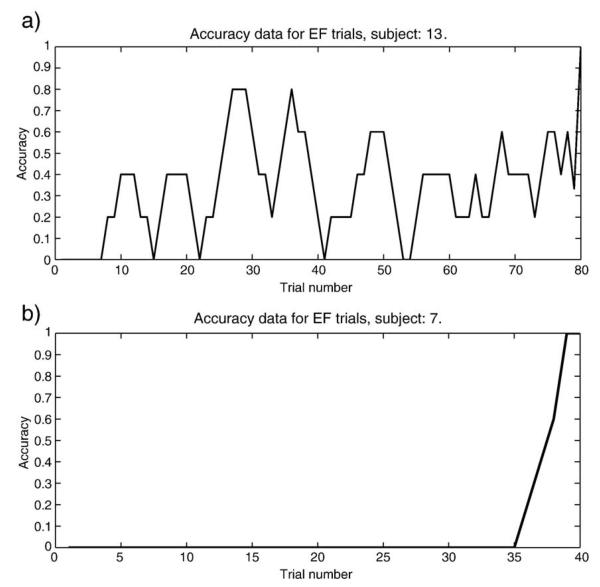
Visual inspection of the instructed training trials also suggested variability in learning about the true contingencies (see Appendix for representative learning curves). While some subjects seemed to gradually move towards the correct stimulus, E, several others abruptly switched response policies from choosing F to choosing E. Classifying subjects on visual inspection of learning curves introduces the bias of the rater. In attempt to reduce such bias, we developed computational models that assess both gradual learning and quick “insight”-type learning (see Q-learning models section).
3. Computational approach and theory sketch
Our approach is to model instruction-following/rule-governance in both biologically constrained neural networks and with simpler analytic models. First, we modify an existing and well supported neural network model of reinforcement learning, and show that our theoretically-motivated modifications to include instructions can replicate the effect seen in human subjects. We explore two possible circuits by which instructions can influence performance. The two hypotheses generated by the neural network simulations are then tested with simpler analytical models fit to subject data. We designed these competing analytical models to map on to, and thereby test between, the core computational accounts by which the networks function. Thus, our network simulations serve not only to generate biologically plausible hypotheses, but also to guide and constrain the types of analytical models used to test these hypotheses. Finally, we fit Bayesian models (which are not strongly constrained by network accounts, but reflect the “ideal observer”) to subject data.
We hypothesize that the rule-governance effect seen in our paradigm is the product of competition and/or cooperation between two neural systems. One of these systems, dependent on the basal ganglia (BG), integrates reinforcement contingencies slowly by trial and error. The other system, dependent on the prefrontal cortex and hippocampus (PFC/HC), rapidly updates representations based on single outcomes or salient details. We expect this system to encode task instructions.
Wide support exists for the key role of the BG, and the neurotransmitter dopamine (DA), in both Pavlovian and instrumental learning (Schultz et al., 1997; Schultz, 2007; O'Doherty et al., 2004), as well as habit learning (Graybiel, 1998; Yin and Knowlton, 2006). Phasic changes in DA levels follow feedback from the environment and constitute a “prediction error” signal, which can be used to drive learning (Montague et al., 1996; Schultz, 2007). Phasic bursts of DA occur when outcomes are better than expected and phasic dips occur when outcomes are worse than expected. These bursts and dips are thought to increase and decrease the likelihood of the action preceding the feedback by facilitating synaptic plasticity, with bursts promoting “Go learning” by means of D1-dependent LTP, and dips promoting “NoGo learning” by means of D2 receptor disinhibition (Nishi et al., 1997; Frank, 2005).
We begin our modeling by assuming that the prefrontal cortex (PFC) and hippocampus (HC) work together to produce the rule-governance effect. By this view, the PFC encodes representations of instructions in an active state that can provide top-down biasing on behavior (Miller and Cohen, 2001). The working memory capacity of the PFC also allows for the flexible updating of behavior in the interest of current goals, as well as robust maintenance of these goals in the face of distractions. A number of neuroimaging studies report PFC activation during rule-based learning (Filoteo et al., 2005; Nomura et al., 2007) as well as during rule-retrieval (Bunge et al., 2003). The HC on the other hand, encodes distributed representations of contexts, setting the occasion for a particular behavior in the presence of a specific context (for more discussion on relative contributions of PFC and HC, see Atallah et al., 2004).
We posit that rule-following involves not only active maintenance of PFC rule representations, but also retroactive retrieval of the rule from episodic memory (HC; see Braver et al., 2007). Recent work supports this view. Nomura et al. (2007) demonstrated that successful categorization of stimuli best grouped by simple verbal rules elicits frontal and hippocampal activation, whereas successful categorization of stimuli best grouped by integrating information over trials elicits striatal activity. Bunge and Souza (2008) review a number of imaging studies of rule representations, and conclude that rule-cue associations are stored in the temporal lobes and retrieved and maintained by PFC. Goto and Grace (2007) suggest that the HC gates PFC activation of the striatum, such that hippocampal episodic contextual memories can influence the degree to which prefrontal rules influence output behavior.
Anatomical studies suggest that the PFC/HC system might produce rule-governance in one of two ways. Although this system projects widely in the brain, the main projections of interest are those terminating in the striatum, and those terminating in motor cortex/premotor planning areas (Wallis and Miller, 2003). Rule-like representations in the PFC/HC may bias the striatum to learn what is described by rules, regardless of the true contingencies experienced. This is consistent with the existence of “split circuits” involving interactions between prefrontal–striatal loops and those involved in motor control (Joel and Weiner, 1999). Alternatively, rule-like representations may bias the behavior at the level of the motor cortex, leaving the striatum to learn the correct environmental contingencies independently, but overriding the expression of this learning in behavior. Our simulations demonstrate the plausibility of either of these circuits in producing rule-governance, but make different predictions for both the underlying neural activation and the extent to which rule-like or reinforcement-driven behavior will generalize to novel situations (e.g., if the rule-based system is taken off-line or if the implicit striatal system is primed in the absence of awareness). Next we report results from neural network simulations, followed by more abstract mathematical “Q-learning” models that can provide quantitative fits to individual subject data using a minimal number of parameters, to determine which (if any) of the various posited mechanisms provide the best fit.
4. Neural network results
4.1. Complete model
4.1.1. Training phase
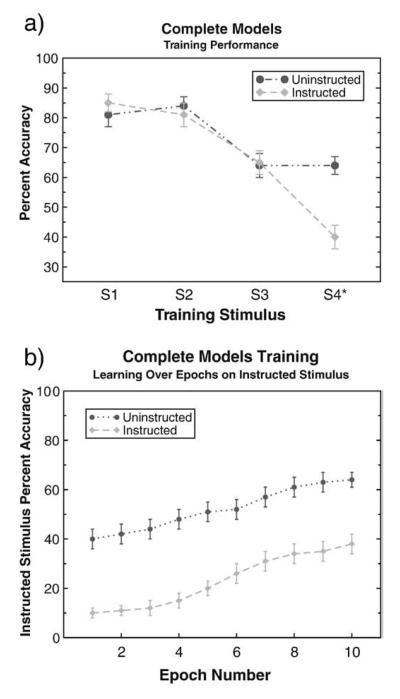
The instructed and uninstructed models produce the same probability matching behavior observed in human subjects on all but the instructed stimulus (Fig. 4a, see Neural network model section for implementational details). After stimulus presentation, the model can make one of two probabilistically rewarded responses such that when stimulus S1 is presented, response R1 is correct 80% of the time, whereas response R2 is correct 20% of the time (as in the human version of the task, on each trial one response is correct while the other is incorrect). For the instructed stimulus, S4, the probability of receiving “correct” feedback for each response matches that used in human subjects (40% for response R1 and 60% for response R2).
Fig. 4.
(a) Complete (dual projection) model performance on a reduced probabilistic selection task involving four stimuli. When presented with stimulus S1 (S2), response R1 (R2) is positively reinforced on 80% of trials. For S3 (S4), R1 (R2) is reinforced on 60% of trials. Instructed models were “misled” in an initial instructed trial that R1 would be correct in response to the critical (instructed) stimulus S4*. The instructed model shows the expected matching behavior on all but the instructed stimulus-response mapping. Choice on the instructed stimulus is suboptimal with respect to actual reinforcement probability, as in human subjects. (b) The instructed model, like human subjects, shows some learning of the true probabilities over time. Over 10 epochs performance on the instructed stimulus drifts up to match the allocation of F stimulus responses seen in human subjects. The uninstructed model begins somewhat below 50%. This occurs because the model does not always clearly choose a specific response early in training, instead producing a blend of responses (which is counted as incorrect). As feedback accumulates in training, the model begins to probability match the S4 stimulus.
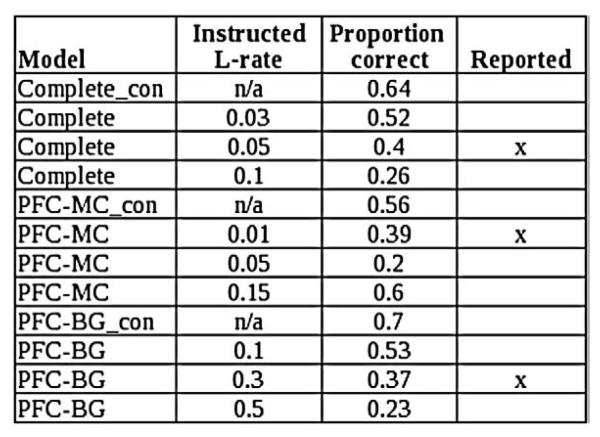
During the training phase, the proportion of instructed stimulus choices is a function of the learning rate applied in the initial trial, with higher instructed learning rates producing more rule-like behavior. Thus, the single instructed learning trial replicates the basic behavioral result seen in the training phase. The actual values of this learning rate parameter are arbitrary. For each simulation, we use the value that provides the best qualitative fit to the behavioral data (see Appendix for learning rates).
Despite exhibiting rule-governed choice, the instructed model demonstrates some learning about the true contingencies over trials, as do humans. Fig. 4b illustrates that the probability of the model selecting the instructed stimulus decreases over epochs, due to the feedback provided about the true environmental contingencies.
Though the qualitative patterns in the uninstructed models and uninstructed subjects are similar, the trajectory of the learning curves are slightly different. Due to the removal of the EF criterion in the behavioral experiment, several subjects were able to proceed to the testing phase before receiving adequate feedback to decipher the probabilities associated with the EF pair. As mentioned above, this caused uninstructed subject group to remain slightly below the expected 60% accuracy on this pair at the end of training (see historical controls Fig. 2a). Removal of subjects receiving insufficient feedback (see Bayesian analysis in Appendix) resulted in greater correspondence in probability matching between subjects and models.
4.1.2. Test phase
During the test phase, the uninstructed model exhibits the expected Go and NoGo activity in the striatum. That is, positive Go activation is observed for responses to stimuli with a high probability of providing “correct” feedback, whereas greater NoGo activation is observed for responses to stimuli with a low probability of providing “correct” feedback. This pattern replicates those described in earlier models without a PFC/HC layer (Frank et al., 2004, 2007b). Thus, our added layer does not alter the basic striatal reinforcement learning characteristics of the model.
In the “complete” instructed model, the PFC/HC projects to both the striatum and the motor cortex. Because we can apply independent learning rates to these projections for the instructed trial, this model can produce two qualitatively different results. If we apply a relatively high learning rate to the weights from the PFC/HC to striatum in the instructed trial, then the striatum shows Go activation for the instructed stimulus even during the test phase, despite having experienced negative feedback on 60% of trials. This result suggests that the PFC/HC trains the striatum (both during the instruction trial itself, and as the instruction is reactivated during each stimulus presentation) to represent the reinforcement probabilities incorrectly. In contrast, if the PFC/HC to motor cortex projection experiences the instructed trial with a relatively high learning rate, the striatum shows NoGo activation for the instructed stimulus. In this case the striatum learns the correct contingencies from experience, but is overridden by the PFC/HC. Because there is no principled way to decide how the brain differentially applies these learning rates (or even if it does), we do not consider these results further, but rather, explore each alternative with the single projection models described below.
4.2. Single projection models
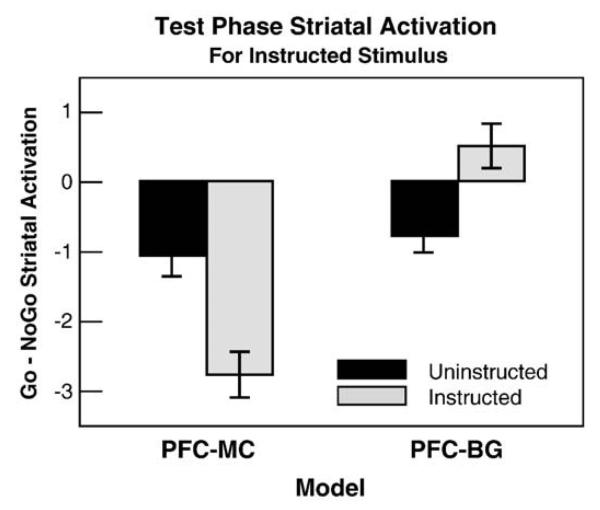
The modeling results suggest that the representations of rules in the PFC/HC either bias what the striatum learns about environmental contingencies or overrides its accurate contingency learning. To distinguish between these “bias” and “override” accounts, we conducted simulations using single projection models (PFC-BG and PFC-MC models respectively), and then probed for differences in striatal activity during the test phase.
During the training phase, the instructed versions of these models produced “behavioral” results virtually identical to that of the complete instructed model. They each exhibited probability matching on all but the instructed condition. On the instructed condition, both models produced the inaccurate, rule-governed response over the accurate, probabilistic response. Differences between the single projection models arise, however, when probing the learned striatal activations in response to the instructed stimulus during the test phase. In this phase, the PFC-BG model showed relatively greater striatal Go activation for the instructed response (Fig. 5). Here, the instruction representations biased the learning of the task by the striatum. This occurs for two reasons. First, the initial instructed trial produces large weight changes such that the representation of instructions in PFC/HC activates the associated striatal Go response. Second, subsequent presentations of the instructed stimulus reactivate these striatal Go representations, and in effect increase the effect of DA bursts following choice of instructed response, while also diminishing the effect of DA dips when the instructed response receives punishing feedback. Thus, the PFC-BG bias model constitutes a neurally plausible instantiation of a “confirmation bias”.
Fig. 5.
Striatal Go and NoGo unit activation-based receptive fields in the test phase when presented with the instructed stimulus. Here positive values indicate greater Go than NoGo activity for selecting R1 compared to R2. Uninstructed models show negative values, indicating a correct preference for R2 over R1 in response to the instructed stimulus, S4. Although both single projection models behaviorally chose response R1 (consistent with the instructions but inconsistent with reinforcement probabilities), their test phase striatal activations show that they learned fundamentally differently. Whereas the striatum in the PFC-MC (override) model appropriately learned NoGo to the instructed response, the PFC-BG (bias) model was biased to learn Go.
The PFC-MC model, in contrast, produced striatal associations similar to those of the uninstructed model (Fig. 5), but even more exaggerated. Here, the striatum learned the correct task-related contingencies, even though the model chose according to the instructions at the output level. Indeed, relative to the control model, the PFC-MC model shows greater striatal NoGo associations for selecting the instructed stimulus. This enhanced NoGo learning arose because the PFC-MC projections override striatal associations, thereby causing the network to select the instructed stimulus, and in turn to experience negative feedback and correspondingly enhanced NoGo representations. Thus whereas in the PFC-BG model, continued choice of the instructed stimulus can further train the striatum to “like” the instructed stimulus, in the PFC-MC model instruction-following increasingly results in striatal NoGo activation. Nevertheless, reactivation of the PFC/HC representations on subsequent instructed trials drive Hebbian learning along the direct PFC/HC to motor cortex pathway, further ingraining the response. Thus, the PFC-MC model predicts that the striatum learns a very negative association to the instructed stimulus despite conflicting choice behavior.
5. Q-learning results
Next we discuss the results of our analytical models which were fit to individual subjects trial-by-trial responses (see Q-learning models section for details). We are primarily interested in model fits to the test phase choices in which all novel pairings are presented without feedback. Because the instructed stimulus is paired with other stimuli of different probabilities, participants relative choice of the instructed stimulus as fit by softmax provides an objective measure of the effective value learned as a result of a combination of actual reinforcement and instructions. Nevertheless, we report model fits for both training and test phases.
5.1. Bias vs. override
On the whole, our modified models produced a marginally better fit in the training phase, and a substantially better fit in the test phase, compared to standard Q-learning models.
These results permit several conclusions. First, compared to the instructed learning model (IL, corresponding to the bias network model) the C-learning model (QC, corresponding to the override network model) yielded a poorer fit of subjects' choice data in both the training and test phases. This lends greater preliminary support to the IL model, which initializes Q-values according to the instructions and then modulates updating of those values over experience to be skewed based on instructions. This suggests that instructions initially operate by endowing a stimulus with value, and then by changing stimulus values to confirm rather than reject the instructions.
A more specific analysis of IL model variants suggests that the good fit is produced by discounting of outcomes inconsistent with the instructions more than by amplification of consistent outcomes. In the IL-A model, we amplified the impact of gains that occurred after following instructions for subjects told to choose F and amplified losses following E choices for subjects told to avoid E. In the IL-D model, we diminished the impact of losses following F choices for subjects told to choose F, and diminished the impact of gains that occurred after violating the instructions for subjects told to avoid E. The IL-D model provided a better fit to both the training and test phases.
5.2. Bayesian “strong prior” and IL models
The “strong prior” model provided improved fits of subject data compared to the basic Bayesian model. As expected, free initial hyperparameters were best fit by high values. For choose F subjects mean α = 286.5 (sd = 441.5), for avoid E subjects mean β = 522.9 (462.2) reflecting strong prior beliefs in the inaccurate instructions. However, this model proved to be inferior to the IL models (for both train and test compared with the non-Bayesian IL model, and for test compared with the Bayesian IL model). The Bayesian IL model not only included a strong prior for instructed stimuli, but also scaled the value updates to “confirm” the bias of the instructions. While this model fit the training phase data slightly less well than the “strong prior” model, it provided a substantially better fit to the test phase. Because the latter phase probes the values actually integrated as a function of training, this result supports the claim that “special” (confirmation bias) learning rules do indeed drive the rule-governance effect, a result consistent across our Bayesian and non-Bayesian frameworks.
5.3. Bayesian override and individual differences in “Insight” learning
The Bayesian override model provided inferior fits to subject data compared to the neurally-motivated Q models. Nevertheless, this model substantially improved training phase results compared to the basic Bayesian model (Table 1). The improved fit is a product of both the capacity to choose according to the instructions during training, and also to shift from this tendency. Interestingly, the best fit subjects were those with learning curves most indicative of “insight” learning (see Fig. 9 Appendix for representative curves). This override model also fit training data marginally better than the Bayesian bias models.
Table 1.
Model fits for training (Trn) and test (Tst) as indicated by Akaike's information criterion (AIC) (Akaike, 1974), pseudoR2 (Camerer and Ho, 1999), and log likelihood estimate (LLE).
| Model | Params | AIC_Trn | AIC_Tst | Trn_pR2 | Tst_pR2 | LLE_Trn | LLE_Tst |
|---|---|---|---|---|---|---|---|
| LG_Con | 3 | 75.88 | 94.87 | 0.16 | 0.288 | −34.94 | −44.44 |
| LG | 3 | 71.34 | 64.59 | 0.214 | 0.296 | −32.67 | −29.29 |
| IL | 4 | 72.07 | 58.56 | 0.23 | 0.392 | −32.04 | −25.28 |
| IL-A | 4 | 73.26 | 64.33 | 0.215 | 0.323 | −32.63 | −28.16 |
| IL-D | 4 | 71.95 | 58.82 | 0.231 | 0.389 | −31.97 | −25.41 |
| QC | 5 | 73.6 | 61.52 | 0.235 | 0.381 | −31.8 | −25.76 |
| B_Con | 2 | 73.24 | 104.66 | 0.158 | 0.193 | −34.62 | −50.33 |
| B | 2 | 79.04 | 71.36 | 0.098 | 0.19 | −37.52 | −33.68 |
| B_OR | 3 | 74.78 | 73.46 | 0.173 | 0.189 | −34.39 | −33.73 |
| B_SP | 3 | 75.06 | 69.96 | 0.17 | 0.23 | −34.53 | −31.98 |
| B_IL | 4 | 77.11 | 65.29 | 0.169 | 0.311 | −34.56 | −28.65 |
| B_IL_LG | 5 | 76.34 | 63.3 | 0.202 | 0.359 | −33.17 | −26.65 |
Higher pseudoR2 and LLE values are indicative of goodness of fit. AIC values penalize fits for models with more parameters, and smaller values indicate a better fit. LG_Con: LG model for control (uninstructed) subjects. LG: gain/loss model for instructed subjects. IL: instructed learning model in which initial values of QE and QF reflect instructions and value updates for instructed stimulus selections are amplified or reduced consistent with the instructions. IL-A: value updates consistent with instructions amplified only. IL-D: value updates inconsistent with instructions diminished only. QC: Q-values and C-values are added in softmax. B_Con: basic Bayesian model for uninstructed subjects. B: basic Bayesian model. B_SP: Bayesian strong prior model with free parameter initializing prior of instructed stimulus. B_OR: Bayesian override model which predicts instruction-consistent choices until it is sufficiently certain that they are incorrect. B_IL: Bayesian instructed learning model with strong prior and an additional free parameter scaling the degree to which outcomes from the instructed stimulus are distorted (as in basic IL). B_IL_LG: same as B_IL with the addition of separate decay parameters for gain and loss (as in LG).
Fig. 9.
Bayesian override model testing the possibility that subjects would abruptly abandon the rule upon accumulating sufficient evidence. Though the model fit the test data poorly compared to other models, the training data produced a good fit. The diversity of fits in the training phase indicate individual differences. Data here smoothed over 5 point moving average. (a) Subjects fit poorly by this model appeared to gradually shift from choosing according to instructions to choosing according to contingencies (this subject: pseudoR2 = 0.03). (b) Subjects best fit by this model also showed a learning curves most indicative of “insight.” (this subject: pseudoR2 = 0.21).
Though modification of the choice rule improved model fit in training, it also reduced fit in the test phase compared to the basic Bayesian model. This result reflects the conceptual difficulty such an account has in explaining the reemergence of instruction-following. If subjects have come to the conclusion that the instructions are inaccurate and adjust their behavior in opposition to those instructions, they should continue to do so at test. But because subjects tended to choose F even over stimuli that had much higher probabilities of positive feedback, these findings are better accommodated by the bias models, in which the system computing reinforcement probabilities is inaccurately trained by that representing instructions, such that the resulting final instructed probability is skewed.
Because of our small sample size and the lack of theoretical biological constraints, strong conclusions about individual differences cannot be drawn. Though some subjects shifted away from the instructed response in the training phase more quickly than others, the cause of this difference is unclear. Future work should seek to investigate these differences at the behavioral and biological levels.
6. Discussion
The computational neural mechanisms of rule-governance or instruction-following, and how they interact with reinforcement learning, remain under-investigated. Our results show that such research may permit not only description of the neural underpinnings of rule-governance, but, by pitting different neural systems against one another, may specify how learning systems cooperate or compete for control of behavior.
Our network simulations explored two routes by which instructions may exert their effects. The first possibility, as explored in the PFC-BG model, is that instructions bias the way the experience-based BG system learns directly. In this case, instructions cause the BG system to develop representations equivalent to those produced by environmental contingencies substantially divergent from those actually present in the environment. These divergent representations develop through “top-down” PFC/HC training signals. This account predicts that the striatum will represent a confirmatory bias to learn what is dictated by higher order structures.
The second possibility, as explored in the PFC-MC model, is that instructions override appropriate trial-and-error learning in the striatum at the level of decision output. In this case, the PFC/HC controls behavior even though the striatum “knows better.” Some neurophysiological data lend support to this idea. Pasupathy and Miller (2005), who recorded from monkey BG and PFC, demonstrated that that, although striatal cells indicate the correct response early in training, the behavior did not. The correct response appeared only when PFC cells also indicated the correct response. Clearly, no instructions appeared this study. Nevertheless, the results indicate that behavior may not always be contingent on the representations of the BG reinforcement learning system, even when it is correct.
Similarly, in a probabilistic reward-learning task, striatal cells were shown to encode Q-values (both positive and negative, consistent with Go and NoGo neuronal populations Samejima et al., 2005). The degree of activation of the associated Q-value striatal neurons predicted choice behavior. Critically, when the animal chose to “explore” by selecting the probabilistically less valuable option, the vast majority of striatal Q-value cells continued to represent the extant reward probabilities rather than the choice actually executed in that trial (see supplement of Samejima et al. (2005) — suggesting that extrastriatal structures control exploratory behavior. Notably, in humans, an explicit decision to “explore” in a probabilistic reinforcement learning environment is associated with anterior prefrontal activation, despite the fact that the striatum faithfully represented current reward probabilities (Daw et al., 2006).
A computational account of BG and PFC by Daw et al. (2005) suggests that each system produces different predictions about optimal behavior. In this framework, of the two systems, that with the more certain prediction controls behavior. The assumption that each system makes independent predictions is more consistent with our PFC-MC model in which the striatum makes its own predictions and the ultimate choice is dictated by motor cortex, depending on the relative strength of basal ganglia or prefrontal projections. The Daw et al. (2005) model is perhaps most closely related to the Bayesian version of our override model, in which the degree of certainty of the reinforcement system's estimations is used as an index to increase the odds of abandoning the instructions. In contrast, because the PFC-BG model suggests that the PFC system directly influences BG representations, and trains them to be skewed, such a clear separation at the neural level would not be expected.
Neither our behavioral experiment nor our network simulations clearly distinguish between the PFC-BG (bias) and PFC-MC (override) accounts. Abstract mathematical models fit to individual subject data suggest the bias hypothesis (IL model) may be more applicable in this context. Consistent findings were very recently reported by Biele et al. (2009), who explored the effects of social “advice” (from one participant to another) on subsequent performance in a gambling task; the best-fitting model was conceptually similar to our IL model. Thus although these authors take a social and cognitive approach, the effect they explore is similar and likely shares similar neural substrates to those we propose here.
Specific analysis of the mechanisms of our IL model suggest that rules control behavior by dismissing outcomes that are inconsistent with the rule (as indicated by the superior fit of the IL-D model). This mechanism maps on to the neural model where the impact of reinforcement inconsistent with instructions is reduced, given the simultaneous top-down bias of the PFC/HC layer onto the striatum. This bias drives Hebbian learning toward the instructed response, and minimizes the effects of DA error signals that would drive learning in the opposite direction.
Though the bias hypothesis is supported by the simulations we described, in absence of further data, we are reluctant to reject the override hypothesis outright. While both the QC model and Bayesian override models did produce overall inferior fits to subject choices, it remains possible that the essence of this type of model is correct, and may accurately reflect a valid cognitive strategy used by some participants. Future work will seek to accept or reject this possibility by correlating model parameters with biological signals, and examining the degree of model fit to functional connectivity between sensory and premotor cortical regions.
6.1. Model predictions
Though the simulations presented here do not provide conclusive answers, they do provide testable predictions. Given the finite working memory capacity of the PFC, it may be possible to take this system “off-line” and probe the striatum for responses. If the PFC is responsible for overriding accurate striatal encoding of reward probabilities, then taxing the PFC with a dual task may prevent this override from taking place. In such a case, instructed subjects would show rule-governed responding in a training phase identical to that described above. By adding second task during the test phase, however, the PFC should be unable to exert its influence and the contingencies learned by the striatum should dictate instructed subjects' choices. It is, of course, possible that contributions from HC in addition to the PFC are necessary to override contingencies learned by the striatum. In light of evidence that the HC and BG systems often compete with each other for behavioral control, such that inactivation of one system leads to enhanced performance in tasks that depend on the other (Atallah et al., 2004; Poldrack and Packard, 2003; Frank et al., 2006), it should be possible to reduce the impact of this system during the test phase. If, on the other hand, the PFC/HC trains the BG, then both systems should reflect the rule-governed contingencies, and the introduction of multiple tasks will not alter choices in the test phase.
Further, a priming paradigm, in which a particular stimulus is presented subliminally, followed by a target response, might reveal striatal “weights” in the absence of PFC/HC influence. If the target response is consistent with the probabilistic reward value of the primed response, we expect enhanced response latencies, whereas if it is inconsistent we expect diminished response latencies. Given that Parkinson's disease affects this kind of priming, revealing behaviorally silent striatal associations, such an approach appears feasible (Seiss and Praamstra, 2004).
Neuroimaging may also help to differentiate these models. Several studies have shown parametric BG responses to stimuli in proportion to their reward value (e.g., Delgado et al., 2003; McClure et al., 2003; ODoherty et al., 2003). Parametric estimation of BG response to each of the stimuli could indicate if the PFC/HC is training this system or if it is learning independently. The PFC-BG model predicts greater BOLD activation for the instructed stimulus F than its statistically superior pair E. The PFC-MC model predicts that, due to more choice and associated NoGo learning, the striatal BOLD response will treat the instructed stimulus F as if its reward value were quite low, even lower than in the uninstructed case (see Fig. 5 and results above).
Another possibility is that there are individual differences in the circuits mediating rule-governance. Recent imaging work documents individual differences in learning (Schönberg et al., 2007), but this approach remains underused. Given that multiple projections from PFC and HC to striatum and to motor outputs exist, it is plausible that individuals differ in the neural and cognitive strategies used to follow task instructions. Hence, those subjects best fit by the C-learning model might reveal greater functional connectivity between PFC and premotor cortex, whereas those better fit by the IL model might show greater functional connectivity between PFC and striatum.
The behavioral data presented here demonstrate that, as training progresses, some people begin to respond to extant probabilistic contingencies rather than misleading instructions. Given this, it is striking that a strong tendency to act according to inaccurate rules reemerges in the test phase (where subjects instructed to choose F, for example, chose it not only over E, with which it was paired during the training phase, but over A and C, stimuli that subjects accurately learned had high probabilities of being correct). One mechanistic interpretation is that during training, the PFC/HC inaccurately trains the BG, but that some portion of the PFC (perhaps orbital prefrontal cortex; Frank and Claus, 2006) with working memory capacity remains sensitive to recent outcomes begins to dominate training phase behavior.
7. Conclusion
Our work builds on lines of research from behavior analysis, cognitive psychology and cognitive neuroscience in attempt to identify and describe the neural correlates of rule-governance. Though computational approaches to cognitive neuroscience continue to proliferate, few have attended to the mechanisms underlying rule-governed behavior. Increasing evidence suggests multiple brain systems fulfill multiple cognitive roles (Sanfey et al., 2003; McClure et al., 2004 see Sanfey et al., 2006 for review). How these systems cooperate and compete for control of behavior remains largely unknown. Our computational investigations into this question generate a number of testable predictions. Future work will test these predictions, and inform future modeling efforts.
8. Experimental procedures
8.1. Subjects
A total of 34 subjects participated in the experiment. Initially, a group of 18 subjects completed the experiment with the instructional manipulation described below. Two of these subjects failed to learn the task to criterion and were excluded from the analysis. Experimental subjects were initially compared to historical controls from a similar demographic (Frank et al., 2007c). Because of differences in training criteria (we removed the EF training criteria in the experimental subjects), data from a group of 16 subjects were subsequently collected. In the analyses that follow we compare these 16 uninstructed controls (hereafter, uninstructed subjects) with the 16 remaining experimental subjects (hereafter, instructed subjects). (A follow-up experiment with controls and experimental subjects run simultaneously produced similar results to those reported here. This experiment was intended to test other aspects of instruction-following which we do not consider here.)
8.2. Probabilistic selection task
8.2.1. Instructed group
Subjects completed a probabilistic selection task (Frank et al., 2004) consisting of a training followed by a test phase (Fig. 1). In the training phase, subjects were presented with one of three stimulus pairs per trial. We refer to these stimuli as AB, CD and EF, although they were displayed to subjects as Japanese Hiragana characters to minimize verbal encoding. Feedback following selection of a stimulus indicated that the choice was either “correct” or “incorrect”. Stimuli were probabilistically rewarded, such that no stimulus was always correct. In stimulus pair AB, for example, choice of stimulus A led to positive feedback in 80% of trials, whereas choice of B led to negative feedback in those trials (CD and EF pairs provided 70/30% and 60/40% positive feedback respectively). During the test phase, subjects received all possible pairings of stimuli without feedback.
The experimenter asked the instructed subjects to read the task instructions on a computer carefully and explained they would receive a quiz to ensure they understood the instructions fully. The instructions read as follows: “Two black symbols will appear simultaneously on the computer screen. One of the symbols will be “correct” and one will be “incorrect,” but at first you won't know which is which. Try to guess the “correct” figure as quickly and accurately as possible. There is no ABSOLUTE right answer, but some symbols have a higher chance of being correct than others. Try to pick the symbol that you find to have the highest chance of being correct.”
Following these instructions, nine subjects read the following (misleading) statement: “The following symbol will have the lowest probability of being correct, so you should avoid selecting it. [The Hiragana symbol for stimulus E was displayed.] You'll have to figure out which of the other symbols you should select when they appear by trying them out. Use the “1” key to select the figure on the left. Use the “0” key to select the figure on the right.”
The remaining instructed subjects received the same instructions, but were shown the symbol for stimulus F and told (again, misleadingly) that it would have the highest probability of being correct, and so it should be selected.3 Both sets of inaccurate instructions, if followed, produce selection of the F stimulus.
After completing the instructions, the experimenter asked the subjects how many figures were to appear on the screen at once and how they would select the figure on either side. Subjects were shown a card with all six characters that would appear in the task and were asked to indicate which had the highest (or lowest, depending on condition assigned) probability of being correct. All subjects answered these questions correctly on the first attempt.
Next, subjects completed the training phase in which they were randomly exposed to 20 trials of each stimulus pair in 60-trial blocks. Previous versions of this task (Frank et al., 2004, 2007c) have required subjects to reach a performance criterion on each stimulus pair within a single block (65% A choices on AB, 60% C choices on CD, and 50% E choices on EF).4 Training blocks are repeated until criteria on all three stimulus pairs are met within a single block. In the current experiment, the AB and CD criteria were retained, but the EF criterion was removed because inaccurate instructions should produce below chance performance on this pair. Two subjects failed to meet training criteria, and their data were excluded from analysis.
After the training phase, the subjects completed a test phase in which they received all novel combinations of stimuli interleaved with the original training pairs. Subjects were told they would see new and old pairings of the stimuli they had learned about, but would not receive feedback following their choice. They were told to simply go with their “gut” feeling in selecting the stimulus most likely to be correct. Each test pair appeared four times in random order. Subjects received no feedback during the test phase.
8.2.2. Uninstructed group
16 uninstructed subjects completed the task described above. These subjects received the standard instructions without instructions about any specific stimulus. Additionally, these subjects received six presentations of each stimulus during the test phase.
9. Neural network model
The basic, uninstructed probabilistic selection task was developed to test predictions from a computational model of the basal ganglia and its modulations by phasic changes in dopamine during positive and negative feedback (Frank, 2005).5 Data consistent with these predictions were reported in several recent studies in which manipulations of the striatal dopamine system produced patterns of learning biases in accord with those simulated (Frank and O'Reilly, 2006; Klein et al., 2007; Frank et al., 2004, 2007a,b,c; Cools et al., 2006).
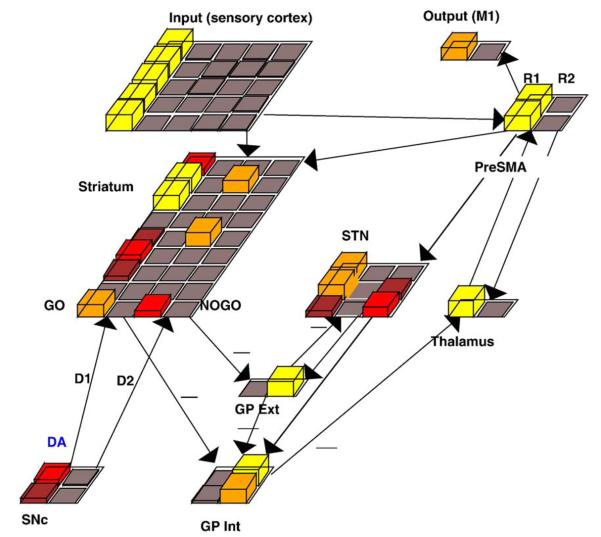
The basic BG model (Fig. 6) is instantiated using the Leabra neural simulation framework (O'Reilly and Munakata, 2000), and uses phasic changes in dopamine during reinforcement to drive synaptic weight changes rather than an explicit supervised error signal (Frank, 2005). A “point neuron” function simulates rate-coded activation of network units, as a dynamic function of their membrane potential, which itself is computed as a differential equation function of three ionic channel conductances (excitation, inhibition, and leak). Parameters of neuronal firing in different BG areas are tuned to match qualitative firing patterns in the various brain regions (see Frank, 2006 for mathematical details and parameters).
Fig. 6.
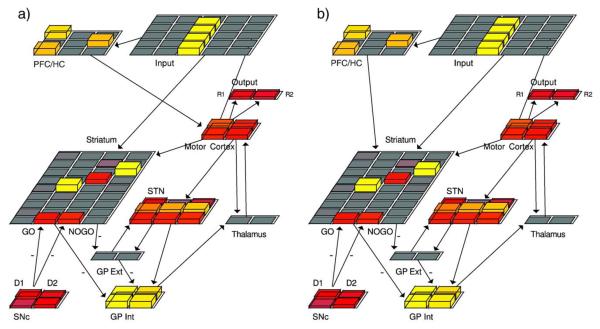
The basic BG model (Frank, 2005, 2006) simulates effects of dopaminergic manipulation on a variety of probabilistic learning tasks using the same network parameters. Stimuli presented in the input layer directly (but weakly) activate motor cortex. In order to execute an action, the motor cortex response requires bottom-up thalamic activation, which occurs via action selection in the BG. When activated, striatal Go units (in left half of Striatum) encode stimulus-response conjunctions and inhibit the internal segment of the globus pallidus (GPi). Because the GPi is normally tonically active and inhibits the thalamus, the effect of striatal Go signal is to release the thalamus from tonic inhibition, allowing it to become activated by top-down projections from motor cortex (PreSMA). In turn, thalamic activation reciprocally amplifies PreSMA activity, thereby generating a response. Striatal NoGo units have the opposite effect, via additional inhibitory projections to the external segment of the globus pallidus (Gpe), which effectively prevents a response from being selected. The net Go–NoGo activity difference is computed for each response in parallel by the BG circuitry and the response with the greatest difference is generally selected. (The subthalamic nucleus (STN) additionally modulates the threshold at which a response is executed, in proportion to cortical response conflict, and is included here for consistency but is not required for the effects reported in this paper).
On each trial, the network receives an input stimulus and executes a given motor response after its associated striatal “Go” representation is sufficiently greater than its corresponding “NoGo” representation. The output of the BG circuitry (the globus pallidus) in effect computes the Go–NoGo activity difference for each response in parallel. The response with the greatest difference is most likely to be facilitated via “disinhibition” of the thalamus, allowing recurrent thalamocortical projections to amplify the corresponding motor cortical response (and suppress the alternatives via lateral inhibitory competition). Thus, following each stimulus presentation, a single response is selected as its corresponding motor cortical units are active and the others suppressed.
Following the network's choice, phasic changes in dopa-mine firing occur to simulate reinforcement feedback: DA bursts for positive outcomes and dips for negative outcomes. Connection weights are adjusted based on the difference between pre and postsynaptic activity states across the response selection (tonic DA) and feedback (phasic DA) phases. Bursts activate the Go units in the striatum (via D1 receptor stimulation) and inhibit the NoGo units (via D2 receptor stimulation). This occurs after correct choices, and increases the probability that Go activity in the striatum will elicit the correct action in motor cortex. DA dips, on the other hand, together with ongoing excitatory (glutamatergic) projections from the cortex, allow the NoGo units to become disinhibited. An increase in the efficacy of NoGo units prevents activation of the incorrect motor response and makes that choice less likely in the future. This results in the training of “Go” and “NoGo” columns in the striatum, which produce stimulus approach or avoidance respectively for each of the two possible motor responses. Initially, the selected response is the product of random connection weights, together with noisy unit activity, but becomes the product of learning as training progresses.
9.1. Simulating the probabilistic selection task
The model experiences a training and test phase much like that experienced by human subjects. During the training phase, the model receives different input stimuli (each represented by a column of four input units). After settling on an action, the model receives probabilistic feedback about the chosen response. Over time, the probabilistically superior and inferior responses are learned. Upon completion of training, the model receives a test phase in which a response is made for each stimulus presentation without feedback. The test phase assesses the degree to which the model striatum had learned Go or NoGo to different stimuli and responses during the training procedure (Frank et al., 2004, 2007b).
The input layer receives each stimulus alone on different trials, and the resulting activity patterns over all striatal units are recorded. The summed relative Go to NoGo activity in the striatum produces an activation-based receptive field for each response to a stimulus. Networks that learned a particular stimulus-response mapping with a high probability of being correct should display strong Go representations for the response associated with choosing that stimulus. Similarly, networks that learn a particular stimulus-response mapping with a high probability of being incorrect should display stronger NoGo associations for the corresponding choice. Simulated changes in striatal dopamine levels can influence the degree to which networks are biased to learn Go or NoGo (Frank et al., 2004, 2007b), as observed in pharmacological experiments.
9.2. Simulating instructions
We assume that experiential learning in the absence of instructions relies on feedback, driving the BG system. The reduced effect of feedback in rule-governed behavior suggests that the BG system is somehow biased, or overridden by the presentation of rules.
The putative neural structures that underlie rule-governance in our manipulation are the PFC and HC. We model the “top-down” bias of these structures on the BG by adding a single abstracted PFC/HC layer that receives input and projects to the striatum and the motor cortex. Upon receiving input, the PFC/HC creates an activation-based distributed representation of the stimulus, which is a product of the layer's initial random weights. These activations then pass through the striatal learning system. The input layer also projects to the striatum and motor cortex as in the standard model.
For the purposes of our simulations, we have ignored some biophysical details with respect to how rules are encoded. The added layer, for example, does not feature the recurrent projections or specialized intracellular ionic currents widely used to capture the working memory capacity of the PFC (e.g., O'Reilly and Frank, 2006; Durstewitz et al., 2000). Nor is the sparse, distributed activity thought requisite for episodic encoding in HC present (O'Reilly and Rudy, 2001). Because we remain agnostic about the specific way in which these neural structures drive rule-governance (i.e., the degree to which the PFC or HC is responsible), these abstractions do not detract from the results. Our current focus is on the downstream (i.e. striatal and motor cortical) effects of these structures during instruction-following. Future models will incorporate top-down modulatory structures in a more biologically detailed manner, and attempt to decipher the relative contributions of PFC and HC in instruction updating, maintenance, and retrieval.
We model instructions by presenting each network with a single trial in which the instructed stimulus and its instructed (misleading) response activation at the output layer occur together. To model the rapid, single-trial acquisition of instructions, we use a much higher learning rate for this trial (see Appendix for parameter values), where this higher learning rate is applied to the weight changes from the input to the PFC/HC and from the PFC/HC to the striatum and motor cortex layers. This single high learning rate trial is an attempt to capture the rapid encoding of task rules in the explicit memory system, a process that should depend on the rapid learning functions of the hippocampus (e.g., O'Reilly and Rudy, 2001) together with the gating of prefrontal working memory representations for task rules (Braver and Cohen, 2000; Frank et al., 2001; O'Reilly and Frank, 2006; Rougier et al., 2005). As a result, networks dramatically increase the weights along these projections, such that the instructed input very likely produces this same “incorrect” response on subsequent presentations (due to reactivation of the PFC/HC “rule” representation and its associated biasing of striatal/motor responses). Following the instructed trial, the learning rate returns to its lower normal level (on the assumption that prefrontal rule representations are only gated once and thereafter only retrieved). The remainder of the training and test phase is completed as described above with no further manipulation. As such, other uninstructed stimuli still activate different distributed patterns of PFC/HC units, but these are not associated with strong biases to choose a given response.
The complete modified model represents the instructions in the abstracted PFC/HC and projects them to both the striatum and the motor cortex. As noted above, rule-governance may result from reactivation of the PFC/HC instruction representations that then bias the BG system to select the probabilistically sub-optimal response. Due to Hebbian learning in corticostriatal projections, repeated reactivation of PFC/HC rules can train the BG such that it never learns the true probabilistic contingencies, but instead continually ingrains the association learned by the instructed trial. Alternatively, the BG may be free to learn the reinforcement contingencies experienced in the environment accurately, but the PFC/HC can override this BG learning directly by simply biasing the premotor cortical decision outputs. The wiring of these structures lends itself to either of these possibilities, where PFC/HC connections to the BG explain the former, and PFC/HC connections to the motor cortex explain the latter. To investigate the differential roles of these projections in our model, we selectively removed them. In the PFC-MC model, the PFC/HC projects only to the motor cortex (Fig. 7a). In the PFC-BG model, the PFC/HC projects only to the striatum (Fig. 7b).
Fig. 7.
Alternative pathways by which rule-based representations can bias responding in the network. (a) In the PFC-MC model, the PFC/HC “rule” layer projects to the motor cortex, but not to the striatum. (b) In the PFC-BG model, the PFC/HC layer projects to the Striatum, but not to the motor cortex. The complete model features both of these projections.
10. Q-learning models
Our neural network simulations examine two potential neurobiological circuits that produce rule-governed behavior in the face of conflicting probabilistic reinforcement, and make different predictions for future experiments (see Discussion). The number of parameters in these network models, however, prevents us from quantitatively fitting models to individual trial-by-trial subject behavior. In contrast, although not specifying the precise mechanisms by which learning and choice behavior is achieved, more abstract reinforcement learning algorithms (e.g. Q-learning, temporal differences) can capture the computational functions that these brain processes are thought to implement and provide quantitative fits to behavior with a minimal number of parameters (O'Doherty et al., 2004; Cohen and Ranganath, 2007; Lohrenz et al., 2007; Daw et al., 2006).
We attempt to capture and test the two hypothesized rule-governance circuits delineated by the neural network simulations via modifications of a simplified Q-learning reinforcement algorithm (Watkins and Dayan, 1992) previously applied to this probabilistic selection task (Frank et al., 2007a). Because any number of abstract analytical models might be developed to account for subject data, we fit only models which conceptually match the “bias” and “override” hypotheses described by the network account above. Investigators increasingly utilize fMRI as a method to constrain analytical models with biological signals (see O'Doherty et al., 2007 for review). Our approach here is similar, though we use the plausible biological circuits identified by our neural network simulations to guide the development of our analytic models. Those models providing the best trial-to-trial fit to behavior might help discriminate between the competing hypothetical mechanisms.
To preview the results, our simulations suggest that subjects continue to learn with their reinforcement system, but that instructions amplify reinforcement experiences consistent with pre-set instructions and diminish reinforcement experiences inconsistent with them. This model is most consistent with the PFC-BG (bias) neural model described above, in which each rule-governed model choice reactivates the associated PFC rule representation which biases the striatum and increments the weight in that trial (despite conflicting reinforcement).
10.1. Standard Q-learning
As a baseline for comparison to our modified models, we use a form of the Q-learning algorithm previously altered for the probabilistic selection task (Frank et al., 2007a). This model incorporates two learning rate parameters, which separately scale value updates for positive (“correct”) and negative (“incorrect”) outcomes. These two learning rates embody our assumption that separate mechanisms within the BG can support Go and NoGo learning. This model computes a Q-value for each stimulus i in the task in the following way:
| 1 |
where αG is a learning rate parameter for positive outcomes, αL is a learning rate parameter for negative outcomes, and r is reward set to 1 for gains and 0 for losses. Q-values range from 0 to 1, and are initialized to 0.5 for all stimuli, in conjunction with subjects' initial uncertainty of value.
No feedback occurs during the test phase, so Q-value updates cannot occur during that phase. Instead, of all training parameters, those producing final (post-training) Q-values that best correspond to subjects' choices in the test phase are derived. This allows us to provide an estimate of the learning rates of a Q′ system in control of behavior during the test phase, based on its learned reinforcement history during training.
The Q′ value-updating equation is similar to that above:
| 2 |
In prior simulations, it was shown that the Q system that responds to trial-to-trial feedback during the training phase likely reflects a different neural and cognitive system than the Q′ system which integrates probabilities across trials, and which is needed to discriminate between subtle differences in these probabilities at test (Frank et al., 2007a). In particular, learning rates associated with trial-to-trial adjustments during training were associated with prefrontal function, whereas those associated with integrating probabilities were associated with striatal function. The assumption is that, during the training phase, working memory capacity of the PFC allows for win-stay/lose-shift strategies, hypothesis testing, and exploration based on uncertainty about reward structure for each stimulus pair. As a result, the best-fitting behavioral learning rates to participants' choices in the training phase are largely influenced by these recency effects, even as the striatal system slowly integrates reinforcement probabilities “under the hood”. Conversely, during the test phase, there is no feedback — and therefore no longer hypothesis testing, exploration, or recency effects. Further, all novel stimulus pairings are presented which can only be discriminated by comparing probabilities based on integrated past experience in the task. In this case, best-fitting learning rates are thought to reflect the striatal integration of reinforcement experiences throughout training, which are then used for choice at test.6
In this basic Q model, and in our bias account, the “softmax” logistic function computes choice. The probability of choosing stimulus A over B on any trial, for example, is
| 3 |
where ζ is an inverse gain parameter controlling the tendency to “exploit” (choose in accordance with established Q-values) or to “explore” and sometimes select the stimulus with the lower Q-value. Probabilities of selecting other stimuli are computed in the same fashion.
10.2. Bias hypothesis: Instructed learning model
According to the neural network simulations, rule-governance may work by inaccurately training the striatum to learn according to the instructions rather than according to the extant contingencies. As described above, the PFC-BG network model exerts this bias in two ways. The initial instructed learning trial inaccurately assigns a high value to the instructed response. Second, the effect of subsequent feedback from the instructed response is increased when it is consistent with the instructions and reduced when it is inconsistent.
To capture these dynamics, we modified the basic algorithm in two ways. To reflect the effects of the initial instructed trial, we altered the initial Q-values of the instructed stimuli. Instructions to choose F should produce results best fit by a high initial value of QF, whereas instructions to avoid E should produce results best fit by a low initial value of QE. We therefore set the Q-value of F to 1 and the Q-value of E to 0 for instructed “choose F” and “avoid E” subjects respectively. All other stimuli had initial values of 0.5 as usual.
To capture the effects of modulating the impact of feedback following an instructed response, we altered the Q-learning algorithm to modify value updating for the instructed stimulus (instructed learning: IL). For subjects instructed to choose F, we amplified value updates when instruction-following led to positive outcomes and reduced value updates when instruction-following led to negative outcomes. The model computes updates for subjects as:
| 4 |
where αI (1 ≤ αI ≤ 10) is a free parameter that amplifies gains and reduces losses following choices of instructed stimulus F. This parameter creates an index of biased learning with values greater than one indicating an amplification of Q-value updates following positive outcomes consistent with instructions, and diminished updating after negative outcomes inconsistent with instructions. We also constrained the maximum αI value by αG and αL.7 For subjects instructed to avoid E, we similarly scaled value updates such that updates consistent with instructions were amplified while those that were inconsistent were diminished. This entailed amplification of losses, and reduction of gains, following choices of stimulus E.
Instructions may exert their effects exclusively by amplifying or reducing outcomes (rather than doing both, as above), be they gains or losses. To investigate this possibility, the IL model was modified to only amplify updates (IL-A, amplify gains for subjects instructed to choose F and losses for subjects instructed to avoid E) and another to reduce outcomes (IL-D, diminish losses for subjects instructed to choose F, and gains for subjects instructed to choose E).
10.3. Override hypothesis: C-learning model
The alternative neural network model indicates that the effect of instructions is to have the PFC/HC directly activate motor cortical responses. By this view, the PFC/HC receives an initial learning trial which rapidly ingrains the instructed stimulus–response mapping. Experience that this instruction is incorrect may reduce instructional control over time, as striatal NoGo associations become large enough to play a role in selection. However, in parallel, continued reactivation of the instructed response in motor cortex upon its selection can slowly drive direct stimulus–response “habits”, in terms of strong synaptic weights due to Hebbian learning between the stimulus representation and the motor cortical response, which become independent of BG functionality over time (Frank, 2005).
To encapsulate these stimulus–response characteristics, we modified the Q-algorithm by introducing a variable that grows with the number of times a stimulus has been chosen. In addition to computing standard Q-values, the model tracks Choice (C) values for each stimulus as
| 4 |
where αc is a free parameter that increments the updates of C-values each time stimulus i is chosen. C-values and Q-values are then summed in “softmax” such that the probability of choosing F over E is
| 6 |
The summation of Q's and C's is based on the combined contributions of the PFC/HC and the BG to follow the instructions or the contingencies respectively. C-values increase over choices and make repeated stimulus selection more likely, independent of the outcomes associated with that selection. Thus, for instructed subjects, relatively large C-values accumulate as F is chosen, further increasing the probability of its selection.
To capture the initial task instructions, the C-value of the F stimulus was initialized as a free parameter (0.01 ≤ CF ≤ 5). This free parameter applies to both instructed groups because instructions to avoid E and to choose F both result in F selection. C-values for all other stimuli were initialized at zero, but nevertheless accumulate and are similarly integrated in the softmax choice function.
10.4. Bayesian Q-learning
We also implemented the Q-learning models described above in a Bayesian framework (Dearden et al., 1998; Daw et al., 2006), with multiple related motives. First, because it reflects the true Bayesian probabilities experienced by each individual, this framework naturally provides an objective measure of whether sufficient feedback information was received to learn the true statistical relationships between the training stimuli, given the probabilistic reinforcement schedule. Second, the Bayesian framework can determine whether subjects' tendency to follow instructions may reflect a strong initial prior distribution over Q-values associated with the instructed stimulus, without having to assume that subsequent learning rules are “special” for the instructed stimulus. That is, it is in principle possible that reduced learning from outcomes inconsistent with instructions (as in the IL model) might be captured by the Bayesian update rule in which the learning rate is effectively diminished when the initial prior is strong enough. Simulation results show that this is not the case, and that addition of an IL-like mechanism is necessary even within the Bayesian framework to fit participants' test choices. Finally, we implement a Bayesian version of the override model which posits that subjects continue to choose according to the instructions until they are sufficiently confident that the evidence rejects the instructions. Such an analysis can potentially indicate the degree to which subjects attained “insight” into the inaccuracy of the rule. We note that, unlike the models above, these analyses are not as directly constrained by mechanisms identified in our network models, but enable us to incorporate the notion that participants may represent different degrees of “belief”.
10.4.1. Basic Bayesian model
In Bayesian learning, rather than representing a single Q-value for each stimulus, the assumption is that subjects represent a distribution of beliefs about the Q-value for each stimulus (see Kruschke, 2008 for a comparison between classical and Bayesian approaches to learning). Because the stimulus outcomes in the probabilistic selection task are characterized by a binomial distribution, we represented beliefs using the beta distribution,8 characterized by hyperparameters α and β. The probability density function of the beta distribution is as follows:
| 7 |
where the integral in the denominator is the beta function B (α,β) and is a normalization factor that ensures that the area under the density function is always 1. The α and β parameters are updated after each outcome by adding to the running counts of “correct” and “incorrect” feedback to the prior α and β respectively. The defining parameters of the posterior distribution for each stimulus i are calculated after each outcome using Bayes rule, which given a beta prior simply amounts to:
| 8 |
| 9 |
where pos= 1 during positive feedback, and 0 during negative feedback, and vice-versa for neg. In addition, the running counts are decayed multiplicatively on each trial by a free parameter γ (1 ≥ γ ≥ 0). This decay parameter represents the subject's potential assumption that the distributions of stimulus outcomes might change with time (without such decay, the distributions become quite narrow, or “confident”, after relatively few trials; Daw et al., 2005).
At each trial, the mode and variance of the current beta distributions for each stimulus i are computed analytically:
| 10 |
| 11 |
Once the beta distributions are calculated, we then apply softmax in the usual way, using the modes of the density function as the best estimate of each Q-value, such that the probability of choosing A in an AB trial is
| (12) |
where ζ is an inverse gain parameter controlling the tendency to choose in accordance with established modal values. Probabilities of selecting other stimuli are computed in the same fashion.
At γ = 1 (i.e., no forgetting), this model computes the optimal Bayesian probability distributions for each subject's set of training data. Comparison of the modes of final distributions for any stimulus pair should reveal the true probabilistic relationship between the stimuli based on actual feedback delivered to each participant. If this relationship of final modes does not reflect the intended probabilistic relationship (i.e., EF has a 60:40 ratio), we conclude that the subject did not receive sufficient feedback to discriminate between the stimuli. Of the 32 subjects included in the analysis, two from the each group (instructed and uninstructed) had final modes for the F stimulus that were higher than those for the E stimulus (see Appendix for representative posterior estimates). As discussed above, exclusion of these subjects, or even of subjects whose F distributions were not at least one standard deviation below those of stimulus E, did not alter the effect of instructions.
10.4.2. Bayesian “strong prior” model
We altered the initial prior Q distributions for instructed stimuli to test the possibility that a model with no “special” learning rules could account for the observed data. In this model, for subjects instructed to choose F, the initial α parameter is allowed to vary for the prior F distribution. High initial α values, with β held to 1 produce distributions with modes close to 1, reflecting subjects' belief that F is correct. Similarly, we allowed β to vary freely for the prior E distributions for subjects instructed to avoid E. High β values with α held to 1 produce distributions with modes around 0, reflecting subjects' belief that E is incorrect. Free initial hyperparameters were bound between 0.01 and 1000. Both ζ and γ were also free to vary and were bound as above.
10.4.3. Bayesian IL model
To provide a strictly comparable comparison for the “strong prior” model, we developed an alternative Bayesian bias model. In this model, we allowed the initial hyperparameters and β to vary for instructed stimuli exactly as above. The defining parameters of the posterior distribution for each uninstructed stimulus i were also calculated as described above. Additionally, for instructed trials, the parameter ω is used to differentially scale consistent and inconsistent outcomes as in the basic (non-Bayesian) IL model.9 Instructed posterior distributions for subjects told to choose F were computed as
| 13 |
| 14 |
where 100 ≥ ω ≥ 1, and modal probability estimates are selected among via the softmax choice rule described above. For subjects instructed to avoid E, the modified update terms, ω and 1/ω, are swapped across hyperparameters such that outcomes are modified in accordance with the instructions that E should be avoided.
10.4.4. Bayesian override model and individual differences
As discussed above, visual inspection of subject learning curves for EF trials in training suggested interesting individual differences. While some subjects gradually increased their allocation of responses to E over F, others appeared to show “insight” into the fact that the instructions were incorrect, and switched from choosing F to choosing E.
A Bayesian framework could in principle provide a prescriptive account for when one might become more likely to abandon the instructions. We fit subject data with a modified version of the basic Bayesian model, which is closer in spirit to the neural override model. Here, standard (Bayesian) probabilistic reinforcement learning proceeds as usual “under the hood”, similar to the override model in which the striatum computes reinforcement probabilities for the instructed stimulus without being distorted by the instructions. Nevertheless, the choice rule is such that the instructed stimulus is highly likely to be chosen until the reinforcement system is sufficiently “confident” that the F stimulus is actually incorrect. This model has a parameter for “confidence” and can therefore be conservative: choices contrary to the instructions occur if the mode of the F distribution is ϕ standard deviations below 0.5, where ϕ represents the required degree of confidence. Estimated probability distributions were initialized and updated as above. For choices involving the instructed stimulus, we altered the choice rule such that the probability that the instruction-inconsistent stimulus (E) is selected (i.e., the probability that the instructions are determined to be inaccurate and should be abandoned), is computed as:
| (15) |
where ϕ (20 ≥ ϕ ≥ 0) represents the degree of confidence, in terms of the number of standard deviations that the mode of the F distribution has to be below 0.5, before a choice inconsistent with the instructions is likely to occur. The probability of continuing to choose in accordance with the instructions is then simply PF(t)=1 − P(E). Note that this modification of the choice rule does not result in a persistent policy switch, but rather computes the likelihood that the subject will choose in accordance with the instructions based on an estimate of their accuracy at each trial. For uninstructed stimulus pairs, the standard “softmax” rule is retained. This model was motivated by a similar implementation of reversal learning (but without the confidence metric, as it did not involve prior instructions), by Hampton et al. (2006).
Once sufficient evidence as to the inaccuracy of the instructions is accumulated, this model predicts a shift in choice strategy, such that there is a higher probability of making a choice inconsistent with instructions. Thus subjects showing learning trajectories in which they initially make instruction-consistent choices and then at some point are more likely to abandon the instructions (possibly reflecting “insight”) may be well fit by this model.
Acknowledgments
We thank Scarlett Coley for assistance with figures, Nathaniel Daw and two anonymous reviewers for helpful comments and suggestions.
Appendix
Network model learning rates
Instructions were simulated in the network models by presenting a single trial in which the instructed (inaccurate) response was clamped to the output layer. The learning rate along projections from the PFC/HC layer was elevated for this trial, then reduced to the learning rate used throughout the network (0.001). Fig. 8 shows results produced using different learning rates for the instructed trial.
Fig. 8.
The effect of different learning rates for the instructed trial on each network model. For each model type we reported the results for the learning rate that provided the best fit of data from human subjects. Proportion correct is the amount of time the model chose according to the actual contingencies (60% for the critical stimulus), rather than the instructions. Higher learning rates in instructed trials generally produce more rule-following and less accurate responding.
Q-learning
Best-fitting parameters in all models were derived using the MATLAB fmincon function, implementing the Simplex method (Nelder and Mead, 1965) using multiple starting locations by maximizing the log likelihood of the data under the model on a trial-to-trial basis for each subject separately.
LLEs for each subject were computed as
| 16 |
where t is trial number and i*,t denotes the subjects choice on trial t. For each subject, the best fit parameters are those associated with the maximum LLE value and are, by definition, the most predictive of the subject's sequence of responses in the probabilistic task.
The pseudoR2 measure compares the improvement in LLE gained by the model compared to a model that choose randomly (p = 0.5 for each trial).
| 17 |
where r is the LLE for the random model.
We also computed the AIC index, which penalizes models with more free parameters:
| 18 |
where k is the number of free parameters. Lower AIC values indicate a better fit. Because of the criteria applied to the training phase, some subjects experienced more training blocks than others. As a result, LLEs for subjects who took longer to reach training criteria are inappropriately high. To control for this we divided the training LLE for each subject by the number of training blocks needed to reach criteria.
To test the validity of our model assumptions specific to the instructed stimulus, we ran control models by serially applying each modified Q-algorithm to each of the uninstructed stimuli, retaining the standard Q-algorithm for the instructed stimulus. These control models indicated that improved fits of the modified Q models were not produced by arbitrarily adding parameters, but rather, reflected computation induced by the experimental manipulation.
Footnotes
Here, we use the word “rule” in the behavior-analytic sense: a verbal statement (in this case, instruction) that controls behavior (Hayes, 1993). While behavior shaped by trial-and-error experiences may be describable by a rule, such behavior is not referred to as rule-governed, but rather, controlled by contingencies in the environment. This is because such behavior is shaped by interactions with contingencies, rather than through interactions with verbal rules.
Although this response profile is sub-optimal (given the static reinforcement probabilities in this experiment, in principle subjects could maximize reward rate by always choosing the more frequently correct response in each pair), the tendency to probability match is thought to reflect the inherent tendency for subjects to explore alternative options to determine whether they might be better than the currently selected option (Daw et al., 2006; Lau and Glimcher, 2005).
In a follow-up experiment the manipulation was presented as a “hint” (e.g. F will be the best) with no specific instruction to select or avoid the instructed stimulus. This manipulation produced similar results to those reported here.
These criteria were used to ensure that participants performed sufficiently well in the test phase (ultimately used to evaluate relative learning from positive and negative feedback) without having to experience excessive numbers of training trials.
Due to space limitations, we primarily confine our discussion of the network model to the modifications undertaken to produce the rule-governance effect. The effects of our modifications are most relevant at the level of the striatum and premotor cortex. Other simulated layers (e.g. globus pallidus, subthalamic nucleus, etc.) support action selection and have particular computational functions but do not play a critical role in the rule-governance effect we replicate here, and therefore are not discussed at length. For a detailed discussion of the basic model, the interested reader should refer to Frank (2005, 2006).
Note that the assumption that the division between training and test choice is binary is likely overly simplistic, and softer choice mechanisms for combining the two systems are possible (Frank et al., 2007a). Nevertheless, these require additional assumptions about when and how to combine the systems, and additional parameters for doing so (see also Daw et al., 2005), and empirical genetic data provide some evidence that training and test choices are primarily influenced by prefrontal and striatal function, respectively.
If αI is greater than 1/αG, Q-values can exceed 1.0, in which cases positive outcomes (with reward values of 1.0) actually lead to negative prediction errors. The resulting instability of Q value updates is detrimental for the optimization algorithm to find best-fitting parameters. To prevent this, we restrict αI to be less than 1/αG for gains and 1/αL for losses.
The use of a beta distribution is motivated by the fact that it forms the conjugate prior to the binomial distribution, such that application of Bayes rule to update the parameters of the prior distribution results in a posterior distribution that is also itself a beta distribution.
For consistency with our basic Q-models which utilized separate learning rates for gains and losses, we also implemented asymmetrical decay parameters, γG and γL in another version of this model. The results of this model, B_IL_LG, are reported in Table 1.
REFERENCES
- Akaike H. A new look at the statistical mode identification. IEEE Trans. Automat. Contr. 1974:716–723. [Google Scholar]
- Allen SW, Brooks LR. Specializing the operation of an explicit rule. J. Exp. Psychol.: Gen. 1991;(1):3–19. [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychol. Rev. 1998;(3):442–481. doi: 10.1037/0033-295x.105.3.442. [DOI] [PubMed] [Google Scholar]
- Atallah HE, Frank MJ, O'Reilly RC. Hippocampus cortex and basal ganglia: insights from computational models of complementary learning systems. Neurobiol. Learn. Mem. 2004;(3):253–267. doi: 10.1016/j.nlm.2004.06.004. [DOI] [PubMed] [Google Scholar]
- Baum WM. Understanding Behaviorism: Behavior, Culture, and Evolution. John Wiley and Sons; 2004. [Google Scholar]
- Biele G, Rieskamp J, Gonzalez R. Computational models for the combination of advice and individual learning. Cognitive Science. 2009;33:206–242. doi: 10.1111/j.1551-6709.2009.01010.x. [DOI] [PubMed] [Google Scholar]
- Braver TS, Cohen JD. On the control of control: the role of dopamine in regulating prefrontal function and working memory. In: Monsell S, Driver J, editors. Control of Cognitive Processes: Attention and Performance XVIII. MIT Press; Cambridge, MA: 2000. pp. 713–737. [Google Scholar]
- Braver TS, Gray JR, Burgess GC. Explaining the many varieties of working memory variation: dual mechanisms of cognitive control. In: Conway AR, Jarrold C, Kane MJ, Miyake A, Towse J, editors. Variation in Working Memory. Oxford University Press; New York, NY: 2007. pp. 76–106. [Google Scholar]
- Bunge SA, Souza MJ. Neuroscience of rule-guided behavior. Chap. Neural Representations Used to Specify Action. Oxford University Press; 2008. pp. 45–65. [Google Scholar]
- Bunge SA, Kahn I, Wallis JD, Miller EK, Wagner AD. Neural circuits subserving the retrieval and maintenance of abstract rules. J. Neurophysiol. 2003:3419–3428. doi: 10.1152/jn.00910.2002. [DOI] [PubMed] [Google Scholar]
- Camerer C, Ho T-H. Experienced-weighted attraction learning in normal form games. Econometrica. 1999:827–874. [Google Scholar]
- Cohen MX, Ranganath C. Reinforcement learning signals predict future decisions. J. Neurosci. 2007;(2):371–378. doi: 10.1523/JNEUROSCI.4421-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cools R, Altamirano L, D'Esposito M. Reversal learning in Parkinson's disease depends on medication status and outcome valence. Neuropsychologia. 2006:1663–1673. doi: 10.1016/j.neuropsychologia.2006.03.030. [DOI] [PubMed] [Google Scholar]
- Daw ND, Niv Y, Dayan P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 2005;(12):1704–1711. doi: 10.1038/nn1560. [DOI] [PubMed] [Google Scholar]
- Daw ND, O'Doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature. 2006;(7095):876–879. doi: 10.1038/nature04766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dearden R, Friedman N, Russell S. Bayesian q-learning. Proceedings of the 15th National Conference on Artificial Intelligence (AAAI); 1998. [Google Scholar]
- Delgado MR, Locke HM, Stenger VA, Fiez JA. Dorsal striatum responses to reward and punishment: effects of valence and magnitude manipulations. Cogn., Affect. Behav. Neurosci. 2003:27–38. doi: 10.3758/cabn.3.1.27. [DOI] [PubMed] [Google Scholar]
- Durstewitz D, Seamans JK, Sejnowski TJ. Neurocomputational models of working memory. Nat. Neurosci. 2000;(suppl. 3):1184–1191. doi: 10.1038/81460. [DOI] [PubMed] [Google Scholar]
- Estes WK. Effects of competing reactions on the conditioning curve for bar pressing. J. Exp. Psychol. 1950:200–205. doi: 10.1037/h0062555. [DOI] [PubMed] [Google Scholar]
- Filoteo JV, Maddox WT, Simmons AN, Ing AD, Cagigas XE, Matthews S, Paulus M. Cortical and subcortical brain regions involved in rule-based category learning. Neuroreport. 2005:111–115. doi: 10.1097/00001756-200502080-00007. [DOI] [PubMed] [Google Scholar]
- Frank MJ. Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and non-medicated Parkinsonism. J. Cogn. Neurosci. 2005:51–72. doi: 10.1162/0898929052880093. [DOI] [PubMed] [Google Scholar]
- Frank MJ. Hold your horses: a dynamic computational role for the subthalamic nucleus in decision making. Neural Netw. 2006:1120–1136. doi: 10.1016/j.neunet.2006.03.006. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Claus ED. Anatomy of a decision: striato-orbitofrontal interactions in reinforcement learning, decision making, and reversal. Psychol. Rev. 2006;(2):300–326. doi: 10.1037/0033-295X.113.2.300. [DOI] [PubMed] [Google Scholar]
- Frank MJ, O'Reilly RC. A mechanistic account of striatal dopamine function in human cognition: psychopharmacological studies with cabergoline and haloperidol. Behav. Neurosci. 2006:497–517. doi: 10.1037/0735-7044.120.3.497. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Loughry B, O'Reilly RC. Interactions between the frontal cortex and basal ganglia in working memory: a computational model. Cogn., Affect. Behav. Neurosci. 2001:137–160. doi: 10.3758/cabn.1.2.137. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Seeberger LC, O'Reilly RC. By carrot or by stick: cognitive reinforcement learning in Parkinsonism. Science. 2004:1940–1943. doi: 10.1126/science.1102941. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Woroch BS, Curran T. Error-related negativity predicts reinforcement learning and conflict biases. Neuron. 2005:495–501. doi: 10.1016/j.neuron.2005.06.020. [DOI] [PubMed] [Google Scholar]
- Frank MJ, O'Reilly RC, Curran T. When memory fails, intuition reigns: midazolam enhances implicit inference in humans. Psychol. Sci. 2006:700–707. doi: 10.1111/j.1467-9280.2006.01769.x. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Moustafa AA, Haughey H, Curran T, Hutchison K. Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proc. Natl. Acad. Sci. 2007a:16311–16316. doi: 10.1073/pnas.0706111104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MJ, Samanta J, Moustafa AA, Sherman SJ. Hold your horses: impulsivity, deep brain stimulation and medication in parkinsonism. Science. 2007b:1309–1312. doi: 10.1126/science.1146157. [DOI] [PubMed] [Google Scholar]
- Frank MJ, Santamaria A, O'Reilly RC, Willcutt E. Testing computational models of dopamine and noradrenaline dysfunction in attention deficit/hyperactivity disorder. Neuropsychopharmacology. 2007c:1583–1599. doi: 10.1038/sj.npp.1301278. [DOI] [PubMed] [Google Scholar]
- Galizio M. Contingency-shaped and rule-governed behavior: instructional control of human loss avoidance. J. Exp. Anal. Behav. 1979;(1):53–70. doi: 10.1901/jeab.1979.31-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goto Y, Grace AA. Dopamine modulation of hippocampal prefrontal cortical interaction drives memory-guided behavior. Cereb. Cortex. 2007 doi: 10.1093/cercor/bhm172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graybiel AM. The basal ganglia and chunking of action repertoires. Neurobiol. Learn Mem. 1998;(1–2):119–136. doi: 10.1006/nlme.1998.3843. [DOI] [PubMed] [Google Scholar]
- Hampton AN, Bossaerts P, O'Doherty JP. The role of the ventromedial prefrontal cortex in abstract state-based inference during decision making in humans. J. Neurosci. 2006;(32):8360–8367. doi: 10.1523/JNEUROSCI.1010-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes S, editor. Rule-governed Behavior: Cognition, Contingencies, and Instructional Control. Plenum Press; 1989. [Google Scholar]
- Hayes SC. Rule governance: basic behavioral research and applied implications. Curr. Dir. Psychol. Sci. 1993:193–197. [Google Scholar]
- Hayes SC, Brownstein AJ, Zettle RD, Rosenfarb I, Korn Z. Rule-governed behavior and sensitivity to changing consequences of responding. J. Exp. Anal. Behav. 1986;(3):237–256. doi: 10.1901/jeab.1986.45-237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertwig R, Barron G, Weber EU, Erev I. Decisions from experience and the effect of rare events in risky choice. Psychol. Sci. 2004;(8):534–539. doi: 10.1111/j.0956-7976.2004.00715.x. [DOI] [PubMed] [Google Scholar]
- Joel D, Weiner I. Striatal contention scheduling and the split circuit scheme of basal ganglia-thalamocortical circuitry: from anatomy to behaviour. In: Miller R, Wickens JR, editors. Conceptual Advances in Brain Research: Brain Dynamics and the Striatal Complex. Harwood Academic Publishers; 1999. pp. 209–236. [Google Scholar]
- Kahneman D. A perspective on judgment and choice: mapping bounded rationality. Am. Psychol. 2003;(9):697–720. doi: 10.1037/0003-066X.58.9.697. [DOI] [PubMed] [Google Scholar]
- Kaufman A, Baron A, Kopp R. Some effects of instructions on human operant behavior. Psychonomic Monograph Supplements. 1966:243–250. [Google Scholar]
- Klein TA, Neumann J, Reuter M, Hennig J, von Cramon DY, Ullsperger M. Genetically determined differences in learning from errors. Science. 2007;(5856):1642–1645. doi: 10.1126/science.1145044. [DOI] [PubMed] [Google Scholar]
- Kruschke JK. Bayesian approaches to associative learning: From passive to active learning. Learning and Behavior. 2008;36:210–226. doi: 10.3758/lb.36.3.210. [DOI] [PubMed] [Google Scholar]
- Lau B, Glimcher PW. Dynamic response-by-response models of matching behavior in rhesus monkeys. J. Exp. Anal. Behav. 2005;(3):555–579. doi: 10.1901/jeab.2005.110-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohrenz T, McCabe K, Camerer CF, Montague PR. Neural signature of fictive learning signals in a sequential investment task. Proc. Natl. Acad. Sci. U. S. A. 2007;(22):9493–9498. doi: 10.1073/pnas.0608842104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure SM, Berns GS, Montague PR. Temporal prediction errors in a passive learning task activate human striatum. Neuron. 2003:339–346. doi: 10.1016/s0896-6273(03)00154-5. [DOI] [PubMed] [Google Scholar]
- McClure SM, Laibson DI, Loewenstein G, Cohen JD. Separate neural systems value immediate and delayed rewards. Science. 2004:503–507. doi: 10.1126/science.1100907. [DOI] [PubMed] [Google Scholar]
- Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Ann. Rev. Neurosci. 2001:167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- Montague PR, Dayan P, Sejnowski TJ. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci. 1996:1936–1947. doi: 10.1523/JNEUROSCI.16-05-01936.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neal A, Hesketh B, Andrews S. Instance-based categorization: automatic versus intentional forms of retrieval. Mem. Cognit. 1995;(2):227–242. doi: 10.3758/bf03197224. [DOI] [PubMed] [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Computer Journal. 1965:308–313. [Google Scholar]
- Nishi A, Snyder GL, Greengard P. Bidirectional regulation of DARPP-32 phosphorylation by dopamine. J. Neurosci. 1997:8147–8155. doi: 10.1523/JNEUROSCI.17-21-08147.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noelle DC, Cottrell GW. A connectionist model of instruction following. In: Moore JD, Lehman JF, editors. Proceedings of the 17th Annual Conference of the Cognitive Science Society; Mahwah, NJ: Lawrence Erlbaum; 1995. pp. 369–374. [Google Scholar]
- Noelle DC, Cottrell GW. In search of articulated attractors. In: Cottrell GW, editor. Proceedings of the 18th Annual Conference of the Cognitive Science Society; Mahwah, NJ: Lawrence Erlbaum; 1996. pp. 329–334. [Google Scholar]
- Noelle DC, Cottrell GW. Individual differences in exemplar-based interference during instructed category learning. In: Gleitman LR, Joshi AK, editors. Proceedings of the Twenty-second Annual Conference of the Cognitive Science Society; Philadelphia: Lawrence Erlbaum; 2000. pp. 358–363. [Google Scholar]
- Nomura EM, Maddox WT, Filoteo JV, Ing AD, Gitelman DR, Parrish TB, Mesulam M-M, Reber PJ. Neural correlates of rule-based and information-integration visual category learning. Cereb. Cortex. 2007;(1):37–43. doi: 10.1093/cercor/bhj122. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Clark SE, Shin HJ. Rules and exemplars in categorization, identification, and recognition. J. Exper. Psychol., Learn., Mem., Cogn. 1989;(2):282–304. doi: 10.1037//0278-7393.15.2.282. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP, Dayan P, Friston K, Critchley H, Dolan RJ. Temporal difference models and reward-related learning in the human brain. Neuron. 2003:329–337. doi: 10.1016/s0896-6273(03)00169-7. [DOI] [PubMed] [Google Scholar]
- O'Doherty J, Dayan P, Schultz J, Deichmann R, Friston K, Dolan RJ. Dissociable roles of ventral and dorsal striatum in instrumental conditioning. Science. 2004;(5669):452–454. doi: 10.1126/science.1094285. [DOI] [PubMed] [Google Scholar]
- O'Doherty JP, Hampton A, Kim H. Model-based fmri and its application to reward learning and decision making. Ann. N. Y. Acad. Sci. 2007:35–53. doi: 10.1196/annals.1390.022. [DOI] [PubMed] [Google Scholar]
- O'Reilly RC, Frank MJ. Making working memory work: a computational model of learning in the prefrontal cortex and basal ganglia. Neural Computat. 2006:283–328. doi: 10.1162/089976606775093909. [DOI] [PubMed] [Google Scholar]
- O'Reilly RC, Munakata Y. Computational Explorations in Cognitive Neuroscience: Understanding the Mind by Simulating the Brain. The MIT Press; Cambridge, MA: 2000. [Google Scholar]
- O'Reilly RC, Rudy JW. Conjunctive representations in learning and memory: principles of cortical and hippocampal function. Psychol. Rev. 2001:311–345. doi: 10.1037/0033-295x.108.2.311. [DOI] [PubMed] [Google Scholar]
- Pasupathy A, Miller EK. Different time courses for learning-related activity in the prefrontal cortex and striatum. Nature. 2005:873–876. doi: 10.1038/nature03287. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Packard MG. Competition among multiple memory systems: converging evidence from animal and human brain studies. Neuropsychologia. 2003:245–251. doi: 10.1016/s0028-3932(02)00157-4. [DOI] [PubMed] [Google Scholar]
- Rougier NP, Noelle D, Braver TS, Cohen JD, O'Reilly RC. Prefrontal cortex and the flexibility of cognitive control: rules without symbols. Proc. Natl. Acad. Sci. 2005;(20):7338–7343. doi: 10.1073/pnas.0502455102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samejima K, Ueda Y, Doya K, Kimura M. Representation of action-specific reward values in the striatum. Science. 2005;(5752):1337–1340. doi: 10.1126/science.1115270. [DOI] [PubMed] [Google Scholar]
- Sanfey AG, Rilling JK, Aronson JA, Nystrom LE, Cohen JD. The neural basis of economic decision-making in the ultimatum game. Science. 2003:1755–1757. doi: 10.1126/science.1082976. [DOI] [PubMed] [Google Scholar]
- Sanfey AG, Loewenstein G, McClure SM, Cohen JD. Neuroeconomics: cross-currents in research on decision-making. Trends Cogn. Sci. 2006;(3):108–116. doi: 10.1016/j.tics.2006.01.009. [DOI] [PubMed] [Google Scholar]
- Schönberg T, Daw ND, Joel D, O'Doherty JP. Reinforcement learning signals in the human striatum distinguish learners from nonlearners during reward-based decision making. J. Neurosci. 2007;(47):12860–12867. doi: 10.1523/JNEUROSCI.2496-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultz W. Multiple dopamine functions at different time courses. Ann. Rev. Neurosci. 2007:259–288. doi: 10.1146/annurev.neuro.28.061604.135722. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997:1593. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seiss E, Praamstra P. The basal ganglia and inhibitory mechanisms in response selection: evidence from subliminal priming of motor responses in Parkinson's disease. Brain. 2004;(2):330–339. doi: 10.1093/brain/awh043. [DOI] [PubMed] [Google Scholar]
- Skinner BF. The Behavior of Organisms. Appleton-Century-Crofts. 1938 [Google Scholar]
- Sloman SA. The empirical case for two systems of reasoning. Pscyhological Bulletin. 1996:3–22. [Google Scholar]
- Thorndike EL. Animal Intelligence: Experimental Studies. MacMillan Press; 1911. [Google Scholar]
- Wallis JD, Miller EK. From rule to response: neuronal processes in the premotor and prefrontal cortex. J. Neurophysiol. 2003:1790–1806. doi: 10.1152/jn.00086.2003. [DOI] [PubMed] [Google Scholar]
- Watkins CJCH, Dayan P. Technical note: Q-learning. Mach. Learn. 1992:279. [Google Scholar]
- Yin HH, Knowlton BJ. The role of the basal ganglia in habit formation. Nat. Rev. Neurosci. 2006;(6):464–476. doi: 10.1038/nrn1919. [DOI] [PubMed] [Google Scholar]