Application of Tsallis Entropy to EEG: Quantifying the Presence of Burst Suppression After Asphyxial Cardiac Arrest in Rats

Abstract

Burst suppression (BS) activity in EEG is clinically accepted as a marker of brain dysfunction or injury. Experimental studies in a rodent model of brain injury following asphyxial cardiac arrest (CA) show evidence of BS soon after resuscitation, appearing as a transitional recovery pattern between isoelectricity and continuous EEG. The EEG trends in such experiments suggest varying levels of uncertainty or randomness in the signals. To quantify the EEG data, Shannon entropy and Tsallis entropy (TsEn) are examined. More specifically, an entropy-based measure named TsEn area (TsEnA) is proposed to reveal the presence and the extent of development of BS following brain injury. The methodology of TsEnA and the selection of its parameter are elucidated in detail. To test the validity of this measure, 15 rats were subjected to 7 or 9 min of asphyxial CA. EEG recordings immediately after resuscitation from CA were investigated and characterized by TsEnA. The results show that TsEnA correlates well with the outcome assessed by evaluating the rodents after the experiments using a well-established neurological deficit score (Pearson correlation = 0.86, p ⪡ 0.01). This research shows that TsEnA reliably quantifies the complex dynamics in BS EEG, and may be useful as an experimental or clinical tool for objective estimation of the gravity of brain damage after CA.

I. Introduction

WITH THE advent of modern cardiopulmonary resuscitation (CPR) accompanied by defibrillation, the mortality from cardiac arrest (CA) has been reduced. However, neurological outcome after CA remains a major cause for concern with poor, long-term neurological sequelae [1]. Cerebral cortex is very sensitive to generalized ischemia caused by circulatory arrest. Presently, no clinically satisfied neurological diagnostic or monitoring tools are available to assess the brain function and its recovery after CA. EEG reflects the postsynaptic potentials generated from cortical neurons. It constitutes a valuable tool for continuous evaluation of brain injury or dysfunction. Quantitative EEG measure may further be useful for accurate injury stratification, and perhaps early prognostication [2]-[5]. Previous research has shown that remarkable EEG recovery patterns are observed following cerebral circulatory deprivation as a result of dynamic changes in brain perfusion and electrophysiological recovery. Moreover, these patterns are tightly correlated with postischemic cerebral damage [6]-[10].

The term burst suppression (BS) is used to describe the EEG pattern characterized by θ and/or δ waves, at times intermixed with faster waves, and intervening periods of relative quiescence [11]. Such BS events often appear in survivors of cerebral circulatory arrest subjected to life-sustaining treatments [12]. Although BS is also reported in anesthetic state and neurosurgically isolated cerebral cortex, this paper focuses on the BS soon after cerebral circulatory arrest. Our previous studies in an animal model of global ischemic brain demonstrated that timely emergence of bursts, leading to a continuous or fused EEG rhythm was associated with a good neurological outcome. On the other hand, persistent BS pattern with lower burst frequency occurred in animals with bad recovery [8], [10]. Thus, although BS observations provide valuable diagnostic and predictive information on the eventual neurological outcome, objective evaluation of the complex data is essential. Developing a quantitative measure that defines this sequence of events will help in the rigorous evaluation of injury severity and the extent of recovery in these subjects.

Among the techniques used to analyze BS EEG, burst count has previously been accepted as a simple method [10], [13]. However, manual burst count is time consuming, and it excludes some important discriminative information such as the shape of burst waveform and the duration of each burst or suppression epoch. Besides burst count, measures such as EEG amplitude in suppression epochs and the duration of BS period are also found to be associated with neurological recovery after CA [10], [12], [14]. For all these measures, the problem of subjectivity cannot be ignored despite established assessment criteria to maintain consistency between different EEG examiners [10]. Given the close prognostic relationship between electrical and neurological recovery from brain injury, and the putative role of BS in the recovery, there is a need to develop objective and reliable methods to quantify the characteristics of BS activity in EEG recordings.

Entropy is a measure of order and disorder in a dynamical system according to information theory [15]. It shows promise in prognosticating the degree of brain injury after CA [3], [4], [16]. Entropy may be an ideal technique for monitoring injury because BS pattern with its rhythmicity or regularity would have low entropy compared with continuous EEG that is more random. Tsallis entropy (TsEn) [17], [18] plays a central role in nonextensive statistical mechanics. It is successful at describing systems with long-range interactions, multifractal space-time constraints, or long-term memory effects [19]. TsEn also allows incorporation of an entropy scaling parameter with which short- and long-range interactions can be probed. EEG spikes, bursts, and continuous or fused rhythms may thus be differentiated with the help of Tsallis statistics. The goal of this paper is to develop a quantitative estimation of BS activity based on Tsallis statistics. A measure called TsEn Area (TsEnA) is proposed. It combines the aforementioned discriminative EEG features during early recovery period after asphyxial CA into a single value. Then, this measure is applied to comprehensively evaluate the incidences of BS events occurring throughout recovery after resuscitation from CA. It is expected that TsEnA correlates closely with a standardized neurological deficit score (NDS), which is a well-established estimation of neurological outcome in clinic [2], [3], [13].

II. Mathematical Method and Physiological Foundation

A. TsEn and Nonextensivity of EEG System

Entropy, which is defined as a measure of uncertainty, could be used to reveal the complexity of a dynamical system. The most basic entropy measure used to analyze system complexity is Shannon entropy (ShEn), which is defined as [15]

$$\mathrm{ShEn}=-\underset{i=1}{\overset{W}{\Sigma }}{p}_i\ln p_i\left(\text{in units of Boltzmann constant}\right)$$ (1)

where {p_i} are the probabilities associated with W microscopic configurations with ${\sum }_{i=1}^W{p}_i=1$. ShEn is based on Boltzmann–Gibbs statistical mechanics and standard thermodynamics in which the effective microscopic interactions and the microscopic memory are of short range [18]. ShEn has extensivity (additivity) as

$$\mathrm{ShEn}(A\bigcup B)=\mathrm{ShEn}\left(A\right)+\mathrm{ShEn}\left(B\right)$$ (2)

where A and B are two independent systems in the sense that

$$p(A\bigcup B)=p\left(A\right)p\left(B\right).$$

In spite of its great success in analysis of extensive systems, ShEn could not properly describe systems with long-range interactions, long-term memory effects, or abrupt changes [20]. A nonextensive statistics, known now as TsEn, was proposed by Tsallis [17], [18], which was defined as

$$\mathrm{TsEn}=\frac{1-{\sum }_{i=1}^W{p}_i^q}{q-1}$$ (3)

when q→1, TsEn in (3) recovers to the definition of ShEn as follows:

$$\begin{array}{cc}\hfill \mathrm{TsEn}& =\frac{1-{\sum }_{i=1}^W{p}_i^q}{q-1}={\Sigma }_{i=1}^W{p}_i\frac{p_i^{q-1}-1}{1-q}\hfill \\ \hfill & ={\Sigma }_{i=1}^W{p}_i\frac{e^{(q-1)\ln p_i}-1}{1-q}\hfill \\ \hfill & \approx {\Sigma }_{i=1}^W{p}_i\frac{[1+(q-1)\ln p_i]-1}{1-q}=-{\Sigma }_{i=1}^W{p}_i\ln p_i.\hfill \end{array}$$ (4)

TsEn is nonextensive and holds the following pseudoadditivity rule [18]:

$$\begin{array}{cc}\hfill & \mathrm{TsEn}(A\bigcup B)\hfill \\ \hfill & =\mathrm{TsEn}\left(A\right)+\mathrm{TsEn}\left(B\right)+(1-q)\mathrm{TsEn}\left(A\right)\mathrm{TsEn}\left(B\right)\hfill \end{array}$$ (5)

where the parameter q measures the degree of nonextensivity [19], with q < 1, q = 1 (i.e., ShEn), and q > 1, respectively, corresponding to superextensive [TsEn(A∪B) > TsEn(A) + TsEn(B)], extensive, and subextensive [TsEn(A ∪ B) < TsEn(A) + TsEn(B)] statistics. TsEn is consistent with Laplace’s maximum ignorance principle, i.e., it is extreme at equiprobability (p_i = 1/W ∀i).This extremum is given by [18]

$${\mathrm{TsEn}}_{\text{extremum}}=\frac{W^{1-q}-1}{1-q}$$ (6)

which, in the limit q→1, gives the extremum of ShEn as

$${\mathrm{ShEn}}_{\text{extremum}}=\ln W.$$ (7)

Tsallis’ work establishes a generalization of Boltzmann–Gibbs statistics that can properly describe the longstanding quasi-stationary state and weakly ergodic phenomenon in long-range interacting systems [18]. Although the generalization of nonextensivity was understood in the thermodynamical sense from earlier times, it now gets broader application beyond thermodynamics, and TsEn has been widely used in biomedical signal processing such as analysis of ECG [21] and EEG [22], [23] recently. Studies showed that the Tsallis environment could provide more detailed information than the conventional Shannon counterpart, especially when used as burst or spike EEG analysis [22], [24], [25].

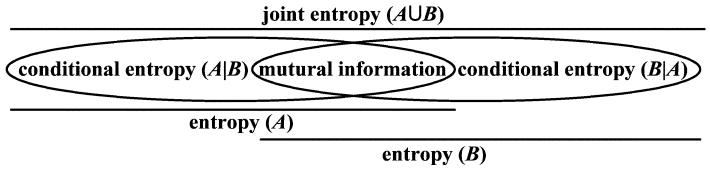
EEG signals result from the temporal and spatial summation of postsynaptic potentials from cortical pyramidal cells [26], which are eventually projected on the scalp. Nonextensivity is inherent in EEG because of long-range interactions [27]: electrical information is transmitted across different cortical areas and feedback loops that are composed of corticothalamic and thalamocortical networks [28]. Therefore, it is rational and necessary to use a nonextensive measure instead of Shannon one to get a grip on the long-range effects in EEG. In addition, since mutual information exists among different neuron clusters, it is reasonable to consider EEG as a subextensive system (i.e., q > 1) [22], [23]. For example, there is TsEn(A ∪ B) < TsEn(A) + TsEn(B), where A and B are two neuronal clusters in cortex that contribute to the EEG activity (see Fig. 1).

Fig. 1.

Entropy relationship between two systems A and B.

This paper analyzes sequential EEG segments with a sliding window of 3000 points (12 s) and an overlap of 1500 points (6 s). At a data length of 3000 points, the entropy bias introduced by the finite window can be neglected [29]. To properly estimate the probability distribution {p_i} and obtain a “smooth” histogram, the number W of microstates is fixed to 50 according to our previous work [22], [23], [25]. Although the parameter q plays an important role in the result of TsEn computation, there has been no established method to optimize its value. When analyzing EEG or other signals, most researchers try different q values, and optimize the selection based on some criteria and their data characteristics [22], [23], [30]. It has been shown previously that the value of TsEn decreases monotonically with the parameter q [17] while “the spike-detection-power” grows gradually with q [22], [23]. Therefore, the TsEn is calculated and compared with four empirically determined values of q = 0.5, 1, 3, and 5 in this paper (TsEn recovers to ShEn when q = 1). In these cases, TsEn/ShEn saturates at the extremum of 12.1, 3.91, 0.500, and 0.250 according to (6) and (7).

B. BS Features in EEG

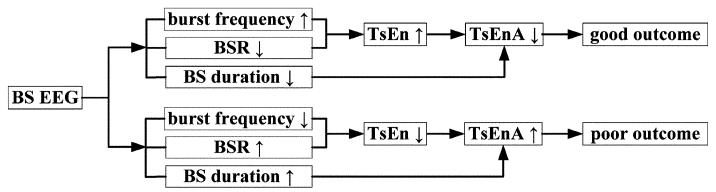
BS is defined as bursts of variable duration separated by periods of generalized suppression lasting at least 1 s [31]. The bursts may range from high-amplitude δ activity or polyspike and slow-wave complexes [5], simultaneously appearing in all EEG channels. BS pattern is generally accepted as a dissociation of the cortex from the intrinsic pacemaker neurons in the reticular thalamic nucleus [26]. Bursts in EEG are a reflection of cortical excitability to input from thalamocortical neurons [26], [32], while the suppression epoch is a reflection of the refractory period of cortical neurons [31]. Our previous studies in animal model have shown that: 1) burst frequency is higher in subjects with good neurological outcomes [10], [13] and 2) the EEGs in poor outcome animals are rather flat during suppression period [9], [14]. It seems that frequent bursts in EEG reveal less dysfunction in cortical neurons and/or relatively unhindered pathway from thalamocortical neurons to cortical neurons. In addition, higher amplitude of EEG background during suppression period very likely denotes that less injury caused by asphyxia in cortical neurons for the generation of slow waves is the intrinsic feature of normal cortical neurons in the isolated cortex [32], [33]. Finally, the time latency of EEG recovery from cerebral circulation arrest also provides diagnostic and prognostic information [6], [10], [12]. We name this discriminative factor as duration of BS (i.e., the time from the first sign of bursts to establishment of continuous EEG). During early recovery period after CA, plentiful oxygen and glucose drive cortical neurons back toward their normal function—eliciting rhythmic potentials from thalamocortical activity [26]. Therefore, the faster the cortical neuronal function normalizes, the shorter the duration of BS in EEG.

C. Relationship Between TsEn and BS Features

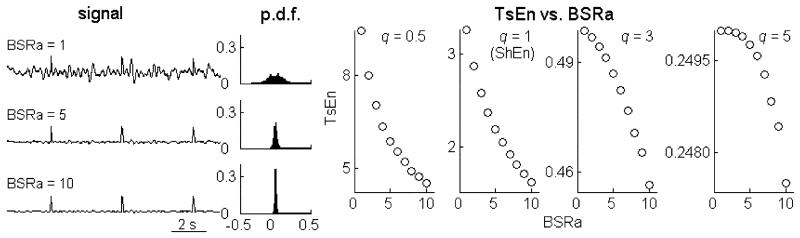
In this section, simulation data are used to illustrate the relationship between the aforementioned BS features and TsEn statistics. Three-thousand-point simulated EEG is composed of intermingled spikes and colored noise with the low-frequency band ranging from 0.5 to 10 Hz (for EEG suppression). The effect of burst frequency on TsEn is shown in Fig. 2. It is found that TsEn increases as more spikes are added to the background time series. Concomitantly with the increase of burst frequency (i.e., suppression epochs with low amplitude are replaced more and more by synthetic bursts), probability density function (pdf) of data, which is estimated using the histogram method, tends toward a flatter and more uniform distribution.

Fig. 2.

Relationship between TsEn and burst frequency. pdf indicates probability density function (as estimated using the histogram method).

To quantify the relative amplitude of burst and suppression in EEG, a measure called BS ratio of amplitude (BSR_a) is defined as the amplitude ratio of burst to suppression. Then, the amplitude of EEG suppression (simulated by low-frequency noise) is varied to test the effect of BSR_a on TsEn. Fig. 3 shows that increasing amplitude of suppression makes the pdf broaden and flatten. In other words, larger BSR_a leads to sharper pdf. As seen in Fig. 3, TsEn decreases monotonically and significantly with increasing BSR_a.

Fig. 3.

Relationship between TsEn and BS ratio of amplitude (BSR_a ).

D. TsEn Area (TsEnA)

According to the illustrations in Section III-B and III-C, the three EEG features (i.e., burst frequency, BSR_a, and duration of BS) are combined into a measure based on TsEn statistics to grade the BS EEG after CA. We define TsEnA as the area in TsEn-time (y–x) plane below the extremum of TsEn and above the curve of TsEn, with the time duration that covers the entire BS pattern period after CA. Mathematically, TsEnA is defined in the following format:

$$\begin{array}{cc}\hfill \mathrm{TsEnA}& ={\sum }_{t_1}^{t_2}({\mathrm{TsEn}}_{\text{extremum}}-\mathrm{TsEn})\hfill \\ \hfill & =\{\begin{array}{cc}\underset{t_1}{\overset{t_2}{\Sigma }}(\ln W+\underset{i=1}{\overset{W}{\Sigma }}{p}_i\ln p_i),\hfill & q=1\hfill \\ \underset{t_1}{\overset{t_2}{\Sigma }}\left(\frac{W^{1-q}-1}{1-q}-\frac{1-{\sum }_{i=1}^W{p}_i^q}{q-1}\right),\hfill & q\ne 1\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (8)

where t₁ and t₂ are the starting time and end time of BS duration. The hypothesized relationships among BS features, TsEnA, and neurological outcomes are shown in Fig. 4.

Fig. 4.

Relationships among BS features, TsEnA, and neurological outcomes.

III. Experiments and Statistical Methods

A. Animal Experiments

The Animal Care and Use Committee of the Johns Hopkins Medical Institutions approved the experimental protocol used in this study. Fifteen adult male Wistar rats (300–350 g, mean = 330 g) were randomly assigned to 7-min (ten rats) or 9-min (five rats) asphyxial insults. CA and resuscitation protocol were performed as previously reported [9], [34]. Anesthesia was induced with 4.5% halothane, followed by tracheal intubation. The femoral artery was cannulated for the monitoring of mean arterial pressure (MAP). After preparation, baseline EEG was recorded for 5 min followed by 5 minutes washout. Then global asphyxia was induced for 7 or 9 min by clamping the tracheal tube and disconnecting the ventilator. After asphyxia, CPR was initiated. Return of spontaneous circulation (ROSC) was defined as achievement of spontaneous MAP > 60 mmHg. To minimize the drug effect on EEG, no anesthesia was provided postresuscitation. The core temperature of the subject was maintained throughout the experiment at 36.5 °C–37.5 °C and for the first 24 h.

The neurologic functional outcomes were evaluated using NDS, which included subsores of general behavioral deficit, brain-stem function, motor and sensory assessment, behavior, and seizures [2]. NDS is scored in the range from 0 (worst outcome) to 80 (best outcome).The NDS of rats was determined 72 h after ROSC by an independent observer. Good neurological outcome is defined as NDS ≥ 60, while NDS < 60 is considered as poor outcome [10].

Two channels of bipolar EEG were recorded using anterior versus posterior differential montage in the right and left parietal areas (DI700 Windaq system). A ground electrode was placed in the midline. Recording continued from baseline to postresuscitation period for a total recording time of 400 min. The signals were digitized using the data acquisition package CODAS (DATAQ Instruments, Inc., Akron, OH). Sampling rate was 250 Hz. A/D conversion of 12 bit was used. EEGs were bandpass-filtered (0.5–70 Hz). The first burst was defined by the following criteria: sharply contoured morphology, after-going slow wave, and conspicuity from background [13].

B. Statistical Methods and Performance Estimation

Pearson correlation of bivariate analysis is used to evaluate the correlation between 72-h NDS and TsEnA measurement. Large correlation coefficient with small p value (i.e., less than 0.01) apparently provides a reliable estimation of neurological outcomes. To quantify the dynamic range of TsEnA values obtained from different rats given certain q, we define a parameter relative dynamic range (RDR, in decibels) as

$$\begin{array}{cc}\hfill & \mathrm{RDR}\hfill \\ \hfill & =20\log \frac{75\text{th percentile}\left(\mathrm{TsEnA}\right)-25\text{th percentile}\left(\mathrm{TsEnA}\right)}{\text{median}\left(\mathrm{TsEnA}\right)}\hfill \end{array}$$ (9)

which gives an objective estimation of the dynamic range of TsEnA among the whole population of subjects. TsEnA measurement with large RDR presents obvious differences between poor-outcome rats and good-outcome rats, and thus provides a better distinguishability in brain injury stratification. In this paper, Pearson correlation coefficient (between TsEnA and NDS) and RDR are chosen as criteria to evaluate the performance of TsEnA measure with q ranging from 0.5 to 5.

IV. Results

EEG becomes highly suppressed and quickly changes to an isoelectric tracing within seconds after CA. About 16 min (16.4 ± 1.9) after ROSC, EEG visibly returns as a BS pattern. Then, the bursts gradually merge into background activity, while the spontaneous EEG recovers. TsEnA values are calculated with q = 0.5, 1, 3, and 5 in all EEG recordings, and the results are averaged between left and right channels (see Table I). The time duration of TsEnA is defined from 22 to 250 min (0 min is the start point of recording). The starting time t₁ in (8) is chosen as 22 min to avoid the artifact induced by CPR (5 min baseline +5 min washout + 7 or 9 min asphyxia + CPR within 2 min). The end time t₂ is selected as 250 min to include almost all the BS activity in EEG. Fig. 5 shows two typical results from animals with good (NDS = 74, rat 1) and poor outcomes (NDS = 46, rat 15), respectively (q = 3). The results show that TsEn (q = 3) is stable during baseline and during the late period of recovery, while it drops and fluctuates distinctly during early recovery due to the BS pattern in EEG. This decrease of TsEn is more prominent in rodents with poor neurological outcomes. In contrast, TsEn (q = 1) fluctuates a lot throughout the entire EEG recording, thus giving less distinctive exhibition of BS pattern in each subject.

TABLE I.

TsEnA in Each Rat With Different q Values

Rat ID	Asphyxia (min)	NDS	TsEnA (averaged between two channels)
			q = 0.5	q = 1	q = 3	q = 5
1	7	74	6855.3	1746.7	7.1003	0.17413
2	7	74	8302.0	2127.1	12.722	0.35800
3	9	71	7670.3	1902.7	6.9706	0.08170
4	7	70	7589.6	1889.3	5.9524	0.05270
5	9	70	8571.5	2166.9	10.246	0.23262
6	7	70	8344.5	2065.7	7.4091	0.08628
7	7	67	9413.2	2497.4	15.409	0.34171
8	7	66	8375.6	2087.7	8.1391	0.11539
9	7	59	9629.7	2557.8	18.488	0.56813
10	9	54	9531.9	2636.5	27.233	1.52073
11	9	53	10201	2745.6	23.797	0.94040
12	9	52	11692	3273.1	44.798	2.68978
13	7	50	10611	3084.9	40.524	2.43142
14	7	49	10695	2960.8	37.898	2.94993
15	7	46	10020	2766.7	23.402	0.92637

Fig. 5.

BS pattern, ShEn, TsEn (q = 3), and TsEnA in EEGs from animals with different neurological outcomes (NDS = 74 versus NDS = 46). EEG signals (left channel) recorded during baseline (10 min), the entire asphyxial duration (7 or 9 min), and resuscitation and recovery periods spanning 400 min are compressed in these plots. Stars denote the artifact induced by CPR.

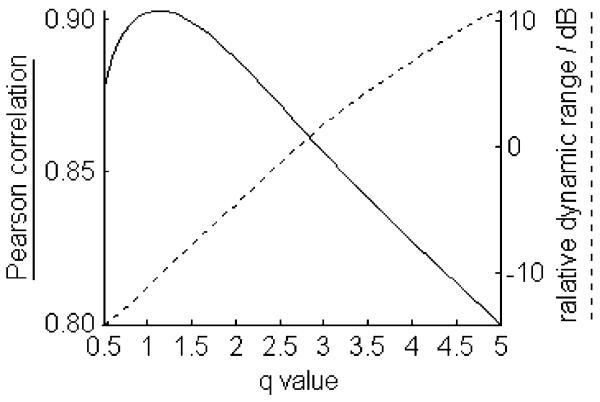
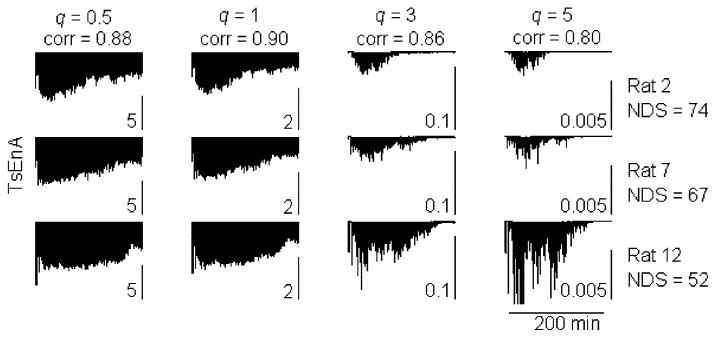
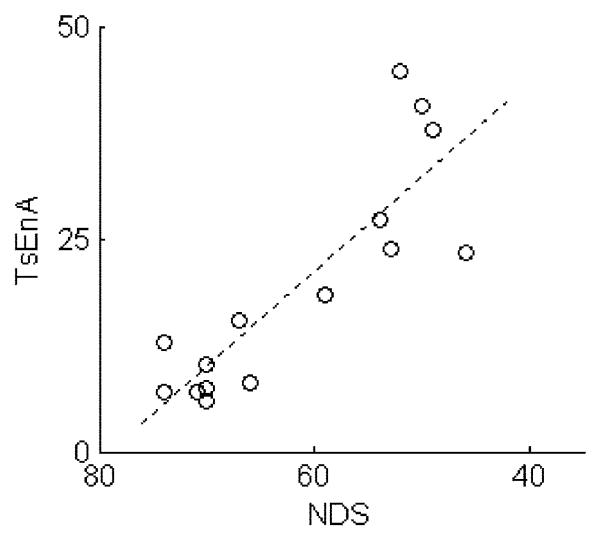
To reveal the effect of parameter q on the RDR, and the correlation of TsEnA and NDS, the average TsEnA (averaged between left and right channels) in each rat is further calculated using different q values ranging from 0.5 to 5 with step size of 0.1. The result is shown in Fig. 6. It denotes that the Pearson correlation coefficient is satisfactorily high (above 0.85) when q < 3 and reaches the maximum with q = 1.1 (p ⪡ 0.01). On the other hand, however, RDR decreases rapidly with smaller q, and it drops below −10 dB when q < 1. Fig. 7 illustrates this effect with typical TsEnA plots from three rats. It shows that when q is too small (e.g., q = 0.5 and 1 in the first two columns), although TsEnA correlates well with the NDS, the differences between TsEnA measurements among rats with various NDS (i.e., NDS = 74, 67, and 52) are diminished because of low RDR. Therefore, a tradeoff should be made between: 1) the linear correlation between TsEnA and NDS and 2) the distinguishability of TsEnA among rats with different neurological outcomes. The results shown in Figs. 6 and 7 suggest that the TsEnA exhibits high performance with q around 3, giving large correlation coefficient and large RDR at the same time. Fig. 8 gives a better illustration of the correlation between TsEnA (q = 3) and neurological outcome (i.e., NDS estimated 72 h after ROSC) (Pearson correlation coefficient = 0.86, p ⪡ 0.01).

Fig. 6.

Pearson correlation coefficient between TsEnA and NDS, and RDR of TsEnA with different q values. p ⪡ 0.01 for all correlation coefficients estimated with q = 0.5–5.

Fig. 7.

Typical TsEnA from three rats calculated with different q. The TsEnA results (left EEG channel) from the same rat with q = 0.5, 1, 3, and 5 are plotted in a row. TsEnA is defined between 22 and 250 min in the whole EEG recording. Subplots in each column hold a same scale. Pearson correlation coefficient (corr) between TsEnA and NDS is also shown on the top of each column.

Fig. 8.

Correlation between TsEnA (q = 3) and NDS. Pearson correlation coefficient = 0.86, p ⪡ 0.01.

V. Discussion and Conclusion

A defining, but elusive, feature of physiologic systems is their complexity. The output of healthy systems reveals a type of complex variability associated with long-range correlations, along with distinct nonlinear interactions; yet, this complexity breaks down with dysfunction [35].To understand the complexity of EEG, it is very much in the need for quantitative tools, i.e., the ability to state clinical data in numerical form that simplifies the analysis of EEG time series [36].We adapt the well-known entropy measure, TsEn, as the TsEnA to demarcate the important period with extensive BS pattern. The sensitivity of Tsallis measure to burst frequency and BSR_a is illustrated by simulated data. The pdf of EEG amplitude during isoelectricity and continuous activity holds the same feature, i.e., a flatter shape, while it sharpens during the BS period. In the latter case, the value of TsEn in EEG is low, and therefore, an area is formed between TsEn curve and the extremum of TsEn. This area could reflect the BS features in EEG after asphyxial CA. Our study applies this measure to quantitative analysis of the BS pattern in EEG immediately after asphyxial CA in rats. To evaluate the TsEnA performance with different q values, Pearson correlation between TsEnA and NDS, and RDR of TsEnA are compared among EEG recordings from 15 rats. The results show that when q is around 3, TsEnA correlates well with neurological outcome (Pearson correlation coefficient > 0.85) and gives high distinguishability among rats with various NDS (RDR > 0dB). Thus, the TsEnA measurement calculated with q = 3 can reliably and effectively provide early prognostic information on cerebral functional recovery.

In conclusion, in order to improve the “readability” of EEG recordings following brain injury, we introduce a method that quantitatively interprets the BS pattern in EEG after CA. Three discriminative BS features, i.e., burst frequency, BSR_a, and the duration of BS are combined to configure a simplified TsEn-based measure, namely TsEnA. This new measure is computed and compared among animals with different neurological outcomes following asphyxial CA. The results show that TsEnA computed with q = 3 could consistently and distinguishably quantify the complex dynamics in BS EEG, and provide early prognostic information on neurological outcomes. The measure proposed in this study may be of value in an accurate and objective estimation of the gravity of post-CA cerebral damage.

Biography

Dandan Zhang received the B.S. degree in biomedical engineering from Xi’an Jiaotong University, Xi’an, China, in 2001. She is currently working toward the Ph.D. degree at the Department of Biomedical Engineering, Tsinghua University, Beijing, China.

From September 2008 to September 2009, she was a Visiting Student in the Department of Biomedical Engineering, Johns Hopkins School of Medicine, Baltimore, MD. Her current research interests include neonatal electroencephalography, neural signal processing, and neurophysiology of brain injury and anesthesia.

Xiaofeng Jia received the M.D. degree in clinical medicine from Zhejiang Medical University, Hangzhou, China, in 1994, the M.S. degree in surgery from Shanghai Medical University, China, in 1997, and the Ph.D. degree in surgery (orthopedics) from Fudan University, Shanghai, China, in 2003.

Since 2007, he has been a faculty member in the Department of Biomedical Engineering, Physical Medicine and Rehabilitation, Johns Hopkins School of Medicine, Baltimore, MD. His current research interests include stem cell therapy for shoulder surgical repair, novel application of neuroelectrophysiology for detection and restoration of spinal cord and peripheral nerve injury, and therapeutic hypothermia of brain and spinal cord after global brain ischemia.

Dr. Jia is a member of the American Academy of Orthopaedic Surgeons, the American Association for Hand Surgery, the Society of Critical Care Medicine, the American Heart Association, and the International Society for Heart Research.

Haiyan Ding received the Ph.D. degree in biomedical engineering from Tsinghua University, Beijing, China, in 2005.

Since 2005, she has been a Lecturer in the Department of Biomedical Engineering, Tsinghua University. Currently, she is the Visiting Scientist in the Department of Biomedical Engineering, Johns Hopkins School of Medicine, Baltimore, MD. Her current research interests include neural signal processing and cerebral function monitoring of neonate, medical metrology, and medical imaging processing.

Datian Ye received the B.S. and M.S. degrees in electrical engineering from Tsinghua University, Beijing, China, in 1970 and 1990, respectively.

He is a Professor and the Supervisor of the Ph.D. Service for the Department of Biomedical Engineering, Medical School, Tsinghua University, Beijing, China, where she is also the Vice Dean of the Department of Electrical Engineering and the Director of the Research Center of Biomedical Engineering, Graduate School at Shenzhen, Tsinghua University. Her current research interests include auditory neural biology and information, digital medical instruments, and medical system on chip. She has authored or coauthored more than 100 papers, and applied for six patents.

Prof. Ye is currently a Reviewer of the National Nature Science Fund Application and the Ministry of Education. She is also the Vice Director of the Shenzhen Branch of Chinese Biomedical Engineering Society.

Nitish V. Thakor (S’78–M’81–SM’89–F’97) received the M.S. degree in biomedical engineering in 1978, and the Ph.D. degree in electrical and computer engineering in 1981, both from the University of Wisconsin, Madison, WI.

He is currently a Professor of biomedical engineering at Johns Hopkins University, Baltimore, MD, where he directs the Laboratory for Neuroengineering. He is the Director of a Neuroengineering Training Program funded by the National Institute of Biomedical Imaging and Bioengineering. His current research interests include neural diagnostic sensors and instrumentation for clinical applications, signal processing, optical and MRI imaging, microsystems for basic neuroscience research, and neural prosthesis. He has authored or coauthored more than 188 refereed journal articles and holds of six patents.

Prof. Thakor is a Fellow of the American Institute of Medical and Biological Engineering, and a Founding Fellow of the Biomedical Engineering Society. He is the Editor-in-Chief of the IEEE Transactions on Neural Systems and Rehabilitation Engineering. He received the Presidential Young Investigator Award as well as the National Institutes of Health Research Career Award.