Stiffness Control of a Continuum Manipulator in Contact with a Soft Environment

Abstract

Stiffness control of a continuum robot can prevent excessive contact forces during robot navigation inside delicate, uncertain and confined environments. Furthermore, it enables the selection of tip stiffnesses that match varying task requirements. This paper introduces a computationally-efficient approach to continuum-robot stiffness control that is based on writing the forward kinematic model as the product of two transformations. The first transformation calculates the non-contact kinematics of the robot and can be formulated based on the specific type of continuum robot under consideration. The second transformation calculates the tip deflection due to applied forces and is efficiently computed using the special Cosserat rod model. To implement a desired tip stiffness, the two transformations are used to solve for the actuator positions that deform the manipulator so as to generate the required tip force at the measured tip position. The efficacy of the proposed controller is demonstrated experimentally on a concentric-tube continuum robot.

I. Introduction

Historically, the study of robot-environment interaction has focused on industrial robots interacting with stiff environments in assembly operations and other manufacturing tasks [1]. In these applications, robot position control is infeasible since uncertainties in both the position and stiffness of the environment lead to excessive contact forces as well as to the jamming and wedging of parts. To avoid these problems, a variety of solutions have been introduced. These include the introduction of passive compliance in the robot, e.g., an RCC wrist [2], as well as hybrid force / motion control [1] and stiffness control [3].

A continuum robot is a manipulator whose curvature can be controlled by adjusting the internal deformation of mechanically coupled elastic components of the body of robot [4]. Continuum robots include steerable catheters [5], multi-backbone snake-like robots [6], [7] and concentric tube robots [8], [9]. Two examples are shown in Figure 1. Since robot shape is controlled by the storage and release of elastic energy in the robot’s component parts, continuum robots are flexible by design.

Fig. 1.

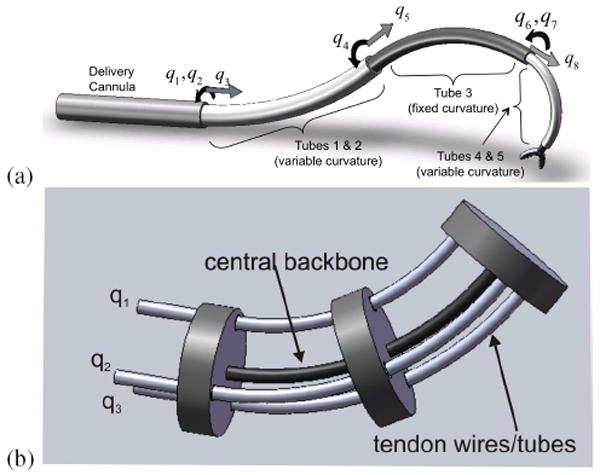
Schematics of two types of continuum robots. (a) concentric-tube robot, (b) tendon-driven robot with flexible backbone.

The resulting robot stiffness may, however, be large enough to generate excessive and damaging contact forces during interactions with soft surgical environments. While it is possible to avoid this problem by building the robot from extremely low stiffness components, e.g., as is done with catheters, such a robot cannot generate the forces required for doing many surgical manipulation tasks such as tissue penetration and suturing. An alternate approach that produces the safety of low stiffness during robot navigation, but also enables high stiffness during tissue manipulation is to employ stiffness control. In this approach, the robot operator can select and modify the robot’s contact stiffness during a procedure. The desired stiffness can be set lower than the inherent stiffness of the manipulator to safely navigate inside confined surgical environments.

This paper introduces a stiffness controller for a continuum robot in the context of the kinematic mapping rather than the force mapping generally used for rigid robots. The kinematic model of the robot in contact is used to map the tip force and tip position to joint positions of the robot. Real-time measurement of tip position is used to calculate robot deflection. The kinematic model is considered as the product of two transformations: the first transformation calculates the unloaded kinematics of the robot while the second calculates the tip deformation due to applied forces. It is assumed that an unloaded forward kinematic model of the specific continuum robot is available, i.e., a model that calculates tip configuration from actuator positions assuming no external forces are applied. These models are readily available in the literature [6], [8], [9].

General applicability to all types of continuum robots is achieved by assuming that, in any given configuration, any continuum robot can be approximated by a single Cosserat rod (of varying mechanical properties along its length) for the purpose of computing deformation due to external loading [10], [11]. The special Cosserat rod model enables computationally efficient calculation of robot deflection due to external forces [10]. Stiffness control is implemented using an iterative method to solve for the actuator positions that achieve the desired tip force. Efficacy of the proposed controller is demonstrated experimentally for a 3 degree of freedom (DOF) concentric-tube robot.

The paper is arranged as follows. Related work is described in the following section. Section III presents the general kinematic and force mappings of continuum robots. The deflection model using the special Cosserat rod model is presented in Section IV. The stiffness controller is presented in Section V and its experimental implementation is described in Section VI. Conclusions appear in the final section.

II. Related Work

Unloaded kinematic models have been developed for a variety of continuum robots. Schematics of two types are shown in Figure 1. Figure 1(a) shows a concentric tube robot which is constructed by telescopically extending concentrically combined pre-curved superelastic tubes. The robot’s shape and tip location are controlled via the kinematic inputs consisting of the relative rotations and translations of the tubes at their proximal ends (q₁, …, q₈). The unloaded kinematic models for this type of robot depend on the modeling assumptions. When the tubes are considered torsionally rigid, the kinematics are described by algebraic equations. For long or highly curved tubes, torsional compliance can be important and the kinematics take the form of differential equations in arc length with split boundary conditions [9].

Figure 1(b) depicts a tendon-driven continuum robot of the type often used in steerable catheters and for distal dexterity enhancement in minimally invasive surgery. These robots possess a central flexible backbone that is deflected by symmetrically arranged wires [6], [5] or tubes [12], [7]. As shown in the schematic, spacer disks are attached to the central backbone. The wires or tubes slide through holes in all disks except for the most distal one to which they are attached. Unloaded kinematic models are developed by relating central backbone shape to tendon length, q₁, q₂, q₃ [6], [5]. While wire tendons are limited to tensile forces, tubes can also be used in compression and their bending stiffness must be accounted for in the kinematics [12], [13]. For this type of continuum robot, the mapping between forces in the actuating tubes and tip forces has also been derived [12]. Using this model, tube forces were used to infer tip forces.

III. Kinematic and Force Mappings of Continuum Robots

All continuum robots can be modeled by a space curve, r(q, s) ∈ ℜ³, that is a function of the n kinematic input variables, q ∈ ℜⁿ, and the arc length, s, together with coordinate frames defined at the robot’s base (frame B) and tip (frames T̂ and T). These are shown in Figure 2. Referring back to Figure 1, the space curve corresponds to the common tube centerline of (a) and the curve of the central backbone in (b). In contrast to rigid robots, two tip frames, T̂ and T, are defined. The former corresponds to the tip configuration when no external loads are applied while the latter includes the deformation arising from a wrench F ∈ ℜ⁶ applied externally at the tip. The first three components of F correspond to the tip force while the latter three are those of the torque applied to the tip [14].

Fig. 2.

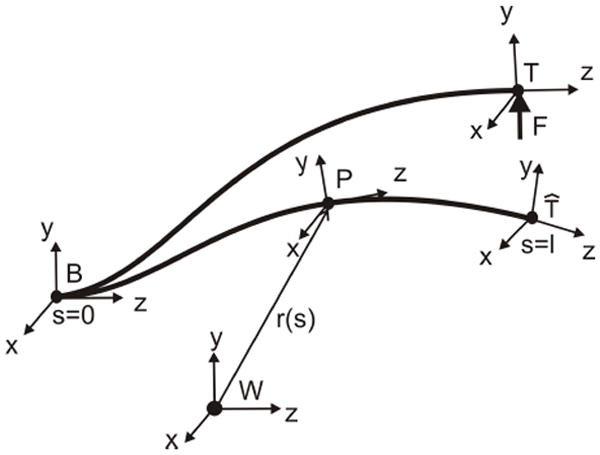
Continuum robot represented as a space curve. W is world coordinate frame while B, P, T̂ and T are robot body frames. T̂ and T are tip frames without and with the application of tip wrench, F, respectively.

The configuration of frame C relative to frame B is a rigid body transformation that can be written in homogeneous coordinates as

$$g_{\mathit{bc}}(q)=\left[\begin{array}{cc}{R}_{\mathit{bc}}(q)& p_{\mathit{bc}}(q)\\ 0& 1\end{array}\right]$$ (1)

where R_bc ∈ SO(3) is the rotation matrix, and p_bc ∈ ℜ³ is the translation vector between frames B and C [14]. This expression also represents a mapping from kinematic input space q ∈ Q to the special Euclidean group SE (3).

For the continuum robot of Figure 2, the configuration of the frame T relative to the frame B, g_bt, can be written as the product of two transformations:

$$g_{\mathit{bt}}(q,F)=g_{b\widehat{t}}(q)g_{\widehat{t}t}(q,F)$$ (2)

where g_bt̂ is the configuration of frame T̂ relative to B and g_t̂t is the configuration of T relative to T̂. The first transformation, g_bt̂(q), corresponds to the unloaded robot kinematic models cited in Section II. The second transformation, g_t̂t (q, F), represents the displacement associated with the deformation of the robot due to the applied loading. Thus, the overall kinematic map, g_bt (q, F), is a function of both the kinematic variables and the external loading.

The force mapping equation for continuum robots can be derived from the principle of virtual work as was done in [12] to obtain

$$\tau =J_{\mathit{bt}}^{T}F+\frac{\partial E(q,F)}{\partial q}$$ (3)

Here, τ ∈ ℜⁿ is the vector of actuator forces and torques, E(q, F) ∈ ℜ is the elastic energy of the manipulator, and J_bt (q, F) is the Jacobian matrix mapping actuator velocities to tip velocity [14]. Of course, for rigid robots, the elastic energy term drops out and this equation reduces to the standard form, $\tau =J_{\mathit{bt}}^{T}F$.

To implement stiffness control in a rigid robot, the force mapping equation must be used to relate desired tip wrenches to actuator forces and torques. For continuum robots, however, it is also possible to implement stiffness control using the kinematic mapping (2). In this approach, (2) is solved for the actuator positions corresponding to the desired tip wrench, F^d, and the actual measured tip configuration, $g_{\mathit{bt}}^m$.

Comparing the two approaches, stiffness control based on the force mapping becomes an actuator force / torque control problem while stiffness control using the kinematic map is an actuator position control problem. Use of the force mapping requires the use of joint force /torque sensors [12] or actuator currents [15]. In contrast, actuator position control can be performed accurately using the existing actuator encoders.

Thus, it may be advantageous to employ (2) if it can be solved efficiently. To explore this question, assume that it is desired to apply a wrench F_d at the tip of a 6 DOF continuum robot that has 6 independent joint variables while its tip is held rigidly fixed at configuration $g_{\mathit{bt}}^m$. Equation (2) can be rewritten in terms of its inputs, measured tip configuration, $g_{\mathit{bt}}^m$, and desired tip wrench, F^d, and its output, desired actuator positions, q^d

$$g_{\mathit{bt}}^m=g_{b\widehat{t}}(q^d)g_{\widehat{t}t}(q^d,F^d)$$ (4)

Driving the actuator displacements to q^d produces deformations of the continuum robot that produce the desired tip wrench F_d at the measured tip configuration of the robot. Note that for the general case of contact with a soft environment, producing a desired tip wrench will also cause the tip configuration to change.

The root finding problem of solving (4) for q^d can be performed efficiently if its right hand side can be computed quickly. The term g_bt̂ (·) is the unloaded forward kinematic model for which numerically efficient formulations are available [6], [5], [12], [9]. The second term, g_t̂t (·, ·), is the tip displacement produced by application of tip wrench on the unloaded robot.

As described below, given g_bt̂ (q^d), an efficiently computed estimate of the product g_bt (q^d, F^d) = g_bt̂ (q^d) g_t̂t (q^d, F^d) can be obtained using the special Cosserat rod model.

IV. Deflection model

To obtain g_bt (q, F) = g_bt̂ (q) g_t̂t (q, F), we approximate any continuum manipulator as a single elastic rod whose curvature and elastic properties match those of the robot for actuator values q and tip wrench F = 0. Thus, the curvature is selected to match the robot’s backbone curve, r(q, s), and its stiffness is selected to match the composite stiffness of all elastic components that comprise the robot.

Deflection of the robot is computed as deflection of the rod in response to tip wrench, F. This model is approximate in that it does not account for relative motions of the robot’s elastic components in response to the tip wrench. As demonstrated in our experiments, the error associated with this approximation is often negligible. It is also assumed that the cross sectional shear and longitudinal extension of the rod are negligible. This assumption is often made in developing unloaded kinematic models for continuum robots; see, e.g., [9].

The special Cosserat rod model is well known in the mechanics literature [11] and has also been employed in the robotics and computer graphics literatures [10], [16], [9]. Here, a concise overview of the model and its numerical solution are presented.

A. Strain and Curvature of a Rod

As shown in Figure 2, coordinate frames can be defined along the backbone curve, r(q, s). In the following, actuator values, q, are assumed constant and are omitted as arguments. Since these frames are intended to track material deformations of the rod’s cross sections, a natural choice for frame orientation is to choose a base frame, B with one axis (i.e., the z axis) aligned with the curve’s tangent and then to slide this frame without rotation about the local z axis along r(s) [17].

The resulting Bishop frame P at arc length s can be written as g_bp(s), s ∈ [0, l] where l is the length of the robot. Its origin lies on r(s) and experiences a rate of change with respect to arc length, v(s) ∈ ℜ³, given by

$$v(s)=\frac{\mathit{dr}(s)}{\mathit{ds}}$$ (5)

The rate of change of frame P’s coordinate axis unit vectors, {e_x(s), e_y(s), e_z(s)}, with respect to arc length satisfy the body-frame equations

$$\frac{{\mathit{de}}_x(s)}{\mathit{ds}}=u(s)\times e_x(s),\frac{{\mathit{de}}_y(s)}{\mathit{ds}}=u(s)\times e_y(s),\frac{{\mathit{de}}_z(s)}{\mathit{ds}}=u(s)\times e_z(s)$$ (6)

in which u(s) ∈ ℜ³.

The vectors u(s) and v(s) are the angular and linear strains, respectively, experienced by the cross section. Thus, u(s) has the units of curvature and its x and y components correspond to bending of the rod while its z component corresponds to twisting of the rod. Similarly, the x and y components of v are the shear strain components of the cross section while the z component is v_z = 1 + ε_z in which ε_z is the longitudinal strain. Given the assumptions of negligible shear and longitudinal strain,

$$v(s)={[\begin{array}{ccc}0& 0& 1\end{array}]}^T,s\in [0,l]$$ (7)

Angular and linear strains, u and v, provide body frame descriptions of the curved shape of the rod. It can be helpful to note that u and v are analogous to body-frame angular and linear velocities if time is substituted for arc length. Thus, coordinate frames, g_bp(s), are obtained as the solution to the differential equation

$$\frac{d}{\mathit{ds}}(g_{\mathit{bp}}(s))=g_{\mathit{bp}}(s)\left[\begin{array}{cc}[u(s)]& v\\ 0& 0\end{array}\right]$$ (8)

in which the square bracket on the vector u indicates the skew-symmetric matrix form

$$[u(s)]=\left[\begin{array}{ccc}0& -u_3& u_2\\ u_3& & -u_1\\ -u_2& u_1& 0\end{array}\right]$$ (9)

This differential equation can be integrated numerically from base to tip or tip to base using a method that preserves the group structure of SE(3). A variety of numerical integration methods are available for this purpose [18], [19].

The initial curvature of the robot prior to the application of external loads is denoted by û(s). Given an unloaded kinematic model that computes g_bp(s), the unloaded shape of the rod used to model robot deflection can be computed as

$$\left[\widehat{u}\left(s\right)\right]=R_{\mathit{bp}}^{-1}\left(s\right){\dot{R}}_{\mathit{bp}}^{-1}\left(s\right)$$ (10)

in which R_bp(s) is the rotation matrix of g_bp(s).

B. Rod Deformation Due to Applied Loads

To compute rod deformations, two equations are needed. The first is a constitutive model that relates cross-section strains u and v to the bending moment, m ∈ ℜ³, and force, n ∈ ℜ³, acting on the cross section. Since shear of the cross section and rod extension are neglected, only the relationship between u and m is needed. The second equation relates cross-section bending moment and force to the external loads. Both are described below.

When a rod with initial curvature û(s) is deformed to a new curvature u(s), a bending moment, m(s), is generated. Assuming linear elastic behavior, the bending moment at any point s along the rod is given by

$$m(s)=K(s)(u(s)-\widehat{u}(s))$$ (11)

where K (s) is the frame-invariant stiffness tensor. For a large class of rods, K (s) is given by

$$K(s)=\left[\begin{array}{ccc}{E}_x(s)I_x(s)& 0& 0\\ 0& E_y(s)I_y(s)& 0\\ 0& 0& J(s)G(s)\end{array}\right]$$ (12)

and E_x(s), E_y(s) are moduli of elasticity, I_x(s) and I_y(s) are area moments of inertia, J(s) is the polar moment of inertia and G(s) is the shear modulus. These values should be selected so that the rod stiffness matches the overall continuum robot stiffness as a function of arc length.

To relate cross-section bending moment and force to the external loads, we employ the equilibrium equation of the special Cosserat rod model [11]. Written in the body frame coordinates of Figure 2, the differential equation governing bending moment m and force n as a function of arc length s is given by

$$\begin{array}{lll}\frac{\mathit{dm}(s)}{\mathit{ds}}& =& \tau (s)-[u(s)]m(s)-[v(s)]n(s)\\ \frac{\mathit{dn}(s)}{\mathit{ds}}& =& \varphi (s)-[u(s)]n(s)\end{array}$$ (13)

where ϕ(s) and τ(s) are the applied force and torque per unit length of the rod and the bracket notation is as defined in (9).

For simplicity of exposition, it is assumed that only tip loads are applied to the robot and so τ(s) = ϕ(s) = 0, s ∈ [0, l]. Combining (11) and (13) results in equations for curvature u and force n,

$$\begin{array}{lll}\frac{\mathit{du}(s)}{\mathit{ds}}& =& \frac{d\widehat{u}(s)}{\mathit{ds}}-[u(s)](u(s)-\widehat{u}(s))+K^{-1}(s)[v]n(s)\\ \frac{\mathit{dn}(s)}{\mathit{ds}}& =& -[u(s)]n(s)\end{array}$$ (14)

The boundary conditions for these equations, u(l), n(l), can be specified from the body-frame wrench, F_b, applied at the robot’s tip

$$\begin{array}{ccc}\hfill {[n^T(l)m^T(l)]}^T& =& F_b\hfill \\ \hfill u(l)& =& K^{-1}m(l)+\widehat{u}(l)\hfill \end{array}$$ (15)

and (14) can be solved numerically by integrating backward in arc length from s = l → 0 [10]. Since (13) is written in body coordinates, the body-frame twist velocity, [v^T, u^T]^T must be simultaneously integrated such that the equations evolve on SE(3). As detailed in [10], a first-order Crouch-Grossman method [18] provides computational efficiency. The result of this integration is the desired estimate of the transformation between the base and tip of the robot, g_bt = g_bt̂ g_t̂t.

In stiffness control, the desired tip wrench is often calculated in a local frame at the tip of the robot whose axes always remain parallel to the axes of the world frame, $F_{\mathit{tw}}^d$ [20]. In this case, the boundary condition is a function of the rotation of the rod tip. Specifically, if the base of the rod is positioned at the origin of the world frame then g_wb in Figure 2 is the identity matrix and the desired body-frame tip wrench, $F_b^d$, to be used in (15) is related to the desired frame tip wrench by

$$F_b^d=\left[\begin{array}{cc}{R}_{\mathit{bt}}^T& 0\\ 0& R_{\mathit{bt}}^T\end{array}\right]F_{\mathit{tw}}^d$$ (16)

where, following (1), R_bt is the rotation matrix of $g_{\mathit{bt}}(q^d,F_b^d)$. While the integral must now be solved iteratively, convergence is rapid when the tip wrench varies smoothly and the solution is seeded using the desired rod shape from the previous time step.

V. Stiffness Controller Using a Modified Position Controller

The task of the controller is to create a user-defined stiffness at the tip of the continuum manipulator. If the stiffness is specified for all degrees of freedom of the robot tip, a pure stiffness controller can be implemented. In many medical applications, however, it is desirable to control the stiffness in certain directions, e.g., tip position, and to control the motion in other directions, e.g., tip orientation. Because of its practical importance, this latter case of hybrid stiffness / motion control is considered here. The framework described below can be easily adapted to other combinations of stiffness- and motion-controlled coordinates.

The desired tip force, f^d ∈ ℜ³, is computed using the user-defined diagonal stiffness matrix, K^d ∈ ℜ^3×3, based on the difference between measured robot tip position, $p_{\mathit{bt}}^m\in {\mathbf{\Re }}^3$, and a reference tip position, $p_{\mathit{bt}}^r\in {\mathbf{\Re }}^3$ as follows

$$f^d=K^d(p_{\mathit{bt}}^m-p_{\mathit{bt}}^r)$$ (17)

The desired tip orientation of the robot is given as $R_{\mathit{bt}}^d\in \mathit{SO}(3)$.

As shown in Figure 3, the stiffness equation (17) can be pictured as a virtual spring of stiffness K^d that connects the reference position $p_{\mathit{bt}}^r$ to the current tip position of the manipulator.

Fig. 3.

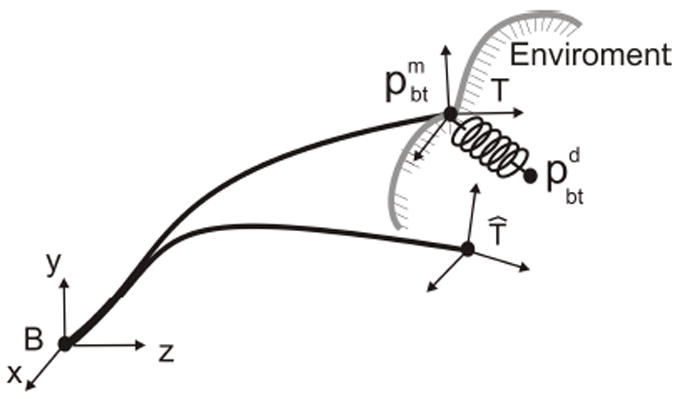
Controller implements a virtual linear spring at the tip of the manipulator. Desired actuator positions are such that when robot is deflected from unloaded tip configuration, T̂, to configuration T, the desired tip spring force is generated and the desired tip orientation is achieved.

The desired force, f^d, and desired tip orientation, $R_{\mathit{bt}}^d$, must be mapped to the actuator positions, q^d, such that the deflected robot will generate the force f^d at the tip configuration

$$g_{\mathit{bt}}^{\mathit{dm}}=\left[\begin{array}{cc}{R}_{\mathit{bt}}^d& p_{\mathit{bt}}^m\\ 0& 1\end{array}\right]$$ (18)

The desired actuator positions are implicitly defined by (4), re-written for $g_{\mathit{bt}}^{\mathit{dm}}$

$$g_{\mathit{bt}}^{\mathit{dm}}=\left[\begin{array}{cc}{R}_{\mathit{bt}}^d& p_{\mathit{bt}}^m\\ 0& 1\end{array}\right]=g_{\mathit{bt}}(q^d,F_{\mathit{tw}}^d)=g_{b\widehat{t}}(q^d)g_{\widehat{t}t}(q^d,F_{\mathit{tw}}^d)$$ (19)

In this equation, $p_{\mathit{bt}}^m$ is directly measured by a tip sensor while $g_{\mathit{bt}}(q^d,F_{\mathit{tw}}^d)$ is computed for values of q^d and f^d from the rod deformation model (14)-(16) using the wrench boundary condition

$$F_{\mathit{tw}}^d=\left[\begin{array}{c}{f}^d\\ {\left[\begin{array}{ccc}0& 0& 0\end{array}\right]}^T\end{array}\right]$$ (20)

and the initial shape (10) obtained from the unloaded kinematic model

$$[\widehat{u}(q^d,s)]=R_{\mathit{bp}}^{-1}(q^d,s){\dot{R}}_{\mathit{bp}}^{-1}(q^d,s)$$ (21)

in which R_bp(q^d, s) is the rotation matrix of g_bp(q^d, s).

Using an efficient numerical implementation, e.g., Gauss-Newton, (19) can be solved iteratively at each time step of the controller for the actuator positions, q^d, that produce the desired combination of tip force and orientation. By driving the actuator variables to q^d, the manipulator is deformed so as to produce the desired tip force at $R_{\mathit{bt}}^d$. Position tracking controllers, e.g., PD, can be used to drive and maintain the actuators of the manipulator at their desired values. The gains of the actuator controllers should be selected so that steady-state tip position error due to actuator error is small compared to the deflection of the manipulator.

Since position controllers already exist for a variety of continuum robots [6], [5], [9], it can be advantageous to leverage the existing controller implementation to achieve stiffness control. This can be accomplished as follows.

A position controller solves the inverse kinematic problem and drives the actuators to the positions given by

$$q^d=I(g_{b\widehat{t}}^d)$$ (22)

where I(·) represents a multi-dimensional inverse kinematic function for the unloaded robot that calculates either numerically or analytically the actuator positions corresponding to the user-defined configuration, $g_{b\widehat{t}}^d$.

To include the tip-applied wrench, the argument of I can be rewritten using (19) to obtain

$$q^d=I(g_{\mathit{bt}}^{\mathit{dm}}{g}_{\widehat{t}t}^{-1}(q^d,F_{\mathit{tw}}^d))$$ (23)

where Cosserat deflection model is used to compute $g_{\widehat{t}t}(·,F_w^d))$.

Since the deflection model computes $g_{\mathit{bt}}(q^d,F_{\mathit{tw}}^d)$ rather than $g_{\widehat{t}t}(q^d,F_{\mathit{tw}}^d)$, (23) can be rewritten using (2) to arrive at

$$q^d=I(g_{\mathit{bt}}^{\mathit{dm}}{g}_{\mathit{bt}}^{-1}(q^d,F_{\mathit{tw}}^d)g_{b\widehat{t}}(q^d))$$ (24)

This equation can be solved for q^d using fixed point iteration [21],

$$q_{i+1}^d=I(g_{\mathit{bt}}^{\mathit{dm}}{g}_{\mathit{bt}}^{-1}(q_i^d,F_{\mathit{tw}}^d)g_{b\widehat{t}}(q_i^d)),i=1,2,\dots$$ (25)

where index i is the iteration number.

In this way, the stiffness controller can be implemented by the on-line iteration of (25). The controller computations for each iteration consist of a single evaluation of (i) the un-loaded kinematic model, $g_{b\widehat{t}}(q_i^d)$, (ii) the deformation model, $g_{\mathit{bt}}(q_i^d,F_{\mathit{tw}}^d)$, and (iii) the unloaded inverse kinematic model, I(·). Assuming that the pre-existing position controller runs at a sufficiently high rate, the changes in controller inputs ( $p_{\mathit{bt}}^r$ and $R_{\mathit{bt}}^d$) and robot tip position ( $p_{\mathit{bt}}^m$) are small from one controller cycle to the next and it is sufficient to evaluate the iteration equation (25) once per cycle.

VI. Experimental Implementation

The stiffness controller was implemented to produce a desired positional tip stiffness on a three DOF concentric tube robot. This is a case of pure stiffness control since the stiffness is specified for each degree of freedom. The robot was comprised of the two 150 mm long tubes shown in Figure 4. Relative rotation of the tubes varies their combined curvature, u(s), from the initial constant pre-curvature value of u(s) = [1/240 0 0]^T mm⁻¹, s ∈ [0, 150] mm, when the curvatures are aligned (q₁ = q₂), to u(s) = [0 0 0]^T, s ∈ [0, 150] mm (robot is straight) when the curvatures are anti-aligned (q₁ = q₂ + π). The robot can also be translated in the z direction by actuator displacement q₃. Varying {q₁, q₂} ∈ SO(2) × SO(2) and q₃ ∈ R produces a cylindrical workspace at the robot’s tip of radius 48 mm and length 254 mm.

Fig. 4.

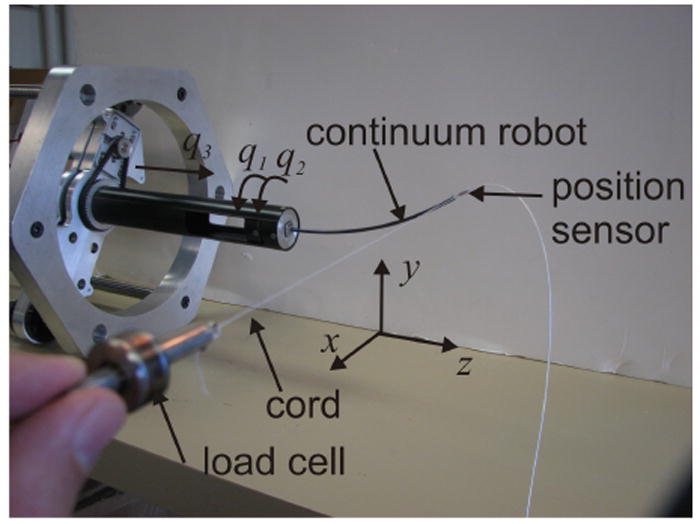
Concentric tube manipulator and drive system. Electromagnetic sensor is shown attached to robot tip. Actuator variables q₁ and q₂ control rotation of tubes and q₃ controls translation of tube pair. Curvature is varied by relative rotation of tubes. Environment motion is produced by manual loading of robot tip through cord attached to load cell.

An existing position control architecture [9] was modified to implement stiffness control. The existing controller consists of a master-slave system in which the concentric tube manipulator is the slave arm and a PHANTOM Omni haptic device (Sensable Technologies, Inc.) is employed as the master arm. The position controller is implemented as a multithreaded process under Windows 2000. The process includes two time-critical user mode threads running at 1 kHz that implement the kinematic model and PD joint controllers and an application thread that updates a GUI.

The stiffness controller requires real-time measurement of the robot’s tip configuration. This was accomplished using an electromagnetic tracking sensor (3D Guidance trakSTAR™, Ascension Technology Corporation). The 2 × 9.7 mm cylindrical sensor (model 180) was attached to the robot’s tip as shown in Figure 4. Sensor accuracy is 1.4 mm RMS in translation and 0.5 degree RMS in rotation with a resolution of 0.5 mm and 0.1 degrees. The update rate of the sensor was set to 100 Hz. The sensor’s electrical leads produced negligible deformation of the robot.

To calibrate the deflection model used in the stiffness controller and to evaluate the controller’s performance, a 22 N tension/compression load cell (Sensotec model 31) was used to measure environment force. The load cell was connected to the tip of the manipulator through a long thin cord to prevent the metal components of the load cell from distorting the magnetic field of the tip tracking system. This loading configuration is depicted in Figure 4.

To evaluate the controller, experiments were performed with a moving environment shown in Figure 4. The environment is produced by manually pulling on the robot tip in a desired direction through a cord attached to a load cell. During these tests, the desired reference tip position, $p_{\mathit{bt}}^r$, of (17) was held constant by fixing the position of the master.

Implementation of the proposed stiffness controller requires an unloaded kinematic model and a calibrated deflection model. Each is described below followed by the results of the control experiments.

A. Unloaded Kinematic Model

To implement stiffness control by modification of a position controller as given by (25), it is assumed that forward and inverse kinematic solutions are already implemented for the non-contact case. Such models have been presented in [9] for concentric tube continuum robots. Modified versions of these models, appropriate to the pair of tubes used in the experiments, are presented here.

While, in general, the combined curvature of two tubes of constant pre-curvature varies along their length due to torsional twisting of the tubes [9], this effect is negligible for the tubes used in the experiments. Thus, it is appropriate to model the combined curvature as a function of actuator values, {q₁, q₂}, that is independent of arc length. It can be written in the world frame of Figure 4 as u^w,

$$u^w=A_{\kappa }(q_1-q_2)\left[\begin{array}{c}\cos ((q_1+q_2)/2+{\varphi }_{\kappa }(q_1-q_2))\\ \sin ((q_1+q_2)/2+{\varphi }_{\kappa }(q_1-q_2))\\ 0\end{array}\right]$$ (26)

Here, A_κ (·) and ϕ_κ (·) compute the magnitude and phase of curvature as functions of the relative tube rotation angle, q₁ − q₂. For curve fitting, A_κ (·) and ϕ_κ (·) are interpreted as the magnitude and phase of a complex function κ(·).

The tip position, assuming no contact forces, is obtained from the curvature, u^w, as [9]

$$p_{b\widehat{t}}(q)=\left[\begin{array}{c}\frac{u_y^w(1-\cos (l\left|u^w\right|)}{{\left|u^w\right|}^2}\\ \frac{-u_x^w(1-\cos (l\left|u^w\right|)}{{\left|u^w\right|}^2}\\ q_3+\frac{\sin (l\left|u^w\right|)}{\left|u^w\right|}\end{array}\right]$$ (27)

in which l is the arc length of the manipulator. To obtain the most accurate kinematic model, the complex function κ(·) was calculated from (26) and (27) as a truncated Fourier series using position measurements obtained with the tip tracking sensor over two complete revolutions of the tubes.

B. Deflection Model Calibration

To calculate robot deflection due to tip loading, the deflection model requires the unloaded body-frame curvature of the robot, û(s), as well its composite stiffness, K(s). While (10) provides a general expression for unloaded curvature, in this case, it can be directly obtained from (26). Due to the choice of Bishop body frames and since the unloaded kinematic model is of constant curvature,

$$\widehat{u}(s)=u^w$$ (28)

The deflection model approximates the composite stiffness of all elastic elements of the robot by the matrix of bending and torsional stiffnesses, K(s), defined in (12). Since the robot is composed of NiTi tubes, K(s) reduces to

$$K(s)=K=\mathrm{diag}(E_c{I}_c,E_c{I}_c,E_c{I}_c/(1+v))$$ (29)

in which E_c and I_c are the composite values for elastic modulus and area moment of inertia, respectively, and v is Poisson’s ratio.

Using the value of v = 0.3 that is appropriate for NiTi, E_cI_c was estimated experimentally using the testing configuration of Figure 4 and the maximum possible value of initial curvature û(s) = [1/240 0 0]^T mm⁻¹. An iterative method was used to solve for the stiffness matrix that minimized the error between the force-displacement response predicted by the model and that obtained by measurement in x and y directions. The resulting calibrated stiffness of

$$K(s)=\mathrm{diag}(0.0490.0490.038)\mathrm{N}­{\mathrm{m}}^2$$ (30)

was used to compare the deflection model and experimental robot tip stiffnesses as shown in Figure 5. (See Figure 4 for the coordinate directions.) The depicted experimental data was collected for cyclic displacements in the x, y and z coordinate directions while holding the robot actuators fixed. While the experimental data reveals a small amount of hysteresis, the deflection model provides a good fit with the loop average in the x and y directions while the high stiffness in the z direction reduces the accuracy of the model fit.

Fig. 5.

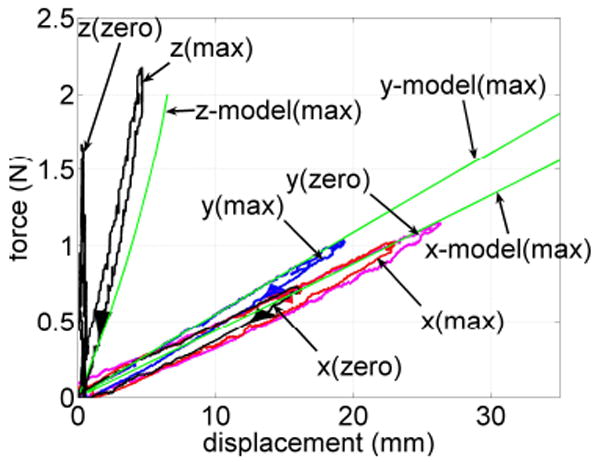
Force versus displacement of the robot tip in coordinate directions {x, y, z}. Both experimental data and predictions from the calibrated deflection model are shown for the maximum curvature configuration, labeled (max), and zero curvature configuration, labeled (zero).

C. Stiffness Controller

Stiffness control was implemented for the three DOF continuum robot depicted in Figure 4 by modifying an existing position controller. The position controller uses Newton’s method to solve (26)-(27) at each time step for the actuator positions associated with the desired unloaded tip position, $p_{b\widehat{t}}^d$,

$$q^d=I(p_{b\widehat{t}}^d)$$ (31)

PD controllers are used to drive the actuators to the values computed in (31).

To achieve stiffness control, (31) was replaced with the iteration equation (25) which, for this robot, reduces to an expression involving only tip positions,

$$q_{i+1}^d=I(p_{\mathit{bt}}^m-(p_{\mathit{bt}}(q_i^d,F_{\mathit{tw}}^d)-P_{b\widehat{t}}(q_i^d)))$$ (32)

Here, $p_{\mathit{bt}}^m$ is the current tip position as measured by the tip tracking sensor. The unloaded tip position, $p_{b\widehat{t}}(q_i^d)$ is computed using (26) and (27).

The deflected tip position, $p_{\mathit{bt}}(q_i^d,F_{\mathit{tw}}^d)$ is calculated from the deflection model (14) using $q_i^d$ to compute the predeflected curvature, û(s), from (26) and (28). The boundary conditions (15) are computed using the desired tip wrench, F^w, as defined by (17) and (20). This wrench is converted to body coordinates using (16) with R_bt computed using the current tip orientation as measured by the tip sensor. The integration was carried out with the discrete (in arc length) formulation detailed in [10] using ten nodes along the 150 mm length of the robot.

D. Controller Evaluation

The testing configuration of Figure 4 was used to evaluate the performance of the controller in the three coordinate directions for various values of robot curvature and tip stiffness. During these tests, the master manipulator was held fixed such that the reference tip position, $p_{\mathit{bt}}^r$, was constant and lay in the y-z plane above the line defined by actuator axis, q₃. (See Figure 4.) In each test, the robot tip was displaced in one of the three coordinate directions. Each displacement started with the robot tip in the unloaded configuration and proceeded until an arbitrary maximum value was obtained. The displacement was then reversed.

Figure 6 depicts the measured tip force and displacement in the three coordinate directions of Figure 4 for an intermediate value of non-contact robot curvature given by $u^w={\left[\begin{array}{ccc}\frac{1}{320\mathit{mm}}& 0& 0\end{array}\right]}^T$. As is also shown, the desired stiffnesses of (17) were set to be equal in the three coordinate directions, K_d = diag(0.04 0.04 0.04) N/mm. The maximum applied displacements in the x and y directions were set to be around 20 mm in order to demonstrate the range of forces over which the stiffness controller can be applied [20]. For most surgical applications, however, the forces and displacements are expected to be smaller than the evaluated range.

Fig. 6.

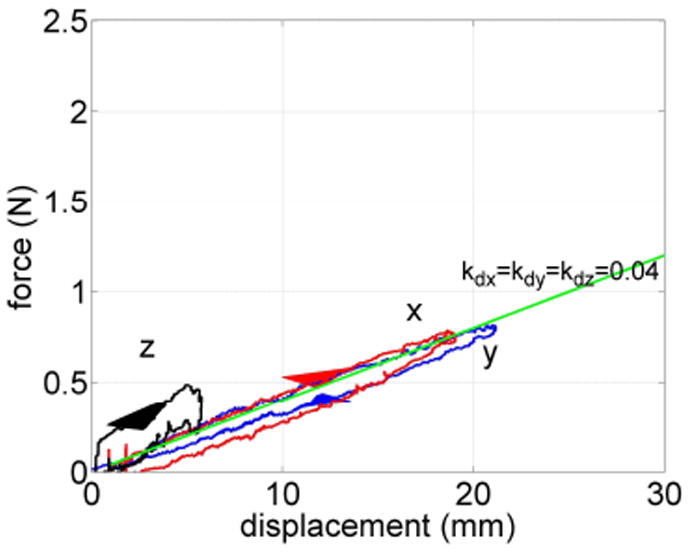
Tip force versus displacement in the three coordinate directions for a non-contact robot curvature of $u^w={\left[\begin{array}{ccc}\frac{1}{320\mathit{mm}}& 0& 0\end{array}\right]}^T$ and desired tip stiffness of K_d = diag(0.04 0.04 0.04) N/mm.

It can be seen that the desired stiffness is accurately achieved in the x and y directions. Stiffness in the z direction is less accurate, especially at direction reversals where imperfect cancellation of friction in the ball screw transmission of actuator q₃ leads to a large amount of hysteresis.

The most difficult configuration for stiffness control corresponds to when the robot is straight, i.e., the non-contact curvature is u^w = [0 0 0]^T. Tip force versus displacement data for this configuration are shown in Figure 7 for a desired stiffness of K_d = diag(0.02 0.08 0.2) N/mm. Recall that the natural stiffness in the x and y directions for the straight robot should be both equal to about 0.048 N/mm as depicted in Figure 5. The stiffness controller has succeeded in reducing the natural robot stiffness by about a factor of two in the y direction and in increasing the natural stiffness by about a factor of two in the in the x direction. Not depicted, the stiffness controller as described is unable to control the stiffness of robot along the z axis when the robot has zero curvature, i.e, is straight. A controller modification described in [20] avoids this limitation and is applicable to backdrivable continuum manipulators.

Fig. 7.

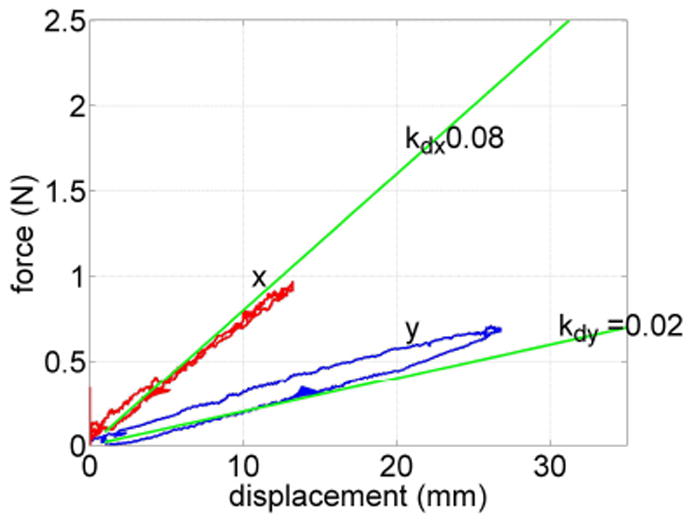
Tip force versus displacement in the x and y coordinate directions for a non-contact robot curvature of u^w = [0 0 0]^T and desired tip stiffness of K_d = diag(0.02 0.08 0.2) N/mm.

VII. Conclusions

The contribution of this paper is to provide an approach for implementing stiffness control on any continuum robot that can be modeled under loading as an elastic rod and for which an unloaded kinematic model is available. Thus, the method is broadly applicable to continuum robots including steerable catheters, multi-backbone robots as well as concentric tube robots.

The efficacy of the proposed stiffness controller was demonstrated on a 3 DOF concentric tube robot. It was found that desired tip stiffnesses could be achieved independent of robot configuration in the lateral or bending directions. Using tip position sensing, stiffness control along the axis of the robot is possible as long as the curvature of the entire robot is not close to zero. A future goal is to evaluate the stiffness controller under surgical conditions.