Corresponding Delay-Dependent Biases in Spatial Language and Spatial Memory

Abstract

The present study addresses the relationship between linguistic and non-linguistic spatial representations. In three experiments we probe spatial language and spatial memory at the same time points in the task sequence. Experiments 1 and 2 show analogous delay-dependent biases in spatial language and spatial memory. Experiment 3 extends this correspondence, showing that additional perceptual structure along the vertical axis reduces delay-dependent effects in both tasks. These results indicate that linguistic and non-linguistic spatial systems depend on shared underlying representational processes. In addition, we also address how these delay-dependent biases can arise within a single theoretical framework without positing differing prototypes for linguistic and non-linguistic spatial systems.

The relationship between linguistic and sensori-motor representations is a fundamental issue in cognitive science (Barsalou, 1999, 2008; Glenberg, 1997; Zwaan, 2004). Spatial language is an ideal domain to explore this issue because it is a clear example of these two systems coming together: sensori-motor systems exist and operate in space and spatial language is language about that space. Although there are numerous questions about how the sensori-motor and the cognitive are integrated in spatial communication (for reviews see Levinson, 2003; van der Zee & Slack, 2003), perhaps the most fundamental question is whether linguistic and non-linguistic spatial behaviors depend on shared or distinct representational processes.

A landmark study by Hayward and Tarr (1995) addressing this question examined performance in both linguistic and non-linguistic spatial tasks. In a phrase generation task, participants looked at a display and described a target object’s spatial relationship to a reference object. In a second experiment, participants looked at a display and rated the applicability of a given term (above, below, left, right) to a depicted spatial relation. Results from both tasks showed that vertically oriented terms (e.g. above, below) were judged to be more applicable when target objects appeared closer to the vertical axis of the reference frame centered on the reference object. Horizontally oriented terms (e.g. right, left) were similarly more applicable when the target object appeared closer to the horizontal axis. These results suggest that linguistic spatial prototypes lie along the canonical vertical and horizontal axes.

Hayward and Tarr also examined non-linguistic spatial representations using both a location discrimination task and a spatial recall task. In these tasks, participants looked at a display, the display was removed, and they either judged whether a new display was the same as or different from the original (discrimination) or they reproduced the location of the target object after a distracter task (spatial recall). Participants were significantly more accurate in discriminating and reproducing target object locations when they appeared along the vertical and horizontal axes. Thus, Hayward and Tarr concluded that non-linguistic spatial prototypes lie along the vertical and horizontal axes, consistent with the linguistic prototypes revealed in the phrase generation and linguistic ratings tasks. Based on this correspondence, Hayward and Tarr argued that linguistic and non-linguistic spatial representations share a common underlying representational structure.

More recently, Crawford and colleagues (Crawford, Regier, & Huttenlocher, 2000) drew starkly different conclusions using a comparable set of tasks. After briefly viewing a display depicting a target object and a reference object, participants rated the applicability of “Above” to the depicted relation. Participants then recalled the location of the target object. As in Hayward and Tarr, “Above” was most applicable for target locations along the vertical axis, leading to the conclusion that the prototype for “Above” lies along this axis. The key difference emerged in the spatial recall task however. Although location memory accuracy was greatest for target locations appearing along the reference axis (i.e., along vertical; see also Munnich, Landau, & Dosher, 2001), memory for targets not located along the axis were systematically biased away from the vertical axis (for similar results see Huttenlocher, Hedges, Corrigan, & Crawford, 2004; Huttenlocher, Hedges, & Duncan, 1991; Spencer & Hund, 2002, 2003).

Crawford and colleagues interpreted these results using the Category Adjustment (CA) model (Huttenlocher et al., 1991). According to this model, people represent a stimulus location in a non-linguistic spatial recall task using two sources of information: fine-grained and categorical. At the fine-grained level, people encode the direction and distance of the target. At the categorical level, people use the cardinal axes as category boundaries with non-linguistic spatial prototypes located at the centers of each spatial region, that is, along the diagonal axes. At recall, people combine fine-grained and categorical information, but weight categorical information more heavily since fine-grained information becomes less reliable during memory delays (see Spencer & Hund, 2002). As a consequence of this categorical weighting, non-linguistic memory responses are therefore biased away from cardinal axes and toward diagonal axes (i.e. towards the non-linguistic spatial category prototype). By this view, there is a fundamental distinction between linguistic and non-linguistic spatial representations: linguistic spatial representations rely on prototypes aligned with cardinal axes, while non-linguistic spatial representations rely on prototypes aligned with diagonal axes (Crawford et al., 2000).

Is it possible to reconcile these findings?

Clearly, Crawford et al.’s “different prototypes” account conflicts with Hayward and Tarr’s “same prototypes” account. Is it possible to reconcile these findings?

Table 1 shows a summary of the tasks used in these two studies. As can be seen, these studies used comparable linguistic tasks and comparable non-linguistic tasks. Table 1 also highlights, however, that both studies probed linguistic and non-linguistic representations at different phases of the task sequence. In the linguistic tasks used by Hayward and Tarr, participants were always asked about visible relations, while in their non-linguistic tasks, participants were asked about either immediate memory for spatial relations or delayed memory for spatial relations. Similarly, the linguistic task used by Crawford et al. probed immediate memory for spatial relations, while their non-linguistic task probed delayed memory for spatial relations.

Table 1.

Summary of tasks used in Hayward and Tarr (1995) and Crawford et al. (2000)

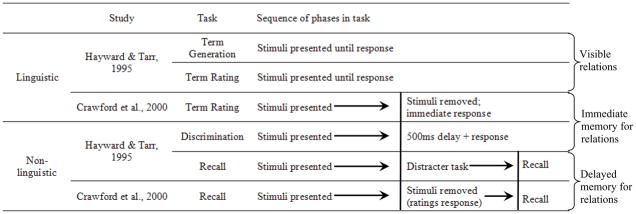The most direct comparison available in Table 1 is between the term rating task from Crawford et al. and the discrimination task from Hayward and Tarr. Both of these tasks probed immediate memory for spatial relations using a linguistic task in one case and a non-linguistic task in the other. Results from these two tasks were comparable: participants judged vertical relations to be most typical of “Above” and they were most accurate in the discrimination task when the target object was located near the vertical and horizontal axes. Thus, it appears that at least in immediate memory, linguistic and non-linguistic processes rely on the cardinal axes.

What about the spatial recall data central to Crawford and colleagues? In this task, participants’ responses were biased away from the cardinal axes and toward the diagonal axes after a memory delay. Unfortunately, the linguistic tasks used by Crawford et al. and Hayward and Tarr did not incorporate a memory delay; thus, we do not know whether biases in language might change over longer memory delays in a manner consistent with the observed spatial recall biases.

The goal of the present experiments was to examine this issue directly to reconcile the starkly different conclusions from these studies. In particular, we asked participants to complete the term rating task and the spatial recall task, but prompted them to respond either immediately after the display was removed or after a 10 s delay. The linguistic and non-linguistic spatial systems were thus both probed after stimulus removal and after the 10 s delay. This allowed us to directly compare linguistic and non-linguistic processes during identical phases in these tasks.

In addition to controlling when linguistic and non-linguistic systems were probed, we also asked participants to verbally count out loud until the response was prompted in both linguistic and non-linguistic tasks. This extra verbal load should prevent participants from forming a verbal response until the end of the delay period, but should minimally interfere with visual-spatial encoding of the spatial relation in the display (see e.g. Baddeley & Andrade, 2000; for related discussion of load effects on language processing, see also Just & Carpenter, 1992). Without this control, it would be possible for participants to form a verbal response when the depicted spatial relation is still visible and then simply draw on this information when later prompted to provide a delayed verbal response (see e.g. Brungart, Rabinowitz, & Durlach, 2000).

Predictions

What does this predict for immediate versus delayed responses in linguistic and non-linguistic tasks? Hayward and Tarr’s argument for shared representations predicts that linguistic and non-linguistic responses will exhibit similar time-dependent changes over delays. By contrast, according to Crawford et al. (2000), people use the cardinal axes as linguistic spatial prototypes and diagonal axes for non-linguistic spatial prototypes. As previously discussed, this claim has been formalized in the CA model (Huttenlocher et al., 1991; Huttenlocher, Hedges, & Vevea, 2000) which posits that at recall, people weight a fine-grained memory with the spatial prototype along the diagonal axis. This produces a bias away from the cardinal axes and toward the diagonal axes over delays. If, based on the generality of such categorical effects across domains (e.g. Hirtle & Jonides, 1985; Huttenlocher, Hedges, & Prohaska, 1988; Huttenlocher et al., 2000; Liberman, Harris, Hoffman, & Griffith, 1957), we assume that linguistic and non-linguistic prototypes are used in a comparable manner, the CA model predicts that spatial language ratings responses should be biased toward the cardinal axes after a memory delay.

Consider, for example, a delayed term rating task where participants are shown a target object 20° away from a vertical reference axis (0°). According to the CA model, people would first encode the fine-grained memory of the target at 20°. Consequently, at recall, it is adaptive to weight this degraded fine-grained memory with categorical information (Huttenlocher et al., 2000), in this case, the linguistic prototype at the vertical axis (0°). This would shift the recalled estimate toward the vertical axis (0°), for instance, to 15°. If we assume that participants transform this recalled estimate to a rating, then they should say that the target is a better example of an “Above” relation after a memory delay, (i.e. the remembered target value of 15° is a better example of “Above” than the encoded target value at 20°).

Experiment 1

The goal of the present study was to directly compare linguistic and non-linguistic processes when responses are probed immediately after the display is removed versus after a memory delay. We focused on two tasks used by Hayward and Tarr (1995) and Crawford and colleagues (2000): the term rating task and spatial recall. As in Crawford et al., we only probed participants rating of a single spatial preposition—”Above”. Because changes in spatial memory over delays between 0s and 20s have been most carefully studied by Spencer and colleagues (e.g. Schutte & Spencer, 2002, in press; Schutte, Spencer, & Schöner, 2003; Spencer & Hund, 2002, 2003), we opted to use the spatial recall task from Spencer and Hund (2002).

Note that participants in Spencer and Hund (2002) showed biases away from the vertical midline axis over delays, and these biases tapered off as targets approached ±90°. Although this is a departure from the pattern of recall biases reported by Crawford et al.—participants show biases toward the centers of left and right regions rather than toward the centers of each quadrant—the advantages of knowing how spatial recall changes over delay in the Spencer and Hund task outweighed this difference.

Method

Participants

Seventeen students from a large Midwestern University (8 females, 9 males; M age = 19.7 yr, SD = 1.7 yr) participated in exchange for course credit or payment. All were native speakers of English who reported having normal hearing and normal or corrected-to-normal vision. One participant repeatedly ignored the task instructions and was dropped from the experiment. All gave informed consent.

Apparatus and Materials

For all tasks, participants were seated at a large opaque table with a homogenous surface (79 cm (h) × 117 cm (w) × 127 cm (l)). Experimental sessions were conducted in a dimly lit room with black curtains covering all external landmarks. A curved border occluded the corners of the table (and therefore diagonal symmetry axes).

Three types of images were used on each trial: a single yellow reference disc (15 mm diameter) located along the vertical midline axis of the table and 30 cm away from the participant, a yellow three-digit number presented along the vertical midline axis of the table 46 cm from the participant, and a blue equilateral triangle “spaceship” (10 mm base). Stimuli were projected onto the surface of the table from below using a Sony VPL-PX LCD Projector.

Procedure

At the start of each trial, the yellow referent disc appeared at midline. Next, the participant moved a computer cursor to this reference disc using the mouse. A randomly chosen number between 100 and 500 then appeared and participants begin counting backwards from that number by 1s aloud. Next, a blue spaceship target appeared on the screen for two seconds. Participants were instructed to keep counting until prompted by a spoken stimulus to make one of two types of responses. On mouse trials, participants moved the mouse cursor to the remembered ship location when the computer said “Ready-Set-Go” and then clicked the mouse button. On spatial language rating trials, participants rated the extent to which the word “Above” described the spaceship’s location relative to the reference disc on a scale of 1 (“definitely not above”) to 9 (“definitely above”) when the computer said “Please give your “Above” rating.” After participants gave their response, all stimuli were removed from the screen and the next trial began.

Experimental Design

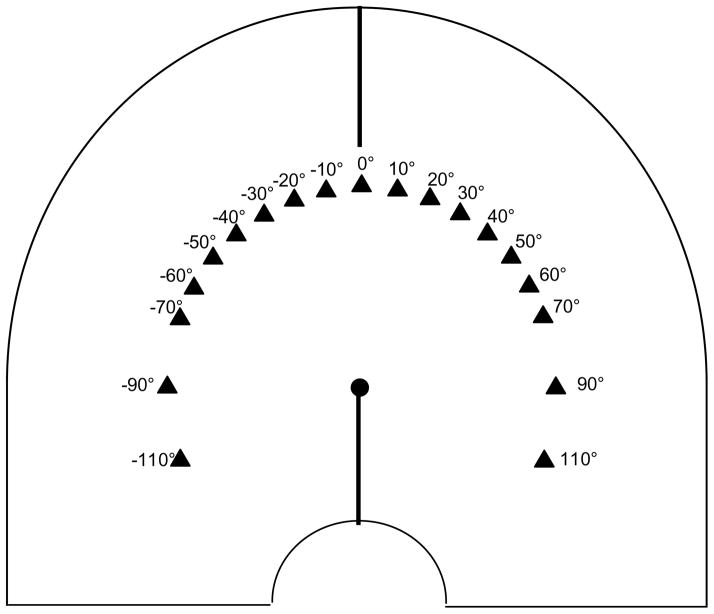
Each individual participated in 2 sessions. The types of experimental trials, mouse (Mouse) and spatial language ratings (Ratings), were randomly intermixed in both sessions. There were two within-subject factors: Target (19 target locations) and Delay (0s, 10s). For the Target factor, spaceships appeared at a constant radius of 15cm from the center of the reference disc at 19 different locations relative to the vertical midline axis (0°): every 10° from −70° to +70° as well as ±90° (see Figure 1). Targets at ±110° were also included to encourage use of the full ratings scale, but were excluded from the final analysis because the term “Above” is not applicable. Completion of the spoken stimulus indicating which response to provide (Ratings or Mouse) occurred at spaceship offset in the 0s Delay condition and 10s after spaceship offset in the 10s Delay condition.

Figure 1.

Target distributions for Experiments 1–3. The disk in the center of the work space corresponds to the yellow reference disk present throughout each trial in all experiments. The black lines along vertical midline axis of the task space depicts the additional perceptual structure used in the Enhanced Midline condition of Experiment 3. See text for additional details.

There were 3 observations for each of the 76 different trial types (2 responses × 2 Delays × 19 Targets) in each session resulting in 228 trials per session. Thirty-eight practice trials (19 Mouse, 19 Ratings) were included at the beginning of Session 1. Nineteen practice trials (9 Mouse/10 Rating or 10 Mouse/9 Rating) were presented in Session 2. Delay was randomized across practice trials.

Methods of Analysis

Directional errors (in °) for each Mouse trial were computed such that positive errors reflect errors in the direction away from the vertical midline. Responses to the same target at the same delay were then grouped together. Outliers (1.8%), defined as any directional errors exceeding the target group mean by 2 standard deviations or more were removed. We set the minimum group standard deviation to 5° and the maximum to 15°.

Ratings responses were recorded as the participant’s verbal rating which was typed into the computer by the experimenter. As with the Mouse responses, ratings to the same target at the same delay were grouped together. Outliers (0.4%), defined as ratings exceeding the target group mean by 2 standard deviations or more, were removed. We set the minimum group standard deviation to 1 and the maximum to 1.7. A ratings range less than 5 indicates a failure to comply with the instructions to use the entire 1–9 scale. Participant with this range were replaced in this and subsequent experiments. No such replacements were necessary in Experiment 1.

In addition to response means, we also analyzed Mouse and Ratings response variability (SD). In the domain of spatial recall, increases in response variability signal a decrease in the stability of spatial working memory (for discussion see Schutte & Spencer, in press). Measures of response variability thus provide an additional index of correspondence between non-linguistic and linguistic representational processes.

Results

Mouse Response Directional Error

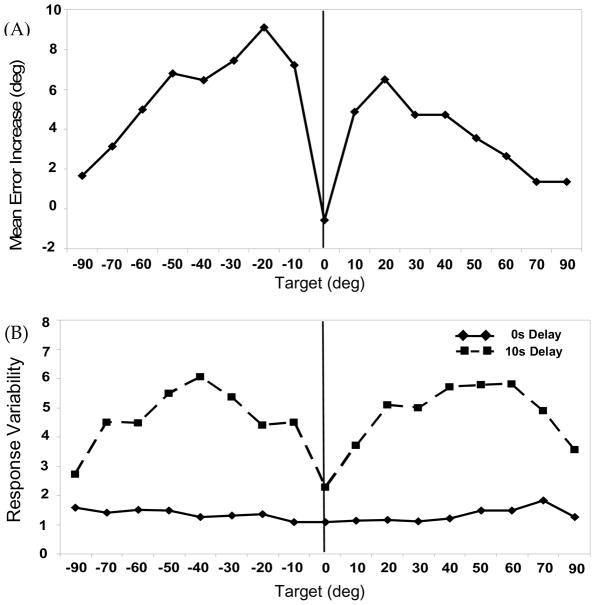
Responses on the 0s Delay trials were highly accurate, with mean directional errors between −.3° and 1.6° for all target locations (M = .79°, SE = .12°). The highly accurate 0s Delay responses contrast with the errors obtained for the 10s Delay trials (M = 5.26°, SE = .49°). Figure 2A displays this change in directional errors over delay as a difference score, computed by subtracting 0s Delay directional errors from 10s Delay directional errors. Consistent with previous research (see Spencer & Hund, 2002; Spencer & Hund, 2003), these difference scores take on a seagull-like shape with minimal bias over delay for the 0° target, increased bias over delay for targets to the left and right of midline, and then a gradual decline in bias over delay as the target locations approach ±90°.

Figure 2.

Experiment 1 Mouse results: (A) Increase in mean directional error over delay across target locations for Mouse trials. Increase in error was measured as 10s Delay mean error −0s Delay mean error. Positive values indicate error increases in the direction away from the vertical midline axis of the task space (solid vertical line in all figures); (B) Response variability (SD) across target locations for 0s Delay (solid line) and 10s Delay (dashed line) Mouse trials.

To analyze these data, we conducted a two-way ANOVA with Delay (0s, 10s) and Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°) as within-subjects factors. Results showed a significant effect of Delay, F(1,15) = 78.71, p < .001, η²_p = .84, and Target, F(16,240) = 11.42, p < .001, η²_p = .43, as well as a Delay × Target interaction, F(16,240) = 12.16, p < .001, η²_p = .45. To probe this interaction, we conducted a contrast analysis comparing the 0°, ±60°, ±70°, and ±90° target group with the ±10°, ±20°, ±30°, ±40°, and ±50° target group because previous work by Spencer and Hund (Spencer & Hund, 2002) has shown that changes in memory responses over delay are greatest for targets to the right and left of the vertical axes and lowest for targets along the vertical axis or near the horizontal axis (i.e., ±90°). Results of this contrast analysis established that targets to the right and left of midline (±10°, ±20°, ±30°, ±40°, and ±50°) did indeed exhibit greater error over delay than targets near the vertical or horizontal axis (0°, ±60°, ±70°, and ±90°), F(1,15) = 38.14, p < .001, η²_p = 72. This confirms that the seagull-like pattern of difference scores in Figure 2A is a statistically robust pattern.

Mouse Response Variability

Response variability (SD; Figure 2B) was quite low across targets in the 0s Delay condition (solid line; M = 1.34°, SE = .12°), consistent with the low mean directional error for these same responses. In contrast to 0s Delay performance, 10s Delay responses were highly variable (M = 4.66°, SE = .28°). Targets lying along the vertical (0°) and horizontal axes (±90°), however, exhibited markedly lower variability, again consistent with the lower directional errors associated with those targets.

To analyze these data, we conducted a two-way ANOVA with Delay (0s, 10s) and Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°) as within-subjects factors. Results showed a significant effect of Delay, F(1,15) = 224.37, p < .001, η²_p = .94, and Target, F(16,240) = 4.33, p < .001, η²_p = .22, as well as a Delay × Target interaction, F(16,240) = 4.44, p < .001, η²_p = .23. As above, we converted the response variability results to difference scores and conducted a contrast analysis comparing differences in variability over delay for targets to the left and right of midline (±10°, ±20°, ±30°, ±40°, and ±50°) to targets near the horizontal and vertical axes (0°, ±60°, ±70°, and ±90°). Results showed that targets to the right and left of midline exhibited a significantly greater increase in response variability over delay relative to targets near the cardinal axes, F(1,15) = 16.94, p = .001, η²_p = .53.

Spatial Language Ratings

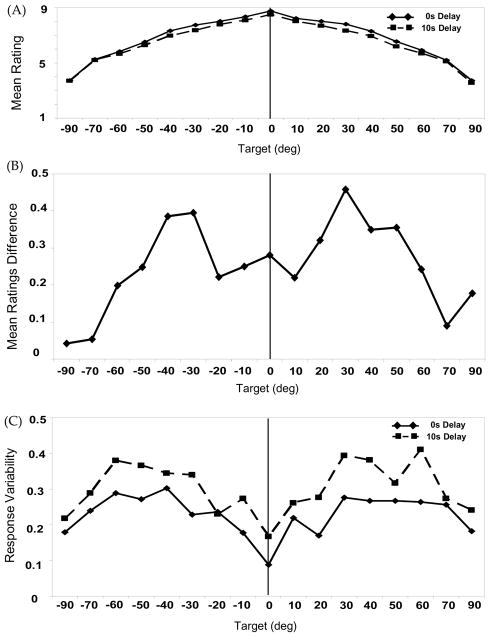
Figure 3A shows the ratings performance for the 0s and 10s Delay condition across the 17 target locations. As in previous studies (e.g. Crawford et al., 2000; Hayward & Tarr, 1995; Logan & Sadler, 1996), “Above” ratings were highest for targets aligned with the vertical midline axis and gradually decreased as targets were moved away from this axis. Note, however, that the 10s Delay ratings are generally lower than those for the 0s Delay condition. The difference scores in Figure 3B (mean 0s Delay ratings condition – mean 10s Delay ratings) further bear this out, revealing a uniformly positive, seagull-like pattern that reflects a general mean ratings decrease for the 10s Delay trials.

Figure 3.

Experiment 1 Ratings results: (A) Mean ratings for the 0s (solid line) and 10s Delay (dashed line) conditions (B) Reduction in mean “Above” ratings across target locations (0s Delay mean rating −10s Delay mean rating). (C) Mean “Above” ratings variability (SD) for 0s Delay (solid line) and 10s Delay (dashed line) conditions.

We analyzed these data in a two-way ANOVA with Delay (0s, 10s) and Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°) as within-subjects factors. Results showed a significant effect of Delay, F(1,15) = 20.79, p < .001, η²_p = .58, and Target, F(16,240) = 108.93, p < .001, η²_p = .88. The Delay × Target interaction was not significant, F(16,240) = 1.14, p = .32, η²_p = .07. Thus, ratings responses differed according to the target location but, most importantly, decreased significantly over delay consistent with the proposal that linguistic and non-linguistic systems share common time-dependent processes.

Spatial Language Ratings Variability

Figure 3C shows ratings variability (SDs) for 0s Delay (M = .45, SE = .05) and 10s Delay (M = .6, SE = .06) trials. Overall, ratings responses produced in the 10s delay condition showed higher variability than those produced in the 0s Delay condition. This delay-dependent increase in ratings variability corresponds to the decrease in mean ratings over delay as well as the delay-dependent increase in response variability for the Mouse trials.

We analyzed these data in a two-way ANOVA with Delay (0s, 10s) and Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°) as within-subjects factors. Results showed a significant effect of Delay, F(1,15) = 30.38, p < .001, η²_p = .67, and Target, F(16,240) = 5.22, p < .001, η²_p = .26. The Delay × Target interaction was not significant, F(16,240) = 1.08, p = .38, η²_p = .07. These results show a clear increase in ratings variability over delay, consistent with the proposal that linguistic and non-linguistic systems share common time-dependent representational processes.

Discussion

Results from the Mouse trials were consistent with previous work showing delay-dependent bias away from the vertical axis for targets to the left and right of this axis (Simmering & Spencer, 2007; Spencer & Hund, 2002, 2003). The delay-dependent increase in Mouse response variability also replicates previously obtained results (Schutte & Spencer, in press; Spencer & Hund, 2002). The most important finding, however, was the delay-dependent decrease in mean Ratings and the associated delay-dependent increase in Ratings variability (see also Lipinski, Spencer, & Samuelson, in press). By probing linguistic and non-linguistic information during the same phases of a trial, that is, immediately or after a delay, we see that these two systems show corresponding delay-dependent biases. Thus, probes of linguistic representations immediately after target disappearance are not directly comparable to probes of non-linguistic representations after a memory delay. This qualifies the conclusions reached by Crawford et al. (see Table 1)—one cannot claim that linguistic and non-linguistic systems rely on different spatial prototypes using their task because linguistic and non-linguistic responses were not probed during the same task phase.

Experiment 2

Experiment 1 suggests that linguistic and non-linguistic spatial cognition share time-dependent processes. It is possible, however, that to cope with the response uncertainty created by our randomization procedure, people may have relied on one type of prototypical representation—the non-linguistic prototypes—in both tasks. Experiment 2 tests this possibility using a blocked design that eliminated response uncertainty.

If the time-dependent correspondence between linguistic and non-linguistic responses was simply an artifact of response uncertainty, then blocking response type by session should eliminate the common delay-dependent effects across tasks. In particular, if participants can rely on separate prototypes in each task—a linguistic prototype along the vertical axis in the ratings task and non-linguistic prototypes at the centers of the left and right regions in the mouse task—then participants performing only the ratings task during the first session (who are therefore naïve to the mouse task) should show a delay-dependent increase in mean ratings, that is, a bias toward the vertical axis. If, however, we observe the opposite—a delay-dependent decrease in ratings in session 1—then this would buttress the claim that linguistic and non-linguistic spatial cognition rely on shared, time-dependent representational processes.

Method

Participants

Twenty-four students from a large Midwestern University (14 females, 10 males; M age = 21.9 yr, SD = 4.3 yr) participated in exchange for course credit or payment. All other participant specifications were the same as in Experiment 1.

Apparatus, Materials, and Procedure

The apparatus, materials, and procedure were the same as in Experiment 1.

Design

Each individual participated in 2 sessions and sessions were blocked by response type (Ratings or Mouse). Participants were randomly assigned to either the Ratings First or the Mouse First condition. Target location (19 targets; see Figure 1) and Delay (0s, 10s) were randomly varied within-subjects as in Experiment 1. There were a total of 6 observations for each of the 38 different response types (2 Delays × 19 Targets) per session. Each participant completed 19 practice trials at the beginning of the session and delay was randomized.

Methods of analysis

The methods of analysis for the mouse and ratings trials were identical to those of Experiment 1. Outliers composed 1.2% of the Mouse trials and 0.6% of the ratings trials.

Results

Mouse Response Directional Error

Figure 4A shows directional difference scores across delays for responses on the Mouse trials.

Figure 4.

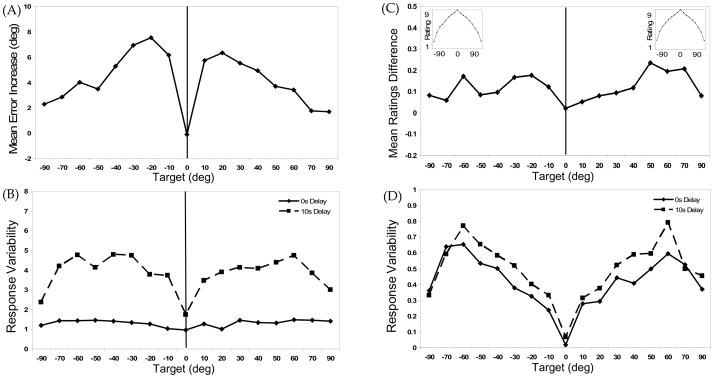
Experiment 2 results: (A) Increase in mean directional error over delay across target locations for Mouse trials (10s Delay mean error −0s Delay mean error). Positive values indicate error increases in the direction away from the vertical midline axis of the task space (solid vertical line in all figures); (B) Response variability (SD) across target locations for 0s Delay (solid line) and 10s Delay (dashed line) Mouse trials; (C) Reduction in mean “Above” ratings across target locations (0s Delay mean rating −10s Delay mean rating). The insets shows the prototypical ratings gradient obtained in the 0s Delay condition for the Ratings First (left) and the Mouse First (right) conditions; (D) Mean “Above” response variability (SD) for 0s Delay (solid line) and 10s Delay (dashed line) conditions.

We analyzed performance using a two-way ANOVA with Delay (0s, 10s) and Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°) as within-subjects factors. This analysis yielded significant effects for both Delay F(1,23) = 53.08, p < .001, η²_p = .7, and Target, F(16,368) = 8.64, p < .001, η²_p = .27, as well as the Delay × Target interaction, F(16,368) = 10.67, p < .001, η²_p = .32. A contrast analysis (±10°, ±20°, ±30°, ±40°, ±50° vs. 0°, ±60°, ±70°, ±90°) indicated that responses to targets to the right and left of midline displayed significantly more directional error over delay than targets near the cardinal axes, F(1,23) = 49.37, p < .001, η²_p = .68. These results replicate the delay-dependent biases from Experiment 1.

Mouse Response Variability

Figure 4B shows response variability in the Mouse task. We analyzed these data using a two-way ANOVA with Delay (0s, 10s) and Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°) as within-subjects factors. There were significant effects of Delay, F(1,23) = 352.47, p < .001, η²_p = .94, and Target, F(16,368) = 8.35, p < .001, η²_p = .27, as well as a significant Delay × Target interaction, F(16,368) = 4.98, p < .001, η²_p = .18. A contrast analysis (±10°, ±20°, ±30°, ±40°, ±50° vs. 0°, ±60°, ±70°, ±90°) once again indicated that targets to the right and left of midline displayed more response variability over delay than targets near the cardinal axes, F(1,23) = 13.38, p = .001, η²_p = .37.

Spatial Language Ratings

The insets of Figure 4C shows the Ratings performance from the 0s Delay condition for the session 1 ratings group (left) and the session 2 ratings group (right). The primary graph in Figure 4C displays the ratings difference scores across delays. Analysis of mean ratings in a two-way ANOVA with Delay and Target as within-subjects factors confirmed significant effects of Delay, F(1,23) = 7.48, p = .01, η²_p = .25 and Target, F(16,368) = 210.36, p < .001, η²_p = .90. This replicates the delay-dependent ratings decrease observed in Experiment 1.

Spatial Language Ratings Variability

Figure 4D shows response variability on the ratings trials. Results of a two-way ANOVA with Delay and Target as within-subjects factors showed significant effects of Delay, F(1,23) = 21.31, p < .001, η²_p = .48 and Target, F(16,368) = 11.32, p < .001, η²_p = .33. This replicates results from Experiment 1 and is again consistent with the delay-dependent increase in response variability observed on the Mouse trials.

Planned Comparisons

To directly test whether the Ratings “drift” in Experiment 1 was caused by response uncertainty we conducted a set of planned comparisons analyzing Ratings responses for those in the Ratings First group. These participants had no knowledge of the Mouse task until session 2.

Mean ratings were analyzed in a two-way ANOVA with Delay and Target as within-subjects factors. This analysis yielded a significant Delay effect, F(1,11) = 5.1, p = .046, η²_p = .32, with the 10s Delay ratings (M=6.1, SD=.29) lower than the 0s Ratings (M=6.27, SD=27). This decrease in ratings over delay indicates that the Experiment 1 ratings results were not an artifact of response uncertainty. The ANOVA also yielded a significant Target effect, F(16,176) = 115.97, p < .001, η²_p = .92, that reflected the canonical ratings gradient discussed above. Ratings variability was analyzed in a two-way ANOVA with Delay and Target as within-subjects factors. This analysis yielded significant effects of Delay, F(1,11) = 16.29, p = .002, η²_p = .6, and Target, F(16,176) = 5.4, p < .001, η²_p = .33, with the variability increasing over delay (0s: M=.46, SD=.05; 10s: M=.56, SD=.06). This result is again consistent with Experiment 1.

Discussion

Experiment 2 blocked response types by session to test whether the delay-dependent effects on spatial language ratings in Experiment 1 were caused by response uncertainty. Results replicated the decrease in ratings over delay as well as the increase in ratings variability over delay, even for participants completely naïve to the Mouse task. These findings rule out the possibility that participants used only the non-linguistic prototypes in the task to contend with response uncertainty. They also highlight, once again, that comparisons of linguistic responses generated immediately after the display is removed are not directly comparable to non-linguistic responses generated after an extended memory delay (see Table 1).

Experiment 3

Experiments 1 and 2 reveal remarkable consistency in delay-dependent effects across the linguistic and non-linguistic spatial tasks. It is possible, however, that the insertion of the delay into the ratings task might simply cause a general degradation in ratings performance, yielding lower ratings (a form of regression to the mean) and higher variability. The link between linguistic and non-linguistic systems in the present report would be more compelling if we could manipulate a factor known to influence non-linguistic spatial memory and show that it has a predictable effect on linguistic ratings. A recent finding from our laboratory provides one way to achieve this goal.

Spencer and colleagues (Schutte & Spencer, 2009; Simmering & Spencer, 2009) have demonstrated that enhanced perceptual structure along the vertical midline axis reduces delay-dependent biases in spatial recall. In the present study, we enhanced the salience of the vertical axis by adding two lines along the midline of the table (see Materials and Figure 1). Increasing the perceptual salience of the vertical midline axis should reduce delay-dependent spatial memory biases. If linguistic and non-linguistic spatial cognition share a set of time-dependent representational processes, then the magnitude of the delay-dependent ratings effect should also be reduced.

Method

Participants

Forty-eight students from a large Midwestern University (24 Mouse only, 24 Ratings only; 29 females, 19 males; M age = 20.8 yr, SD = 4.7 yr) participated in exchange for course credit or payment. All were native speakers of English who reported having normal hearing and normal or corrected-to-normal vision. Two participants with a ratings range of less than 5 were replaced. A third participant was removed from the analyses for failing to fully engage in the task. A total of 23 participants were therefore included in the Ratings analyses and 24 participants for the Mouse analyses.

Materials and Apparatus

The materials and apparatus for the Standard Midline trials were identical to those of Experiments 1 and 2. Enhanced Midline trials were also identical to those Experiments 1 and 2 with one exception: two green vertical lines aligned with the midline symmetry axis were added to the display, providing enhanced perceptual structure along this axis. The first green line was 5 mm wide and 21 cm long, extending from the bottom edge of the table (the edge closest to the participant) to the bottom edge of the reference disc. The second green line, also 5 mm wide, began 30 cm above the reference disc and extended 36 cm to the top of the table (away from the participant). The gap in the line permitted us to enhance the midline without interfering with target presentations.

Design

Participants were randomly assigned to either the Mouse condition or the Ratings condition. Six trial blocks were presented to each participant (3 Enhanced, 3 Standard) with the midline structure alternating each block. Block order was counterbalanced across subjects. Target and Delay were randomly intermixed within each block. We presented each non-midline target at each delay one time within each experimental block. In addition, midline (0°) targets were presented twice at each delay within each block. to permit the calculation of response variability collapsing across targets equidistant from midline on the left and right sides (e.g., ±10°). Due to baseline differences in variance to the left and right of midline, however, we did not conduct analyses of response variability.

Two short practice blocks were completed before the experimental trials, one for each Midline condition. The number of targets presented within a single practice block (9 or 10) was counterbalanced across subjects and Delay was randomized.

Procedure

The procedure was identical to that of Experiments 1 and 2 with one exception. Rather than having participants look back at the reference disc during the 10s delay, participants were instead instructed to look up from the display table and subsequently reorient themselves to the task space when they heard the response prompt. This was done to maintain consistency with the procedure used in Simmering and Spencer (2009).

Methods of analysis

Mouse directional errors were coded in the same manner as Experiments 1 and 2. Because of the limited number of observations per cell (3 trials), responses to the same target within the same Midline condition, collapsing across Delay, were grouped together when determining outliers. Ratings responses were grouped in the same manner. All other outlier procedures were identical to those of Experiments 1 and 2. Outliers composed 5.6% of the Mouse trials and 1.1% of the Ratings trials.

Results

Mouse Response Directional Error

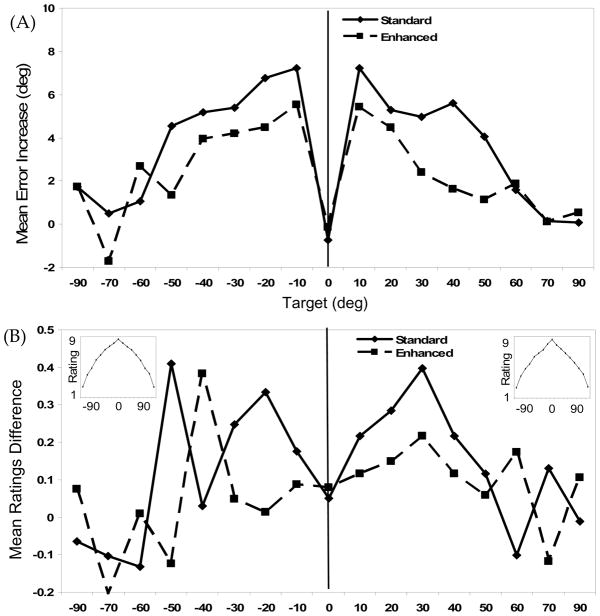
Figure 5A shows difference scores (10s Delay – 0s Delay) for the Enhanced and Standard Midline conditions at each target. Results of a three-way ANOVA with Delay (0s, 10s), Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°, 0°), and Midline (Standard, Enhanced) as within-subjects factors yielded significant main effects of Midline, F(1,23) = 11.72, p = .002, η²_p = .34, Delay, F(1,23) = 57.35, p < .001, η²_p = .71, and Target, F(16,368) = 11.99, p < .001, η²_p = .34. We also obtained significant Midline × Delay, F(1,23) = 11.51, p = .003, η²_p = .33, Midline × Target, F(16,368) = 2.8, p < .001, η²_p = .11, and Delay × Target, F(16,368) = 12.55, p < .001, η²_p = .35, interactions. These effects were subsumed by a Midline × Delay × Target interaction, F(16,368) = 2.09, p = .008, η²_p = .08.

Figure 5.

Experiment 3 results: (A) Increase in mean directional error over delay across target locations for Mouse trials in the Standard (solid line) and Enhanced (dashed line) midline conditions. Positive values indicate error increases in the direction away from the vertical midline axis of the task space (solid vertical line in all figures); (B) Reduction in mean “Above” ratings across target locations, measured as the 0s Delay mean rating −10s Delay mean rating, for the Standard (solid line) and Enhanced (dashed) midline condition. The insets show the prototypical ratings gradient obtained in the 0s Delay condition for the Standard (left inset) and Enhanced (right inset) midline conditions.

Two contrast analyses analogous to those in Experiments 1 and 2 examined this interaction in detail. In the first contrast analysis, we compared directional difference scores for targets to the left and right of midline (±10°, ±20°, ±30°, ±40°, ±50°) across the Enhanced and Standard conditions. We expected the enhanced perceptual structure to significantly alter difference scores for this target grouping. Results showed a significant reduction in difference scores for the ±10° to ±50° target set in the Enhanced Midline condition relative to the Standard Midline condition, F(1,23) = 27.86, p < .001, η²_p = .55. Examination of mean errors in the Standard condition for this target set across delays showed an increase in directional error of 5.62°. By contrast, directional error for the Enhanced condition showed an increase of only 3.46°. The enhanced perceptual structure along the midline therefore reduced delay-dependent drift by 38% for this target set.

In the second contrast analysis, we compared directional difference scores across conditions for the targets near the cardinal axes (0°, ±60°, ±70°, ±90°). Given the smaller delay-dependent errors for this target set, we did not expect the enhanced perceptual structure to significantly alter difference scores for this target grouping. As expected, there was no significant change in difference scores across conditions for this target set, F(1,23) = .065, p = .8, η²_p = .003. Overall, then, results from Mouse trials reveal a significant reduction in delay-dependent drift in the Enhanced condition that was isolated to the ±10° to ± 50° target set.

Spatial Language Ratings

The insets in Figure 5B show the 0s Delay ratings for the Standard (left inset) and Enhanced (right inset) Midline conditions, indicating that the canonical ratings gradients were obtained in both conditions. The primary plot in Figure 5B shows ratings difference scores across target locations for each Midline condition. Although these difference scores are clearly variable across targets, difference scores in the Standard condition were higher than difference scores in the Enhanced condition for 9 of the 10 targets in the critical ±10° to ± 50° target range, suggesting a general reduction of the delay-dependent ratings effect in the Enhanced Midline condition.

A three-way ANOVA with Delay (0s, 10s), Target (±90°, ±70°, ±60°, ±50°, ±40°, ±30°, ±20°, ±10°,0°), and Midline (Standard, Enhanced) as within-subjects factors yielded significant main effects of Midline, F(1,22) = 13.27, p = .001, η²_p = .38, Delay, F(1,22) = 7.27, p = .013, η²_p = .25, and Target, F(16,352) = 233.54, p < .001, η²_p = .91. There were also significant Midline × Target, F(16,352) = 3.07, p < .001, η²_p = .12, and Delay × Target, F(16,352) = 2.22, p = .005, η²_p = .09 interactions. These effects were subsumed by a significant Midline × Delay × Target interaction, F(16,352) = 2.87, p,< .001, η²_p = .12.

We examined this interaction in greater detail using the same two contrast analyses discussed above. For the ±10° to ±50° target set, the Enhanced Midline (M=.11 SE=.06) ratings difference scores were substantially (54%) and significantly lower than those for the Standard Midline condition (M=.24 SE=.06), F(1,22) = 8.80, p = .007, η²_p = .29. This was not the case, however, for targets close to the cardinal axes (0°, ±60°, ±70°, ±90°), F(1,22) = 2.35, p = .14,, η²_p = .1. Thus, the enhanced perceptual structure along the vertical midline axis reduced delay-dependent ratings drift only for targets in the ±10° to ±50° range—precisely the same reduction effect observed on Mouse trials.

Discussion

Overall, results from the present experiment showed robust overlap between performance in the Enhanced and Standard Midline conditions across linguistic and non-linguistic tasks. In particular, ratings results across conditions mirrored results from the Mouse task, exhibiting a reduction in delay-dependent effects in the Enhanced condition only for targets to the right and left of midline. This isolation of the enhanced midline effect to the same targets across tasks strongly suggests that perceived reference axes are used in a similar, time-dependent manner in both the linguistic and non-linguistic tasks probed here. These findings provide additional evidence that linguistic and non-linguistic spatial cognition depend on shared, time-dependent processes.

General Discussion

One of the key questions to emerge from the spatial cognition literature (for reviews see Levinson, 2003; van der Zee & Slack, 2003) is whether linguistic and non-linguistic spatial behaviors depend on shared or distinct representational processes. The goal of the present paper was to reconcile the contradictory conclusions from two landmarks studies, one (Hayward & Tarr, 1995) arguing for shared processes, the other (Crawford et al., 2000) for distinct processes. To this end, we noted that the tasks in these studies tapped the linguistic and non-linguistic spatial systems in different phases (see Table 1). Based on this summary, we suggested that the contradictory claims in the literature might be reconciled if linguistic and non-linguistic processes were probed at the same experimental phases—immediately after the display is removed and following a 10 s delay. Moreover, we were able to generate precise predictions from the Category Adjustment model (Huttenlocher et al., 1991) which Crawford et al. used to interpret their results.

Results across Experiments 1–3 were consistent—in all cases, linguistic and non-linguistic biases showed surprisingly similar delay effects. Experiment 1 first showed a significant delay-dependent decrease in mean ratings and the associated delay-dependent increase in ratings variability, effects analogous to those for the non-linguistic spatial recall task. Experiment 2 showed that these analogous delay-dependent effects arise even when the tasks were performed in different sessions and, most tellingly, replicated the delay-dependent ratings effect for those naïve to the non-linguistic task. This rules out the possibility that the Experiment 1 results arose from an artificial reliance on non-linguistic prototypes due to response uncertainty. Finally, in Experiment 3, we probed the robustness of this link between the linguistic and non-linguistic spatial systems, showing that additional perceptual structure along the vertical axis reduced delay-dependent effects in both tasks. Critically, the effects of this change were isolated to the same subset of target locations across the tasks.

These data support our concern about the comparison of linguistic and non-linguistic systems at different phases of a trial. This is a critical methodological point that tempers conclusions from previous studies that have examined the relation between linguistic and non-linguistic representational processes. Our data show that one cannot compare linguistic responses using visible relations or immediate memory to non-linguistic responses given after a memory delay.

Beyond this methodological point, our data have implications for the general question addressed by previous studies. Most directly, our results are not consistent with the claim by Crawford et al. that linguistic and non-linguistic systems rely on different spatial prototypes. A central concept of the CA model is that recall responses reflect a weighting process at recall. Thus, even if linguistic and non-linguistic systems must use the same fine-grained memory under both immediate and memory conditions because that is the only location information currently available, the response at the moment of estimation should nonetheless be biased in the direction of the relevant spatial prototype—toward cardinal axes in linguistic tasks and toward the centers of spatial regions in non-linguistic tasks. The absence of this effect falsifies this claim.

By contrast, our data appear to be more consistent with arguments from Hayward and Tarr (1995) favoring shared representational processes. Nevertheless, their account does not explain the source of location memory biases away from the vertical axis in the non-linguistic task—the very data explained by the CA model.

How, then, do we explain our data? As a first step, consider our data outside the scope of the debate in the literature. In our task, participants were forced to rely on a common memory of the target location when generating either the linguistic or non-linguistic response at the ‘go’ signal. This makes intuitive sense because, after all, what else can the sensori-motor and linguistic systems use except a memory of the target location? This intuition was the starting point for our application of the CA model as well—we assumed that people must use a fine-grained memory of the target in both cases, but that they weighted this memory with different, task-dependent prototypes. Our results suggest that this latter claim requires closer examination.

A different spatial memory model—the Dynamic Field Theory of spatial cognition (Schutte & Spencer, in press; Simmering, Schutte, & Spencer, 2008; Simmering & Spencer, 2008; Simmering, Spencer, & Schöner, 2006; Spencer, Simmering, Schutte, & Schöner, 2007)—provides a useful context for this reevaluation. The DFT (Erlhagen & Schöner, 2002) is a formalized, time-dependent process model based on principles of neural population dynamics (Amari, 1977; Schöner, 2008; Wilson & Cowan, 1972). According to the DFT, perceptually-based reference frames such as the vertical symmetry axis (e.g. Palmer & Hemenway, 1978; Wenderoth, 1994) serve as a source of input into the system. Although this reference-related activation is hypothesized to support the coordination of spatial information across differing reference frames (e.g. between a retinotopic and an object-centered frame; for further development of these ideas see especially Spencer et al., 2007), this reference-related activation can also bias location memories away from this reference axis over delays (for extensive discussion of these and related processes in the DFT see Schutte & Spencer, in press; Simmering et al., 2008; Simmering & Spencer, 2008; Simmering et al., 2006; Spencer et al., 2007).

The critical point for our current purposes is that non-linguistic memory biases like those found in Experiments 1–3 are biases away from the cardinal axes, not biases towards a prototype at the centers of the left and right regions. Characterizing non-linguistic memory biases as reflecting spatial “drift” away from the vertical midline symmetry axis provides for a consistent account of delay-dependent ratings effects because non-linguistic spatial memory and spatial language can both be anchored to the same representational structure, namely, the cardinal axes in the local workspace. Moreover, both systems can rely on the same actively maintained working memory for the target location. By this view, then, perceptual and time-dependent processes that alter non-linguistic recall performance should likewise shape linguistic ratings. This conceptualization is congruent with the delay-dependent ratings effects established in our experiments, most notably, the target-specific reduction of effects in Experiment 3. Although future research will need to fully explore how the DFT can capture ratings data, initial work in this direction integrating connectionist-style, localist spatial term representations is promising (Lipinski, Spencer, & Samuelson, 2009; Lipinski et al., in press). The DFT account of spatial working memory therefore not only explains the non-linguistic delay-dependent drift away from the vertical axis without recourse to prototypes but also provides the basis for integrating spatial language behaviors in a manner consistent with our findings.

Conclusion

Our work shows how analogous delay-dependent biases in both spatial language and spatial memory can emerge without positing differing prototypes for the differing systems, reconciling two prominent but conflicting accounts of representational processes in spatial cognition (Crawford et al., 2000; Hayward & Tarr, 1995). By establishing delay-dependent changes in spatial language with the context of the DFT, the present work takes an early but promising step towards an expanded theoretical framework integrating linguistic and non-linguistic spatial processes.

In doing so, we also draw attention to two key insights. The first is that probes of linguistic and non-linguistic systems must be comparable across tasks to assess the underlying representational processes. Second, linguistic and non-linguistic spatial processes appear to travel together through time from immediate to delayed memory conditions. Given the frequent dependence of spatial language on remembered rather than visible spatial relations, our findings directly address how spatial memory processes may be brought to bear on spatial communication in the real world.

These observations give rise to a host of novel questions. For example, how is this relationship influenced by processes occurring over the longer time scales of learning and development? If spatial language representations are tied to spatial working memory processes, might spatial language also influence spatial working memory? Clearly, substantial empirical and theoretical work remains before we can answer such questions. The present work, however, suggests that an emphasis on the fine-grained shifts of linguistic and non-linguistic behaviors over time can provide a new and useful tool for addressing these bigger questions and resolving outstanding conflicts in the literature.