Identity-by-descent filtering of exome sequence data for disease–gene identification in autosomal recessive disorders

Abstract

Motivation: Next-generation sequencing and exome-capture technologies are currently revolutionizing the way geneticists screen for disease-causing mutations in rare Mendelian disorders. However, the identification of causal mutations is challenging due to the sheer number of variants that are identified in individual exomes. Although databases such as dbSNP or HapMap can be used to reduce the plethora of candidate genes by filtering out common variants, the remaining set of genes still remains on the order of dozens.

Results: Our algorithm uses a non-homogeneous hidden Markov model that employs local recombination rates to identify chromosomal regions that are identical by descent (IBD = 2) in children of consanguineous or non-consanguineous parents solely based on genotype data of siblings derived from high-throughput sequencing platforms. Using simulated and real exome sequence data, we show that our algorithm is able to reduce the search space for the causative disease gene to a fifth or a tenth of the entire exome.

Availability: An R script and an accompanying tutorial are available at http://compbio.charite.de/index.php/ibd2.html.

Contact: peter.robinson@charite.de

1 INTRODUCTION

The identification of genes underlying Mendelian disorders for the past several decades has mainly proceeded by means of positional cloning to identify chromosomal linkage intervals followed by the sequencing of candidate genes (Collins, 1995). Efforts at disease-gene identification involving linkage analysis or association studies usually result in a genomic interval of 0.5–10 cM containing up to 300 genes (Botstein and Risch, 2003). Although computational methods can be used to prioritize candidate genes (Köhler et al., 2008), sequencing large numbers of candidate genes remains a time consuming and expensive task, and it is often not possible to identify the correct disease gene by inspection of the list of genes within the interval. Recently, whole-exome sequencing, i.e. the targeted capture of protein coding exons followed by massively parallel, ‘next-generation’ sequencing (NGS), has been demonstrated as an effective approach to identify genes underlying Mendelian disorders using a small number of affected individuals (Biesecker, 2010).

Sequenced individuals typically have on the order of five to ten thousand variant calls representing either non-synonymous substitutions in protein coding sequences, alterations of the canonical splice-site dinucleotides or small indels (NS/SS/I) (Gilissen et al., 2010; Ng et al., 2009; Rios et al., 2010). Even after filtering out common variants using data from dbSNP, the HapMap project and related resources such as the 1000 Genomes project, the number of potentially disease-causing NS/SS/I variants can remain high if the exome of a single patient is considered in isolation. Many disease-causing mutations were completely unsuspected on the basis of previous knowledge (Altshuler et al., 2008), and software tools that aim at predicting the damaging effect of non-synonymous variants (Adzhubei et al., 2010; Kumar et al., 2009; Schwarz et al., 2010; Sunyaev et al., 2001) are currently unable to reliably distinguish between disease-causing mutations and other variants.

Groups who have performed disease–gene identification projects by exome sequencing (Choi et al., 2009; Hoischen et al., 2010; Ng et al., 2009, 2010b) have developed analysis strategies based upon searching for potentially damaging rare variants found in the same gene in sets of multiple unrelated patients affected by the same Mendelian disorder. Although this strategy has been applied successfully in sequencing projects with two affected individuals (Gilissen et al., 2010; Lalonde et al., 2010) and occasionally even with a single affected individual (Pierce et al., 2010; Rios et al., 2010), in many cases multiple candidate genes remain after applying computational filters based on rarity or presence of a mutation in multiple affected patients (Hoischen et al., 2010; Ng et al., 2009, 2010a, b). This means that additional analysis of multiple candidate genes or other procedures would often be needed to identify the disease gene following exome sequencing of single families with a Mendelian disorder.

We will refer to the above-described procedure for searching for a disease gene by exome sequencing in multiple unrelated patients as the ‘intersection’ approach. Although the intersection strategy has been useful in identifying Mendelian disease genes in the studies cited above, it is not always applicable. Many of the thousands of Mendelian disorders listed in OMIM, whose genetic basis is unknown, are often only clinically well characterized in members of a single family. Obviously, a filtering approach that focuses on genes that are affected by variants in which multiple unrelated patients harbor potential disease-causing mutations (Hoischen et al., 2010) is unsuitable. Rather, linkage analysis (Botstein et al., 1980; Lander and Green, 1987) has proved to be the method of choice that led to most of the disease–gene discoveries in such cases, and more recently linkage analysis including homozygosity mapping has been combined with NGS approaches to identify disease genes (Bilgüvar et al., 2010; Johnston et al., 2010; Nikopoulos et al., 2010; Rehman et al., 2010; Sun et al., 2010; Volpi et al., 2010; Walsh et al., 2010). However, existing tools for linkage analysis require pedigree data over at least two generations and are not optimized for the relatively high error rates of variant calls in NGS data.

In this work, we describe a procedure for efficiently filtering exome sequencing data obtained from two or more affected siblings with an autosomal recessive Mendelian disorder based upon the identification of chromosomal regions identical by descent (IBD) in the presence of noisy sequence data. In consanguineous families, affected individuals share two IBD haplotypes inherited from a single common ancestor. The disease gene is located somewhere within the IBD haplotype block, which is the basis of homozygosity mapping (Lander and Botstein, 1987). In the general case in which the parents are not consanguineous, each affected person inherits the same haplotype from each parent. That is, although the maternally and parentally inherited haplotypes surrounding the disease gene may differ from one another, each affected person inherits a maternal and a paternal haplotype that are IBD to the maternal and paternal haplotypes in other affected siblings. We will refer to the intersection between the maternal and paternal IBD haplotypes among all affected individuals in a family as an IBD = 2 region. We note that the disease gene must be located within an IBD = 2 region, but that affected siblings may also share other IBD = 2 regions by chance. Our method can be used to identify the chromosomal regions that are compatible with the inheritance patterns of a recessive monogenic disorder and can be combined with previous methods for filtering out common variants and for predicting potentially pathogenic sequence changes using computational tools. This approach was first successfully used in identifying PIGV as the disease gene in Hyperphosphatasia with Mental Retardation (HPMR) syndrome (Krawitz et al., 2010).

We will use simulated exome datasets as well as real exome datasets to show that our method can efficiently reduce the number of candidate mutations in exome sequencing projects comprising more than one affected sibling and additionally to identify chromosomal positions with a high probability of false variant calls. The article is structured as follows: we will first describe in detail the algorithm used to classify a genomic position as either IBD = 2 or IBD ≠ 2. We will derive a posterior probability that indicates how likely the classification of a position is to be correct under the assumptions of our model. Based on simulated data, we trained the classifier to a false negative classification error rate of less then 0.01. Finally, we classified three exome triplets into IBD = 2 and analyzed a subset of genomic locations that showed a conflict in IBD = 2 classification and variant calls. By validating this subset, we show that candidate locations can be identified using IBD = 2 classification that would otherwise have been lost by mere intersection filtering.

2 METHODS

In autosomal recessive disorders, all affected children share two haplotypes that are identical by descent (IBD = 2). We model the exome sequencing results using a hidden Markov model (HMM), in which the meiotic process yielding individual genomes is statistically modeled as a Markov process. The goal of HMMs is to predict the most likely sequence of hidden states that best explain the observed data (Fig. 1A). Here, we use an HMM to predict the most likely sequence of IBD = 2 and IBD ≠ 2 states in chromosomal segments on the basis of the observed exome sequences of two or more persons affected with a Mendelian disease. We note that the algorithm described here is an enhanced version of the algorithm recently used by our group to identify the disease gene in HPMR (Krawitz et al., 2010). For simplicity, we will describe the algorithm in terms of the affected siblings of unrelated parents, but note that the algorithm is equally applicable to more complex pedigrees in which multiple affected relatives share the same two disease haplotypes, as well as to pedigrees of consanguineous unions in which affected persons share two haplotypes that are identical by descent.

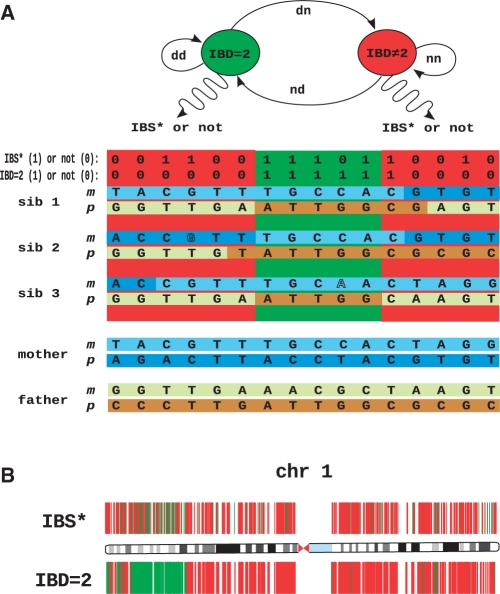
Fig. 1.

HMM to identify regions identical by descent in exome sequencing data. (A) In siblings affected with an autosomal recessive disorder, both the maternal and the paternal haplotypes surrounding the disease gene are identical by descent (IBD = 2). It is not possible to measure the IBD = 2 state directly, but only whether each sibling was called to the same homozygous or heterozygous genotype (referred to as IBS*). In this model, every genetic locus is either IBD = 2 or IBD ≠ 2 and the transition probabilities between these two states are defined by locus-specific transition rates, dd, nd, dn, nn. According to the HMM, these states emit genotypes that are IBS* or not, according to the appropriate probability distributions. Note that genotypes in IBD ≠ 2 may be IBS* by chance and genotypes in IBD = 2 may not be IBS* due to calling errors (displayed with outlined letters). The HMM and the observed exome sequence are used by the IBD = 2 classifying algorithm to identify regions of the genome that are IBD = 2. The disease gene must be located in such an IBD = 2 region. (B) Exome variant data of chromosome 1. Any chromosomal position that was called to a different genotype in at least one of three sibs on chromosome 1 with respect to the haploid reference sequence hg18 is depicted as a colored vertical line. In the upper panel, green indicates a genomic position that is IBS* in all three sibs, and red indicates ¬IBS* (non-IBS*). In the lower panel, green indicates genomic positions classified as IBD = 2, whereas red indicates IBD ≠ 2.

2.1 Structure of the HMM model

We model the exome sequencing results using an HMM that can transition between hidden (unobservable) states, each of which ‘emits’ observable tokens. The goal of HMMs is typically to predict the most likely sequence of hidden states that best explain the observed data. HMMs have been used in many applications in linkage analysis including the Lander–Green algorithm (Lander and Green, 1987).

We denote the state of descent of a chromosomal position t ∈ {1,…, T} for a particular chromosome with T relevant sites by the Boolean random variable X_t. The relevant sites comprise all nucleotide positions for which at least one call different from the reference sequence was made in at least one of the sequenced siblings. If the chromosomal position t is identical by descent in its two parental haplotypes in n studied siblings, then X_t = 1, otherwise X_t = 0. We assume that recombinations during meiosis occur mutually independently according to locus-specific recombination rates.

A locus t is IBD = 2 in n siblings if all n siblings share the same inheritance pattern for t. The inheritance pattern may be represented by a Boolean vector with two coordinates that describe the outcome of the paternal and the maternal meioses. For each locus under consideration, the inheritance vector is a binary vector of length 2n corresponding to the 2n gametes that gave rise to the individuals. A coordinate is 0 if the gamete carried DNA from the parent's paternally derived chromosome and 1 otherwise. There is one coordinate for the maternal and paternal loci of each of the sibs (Lander and Green, 1987). As there are four possible combinations for each sib, the probability of the event X_t = 1 is given by .

The a priori chance that a given coordinate in the inheritance vector differs between two adjacent positions t − 1 and t is the recombination fraction θ. Recombination frequencies depend on the chromosomal region and on sex. In other words, the inheritance vectors arise during meiosis from an inhomogeneous Markov process with position-dependent transition probabilities that are calculated for each variant call position on each chromosome based on the interpolated paternal and maternal recombination rates between position t − 1 and t. The transition probabilities between IBD = 2 and IBD ≠ 2 will be derived in the next section. The parameters dd and dn specify the probability of staying in the IBD = 2 state or transition from it to the IBD ≠ 2 state, and nn and nd are defined analogously for staying in or transition from the IBD ≠ 2 state.

Thus, we assume that the state of X_t depends only on the state of the previous position, but not on the other positions, i.e. P_t(X_t|X_t−1,…, X₁) = P_t(X_t|X_t−1). The model is fully described by a first-order inhomogeneous Markov process, whose transition probabilities P_t(X_t = j|X_t−1 = i) are described by T_t−1,t[i, j], a 2 × 2, position-specific matrix of transition probabilities between states i, j ∈ {0, 1} and from variant position t − 1 to position t.

The true state of descent of the chromosomal positions is not directly observable. Even in the absence of sequencing errors, it is only possible to observe identity by state (IBS), and our observations of the IBS status can be disturbed by sequencing and calling errors. We describe the event of observing genotypes at chromosomal position t in n examined samples by the Boolean random variables Y_t. If Y_t = 1 then an identical genotype was called in all examined samples at chromosomal position t—an event we also refer in the following for brevity as identity by observed state (IBS*). The state propagation between the hidden state X_t and the observed state Y_t is determined by local probabilities P(Y_t = i|X_t = j) for each i, j ∈ {0, 1}. These probabilities are referred to as the emission probabilities e_ij. This class of probabilistic model is commonly referred to as a HMM (Durbin et al., 1998).

2.2 Transition rates

Let v_t(m, p) ∈ {(0, 0), (0, 1), (1, 0), (1, 1)} be the inheritance vector at a chromosomal position t that indicates, which allele was inherited from the parents: v_t(m) = 0 for the grandmaternal or v_t(m) = 1 for the grand paternal allele from the mother's side and v_t(p) = 0 for the grandmaternal or v_t(p) = 1 for the grand paternal allele from the father's side. The a priori chance that a given coordinate in an inheritance vector differs between two adjacent positions t − 1, t, is the recombination fraction θ. The recombination frequencies depend on the chromosomal region and on the gender, thus θ(t − 1, t, s) is a function of both chromosomal positions and the gender s. In other words, the inheritance vectors arise during meiosis from an inhomogeneous Markov process with a position-dependent transition probability matrix T.

(1)

We will assume that the distribution of IBD = 2 and IBD ≠ 2 regions is in equilibrium. T therefore represents a regular transition matrix for which a unique equilibrium distribution exists. If we define D as the set of IBD = 2 loci among the measured variants and N as the set of IBD ≠ 2 loci, then N + D = G is the total number of measured variants and

(2)

and

(3)

Letting w = [N D] be the probability vector for being in state IBD = 2 or IBD ≠ 2, we have w = wT. This yields two equations of five variables.

(4)

(5)

The probability that the paternal coordinate of the inheritance vectors is IBD in n siblings at two randomly chosen positions is a function of the recombination rates θ:

(6)

The probability for the maternal coordinates of the inheritance vectors is defined analogously. The probability that two randomly chosen positions t_i, t_j have an identical vector of inheritance in n siblings, i.e. are IBD = 2, is thus:

(7)

This equation effectively averages the maternal and paternal recombination rates, so that T represents a sex-averaged transition matrix. With the identities nn + nd = 1 and dn + dd = 1 and Equations (4) and (5) the remaining transition rates dn, nd and nn are thus:

The recombination rates and the corresponding transition probability matrices for any two randomly chosen positions were interpolated from the deCODE recombination rate data (Kong et al., 2002) for hg 18 as downloaded from the UCSC Genome Browser (Karolchik et al., 2009).

2.3 Emission rates with integrated genotyping errors

In autosomal recessive disorders, the disease gene must be located in an chromosomal region that is IBD = 2 in all affected siblings. However, as already mentioned, we are not able to measure IBD = 2 directly, but only whether the siblings were observed to have the same diploid genotypes at a chromosomal locus (IBS*) or whether the observed genotypes differ from one another (not IBS*, denoted ¬IBS*). On the one hand, it is possible that all affected siblings share the same sequence at a random chromosomal locus by chance. On the other hand, it is also possible that sequencing or calling errors obscure the true IBS/¬IBS status.

The emission probability for the hidden state IBD = 2 refers to the probabilities that we observe IBS* or ¬IBS* at a locus that is IBD = 2. We will refer to the probability of a false genotype call at a single variant position as ε. Harismendy et al. (2009) estimated the variant accuracy of the three main NGS platforms to be on the order of 95% at high sequencing coverage, whereby variant accuracy was defined to be the proportion of ABI-Sanger validated sequence variants that are correctly called as homozygous or heterozygous variants on the basis of NGS read alignments. Therefore, we take the variant calling error rate to be on the order of ε = 0.05. The probability that one actually calls a locus as identical by state, IBS*, in n siblings is thus approximately (1 − ε)ⁿ. Additionally, there is a small probability of multiple sequencing errors leading to genotype calls that are erroneous but still consistent with IBS*. For instance, if the true genotype is A/C in all n siblings, n or more sequence errors could cause the genotypes to be observed as A/G. The total probability of such events was estimated from our simulated datasets and is small enough that it can be neglected (< 5.1 × 10⁻⁵).

The probability that an IBD ≠ 2 genetic locus is IBS* depends on the variability of the genomic region in its specific population context (International HapMap Consortium, 2007). In reference-guided resequencing, however, genotypes will only be considered as variant if they differ from the haploid reference sequence. In our context, we are thus interested in the probability that a called (diploid) genotype of a chromosomal position that is IBD = 2 or IBD ≠ 2 differs from the haplotype of the reference exome sequence and is IBS* in n siblings. We sampled these emission probabilities on our simulated exome datasets for n = 2 and n = 3 siblings.

2.4 Simulation of exome sequencing data

Genotype data of 30 HapMap trios of Central European descent was used to construct diploid genomes of parental individuals. For each such individual, the sex-specific meioses were simulated in the following way: the recombination rate between any two neighboring chromosomal positions that differed from the reference sequence was interpolated from the sex-specific physical map of the human genome (Matise et al., 2007). A haploid chromosome set of a gamete was simulated from the diploid parental genome according to these recombination frequencies. Two such haploid chromosomal sets of a male and female gamete yielded the diploid chromosomal set of each child. In total, 25 000 families consisting of n = 2, and n = 3 siblings were simulated. Variant calls in all siblings were restricted to exome CCDS coordinates (Pruitt et al., 2009) and were defined as genotypes differing from the haploid reference sequence hg 18. Genotype calling errors were simulated by randomly changing the genotype call at any variant position with probability ε. Additionally, assuming a sequencing accuracy (number of concordant calls between ABI Sanger and an NGS platform) of 0.999 over the entire exome (Harismendy et al., 2009), false-positive calls were randomly distributed over the entire exome with a probability of 0.001 per nucleotide.

2.5 Classifying IBD = 2 regions

We denote the vector of the observed IBS* status for each called position as y = (y₁,…, y_T). x = (x₁,…, x_T) is the vector describing the corresponding IBD = 2 and IBD ≠ 2 states. x can be estimated using the Viterbi algorithm adapted to a inhomogeneous Markov model (Durbin et al., 1998; Viterbi, 1967), which yields a maximum a posteriori estimate of the most likely path of hidden states:

(8)

Viterbi's algorithm delivers a single configuration of the states that jointly describe the observation best by classifying each position as either IBD = 2 or IBD ≠ 2, but it does not provide a confidence of that classification. We therefore also report the marginal posterior probability for each chromosomal position t to be IBD = 2, that is P(X_t = 1|Y = y). This probability can be calculated using the Forward/Backward algorithm (Durbin et al., 1998). The logarithmic ratios of the marginal probabilities of being IBD = 2 versus IBD ≠ 2 are well suited for graphical representation: 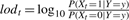(See Fig. 2C).

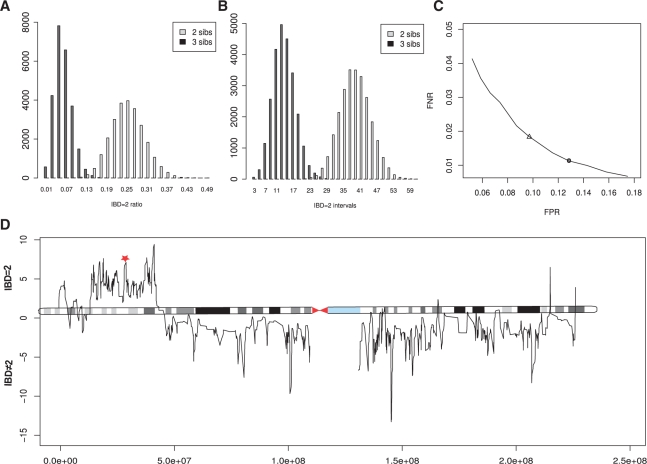
Fig. 2.

(A and B) Distribution of the IBD = 2 ratio and the number of IBD = 2 intervals. Exome datasets were simulated for 25 000 families consisting of n = 2 and n = 3 siblings using HapMap variant frequency data (International HapMap Consortium, 2007). (A) The mean proportion of the genome that is IBD = 2 is μ = 1/4 for n = 2 and μ = 1/16 for n = 3. (B) The mean number of intervals that are IBD = 2 is 38 in two and 14 in three siblings. (C) Robustness of IBD = 2 classification. The in silico exomes were simulated with a sequencing accuracy of 0.999 and a variant calling error rate of ε = 0.05. This yielded emission probabilities of e₁₁ = 0.77 and e₀₁ = 0.28. Using these emission probabilities as HMM parameters in the IBD = 2 classifier, the simulated 3 sib exome data could be classified with a false negative rate of fnr = 0.016 and a false positive rate of fpr = 0.095 (triangle). Decreasing the emission probabilities increases sensitivity but lowers specificity. The default parameters for the classification of real exome datasets of three siblings, the emission probabilities were set to e₁₁ = 0.75 and e₀₁ = 0.26, to increase sensitivity above 99% for the expected error rates (filled circle). (D) Posterior probabilities of IBD = 2 classification. The logarithmic ratio of the posterior probabilities of being IBD = 2 versus IBD ≠ 2 are plotted for all classified variant positions on chromosome 1. A disease-causing mutation (red star) was identified in a IBD = 2 region of high posterior probability (Krawitz et al., 2010).

The full procedure has been implemented in a freely available R program that requires a minimal amount of memory and running time on a standard desktop computer. The program code as well as online tutorial can be found on our web site.

2.6 Whole-exome enrichment and sequencing

Genomic DNA was enriched for the target region of all human Consensus CDS (CCDS) exons (Pruitt et al., 2009) with Agilent's SureSelect Human All Exon Kit and subsequently sequenced on a SOLiD version 3 sequencing platform with 50 bp reads (family A and B) and on a Illumina Genome Analyzer II with 100 bp reads (family C). The raw data of ∼5 GB per exome was mapped to the haploid human reference sequence hg18 and variants were called using the platform's standard software pipelines.

3 RESULTS

The algorithm presented here infers the locations of IBD = 2 chromosomal segments from the exome sequences of siblings affected by an autosomal recessive hereditary disease without requiring sequence data from the parents. The disease gene must be located in such an IBD = 2 region.

3.1 Distribution of IBD = 2 regions over the exome

To evaluate the performance of our algorithm, exome data were simulated for families of two and three siblings based on 30 HapMap trios. In reference-guided resequencing, only variants that differ from the haploid reference sequence are called. In our simulation, only those chromosomal positions that show heterozygous or homozygous variants with respect to the haploid reference sequence are potential variant alleles in a child of those parents. We restricted our analysis to the 38 Mb of the exonic regions of the human genome as defined by CCDS (Pruitt et al., 2009). The mean number of such varying positions was in the order of 20 thousand per individual corresponding to roughly one variant position in every 1900 bp. The proportion of the genome that is IBD = 2 in two and three siblings is shown in Figure 2A. The mean fraction of IBD = 2 is 1/4 for n = 2 and 1/16 for n = 3 (Table 1), which is in agreement with the expected values, according to . Thus, identification of IBD = 2 regions reduces the exomic search space exponentially in the number of siblings.

Table 1.

IBD = 2 classification of simulated datasets

	n = 2		n = 3
	Total	Percentage	Total	Percentage
Variant sites	21 150 (±1414)	100	22 034 (±1687)	100
IBS*	6615 (±867)	31	6842 (±735)	31
True IBD = 2	5260 (±553)	25	1494 (±457)	6.5
Classified IBD = 2	7754 (±1332)	36	2198 (±683)	10

The mean number (±1SD) of variants called on an CCDS exome of European ethnicity as expected from HapMap data is in the order of 20K. The fraction of exome positions that are expected to show identical genotypes IBS* is 0.31. The mean fraction of the exome that is IBD = 2 is 1/4 in 2 sibs and 1/16 in 3 sibs. With a false negative rate of fnr < 0.01 about a third of the exome is classified IBD = 2 for 2 sibs and about a tenth for 3 sibs. Chromosomal positions classified as IBD = 2 but that are not IBS* are either misclassifications or are ¬IBS* due to calling errors. Therefore, besides reducing the search space, IBD = 2 classification can help identify calling errors.

Also, the mean number of continuous IBD = 2 intervals decreases with the number of analyzed siblings. The distribution of IBD = 2 intervals is shown in Figure 2B for n = 2 and n = 3. The expected mean number of IBD = 2 intervals for n siblings can be derived as follows: the total sex-averaged map length of the human genome is 3790 cM (Matise et al., 2007). This translates to an expected number of roughly 38 recombinations per meiosis. Given the length of the human genome, all recombination events may be assumed to occur at different positions in different meioses. We may thus expect that when comparing n ≥ 2 diploid genomes, we will encounter 2n · 38 transitions between chromosomal segments with differing inheritance vectors among the n siblings. The expected number of IBD = 2 intervals in n siblings is thus , which is in perfect agreement with our simulations (Fig. 2B).

3.2 Evaluation of classifying simulated datasets

Genotype calling was simulated by adding sequencing and calling errors at frequencies representative of NGS data. The binary input vector of IBS*/¬IBS* observations was generated on these simulated observation datasets and classified into IBD = 2 or not using our algorithm. The rates of false negative and false positive classification were analyzed depending on different sets of emission probabilities: e₀₁ ∈ [0.22, 0.33], e₁₁ ∈ [0.70, 0.80] Using the mean emission probabilities from the simulated datasets of three siblings, e₀₁ = 0.28 and e₁₁ = 0.77 yielded classification error rates of fnr = 0.016 and fpr = 0.095 (triangle in Fig. 2C). The emission probabilities are a function of the error rates of the actual sequence data, and increasing error rates will decrease the probability of observing IBS* sequences for both IBD = 2 and IBD ≠ 2 states. The error rates of false positive and false negative classification in turn depend on the emission probabilities. Lowering e₀₁ and e₁₁ will increase the number of chromosomal positions that are falsely classified as IBD = 2, but on the other hand, it will decrease the number of chromosomal positions that are falsely not identified as IBD = 2 (Fig. 2C). When optimizing the emission probabilities for a minimal combined error, emission probabilities should be chosen according to the expected error rate in the real sequencing data. However, if an experiment is being performed to search for a novel disease gene, sensitivity is typically of higher importance than specificity. For classifying our real exome data, we thus set the emission probabilities to e₀₁ = 0.26 and e₁₁ = 0.75. These parameters yielded a IBD = 2 classification sensitivity of over 99% for three siblings in the simulated datasets and reduced the exomic search space on average to less than a tenth of the original search space (Table 1).

3.3 Classification of real NGS exome datasets

We first successfully used our IBD = 2 classifying algorithm to confine the exomic search space in a non-consanguineous family of three siblings affected by HPMR (Krawitz et al., 2010). In this case, about a fifth of the exome was classified IBD = 2 (family A in Fig. 3), reducing the number of genes affected by protein changing mutations that were called in all three siblings and that established a candidate set under an autosomal recessive disease model from 14 to 2. The disease-causing mutation mapped to a region on chromosome 1 with a high posterior IBD = 2 probability as depicted in Figure 2D.

Fig. 3.

Filtering of exome variant calls. Variants to hg18 were called in exomes of all three sibs of families A, B, and C. Subsequently, every position was classified as IBD = 2 or IBD ≠ 2 and as common or rare variants. Variants classified as IBD = 2 and rare represent the set of candidate mutations for rare monogenic diseases. Variants that are classified as IBD = 2 are either false IBD = 2 classifications or have been called to wrong genotypes in at least one of the probed samples.

To test the robustness of our IBD = 2 classifier, we subsequently analyzed the exome datasets of two families of different population backgrounds that were sequenced on two different NGS platforms (Fig. 3). Family B is of Turkish ethnicity and family C is of Syrian ethnicity. In both families, a higher number of total variant (about 30 thousand each) was called, which is probably due to their population backgrounds. The haploid reference sequence has a bias toward an European population background (International Human Genome Sequencing Consortium, 2004) and consequently variants that represent the major allele in the Syrian or Turkish population may be called as polymorphisms with respect to hg18. Regardless of the higher number of total variants called, the fraction of the IBD = 2 classified exome was 0.10 for family B and 0.07 for family C (Fig. 3) as expected from our simulations.

3.4 False positive variant calls and false positive IBD = 2 classifications

It is important to realize that current exome-capture and NGS technologies are not able to provide adequate and error-free coverage of the entire exome. Mutations in poorly covered genes can be missed by current analysis strategies if no or an insufficient number of mutant reads are sequenced. In projects in which the causative gene cannot be identified by exome sequencing, manual inspection or Sanger sequencing of poorly covered genes that are located in IBD = 2 regions and are thought to be good candidates may be a reasonable strategy.

Genes that have divergent calls for the affected sibs would be excluded from further analysis by the intersection strategy described in the Section 1. However, variants that are observed as ¬IBS but are located in IBD = 2 regions are likely to reflect a sequencing error (or rarely a de novo mutation in one of the sibs). Alternatively, the IBD = 2 classification could be false. To test this, we examined rare variants (not in dbSNP) that were observed to be ¬IBS but located within chromosomal regions classified as IBD = 2. There were 254 such variants in family A, 220 in family B and 53 in family C (Fig. 3). Each variant thus represents a conflict between the IBS* observation and the IBD = 2 classification. We picked 29 of these calls at random and validated their genotypes by ABI Sanger sequencing. Of total, 27 of these positions were validated as IBS*, indicating false NGS calls, and 2 were validated as ¬IBS*, indicating false positive IBD = 2 classification. The rate of false IBD = 2 classifications is thus in the expected false positive range for the parameters chosen for the analysis. Although most false NGS calls were found to be wild-type genotypes in the Sanger sequences, we also identified two positions as heterozygous in all samples, thus representing a candidate mutation that would have been missed under simple intersection filtering. Besides being a powerful filtering approach, IBD = 2 classification is thus also an effective approach to identify false NGS calls.

4 DISCUSSION

The analysis of chromosomal regions that are identical by descent is a fundamental tool in linkage analysis of pedigree data and in population genetics studies such as genome-wide association studies (Browning and Browning, 2010). In this work, we have presented a method for detection of IBD = 2 regions in the exome sequences of two or more related individuals affected with an autosomal recessive disease. In contrast to homozygosity mapping approaches designed for the analysis of children of consanguineous matings (Lander and Botstein, 1987), our procedure was developed to work for consanguineous or non-consanguineous families. With the recent advent of exome and genome sequencing for medical diagnostics, there is a pressing need for computational procedures that make maximum use of the information provided by the sequences for the rapid and correct identification of medically relevant mutations. Recent results have shown that even in populations such as Europeans that are well represented in dbSNP and HapMap, very high numbers of novel SNPs still remain to be found (Roach et al., 2010). This is likely to be even more the case in other population groups, and this will be an important issue given that many families affected by rare recessive syndromes come from small populations for which only scarce variational data are available.

The main drawback of filtering approaches that rely on a computational prediction of pathogenicity, as well as filtering approaches that focus on sets of variants that intersect in all analyzed samples of affected individuals (Ng et al., 2009, 2010b), is the possibility of false negative results. Not all disease-associated mutations are predicted to be pathogenic by current algorithms (Raymond et al., 2009), and not all disease-causing mutations are called to the correct genotype in all samples (Roach et al., 2010). The benefit of error-robust IBD = 2 classification is thus 2-fold: on the one hand, it is an effective tool for reducing the genomic search space, and on the other hand, it is an effective means for identifying sequencing errors.

The posterior probability computed by our algorithm additionally provides an estimator of how likely the classification is to be correct. The interpretation of these values is difficult. It has to be noted, that error probabilities, as well as IBD = 2 classification probabilities are often of a conditional nature. The constraint of being a rare variant increases the error probability tremendously. That is, a variant call at a dbSNP130 position is much more likely to be a correct one, compared with a call at a non-dbSNP position. The same holds true for IBD = 2 classification errors. A limitation of our method is the fact that regions of high linkage disequilibrium in a population (Browning and Browning, 2010) are more likely to be falsely classified as an IBD = 2 region. In future work, we plan on analyzing how homozygosity runs as well as population-specific linkage disequilibria may be incorporated to further reduce error rates in IBD = 2 classification.

Funding: Bundesministerium für Bildung und Forschung (BMBF, project number 0313911); NHLBI (5R01HL094976), NHGRI (5R21HG004749), NHGRI (1RC2HG005608), NICHD (1R01HD048895).

Conflict of Interest: none declared.