Simulated village locations in Thailand: A multi-scale model including a neural network approach

Abstract

The simulation of rural land use systems, in general, and rural settlement dynamics in particular has developed with synergies of theory and methods for decades. Three current issues are: linking spatial patterns and processes, representing hierarchical relations across scales, and considering nonlinearity to address complex non-stationary settlement dynamics. We present a hierarchical simulation model to investigate complex rural settlement dynamics in Nang Rong, Thailand. This simulation uses sub-models to allocate new villages at three spatial scales. Regional and sub-regional models, which involve a nonlinear space-time autoregressive model implemented in a neural network approach, determine the number of new villages to be established. A dynamic village niche model, establishing pattern-process link, was designed to enable the allocation of villages into specific locations. Spatiotemporal variability in model performance indicates the pattern of village location changes as a settlement frontier advances from rice-growing lowlands to higher elevations. Experiments results demonstrate this simulation model can enhance our understanding of settlement development in Nang Rong and thus gain insight into complex land use systems in this area.

Introduction

Land use and land cover changes are central to the study of complex coupled human-environment systems. Among such changes, the development of settlement systems has a long tradition of study (Garner 1967; Hudson 1967, 1969; Weidlich and Munz 1990; Popkov et al 1998; Pumain 2000; Page et al 2001; Brown et al 2005; Malanson et al 2006; Entwisle et al 2008). While settlement development is driven by a combination of such factors as environment, economy, population, and culture, it has its own endogenous dynamics in which each new settlement changes the conditions for all future settlements. Distance plays an important role in settlement development because the choice of settlement location depends on movement minimization inherently associated with geographic accessibility (Garner 1967), which combines the influence of resources, employment, markets, and social networks (cf. Schmit and Rounsevell 2006). The organization of human activities in settlement systems, as Garner (1967) highlighted, is hierarchical in two ways: horizontally in terms of spatial arrangements, and vertically in terms of organizational structures (e.g., rank-size relations and land use). Most traditional settlement models, often based on central place theory (establishing the relationship between the size and spatial arrangements of settlement; see Christaller 1966), focus on the relations of spatial patterns per se (see Garner 1967; Semple and Golledge 1970; Upton 1986; Pumain 2000), and thus are inadequate in explicitly representing dynamic processes (e.g. biophysical, social, and human decision-making) that inherently drive the choice of settlement location (Pumain 2000). Therefore, simulation models have been recognized to remedy this limitation by integrating factors in horizontal and vertical arrangements to represent explicitly complex settlement processes (e.g. Hudson 1967).

As research focus in settlement modeling has shifted from pattern-based to process-oriented for understanding complex settlement dynamics (Bell and Church 1985; Pumain 2000), suites of simulation models of settlement systems have been developed, differing in their mathematical treatment of time and events as continuous or discrete (see Zeigler et al 2000 for detail). For example, in the continuous-time simulation approach differential equation models have been developed for settlement studies (see Weidlich and Munz 1990; Popkov et al 1998). In contrast, discrete-time and discrete-event simulation approaches are often combined to support the modeling of settlement dynamics, exemplified by cellular automata models (Batty and Xie 1994; White and Engelen 1994; Clarke et al 1997) and agent-based models (Bura et al 1996; Kohler and Eric 1997; Sanders et al 1997; Dean et al 2000; Huigen 2004; Brown et al 2005). Three key issues have been recognized in the development of these simulation models and are what we focus our discussion on in this paper.

The first issue is the link between spatial patterns and their driving processes in settlement dynamics (Hudson 1967, 1969; Kohler et al 1997; Sanders et al 1997; Page et al 2001; Brown et al 2005). Hudson (1967) identified a theoretical model of rural settlement systems that combines ecological niche theory and location theory to explain settlement development. Three spatial processes were identified to characterize settlement dynamics: colonization (initial establishment of settlements by immigration), spread (establishment of new settlements or land occupation by local residents) and competition (leading to the loss of settlements). Hudson (1967) emphasized the potential that a region is settled is a function of influential variables that construct the niche space of a settlement system—i.e., a settlement niche (similar to the concept of ecological niche; see Hutchinson 1958), characterized by a set of influential factors that determine the location of settlement units (e.g., cities, villages, or households). A settlement niche can change due to, for example, socio-economic development (Hudson 1967). Agent based models, in which the processes are represented at the level of individual actors (Macy and Willer 2002), are increasingly used for settlement modeling (e.g., Kohler et al 1997; Sanders et al 1997; Dean et al 2000; Huigen 2004; Pumain 2007). In these models settlement units, represented by cities and towns (see Sanders et al 1997; Sanders 2006) or households (see Kohler et al 1997; Dean et al 2000), are modeled as either immobile or mobile agents that establish the link between settlement patterns and their driving processes (e.g., biophysical, cultural, social, and decision-making). In this study we develop a niche basis for the choice of settlement allocation at the village level to achieve the pattern-process link.

Hierarchy is the second issue in the study of land use systems, in general, and settlement systems in particular (Garner 1967; Veldkamp and Fresco 1997; Page et al 2001; Walsh et al 2001; Wu et al 2003; Verburg 2006; Verburg et al 2008). The importance of scale is implied in Hudson's theoretical settlement model (Hudson 1969). Veldkamp and Fresco (1997) emphasized that hierarchical approaches are well-suited to representing processes underlying land-use changes across various spatial scales. Likewise, Verburg et al (1999) incorporated a spatially hierarchical framework into land use study by considering both macro- and micro-level land use development. Agarwal et al (2002) stressed that land use complexity relies on the scales of space, time, and decisionmaking, and biophysical and social changes at a high level affect low-level interactions, and vice versa. Hierarchical modeling frameworks have been successfully applied in the design of a suite of land-use simulation models, represented by the CLUE family (Veldkamp and Fresco 1996; 1997; Veldkamp et al 2001; Verburg et al 2002, 2008) and SIMPOP (Pumain 2000, 2007; Sanders et al 1997; Sanders 2006). The consideration of hierarchy facilitates the modeling of settlement patterns and processes that may operate across different scales. We will use a hierarchical simulation framework to address such multi-scale processes to capture what appear to be multi-scale patterns because only then can possible feedbacks be represented correctly.

The third issue involves the consideration of nonlinearity into settlement models (Page et al 2001; Malanson et al 2006). Settlement systems have been identified as complex adaptive systems (Sander et al 1997; Pumain 2000; Malanson et al 2006; Manson and O'Sullivan 2006), characterized by self-organization, nonlinearity, path-dependence, and adaptation (Levin 1998; Malanson 1999). Traditional analytic models (e.g., mathematic or statistical) have imposed a great reliance on prior knowledge and strict assumptions (e.g., linearity, stationarity, and independence, see Gahegan 2003) and, thus, are ill-suited to capturing complex responses in settlement systems. Consideration of nonlinear relationships between landscape patterns and their driving processes, and between inputs and outputs of data used for inferring interesting structural and functional patterns enhances our understanding of complex characteristics in settlement systems. The explicit representation of driving processes in simulation models help explore nonlinear pattern-process interactions; the use of machine learning techniques, an important sub-domain of artificial intelligence (Mitchell 1997), allows the inference of nonlinear input-output relationships among land-use data and, thus, offers insights into relaxing assumptions in traditional modeling approaches (Openshaw and Openshaw 1997; Page et al 2001; Parker et al 2003; Pijanowski et al 2005). Machine learning algorithms mainly includes artificial neural networks, evolutionary computation, decision-tree learning, and reinforcement learning (Russell and Norvig 1995). These algorithms are inductive approaches that iteratively search for optimal solutions and allow the consideration of nonlinear input-output relationships among data (Gahegan 2003). Machine learning has a wide range of applications in such domains as pattern recognition, classification, and optimization (Russell and Norvig 1995; Openshaw and Openshaw 1997; Gahegan 2003; Bennett and Tang 2006; Tang 2008). The consideration of nonlinearity into settlement models is, therefore, instrumental in capturing complex characteristics in settlement systems. In this paper, we examine the utility of this consideration using the settlement niche-driven simulation model for nonlinear pattern and process interaction and neural networks (a representative machine learning approach that emulates neuronal activities of the brains for problem-solving; see Bishop 1995; Openshaw and Openshaw 1997; also cf. Li and Yeh 2002; Pijanowski et al 2005 for land-use modeling) for modeling nonlinear input-output relationships among empirical data.

The general purpose of this paper is to examine the identified three issues involved in the development of simulation models of settlement systems and, thus, to investigate how the incorporation of these issues into simulation facilitates the representation and interpretation of complex settlement dynamics. These three issues are common themes in landscape ecology, and our approach is part of broader analyses of landscape dynamics (Entwisle et al 2008). Specifically, in this paper we develop a hierarchical discrete simulation framework that is based on the settlement niche theory and a neural network-driven space-time model to provide insight into the identified issues in settlement modeling and associated regional land use. This development is placed within the context of investigating village dynamics on a (re)settlement frontier in Thailand.

Study area

Our study area is Nang Rong (Fig. 1), a rural district in Northeast Thailand. The topography is generally flat, with some higher elevations in the south, including gently rolling terrain in the southwest and two extinct volcano remnants in the southeast. Drainage is generally poor, resulting in a moderately dense network of small streams draining toward the north.

Fig. 1.

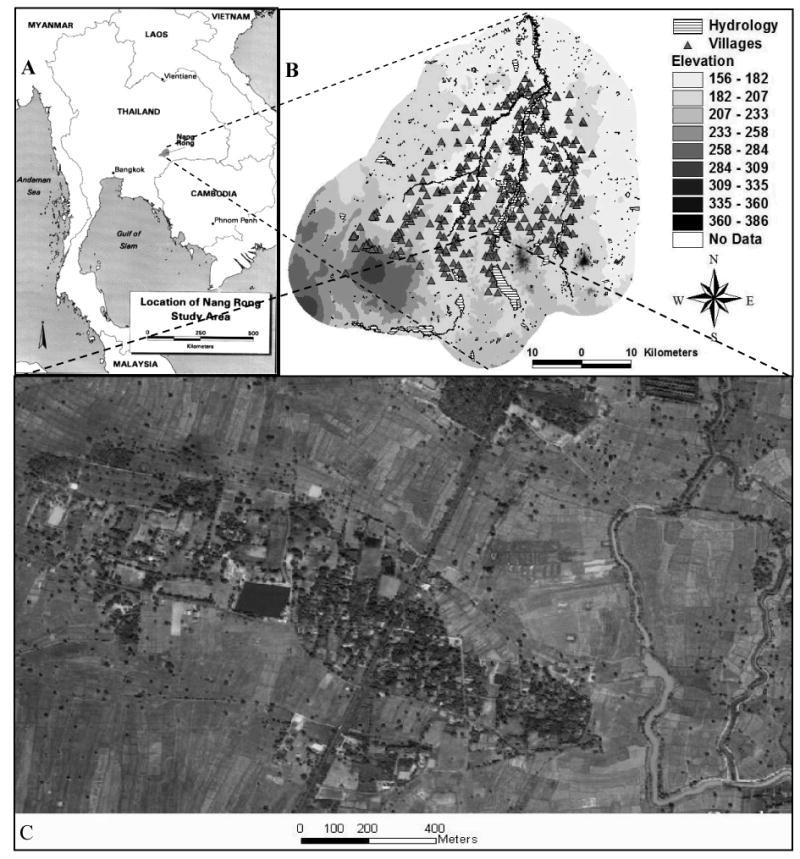
Maps of the study area (A: the location of Nang Rong district, Thailand; B: village patterns at 2000 in Nang Rong, including elevation and water distribution; elevation units: meters; C: clustering pattern of household settlement; adapted and georeferenced using a remote sensing image from Google Earth; see http://earth.google.com/).

Although occupied in the Khmer period (c. 800-1400 AD), the district had only 22 villages prior to 1900. The number increased steadily from 83 to 352 from 1950 to 2000 (see Fig. 1B), accompanying rapid socio-economic changes of modernization. Settlement evolved in two ways. First, new villages were created by colonization. Second, during spread, because villages are defined administratively and kept in the range of 100 – 200 households, when a village grows larger it is administratively split into two villages. Further splits can also occur.

Household settlement presents a nuclear pattern in Nang Rong. Households are clustered to form a village, and farming plots for households surround them (see Fig. 1C). Farming is the principal occupation. Rice is grown in the extensive lowlands, while crops such as cassava, sugar cane, and kenaf are grown in the uplands of the southwestern corner of the district. Some rubber and fruit trees have recently been added in the uplands. The availability of surface water is extremely important in determining land use and the settlement pattern prior to 1970 when rice was the dominant crop. The uplands were developed following exogenous socio-economic shocks in the late 1960s and early 1970s, which included the extension and upgrading of roads and the development of a European market for cassava.

Data sets available for our model include elevation, hydrographic coverage, and observed villages from 1950 to 2000. Fieldwork, including interviews with villagers and GPS positioning of village centers, and remote sensing allow us to compile these data sets. Three variables (elevation, distance to water, and distance to nearest village) have been recognized to be important in village establishment with respect to subsistence requirements (Entwisle et al 1998). Distance to water is skewed with a mode of 300 – 600 m. Most villages were located in low-elevation areas that are close to existing villages and water. Villages located at high elevation have short distances to water and to nearest village.

Methods

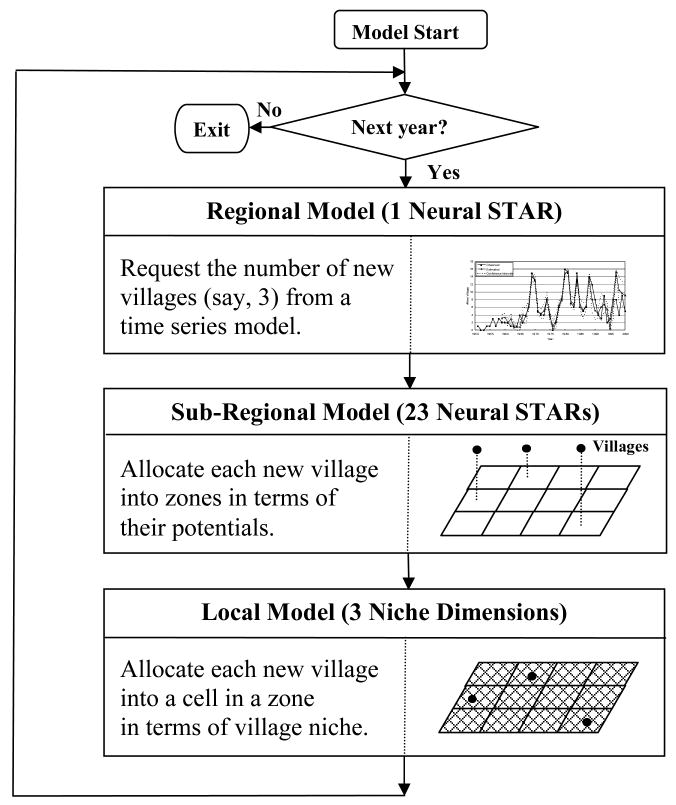
Our simulation model is based on a hierarchical discrete-time and discrete-event framework that includes three sub-models at different spatial scales: a regional model at a macro-scale, sub-regional models at a meso-scale, and a local model at a micro-scale (see Fig. 2 for a flow chart and conceptual illustration of the framework). Settlement development in our current model is represented at the village level: village establishment is modeled at a yearly level and the occurrence of new villages functions as discrete events that drive settlement development in our study area. In a top-down manner, the total number of new villages each year is obtained from the regional model, and these villages are then allocated into sub-regions with respect to their potential of creating new villages. The regional and sub-regional models are based on a space-time autoregressive model (defined and discussed later) that estimates the number of villages to be established using empirical time-series data. The local model, derived from Hudson's settlement niche theory for representing the choice of settlement allocation (Hudson 1969), determines the specific location of a new village within a sub-region through stochastic simulation in a bottom-up manner. The allocation of a new village is performed in a hierarchical manner, which significance has been well recognized in the CLUE modeling family (see Veldkamp and Fresco 1996; Verburg et al 1999). We need to use a hierarchical approach for our context because 1) we cannot fit the choice of a village location for the entire region and as a stationary process; and 2) the consideration of cross-scale village development may further enhance our understanding of complex multi-scale settlement dynamics.

Fig. 2.

The flowchart of the simulation model for the allocation of new villages in a hierarchical context.

We focus on the development of all administratively split villages because they have similar spatial relations as those newly colonized. Thus we model colonization and spread together (see Hudson 1969). In our model villages do not die due to competition. There is some indication that villages moved if their original location turned out to be problematic (e.g., too far from water), but it was rare and so we ignore this change. Subsequent to splitting, the administrative villages do not have the same GPS-positioned centers as their original villages, but the distances are small compared to our other measures (e.g., distance to water). As time progresses, not all options remain available in their initial proportions.

Model description

A general space-time autoregressive model

We developed a general spatiotemporal model to capture village development at large spatial scales. This model is a space-time autoregressive (STAR) model, which belongs to the family of STARMA (space-time autoregressive and moving average) models (Pfeifer and Deutsch 1980) extending from ARMA models in time series studies (Chatfield 2004). A STARMA model is a hybrid of a time-series forecasting model and a spatial prediction model (Pace et al 1998). STARMA models have been used to study diffusion processes, including disease spread (Cliff et al 1981), traffic flow (Kamarianakis and Prastacos 2005), and spatial econometrics (Pace et al 1998). Here we used a STAR model to investigate village diffusion.

Mathematically, the spatiotemporal model can be formulated as follows. Let D be the whole study area, and D can be partitioned into a set of sub-regions B₁, B₂,…, B_l, l is the number of sub-regions. Thus we have

$$D=\left\{B_i\right|B_i\subseteq D,i\in [1,l]\}$$ (1)

Let N(i,t) the number of new villages in a sub-region B_i at time t (t∈[1,n], n is the length of the data series in B_i). Thus, for a region B_i, a STAR model (see equation 2) establishes the relationship between the current response (i.e., N(i,t)) and its spatially and temporally neighboring responses.

$$N(i,t)=\sum _{j\prime =1}^k{\alpha }_{j\prime }N(i,t-j\prime )+\sum _{j=1}^l{w}_{ij}{\beta }_{j}N(j,t-1)+{\varepsilon }_{i_t}$$ (2)

where k is the order of the autoregressive (AR) process (simply, temporal order); α_j′ is the coefficient of the autoregressive process for N(i,t-j′); w_ij is the weight that illustrates the neighboring relationship between region B_i and B_j; β_j is the coefficient for the spatially-neighboring variable N(j,t-1); ε_it is a normally-distributed white noise with a zero mean.

Equation (2) defines a linear STAR model including two parts: temporal and spatial components. The former is an autoregressive process that models the historical responses of the current region B_i; the latter interprets effects from the spatially-neighboring regions at time t-1. The temporal order of spatially-neighboring regions is 1. Coefficients α_j′ and β_j can be estimated using, for example, maximum-likelihood approaches (Pace et al 1998). It is assumed that village development in Nang Rong is not affected by its surrounding districts.

A nonlinear STAR model using neural networks

Traditional ARMA models are mostly limited to capturing linear relationships between explanatory and dependent variables, and require rigid assumptions (Chatfield 2004). STARMA models face the same issues, which limit their use for time series exhibiting complex characteristics (e.g., nonlinearity and discontinuity). Artificial neural networks (ANN) provide a nonlinear approach for modeling complex time series and offer insights into these issues (Faraway and Chatfield 1998; Zhang et al 1998). Also, the applicability of ANN for the modeling of space-time series has been identified (French et al 1992; Gould 1994). In this paper, we developed a nonlinear STAR model to investigate the utility of ANN in space-time series modeling. Before delving into the nonlinear STAR model, we need to introduce ANN.

ANN are an inductive machine learning approach that emulates brain functions for problem-solving (Bishop 1995; Russell and Norvig 1995). While ANN can be seen as a black-box modeling approach, they exhibit flexibility, fault-tolerance, and nonlinearity (Bishop 1995). Typically, nonlinearity in ANN is achieved by applying nonlinear activation functions, represented by sigmoid functions, on neurons. Equation (3) is a sigmoid-type activation function.

$$\phi (\mathit{\text{In}})=1/(1+{\text{exp}}^{-\mathit{\text{In}}})$$ (3)

where In is the weighted sum of signals from the previous layer for the current neuron. Network topologies, link weights, and learning algorithms determine the problem-solving capabilities of ANN (Bishop 1995). In particular, the utility of multi-layer feed-forward neural networks (a form of neural networks that are acyclically connected by multiple layers of nodes in a direction from inputs to outputs; see Bishop 1995 for detail) in complex problem-solving (e.g. prediction, classification, and optimization) has been well-recognized (Bishop 1995; Russell and Norvig 1995) because of their proven universal approximator characteristics (Hecht-Nielsen 1987). The number of hidden layers and hidden nodes are important parameters that affect the performance of ANN.

Learning is essential in the use of ANN for problem-solving (Bishop 1995). We focus on back-propagation supervised learning. Back-propagation learning involves a procedure in which the estimated errors are propagated from output layers back to the previous layers and the corresponding link weights are then adjusted to minimize the error function according to the gradient information of these errors (Rumelhart et al 1986). While back-propagation learning may converge to local minima, it has been identified as an efficient learning approach for ANN and, thus, leads to a wide range of applications in neural-network modeling (Bishop 1995).

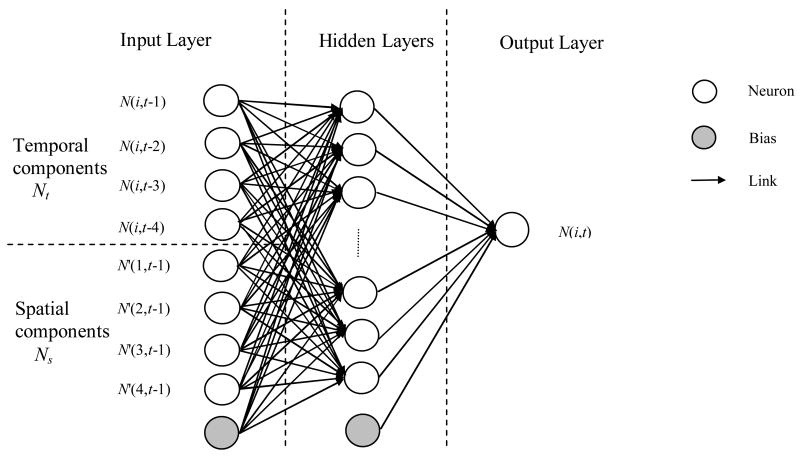
We used multi-layer feed-forward neural networks to construct nonlinear STAR models. Each sub-region is associated with a neural network. An example in Fig. 3 shows the structure of a fully-connected neural network with one hidden layer for a nonlinear STAR model in which the temporal order is 4, the spatial lag is 1, and the shape of sub-regions is rectangular.

Fig. 3.

A nonlinear space-time autoregressive model based on a fully-connected multi-layer feed-forward neural network.

Inputs nodes in each neural network receive data including temporal and spatial components, corresponding to those in the linear STAR model (see equation 2). Temporal components N_t are a vector of variables as follows

$$N_t=[N(i,t-1),N(i,t-2),\dots ,N(i,t-k)]$$

Spatial components N_s are a vector of variables N(j,t-1), which meet w_ij ≠ 0 —i.e. only those variables with non-zero weights are considered. The vector is denoted as

$$N_s=[N\prime (1,t-1),N\prime (2,t-1),\dots ,N\prime (k\prime ,t-1)]$$

where N′ (j′,t-1) = N (j,t-1), 1 ≤ j′ ≤ k′, 1 ≤ j ≤ 1, w_ij ≠ 0 For example, if spatial order is 1 for a rectangular region, then spatial components are represented by four input nodes, which correspond to the responses of four immediately-adjacent neighbors at time t-1 (i.e., k′ = 4). The neural-network model has one output node corresponding to the variable N(i,t) in the linear model. Thus, our neural STAR model (1 hidden layer and 1 output) for establishing the relationship between the number of current villages for a region and its spatial and temporal components (cf. equation 2) can be written as in equation (4):

$$N(i,t)=f(N,A)={\phi }_o(\sum _{i\prime =1}^{n_h}{a}_{i\prime }^{″}{\phi }_h(\sum _{j=1}^k{a}_{j}N(i,t-j)+\sum _{j\prime =1}^{k\prime }{a}_j^{\prime }N\prime (j\prime ,t-1)+a_0)+a_0^{″})$$ (4)

where f(N, A) is the nonlinear function in the model. N = {N_t, N_s}.A = {a, a′, a″} is the set of link weights. a₀ and ${\mathit{\text{a}}}_0^{″}$ represent noise introduced from bias nodes.φ₀ and φ_h are activation functions (sigmoid functions used in this model) for output and hidden layers. n_h is the number of hidden nodes. The number of input nodes is n_in = k+k′.

The error function for neural networks is based on the sum-of-square error function (Bishop 1995). Mean squared error (MSE, see equation 5) associated with the error function is one of the metrics that are often used to evaluate network performance.

$$\mathit{\text{MSE}}=(\sum _{t=\mathit{\text{lag}}}^n{(N(i,t)-\widehat{N}(i,t)))}^2)/(n-\mathit{\text{lag}}+1)$$ (5)

where N̂(i,t) is the estimated or predicted value of N(i,t) at time t (t∈[1, n], n is the length of the data series); lag is the temporal order. In addition, data normalization is often used to avoid unnecessary computation and the whole data set is partitioned into a training set and a test set for supervised learning (Bishop 1995). In our model, a linear transformation approach (Lapedes and Farber 1988; Zhang et al 1998) is used to normalize the input data to the range of [0,1] and the output data are then scaled back to the range of the input data. The output data in real numbers (i.e., the potential for creating new villages) are rounded up to convert to the number of villages in integers.

A regional model at a macro-scale

The regional model determines the total number of new villages each year. From the STAR model, we know that the number of regions in our study area is 1. Thus, our STAR model becomes an autoregressive time-series model. Let N(1,t) denote the number of villages at time t. The regional model only needs to consider the historical responses and can be simplified from equation (4) into equation (6) as follows:

$$N(1,t)=f(N,A)={\phi }_o(\sum _{i\prime =1}^{n_h}{a}_{i\prime }^{″}{\phi }_h(\sum _{j=1}^k{a}_{j}N(1,t-j)+a_0)+a_0^{″})$$ (6)

Data from 1951 to 1988 and from 1989 to 2000 were used for training and tests. We used incremental back-propagation learning to train networks and weight-decay regularization to avoid overfitting (Bishop 1995). We performed model selection by systematically experimenting different parameter sets, including the number of inputs k (5 to 10), the number of hidden nodes (k to 2k), learning rates (0.2, 0.4, 0.6, and 0.8) with momentum factors (0.2 and 0.6), ranges of initial weights ([-0.5, 0.5] and [-0.8, 0.8]), weight-decay coefficients (0 to 10^-3 with a step size of 10^-4), and the number of maximum epochs (300, 400, and 500). Termination criteria are that either the maximum number of epochs or an expected threshold error is reached. For each parameter set, 100 neural networks were trained to reduce the local-minima effect and the one with a minimum generalization error on the test set were compared with networks from other parameter sets. The network with the minimal error was found with 8 inputs, 10 hidden nodes, the learning rate of 0.6 with the momentum of 0.6, initial weights within the range of [0.8, 0.8], the weight-decay coefficient of 10^-4, and the number of maximum epochs of 500.

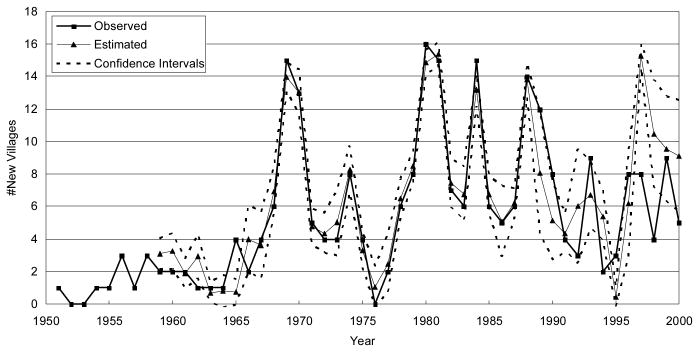
The observed and predicted numbers (with a 95% confidence interval) of villages in the regional model are compared in Fig. 4. The confidence interval, estimated using the bootstrap residual sampling technique (Tibshirani 1996) with 50 repetitions, suggests that the learned neural model provides reliable estimation for village development at the regional level. As an outlier case, the predicted number for 1997, which was the year of the Asian economic crisis when the Thai currency value crashed, is overestimated. Thus the model proved capable of reproducing the ongoing pattern until a sudden exogenous event, for which it was not calibrated (in part explains the outlier), occurred.

Fig. 4.

The observed and predicted numbers (with a 95% confidence interval) of new villages over time.

Sub-regional models at a meso-scale

Models at the meso-scale capture spatiotemporal development of villages. The whole study area was partitioned into a set of zones or sub-regions. A quadrat grid defines a zone. Each zone is a unit that aggregates spatiotemporal data (e.g. a time series of new villages) and can determine the potential of allocating a new village (simply, village potential). While socio-economic data are well suited to defining these zones, the current unavailability of these data for this study drives us to use a standard quadrant grid to divide the region geographically. Although we did not quantify spatial autocorrelation across the study area, the spatial scale chosen for sub-regional models approximates the areal extent of land use subdivisions observed from available satellite imagery (e.g., the southwest uplands, the central town, the eastern plain) and, in particular, covers the maximal observed values of distance-based influential variables (i.e., distance to nearest villages and to water) that drive village spread. As a result, the whole area of Nang Rong district was divided into a 5 × 6 grid with the cell size of 9 600 m × 9 600 m. Observed villages are found in 23 zones, which are the only ones modeled; the other 7 zones are empty. The number of new villages in each zone per year was used to model village potential.

Each zone is associated with a neural network that determines village potential. The temporal order is fixed at 8, and the spatial order is 1. Thus, the number of input nodes is 12. We used the same data-splitting strategies as in the regional model for network learning. Neural networks were trained using incremental back-propagation learning with weight-decay regularization. Model selection was used to increase the likelihood that neural networks converge to globally optimal solutions. To reduce heavy computation, we fixed the learning rate at 0.6 with a momentum of 0.6 and the range of initial weights from -0.5 to 0.5. For each zone, we examined the number of hidden nodes from 5 to 15 for model selection. Each experiment was repeated 100 times and networks with minimum generalization errors retained. The spatial distribution of errors associated with zones can reflect the complexity of spatiotemporal development of villages. Maps in Fig. 5 represent the spatial distribution of MSE and residuals of the neural models over 50 years. Observed from Fig. 5, zones with high errors are located in the center and southwest of the study area; overpredicted zones dominate the whole region and overall highest error is located in the overpredicted center.

Fig. 5.

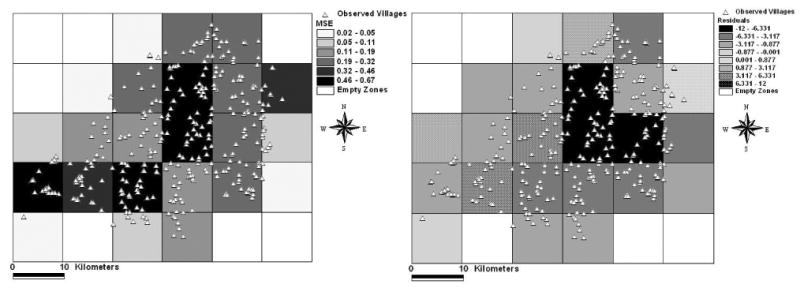
Spatial distributions of mean square errors and residuals of neural network models at the sub-regional level (using a 5 × 6 grid; MSE: mean square errors (based on normalized data); residuals are scaled back to the range of the corresponding data series).

Given village potential, the probability that a zone B_i is chosen, p_z(i), is equal to the ratio of the potential of zone B_i to the sum of the potentials of all zones (see equation 7).

$$p_z(i)=P(i,t)/\sum _{j=1}^{l}P(j,t)$$ (7)

where P(j,t) is the potential of zone B_j at time t, and P(j,t) = N̂(j,t); l is the number of zones.

A simulation model at a micro-scale

While models at the macro- and meso- levels determine the number of new villages each year and in which zone a new village is allocated, a micro-scale simulation model was used to specify the location of a new village. In this paper, a village niche model, extended from Hudson's settlement niche theory (Hudson 1967, 1969), was designed to simulate the village allocation process at a fine spatial scale. Note that while the use of niche theory may have its limitations (Austin 1985; Alterti et al 2003), the utility of niche theory (with its assumptions relaxed) in the study of coupled human-nature systems has been acknowledged (see Laland et al 2000; Alterti et al 2003; Odling-Smee et al 2003; Laland and Brown 2006). In particular, in this paper the niche concept is employed to generally represent relationships between village patterns and their driving factors modeled as niche variables. Specifically, a village niche is a hypervolume (a multi-dimensional space of influential factors; see Hutchinson 1958) that changes over time (i.e., a temporal niche). Three niche variables (i.e., influential factors) include elevation (X₁), distance to water (X₂) and distance to nearest village (X₃). The influence of other factors on village development is assumed to be insignificant to village niche (Vandermeer 1972).

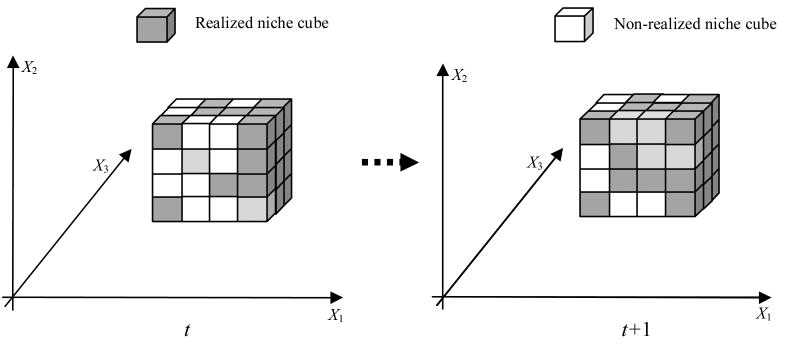
A discrete approach is used to represent a village niche, in which each niche variable is discretized into a sequence of intervals. The intersection of the sets of niche variables constructs a realized village niche, which is a set of hyper-cubes and is dynamic—i.e., it may shrink, expand, or shift due to, for example, socio-economic development (cf. Hudson 1969). These niche cubes can be (re)realized over time. Each niche cube (the minimal niche unit) is, therefore, a dynamic entity with a set of lifespan. Only within a lifespan, a niche cube can realize new villages. We assume that the lifespan length of niche cubes is fixed. Village density, defined as the number of villages in each cube, represents niche fitness. The temporal village niche (denoted as S; see equation 8) is represented as a set of village niche classes, each of which is a 5-tuple entity that establishes relationships between village density and niche variables. Figure 6 is a conceptual illustration of the temporal village niche.

Fig. 6.

Illustration of a dynamic village niche (X₁: elevation; X₂: distance to water; X₃: distance to nearest village; t: current time step; t+1: next time step; niche cubes with various number of realized villages are colored in grey).

$$S=\left\{s\right|s=[{\overline{X}}_1,{\overline{X}}_2,{\overline{X}}_3,t,y],{\overline{X}}_j=[x_j,x_j+{\sigma }_j],t\in [t_1,t_m],j\in \{1,2,3\}\}$$ (8)

where

• s: a village class;

• X̄₁, X̄₂, X̄₃: intervals of niche variables in s;

• y: number of villages realized in class s—i.e., village density;

• x_j: starting values of the interval of a niche variable;

• σ_j: interval length of a niche variable;

• t: time that the niche cube in s was realized;

• t₁, t_m: starting and ending years of the model;

• m: time duration of the model.

Let y(s) denotes the number of villages realized in s; similar for obtaining other variable values in s. The temporal village niche (i.e., the realized village niche) at time t′, S(t′), is illustrated as follows:

$$S(t\prime )=\left\{s\right|s\in S,t(s)\in [t\prime -\sigma ,t\prime +\sigma )\},S(t\prime )\subseteq S$$ (9)

where σ is the buffering time length, associated with the lifespan length of a village class via the formula 2σ+1. The boundary conditions for S(t′) are:

$$\{\begin{array}{ccc}t\prime -\sigma =t_1& if& t\prime -\sigma <t_1\\ t\prime +\sigma =t_m& if& t\prime +\sigma >t_m\end{array}$$ (10)

A village class s_i in the current village niche is randomly chosen for allocating a new village V(t_p) at time t_p. The probability of the occurrence of the new village V(t_p) in the class s_i is the ratio of the number of villages occurred in this class over the sum of the total number of villages realized at time t_p (see equation 11):

$$p_v(s_i)=y(s_i)/\sum _{j=\mathit{1}}^{n_s}y(s_j),s_i,s_j\in S(t_p),i,j\in [1,n_s],p\in [1,m]$$ (11)

where y(s_j) is the number of villages in class s_j; n_s is the size of S(t_p).

Each class s_i in the village niche corresponds to a set of locations (cells), referred to as a potential zone and written as C(s_i) (see equation 12). Each corresponding cell is a candidate for the location of a new village. A potential zone is a subset of the biotope space of village distribution (Hudson, 1969).

$$C(s_i)=\left\{c\right|c=[xx,yy,x_1,x_2,x_3,V],x_j(c)\in X_j(s_i),s_i\in S,j=\{1,2,3\}\}$$ (12)

where

• c: a cell in the potential zone;

• xx, yy: coordinates of cell c;

• x₁, x₂, x₃: niche variables for cell c;

• V: collection of villages in c.

The realized village niche is updated each year. The potential zone of a village class is constructed by searching the landscape for cells that satisfy the niche cube defined by the class. Each cell in the potential zone has an equal probability to be chosen. If the potential zone is a null set, a new village class will be picked and the above operations repeated until the potential zone is nonempty. Thus, the location of a new village is determined.

Model implementation

The time duration of our model is from 1950 to 2000 with a discrete time step of 1 year. The spatial resolution of the local model is 120 m × 120 m to keep the problem size manageable; actual observations find that almost no measures (distance to water or villages or detectable change in elevation) are less than 120 m. At finer resolution the number of possible cells is so much greater than the number of villages that the cell-to-cell match of observed and simulated is not informative. The spatial extent is 592 × 561 cells. The whole model was implemented using object-oriented programming language C++. The Fast Artificial Neural Network Library (http://fann.sourceforge.net/) was used to construct neural-network models.

Experiments and results

Because of stochasticity in our model, we used Monte Carlo methods to investigate the impact of hierarchical allocation of new villages and temporal niche on the development of village patterns in Nang Rong. Accordingly, two experiments were designed. First, we introduce approaches to quantitatively compare simulated village patterns with the observed.

Pattern comparison

Since villages are modeled as points constrained by raster cells, two choices are available for comparing village patterns: spatial point pattern (SPP) analysis (as points) and categorical map comparison (as cells). These approaches have been extensively used in the quantitative analysis of land-use patterns (Getis 1964; Haining 1982; Congalton 1991; Pontius 2002). We chose three methods in bivariate SPP analysis: quadrat analysis, point-to-nearest-event distance analysis, and second-order nearest-neighborhood analysis (Diggle 2003). These methods use different spatial characteristics (including area, distance, and both) of bivariate SPPs to compare their dependence or similarity.

At the categorical-map level we used kappa statistics (Cohen 1960; Pontius 2002) and quadrat analysis. Quadrat analysis, an areal-based approach (Greig-Smith 1983), adopts a contingency table that uses the presence and absence of point events to compare point patterns (a simulated village pattern and the observed in our model). We used a corrected version of chi-square test (see Greig-Smith 1983, pp. 38) to evaluate pattern similarity. Since points are constrained by quadrats (cells), quadrat analysis can be seen as an approach of categorical-map comparison based on cell-by-cell evaluation that only considers the presence or absence of point events. We thus used as comparison Pontius's multi-scale kappa indices (Pontius 2002), which utilize the proportion of categories (villages and nonvillages in our model) within quadrats to estimate pattern similarity across multiple spatial resolutions. We chose standard kappa index (Kstandard, Kstandard ∈ [-1,1]) (see Pontius 2002) for pattern comparison. Positive (negative) values of the index represent the degree of similarity (dissimilarity) between maps. Complete similarity (dissimilarity) is achieved when Kstandard=1 (-1). We applied the z-test to examine the significance of the kappa statistics (see Congalton and Green 1999; Koukoulas and Blackburn 2001).

The second method is point-to-nearest-event distance analysis, a distance-based approach (Diggle and Cox 1983). The centroids of a 60 × 60 grid were used as control points to calculate nearest-neighborhood distances. We considered the correlation of paired point-to-nearest-event distances. The Kendall's test (Kendall 1970) was used to evaluate pattern similarity. For Kendall's ranked correlation coefficient, τ, positive (negative) values represent similarity (dissimilarity). Absolute correlation values represent the magnitude of (dis)similarity.

The third method is second-order nearest-neighborhood analysis, also referred to as Ripley's K-function approach (Ripley 1977). L(h) is used to examine pattern similarity (equation 13; see Dale 1999):

$$L(h)=h-{((n_2{K}_{12}(h)+n_1{K}_{21}(h))/(\pi (n_1+n_2)))}^{1/2}$$ (13)

where h is the distance lag; n₁ and n₂ are the number of points in pattern 1 and 2; K₁₂(h) and K₂₁(h) are estimates of K functions for both patterns. Negative (positive) L(h) represents pattern similarity (dissimilarity). The absolute value of L(h) determines the magnitude of (dis)similarity. The method of toroidal shifts (Diggle 2003) is employed in this paper to assess the significance of this approach.

Experiment 1—Impact of hierarchical allocation

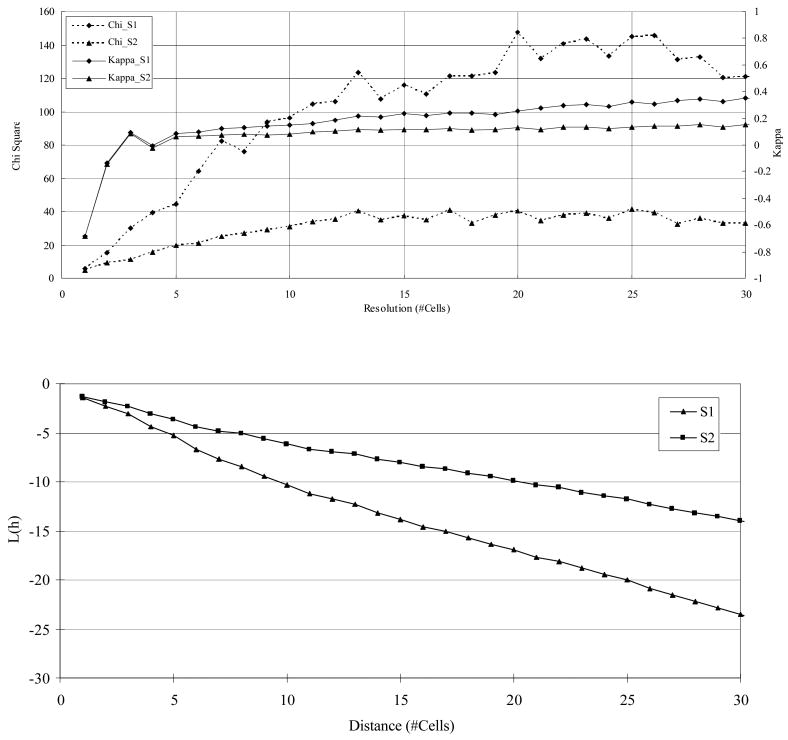
In this experiment, two treatments were compared in terms of using sub-regional models (S1) or not (S2) for village allocation. The whole village niche was used for both treatments. We compared simulated and observed patterns in 2000 (villages before 1951 were not included). 100 repetitions were performed for each treatment. Fig. 7 shows village patterns (including observed and simulated) for both treatments. From visual inspection, the use of spatial hierarchy for village allocation exhibits a more aggregated pattern than the treatment without the use of spatial hierarchy. The mean values of chi-square and kappa indices over quadrat size are illustrated in Fig. 8. Under the 5% conventional level, both treatments are significant. Chi-square values for both treatments tend to increase at the early stage of aggregation and decrease for the late stage. Kappa values also increase with quadrat size (Fig. 8). While kappa values are negative at the early-stage aggregation, they indicate increasing pattern similarity over quadrat size. Kappa results become significant at 5% conventional level when the distance lags (as in number of cells) are larger than 5. In total, the corresponding chi-square and kappa values for S1 are higher than those for S2. This suggests that simulated patterns in S1 are more similar to the observed than those in S2.

Fig. 7.

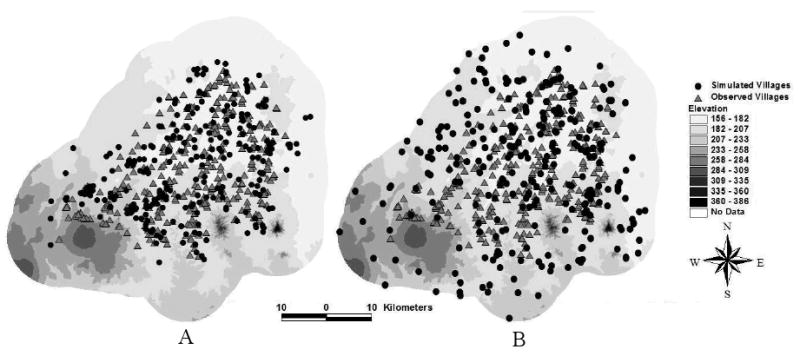
Spatial patterns of villages for experiment 1 (A: village patterns in treatment S1 that uses a spatial hierarchy; B: village patterns in treatment S2 without a spatial hierarchy; elevation in meters).

Fig. 8.

Chi-square tests, kappa statistics, and second-order nearest neighborhood analysis over distance in experiment 1.

For point-to-nearest-event distance analysis, Kendall's τ values for the two treatments are 0.785 and 0.616 (both p-values are 0.000). This indicates a higher pattern similarity in S1 than in S2. The mean L(h) values of second-order nearest-neighborhood analysis is shown in Fig. 8. Similarity between patterns can be observed because all L(h) values are negative. The absolute values of L(h) for S1 are larger than those for S2. Based on the method of toroidal shifts, the L(h) results are significant at 5% conventional level (corresponding to 100 shifts; see Diggle 2003). Statistical results of bivariate SPP analysis and categorical map comparison indicate that the model with sub-regional allocation produces simulated patterns that are more similar to the observed than without recruiting sub-regional allocation.

Experiment 2—Impact of temporal niche widths

To examine the impact of temporal niche widths, we designed an experiment with 7 treatments: T1-T7. The buffering time lengths (σ in equation 9) are 0, 1, 2, 3, 4, 5, and 50 years—i.e., models with niche widths of 1, 3, 5, 7, 9, 11, and 101 years. Based on the possible cyclic patterns from empirical data (see Fig. 4), niche widths for the first six treatments were chosen. T1 and T7 are extremes of niche widths, corresponding to the narrowest and widest. In particular, the whole niche was used in treatment T7 (as a reference treatment) by arbitrarily setting the width to 101. Each treatment was replicated 100 times. To test the temporal development of villages, we compared three years of village patterns: 1960, 1980, and 2000. Villages before 1951 were not included.

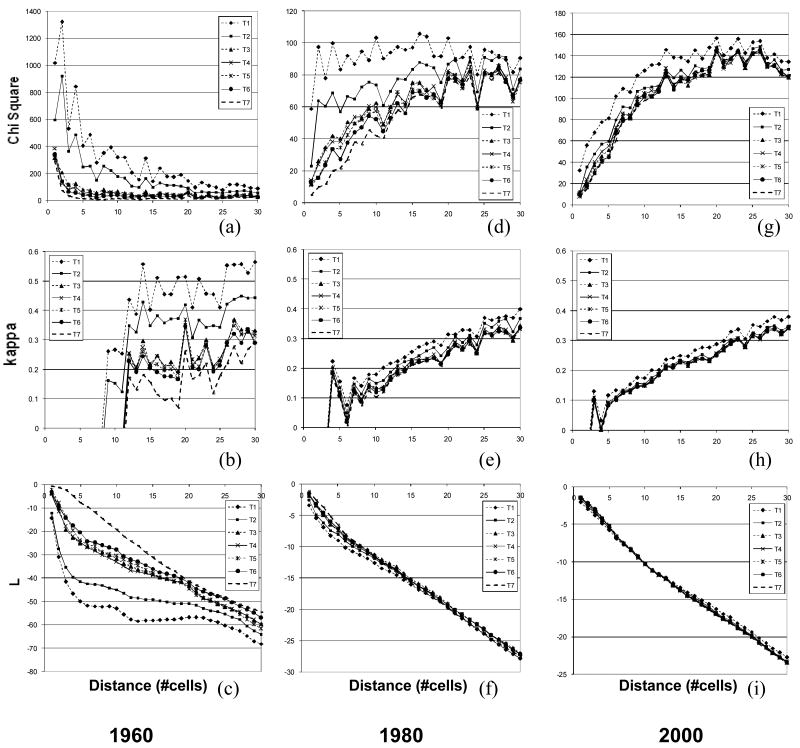
The results of chi-square analysis, kappa statistics, and second-order nearest-neighborhood analysis for the treatments are shown in Fig. 9. All results of chi-square tests are significant under the 5% conventional level. We only show nonnegative kappa results that are of interest in this research for the purpose of pattern similarity. Kappa results for comparison at 1960 (1980 and 2000) become significant (5% conventional level) when the distance lags are larger than about 10 (5) cells. The results for point-to-nearest-event distance analysis are shown in Table 1. All p-values for Kendall's test are 0.000. L(h) results are also significant at the 5% conventional level based on 100 toroidal shifts.

Fig. 9.

The plot of chi-square, kappa, and second-order neighborhood values versus distance for different niche widths over time (a-c for 1960, d-f for 1980, and g-i for 2000).

Table 1.

Point-to-nearest-event distance analysis for treatments in experiment 2 (the p-values for all treatments are 0.000).

Treatments	Niche Widths	Kendall's τ
		1960	1980	2000
T1	1	0.9010	0.6959	0.6835
T2	3	0.8415	0.7002	0.6649
T3	5	0.8354	0.6950	0.6607
T4	7	0.8297	0.6885	0.6639
T5	9	0.8257	0.6950	0.6660
T6	11	0.8184	0.6948	0.6692
T7	101	0.8144	0.6894	0.6641

Observed from Fig. 9 and Table 1, similarities between simulated and observed patterns are negatively associated with niche widths: the narrower the niche widths are, the higher similarities between simulated and observed patterns are. This trend is particularly apparent for the early and middle stages of village development (e.g., 1960 and 1980). The influence of niche widths becomes insignificant once niche widths are larger than 5 years. Treatments T1 and T7 correspond to the highest and lowest similarities. Differences in pattern similarity for various niche widths tend to decrease as the development of villages.

Discussions

The combination of STAR, neural networks, and niche theory in our hierarchical simulation model allows for the investigation of complex village dynamics in which settlement patterns and their driving processes interact nonlinearly and across various spatial and temporal scales. STAR models with neural networks capture the development of villages at macro spatial scales and this development information (i.e., the number of new villages per year) is then fed to the micro-level village niche, which links spatiotemporal patterns and their driving factors (as niche variables). This hierarchical allocation, as suggested by Verburg et al (1999; 2004), facilitates the representation of land-use dynamics (village development in our context) that often exhibit cross-scale characteristics (see Veldkamp and Fresco 1997; Veldkamp et al 2001; Walsh et al 2001; Verburg et al 2008).

The local niche model alone (i.e., without the use of spatial hierarchies) was not satisfactory for allocating villages spatially in Nang Rong. Simulated villages often did not coincide with observed villages in space and time. The southwestern corner of the district, at the edge of the cassava-growing plateau, was poorly simulated (Fig. 7B). While model simplification is always an issue that possibly leads to this mismatch, comparison between simulated patterns and observed changes that have occurred in this sub-region provides insight into understanding complex village dynamics in this area. More specifically, new villages in this sub-region established relatively far from others, so the simulation usually allocates few in this area. The mismatch between simulated and observed patterns was caused by the change of the agroeconomic structure (as processes) in this sub-region in the 1960s, when changes in European tariffs on cassava led to the development of this agricultural frontier and a change from rice-based agriculture, which drove our choice of a temporally-sensitive approach within a hierarchical framework.

A spatially-hierarchical approach leads to accuracy improvement in the current simulation model in part because simulated villages are not allocated to sub-regions without villages observed. This accuracy improvement suggests the existence of spatial heterogeneity of village patterns and may entail spatial imbalance in the agroeconomy development of Nang Rong. Of more interest, however, is what the pattern of remaining errors tells us about modeling and about Nang Rong (see Fig. 5). In our NN-STAR approach, the predictive accuracy depends on the complexity of a space-time series and the settings of the corresponding neural network. The former is a main determinant that influences predictive accuracy. The center of the region (row 3 and column 4), which has a relatively high error, is the location of Nang Rong town. Because we are focusing on new villages, the effect of the growth of what became the large town of Nang Rong in this area is not accounted for. The growth of the town inhibits the creation of new villages, which made the space-time series in this sub-region complex. A gravity model (or generally spatial interaction model; see Fotheringham and O'Kelly, 1989) that incorporates the growth of Nang Rong and the splitting into administrative villages as the mass in the model can be used to describe and estimate the local niche into which new villages locate.

The use of temporally-shifting niche facilitates our understanding of village development on the spatial and temporal domain. While all spatial indices compare village patterns well at the early stage of village development (see Fig. 9), chi-square analysis and kappa statistics may be well suited to revealing similarity differences at the late stage. More importantly, these results may suggest temporal heterogeneity in village development with respect to the choice alternatives available for village allocation. The temporally-shifting niche, which establishes the pattern-process link, captures the possibility that the relative importance of water, elevation, and distance to other villages can change with time. The first two can change because the type of agriculture that is practiced can change, as it did in our study area from a subsistence rice-based system to, for the southwestern region, an export cassava-based system. The change in the importance of distance to other villages could reflect a change in the agricultural system, with spacing changing with the extent of farmed area needed per household varies (rice is more intensive than cassava), or it could reflect the change in processes from colonization through spread to competition theorized by Hudson (1969).

Although the processes are not temporally stationary, neural networks can capture gradual nonlinear change. Our model, developed using the proposed framework, was able to cope with the change in the agricultural system from primarily lowland rice through the addition of upland cassava, although this change is still evident in some errors of our model (see Fig. 4 and 5). Where we encountered the greatest problem was in temporal projections across an abrupt exogenous shock of the economic crisis of 1997. Such exogenous forcings are a general problem for modeling, but our neural networks may have been able to cope with this change had it occurred in the middle of a calibration period, unlike less dynamic models.

Conclusions and Future Work

Our discrete simulation model, developed in a hierarchical framework and combined with a neural network approach, provides a platform to capture complex village dynamics in our study area and, thus, gain insight into regional land use changes. This simulation advances the modeling of settlement systems by providing suggestion for resolving the three modeling issues that can be generalized to other land-use systems (Veldkamp et al 2001; Verburg et al 2004; Verburg 2006). We link pattern and process by both zoning and using spatial dimensions for niche; we include scaling by nesting models in a spatial hierarchy (single neural STAR model/multiple neural STAR models/local niche model); and we incorporate a settlement niche model and neural networks for consideration of nonlinearity, representative of complex characteristics in dynamic ecological and social systems (Levin 1998; Parker et al 2003). While this simulation framework enhances our understanding of complex village dynamics in the study area, such modeling is well-suited to the identification of where further field study is needed.

Currently, village development is driven by events of creating new villages and village niche calibrated using empirical data. Future work will be focused on the integration of this simulation model with an agent-based model that explicitly takes into account the land-use decision processes of household agents (i.e., the incorporation of a finer spatial scale into the current region-subregion-village hierarchy) in the development of complex settlement systems. This integration, as highlighted in the current literature of land use modeling (Parker et al. 2003; Verburg et al 2004; Verburg 2006; Pumain 2007), will facilitate the capturing of nonlinear pattern-process interactions in a bottom-up manner. In addition, the use of socio-economic data for the partitioning of the study area and the introduction of more advanced spatial similarity metrics will be conducted in future study to further support the modeling of village diffusion over space and time.