Three-dimensional Molecular Modeling with Single Molecule FRET

Abstract

Single molecule fluorescence energy transfer experiments enable investigations of macromolecular conformation and folding by the introduction of fluorescent dyes at specific sites in the macromolecule. Multiple such experiments can be performed with different labeling site combinations in order to map complex conformational changes or interactions between multiple molecules. Distances that are derived from such experiments can be used for determination of the fluorophore positions by triangulation. When combined with a known structure of the macromolecule(s) to which the fluorophores are attached, a three-dimensional model of the system can be determined. However, care has to be taken to properly derive distance from fluorescence energy transfer efficiency and to recognize the systematic or random errors for this relationship. Here we review the experimental and computational methods used for three-dimensional modeling based on single molecule fluorescence resonance transfer, and describe recent progress in pushing the limits of this approach to macromolecular complexes.

Introduction

Detailed structural studies extending to the atomic level are effective approaches to reveal the molecular mechanisms underlying function of biological molecules. High-resolution methods such as X-ray diffraction crystallography and nuclear magnetic resonance have led the way in providing the highest spatial information, but a host of other methods, such as small angle X-ray scattering, cryo-electron microscopy, hydrodynamic assays (gel filtration chromatography, light scattering, and analytical ultra centrifugation), and spectroscopic measures of circular dichroism and fluorescence also can provide a wealth of knowledge about molecular structure. Among these approaches, fluorescence resonance energy transfer (FRET) studies have flourished in recent years as a result of the capability to detect the signal reporting intra and intermolecular distances from samples as small as single molecules (Deniz et al., 2008; Roy et al., 2008).

The benefits of studying single molecules have opened new avenues of investigation in biomolecular science. By recording properties and dynamics of single molecules one at a time, the effects of averaging that are inherent in ensemble studies are absent, allowing discovery of phenomena not otherwise observable. The single molecule approach is particularly effective at revealing heterogeneous behaviors across different individual molecules within a sample and also reporting dynamic trajectories of molecules without the need for synchronous behavior across a population. Single molecule FRET (smFRET) is well suited for structural studies because it provides a unique tool with the applicability to transient and dynamic molecular conformations and can reveal weak interactions that often are not resolvable when averaging over a larger sample.

Motivated by the dramatic successes of smFRET in the past decade, there has been a rapid development of instrumentation, sample preparation, and data analysis. Furthermore, development of new fluorescent organic dyes with desirable properties for single molecule imaging and discovery of additives to improve behavior of existing fluorophores have allowed greater signal to noise ratios to be achieved and extended the observation period before fluorophores undergo photobleaching (Rasnik et al., 2006; Dave et al., 2009). Other efforts have defined optimal procedures to correct single molecule measurements for instrumental and environmental effects to allow more accurate determinations of fluorophore separation distances (McCann et al., 2010). Independent developments are extending the range of applicability of single molecule FRET investigations into live cells (Sakon and Weninger, 2010).

By combining multiple smFRET experiments involving different labeling site combinations one obtains a network of FRET-derived distances between the labeling sites. If the distance network is augmented by structural information about the molecules to which the fluorophores are attached, powerful computational approaches can be used to obtain three-dimensional models of the entire system. One particular approach is based on computational docking of molecular components using smFRET-derived distance information, similar to approaches used for nuclear magnetic resonance spectroscopy studies of macromolecular complexes (Clore and Schwieters, 2003; Domingues et al., 2003; Choi et al., 2010).

Here we review recent advances in translating sets of single molecule FRET measurements between fluorescent dye locations in biomolecules into three-dimensional models. Approaches for such modeling range from simple three-point triangulation to sophisticated computational docking algorithms using smFRET-derived distances (Margittai et al., 2003; Rasnik et al., 2004; Schröder and Grubmüller, 2004; Andrecka et al., 2008; Muschielok et al., 2008; Wozniak et al., 2008; Choi et al., 2010). As a particular example for multi-molecule docking we discuss the determination of the model of the synaptotagmin 1 (Syt1): SNARE complex derived from smFRET-derived distances (Choi et al., 2010).

Förster Theory

FRET occurs between two fluorescent dyes when the emission spectrum of an excited donor fluorophore overlaps the absorption spectrum of a nearby acceptor fluorophore (Förster, 1948). For applications with biomolecules, site specific chemistry is generally used to link the fluorescent dyes at known locations on the molecule so that FRET between the fluorophores is interpretable at the distance between those points (Stryer and Haugland, 1967). The FRET efficiency E_FRET depends strongly on the distance R between fluorophores:

$$E_{\text{FRET}}=\frac{1}{1+{(R/R_0)}^6}$$ (1)

where the Förster radius R₀ is a donor/acceptor-pair specific constant (the distance at which the FRET efficiency is 50%). When the distance between the donor and acceptor fluorphores is ½ R_0, the FRET efficiency is nearly maximal and, so, any further decrease in distance is difficult to measure. Conversely, if the distance increases beyond 2 R₀ then, the distance dependence is also very shallow. Thus, the most sensitive range for a typical FRET experiment is in the distance range ½ to 2 R₀.

The Förster radius R₀ depends on the spectroscopic properties of the FRET fluorophore pair and the surrounding medium of the fluorophores:

$$R_0^6=\frac{0.529·{\kappa }^2·{\phi }_{D}J(\lambda )}{N·n^4}$$ (2)

where the units of R₀ and the wavelength λ are centimeters, κ² describes the relative orientation of the fluorophores, φ_D is the quantum yield of the donor (ratio of the number of emitted photons to absorbed photons, a parameter that depends on the fluorophore itself and its environment), N is Avogadro’s number, n is the index of refraction of the medium, J(λ) is the overlap between the donor’s emission spectrum and the acceptor absorption spectrum, given by:

$$J(\lambda )=\frac{{\int }_0^{\infty }{f}_D(\lambda )·{\epsilon }_A(\lambda )·{\lambda }^{4}d\lambda }{{\int }_0^{\infty }{f}_D(\lambda )d\lambda }$$ (3)

where f_D(λ) is the spectral shape of the donor emission and ε_A(λ) is the spectral shape of the acceptor excitation in units of (M⁻¹ cm⁻¹). The orientation factor between fluorophores is given by

$${\kappa }^2={(cos{\mathrm{\Theta }}_T-3·cos{\mathrm{\Theta }}_D·cos{\mathrm{\Theta }}_A)}^2$$ (4)

where Θ_T, Θ_D, Θ_A are the angles between donor and acceptor dipole, between donor and the line connecting the two fluorophores, and between the acceptor and the line connecting the two fluorophores, respectively. It is often assumed that the fluorophores undergo isotropic reorientation in a time much shorter than the excited state lifetime of the donor which leads to κ² = 2/3 (Dale et al., 1979).

FRET efficiency can be obtained by measuring either the donor and acceptor fluorescence intensities, or the donor lifetimes in the presence and absence of an acceptor (Rothwell et al., 2003),

$$E_{\mathit{FRET}}={\left[1+\gamma \left(\frac{I_D}{I_A}\right)\right]}^{-1}=1-\frac{{\tau }_{D(A)}}{{\tau }_{D(0)}}$$ (5)

where I_D and I_A are donor (D) and acceptor (A) fluorescence intensities. The factor γ combines the probabilities of the donor and acceptor fluorophores to relax to the ground state from the fluorescent excited state by emitting a photon and the likelihood of experimentally detecting emitted photons as

$$\gamma =\frac{{\phi }_A{\eta }_A}{{\phi }_D{\eta }_D}$$ (6)

where η is the instrumental detection efficiency and φ the fluorophore quantum yield for the acceptor (A) and donor (D) fluorophore, as indicated by the subscript. τ_D(A)and τ_D(0)are the donor (D) lifetimes in the presence (A) and absence (0) of the acceptor fluorophore, respectively. In this review we primarily focus on the approach that uses measurements of the donor and acceptor fluorescence intensities.

Conversion of FRET efficiency to distance

The Förster theory that relates measured donor and acceptor intensities (I_D and I_A) to the interfluorophore distance R is dependent on two factors involving fluorophore and instrument properties: R_o (the Förster Radius) (Eq. 1) and γ (Eq. 5). R_o is generally different for each specific pair of fluorescent dyes. The γ factor depends on a combination of fluorophore and instrument properties (Eq. 6).

Corrections to raw single molecule fluorescence intensity data

The raw fluorescence intensity data (I_A and I_D Eq. 5) must be corrected by background scattering, leakage of fluorescence intensity of donor and acceptor fluorophores into each other’s detection channels, and by the γ factor. Leakage of one fluorophore’s emission into the detection channel of the other fluorophore is typically characterized using measurements of samples prepared with only one of the fluorophores. The fraction of the emission for each fluorophore that appears in the unintended channel is a fixed function of the specific configuration of the detection channel as long as the emission spectral density is constant during the experiment (see ref. (Chung et al., 2009) for a notable exception where emission spectral density changes). This fraction is subtracted from measured intensities when analyzing the FRET efficiency data. There are several approaches to background subtraction for experiments using immobilized molecules. They all are generally based around the fact that if the surface density of immobilized molecules is sufficiently dilute then background contributions to the emission intensity can be estimated from locations near observed fluorescent spots that are free of other fluorescent molecules.

Empirical determination of γ

The γ factor accounts for differences between the donor and acceptor fluorophores in the probability that emitted photons will be detected (detector efficiency) and the probability of photon emission upon excitation (quantum yield) and (Eq. 6). These properties can be determined experimentally by measuring the detected intensities of acceptor and donor fluorophores separately as a function of illumination power, and by measuring the relative quantum yields of the fluorophores attached to the particular biomolecule under study. Quantum yields are commonly measured by comparing ensemble fluorescence measurements of samples with known concentrations to the emissions of quantum yield standards (for example, rhodamine 101 in ethanol). For single molecule studies of freely diffusing molecules, alternative approaches to determine the γ factor that do not require independent determination of detection efficiencies and quantum yields are available. One such method exploits the linear relationship between the apparent FRET ratio and the stoichiometry by using an alternative laser excitation scheme (Lee et al., 2005). Another approach relies on measurement of the lifetime of the fluorescent dye excited states (Rothwell et al., 2003).

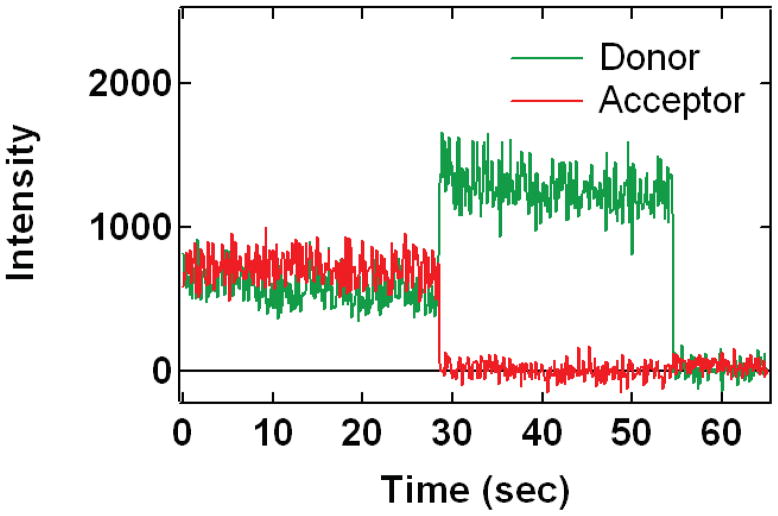
Determination of the γ factor is particularly straightforward and does not require such additional experiments if molecules are immobilized so that observation times of each molecule are long. Single molecule fluorescence time traces that contain an instance of photobleaching (Figure 1) can be efficiently utilized to estimate the γ factor for this particular fluorophore pair (McCann et al., 2010). Specifically, γ is obtained by measuring the change in donor and acceptor fluorescence intensity before and after photobleaching (Ha et al., 1999):

$$\gamma =\mathrm{\Delta }{I}_A/\mathrm{\Delta }{I}_D$$ (7)

whereΔI_A and ΔI_D are the intensity changes of the donor and acceptor intensities upon acceptor photobleaching, respectively. Anticorrelated photobleaching is a frequent event in single molecule measurements, so this method does not require any additional measurements. However, it is important to measure the fluorescence intensities for sufficiently long periods before and after photobleaching in order to obtain reliable mean intensities. For specific pairs of labeling sites, one has to use instances where the acceptor fluorophore photobleaches before the donor fluorophore (leading to anticorrelated intensity changes within a single detection time interval).

Figure 1. Typical single-molecule fluorescent emission time courses from FRET coupled fluorophores.

Alexa555 (green curve, donor) and Alexa647 (red curve, acceptor) fluorophores are attached to Syt1 at cysteine mutations E140C Q154C, both in the C2A domain. The donor fluorescence is directly excited by the 532 nm illumination that is present for the entire observation interval. The high acceptor emission at the beginning is due to FRET coupling to the donor. The bleaching of the acceptor around 28 seconds and the resultant, anticorrelated recovery of the donor allow calculation of the γ factor as discussed in the text. For this case, gamma is around 0.95. The donor finally bleaches around 55 seconds.

The donor and acceptor intensities for these molecules are then determined in the intervals before and after the photobleaching event (omitting the intervals both immediately before and after the event (Choi et al., 2010) (Figure 1). These averaged intensities are used to calculate the changes in donor and acceptor intensity upon bleaching ΔI_A and ΔI_D

In one particular example, distributions of γ factors were acquired from individual measurements involving the donor/acceptor pair (Alexa555:Alexa647) conjugated to synaptotagmin 1 (Syt1) at various amino acid locations (Choi et al., 2010). Remarkably, the measured γ distributions were similar for all 16 amino acid labeling pairs used in this study. Gaussian fits to these distributions generally produced a mean center value for γ of 0.968 +/− 0.11. The similarity of the γ factors for all of the 16 different labeling pairs (covering all of the label sites used for the docking calculations of the Syt1: SNARE complex described below) demonstrates that no specific amino acid labeling site results in a significant change in critical fluorophore parameters such as quantum efficiency, supporting the use of a single R_o parameter for all the 34 label pairs used in the subsequent docking calculations. Interestingly, no systematic difference in γ factor between the different experimental conditions was found (Syt1 encapsulation in liposomes vs. SNARE bound Syt1 and presence of EDTA vs. Ca²⁺) (Choi et al., 2010).

Empirical determination of R₀

In principle, R₀ can be calculated from the spectral overlap of the fluorophore pairs, the donor quantum yield, and the orientation factor (Eq. 2). Some of these parameters can be obtained experimentally, but the orientation factor requires some knowledge of the fluorophores’s dynamics with respect to the attached molecule.

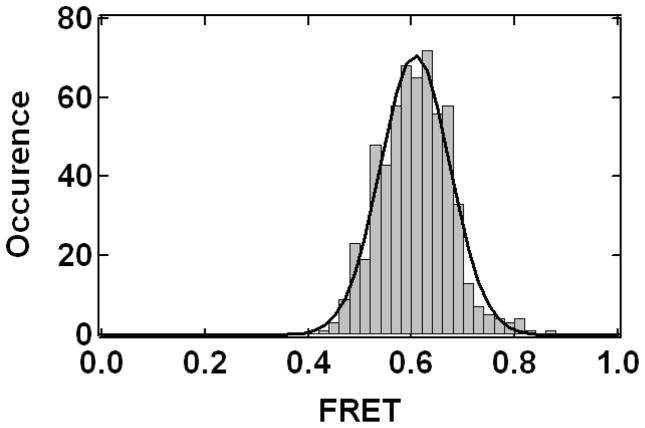
A combination of single molecule experiments and Monte Carlo simulations of the allowed volume for the fluorophores has been used to estimate R₀ (Muschielok et al., 2008). In contrast, for the synaptotagmin-SNARE study (Choi et al., 2010), we used an entirely empirical approach to calibrate R_o inspired by previous work (Amir and Haas, 1987; Amir and Haas, 1988). For a fluorophore pair (Alexa555:Alexa647) attached to one of the two rigid C2 domains of Syt1 we measured the FRET efficiency and calculated the fluorophore separation from a crystal structure of Syt1 (Fuson et al., 2007). It should be noted that the resulting FRET efficiency distributions produced a single Gaussian peak with a width consistent with shot noise (Figure 2) (see section Assignment of FRET efficiency values from a distribution). The FRET efficiency and fluorophore separation yielded an empirical value of R_o = 5.55 nm (using γ = 1, Eqs. 1 & 5), compared to the theoretical R_o for the Alexa555:Alexa647 fluorophore pair of 5.1 nm (Haugland, 2005). R_o is expected to deviate from the theoretical value due to changes in the fluorophore microenvironment when conjugated to the molecule of interest. In our work with Syt1, the spread of the R_o values derived from three label-site combinations (using the same fluorescent dyes but different amino acid attachment sites) was 0.23 nm, which is smaller than the error bounds used in the docking calculation (Choi et al., 2010).

Figure 2. FRET Histogram.

A histogram of FRET efficiency measurements calculated at each time point (100 msec time bin) from donor and acceptor fluorescence intensity trajectories and accumulated for four Syt1 molecules with Alexa555 and Alexa647 fluorophores attached at E140C Q154C as in Figure 1. The solid line is a least squares fit to a Gaussian function.

As a check on the validity of our empirical calibration scheme for R₀, we compared results obtained for the same amino acid labeling pair, but using a different pair of fluorescent dyes with a very different value of R₀. Using the Alexa488:Alexa555 pair (instead of Alexa555:Alexa647) the measured FRET efficiency (Eq. 5) was on average 0.23. Using the method of analyzing single molecule photobleaching events (Section on empirical determination of γ), we experimentally determined the γ factor (Eq. 7) to be 1.83. We used this γ value and Eq. 5 to obtain a FRET efficiency of 0.55 for Alexa488:Alexa555 labeled Syt1 at amino acids 254 and 396. Using the interfluorophore distance derived from the Alexa555:Alexa647 measurement of this amino acid label pair (6.78 nm, using the empirically determined R₀ = 5.55 nm and γ = 1 parameters for the Alexa555/Alexa647 pair, Eqs. 1 & 5) along with the Alexa488-Alexa555 measured FRET efficiency yields an empirical R₀ for the Alexa488:Alexa555 pair of 7.02 nm. Table 1.6 in the Molecular Probes Handbook (Haugland, 2005) gives a theoretical R₀ = 7.0 nm for this fluorophore pair. Observing the expected R₀ for this different pair of fluorophores lent confidence to our empirical calibration scheme for R₀.

Assignment of FRET efficiency values from a distribution

If the distance between a donor/acceptor pair of fluorophores remains constant, then the noise in the measurement of the FRET efficiency is dominated by the shot noise of the random statistics of counting detected photons in each time bin. This shot noise leads to histograms of FRET efficiency that are distributed in an approximately Gaussian manner and with a predictable width (Gopich and Szabo, 2005; Nir et al., 2006; Cherny et al., 2009; Chung et al., 2009; Kalinin et al., 2010) (Figure 2). However, conformational dynamics of the molecule(s) can lead to temporal variations in the distance between a donor/acceptor pair and correspondingly dynamic variations in FRET efficiency levels. If the timescale for transitions among distinct conformational states is much slower than the integration time of the measurement, then the measured FRET histograms will converge to a set of peaked Gaussian-like functions, each with a shot noise limited width. As the integration time of the measurement is lengthened to be similar to the transition time between states then the peaks merge into wider peaks with averages of the individual FRET efficiencies. In the limit when the integration time of the measurement is much longer than the transition times so that many states are visited within each measurement, a FRET histogram is formed with a single Gaussian peak at a value related to the average of the underlying states (Gopich and Szabo, 2005)

The FRET measurements used for the Syt1: SNARE complex study (Choi et al., 2010) were acquired with a 0.1 sec integration period (referred to as “time bin”). The histograms of FRET efficiency for the different sets of label attachment sites were characterized by either one or two well defined Gaussian peaks whose width was near the shot noise expected width or up to a factor of two wider. The center of a Gaussian function fitted to the histograms was used to represent the FRET efficiency value for a defined state of the complex. The fraction of area under that Gaussian compared to the area under the complete histogram indicated the fractional population within that FRET efficiency state. In this system, 26 out of 34 label site combinations had dominant states with at least 70% fractional population. These states were used to generate distance restraints for molecular modeling. The remaining label site combinations indicated a mixture of states with none reaching 70 % occupancy. For these cases we selected the state using an iterative modeling approach to make use of these mixed-state FRET efficiency distributions. An intermediate model was generated using only the restraints derived from FRET states with >70 % in one Gaussian and the mixed states were compared to this preliminary model. The FRET value in the mixed states that was more consistent with the intermediate model was selected and then the entire set of restraints was used for a final round of modeling.

The presence of distinct FRET states for some label pairs along with the fact that the widths of some FRET efficiency peaks were wider than expected from shot noise alone indicate some degree of heterogeneity within the Syt1: SNARE complex. For most fluorophore attachment site combinations a dominant configuration could be identified, highlighting one of the advantages of the single molecule approach. On the other hand, this example serves as a warning that in future applications possible heterogeneity within a configurational ensemble may prevent convergence of the modeling calculations to a single solution. Advances in single-molecule imaging technology that allow improved temporal resolution in single molecule FRET studies will allow multiple interconverting states to be better resolved and will extend the applicability of the modeling approaches discussed here.

Accuracy of FRET-derived distances

A number of studies have investigated the accuracy of smFRET-derived distance measurements. In one study, smFRET efficiency distributions were measured for donor and acceptor fluorophores attached to the ends of freely diffusing polyproline molecules of various lengths (Schuler et al., 2005). The observed smFRET efficiencies agreed with those determined from ensemble lifetime measurements but differed from values expected from Eq. 1 when the polyproline peptide was treated as a rigid rod. At distances less than R₀, the observed FRET efficiencies were lower than predicted, whereas at other distances, they were much higher. Possible explanations of this discrepancy are incomplete rotational averaging of the fluorophores, and bending of the polyproline peptide for larger numbers of residues. Indeed, in related work, a 23 Å persistence length wormlike chain model appears to fit single molecule FRET measurements for polyproline peptides of varying lengths ranging 8 to 24 residues (Watkins et al., 2006).

The orientation factor κ² (Eq. 4) potentially has a large uncertainty associated with it. If both fluorophores undergo random isotropic motion on a timescale that is much shorter than the lifetime of the donor then κ² = 2/3 (Dale et al., 1979). This assumption can break down depending on the fluorophore pair, the particular macromolecule that the fluorophores are attached to, and the length of the linkers. For example, for a tethered DNA duplex that was terminally labeled with Cy3 and Cy5, the single molecule FRET efficiency dependence as a function of duplex length exhibits a modulation that is proposed to be caused by preferential stacking interactions between fluorophores and the DNA bases (Iqbal et al., 2008). However, the actually observed modulation is much smaller than if there were perfect stacking. In related work, the FRET efficiencies between fluorophores at various positions within a DNA duplex were measured using smFRET measurements on freely diffusing DNA molecules (Wozniak et al., 2008). In this case, the observed modulation of the FRET efficiency dependence by fluorophore position could be explained by an averaging model that uses distinct time scales for the rotational and translational (diffusional) motions of the fluorophores. This model used a molecular dynamics simulations of cyanine fluorophores attached to rigid DNA models. Surprisingly, the best agreement with experiment was obtained when the orientational motions were treated by the κ² = 2/3 approximation, but the diffusional motions were treated as slower than the fluorescence lifetime of the donor. In this model, the average FRET efficiency is simply a function of the R⁻⁶ average of the inter-fluorophore distances obtained from the molecular dynamics simulation.

Ensemble measurements of emission anisotropy of donor and acceptor fluorophores can be used to obtain a more precise estimation of the orientation factor κ² (Ivanov et al., 2009), again assuming that the motions are faster than the lifetime of the excited state of the donor fluorophore. Using the of the HIV-1 integrase complex as a model system the authors showed that the error of the FRET-derived distance is typically only 10–20% if the fluorophore emission anisotropies are not accounted for. The authors also proposed an iterative scheme to calculate the orientation factor κ² from the measured emission anisotropies and the current estimate of the distance between fluorophores. It should be noted that the interfluorophore distance refers to the distance between fluorophore centers, so the effect of flexible linkers to their attachments on the molecule(s) of interest adds to this uncertainty. Similarly, (van der Meer, 2002) make the important point that rather than focusing on worst case scenarios for the errors in converting FRET measurements to distances arising from uncertainty in κ², examination of most probable values of derived distances and associated confidence intervals are more meaningful. Those authors conclude that, under reasonable assumptions, the error in a FRET distance derived using the assumption κ² = 2/3 is less than 8% within a 67% confidence interval, i.e., for most cases the error introduced by the isotropic motion assumption is substantially smaller than worst case scenarios. Of course, particular combinations of anisotropic behaviors can still conspire to give highly anomalous results, but these situations can be used to obtain details of fluorophore rotational freedom (van der Meer, 2002). As a case in point, the FRET-derived distances in the actin: DNase 1 complex were compared with the distances of the attachment points obtained from corresponding X-ray crystal structures (dos Remedios and Moens, 1995) and the authors suggested that the assumption of a freely rotating fluorophore is a reasonable one, even for relatively large organic fluorophores attached by flexible linkers to macromolecules.

Photo-physics vs. conformational variability

Observed single molecule FRET efficiency distributions often show relatively broad distributions. Shot noise is one source that broadens a FRET distribution. However, the distributions are often broader than what is expected from counting statistics. Possible sources can be photo-physics of the fluorophores themselves or conformational changes of the molecule that is studied (for examples, see the section on Assignment of FRET efficiency values from a distribution).

An example of photo-physics is called “blinking”, i.e., transient instances of dark states of fluorophores. Typically, blinking events are relatively short (less than 1 sec). However, longer dark states, lasting several seconds, have also been observed (Sabanayagam et al., 2005). Blinking of the acceptor fluorophore produces anticorrelated donor-acceptor intensity fluctuations which can be mistaken as variations in interfluorophore distance. By periodically switching between donor and acceptor excitation wavelengths it is possible to distinguish between variations of distance vs. long-time blinking (as long as the acceptor fluorophore stays in the evanescent field of typical single-molecule total internal reflection (TIR) experiment, which a reasonable assumption in most cases). A comprehensive theory for the effects of blinking, conformational dynamics, and diffusion in and out of the illuminated region for studies of freely diffusing molecules has been developed by (Gopich and Szabo, 2005).

Other photo-physics effects include quenching by other factors, and a photoinduced redshift of the donor fluorophore if the donor and acceptor absorption spectra are relatively close (Chung et al., 2010). Both situations can in principle be avoided by judicious choice of fluorophores and sample preparations. The quantum yield of a fluorophore may change significantly upon conjugation to different locations, even within a single biomolecule, altering the Förster radius for a FRET pair. For accurate structural interpretations of FRET signals, R₀ should be carefully assessed for different label sites either by ensemble characterization of the various contributing parameters or the empirical approach discussed in the section on Empirical determination of R₀.

Generation of models from FRET distances

Simulation of fluorophore center positions

As a pre-requisite for docking and fitting calculations, the average fluorophore center positions have to be computed relative to the position of the molecule or domain that the fluorophore is attached to. Depending on the particular fluorophore and linker, the fluorophore center position is separated from the coordinates of the covalently attached residue (often generated by site-specific mutagenesis) by ~ 1 nm. In earlier work, the fluorophore center position was simply taken at the protein residue site or displaced by a certain amount away from the molecule’s center (Rasnik et al., 2004). To obtain a more precise estimate, we used a molecular dynamics simulation to obtain the average position of the fluorophore center using an atomic model of the fluorophore linked to a protein at the residue position used for labeling (Choi et al., 2010; Vrljic et al., 2010). For these particular simulations, the protein atoms of the molecule to which the fluorophore is attached were kept fixed while the linker and the fluorophore atoms were allowed to move. Chemical structures are available for some of the commonly used fluorescent fluorophores, such as Cy3, Cy5, and Alexa 647 (Vrljic et al., 2010). A large number of simulations were performed starting from different initial velocities in order to obtain good conformational sampling. Similar molecular dynamics simulations were used for modeling the conformations of fluorophores attached to nucleotides (Wozniak et al., 2008).

Model fitting

If structures of individual domains are available, it is possible to generate a three-dimensional model based on the known structures and the sm-FRET derived distances. Clearly, the model must not have more degrees of freedom than there are observations, restricting this approach to rigid-body three-dimensional modeling of complexes or determination of large-scale motions, such as hinge bending. For example, the degree of bending of kinked DNA duplexes was determined from a set of single molecule FRET experiments of labels placed in different places along the DNA (Wozniak et al., 2008). The model was obtained using a torsion angle sampling method that fit the observed FRET efficiencies with FRET efficiencies calculated from the three-dimensional model using isotropic averaging to take into account the fluorophore’s translational motion (see also section on Accuracy of FRET-derived distances).

Docking calculations

Determination of a three-dimensional model from smFRET derived distances is reminiscent to rigid body docking approaches using nuclear magnetic resonance (NMR)-derived distances between protons (Schwieters and Clore, 2001; Dominguez et al., 2003). In the application to smFRET data, the distances refer to distances between fluorophore centers. In our approach, the fluorophore center position is treated as a “pseudoatom” that is rigidly associated with the molecule to which the fluorophore is covalently attached; the position of the pseudoatom is taken as the average position of the fluorophore center relative to the molecule, as obtained from a molecular dynamics simulation (see above) (Choi et al., 2010). The term pseudoatom is used since these points have no chemical energy terms associated with them during the docking calculation, but are rather restricting the possible conformations of the rigid molecule or domain that the pseudoatom is attached to. We then perform extensive torsion angle/rigid body molecular dynamics simulations (Rice and Brunger, 1994) using a simulated annealing slow-cooling protocol. The total energy function consists of a repulsive term for the nonbonded interactions (i.e., excluding electrostatic and attractive van der Waals terms) (Engh and Huber, 1991) and the distance restraints term. This type of energy function is widely used for three-dimensional structure determination based NMR data (Brunger and Nilges, 1993). We use a harmonic square-well potential to the fluorophore center pseudoatom positions (Brunger, 1992). The smFRET efficiencies were converted to distances as described in the section on FRET efficiency to distance. FRET efficiency becomes less sensitive to fluorophore separation at distances much less and much greater than R_o (see Eq. 1). Therefore, we use variable bounds for the square well potential depending how close the expected distance is to R_o (Choi et al., 2010).

Many trials (typically ~ 1000) with different randomly assigned orientations of domains and molecules, different relative conformations of flexible domains, and initial velocities are performed for each set of calculations. Each resulting model is then characterized by the root mean square (rms) deviation between the distances predicted by the model and the distance ranges used as the square well potentials derived from the FRET efficiency measurements. The solutions of the docking simulations are sorted by rms deviation satisfaction in increasing order. The solutions are then clustered according to the rms deviation using an algorithm implemented in the program HADDOCK (de Vries et al., 2007). For each cluster, the structure with the best distance satisfaction is used for analysis. The derived models can also be further refined using local perturbation and refinement in docking programs to optimize local interactions. This step allows for side chain refinement and includes electrostatics and van der Waals energy terms.

Example: synaptotagmin 1/SNARE complex

We performed extensive smFRET measurements between a set of 34 fluorophore pairs located at various amino acid positions in the C2AB fragment of Syt1 and the cis (post-fusion) state of the neuronal SNARE complex (Choi et al., 2010). The SNARE complex, and the two C2 domains of Syt1 were treated as independent rigid bodies (residues 140:262 and 273:418, respectively), while the torsion angles of the linker connecting the two domains (residues 263–272) were simulated in torsion angle space, i.e., with bond lengths and bond angles fixed. The coordinates for the SNARE complex were obtained from the crystal structure of the neuronal SNARE complex (PDB ID 1SFC) (Sutton et al., 1998) and those of the C2 domains of Syt1 from the Ca²⁺-free crystal structure of Syt1 (PDB ID 2R83) (Fuson et al., 2007).

Some of the 34 distance restraints involved multiple distinct FRET populations as described in the section on Assignment of FRET efficiency values from a distribution. Therefore, the docking calculations proceeded in two steps. FRET efficiency distributions were analyzed by fitting to sums of two or more Gaussian functions. As described above, for 26 of the 34 measured FRET pairs, the major fitted peaks capture 70% or more of the total non-zero smFRET distribution; ten label pairs have distributions with a major peak comprising 90% of the total distribution, seven label pairs between 90% and 80%, nine between 80% and 70%. The assignments of the dominant FRET states at the 70% level were robust against run-to-run variation. Repeating measurements of single label pair combinations generated the same central FRET efficiency values within experimental error for all label pairs and for most label pairs the dominant population was consistently above the 70% value. For all pairs the dominant population was observed at levels above 70% in at least 66% of the repeated experiments. Many were confirmed greater than 70% dominant in all repeats.

For final docking calculations we pooled all of the repeated experiments for each label pair into a single histogram to address the most probable configuration observed across multiple repeated experiments (at least three repeats for every label site pair). For label pairs with FRET efficiency distributions with a dominant peak of >70% of the total area, the FRET measurements were converted to distances and used as restraints for a first round of docking calculations (26 out of 34 pairs were included at this first step). The FRET histograms for the remaining eight label combinations required sums of two Gaussians to fit where neither comprised more than 70% of the total population. These measured distances were compared to the best model from the first simulation using the first 26 distances and the measured distance that was closer to the model distance was selected. Then the simulation was repeated using all 34 restraints. The resulting models did not change significantly upon inclusion of the eight additional restraints.

We also performed a docking simulation using the minor populations from each of the FRET efficiency distributions (if only one FRET population was present, it was used for both the major and minor population simulation) but convergence was much poorer than for the calculations with the major population. Thus, the conformations arising from docking using the major FRET population restraints are much more likely to occur than those derived using the minor FRET populations.

Uniformly increasing or decreasing all major FRET derived distance restraints by 1 nm led to non-physical results where the proteins were far away from each other or overlapped in space respectively. If the intra-C2 domain restraints were released then the models converged to the same C2B docking state, but the location of the C2A domain became variable.

Cross-validation of the model of the Syt1-SNARE complex

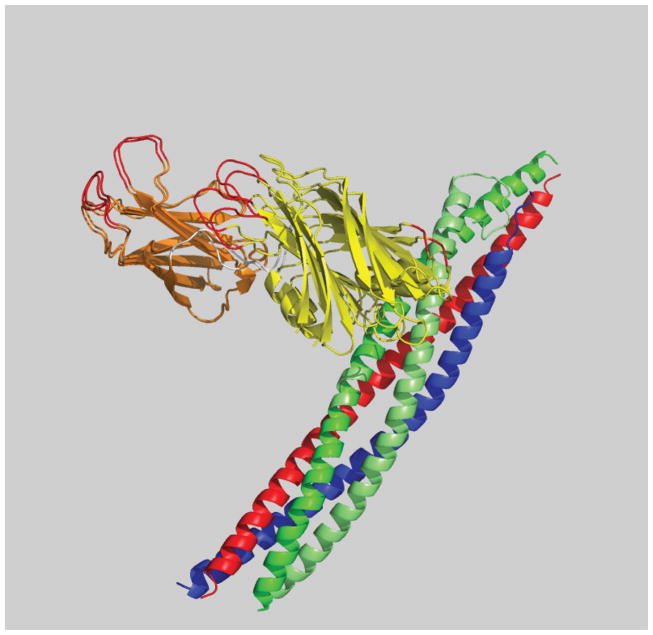
In order to cross-validate our model, we repeated the docking calculations omitting all of the restraints that involved one particular fluorophore position on Syt1. This site showed some of the highest FRET efficiency values when combined with acceptor fluorophores on the SNARE complex. Remarkably, the resulting top model was very similar to the docking calculation using all distances. Because the number of restraints exceeds the number of degrees of freedom for our docking calculations, it is reasonable that omitting a few restraints does not lead to drastically different solutions. The similarity of the top models with and without distances involving the Syt1-383 site (Figure 3) illustrates the robustness of the top solution with respect to such cross-validation.

Figure 3. Cross-validation of smFRET derived three-dimensional models.

Showing a superposition of the top models of the Syt1: SNARE complex using all smFRET-derived distances and all smFRET distances except those involving labeling site Syt1-383 (Choi et al., 2010). The quality of the model was assessed by satisfaction of the model with the observed smFRET-derived distances. The C2A domain of Syt1 is colored orange, C2B of Syt1 yellow, SNAP-25 green, synaptobrevin blue, and syntaxin red. The resulting models are very similar regardless of inclusion of the distances involving the Syt1-383 site.

Alternative to docking or fitting calculations

An alternative to docking or fitting calculations consists of calculating positional distribution functions for the fluorophore center positions taking into account the excluded volume produced by the molecule(s) to which the fluorophores are attached to (Muschielok et al., 2008). Thus, rather than calculating set of three-dimensional models, this method produces probability distributions of fluorophore positions.

In earlier work, a computational method was described for determining the positions of multiple fluorophores from several FRET-efficiency derived distances (Schröder and Grubmüller, 2004). A minimization method was used to minimize the least-squares residual between observed and calculated distances as a function of the fluorophore positions. This approach has been used for modeling of molecular conformations, such as the open and closed form of syntaxin 1 (Margittai et al., 2003). Distance-based triangulation was also used to model the study the conformation of E. coli Rep helicase bound to DNA (Rasnik et al., 2004). We also note that use of single molecule derived data is not absolutely necessary for conformational modeling. In cases where heterogeneity or dynamics are absent, distance restraints derived from multiple ensemble FRET measurements can guide such modeling (Mekler et al., 2002; Knight et al., 2005; Sun et al., 2006).

Simulation of FRET efficiency from models

Direct calculations of FRET efficiencies from molecular models

A FRET efficiency distribution can be simulated by performing molecular dynamics simulations of a fluorophores pair attached to a fixed framework of molecules(Wozniak et al., 2008; Choi et al., 2010; Vrljic et al., 2010). From such simulations, average fluorophore positions and mean orientations factors can also be calculated.

In one particular example, the C2A-C2B fragment of Syt1 was simulated with the two C2 domains treated as rigid bodies, while the torsion angles of the linker connecting the two domains were kept variable (Choi et al., 2010). Pseudoatoms were rigidly associated with the C2 domains at the indicated labeled residue positions. The position of the pseudoatom relative to the rigid bodies was derived from the simulated fluorophore center positions (see section on Simulation of fluorophore center positions). Only repulsive van der Waals energy terms were included in the simulation. This was not meant to be a realistic simulation which would require inclusion of solvent and electrostatics but rather to provide information about the range of possible conformations of Syt1. Distances were then converted to FRET efficiencies using Eq. (1) and the resulting FRET efficiencies represented as a histogram. The calculated distributions shared the broad character of the observed FRET efficiency distributions and their maxima were approximately at the same distance.

Conclusions and outlook

Many important biological structures have resisted analysis by high-resolution structural methods. The causes of these difficulties are often multiple and wide-ranging. Some proteins are not stable at the high concentrations required; some molecular systems do not reside in a single stable configuration; other interesting complexes are present only rarely within an ensemble. Single molecule FRET has proven to be an effective tool that can provide a window into these difficult systems. Although the distance resolution provided in any single FRET pair measurement does not approach the atomic dimensions, detailed structural information can be gleaned by oversampling in distance space with combinations of multiple FRET measurements across different locations.

The study of the Syt1: SNARE complex is an example of a particularly effective combination of single molecule FRET with available high-resolution structures of individual domains. The domains are either connected by flexible linkers or are bound to other stable domains in the final complex. Single molecule FRET measurements restrained docking calculations of the known high-resolution structures of the individual domains and allowed us to obtain three-dimensional models of the Syt1: SNARE complex ranked by distance satisfaction. This hybrid strategy will likely be useful to determine the configuration of other biological complexes.

As technologies for single molecule fluorescence measurement advance, the utility of smFRET for structural biology will also grow. Development of new fluorophores can lead to increased signal to noise ratios, longer observation periods, and fewer interactions between fluorophores and the molecules being studied. These improvements can be combined with instrumental advances that are expected to allow data acquisition at increased time resolution (e.g., sCMOS technology) and thus provide the capability to discriminate distinct states with similar FRET efficiencies. With these developments, it will be possible to resolve fast dynamic transitions that presently average to a single state.

Technological challenges remain. In present applications of smFRET only a limited range of distances can be probed. The Förster radii that can be obtained from fluorophores that are sufficiently bright and stable for smFRET experiments are limited typically to 4 – 8 nm. Therefore, only distances between 2 and 16 nm (~ 1/2 to 2 R₀) are practical to observe with smFRET measurements. While this range is useful for many biological molecules, certain applications would benefit from expanding this accessible distance range. Alternate methodologies may assist in addressing these other distance ranges and thus complement FRET measurements. For example, single molecule electron transfer (Yang et al., 2003) can provide access to shorter length scales while single molecule plasmon coupling to nanoparticles (Reinhard et al., 2007) is sensitive to much longer distances.

Another limitation is related to the site-specific attachment of the fluorescent probes. The cysteine mutation approach that is most common for work with proteins is not universally applicable. Sometime native cysteines are important for function or conformational stability. Sometimes cysteines are too plentiful to completely mutate in any practical manner. Incorporation of unnatural amino acids into proteins to allow fluorophore labeling with unique chemistries is showing great promise to overcome this limitation (Brustad et al., 2008).

In conclusion, smFRET is emerging as a new tool for structural biology. Three-dimensional molecular modeling using smFRET provides access to dynamic and transient conformations that are difficult to resolve by ensemble methods such as X-ray crystallography or nuclear magnetic resonance spectroscopy. The continued development of smFRET methodologies will be paralleled by equally exciting applications in structural biology.