Static and Dynamic Discharge Properties of Vestibular-Nerve Afferents in the Mouse are Affected by Core Body Temperature

Abstract

The goal of this study was to determine the effect of changes in core body temperature on the resting discharge rate and sensitivity of vestibular-nerve afferents. Extracellular recordings were made from vestibular-nerve afferents innervating the semicircular canals in anesthetized C57BL/6 mice maintained at a core body temperature of either 30 – 32° (T₃₁) or 35 – 37° (T₃₆) C. The resting rates of regular (CV* < 0.1) and irregular afferents (CV* > 0.1) were lower at T₃₁ than at T₃₆. Sensitivity and phase were compared for rotations ranging from 0.1 – 12 Hz by calculating coefficients of a transfer function, g·t_c1s·(t_zs + 1)/(t_c1s + 1), for each afferent. The sensitivity (g) increased with CV* and with higher core body temperature. The value of the coefficient representing the low-frequency dynamics (t_c1) varied inversely with CV* but did not change with core body temperature. The high-frequency dynamics represented by t_z increased with CV* and decreased with higher core body temperature. These findings indicate that changes in temperature have effects on the static and dynamic properties of vestibular-nerve afferents.

INTRODUCTION

Temperature can have profound effects on the properties of the vestibular endorgans. The caloric test, a common clinical test that examines the function of the labyrinth, uses warm and cold water or air administered to the external auditory canal. The temperature gradient created across the horizontal canal by the thermal stimulus causes the convective flow of endolymph in the horizontal semicircular canal which results in a nystagmus (Barany, 1906). The velocity of the slow-phase components of the nystagmus provides a quantitative measure of function in the labyrinth. In addition to the convective flow of endolymph resulting from caloric stimuli, there is also a direct effect of temperature on vestibular-nerve afferents and/or hair cells (Young and Anderson, 1974; Suzuki et al., 1998; Minor and Goldberg, 1990).

In vitro experiments involving vestibular hair cells and afferents are frequently performed at temperatures that are considerably lower than the body temperature of the animals (Rusch and Eatock, 1996a; Rusch and Eatock, 1996b; Holt et al., 1997; Eatock et al., 1998; Rusch et al., 1998; Lee et al., 2005). The effect of changes in core body temperature on the resting discharge rate and sensitivity to motion of vestibular afferents has not previously been defined. The core body temperature of mice, a species that is being used with increased frequency in vestibular research, can vary between 20 and 37° C in accord with the time of day and physical activity of the animal (Swoap, 2008).

In this study, we investigated the effects of changes in core body temperature on the discharge properties of vestibular-nerve afferents in mice. Our findings show that both resting rate and sensitivity are affected by core body temperature. These temperature-dependent changes are more pronounced in irregular compared to regular afferents.

METHODS

Surgical procedure & recording technique

Data were obtained from 62 adult (6 – 8 weeks old) C57BL/6 mice purchased from Charles River Laboratories. Each animal was anesthetized with an IM dose of ketamine (100 mg/kg) and an IP dose of xylazine (10 mg/kg). A heating pad (FHC, Bowdoinham, Maine) was connected to an external servomechanism (FHC, model 40-90-8B) and was used to keep the animal’s core body temperature between 30 – 32° C or between 35 – 37° C. During the experiment, saline (5% of body weight) was injected subcutaneously and the heart and respiratory rate were monitored to maintain good physiologic status.

The animal was then placed in a stereotaxic frame such that the top of the skull was parallel to the horizontal plane. The surgical approach has been described previously (Lasker et al. 2008a) and will be summarized as follows. A suboccipital craniotomy on the left side was made under microscopic visualization exposing the cerebellar cortex and paraflocculus. These were aspirated, exposing the medial face of the temporal bone. Care was taken not to damage the transverse sinus or the temporal bone. The brain stem was then retracted minimally to expose the vestibular nerve as it traversed the internal auditory meatus. The superior and inferior branch of the vestibular nerve exited the temporal bone at different sites with the superior branch projecting more rostrally than the inferior nerve. All surgical and experimental procedures were approved by the Animal Care and Use Committee of The Johns Hopkins University School of Medicine.

Glass micropipettes (WPI Corp., M1B100F-4) with impedances of 20–60 MΩ were filled with 3 M NaCl and adjusted into position over the nerve using a minimanipulator (You, model US-3F). This minimanipulator could maneuver in three dimensions and was attached to a microdrive (Narishige International USA, model MO-22) mounted on the stereotaxic frame. The micropipette was advanced using the microdrive until it entered the vestibular nerve as it emerged from the internal auditory meatus. Signals from the micropipette were amplified and band-pass filtered (100 – 3kHz) (Dagan, model 2400A). Extra-axonal activity of afferents was identified by the use of an external auditory speaker. A window discriminator was used to identify action potentials (Mentor, model N-750). The timing of action potentials was recorded through a digital event channel with a resolution of 100nS (CED, micro1401). The voltage from the microelectrode was also digitized with a 16-bit A/D converter with a sample rate 5 kHz for off-line comparison with the spike-times. The angular head position was obtained using a high-resolution digital encoder that was also digitized with a sample rate of 2 kHz. These signals were then recorded to a PC for off-line analysis.

Rotational stimulation

Once a canal afferent was identified, a Fick gimbal was used to position the animal such that the afferent was within 20 % of the maximum sensitivity for that canal plane. We estimated the maximum sensitivity for each afferent by using an equation representing the optimal canal plane derived in our earlier study (Lasker et al. 2008a). Animals were than rotated at frequencies ranging from 0.1 – 12 Hz at peak velocities of 25 °/s via a position servomotor. Responses during each sinusoid were recorded for 30 seconds. Angular head velocity was obtained by differentiating the signal from an angular position transducer mounted to the shaft of the turntable. The accuracy of the turntable position was confirmed via a linear accelerometer mounted eccentric to the head of the mouse. The phase difference between the accelerometer and the table position was 180 ± 3° (mean ± SD) at all frequencies.

Data analysis and transfer function fits

A cycle histogram was created from average spike rates. Resting rate and CV* were calculated as we have described (Lasker et al. 2008a). All statistical comparisons were performed using an analysis of variance model (ANOVA). A least squares fit was performed to the first harmonic of the averaged head velocity and cycle histogram of instantaneous firing rate to calculate the sensitivity and phase at each frequency. The sensitivity was then calibrated using the individual canal's maximum sensitivity vector. Transfer functions were fit using a least squares technique to the average sensitivity and phase after normalizing the sensitivity for each afferent to a sensitivity of 1.0 at 0.75 Hz. Normalization of the average data was necessary because responses were not recorded at every frequency for each afferent. The order of the resulting transfer function (i.e. number of poles and zeros) was determined using the Bayesian Information Criteria (BIC) (Lasker et al. 2008a). It was determined from the average data that the best transfer function fit consisted of an equation that contained a zero (t_z) and a pole (t_c) [see Results - Equation 2]. Individual transfer functions were then fit to the raw data for each afferent with a transfer function containing one zero and pole. It was necessary to constrain the order of the fits in this way in order to make meaningful comparisons of the dynamics among individual afferents.

RESULTS

Resting discharge rate and coefficient of variation

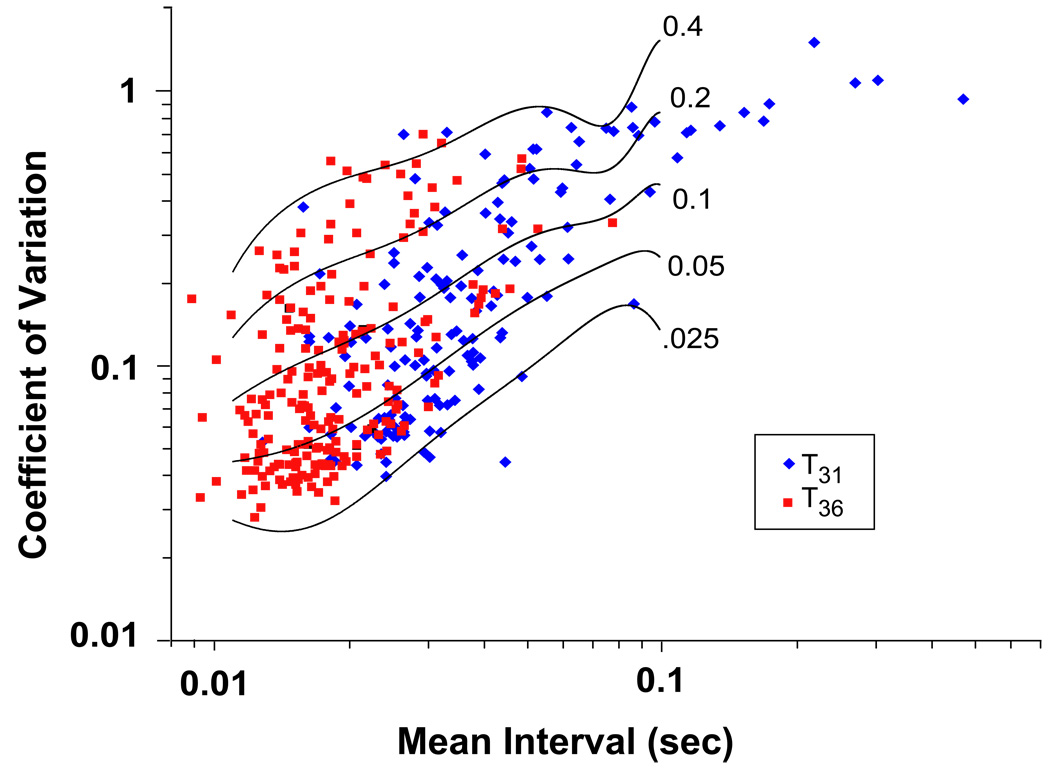
We obtained a resting discharge rate and a corresponding coefficient of variation in a total of 368 canal afferents recorded in 62 mice at ages 6 – 8 weeks (Fig. 1). Of these, 160 were recorded in 29 animals while keeping the core body temperature of the mouse between 30 – 32° C (T₃₁) and 208 were recorded in 33 animals while keeping the core body temperature between 35 – 37° C (T₃₆). CV* was calculated for 351 of these units. There were 17 units for which CV* could not be calculated because the resting rates of these afferents were either too low (< 10.1 spikes.s⁻¹) or too high (> 90.1 spikes.s⁻¹) thereby placing the units outside the range of our normalization technique (Figure 1). The remaining units were classified based upon discharge regularity into either regular (CV* < 0.1) or irregular (CV* > 0.1) groups (Goldberg et al., 1984; Baird et al., 1988; Hullar et al., 2004; Lasker et al., 2008a). The results are listed in Table 1. There was no difference between the coefficient of variation or the distribution of regular versus irregular afferents. The resting rate was, however, greater at the higher core body temperature for both regular and irregular afferents.

Figure 1.

Values for the coefficient of variation (CV) and the corresponding interspike interval (ISI) during a 5-sec interval of resting activity for vestibular-nerve afferents innervating the semicircular canals in the mouse. Data obtained with the core body temperature kept at T₃₁ are plotted in blue while those at T₃₆ are plotted in red. Curves are plotted relating the ISI and CV for 5 values of CV* (0.025, 0.05, 0.1, 0.2, 0.4).

Table 1.

Resting discharge rate and coefficient of variation at the two core body temperatures.

Core body temperature	Regular			Irregular
	Resting Rate (sp/s)	CV*	No. of afferents	Resting Rate (sp/s)	CV*	No. of afferents
T31 (29 mice)	36.2 ± 12.3a	0.05 ± 0.02b	96 (64%)c	22.4 ± 13.5a	0.20 ± 0.10d	53 (36%)c
T36 (33 mice)	56.5 ± 15.5a	0.05 ± 0.02b	139 (69%)c	43.8 ± 15.1a	0.22 ± 0.11d	63 (31%)c

The p values for the comparisons indicated by superscripts are as follows:

^ap < 0.001,

^bp > 0.3,

^cp > 0.1,

^dp > 0.4

Response dynamics

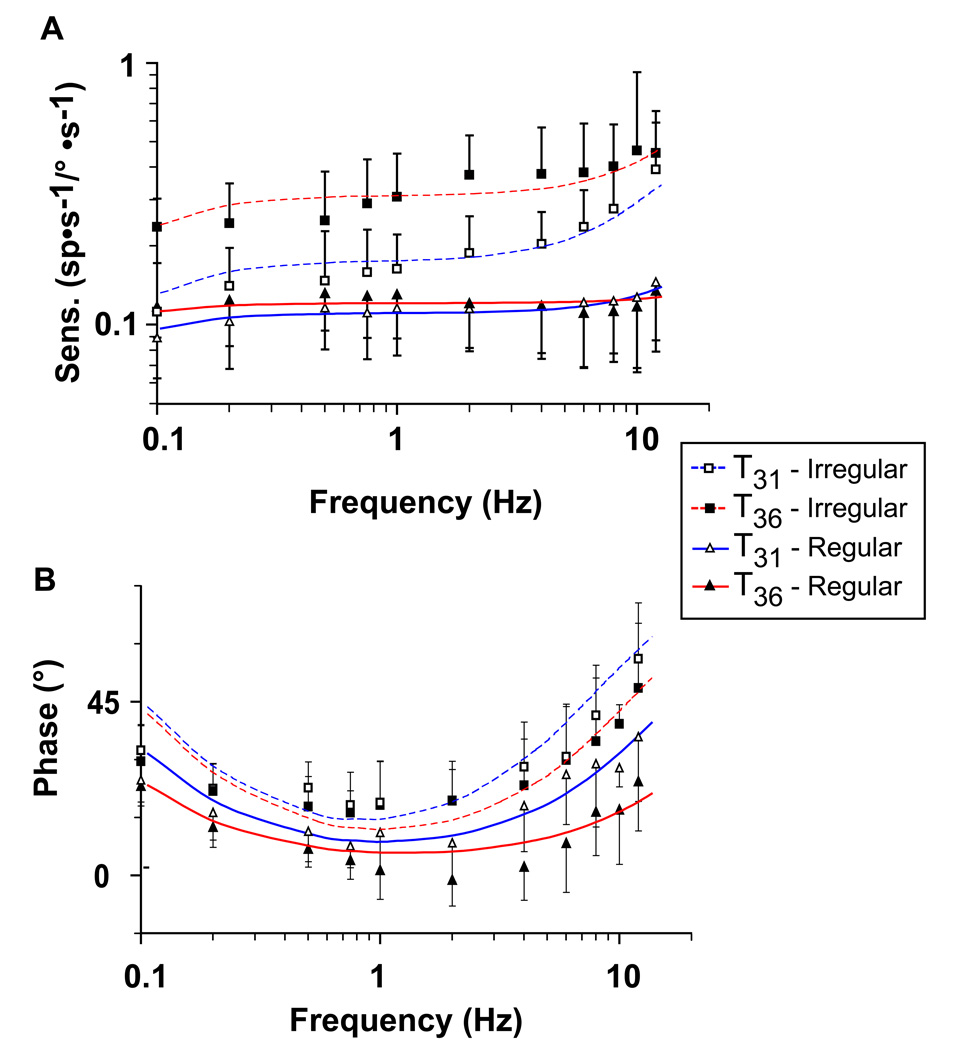
Responses to sinusoidal rotations were studied for 42 regular and 22 irregular afferents at T₃₁ and for 60 regular and 24 irregular afferents at T₃₆. Data were only included in this set if sensitivity and phase were measured at 0.75 Hz and at least one other frequency. In order to obtain an average sensitivity for regular and irregular afferents, we normalized the sensitivity values to 1.0 at 0.75 Hz for each individual afferent. The average sensitivity and phase are plotted versus frequency in Figure 2.

Figure 2.

Average sensitivity (A) and phase (B) plotted versus frequency at T₃₁ and at T₃₆ for regular and irregular afferents. Fits to the average sensitivity and phase are plotted versus frequency in blue at T₃₁ and in red at T₃₆. The number of data points at T₃₁ for each frequency used in the fits of the transfer function for regular afferents was as follows: 0.1 Hz = 24, 0.2 Hz = 30, 0.5 Hz = 21, 0.75 Hz = 42, 1 Hz = 17, 2 Hz = 27, 4 Hz = 19, 6 Hz = 15, 8 Hz = 16, 10 Hz = 5, 12 Hz = 11. The number of data points at T₃₁ for each frequency used in the fits of the transfer function for irregular afferents was as follows: 0.1 Hz = 12, 0.2 Hz = 19, 0.5 Hz = 16, 0.75 Hz = 22, 1 Hz = 15, 2 Hz = 21, 4 Hz = 15, 6 Hz = 15, 8 Hz = 10, 12 Hz = 6. The number of data points at T₃₆ for each frequency used in the fits of the transfer function for regular afferents was as follows: 0.1 Hz = 13, 0.2 Hz = 22, 0.5 Hz = 9, 0.75 Hz = 60, 1 Hz = 48, 2 Hz = 43, 4 Hz = 37, 6 Hz = 33, 8 Hz = 26, 10 Hz = 19, 12 Hz =18. The number of data points at T₃₆ for each frequency used in the fits of the transfer function for irregular afferents was as follows: 0.1 Hz = 6, 0.2 Hz = 8, 0.5 Hz = 8, 0.75 Hz = 24, 1 Hz = 18, 2 Hz = 18, 4 Hz = 15,6 Hz = 13, 8 Hz = 9, 10 Hz = 4, 12 Hz = 6.

Transfer functions were fit to the average sensitivity and phase to describe the dependence of these parameters on frequency. In every case, we fit higher orders (different combinations of poles and zeros) and determined from the values obtained for the BIC that the resulting data were best fit with a transfer function of the form:

$$\text{DR}=\frac{\mathrm{g}·({\mathrm{t}}_{\mathrm{c}}\mathrm{s})({\mathrm{t}}_{\mathrm{z}}\mathrm{s}+1)·\text{Hv}}{({\mathrm{t}}_{\mathrm{c}}\mathrm{s}+1)}$$ eq 1

where DR = canal afferent discharge rate and Hv = angular head velocity. The average values obtained for each set of afferents are shown in Table 1.

Equation 1 has three parameters (g,t_c,t_z) describing the response properties of vestibular afferents across a wide range of frequencies. The value of g is a measure of the sensitivity to head velocity (spikes/s/deg/s) for frequencies that range from approximately 0.5 – 2 Hz. The coefficient (t_z) is a time constant that describes how an afferent responds at high frequencies (> 2 Hz.). The higher the value of t_z, the lower the frequency at which the response will begin to display dynamics that are more closely aligned with head acceleration instead of head velocity. The value of t_c is the time constant that describes responses of the afferent at low frequencies (< 0.5 Hz). If an animal is rotated at a constant velocity the afferent will initially fire in proportion to the speed of rotation as denoted by the parameter g. With sustained rotation at a constant velocity, the afferent response will begin to decay at an exponential rate back to its base line firing rate. The parameter t_c is the time in seconds required for the response to decay by 63%.

Effect of CV* and core body temperature on afferent dynamics

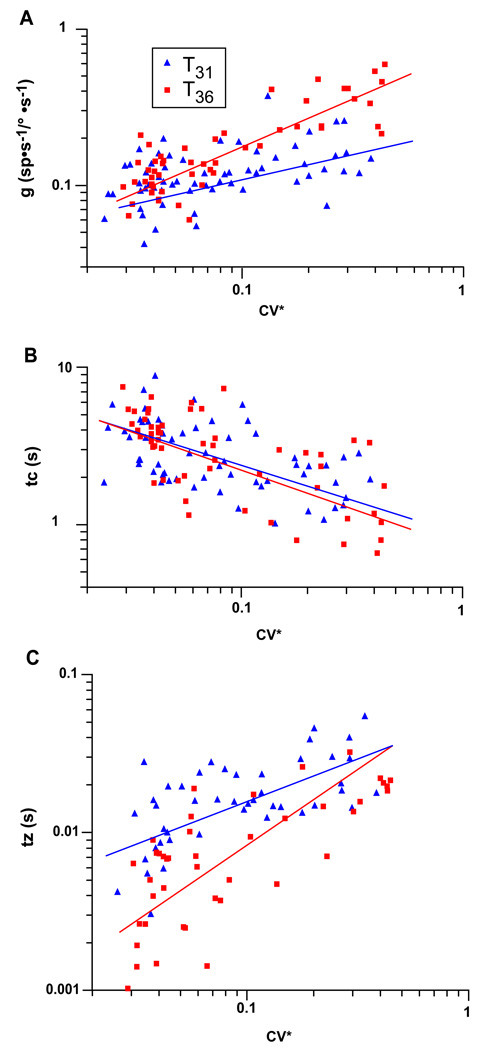
In order to determine the relationship of afferent dynamics, discharge regularity, and core body temperature, we fit each individual afferent with the transfer function from Equation 1. The averaged values obtained from the individual fits are shown in Table 1. We plotted the three parameters of our transfer function (g, t_z, and t_c) versus CV* on a logarithmic scale (Figure 3). Regression equations were produced with the following relationship: Y = a·CV*^b, where Y is either g, t_z, or t_c. We used the data shown in Figure 3A to obtain the following regression equations for the mid-band sensitivity (g) versus CV*.

$$\begin{array}{c}{\mathrm{g}}_{31}=(0.214+0.034){({\text{CV}}^{*})}^{0.235\pm .059},{\mathrm{R}}^2=0.22\hfill \\ {\mathrm{g}}_{36}=(0.665+0.087){({\text{CV}}^{*})}^{-0.563\pm 0.049},{\mathrm{R}}^2=0.72\hfill \end{array}$$

Figure 3.

Parameters of the transfer function describing afferent dynamics are plotted vs. CV* [Panel A, sensitivity (g); Panel B, long time constant (t_c); and Panel C, short time constant (t_z)]. Values taken with the core body temperature kept at T₃₁ are plotted in blue while values taken at T₃₆ are plotted in red. Power law regressions were fit to the data and are plotted as solid lines in blue for T₃₁ and red for T₃₆.

We determined that the values for a and b (the coefficients in these equations) differed between the two temperature conditions (p < 0.001 for both a and b).

We used the data shown in Figure 3B to obtain the following regression equations for the low-frequency time constant of the transfer function (t_c) versus CV*:

$$\begin{array}{c}{\mathrm{t}}_{\mathrm{c}31}=(1.167+0.219){({\text{CV}}^{*})}^{-0.326\pm 0.069},{\mathrm{R}}^2=0.27\hfill \\ {\mathrm{t}}_{\mathrm{c}36}=(0.824+0.165){({\text{CV}}^{*})}^{-0.472\pm 0.075},{\mathrm{R}}^2=0.44.\hfill \end{array}$$

There was no difference between the values of a or b for the two different temperature conditions (p > 0.2 for a and p > 0.15 for b).

We used the data shown in Figure 3C to obtain the following regression equations for the high-frequency time constant of the transfer (t_z) versus CV*:

$$\begin{array}{c}{\mathrm{t}}_{\mathrm{z}31}=(0.051+0.012){({\text{CV}}^{*})}^{-0.488\pm 0.091},{\mathrm{R}}^2=0.40\hfill \\ {\mathrm{t}}_{\mathrm{z}36}=(0.039+0.011){({\text{CV}}^{*})}^{-0.702\pm 0.107},{\mathrm{R}}^2=0.52.\hfill \end{array}$$

There was no difference in the values of a and b for the two temperature conditions (p > 0.5 for a and p > 0.09 for b).

DISCUSSION

As previously shown, sensitivity to rotations of canal afferents in mice is about 3-fold lower than in larger animals such as cats, chinchillas or monkeys (Yang and Hullar, 2007; Lasker et al., 2008a). The static and dynamic discharge properties of vestibular afferents in mice are, however, qualitatively similar to those in other animals in virtually every other respect. Our findings from afferents recorded when the core body temperature was 35–37° C (T₃₆) were similar to those reported previously (Lasker et al., 2008a). Our goal in this study was to determine the effect of lowering the core body temperature to 30–32° C (T₃₁) on the properties of vestibular-nerve afferents. We found that there were three effects: a decline in resting rate, a decline in sensitivity to head velocity that was much greater in irregular afferents, and an increase in t_z.

Discharge regularity and coefficient of variation

The resting rates obtained from both regular and irregular afferents were larger at the warmer (T₃₆) than at the colder (T₃₁) core body temperature. One likely explanation for this finding is that core body temperature has a direct temperature effect on vestibular hair cells and/or nerve fibers. The resting discharge rate rose by ~50% for regular afferents and by ~90% for irregular afferents when temperature was increased by ~5° C. These findings agree with estimates of the direct effect of temperature on the vestibular periphery determined from analysis of the caloric nystagmus in squirrel monkeys (Minor and Goldberg, 1990). In that study the nystagmus resulting from changes of the temperature of the inner ear had a convective and a nonconvective component. The nonconvective component was thought to result from direct effects of temperature on the neuroepithelium and might be mediated at least in part by differences in channel kinetics, transmitter release, diffusion rates, enzyme reaction rates and other mass action processes within cells. It was concluded that the average background discharge should change due to this nonconvective component by approximately 10% per °C. This value corresponds to the changes we observed in regular afferents, the afferents that are likely to make the largest contribution to low-frequency responses such as caloric nystagmus (Minor and Goldberg, 1990). This change in resting rate also corresponds to predicted changes in ion channel conductance. Quantitative measurements of the gating of K⁺ and Na⁺ ion channels in the squid giant axon indicate that conductance rises 2–4 fold for each 10° C increase in temperature [Hodgkin-Huxley, reviewed in Hille (2001)]. Our data are consistent with the existence of a direct relationship between resting discharge rate and ion channel conductance.

The larger dependence of the resting rate on temperature for irregular in comparison to regular afferents might be explained based upon differences in the post-spike recovery functions for these two groups of afferents. Irregular afferents have an after-hyperpolarization following each action potential with rapid repolarization to near threshold. In contrast, the repolarization for regular afferents follows a slower, more linear trajectory (Smith and Goldberg, 1986). The increased transmitter release from hair cells that occurs with a rise in temperature would, therefore be expected to cause a greater change in resting rate for irregular than for regular afferents.

Dynamics versus CV*

The mid-band sensitivity (g) is higher at T₃₆ than at T₃₁. This finding raises a number of interesting, and heretofore unexplored, questions regarding the temperature-dependence of vestibular processes. The changes in sensitivity are most pronounced for irregular afferents (Table 1). In primates, these afferents have been shown to provide the major inputs to vestibulospinal pathways (Boyle et al., 1992). Irregular afferents also appear to be important for vergence-mediated changes in the vestibuloocular reflex (Chen-Huang and McCrea, 1998; Lasker et al., 2002; Migliaccio et al., 2008). Unless there are reciprocal temperature-dependent changes in the sensitivity to motion of central neurons, then responses of central processes and reflexes receiving irregular afferent inputs would be expected to decline as temperature falls. Smaller changes would be predicted for reflexes receiving inputs predominantly from regular afferents such as the angular VOR in response to lower frequency head movements (Minor and Goldberg, 1991; Minor et al., 1999).

The long time constant (t_c) varies inversely with CV* with regular afferents having a time constant of approximately 3.5 s versus irregular afferents having a time constant of only 2.0 s. Variations in the long time constant between regular and irregular afferents have been shown in other mammals (Goldberg and Fernandez, 1971). However, there is no difference between the long time constant (t_c) at T₃₁ versus T₃₆ for regular and irregular afferents. The long time constant is believed to reflect the specific biomechanical properties of the semicircular canals and this finding supports the notion that the change in core body temperature does not significantly affect the properties of the cupula and/or endolymph.

The short time constant (t_z) varies proportionally with CV*. A similar relationship has recently been shown in the mouse and chinchilla (Hullar et al., 2004; Lasker et al., 2008a). The change in core body temperature also affects the high frequency dynamics of the canal afferents with the value of t_z being greater at T₃₁ in comparison to T₃₆. This increase was significant only for regular afferents and not for irregular afferents. It is been shown that most of the dynamics associated with t_z occur prior to the post-synaptic spike initiation zone (Goldberg et al. 1982; Goldberg et al. 1984; Lasker et al. 2008b). The reason for this difference between afferent groups is not apparent. Recent studies have speculated that differences in the proportion of GABA to glutamate transmitted from the hair cell to the axon could be responsible for the variation in the high frequency dynamics between afferent sub-types in the toadfish (Holstein et al., 2004). The administration of a GABA antagonist had two specific effects on the most "acceleration sensitive" neurons (i.e. those neurons with the largest value of t_z). The first effect was an increase in sensitivity to head motion that could be explained by the removal of GABA, an inhibitory neurotransmitter. The second effect was to reduce the afferent's sensitivity to acceleration (i.e., reduce the value of t_z). Holstein et al. (2004) postulated that a delayed contribution of GABA could act as a differentiator, thereby converting sensitivity to head velocity into sensitivity to head acceleration. Interestingly, we see a similar dual effect when comparing the effects at the two core body temperatures. When the animals were at the cold core body temperature the overall effect was a decrease in the sensitivity with a concomitant increase in its sensitivity to acceleration (larger values of t_z). This finding suggests that if a mechanism similar to that in the toad fish exists in the mouse then changes in core body temperature could preferentially affect the afferents that are more sensitive to GABA than glutamate. Previous studies have shown that inhibitory neural transmitters are more thermosensitive than excitatory ones (Adolph 1973; Raiteri and Levi 1973).

Table 2.

Parameters obtained for best fits to normalized data and individual afferent data to the transfer function of the form: g·(t_cs)(t_zs + 1)/(t_cs + 1).

Afferent Cat.	g (sp·s−1/deg·s−1)		tc (s)		tz (s)
	Best fit to normalized data	Fit to individual afferents	Best fit to normalized data	Fit to individual afferents	Best fit to normalized data	Fit to individual afferents
Regular –T31	0.11	0.11 ± 0.04a	2.9	3.5 ± 1.6c	0.010	0.014 ± 0.008e
Regular –T36	0.13	0.13 ± 0.04a	4.1	3.9 ± 1.6c	0.005	0.005 ± 0.003e
Irregular –T31	0.18	0.16 ± 0.07b	1.8	2.2 ± 1.1d	0.022	0.024 ± 0.012f
Irregular –T36	0.31	0.34 ± 0.12b	2.0	1.8 ± 0.9d	0.015	0.017 ± 0.007f

The p values for the comparisons indicated by superscripts are as follows:

^ap < 0.05,

^bp < 0.001,

^cp > 0.1,

^dp > 0.15,

^ep < 0.001,

^fp > 0.06