Summary
How are local motion signals integrated to form a global motion percept? We investigate the neural mechanisms of tactile motion integration by presenting tactile gratings and plaids to the fingertips of monkeys, using the tactile analogue of a visual monitor, while recording the responses evoked in somatosensory cortical neurons. In parallel psychophysical experiments, we measure the perceived direction of the gratings and plaids. We identify a population of somatosensory neurons that exhibit integration properties comparable to those observed in area MT to analogous visual stimuli. We find that the responses of these neurons can account for the perceived direction of the stimuli across all stimulus conditions tested. We show that the preferred direction of the neurons and the perceived direction of the stimuli can be predicted from the weighted average of the directions of the individual stimulus features (edges and intersections).
INTRODUCTION
A common problem faced by neural systems is to integrate information across locally ambiguous cues to infer a global stimulus property, a problem solved by implementing adequate algorithms or heuristics. A well-studied visual example of such an integration problem is the aperture problem (Wallach, 1935). Indeed, the direction of motion of one-dimensional edges is ambiguous because information about the motion component parallel to their orientation is not available. To acquire a veridical direction percept, it is necessary to integrate motion information across multiple stimulus contours that differ in orientation or to rely on terminators. Early in sensory processing, motion is encoded in the responses of neurons whose receptive fields are spatially restricted and are thus susceptible to the aperture problem. Hence, integrating motion information across the sensory image is necessary to recover the veridical velocity of the object by integrating stimulus contours that differ in orientation (Rust et al., 2006;Simoncelli and Heeger, 1998) or by relying on motion signals emanating from terminators (i.e., corners and intersections) whose velocity is unambiguous (Pack et al., 2003;Shimojo et al., 1989).
In both the visual and somatosensory systems, stimulus motion is inferred from a spatio-temporal pattern of activation across a two-dimensional sensory sheet (i.e., the retina and the skin). Not surprisingly, motion processing in the somatosensory system shares many similarities with its visual counterpart. First, a large proportion of neurons in somatosensory cortex, particularly in area 1, are strongly tuned for direction of motion (Costanzo and Gardner, 1980;Pei et al., 2010;Ruiz et al., 1995;Warren et al., 1986;Whitsel et al., 1971) (Supplemental Fig. 1), as has been shown in primary visual cortex (Hubel and Wiesel, 1968) and in the middle temporal area (area MT) (Albright, 1984;Maunsell and Van Essen, 1983;Zeki, 1974). Second, in a subpopulation of these neurons, the tuning is consistent across a variety of different stimulus types, including bars, dot patterns, and random dot displays (Pei et al., 2010). Third, the responses of this subpopulation of area 1 neurons can account for the perceived direction of these stimuli (Pei et al., 2010). Fourth, the perception of stimuli comprising ambiguous motion cues, such as barber poles and plaids, is similar in vision and in touch (Bicchi et al., 2008;Pei et al., 2008).
In somatosensory cortex, a processing hierarchy has been established: neurons in the earliest stages of motion processing – in area 3b – respond to the motion of local elements, whereas neurons in higher processing stages – in area 1 – are apt to encode global motion, for instance, when stimulated with random dot patterns (Pei et al., 2010). The question remains, then, how motion signals in area 1 are constructed. Specifically, what algorithm or heuristic is implemented in somatosensory cortex to compute from locally ambiguous cues the direction in which a stimulus moves across the skin?
Plaids, consisting of two superimposed gratings, have been widely used in neurophysiological experiments to characterize how neurons in MT integrate motion information. At one end of the spectrum of integration properties, “component” neurons respond to the individual component gratings forming the plaid. At the other extreme, “pattern” neurons encode the veridical motion of the plaid by integrating motion information across stimulus contours and/or terminators. Because plaids comprise ambiguous local motion cues, these stimuli are well suited to characterize the computations implemented in sensory systems to extract information about the global motion of a stimulus.
RESULTS
We recorded the responses of 113 neurons in somatosensory cortex: 66 neurons in area 1, 28 neurons in area 2, and 19 neurons in area 3b. We sampled more sparsely from areas 3b and 2 because neurons in these areas exhibit only weakly direction-tuned responses to gratings (Supplemental Fig. 1) and to other spatially complex stimuli (Pei et al., 2010).
Integration properties of neurons in somatosensory cortex
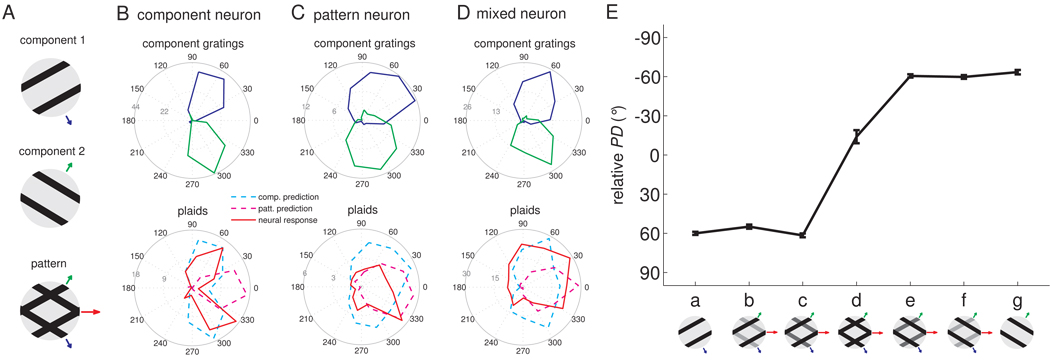
A first set of plaids (type 1 plaids) were constructed by superimposing non-additively two square-wave gratings whose directions of motion were separated by 120° (Figure 1A). Figure 1 shows the responses to type 1 plaids of typical direction-sensitive neurons in area 1: One neuron (Figure 1B), akin to component neurons in MT, yielded a bi-modal distribution of responses to plaid stimuli, the two modes separated by 120°. This neuron thus responded whenever one of the component gratings moved in its preferred direction (PD). The second neuron (Figure 1C,E) yielded a unimodal distribution of responses to the stimuli, exhibiting responses analogous to that of pattern neurons in MT (Movshon et al., 1983;Movshon and Newsome, 1996): it produced its highest response when either a plaid or a pure grating moved in its PD. The third neuron (Figure 1D) exhibited intermediate integration properties. Across the population, neurons in area 1 exhibited responses that ranged from pure pattern to pure component tuning (Figure 2A). In contrast, neurons in areas 3b and 2 did not exhibit pattern tuning or exhibited only very weak pattern tuning (Figure 2A), in part because relatively few neurons in these areas were tuned for direction when stimulated with plaids (Supplemental Fig. 1). At both single-cell and population levels, when the pattern was morphed from a grating to a plaid, the PD of pattern neurons dramatically shifted from that corresponding to the direction of the simple grating (Figure 1E-a,g and 2B-a,g) to that bisecting the directions of the two component gratings (Figure 1E-d and 2B-d); the PD of pattern neurons matched the perceived direction measured in human psychophysical experiments (Figure 2B). Our results are therefore consistent with the hypothesis that area 1 comprises a population of neurons whose responses mediate our perception of tactile motion. However, the neuronal and behavioral data were obtained from different species; this hypothesis could be tested in future experiments by assessing whether electrically stimulating clusters of direction selective neurons systematically affects the animal’s performance in a direction discrimination task (Salzman et al., 1990) or by ascertaining whether the responses of direction selective neurons are predictive of a monkey’s behavior (Britten et al., 1996;Shadlen et al., 1996). Note, however, that human perceptual discrimination has been successfully predicted from macaque neuronal responses across a variety of contexts (Bensmaia et al., 2008;LaMotte and Mountcastle, 1975;Mountcastle et al., 1972;Pei et al., 2010, e.g.), and that the human and macaque somatosensory systems bear many similarities (Mountcastle, 2005). To further characterize the integration properties of somatosensory cortical neurons, we presented plaids with reversed polarity (so-called positive plaids) (Pei et al., 2008) and obtained similar results to those described above (Supplemental Fig. 2).
Figure 1.
The motion integration properties of somatosensory neurons estimated from their responses to type 1 plaids. A. The plaid is constructed by non-additive superimposition of two component gratings that move in directions separated by 120°. The velocity (direction and speed) of the two components and of the resulting plaid are denoted with blue, green and red arrows, respectively; the length of the arrows is proportional to the speed of the components (blue and green) or of the pattern (red). Responses of a typical (B) component neuron, (C) pattern neuron, and (D) “mixed” neuron. The angular coordinate denotes the direction of motion of the stimulus (in degrees), the radial coordinate the response (in impulses per second). The blue and green traces are the neural responses to component gratings 1 and 2, respectively, and the red trace shows the neural response to plaids (with the two component gratings at equal amplitude). Component predictions (dashed cyan traces) are constructed by summing the responses to the component gratings and corrected for baseline firing rate. Pattern predictions (dashed magenta traces) are tuning curves measured using simple gratings. Component neurons yield bimodal tuning curves when tested with plaids (red trace in B), similar to those obtained when each component grating is presented alone. In contrast, pattern neurons yield a unimodal tuning curve when tested with plaids (red trace in C), centered on the veridical direction of motion of the plaid. Interestingly, many pattern neurons exhibited asymmetric tuning curves when tested with plaids. The “mixed” neuron (D) exhibited an intermediate pattern of responses to plaids. E. Neuronal PD of the example pattern neuron shown in C as component 1 is morphed into a plaid, which is then morphed into component 2 (0° corresponds to pattern motion).
Figure 2.
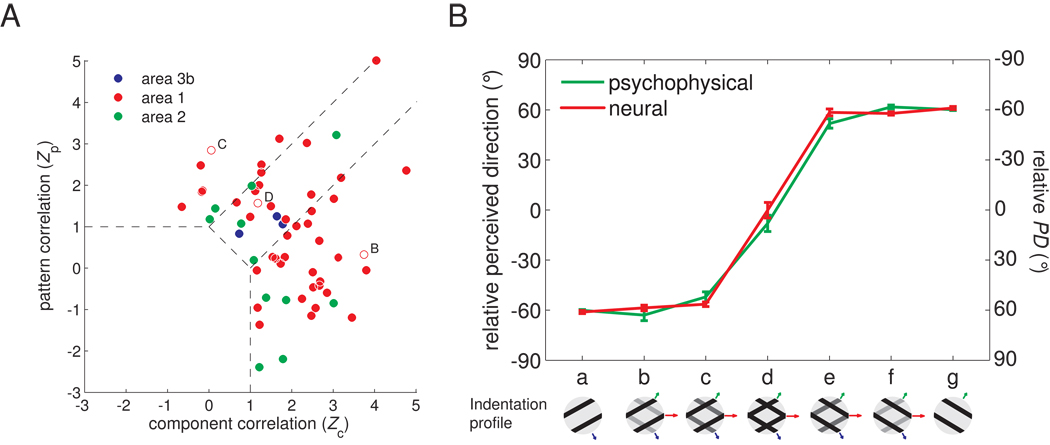
Quantifying the motion integration properties of somatosensory cortical neurons. A. Integration properties of somatosensory cortical neurons derived from their responses to type 1 plaids (cf. Movshon and Newsome, 1996). Each neuron’s integration properties are indexed by characterizing the degree to which each of its responses to plaids matches the corresponding response of an idealized component or pattern neuron. Zc and Zp are the Fisher’s z-transforms (Hotelling, 1953) of the partial correlation between the measured responses and the responses of an idealized component and pattern neuron, respectively. Zc and Zp are shown for all motion-sensitive neurons in somatosensory cortex (blue: area 3b; red: area 1; green: area 2). Data points in the upper left quadrant indicate pattern tuning, whereas points in the lower right quadrant indicate component tuning. Data points intermediate between those two indicate “mixed” tuning properties. The two dashed lines denote the criteria at which the absolute difference between Zp and Zc is 1 and separate “pattern,” “mixed,” and component neurons from one another. The open symbols correspond to the example neurons shown in Figure 1 (B. the component neuron; C. the pattern neuron; D. the “mixed” neuron). B. PD of pattern-like neurons and perceived direction as component 1 is morphed into a plaid, which is then morphed into component 2. Neurons whose plaidness index (PI = Zp-Zc) was greater than the median value were used to compute the population PDs. Note that matching relative PDs and perceived directions are of opposite polarity. For example, a neuron with a relative PD of −60° would yield a perceived direction of 60°.
Models of motion integration
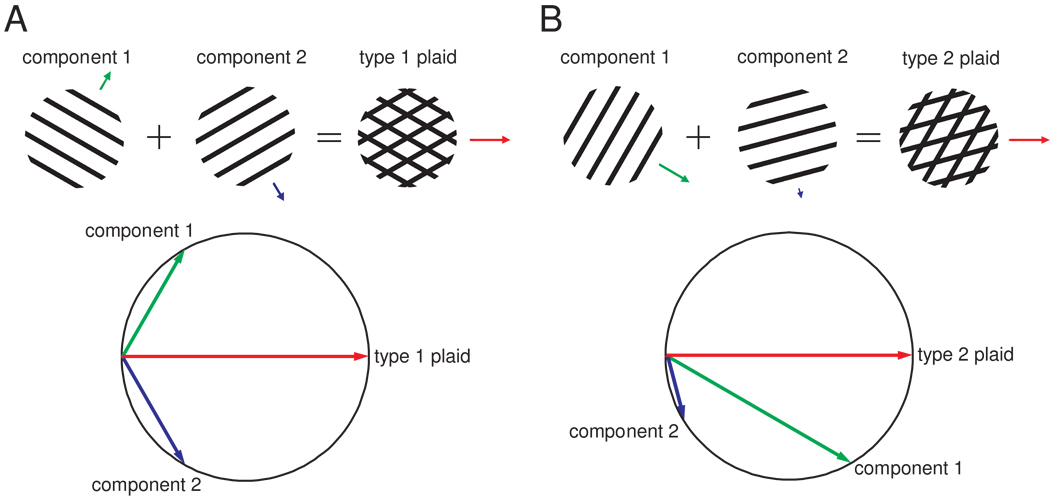
Responses of area 1 neurons to plaids, then, are analogous to the responses of MT neurons to visual plaids. This similarity suggests that the mechanisms of integration are similar in the two sensory modalities. Two models of motion integration have been fruitfully applied to visual motion integration, namely the Intersection of Constraints (IOC) and Vector Average (VA) models. The IOC model (Adelson and Movshon, 1982;Fennema and Thompson, 1979;Movshon et al., 1983;Simoncelli and Heeger, 1998) appeals to the fact that the speed and direction of each stimulus contour constrains the possible interpretations of the motion of the stimulus as a whole. Two such constraints are sufficient to determine the veridical direction of stimulus motion (see Figure 3). According to the VA model (Movshon et al., 1983;Treue et al., 2000;Weiss et al., 2002), the response of a pattern neuron is determined by the mean direction of the component contours making up the stimulus, each direction normal to the contour’s orientation. These two models imply very different mechanisms to extract the global direction of motion. Both VA and IOC models make similar or identical predictions as to the perceived direction of the plaids described above, dubbed type 1 plaids. In contrast, another category of plaids (type 2 plaids), which consist of two superimposed gratings that differ in both speed and direction of motion, draw divergent predictions from the two models. Specifically, the IOC model always predicts the veridical direction of motion, which, for type 2 plaids, falls outside of the angle delimited by the directions of the component gratings (Figure 3B). In contrast, the direction of motion predicted by the VA model is confined to the angle delimited by the component directions (unless terminator signals are also included in the computation, see below).
Figure 3.
Constructing plaids: Type 1 and 2 plaids and their perceived directions estimated using the Intersection of Constraints model. The vector’s length and direction represent the grating’s speed and direction, respectively. In each panel, we show how the plaid is constructed by superimposing two component gratings. The Intersection of Constraints model estimates the direction of motion of the plaid pattern by finding the only solution that is compatible with the velocity (speed and direction of motion) of both component vectors. The direction predicted by the Intersection of Constraints model is the veridical direction of the resultant plaid. A. Example of a type 1 plaid whose direction of motion lies between those of its two components. B. Example of a type 2 plaid whose direction of motion lies outside of the angle spanned by the two component directions.
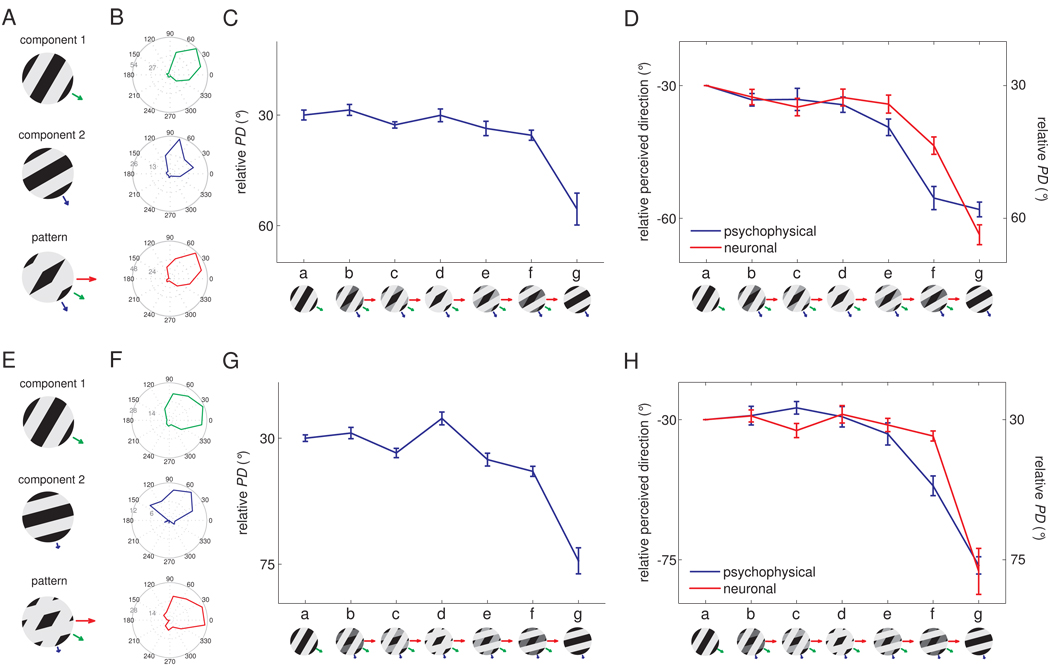
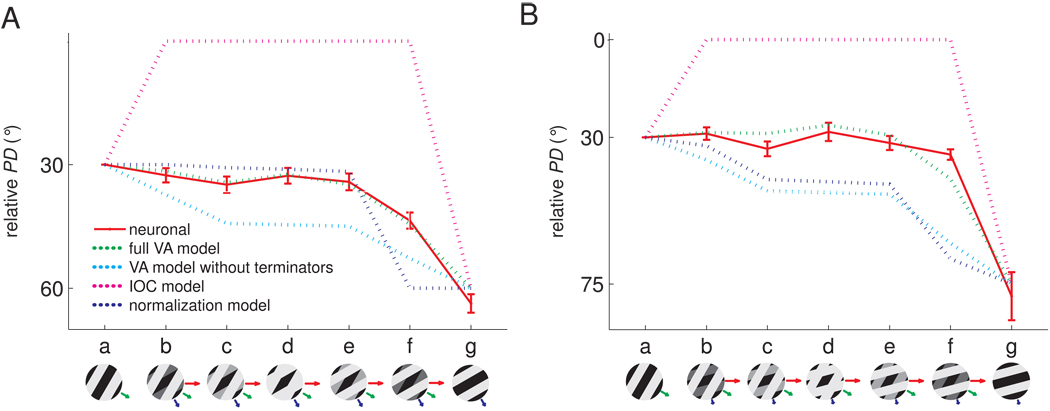
In vision, the IOC model accounts for perceived direction under most circumstances (since the veridical direction of motion is generally recovered, see Supplemental Fig. 3), suggesting that the IOC model is implemented in the visual system through non-linear neural mechanisms or that the perceived direction of visual motion is dominated by terminators (Pack et al., 2003;Pack et al., 2004). To ascertain whether the same holds true for touch, we recorded the responses of neurons in somatosensory cortex to type 2 plaids and measured the perceived direction of these stimuli in paired human psychophysical experiments. Figure 4 shows the responses of an individual neuron in area 1 to type 2 plaids with component directions separated by 30° (A–C) and 45° (E–G). The PD seemed to be determined predominantly by the direction of the faster component (component 1) over a range of relative amplitudes (shown as a series of insets from a to g); beyond this range, the perceived direction shifted towards the direction of motion of the slower component (component 2). This pattern was observed over the population of direction-sensitive neurons in area 1 (Figure 4D, H, red traces). Furthermore, the perceived direction of these plaids matched the PD of these neurons (Figure 4D, H, blue trace). We verified that the dominance of component 1 over component 2 in driving neural responses was not due to speed tuning (Supplemental Fig. 4A,B).
Figure 4.
Responses of example neurons in area 1 to type 2 plaids. A. Component gratings at −30° and −60° and resulting type 2 plaid (veridical direction = 0°). B. Responses of a neuron in area 1 to these plaids scanned in each of 16 directions. C. Preferred direction (PD) of this neuron for each grating/plaid morph. D. Mean preferred direction of all significantly direction-tuned area 1 neurons (red) and perceived direction (blue) for each grating/plaid morph; 26 out of 45 area 1 neurons were sensitive to the direction of motion of the −30°/−60° plaids E. Component gratings at −30° and −75° and resulting type 2 plaid (veridical direction = 0°). F. Responses of a neuron in area 1 to plaids (with components separated by 45°) scanned in each of 16 directions. G. Preferred direction of this neuron for each grating/plaid morph. H. Mean preferred direction of all significantly direction-tuned area 1 neurons (red) and perceived direction (blue) for each grating/plaid morph; 16 out of 32 area 1 neurons were sensitive to the direction of the −30°/−75° plaids.
Vector average model
As mentioned above, the IOC model predicts that the veridical direction of the gratings or plaids will be recovered (magenta traces in Figure 5A,B), a prediction that is not borne out in the data. In contrast, the VA model predicts that the PD will shift gradually – as the stimuli are morphed from component 1 to a plaid to component 2 – from the direction of component 1 to the direction of component 2 but VA predictions did not adequately capture neuronal responses (cyan traces in Figure 5A,B).
Figure 5.
Model comparison with type 2 plaids. Comparison of the relative PDs of neurons in area 1 and those predicted by four candidate models for (A) type 2 plaids with components moving at −30° and −60 ° relative to the veridical direction and (B) type 2 plaids with components moving at −30° and −75 ° relative to the veridical direction. The full Vector Average (VA) model (green dashed traces) that includes motion signals from both local contours and terminators yielded the best prediction. The VA model that includes only the directions of local contours (dashed cyan traces) is not as effective as the full model (for this model, we used the same speed weighting as for the full model; without this speed weighting, the predictions are even more divergent from the observed data). The VA model with terminators yielded significantly better fits than without (F(1,6) = 86.5 and 108.5, p < 0.001, for the −30°/−60° and −30°/−75° plaids, respectively). The Intersection of Constraints (IOC) model (dashed magenta traces) failed to explain the direction signals for type 2 plaids, as did the normalization model (dashed blue traces). For all models, the contours (and terminators when applicable) were computed using algorithms inspired by computer vision from the strains produced in the skin by the various stimuli, estimated using a model of skin mechanics (Sripati et al., 2006).
One possibility is that the PD and perceived direction of motion are determined by a VA mechanism, with the faster component weighted disproportionately more heavily than the slower component. Indeed, the responses of mechanoreceptive afferents are stronger when stimuli are scanned more rapidly across their receptive fields. Thus, all other things being equal, faster contours may be more salient and are accordingly weighted more strongly than slower ones in the determination of perceived direction (Goodwin et al., 1989;Phillips et al., 1992). In generating the VA prediction shown in Figure 5A,B, we incorporated a speed-weighting derived from the function relating the strength of afferent responses to scanning speed (Supplemental Fig. 4C,D). However, this speed weighting may not have fully captured the effect of speed on stimulus feature salience. To examine this possibility, we developed a model according to which PD was determined by a vector average of the two components, weighted by their speed and amplitude, with the speed-related weights as free parameters. Although the model could account for PD and perceived direction across stimuli (data not shown), we found that the ratio of the weight of the faster component to that of the slower component was 4.6:1 for the −30°/−60° plaids and 33.3:1 for the −30°/−75° plaids. Thus, the ratios of the weights assigned to the two components were disproportionately large and exhibited a non-monotonic relationship to their relative speeds. We examined whether this non-linearity in the weighting of the components could be accounted for using a normalization model, according to which signals stemming from the more intense of the two components effectively inhibit signals stemming from the less intense one (Busse et al., 2009), and found that this model could not account for neuronal PDs or perceived directions (see Experimental Procedures, Figure 5A,B). Thus, the PD and perceived direction could not be expressed based solely on the components’ directions.
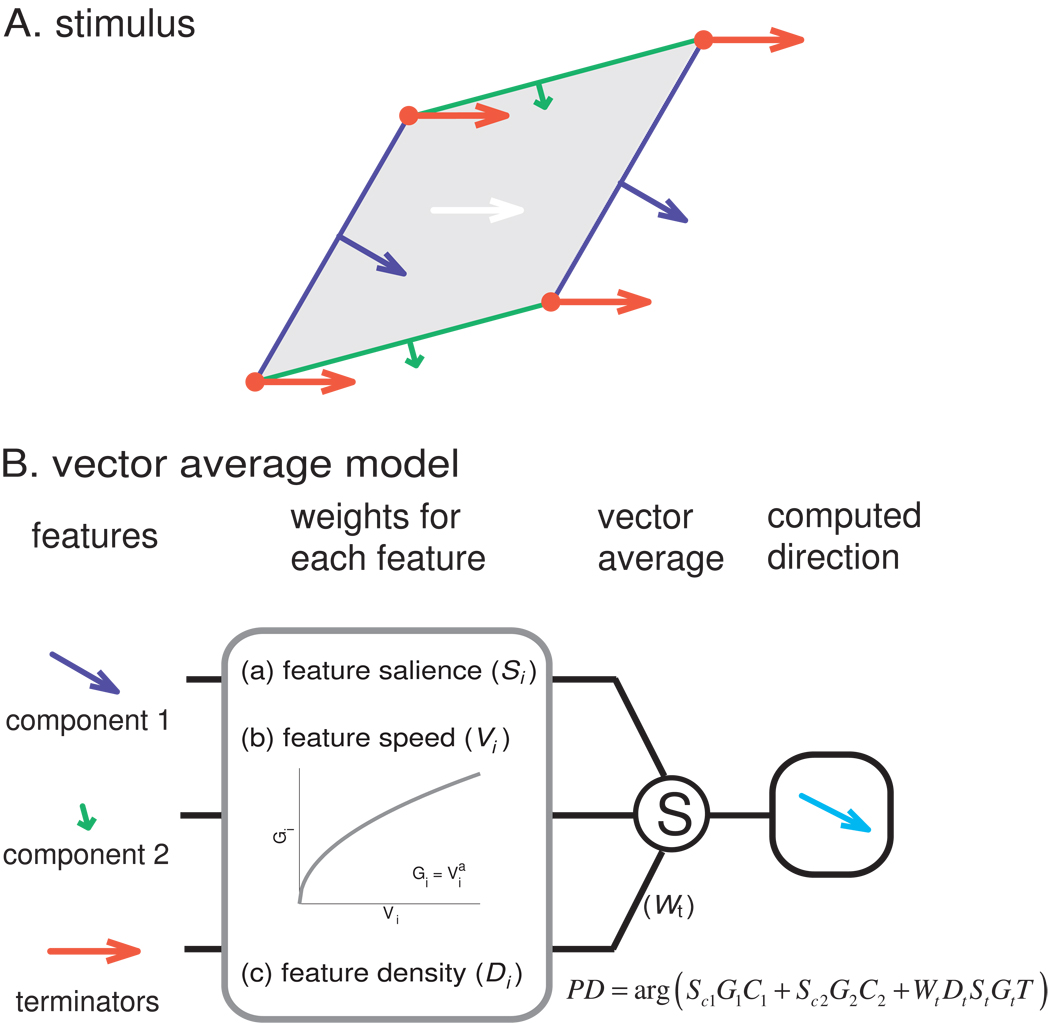
Another possibility is that the PD and perceived directions are determined by a vector average of the directions of components and the terminators. Indeed, for type 2 plaids, predictions from the VA model tend to deviate too far towards the direction of the components and away from the veridical direction. One possibility, then, is that signals from the terminators pull the PD towards the veridical direction, but do not do so sufficiently. We tested this possibility by implementing a model that included the two components and the terminators, each weighted according to their speeds and amplitudes (Figure 6). Specifically, we computed the patterns of strains produced in the skin – at the depth where mechanoreceptors are located – by the various gratings and plaids using a model of skin mechanics (Sripati et al., 2006). Indeed, the spatial filtering of the skin affects the degree to which terminators will be tangible. Then, using algorithms inspired by computer vision, we identified the edges and terminators in each pattern of strains. The perceived direction or neuronal responses were then predicted based on a vector average of edge and terminator motion vectors. The only parameter in the model was the weight assigned to the terminators (all other factors, including speed and amplitude weighting, were computed from the stimulus and from known response properties of mechanoreceptive afferents, see Experimental Procedures).
Figure 6.
Vector average model. A. Breakdown of the stimulus features for input into the vector average model. Green and blue contours and arrows correspond to the component edges and their respective directions of motion; red vertices and arrows correspond to the terminators and their direction of motion. B. Computation of the stimulus based on the direction of its components. Each feature is weighted according to its density (length of the edges, density of the terminators), its amplitude, and its speed. Weighted unit direction vectors are then summed to compute the direction of the plaid. The speed weighting function (Gi) was derived empirically (see Supplemental Fig. 4C,D). Please see Methods and Supplemental Fig. 5 for details.
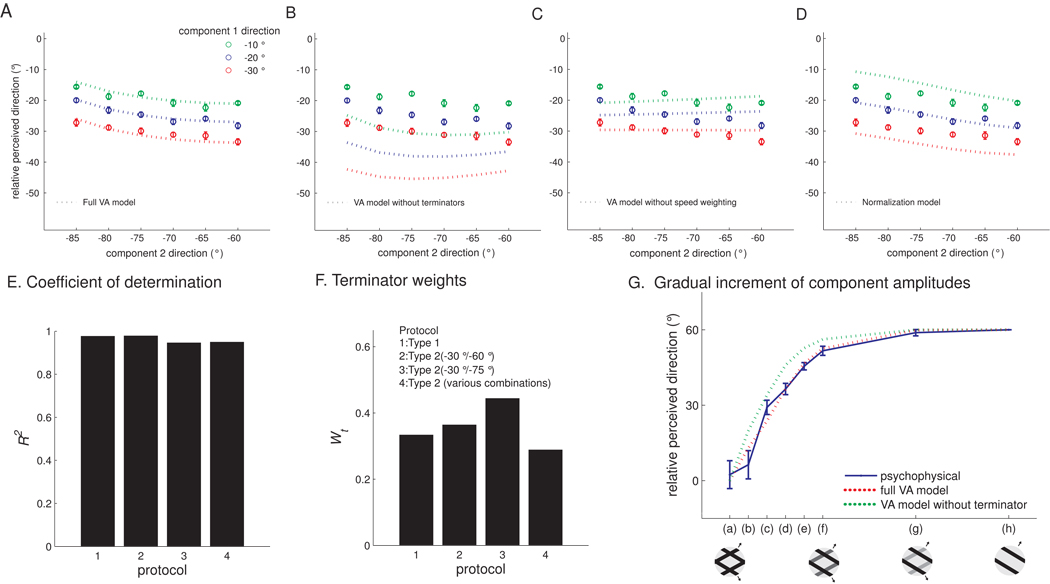
We found that a VA model that included both components and terminators could account for both the neuronal PDs and perceived directions (Figure 5A,B, green dashed traces). To further test models of motion integration, we tested the perceived directions of a variety of additional type 2 plaids, with component gratings at different relative angles and speeds (Figures 7A–D), and found that the VA model could account for these as well (Figure 7A), as evidenced by high coefficients of determination (R2 ≥ 0.95) (Figure 7E). Importantly, the weight attributed to the terminators, which gauges their contribution to the motion signal and is the only free parameter in the model, was consistent across stimuli (around 0.35, see Figure 7F).
Figure 7.
Assessing the performance of models of motion integration. The relative perceived directions of additional type 2 plaids (0° corresponds to the veridical direction), measured in human psychophysical experiments. Components were systematically varied in a factorial design: component 1 was scanned at −10, −20, or −30° and component 2 was scanned at −60, −65, −70, −75, −80, or −85° relative to the direction of the plaid pattern. Again, the full Vector Average model predicts the performance of human subjects. The psychophysical data (circles with error bars) are shown with the predictions (dotted traces) of (A) the full Vector Average model, (B) the Vector Average model without the terminator term, (C) the Vector Average model without speed weighting, and (D) the contrast normalization model (Busse et al., 2009), which has been shown to effectively predict the responses of V1 neurons to superimposed gratings. E. The Vector Average (VA) model predicts that, as the relative amplitudes of the component gratings are varied in small increments, the perceived direction will shift gradually. As predicted by the model, the distribution shifted gradually from component to pattern motion. Mean perceived direction measured from seven subjects (blue trace) along with the predictions from the full Vector Average model (red dashed trace) and the Vector Average model without the terminator term (green dashed trace). The full Vector Average model prediction matches the psychophysical data almost perfectly. F. In the full Vector Average model, Wt is relatively constant (around 0.35) across the four protocols (identified in the legend; protocol 4 refers to the psychophysical data shown in panels A–D). F. The Vector Average model accounts for most of the variance in perceived direction across the four protocols (identified in the legend of panel E).
We also compared the predictions of the Vector Average model to that of less complex models to determine whether all of the terms in the full model were necessary to account for the data. Figure 7B shows the predictions from the Vector Average model and from an alternative Vector Average model that did not include terminators. As can be seen from the figure, the alternative model yielded systematically erroneous predictions. We also found that we could not account for the perceived direction if weighting by component speed was eliminated (Figure 7C) or if the component signals were non-linearly transformed using a population normalization model (Busse et al., 2009) (Figure 7D). Thus, only the Vector Average model with terminator signals could account for PD and perceived direction across conditions.
The influence of terminators on perceived direction can be interpreted as evidence that a population of local motion detectors in somatosensory cortex encodes the motion of terminators, analogously to end-stopped neurons in primary visual cortex. Signals from these neurons then contribute to the motion signal of pattern neurons in area 1 (Pack et al., 2003). The model predicts that the perceived direction will shift gradually from component to plaid pattern if the relative amplitudes of the two gratings forming the type 1 plaid are sampled sufficiently densely, a prediction that is borne out in the data (Figure 7G).
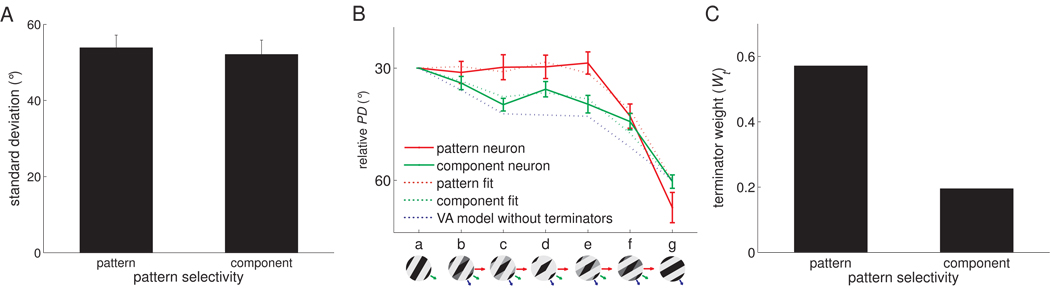
Neurons in area 1 exhibit a range of motion integration properties, ranging from component to pattern tuning. We wished to establish what determines the position of neurons along this continuum. We tested the possibility that component and pattern neurons differ only in the width of their tuning, with pattern neurons being more widely tuned than their component counterparts (Tsui et al., 2010), and found this not to be the case (Figure 8A). Another possibility is that pattern neurons receive stronger terminator signals than do component neurons. To test this hypothesis, we fit the VA model to responses evoked in pattern and component neurons and found that the former yielded higher terminator weights than the latter (Figure 8B,C). In other words, pattern neurons seem to receive stronger terminator signals than do component neurons.
Figure 8.
Comparing the properties of pattern and component neurons. A. Tuning width (circular standard deviation) of component and pattern neurons. The direction tuning of pattern neurons was not significantly wider than that of component neurons (t(40) = 0.24, p = 0.73). We used the median of the plaidness index (PI = Zp-Zc, see Figure 2) to discriminate pattern from component neurons. B. Mean of relative PD obtained from the responses to −30°/−60° type 2 plaids of pattern (red, N=13) and component (green, N=13) neurons, respectively, along with their corresponding VA predictions and predictions derived from a VA model without terminators. C. Pattern neurons receive stronger terminator signals, as evidenced by a higher terminator weight (Wt) compared to their component counterparts.
DISCUSSION
In most conditions, the responses of neurons in area MT and the perception of visual motion are consistent with predictions from the IOC model. Only under certain stimulus conditions does the visual system’s behavior defy IOC predictions, for example when type 2 plaids are presented at low-contrast or when bar fields are presented at short durations (Lorenceau et al., 1993;Pack and Born, 2001;Weiss et al., 2002;Yo and Wilson, 1992). Tactile motion integration seems to be incompatible with the IOC model and, instead, can be accounted for using a VA model, which is heuristic rather than algorithmic. Then again, the motion integration problem faced by the somatosensory system may be adequately solved using a VA mechanism, i.e., by computing the average of motion signals stemming from local motion detectors, a computation that can be implemented using a relatively simple neural network. Many of the mechanisms that are thought to contribute to visual motion integration, including non-linear interactions between simple motion detectors (Busse et al., 2009;Heeger, 1992;Rust et al., 2006;Simoncelli and Heeger, 1998) and/or parallel pathways for processing edges and terminators (Barthelemy et al., 2008;Wilson et al., 1992), thus seem unnecessary to explain tactile motion integration.
We propose that neurons encode the direction of motion of individual contours, including edges and terminators, at the first stage of processing in somatosensory cortex. The responses of these simple motion detectors are sensitive to the direction, amplitude and speed of the individual contours (Pei et al., 2010). Signals from these motion detectors then converge onto neurons in area 1, where they are combined according to a vector average mechanism. The perceived direction of the stimuli is then determined by the responses of this subpopulation of neurons in area 1. A strong prediction from this model that remains to be tested is that somatosensory cortex contains a subpopulation of end-stopped neurons that signal the direction of terminators, as is the case in V1(Pack et al., 2003).
Importantly, the full VA model makes identical predictions to those of the IOC model if terminator weights are sufficiently high. Differences between tactile and visual motion integration might then be explained in terms of the weighting assigned to the terminator signals: In vision, these may be weighted much more strongly (Pack and Born, 2001;Weiss et al., 2002), resulting in more veridical percepts of motion direction. In fact, processing of visual motion direction resembles a VA for short stimulus durations (Pack and Born, 2001). A parsimonious interpretation is that motion integration mechanisms are analogous in the two modalities, but that the visual system assigns greater weight to terminators as the motion signal is elaborated over time.
Although the integration properties of area 1 neurons are analogous to their MT counterparts, the overall preponderance and strength of pattern selectivity is lower in somatosensory than in visual cortex. The relative weakness of tactile pattern tuning reflects the lower motion sensitivity in touch than in vision (Pei et al., 2010). The lower incidence of strong pattern selectivity is likely due to the fact that area 1 also comprises a strong representation of stimulus orientation (Bensmaia et al., 2008) and texture (Randolph and Semmes, 1974), which suggests that it serves other functions and is not an area dedicated to motion processing. The contiguity of form, texture, and motion representations in somatosensory cortex is not surprising given that motion is a hallmark of tactile exploration. Motion information may indeed be necessary to resolve the spatial relationships between stimulus features during scanning. That responses of area 1 neurons can account for perception across a broad range of stimulus conditions (Pei et al., 2010) suggests, however, that the motion signal in this area 1 is the tactile analogue of its counterpart in area MT.
Experimental Procedures
Apparatus
The tactile stimuli were delivered using a dense tactile array, consisting of 400 independently-controlled probes arrayed in a 20 × 20 matrix (Killebrew et al., 2007). The tips of the probes, spaced at 0.5 mm, center to center, cover a 10mm ×10mm area. The depth of indentation of each probe is specified every millisecond. To simulate motion, adjacent probes were indented in succession at a rate that was determined by the nominal speed of the stimulus. The indentation of one probe overlapped in time with the retraction of the other to create a smooth percept of motion. The density of the probes is greater than the innervation density on the fingertip, which leads to a smooth motion percept despite the inherent pixilation of the array.
Stimuli
Negative type 1 plaids
On each trial, we presented a stimulus consisting of two superimposed square-wave gratings moving in directions separated by 120° (Figure 1A–C). We used a separation of 120° because pattern motion and component motion can be readily distinguished empirically as demonstrated in human psychophysical experiments (Pei et al., 2008) (the separation between pattern and component motion is 60°). The wavelength of the component gratings was 6mm and their duty cycle 30% (3/10). The direction of motion of the components varied from 0 to 330° in steps of 30° relative to the preferred direction (PD) of each neuron. The PD was determined using simple gratings (with a wavelength of 6mm and a duty cycle of 30%) drifting at a speed (20, 40, or 80 mm/s) at which the direction tuning was strongest. The difference in amplitude between the two component gratings ranged from +500µm to −500µm in steps of 167µm, yielding a set of patterns that gradually morphed from a simple square wave grating into a standard plaid pattern (Figure 1E, a–d). Specifically, the amplitude of one component grating was 500µm while the amplitude of the other was 0, 167, or 334µm. The plaid pattern consisted of diamond-shaped grooves bounded by an indented grid. If I1(x,y) and I2(x,y) are the displacements of components 1 and 2, at position (x,y), respectively, the displacement, I(x,y), of the pattern was the greater of I1(x,y) and I2(x,y). In other words:
| (1) |
The maximum displacement of the pattern at any location was therefore 500µm. If instead of a max, we had adopted a sum operation, the depth of indentation at the intersections would be the sum of the depths of indentation of the individual gratings. We determined, using skin mechanical modeling (Sripati et al., 2006) and in psychophysical experiments (Pei et al., 2008), that the intersections (terminators) almost completely masked the edges in additive plaids. Six to fifteen trials (specifically: 2–5 repetitions × 3 phase combinations) were presented for each condition and the starting position (phase) of the pattern was pseudo-randomized so that phase effects could be averaged out. Each stimulus was presented for a duration of 1s, followed by a 100-ms blank interval.
Positive type 1 plaids
The positive plaids were similar to negative plaids with several modifications: Their duty cycle was 42% (5/12) and the displacement at location (x,y), I(x,y), was 500µm minus the maximum of the component displacements I1(x,y) and I2(x,y). In other words:
| (2) |
Type 2 plaids
Type 2 plaids (Figure 4A, E) were similar to positive type 1 plaids with the following differences: The two components moved at different speeds: component 1 moved at 20, 40, or 80mm/s (tailored to each neuron; we determined, in preliminary experiments, the speed that yielded the strongest direction tuning using gratings), and component 2 moved at a speed determined by the constraints outlined in Figure 3B. The directions of motion of the two components differed by 30° or 45° (rather than 120° for type 1 plaids). Thus, one type 2 plaid had one component moving at −30° and the other at −60° relative to the veridical direction of pattern motion (as determined by the IOC or by terminator motion); the speed of the second component was about 6/10 of the speed of the first. The other plaid had one component moving at −30° and the other at −75° relative to the veridical direction of motion (the ratio of speeds was about 3/10). Each stimulus was presented for 1s, followed by a 100-ms blank interval. Each plaid was presented five times with phase randomized.
Neurophysiological procedures
Before the microelectrode recordings, surgery was performed to secure a head-holding device and recording chambers to the skull. Surgical anesthesia was induced with ketamine HCl (20 mg/kg, i.m.) and maintained with pentobarbital (10–25 mg · kg−1 ·hr−1, i.v.). All surgical procedures were performed under sterile conditions and in accordance with the rules and regulations of the Johns Hopkins Animal Care and Use Committee.
Extracellular recordings were made in the post-central gyri of three hemispheres of two macaque monkeys using previously described techniques (Bensmaia et al., 2008;Pei et al., 2010). The animals were trained to sit in a primate chair with their hands restrained while tactile stimuli were delivered to the distal pads of digits 2, 3, 4 or 5. All recordings were performed with the monkeys in an awake state, which was maintained by offering them liquid rewards at random intervals. On each recording day, a Reitbock multielectrode microdrive (Mountcastle et al., 1991) was loaded with seven quartz-coated platinum/tungsten (90/10) electrodes (diameter, 80µm; tip diameter, 4µm, impedance 1– 3MΩ at 1000Hz).
When recording from area 3b, the electrodes were driven 2–3 mm below the depth at which neural activity was first recorded. As one descends from the cortical surface through area 1 into area 3b, the RFs progress from the distal, to middle, to proximal finger pads, then to the palmar whorls. Within area 3b, the RFs proceed back up the finger, transitioning from proximal, to medial, and ultimately to distal pads. Because responses from the distal pad were never encountered in the more superficial regions of 3b (where the palmar whorls or proximal pad typically were most responsive), there was never any difficulty distinguishing neurons in area 1 from neurons in area 3b. On every second day of recording, the electrode array was shifted ~200µm along the postcentral gyrus until the entire representation of digits 2–5 had been covered. On the third day, we moved the electrodes posterior-laterally to record from area 2. Multi-units in this area had larger RFs and responded to both cutaneous stimulation and joint manipulation, so were easily distinguishable from their counterparts in area 1.
Recordings were obtained from neurons that met the following criteria: (1) the neuron responded to cutaneous stimulation; (2) action potentials were completely isolated from the background noise; (3) the RF of the neuron included at least one of the distal finger pads on digits 2–5 (only the distal fingerpads of digits 2–5 could be accessed with the stimulator); (4) the stimulator array could be positioned so that the RF of the neuron was centered on the array. The mean firing rate of the neurons was computed for each stimulus interval (lasting 1s).
Human Psychophysical procedures
All testing procedures were performed in compliance with the policies and procedures of the Institutional Review Board for Human Use of the Johns Hopkins University. Twenty-six subjects (10m16f) participated in some or all of the psychophysical experiments. Nine subjects (4m5f) were tested with −30°/−60° type 2 plaids and eight (4m4f) with −30°/−75° type 2 plaids. In addition, five (2m3f) participated in the experiment examining the effect of speed on perceived direction, nine (3m6f) in the experiment investigating the perceived directions of plaids with different combinations of component directions, seven (2m5f) participated in the experiment testing the perceived direction of tactile plaids with component gratings whose relative amplitudes varied in small increments, and five (1m4f) in an experiment testing the perceived direction of visual plaids.
In the human psychophysical experiments (cf. Pei et al., 2008), the subject’s finger, ventral side up, was pressed against the array with a force of 100g using a counterweight mounted on a vertical stage (L.O.T Oriel GmbH & Co., Darmstadt, Germany). This assembly allowed for accurate and repeatable finger positioning on the probe array. On each trial, a moving tactile pattern, lasting 1s, was presented to the subject’s left distal index fingerpad. To eliminate spatial cues, only probes within 5mm of the center of the array were active (such that the tactile display was circular and thus radially symmetric). The subject’s task was to indicate the direction of motion by selecting by mouse click using his free hand one of a set of arrows, presented on the computer screen. The arrows ranged in direction from 0 to 345° in 15-degree steps. There was a 500-ms interval between the subject’s response and the next stimulus.
The psychophysical results with type 1 plaids shown in Figure 2B and in Supplemental Fig. 2D are reproduced from a previous study (Pei et al., 2008). In the present study, we performed additional psychophysical experiments using the same type 2 plaids used in the neurophysiological experiments to assess the extent to which neuronal responses could account for perception. We designed three additional psychophysical experiments to characterize the perception of plaids over a wider range of conditions. In all psychophysical experiments, subjects also identified the direction of motion of simple gratings to establish a baseline performance to correct for any systematic biases (Pei et al., 2008).
Speed invariance of perceived direction
In this experiment, we wished to assess the extent to which the perceived direction is stable across a range of scanning speeds. As we have shown that PDs of neurons are relatively invariant to changes in speed, we examined whether this invariance was reflected in perception. The plaid stimuli were identical to the −30°/−75° type 2 plaids described above except that the speed of component 1 was 10, 20, 40 or 80mm/s. Subjects performed the direction identification task described above.
Combinations of component directions
In this experiment, we wished to measure the perceived direction of type 2 plaids over a wide range of conditions to provide a stringent test for the model of motion integration described below. To this end, we presented subjects with type 2 plaids with components that varied in their relative directions of motion (relative to the direction of pattern motion). Specifically, component 1 was scanned at −10, −20, or −30° and component 2 was scanned at −60, −65, −70, −75, −80, or −85° relative to the direction of plaid motion. The speed of component 1 was 40mm/s and that of component 2 was computed using the Intersection of Constraints model (Figure 3B for an illustration). The amplitude and duty cycle were identical to those of the −30°/−75° plaids described above.
Type 1 plaids with small increments in relative amplitude
The stimuli were identical to the type 1 positive plaids described above, except that the amplitude of the non-dominant grating was incremented in steps of 25µm over the range in which the transition from component to pattern motion perception is observed. Subjects identified the direction of motion using the procedure described above.
Analysis
Tuning properties
As an index of tuning strength, we used vector strength, given by:
| (3) |
where R(θi) is the neuron’s mean firing rate to a stimulus scanned in direction θi (Mardia, 1972). Values of DI ranged from 0, when a neuron responded uniformly to all scanning directions, to 1, when a neuron only responded to stimuli scanned in a single direction. The statistical reliability of DI was tested using a standard randomization test (α = 0.01).
The PD was determined by computing the weighted circular mean:
| (4) |
Quantifying integration properties
Each neuron’s integration properties were indexed by characterizing the degree to which its responses to plaids matched the responses of an idealized component neuron or pattern neuron (Movshon and Newsome, 1996). The idealized predictions were computed for an individual neuron using its responses to simple gratings. Specifically, the idealized component prediction was constructed by summing the responses to the component gratings, correcting for the baseline firing rate. Accordingly, the component prediction yielded a bimodal tuning curve. The idealized pattern prediction was the tuning curve measured using simple gratings, shifted by the angular difference between component grating and the plaid it yielded. As a result, the pattern prediction yielded a unimodal tuning curve that peaked at the neuron’s preferred direction.
We then represented the degree to which a neuron’s responses to plaids fit its component and pattern predictions using the Z scores of the partial correlation between the measured responses and the respective idealized predictions. Specifically, we first computed the partial correlations coefficients, Rp and Rc, between the observed and predicted responses:
| (5) |
| (6) |
where rc and rp are the correlations between a neuron’s measured responses and its component and pattern predictions, respectively; rpc is the correlation between the two predictions. Finally, we performed a Fisher’s z-transformation (Hotelling, 1953) on Rp and Rc to obtain Zp and Zc. Accordingly, a pattern neuron will yield a relatively high Zp and a low Zc and a component neuron the opposite pattern.
The Vector Average model
According to the Vector Average model, the PD of a neuron or the perceived direction of a stimulus is determined by the mean direction of the individual stimulus features (as summarized in Equation 16). A fundamental assumption underlying the present approach is that individual features (such as edges and terminators) of the stimulus contribute to the global motion percept differentially, depending on their salience. We assume that “pattern” neurons receive motion information from multiple local motion detectors, which have small RFs and only process local stimulus features. Furthermore, an edge impinging on the RF of a local motion detector can provide information only about the direction of motion orthogonal to the edge’s orientation, whereas a local terminator can indicate the veridical direction of motion of the pattern.
In the proposed model, edges and terminators were identified using algorithms inspired by computer vision. Specifically, we first estimated, for each location on the stimulus image, the partial derivatives of the image along the x- and y-axes using a Sobel filter; the derivatives were then used to compute the magnitude and orientation of local image gradients. The salience of edges contributed by a component grating was gauged by the total magnitude of local motion gradients at the grating’s orientation. Note that the direction of motion of these edges is orthogonal to their orientation because of the aperture problem. Individual terminators were detected by identifying regions of the image that include edges at different orientations and their salience was modulated by their density. As mentioned above, terminators signal the veridical direction of motion.
Because we computed the edges and terminators from static images, these calculations did not take into consideration the relative speeds of these stimulus features. Since speed has been shown to modulate neuronal responses (Pei et al., 2010;Phillips et al., 1992), we determined how the salience of edges and terminators was modulated by their speed. To that end, we measured the responses of neurons in areas 3b and 1 to bars scanned at various speeds and found that the response magnitude of neurons increased as a power function of speed (Supplemental Fig. 4C,D). The idea is that a local contour moving at a faster speed evokes a higher response in local motion detectors and thus is weighted more in the computation of direction.
Finally, we constructed a motion integration model to predict both the PD of pattern neurons in area 1 and the perceived direction measured from human observers. According to the model, PD and perceived direction were determined by the sum of the directions of the stimulus features (edges and terminators) weighted by their salience. The model is described in greater detail in the following text (and summarized in Supplemental Fig. 5).
Skin mechanics
First, we transformed the indentation profile (the spatial pattern indented into the skin) to a corresponding strain profile using a continuum mechanical model of skin mechanics (Sripati et al., 2006). We carried out the analysis on strain rather than indentation because the former more closely reflects the stimulus impinging upon the sensory sheet (SA1 receptors embedded in the skin)(see ref. Pei et al., 2008 for a more in-depth treatment of this issue).
Edge salience
The edge salience gauges the degree to which an edge moving in a particular direction (perpendicular to its orientation) contributes to the neuronal response or global motion percept. We estimated the spatial gradients (spatial derivatives) of the image S using the Sobel filter:
| (7) |
| (8) |
such that Lx and Ly are the gradients of S along the x- and y-axes, respectively. The orientation θ(x,y) of the local gradient vector at location (x,y) was then:
| (9) |
and its magnitude M(x,y) was:
| (10) |
To quantify the magnitude of the gradient at each orientation, we computed the orientation histogram E(ω) for each image:
| (11) |
where E(ω) is the sum of the magnitudes of the local gradient vectors when their orientation was ω (ω varied from –π/2 to π/2 (bin width= π/90). Notice that we pooled the gradient magnitude with orientation ω and ω ± π altogether, by assuming that the leading and trailing edges of a moving object yield comparable motion strength.
E(ω) is distributed exponentially with peaks at orientations corresponding to the edges of the component gratings (Supplemental Fig. 5) that form the plaid. E(ω) can thus be described as a linear combination of two exponential functions in circular space (moment = 2):
| (12) |
where, to circularize the function,
| (13) |
and θ c1 and θc2 are the scanning directions of the two component gratings, respectively (e.g., −60° and +60° in type 1 plaids). We used a standard least-squares fitting method to obtain the best-fitting parameters a0, Sc1, Sc2 and λ; a0 is the intercept, and Sc1 and Sc2 are salience of the edges corresponding to the two component gratings; λ defines how sharply the gradient magnitude decreased as the ω moved away from the peak orientation.
Terminator salience
A terminator is defined as the intersection of two edges. Consider a circular neighborhood with a diameter of 1.9mm centered at location (x,y), the structure tensor matrix C is defined as (Harris and Stephens, 1988):
| (14) |
where the sums are taken over the neighborhood and Lx and Ly are the gradients defined in Equations 3 and 4, respectively. We then derive the two eigenvalues, λ1 and λ2, from C (λ1 ≥ λ2 ≥ 0). If location (x,y) contains no features, then both λ1 and λ2 are near zero. If location (x,y) is characterized by the presence of a single edge, λ1 takes on a non-zero value and λ2 is near zero. If two edges converge on this location, then both λ1 and λ2 take on comparable non-zero values (and this location contains a terminator). The ratio of λ2 to λ1 can be used to signal the presence of a terminator. We can then weight this quantity by λ1 to gauge the salience of the terminator. The total terminator salience is defined as sum of the local terminator salience λ2(x,y) across the image S:
| (15) |
For the analysis of each morph from pure grating to pure plaid, we normalized the edge strength such that Sc1 was 1 when component grating 1 was presented alone, 0 when component grating 2 was presented alone, and vice versa for Sc2. Similarly, the terminator strengths were normalized such that St was 0 when a simple grating is presented and 1 when a pure plaid was presented. St fell between 0 and 1 when one of the edges was more salient than the other. St thus denotes the salience of individual terminators.
Model fitting
The PDs of individual neurons and perceived directions in human psychophysical experiments were fit to the following model using a standard least squares method:
| (16) |
| (17) |
| (18) |
where Wt, the weight of the terminator, is the only free parameter in the model; S1, S2, and St are the salience of components 1, 2 and of the terminators, respectively (computed as described above from each of the stimuli); vi denotes the speeds of the components or terminators; α, the exponent that relates the relative weight of the stimulus features (edge, terminator), Gi, to its speed, vi, as determined in preliminary measurements (α = 0.49, Supplemental Fig. 4C,D); Dt denotes the density of terminators. Dt is a sinusoidal function of the difference between the component directions because the wavelength of the component gratings was fixed. Finally, C⃗1, C⃗2 and T⃗ are the unit vectors corresponding to the directions of motion of components 1 and 2 and of the terminators, respectively.
Normalization model
We examined whether the nonlinearity of the input of the Vector Average model can be explained by the population normalization mechanism proposed by Busse et al. (Busse et al., 2009), rather than by nonlinearities originating from the neuronal responses to terminators in our Vector Average model. The major difference between these two models is that the former relies on untuned normalization, which is likely to be a generic feature of low-level sensory processing, while the latter involves end-stopping which can be viewed as a type of tuned normalization. In the normalization model, the neuronal response to superimposed gratings is the sum of the response elicited by each individual gratings when their depth of indentations are comparable. However, the neuronal response is disproportionally dominated by one dominant component grating when depths of indentations differ substantially, resembling a winner-take-all phenomenon. Winner-take-all behavior in the responses of populations of neurons in primary visual cortex can be described using a modified Naka-Rushton equation (see Equations 20 and 21).
Within this framework, we computed the perceived direction of motion and neuronal PD from the sum of the unit component vectors weighted by the component saliency and adjusted by the aforementioned normalization processing. Specifically, we first obtained the salience (Sc1 and Sc2) for the two components, C1 and C2, using Equation 12 and empirically derived speed weights (Gc1 and Gc2) using the Equation 18. Initially, the weight (Wi) assigned to each component grating is determined by the product of its salience (Si) and its speed weighting (Gi):
| (19) |
We then computed the root-mean-square (Wrms) of the initial tentative weights obtained for the two component gratings and then applied the normalization process as follows (Busse et al., 2009):
| (20) |
| (21) |
where n, the exponent of an accelerating nonlinearity, and C50, the constant that determines the value of semisaturation, are the two free parameters in the model; Ri correspond to the population neuronal responses elicited by each component grating after having been normalized. Finally, the PD is determined by a simple vector sum of component unit vectors weighted by the corresponding neuronal responses
| (22) |
where C⃗1 and C⃗2 are the unit vectors corresponding to the moving directions of two components, respectively. In contrast with the full Vector Average model in Equation 16, the present equation did not include the terminator term.
Supplementary Material
ACKNOWLEDGMENTS
We would like to thank Justin Killebrew and Frank Dammann for invaluable technical assistance and Ishanti Gangopadhyay, Melissa Solis, and Doyeon Kim for collecting psychophysical data. We are also grateful to Sung Soo Kim, Yoonju Cho, Chia-Chung Hung, Yi Dong, Anne Baldwin, Philip O’Herron, Leslie Osborne, David Freedman and Jason Maclean for their comments on previous versions of this manuscript. This work was supported by National Institutes of Health grants NS-18787, and NS-38034 and by Chang Gung Memorial Hospital grant CMRPG-350963.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
COMPETING INTERESTS STATEMENT
The authors declare that they have no competing financial interests.
Reference List
- Adelson EH, Movshon JA. Phenomenal coherence of moving visual patterns. Nature. 1982;300:523–525. doi: 10.1038/300523a0. [DOI] [PubMed] [Google Scholar]
- Albright TD. Direction and orientation selectivity of neurons in visual area MT of the macaque. J. Neurophysiol. 1984;52:1106–1130. doi: 10.1152/jn.1984.52.6.1106. [DOI] [PubMed] [Google Scholar]
- Barthelemy FV, Perrinet LU, Castet E, Masson GS. Dynamics of distributed 1D and 2D motion representations for short-latency ocular following 1. Vision Res. 2008;48:501–522. doi: 10.1016/j.visres.2007.10.020. [DOI] [PubMed] [Google Scholar]
- Bensmaia SJ, Denchev PV, Dammann JF, III, Craig JC, Hsiao SS. The representation of stimulus orientation in the early stages of somatosensory processing. J. Neurosci. 2008;28:776–786. doi: 10.1523/JNEUROSCI.4162-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bicchi A, Scilingo EP, Ricciardi E, Pietrini P. Tactile flow explains haptic counterparts of common visual illusions. Brain Res. Bull. 2008;75:737–741. doi: 10.1016/j.brainresbull.2008.01.011. [DOI] [PubMed] [Google Scholar]
- Britten KH, Newsome WT, Shadlen MN, Celebrini S, Movshon JA. A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis. Neurosci. 1996;13:87–100. doi: 10.1017/s095252380000715x. [DOI] [PubMed] [Google Scholar]
- Busse L, Wade AR, Carandini M. Representation of concurrent stimuli by population activity in visual cortex. Neuron. 2009;64:931–942. doi: 10.1016/j.neuron.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costanzo RM, Gardner EP. A quantitative analysis of responses of direction-sensitive neurons in somatosensory cortex of awake monkeys. J. Neurophysiol. 1980;43:1319–1341. doi: 10.1152/jn.1980.43.5.1319. [DOI] [PubMed] [Google Scholar]
- Fennema C, Thompson W. Velocity determination in scenes containing several moving objects. Computer Graphics Image Processing. 1979;9:301–315. [Google Scholar]
- Goodwin AW, John KT, Sathian K, Darian-Smith I. Spatial and temporal factors determining afferent fiber responses to a grating moving sinusoidally over the monkey's fingerpad. J. Neurosci. 1989;9:1280–1293. doi: 10.1523/JNEUROSCI.09-04-01280.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris C, Stephens MJ. A combined corner and edge detector; Proceedings of the 4th Alvey Vision Conference; 1988. pp. 147–152. Ref Type: Conference Proceeding. [Google Scholar]
- Heeger DJ. Normalization of cell responses in cat striate cortex. Vis. Neurosci. 1992;9:181–197. doi: 10.1017/s0952523800009640. [DOI] [PubMed] [Google Scholar]
- Hotelling H. New light on the correlation coefficient and its transforms. J. R. Stat. Soc. B. 1953;15:193–232. [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 1968;195:215–243. doi: 10.1113/jphysiol.1968.sp008455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Killebrew JH, Bensmaia SJ, Dammann JF, Denchev P, Hsiao SS, Craig JC, Johnson KO. A dense array stimulator to generate arbitrary spatio-temporal tactile stimuli. J. Neurosci. Methods. 2007;161:62–74. doi: 10.1016/j.jneumeth.2006.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaMotte RH, Mountcastle VB. Capacities of humans and monkeys to discriminate between vibratory stimuli of different frequency and amplitude: a correlation between neural events and psychophysical measurements. J. Neurophysiol. 1975;38:539–559. doi: 10.1152/jn.1975.38.3.539. [DOI] [PubMed] [Google Scholar]
- Lorenceau J, Shiffrar M, Wells N, Castet E. Different motion sensitive units are involved in recovering the direction of moving lines. Vision Research. 1993;33(9):1207–1217. doi: 10.1016/0042-6989(93)90209-f. Ref Type: Generic. [DOI] [PubMed] [Google Scholar]
- Mardia KV. Statistics of Directional Data. London: Academic Press; 1972. p. -357. [Google Scholar]
- Maunsell JH, Van Essen DC. Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation. J. Neurophysiol. 1983;49:1127–1147. doi: 10.1152/jn.1983.49.5.1127. [DOI] [PubMed] [Google Scholar]
- Mountcastle VB. Neural Mechanisms in Somatic Sensation. Cambridge, MA: Harvard Uni Press; 2005. The Sensory Hand. [Google Scholar]
- Mountcastle VB, LaMotte RH, Carli G. Detection thresholds for stimuli in humans and monkeys: comparison with threshold events in mechanoreceptive afferent nerve fibers innervating the monkey hand. J. Neurophysiol. 1972;35:122–136. doi: 10.1152/jn.1972.35.1.122. [DOI] [PubMed] [Google Scholar]
- Mountcastle VB, Reitboeck HJ, Poggio GF, Steinmetz MA. Adaptation of the Reitboeck method of multiple microelectrode recording to the neocortex of the waking monkey. J. Neurosci. Methods. 1991;36:77–84. doi: 10.1016/0165-0270(91)90140-u. [DOI] [PubMed] [Google Scholar]
- Movshon JA, Adelson EH, Gizzi MS, Newsome WT. The Analysis of Moving Visual Patterns. PONTIFICIAE ACADEMIAE SCIENTIARVM SCRIPTA VARIA. 1983;54:117–151. [Google Scholar]
- Movshon JA, Newsome WT. Visual response properties of striate cortical neurons projecting to area MT in macaque monkeys. J. Neurosci. 1996;16:7733–7741. doi: 10.1523/JNEUROSCI.16-23-07733.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pack CC, Born RT. Temporal dynamics of a neural solution to the aperture problem in visual area MT of macaque brain. Nature. 2001;409:1040–1042. doi: 10.1038/35059085. [DOI] [PubMed] [Google Scholar]
- Pack CC, Gartland AJ, Born RT. Integration of contour and terminator signals in visual area MT of alert macaque. J. Neurosci. 2004;24:3268–3280. doi: 10.1523/JNEUROSCI.4387-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pack CC, Livingstone MS, Duffy KR, Born RT. End-stopping and the aperture problem: two-dimensional motion signals in macaque V1. Neuron. 2003;39:671–680. doi: 10.1016/s0896-6273(03)00439-2. [DOI] [PubMed] [Google Scholar]
- Pei YC, Hsiao SS, Bensmaia SJ. The tactile integration of local motion cues is analogous to its visual counterpart. Proc. Natl. Acad. Sci U. S. A. 2008;105:8130–8135. doi: 10.1073/pnas.0800028105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei YC, Hsiao SS, Craig JC, Bensmaia SJ. Shape invariant representations of motion direction in somatosensory cortex. PLoS. Biol. 2010 doi: 10.1371/journal.pbio.1000305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips JR, Johansson RS, Johnson KO. Responses of human mechanoreceptive afferents to embossed dot arrays scanned across fingerpad skin. J. Neurosci. 1992;12:827–839. doi: 10.1523/JNEUROSCI.12-03-00827.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randolph M, Semmes J. Behavioral consequences of selective ablations in the postcentral gyrus of Macaca mulatta. Brain Res. 1974;70:55–70. doi: 10.1016/0006-8993(74)90211-x. [DOI] [PubMed] [Google Scholar]
- Ruiz S, Crespo P, Romo R. Representation of moving tactile stimuli in the somatic sensory cortex of awake monkeys. J. Neurophysiol. 1995;73:525–537. doi: 10.1152/jn.1995.73.2.525. [DOI] [PubMed] [Google Scholar]
- Rust NC, Mante V, Simoncelli EP, Movshon JA. How MT cells analyze the motion of visual patterns. Nat. Neurosci. 2006;9:1421–1431. doi: 10.1038/nn1786. [DOI] [PubMed] [Google Scholar]
- Salzman CD, Britten KH, Newsome WT. Cortical microstimulation influences perceptual judgments of motion direction. Nature. 1990;346:174–177. doi: 10.1038/346174a0. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Britten KH, Newsome WT, Movshon JA. A computational analysis of the relationship between neuronal and behavioral responses to visual motion. J. Neurosci. 1996;16:1486–1510. doi: 10.1523/JNEUROSCI.16-04-01486.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimojo S, Silverman GH, Nakayama K. Occlusion and the solution to the aperture problem for motion. Vision Res. 1989;29:619–626. doi: 10.1016/0042-6989(89)90047-3. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Heeger DJ. A model of neuronal responses in visual area MT. Vision Res. 1998;38:743–761. doi: 10.1016/s0042-6989(97)00183-1. [DOI] [PubMed] [Google Scholar]
- Sripati AP, Bensmaia SJ, Johnson KO. A continuum mechanical model of mechanoreceptive afferent responses to indented spatial patterns. J. Neurophysiol. 2006;95:3852–3864. doi: 10.1152/jn.01240.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treue S, Hol K, Rauber HJ. Seeing multiple directions of motion-physiology and psychophysics. Nat. Neurosci. 2000;3:270–276. doi: 10.1038/72985. [see comments] [DOI] [PubMed] [Google Scholar]
- Tsui JM, Hunter JN, Born RT, Pack CC. The role of V1 surround suppression in MT motion integration 1. J. Neurophysiol. 2010;103:3123–3138. doi: 10.1152/jn.00654.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallach H. Ueber visuell wahrgenommene Bewegungsrichtung. Psychologische Forschung. 1935;20:325–380. Ref Type: Generic. [Google Scholar]
- Warren S, Hämäläinen HA, Gardner EP. Objective classification of motion- and direction-sensitive neurons in primary somatosensory cortex of awake monkeys. J. Neurophysiol. 1986;56:598–622. doi: 10.1152/jn.1986.56.3.598. [DOI] [PubMed] [Google Scholar]
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat. Neurosci. 2002;5:598–604. doi: 10.1038/nn0602-858. [DOI] [PubMed] [Google Scholar]
- Whitsel BL, Dreyer DA, Roppolo JR. Determinants of body representation in postcentral gyrus of macaques. J. Neurophysiol. 1971;34:1018–1034. doi: 10.1152/jn.1971.34.6.1018. [DOI] [PubMed] [Google Scholar]
- Wilson HR, Ferrera VP, Yo C. A psychophysically motivated model for two-dimensional motion perception 2. Vis. Neurosci. 1992;9:79–97. doi: 10.1017/s0952523800006386. [DOI] [PubMed] [Google Scholar]
- Yo C, Wilson HR. Perceived direction of moving two-dimensional patterns depends on duration, contrast and eccentricity. Vision Res. 1992;32:135–147. doi: 10.1016/0042-6989(92)90121-x. [DOI] [PubMed] [Google Scholar]
- Zeki SM. Functional organization of a visual area in the posterior bank of the superior temporal sulcus of the rhesus monkey. J. Physiol. 1974;236:549–573. doi: 10.1113/jphysiol.1974.sp010452. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.