Signaling pathways that control cell migration: models and analysis

Abstract

Dissecting the intracellular signaling mechanisms that govern the movement of eukaryotic cells presents a major challenge, not only because of the large number of molecular players involved, but even more so because of the dynamic nature of their regulation by both biochemical and mechanical interactions. Computational modeling and analysis have emerged as useful tools for understanding how the physical properties of cells and their microenvironment are coupled with certain biochemical pathways to actuate and control cell motility. In this focused review, we highlight some of the more recent applications of quantitative modeling and analysis in the field of cell migration. Both in modeling and experiment, it has been prudent to follow a reductionist approach in order to characterize what are arguably the principal modules: spatial polarization of signaling pathways, regulation of the actin cytoskeleton, and dynamics of focal adhesions. While it is important that we “cut our teeth” on these subsystems, focusing on the details of certain aspects whilst ignoring or coarse-graining others, it is clear that the challenge ahead will be to characterize the couplings between them in an integrated framework.

Cell migration is governed by a complex network of signal transduction pathways that involve lipid second messengers, small GTPases, kinases, cytoskeleton-modifying proteins, and motor proteins. For cells to achieve productive movement, these signaling processes must be differentially and persistently localized to particular regions of the cell [1], yet they must also respond in a dynamic fashion to extracellular cues. This spatial patterning or “symmetry breaking” dilemma is resolved in a variety of ways in different cell/environmental contexts; however, the underlying, molecular-level mechanisms are only partially understood. In cells of mesenchymal origin, such as fibroblasts, a broad, flat lamellipodium with newly formed adhesive contacts at its leading edge protrudes as a consequence of integrin-mediated signaling and associated actin polymerization. A fraction of these nascent adhesions mature in conjunction with actomyosin-dependent forces to form large, long-lived adhesions, which disengage or disassemble in the rear of such cells. In contrast, amoeboid cells exhibit protrusion of the cell front that is unfettered by stable adhesions and balanced by myosin-dependent squeezing forces at the rear. Intriguingly, some cell lineages and cancer cells exhibit a transition from one form of migration to the other as a characteristic of their differentiation/dedifferentiation program [2].

Another aspect of cell migration signaling that makes it difficult to analyze using traditional, reductionist approaches is that all of the functional components required for productive movement must work in unison, and they do not function normally without the feedbacks and couplings between them. This is in stark contrast with certain aspects of gene regulation and the cell cycle, for instance, where certain checkpoint conditions must be met to ensure that each step is initiated sequentially but otherwise independently. Membrane protrusion is accelerated by signals that originate from adhesions, and adhesions in turn grow in response to motor-driven mechanical forces that ultimately move the cell body forward [3]. Failure of any of these individual subprocesses, or failure to couple them appropriately, results in defective migration phenotypes. Further, the presence of feedback loops in signaling networks offers the potential for amplified sensitivity or adaptation to stimuli, but such complexities complicate the analysis of experiments [4].

Over the past decade, mathematical modeling and sophisticated image analysis approaches have emerged in combination with live-cell fluorescence microscopy to help interpret the dynamics of intracellular signaling and regulation of cell motility. In this focused review, we highlight recent efforts wielding these complementary approaches to quantitatively characterize three important signaling modules: polarization of intracellular signaling, regulation of the actin cytoskeleton, and focal adhesion signaling. The goal here is to concentrate attention on the integration of experimental and theoretical efforts in the field of cell migration, rather than on the understanding of a particular motile cell type.

Polarization of Intracellular Signaling

To execute persistent migration, cells establish leading and trailing ends in which different signaling pathways promote membrane protrusion and retraction, respectively. Most often, cell orientation is biased, with commensurate asymmetric localization of intracellular signaling processes, by external gradients of soluble and/or adhesive ligands. Directed migration, or taxis, of cells in culture has also been observed in response to gradients of mechanical stiffness, temperature, and electric field. The diversity of conditions capable of inducing directed migration suggests that the signaling systems responsible for sensing such gradients converge upon common intracellular regulators of cell polarity. In the absence of such cues, cells that exhibit random changes in migration direction also demonstrate spatial organization of intracellular signaling that correlates with cell migration behavior, and recent evidence suggests that random migration might be a consequence of unbiased firing of stochastic protrusion events [5]. Likewise, directed migration might reflect a spatial bias in the execution of the same processes [6, 7].

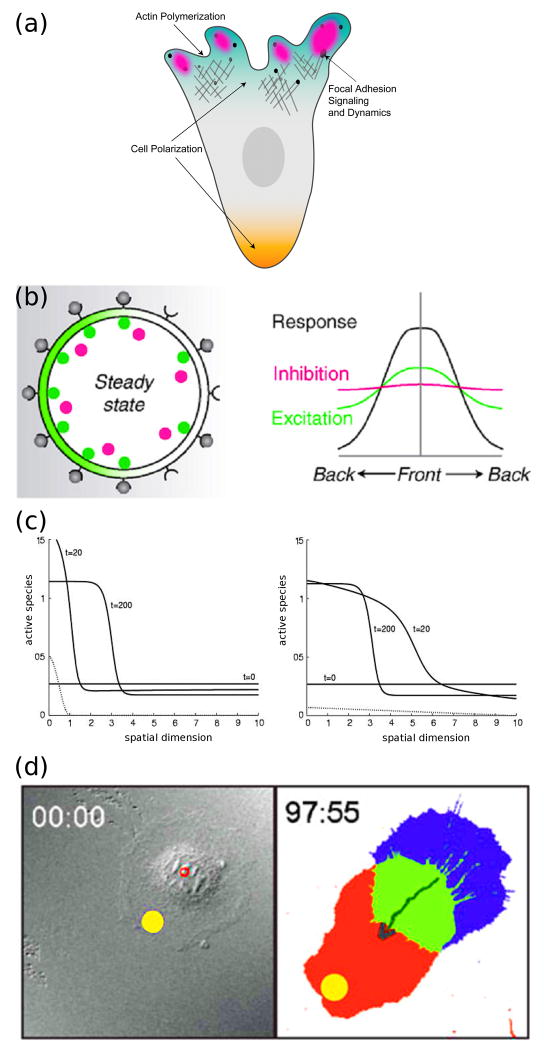
It is widely believed that maintenance and/or dynamic remodeling of cell morphological polarity is governed through the asymmetric spatial distribution and activation of certain signaling proteins, and numerous mathematical models and analysis approaches have been developed and applied to test their roles in cell orientation (Figure 1). Many such models have implemented variations of the local excitation global inhibition (LEGI) mechanism, which achieves sensitivity by generating localized regions of slow-diffusing signaling activity at the plasma membrane (often with positive feedback) in a background of similarly responsive negative regulation that is distributed by rapid diffusion in the cytosol [8-10]. Recent stochastic modeling work by Altschuler et al. explored the alternate possibility that spontaneous cell polarization might be achieved by a simple generalized positive feedback mechanism whereby a membrane-bound species is self-recruited to the membrane, with corresponding depletion from a cytosolic pool [11]; the same mechanism had previously been proposed in a deterministic model of spatial gradient sensing [12]. In the mathematical sense, depletion of a fast-diffusing precursor is completely analogous to the activation of a fast-diffusing inhibitor in LEGI models.

Figure 1. Breaking symmetry of intracellular signaling in migrating cells.

(a) Signaling pathways are coordinately localized at the cell front and rear (polarization). They affect, and are in turn affected by, the dynamics of the actin cytoskeleton and cell-matrix adhesion complexes. (b) Local Excitation Global Inhibition (LEGI) models develop intracellular asymmetry in the face of shallow extracellular gradients by amplifying receptor occupancy (gray) via localized activation with positive feedback or cooperativity (green), in tandem with an inhibition mechanism dispersed by fast diffusion (red). (Reprinted with permission from [9]. Copyright 2008 Elsevier Inc.). (c) Polarized signaling responses to two different external gradients, as computed from the “wave pinning” mechanism, are shown by solid lines. The final position of the wavefront (t = 200) does not depend on the stimulus (dotted lines), but rather on the total amount of the signaling protein, which is the same in both cases. (Reprinted with permission from [19]. Copyright 2008 Elsevier Inc.). (d) Guidance of cell migration by focal photo-activation of Rac (yellow spot). (Reprinted with permission from [22]. Copyright 2009 Macmillan Publishers Ltd).

Since the late 1990’s, the localized activities of phosphoinositide 3-kinases (PI3Ks) and the 3′-phosphoinositide phosphatase PTEN have received much attention in the arena of cell migration and chemotactic signaling, although it is currently appreciated that the precise role of PI3K signaling in promoting gradient sensing and cell motility is context-dependent [13]. Phenomenological models of the PI3K/PTEN system have been used to explore the relationships between intrinsic polarity and gradient-induced polarization, and analysis of these models suggests that these opposing enzymes work together to control and adjust cellular orientation based on the LEGI principle [14, 15]. This work also highlights the importance of designing experiments to investigate specific properties of biochemical signaling systems; for example, the authors suggest evaluating the effect of identical chemotactic gradients on cells with different internal states to test the importance of intrinsic polarity. Whereas LEGI and depletion models generally incorporate positive and negative feedback loops to explain signal amplification and adaptation in amoeboid cells, spatial models have also been used to rule out the need for such mechanisms to explain the relatively insensitive gradient sensing mechanism in fibroblasts [16, 17].

Several members of the Rho GTPase family, notably Rac1, RhoA, and Cdc42, have been even more strongly implicated in cell polarization. To explain their spatial segregation, a number of investigators have proposed models invoking synergistic and antagonistic interactions among Rho family members. Otsuji et al. compared different models of Rac/Rho/Cdc42 regulation to assess the general properties of this signaling system, concluding that mass conservation and diffusion-driven instability may be the fundamental properties that lead to polarization of signaling [18]. Further work based on a generalized description of the properties of the GTPase signaling network has shown that a single Rho family member, cycling between a slow-diffusing, membrane-bound form and a fast-diffusing, cytosolic form, may display the requisite bistability and pattern formation characteristics necessary for cell polarization [19]. To capture the requisite behavior, this model includes cooperative, saturable positive feedback in the activation of the small GTPase [mediated by guanine nucleotide exchange factors (GEFs)] and a corresponding depletion of the more homogeneous, cytosolic pool of inactive protein.

To date, most experimental studies of directed migration have involved generation of gradients or heterogeneous conditions of cellular stimulants [20], and continued use of these approaches in combination with progress in analysis techniques will further develop our understanding of cell polarization. Recently, the prospect of using small molecules [21] or light [22] to control the localized activity of signaling proteins has emerged as a powerful and potentially general tool for exploring how spatial segregation of cell signaling contributes to cell orientation and migration.

Regulation of the Actin Cytoskeleton

The actin cytoskeleton is in large part responsible for formation of protrusive structures and transducing the forces necessary for cell translocation, and thus it serves as a central integrator of signaling pathways that control cell migration. Accordingly, analysis of the mechanisms by which the actin cytoskeleton is regulated has produced a rich literature leveraging both theoretical and experimental approaches, and the functions of a host of actin-modifying proteins have been delineated as a result [23]. Recent work has extended our understanding of how actin dynamics are modulated by multiple regulatory proteins and has provided insight into how spatial organization of actin and myosin activity affects cell shape (Figure 2).

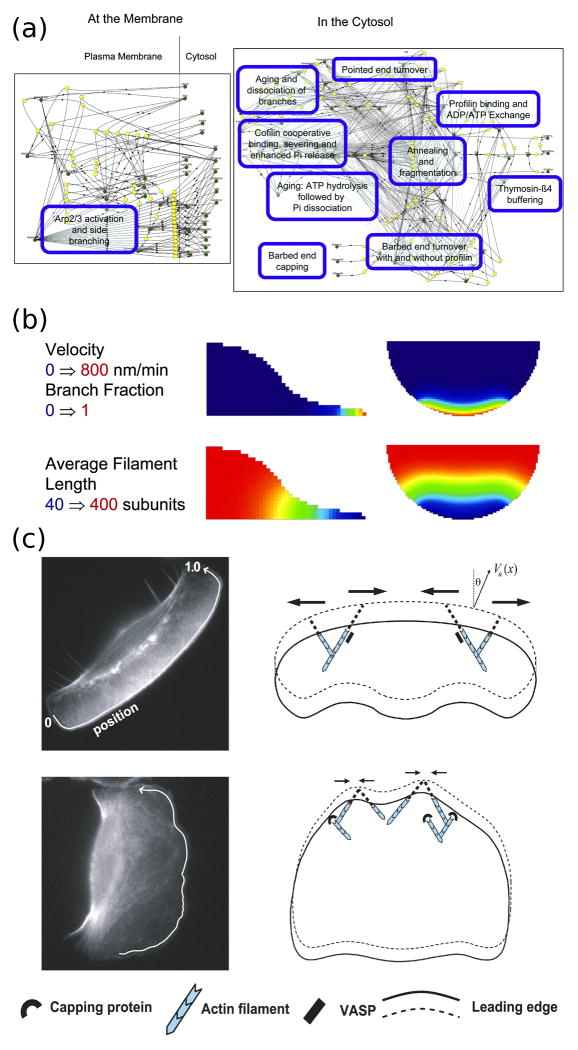
Figure 2. Computational modeling of actin cytoskeletal dynamics.

(a) The continuum model assembled by Ditlev et al. encompasses an extensive actin modification network. In the diagram, green circles represent different species or state variables, connected to the reactions (yellow) by solid lines, and the dashed lines represent catalytic interactions. (Reprinted with permission from [24]. Copyright 2009 Elsevier Inc.). (b) Implementation of the model by Ditlev et al. in three dimensions following activation of dendritic nucleation at the cell edge. The top row shows how the protrusion velocity (calculated as a function of actin branching) is localized to the cell front and decays rapidly behind the leading edge. The bottom row shows how actin filament length depends on the rapid nucleation and capping of actin filaments at the cell front that results from depletion of G-actin. (Reprinted with permission from [24]. Copyright 2009 Elsevier Inc.). (c) The model of actin filament dynamics by Lacayo et al. shows how excessive filament capping at the leading edge can produce rough cell morphologies. In cells with high VASP activity at the leading edge (top row), actin filaments are protected from capping and are subject to lateral flows that smooth heterogeneities in protrusive force at the leading edge. (Reprinted with permission from [26]).

Ditlev et al. recently assembled a detailed model of actin polymerization and depolymerization kinetics, which stands as a compendium of quantitative rate parameters and other experimental evidence accrued in the literature and allows for solution of the corresponding partial differential equations with realistic cellular geometries [24]. Implemented in the openly accessible Virtual Cell software environment, the model quantitatively synthesizes the known activities that influence actin filament growth, capping, severing, and branching. This effort highlights how large-scale signaling models will be important in developing a more cohesive, integrated view of cell migration; the challenge ahead is that we do not yet have a quantitative handle on how upstream signaling pathways influence actin dynamics.

Compared with the comprehensive, continuum model of Ditlev et al., a model of a single, actin-rich filopod implements a much smaller reaction network but simulates the stochastic dynamics of such motile structures at the level of discrete actin monomers [25]. This model incorporates feedback from the forces that arise from actin filaments pushing against the plasma membrane and successfully explains how experimentally observed growth and retraction behaviors of filopodia might arise from stochastic noise intrinsic to their mechanochemical network.

A coarser and also less comprehensive level of detail is often most appropriate for models driven by experimental data, exemplified by a study of how the localization and activity of a specific actin-interacting protein, VASP, affects the morphology and speed of migrating fish keratocytes [26]. VASP effectively increases the local polymerization rate by inhibiting capping of F-actin barbed ends, which smooths out fluctuations in actin dynamics and thus promotes a smoothly curved shape of the leading edge; conversely, low VASP activity results in the “rough” cell shapes that are characteristic of slow-migrating cells. Following up on that work, the same group showed that the lateral gradient of F-actin along the keratocyte lamellipod determines the cell’s radius of curvature and thus its overall shape [27].

Mechanical forces influence cell migration signaling in important yet incompletely understood ways, and a great deal of work has been devoted to the quantitative characterization of cytoskeletal mechanics and the role of non-muscle myosin II motors [28]. Theoretical work in this area has accelerated recently. Chandran et al. invoked a continuum mechanical model to show how actin stress fibers emerge and spread in a band-like manner as a result of forces opposed by F-actin resistance [29]. By formulating a detailed model describing the forces generated in an actin gel as a cell forms multiple points of adhesion, Shemesh et al. showed that the lamellipodia/lamella interface might arise as a consequence of high stretching stresses that dissolve the actin gel to create two distinct zones at the cell’s leading edge [30]. A two-dimensional model of myosin transport and myosin-powered viscoelastic flow of the F-actin network in a realistic, two-dimensional lamellipod geometry was used to generate maps of the traction forces and stresses present in a migrating keratocyte and to show how myosin-induced flows can give rise to various, experimentally observed cell shapes [31].

Recent experimental studies have likewise contributed rich quantitative information characterizing actin dynamics and the attendant forces applied during cell migration. Fournier et al. simultaneously monitored actin movement in, and substrate deformation by, migrating keratocytes to determine where actin-based forces are applied and thus demonstrated how this highly motile cell type maintains persistent motion by a combination of actomyosin contraction and actin assembly [32]. Such quantitative, spatially resolved measurements are immensely valuable for critical validation and/or refinement of models and of the current mechanistic understanding in general.

Focal Adhesion Signaling

Especially in cells that exhibit movement of the mesenchymal type, an important step of the migration cycle is formation of firm attachment points called focal adhesions, which transduce adhesive forces from the cell cytoskeleton to the extracellular matrix (ECM) via adhesion receptors, most notably integrins. These adhesive structures have two important properties that are ripe for quantitative studies: their ability to activate signal transduction pathways locally, thus reinforcing the polarization of signaling during directionally persistent movement, and their dynamic responses to tensile stress, as dictated by the mechanical forces applied internally and externally and the viscoelastic properties of the cell and ECM [33] (Figure 3).

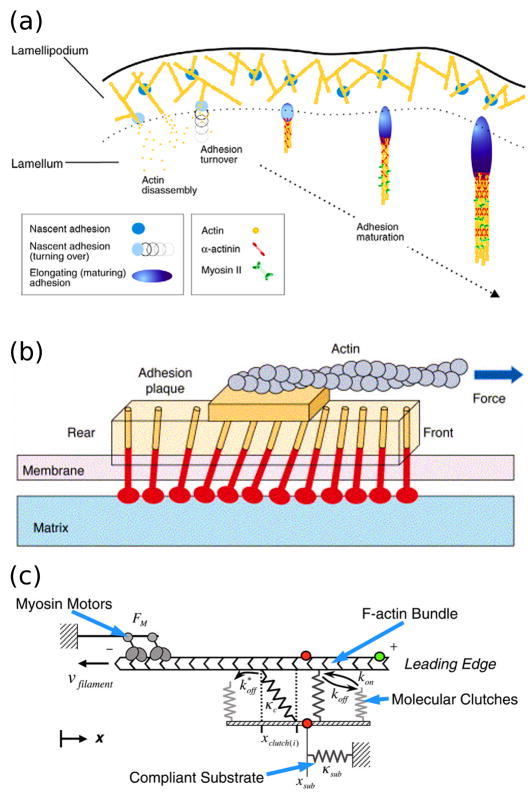
Figure 3. Focal adhesion signaling and remodeling.

(a) Formation, maturation, and turnover of adhesions at the leading edge occur in different locations and in response to different mechanical and biochemical cues. (Reprinted with permission from [52]. Copyright 2009 The Company of Biologists). (b) Conceptual model of focal adhesion remodeling in response to mechanical strain. The mechanosensitive lower layer of the adhesion complex experiences strain induced by the coupling of actin filaments to the upper layer, inducing growth of the focal adhesion in the direction of force. (Reprinted with permission from [33]. Copyright 2006 Elsevier Inc.). (c) The computational model proposed by Chan and Odde recapitulates the mechanical “clutching” observed between moving actin filaments and adhesion receptors bound to a compliant substrate. (Reprinted with permission from [44]. Copyright 2008 The American Association for the Advancement of Science).

It has been appreciated for some time that signaling pathways mediated by ligated integrins, including the aforementioned PI3K- and Rho-family GTPase-dependent pathways, regulate cytoskeletal dynamics and myosin-dependent contraction [34]; however, our understanding of how they are dynamically localized during cell migration is relatively nascent, developing in tandem with the application of live-cell fluorescence microscopy approaches [35]. For example, Forster resonance energy transfer (FRET) microscopy has been used in combination with microcontact printing of small ECM islands on the surface to show that Rac activation by focal adhesion signaling in fibroblasts is highly localized [36], consistent with estimates of Rac1 membrane diffusion and GTP hydrolysis rates in fibroblasts spreading on ECM [37]. These properties are important because they govern how Rac-mediated protrusion waves might propagate along the leading edge, as considered in recent computational models [38, 39].

After integrin-mediated adhesion complexes form in response to ECM ligation, further changes in their properties, most notably focal adhesion maturation, are observed in response to applied forces. Two competing theories have emerged to explain the observed phenomenon, one postulating strain-induced changes in the conformations of constituent proteins, and the other based on thermodynamic arguments where forces applied to the interfaces between constituent proteins affect binding affinities within the complex [33]. Recent theoretical work extending the concept of mechanosensitive focal adhesion growth predicts how the dynamics of the process depends on the compliance of the adhesive substratum [40]. Of interest to experimentalists, the theoretical results emphasize the notion that, in traction force measurements on elastic gels, both the measured force and mechanical feedback affecting focal adhesion dynamics depend on substrate stiffness.

Another intriguing aspect of focal adhesions is that they exhibit “clutching” behavior, whereby slippage can occur between moving actin stress fibers and bound adhesion receptors [41]. Traction force microscopy and fluorescence speckle microscopy have been used to show that the speed of F-actin flow within a cell is related to traction forces applied by focal adhesions in a highly nonlinear fashion, suggesting a viscous coupling between actin flow and adhesion forces [42]. This phenomenon has been examined in terms of the kinetic parameters that might characterize this behavior in different cell types [43], and in terms of the stochastic behavior of filopodia [44]. In the latter study, the model proposed by Chan and Odde predicts emergence of an oscillatory “load and fail” cycle on soft substrates and clutch slippage on hard substrates. Specifically, the model predicts a range of substrate stiffness where actin flow rate is sensitive to substrate stiffness, in accord with experimental measurements.

Integrative Efforts

The studies highlighted above illustrate a common trade-off in modeling and analysis of biological processes. On the one hand, there is a need to develop a broad understanding of how disparate subprocesses work together, but more comprehensive models need to be coarse-grained in order to fill the gaps in our current understanding and so that the model may be tractably parameterized. On the other hand, the reductionist agenda demands that we also drill down to the fine details of each modular subprocess. A judicious balance between these competing interests is generally dictated by the availability of quantitative data, and hence the challenge in formulating a multi-scale model of cell migration will be to decide how best to connect the various modules, recognizing too that certain modules might need to be substituted or modified to capture the peculiarities of different cell and environmental contexts. Recent work at the interfaces between the subprocesses outlined above suggests how we might proceed towards this goal.

Three recent experimental studies have employed sophisticated microscopy and image analysis techniques to further our understanding of how cell signaling correlates in time and space with protrusion of the cell’s leading edge. Machacek et al. developed an elegant method for edge tracking with fine spatial resolution and correlated protrusion velocity with the fluorescence intensities of three FRET biosensors, imaged pair-wise, monitoring the active forms of Rho, Rac, and Cdc42 in migrating fibroblasts [45]. Somewhat surprisingly, they found that localized Rho signaling coincides with protrusion, whereas Rac and Cdc42 signaling lags by about 40 seconds at a distance of about 2 μm from the cell edge in fibroblasts. In a separate study by Tsukada et al., it was found that over a slightly longer spatial scale Rac and Cdc42 signaling typically follows membrane protrusion by 6-8 minutes in human fibrosarcoma cells [46]. These studies suggest a dynamic spatiotemporal interplay among the Rho-family GTPases that is likely to be critical for controlling actin polymerization. In another quantitative study, Weiger et al. imaged and analyzed the spatiotemporal dynamics of PI3K signaling in fibroblasts and showed that its spatial pattern correlates strongly with the persistence of membrane protrusion and overall cell movement, and further that the signaling dynamics in distant regions of the cell are coupled in an antagonistic or competitive way [47]. Continued development and application of novel analysis techniques, in conjunction with mathematical models, should further elucidate how localized signaling is integrated with cell mechanics.

As a step in that direction, models integrating signaling through PI3K and Rho-family GTPases along with a simple representation of actin polymerization have been formulated to explore how spatial polarization of motility may be initiated and maintained in amoeboid cells [48, 49]. The accompanying analysis suggests that coupling between the two signaling modules is important for stabilizing polarity in the face of stochastic noise, while allowing for changes in direction. Two stochastic models published more recently integrate integrin-mediated Rac signaling, membrane protrusion, and adhesion dynamics at the leading edge to show how multiple feedback loops might shape the dependence of mesenchymal cell motility on ECM density and actomyosin contractility [38, 39]. Whereas those models focus on the molecular details of the signaling biochemistry and coarse-grain the mechanics, others attack the problem from the opposite direction. The model of Stéphanou et al. incorporates a force balance on the actin cytoskeleton to solve for the position of the cell membrane subject to spontaneous protrusion and mechanically responsive adhesion dynamics [50]. An interesting prediction arising from this work is that the persistence of cell migration may be affected by the relative lifetimes of different adhesion complexes. The model by Pathak et al. integrates stress fiber formation along with mechanosensitive adhesion dynamics to recapitulate the observed two-dimensional arrangements of stress fibers and adhesion proteins in cells plated on different ECM patterns [51].

Conclusions

As live-cell imaging and other experimental approaches promise to reveal more quantitative details of cell motility at the molecular level, it is anticipated that analytical methods and mathematical models will play an increasingly important role in the mechanistic interpretation of data. Although the work highlighted here represents the cutting edge in that regard, much of the work in the field remains (appropriately) reductionist in approach. As we move towards a more complete understanding of the individual parts of the cell migration machinery, it will be vital to continually evaluate how they are integrated to regulate cell migration phenotypes.

An important issue that has been touched upon throughout this review is the need to more quantitatively characterize the similarities and differences among various motile cell types. If we consider too the environmental context, the regions of the experimental parameter space that have been sampled to date are collectively rather tiny. Computational modeling promises to remedy this situation at least partially through its ability to generate testable predictions, effectively “interpolating” between different contexts. A related point is that cells are traditionally imaged as they migrate on flat, stiff surfaces, as this is most amenable to a variety of microscopy techniques. As researchers move to study cell migration in more physiological, three-dimensional environments, methods of image analysis and refinements of existing mathematical models and theoretical concepts will need to keep pace. Finally, we see the development of new fluorescent biosensors/molecular beacons, with specificities for a much larger array of intracellular targets than is currently available, as another key process that is likely to determine the rate of progress in the field.