Anterior-posterior and medial-lateral control of sway in infants during sitting acquisition does not become adult-like

Abstract

We examined 1) how sitting postural control in infants develops in the anterior-posterior (A/P) and medial-lateral (M/L) directions of sway, and 2) whether this control is already adult-like during the late phase of infant’s sitting acquisition. COP data were acquired from 14 healthy infants (from the onset of sitting until independent sitting) and 21 healthy adults while sitting on a force platform. Attractor dimensionality (CoD: correlation dimension), attractor predictability (LyE: largest Lyapunov exponent), and sway variability (RMS: root-mean square) were calculated from the COP data to evaluate postural control. In the A/P direction, sitting was mastered by the infants by decreasing the active degrees of freedom of the postural system (decreased CoD), using a more predictable and (locally) stable sway (decreased LyE), and increasing sway variability (increased RMS). Control of sitting became practically simple, stable and exploratory with infant development. This may support the hypothesis that the sitting posture serves as the foundation for the development of other motor skills, as reaching. In the M/L direction, only sway variability decreased with development, possibly due to changes in the infant’s body dimensions. Taken together, these findings indicate that early in development the focus is more in the A/P than the M/L direction. Adults’ postural control was found more adaptable than the infants in both directions, involving more active degrees of freedom and less predictable sway patterns. Identifying the factors that make the dynamics of the postural system adult-like requires further research.

1. Introduction

The achievement of independent sitting is a major motor milestone, requisite for the development of other activities such as reaching, grasping, eye/hand coordination, standing posture and locomotion [1–5]. Therefore, several studies have examined how this skill is acquired as part of the infant’s motor development [6–9]. While most of the literature on this subject focuses on the processes operating within the central nervous system [e.g., 6,7], a few recent studies used as a theoretical background the dynamical systems approach to motor development [8,9]. This approach emphasizes the self-organizing principles underlying skills acquisition over time, under the shaping influence of environmental, task, and biomechanical constraints [10]. Specifically, sitting is viewed as a high-dimensional task in which the many degrees of freedom (DFs) of the sensory-motor system are compressed into a low-dimensional space of a few active DFs [10,11]. Maintaining sitting posture results thus from mastering the active DFs.

Using this theoretical framework, Harbourne and Stergiou [8] used center of pressure (CoP) data to show that infants achieve sitting posture in the anterior-posterior (A/P) direction of sway by freezing and freeing the active DFs during the intermediate (~ six to seven months) and late (~ seven to eight months) phases of sitting acquisition, respectively. Moreover, they found that postural control becomes more stable with development. They postulated that the freezing to freeing strategy of the active DFs allows the infant to first assemble a safe sitting skill and second to interact with the environment while sitting. A remaining issue is now to determine whether infants’ postural control during the late phase of sitting acquisition is already comparable to that of adults. Considering that active DFs are already released in this phase, possibly to make postural control more complex (perhaps for exploration purposes), we hypothesized that an adult-like control of sitting posture is already present at that time.

Another issue of interest is whether infants achieve sitting by solving the DFs problem in the medial-lateral (M/L) direction of sway the same way as they do in the A/P direction. It is known that a differentiated control of sway is evident in the A/P and M/L directions in adult standing [12,13]. Harbourne et al. [9] also supported the need to consider separately the A/P and M/L directions of sway in infant sitting. These authors used a principal component analysis and found that sway variables from the A/P direction loaded onto different factors than variables from the M/L direction. This finding suggested that the two directions describe different features of sitting postural control. Therefore, determining changes in the M/L direction during the development of sitting represents an important step to improve our understanding of the sitting skill acquisition. Since new skills are commonly mastered by freezing and/or freeing the active DFs [10,11,14], we hypothesized that one of these pathways of change will also be observed in the M/L direction, with the control of sway becoming comparable to that of adults.

2. Methods

2.1 Subjects

Fourteen typically developing infants (six males, eight females; age at onset: 150.8±15.01 days) and 21 healthy adults (nine males, twelve females; age: 23±2.45 years, height: 1.65±0.32 m; weight: 63.95±9.39 kg) participated in the study. The infants were followed over a period of four months (from the age of five to eight months), the time for them to sit independently. Inclusion entry criteria for the infants into the study were: a) a score on the Peabody Gross Motor Scale (PGMS) within 0.5 SD of the mean, b) an age of about five months at the time of initial data collection, and c) abilities to hold up their head when supported at the thorax, to reach for objects dangled in front of them in supported sitting or lying on their back, to prop on their elbows for thirty seconds and to prop on both arms to maintain sitting. The exclusion criteria were: a) a score on the PGMS greater than 0.5 SD below the mean, b) diagnosed visual deficits, and c) diagnosed musculoskeletal problems. The inclusion criteria for the adults were the absence of any neurological, visual, vestibular, or musculoskeletal problems that might affect postural steadiness. Adults were also excluded from the study if they were unable to sit on the force platform surface (0.6 m × 0.4 m) without any part of them touching the floor around the platform (Fig. 1). An informed consent form was signed by the parents of the infants and by the adults before the experiment.

Fig. 1.

Illustration of the experimental set-up for an adult and an infant during the late phase of sitting acquisition (i.e., stage 3 of sitting).

2.2 Experimental design

Each infant underwent nine experimental sessions. The first session lasted for 45 min and was used to perform the PGMS which is a norm and criterion referenced test that examines gross motor function from birth to 83 months. The other eight sessions were sitting sessions, distributed every month of the four-month period, during which the infants performed a sitting skill on a force-plate (Fig. 1). Specifically, the infants were tested twice in one week at each of the four months of the study. A physical therapist identified each session’s sitting behavior according to three stages of sitting: 1) prop sitting (i.e., early phase of sitting acquisition), 2) prop sitting with periods of 10 s independent sitting (i.e., intermediate phase of sitting acquisition), and 3) independent sitting (i.e., late phase of sitting acquisition). Stage of sitting was considered as a more appropriate independent variable of development than the age since infants presented similar sitting behaviors at different ages, and, two or more sessions were identified at the same stage of sitting. Although more than one session could correspond to the same stage of sitting, the data presented in the study for each infant’s phase of development were always chosen from the same session, considered as the best sitting performance session.

The adults took part in three experimental sessions of 5 min each. They were asked to sit on a force-plate in a yoga style position with their hands resting comfortably in their lap and head facing forward (Fig. 1).

2.3 Data collection

Infants’ COP data in the A/P and M/L directions were obtained using an AMTI force-plate (Advanced Mechanical Technology Inc., Model OR6-7-1000) interfaced with a VICON 370 3-D Motion Capture System (Fig. 1). Specifically, the COP coordinates were obtained (240 Hz) from the components forces (F_x, F_y, F_z) and moments (M_x, M_y, M_z) using the VICON 370 v. 2.5 software (Oxford Metrics Ltd., Oxford, UK). The sampling frequency was selected based on a frequency analysis of both A/P and M/L COP data which indicated a range of signal frequencies that contains the entire signal power spectral density between 1 and 30 Hz. For each infant and stage of sitting, three segments of 8.3 s, corresponding to 2000 data points each, were then selected over the sitting sessions for analysis.

Adults’ COP data in the A/P and M/L directions were acquired by means of a Kistler force-plate (Model: 9281-B11; Amherst, NY) interfaced with a Peak Technologies Motus 7.2 system (Englewood, CO) (Fig. 1). The sampling frequency was set at 10 Hz as the frequency range of the A/P and M/L COP signals was found below 1 Hz. Three segments of 200 s were selected from the 5 min collecting sessions. The 200 s duration allowed the COP time series for the adults to count a similar number of points (i.e., 2000 data points) as those used for the infants and eliminated any artificial differences in the nonlinear measures (see below) due to uncontrolled time series length. No filtering was performed on the COP time series as has been prescribed when calculating nonlinear measures [15].

2.4 Data analysis

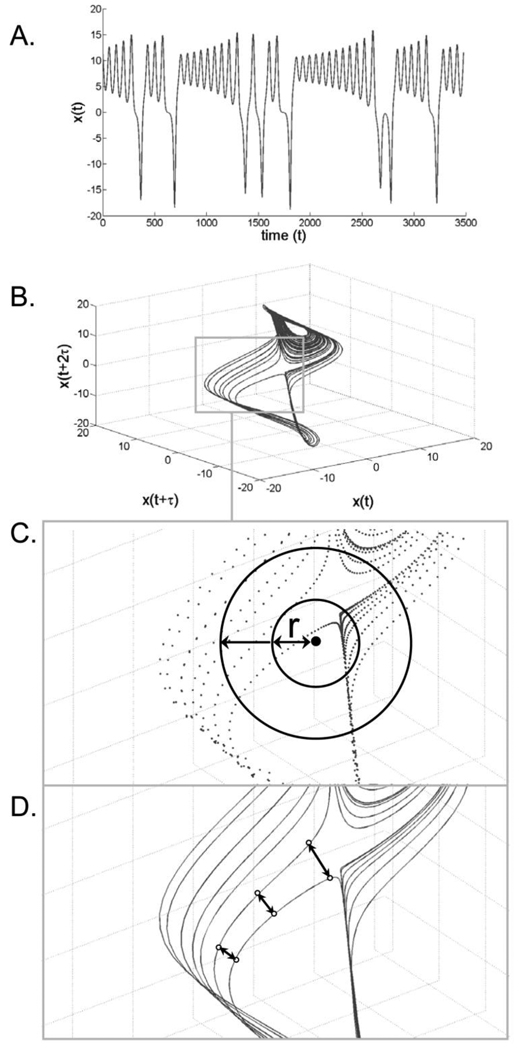
To quantify the active DFs involved in the control of sitting, the (multi-dimensional) attractor underlying the postural system was first reconstructed from each scalar COP time series using the time-delay method (Fig. 2A & 2B) [16]. In order to unfold the attractor with no overlap in the reconstructed trajectories, the number of dimensions was selected where the percentage of the global false nearest neighbors (GFNN) approached zero [17]. The GFFN analysis of the COP time series was conducted using Tools for Dynamics software [18]. Five and six embedding dimensions were found adequate to unfold the attractor from the infants and adults COP time series, respectively. The correlation dimension (CoD) was then calculated from the reconstructed attractor using the Chaos Data Analyzer software [19]. CoD is an estimate of the attractor’s dimensionality and identifies the least number of independent variables (i.e., active DFs) needed to characterize a complex system. Technically, the fraction of points C(r) contained within a (hyper) sphere of radius r centred about some points on the attractor is evaluated for various r values (Fig. 2C). CoD is then obtained from the slope of the relation between log[C(r)] and log[r] [20]. Practically, the higher the CoD value, the larger the active DFs [21]. The largest Lyapunov Exponent (LyE) was also calculated from the reconstructed attractor using the same software. The LyE quantifies the average exponential rate of divergence of neighboring trajectories in phase space (Fig. 2D) [22]. This is a direct measure of the attractor’s predictability and sensitivity to infinitesimal (local) perturbations of the (postural) system, with larger exponents indicating lower attractor predictability and greater sensitivity to local perturbations (i.e. greater local instability) [21,23].

Fig. 2.

Schematic representation of the attractor-based analysis. (A) A time series data, x(t), plotted as a function of time t (arbitrary units). (B) Reconstruction of the attractor from x(t) using the time delay method. As an example, the attractor presented here is three-dimensional [x(t), x(t+τ), x(i+2τ)]. (C) Calculation of the correlation dimension (CoD) by evaluating the way in which the fraction of points contained within a (hyper) sphere of radius r centred about some points on the attractor scales with r. (D) Calculation of the largest Lyapunov exponent (LyE) by measuring the (average exponential) rate of divergence of neighboring trajectories of the attractor.

Finally, the Root-Mean Square (RMS) of the COP time series was also calculated using Matlab (Matlab 7.1, The Mathworks, USA). This parameter, which measures the magnitude of varying COP displacements, was included in the study since it is a standard descriptive variable of postural strategies relatively independent of biomechanical factors (e.g., height and weight) which are expected to change with development [24].

2.5 Statistical analysis

Individual mean values of CoD, LyE and RMS were calculated for the different stages of sitting (i.e., stages 1 to 3 and adult’s stage) and for both the A/P and M/L sway directions. To evaluate changes in the development of sitting postural control, (i) repeated measures analyses of variance (ANOVAs) across the stages 1 to 3 of infant sitting, and (ii) independent t-tests between the stages of infant sitting and adult sitting, were performed on the above dependent variables. For all ANOVAs, post-hoc Newman–Keuls tests tallied differences between the infant stages of sitting. To control type I errors when performing multiple independent t-tests, Bonferroni corrections were used by testing each comparison at a significance level of α/n, with n the number of comparisons. Dependencies among the dependent variables, for each sitting stage, were also tested by means of Pearson's correlation. The level of statistical significance was set at 0.05.

3. Results

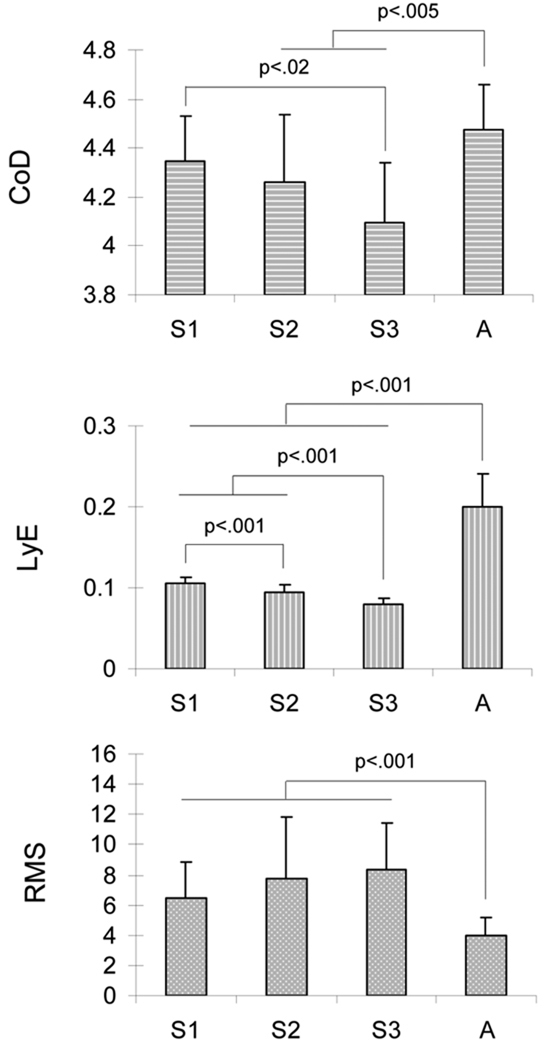
In the A/P direction, ANOVA results showed significant differences for both CoD and LyE values between the stages of infant sitting (F_(2,26)=4.31, p=.02; F_(2,26)=35.55, p<.001; respectively) (Fig. 3). The post-hoc analyses revealed (i) a higher CoD value in stage 1 as compared to stage 3, and (ii) a significant decrease of the LyE values from stage 1 to 3 (Fig. 3). In addition, the t-tests indicated significant differences between the infant stages and adult sitting. Both the CoD values at stages 2 and 3 and the LyE values from stages 1 to 3 were lower than the values observed for the adult stage (Fig. 3). Regarding the RMS values, significant difference was only identified between the infant sitting stages and adult sitting. Specifically, the values from infants were higher than that from adults (Fig. 3). At last, no significant correlations were observed between the dependant variables per sitting stage, with a range of r-values between −0.16 and 0.23 for all stages.

Fig. 3.

Evolution of the sway dimensionality (CoD), predictability (LyE) and variability (RMS) as a function of stage of sitting (from S1 to A) in the A/P direction. S1: stage 1 of infant sitting. S2: stage 2 of infant sitting. S3: stage 3 of infant sitting. A: adult sitting.

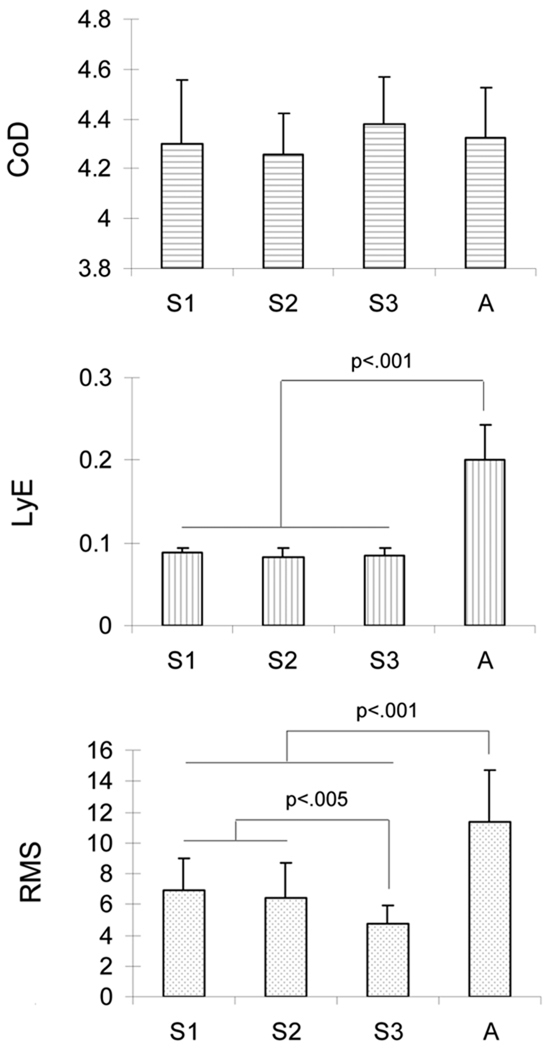
The results in the M/L direction were different from those in the A/P direction. Only the LyE values from the infant sitting stages were lower than those from the adult sitting stage (Fig. 4). On the other hand, significant differences were present for the RMS, with (i) decreased values from the stages 1 to 3 of infant development (F_{(2, 26)}=7.98, p=.001), and, (ii) lower values for the infant stages as compared to the adult stage (Fig. 4). As in the A/P direction, no correlations were found to be significant between the dependent variables per sitting stage, with a range of r-values between −0.48 and 0.44 for all stages.

Fig. 4.

Evolution of the sway dimensionality (CoD), predictability (LyE) and variability (RMS) as a function of stage of sitting (from S1 to A) in the M/L direction. S1: stage 1 of infant sitting. S2: stage 2 of infant sitting. S3: stage 3 of infant sitting. A: adult sitting.

4. Discussion

The aims of the present study were to investigate how sitting posture develops in the A/P and M/L directions of sway during infancy and to examine whether an adult-like control of the sway is already present during the late phase of sitting acquisition in infants. Changes in the control of postural sway were approached within the framework of “the active DFs problem” that accompanies motor development, exploring variations in attractor dynamics of the postural system.

In the A/P direction the decreased CoD that was observed during the sitting skill acquisition, reflected an attractor that was becoming lower-dimensional, indicating a skill that was mastered by decreasing the active DFs. This pathway of organizational change has been commonly observed in motor learning and motor development [10,11]. From a dynamical systems theoretical perspective, this renders the postural system much simpler to control, with fewer collective variables (or order parameters) [10]. Consequently, in contrast with the findings of Harbourne and Stergiou [8], a freezing to freeing strategy of the active DFs does not underlie infant sitting acquisition so that postural control is not becoming more complex in the late phase of sitting acquisition. Instead, the lower LyE values revealed in this late phase indicated a COP path that was more predictable with much more convergence in the attractor’s trajectories, a strategy reminiscent of a process of fine tuning to a most successful solution as shown in reaching, clapping and walking [25–29]. More importantly, this finding shows that sway became more (locally) stable. This replicates a finding of Thelen and Spencer [3] who concluded that the postural system in infancy is working on stability, to promote reaching. However, their results favored a motionless behavior of the postural system while the increased RMS observed here with infant development reflects a higher amount of sway variability. Considering that sitting and reaching are ‘embedded’, a more variable and stable sway would represent a proficient solution, allowing the infant to increase the reaching area as well as counteract the inertial effects of arm movements that may cause to miss the intended target. Another important finding in the A/P direction is that postural control in infants at the time of independent sitting is drastically different from adults, with higher CoD and LyE values found in the latter group. In contrast to our hypothesis, adults are then more skilful (i.e. flexible) in sitting, controlling simultaneously more active DFs and exploring more sway patterns. Such a difference certainly results from changes in variables associated with age as body dimensions, motor competence, perceptual acuity, and intentional constraints that shape attractor dynamics throughout the lifespan [26].

In the M/L direction, the CoD values and thus the active DFs remained the same during infant sitting development. Although this result was unexpected and opposed to other findings revealing DFs variations with motor development [10,11], it is not irrational. Indeed, Mégrot and Bardy [30] reported that in some cases, learning is not manifested through dimension modulations of the intrinsic dynamics of the movement (from complex to simple or simple to complex), but rather through changes in the structure and/or (spatio-temporal) characteristics of the movement itself. In the present case, the geometrical structure of the postural attractor in the M/L direction remained the same, with patterns equivalently predictable through sitting development (i.e., unchanged LyE values). However, sway became less variable in the late phase of sitting acquisition with a decreased RMS. Potentially this may be the result of changes in the infant’s body composition with age due to changes in the base of support. The infant’s base of support is affected during development through changes in the amount of body fat stored around the hips. Finally, while the active DFs were found to be similar between infants and adults, their postural control differed with less predictable (i.e., higher LyE) and more variable (i.e., higher RMS) sway patterns in the adults. As in the A/P direction, postural control in the M/L direction was more flexible in adults than in infants, allowing more proficiency in producing goal-directed actions.

From a methodological standpoint, the absence of a correlation between the dependent variables (i.e., CoD, LyE, and RMS) within each sitting stage, in both A/P and M/L directions, provided evidence that these variables are complementary and quantify different aspects of postural sway control. This supports the contemporary view that changes in the behavioral organization that occur during the development of sitting postural control should be captured by incorporating multiple levels of analysis (dimensionality, predictability, and variability) of postural sway [8,9].

5. Conclusion

In conclusion, infant sitting posture develops differently in the A/P and M/L directions of sway. In the A/P direction, a major finding is that the sitting skill is progressively mastered by decreasing the active DFs, relying on a more predictable and (locally) stable sway, and increasing sway variability. This pathway of change would promote the acquisition of new skills, as reaching. Determining the health of the developing postural control system in this direction may then be critical for the early diagnosis of motor disability. In the M/L direction, only the sway variability was found decreased, so that an early monitoring of sitting development is this direction appears to be less important.

Moreover, infant sway control at the time of independent sitting is not adult-like, lacking in adaptability. Further studies are then needed to delineate the factors (e.g., neuro-maturation, motor experience) responsible for such a difference, in order to get a more complete account of sitting posture development throughout the lifespan.