The Use of Computational Fluid Dynamics in the Development of Ventricular Assist Devices

Abstract

Progress in the field of prosthetic cardiovascular devices has significantly contributed to the rapid advancements in cardiac therapy during the last four decades. The concept of mechanical circulatory assistance was established with the first successful clinical use of heart-lung machines for cardiopulmonary bypass. Since then a variety of devices have been developed to replace or assist diseased components of the cardiovascular system. Ventricular assist devices (VADs) are basically mechanical pumps designed to augment or replace the function of one or more chambers of the failing heart.

Computational Fluid Dynamics (CFD) is an attractive tool in the development process of VADs, allowing numerous different designs to be characterized for their functional performance virtually, for a wide range of operating conditions, without the physical device being fabricated. However, VADs operate in a flow regime which is traditionally difficult to simulate; the transitional region at the boundary of laminar and turbulent flow. Hence different methods have been used and the best approach is debatable. In addition to these fundamental fluid dynamic issues, blood consists of biological cells. Device-induced biological complications are a serious consequence of VAD use. The complications include blood damage (haemolysis, blood cell activation), thrombosis and emboli. Patients are required to take anticoagulation medication constantly which may cause bleeding. Despite many efforts blood damage models have still not been implemented satisfactorily into numerical analysis of VADs, which severely undermines the full potential of CFD. This paper reviews the current state of the art CFD for analysis of blood pumps, including a practical critical review of the studies to date, which should help device designers choose the most appropriate methods; a summary of blood damage models and the difficulties in implementing them into CFD; and current gaps in knowledge and areas for future work.

1. Introduction

Cardiovascular disease is the leading cause of mortality globally ¹. Among various forms of cardiovascular disease, heart failure (HF) affects 5.8 million patients in the US ² and in 2006, HF contributed to almost 300,000 deaths ². The fatality rate for HF is high, with one in five people dying within 1 year and fewer than 60 % surviving 5 years ². The estimated direct and indirect cost of HF in the United States for 2010 is $39.2 billion ². Many therapies are available to treat patients with HF, including lifestyle changes, medications, transcatheter interventions and surgery. However, despite optimal medical and surgical therapies, some patients with the most advanced stage of HF still do not improve; for them, cardiac transplantation may be the only treatment option.

The problem with transplantation is that only about 2300 donor hearts become available each year resulting in around 2200 transplants ², or only about 6 % of the estimated 35,000 US patients who would benefit from a heart actually receiving a transplant ^{3, 4}. The mortality rate for patients waiting for scarce donor organs to become available was 142 per 1000 patient years in 2007 ⁵. To address the need to support the circulation in patients with end-stage HF a wide variety of mechanical circulatory support devices (MCSDs) have been developed over the past four decades. These devices include aortic balloon pumps ⁶, total artificial hearts ⁷, extracorporeal membrane oxygenation systems ⁸, portable pump-oxygenators ⁹ and ventricular assist devices (VADs).

VADs are mechanical pumps designed to augment or replace the function of one or more chambers of the failing heart. VADs have been developed as a bridge to transplant, a bridge to recovery, and as an end stage treatment. They can be implanted to support the left ventricle (LVAD) or the right ventricle (RVAD) or two devices are used to support both left and right ventricles (Bi-VAD). In some cases, VADs are placed between the left atrium and descending aorta or the right atrium and pulmonary artery. In addition to adult patients with end stage HF, paediatric patients with ventricular dysfunction (congenital or acquired) constitute another group requiring circulatory support. Development of VADs for paediatric patients has been slower, due to fewer potential patients and the complexity of paediatric pathophysiologies, and the intrinsic difficulty of producing small nonthrombogenic devices ^{10, 11}. The widely acknowledged need for pumps specifically designed for these patient groups has lead to the development of several new devices in the last five years, in part due to funding from the NIH¹².

The two main types of blood pumps which have been developed are: rotary continuous flow and positive displacement pulsatile pumps. Whilst displacement pumps maintain the physiological pulsatility of the flow they typically experience problems with mechanical failure of diaphragms and valves. The impact of removing the pulsatility of the blood flow on the circulation and organ function is debatable, but the advantages of continuous flow pumps are the simpler designs, involving fewer moving parts, the smaller size and lower power consumption.

Rotary pumps can be further subdivided into centrifugal and axial flow pumps. Centrifugal pumps convert the rotational flow to linear flow by positioning the outlet tangentially with the pump housing while in axial pumps the outlet is collinear with the rotating section and the impeller blades are shaped to move the blood both rotationally and axially. While centrifugal pumps produce higher pressures at lower flow rates, axial pumps typically generate higher flows with lower pressure rises, and require much faster rotational speeds to do so. Axial flow pumps are smaller and lighter than centrifugal pumps, and have a tubular configuration, which makes them easier to implant. The current state of rotary pumps has been recently reviewed in references 13, 14.

In pulsatile pumps the flow is driven either pneumatically or by a pusher plate against a segmented polyurethane blood sac. An inlet valve and an outlet valve are used to ensure blood enters and leaves the chamber at the correct times and in the correct direction. The flow is characterized by inlet jets that establish a large vortex during filling which washes the whole chamber. Wall shear stresses in the pump chamber are generally low, while high velocities in the jets create large shear rates in these regions.

VADs have benefitted many patients already, however however, there are still a number of significant challenges to overcome. The biggest of these is damage to the blood components, in particular ^{15, 16} thrombosis and embolisation. Thrombus can form within the device possibly leading to device failure or necessitating device explant. Emboli are transported along the blood stream to the brain, heart, kidneys and liver, leading to strokes ^{17, 18, 19}, heart attacks and impairment of kidney and liver function ²⁰. The thrombogenicity of VADs requires patients to take anti-coagulation medication, which can in turn lead to bleeding. Infection is currently another drawback with VADs; bacteria can enter the body along drivelines and transcutaneous cannulae but infections have also been found inside the devices ²¹. Currently, VADs which can provide full support to the heart, while significantly smaller than their predecessors, are still bulky and difficult to wear, in particular for paediatric patients. Implantable devices necessitate a body of a certain size while extracorporeal devices are uncomfortable and worrisome for patients ²². As the size of devices is reduced, gap widths will decrease and impeller speeds increase to provide the desired pressures, and haemolysis and platelet activation may be a more pertinent issue. If these weaknesses could be eliminated more patients could benefit from VADs, they would live longer and their quality of life would be improved.

Solution of these issues is a multidisciplinary task employing in vitro models, animal models, clinical trials and numerical modelling. Since the devices involve fluid flow, and some of the problems are flow related, computational fluid dynamics (CFD) forms a large part of this numerical modelling and, as in many fields of engineering ²³, has become widespread in biomedical engineering in general (see, as examples ^{24, 25, 26}) and in particular has many uses in studying the cardiovascular system ^{27, 28, 29, 30}. CFD has been used in the analysis and design of blood pumps since the early 1990s ^{31, 32, 33, 34, 35}. Calculations are performed for new pump designs to determine pressure-flow relationships and efficiencies before constructing prototypes. Simultaneously CFD allows for appreciation and understanding of the flow characteristics such as velocity profiles, shear rate, recirculation and stagnation. As new designs are developed, in the effort to reduce the VAD limitations described above, there is a continuing need for computational analysis of their functionality. Improvements in modelling technique are desirable to increase the accuracy of the model predictions. Some of the issues described above involve biology, and therefore require the development of specific modelling techniques to assist with solving them. For example, the problems of thrombosis and embolism within the device require models of blood clotting and emboli formation, while analysis of the circulating emboli requires coupling the device model to a model of the vasculature. All of this understanding of device function then needs to be incorporated into the design, a process which can be improved by automated techniques.

This article discusses the current state of the art in simulating blood flow in VADs, starting with the computational techniques used (section 2) and then sections on: preprocessing (section 3), including pump geometries and meshing; simulation of moving parts (section 4); turbulence (section 5); hydraulic analysis (section 6); blood damage (section 7); interaction of the artificial device and the native cardiovascular system (section 8); blood rheology (section 9); design optimization (section 10); validation of computational results (section 11); and some future directions (section 12).

2. Computational Techniques

The following basic steps are involved in mesh based solution of the Navier-Stokes equations: definition of the problem, or pre-processing; solution of the flow; and analysis of the results, or post-processing. The first step in pre-processing is to define the geometry, or physical bounds, of the problem. Simple flow domains can be represented by a set of equations while complex geometry, such as in VADs, is often created with computer-aided design (CAD) software and represented in a format which can be imported into specific CFD meshing software. Meshing, or grid generation, means discretizing the continuous spatial domain of the fluid into a number of small tessellating elements. Once the meshing is completed, the physical phenomena to be modelled must be specified, for example: turbulence, species concentration, chemical reactions and heat transfer. The rheology of the working fluid must be defined, for example whether it has constant viscosity (Newtonian fluid) or variable viscosity (non-Newtonian). Blood has complicated rheology and there are many models to describe it on different scales, from microscale models incorporating the time history of agglomerates to Eulerian models of shear dependent viscosity. In VADs shear rates are usually considered high enough to be in the shear independent range, so the complexities of blood rheology can usually be ignored. However, if slow moving and stagnant flows are important the shear dependent nature of the viscosity must be modelled. Boundary conditions for the mesh elements in contact with the domain boundary must be specified according to the problem: usually there is zero velocity of the fluid relative to a wall (no-slip), an inlet may have the fluid velocity or pressure specified and an outlet often has a spatially uniform pressure (in agreement with fully developed flow).

The majority of works on VADs in the literature are conducted using commercially available CFD software packages with some user defined functions. The implementations of these CFD packages are either based on the finite volume²³ method or finite element method. Fluent ^{36, 37, 38, 39, 40, 41} and CFX ^{42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 11, 57, 58, 59}, both available from ANSYS, Inc. (Canonsburg, PA) and STAR-CD from CD-Adapco ^{60, 61} (Melville, New York) are the CFD software packages used most often for analysis and modelling of blood flow in VADs. In addition, AcuSolve from ACUSIM Software ⁶² (Mountain View, CA) and Adina from Adina R&D (Watertown, MA) are also used. Some research groups have developed their own CFD solvers to suit their specific problems. An example of an alternative approach is the Deformable-Spatial-Domain/Stabilized Space-Time finite element formulation of Behr et al ⁶³ which they used for calculating flow in the GYRO pump. They have implemented viscoelastic fluid modelling with blood as a viscoelastic fluid in a shear thinning solvent ⁶⁴ and pressure head calculations agreed well with experimental measurements: calculations at most operating conditions were within 5 % of experiments but at the fastest speed the error was up to 12 %. While solution of the Navier-Stokes equations using mesh based methods are now commonly used for flows in VADs, there are a number of other ways to calculate fluid flows, including smoothed particle hydrodynamics ⁶⁵, spectral methods ⁶⁶ and the Lattice Boltzmann method ⁶⁷. Some of these have been used for calculations related to blood flow ^{68, 69}, and may in the future prove useful for studying different aspects of flow through VADs.

Since CFD uses iterative methods to solve the governing equations, convergence is an important consideration. Different researchers use different measures of convergence but it is common to look at the residuals, which should decrease below a threshold value, and examples of local and global flow which should have reached a steady state. The convergence criterion for the residuals should be determined by examining how much the important flow characteristics change between different values.

3. Preprocessing for CFD Analysis of Ventricular Assist Devices

3.1 Geometry Representation

First it is necessary to obtain the geometry of the flow domain in a format which can be represented computationally. The sophisticated designs of the latest VADs are often developed using computer aided design (CAD) software. It is then straightforward to import the blood contacting parts into meshing software and use these shapes to define the exact flow domain through the device. For some purposes it is not necessary to model the whole device, and the imported geometry can be cut to make use of symmetry, or otherwise simplified as appropriate.

An understanding of how the device fits in vivo is important for accurate modelling of the in- and outflows. For example, while many pumps are attached to the ventricle and aorta with cannulae, others, such as the Jarvik hearts fit directly into the ventricle, and pumps such as the Impella are located inside the heart itself. Consideration of the effects of these geometries may influence the flow field within the device. Descriptions of centrifugal, axial and pulsatile pumps are given in the following three sections.

3.2 Continuous Flow Pumps

3.2.1 Centrifugal Blood Pumps

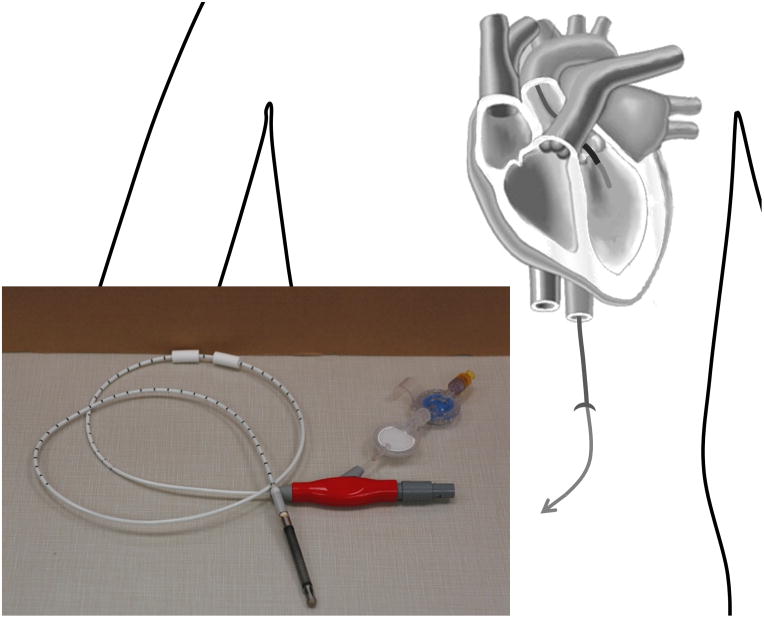
Centrifugal rotary VADs have impeller radii between 20 and 30 mm, and are designed to produce optimum flow rates of 3 to 7 l/min and pressure rises of 90 to 350 mmHg, operating at speeds of 2000 to 7000 rpm (see Appendix). While the earliest centrifugal pumps used mechanical contact bearings (for example Vienna Pump ³⁴, Nikkiso HPM-15 ⁷⁰), recently magnetic levitation technology has been used in some centrifugal VADs to suspend and drive the impeller ¹⁴. The Terumo DuraHeart^{™ 71} and the Levitronix^® CentriMag^{® 72, 73} are now in clinical use. The overall size of the CentriMag^®, including the motor, is relatively large (height 70 mm, diameter 87 mm ¹⁴) as it was designed for extracorporeal use. Figure 1 shows a centrifugal pump placed extracorporeally. However, the DuraHeart^™ is smaller (height 45 mm, diameter 72 mm, weight 540g ¹⁴) and can be implanted into a pocket created in the preperitoneal space in the left upper quadrant ⁷¹. Several more implantable devices are currently under development (HeartQuest ⁷⁴, HeartMate III ⁷⁵, Tokyo Medical and Dental University and Tokyo Institute for Technology’s Heart ⁷⁶, Ibaraki University’s Heart ⁷⁷, Levitronix^® UltraMag^{™ 78} and MiTiHeart^{™ 79}). The HeartQuest has been developed with extensive use of CFD ^{44, 45, 46, 48}. It is 35 mm high, 75 mm diameter, weighs 440 g and is fitted into the upper left quadrant of the abdomen. The inflow cannula is rigid titanium and the outflow cannula is reinforced 12 mm vascular graft. Details of centrifugal VADs for which CFD studies have been executed are given in the appendix (Table 1).

Figure 1.

A centrifugal VAD placed extracorporeally and inset showing the Levitronix^® CentriMag^®.

Table 1.

Details of centrifugal pumps studied with CFD

Pump name	References	Impeller Radius (mm) r	Flow rate (l/min)		Pressure (mmHg)		Speed (rpm)		Clearance (mm)	${\mathit{MaxRe}}_{in}=\frac{vd}{\upsilon }$	${\mathit{MaxRe}}_{\mathit{imp}}=\frac{2r^2\omega }{\upsilon }$
			Optimum	Maximum (Q)	Optimum	Maximum	Optimum	Maximum
Adult pumps
HeartQuest CF4/Levacor	47 46 74 109 194	22.225	6.0	10	100	190	2000	2500			77,590
HeartQuest CF3	45 44 43	30.5	6.0	13.26	100		2000	2400	7.62 0.75		140,280
CentriMag®	108 72 73	21.2	5.0	9.9	352	600	4000	5500	1.5	6,617	155,320
HeartMate III	36 75 195		7.0	10	90	120	3000	5500
UltraMag	96 78		1.0–3.0	6.0			5–7000	9000		7,003
Kyoto-NTN	189 188 38 37	25	6.5		120		2000		0.2		78,540
Nikkiso HPM-15	112 49 103 111 70	25	5.0		300		3100				121,740
Pediatric pumps
PediVAS/Pediatric CentriMag®	39 196	13.6		3.0		200		5500	1	3,007	63,918
TinyPump	42 197	15	2.0	4.0	86	120	3000	3000	0.1	4,011	42,412

3.2.2 Axial Flow Blood Pumps

Axial rotary VADs have impeller radii between 2 and 10 mm, and are designed to produce optimum flow rates of 1.5 to 6 l/min and pressure rises of 50 to 140 mmHg, operating at speeds of 6000 to 45000 rpm (see Appendix). The earliest axial pump, the Hemopump, was cable driven by an external electric motor⁸⁰. The device featured a small impeller positioned at the tip of a long cable housed in a cannula and used lubricating fluid to reduce the friction between the rotating cable and the stationary bearing in the cannula. The first clinical trial of the Hemopump was in 1988 ⁸⁰. Developed from the Hemopump concept and similar in design is the Impella, which had its first clinical use in 1999 ⁸¹. The use of fixed axels and pivot bearings, along with sealed, brushless, electromagnetic motors, such as in the MicroMed DeBakey (which was first implanted clinically in 1998 ⁸²), the Jarvik Heart^{® 83, 84} (first destination therapy implant 1999 ⁸⁵), and the HeartMate II ^{13, 86, 75} (first clinical implant 2000 ⁸⁷), reduces the contact surface between moving and stationary parts, and thus alleviates the need for lubricating fluids. While durability of the bearings is thought not to be an issue, indeed the MicroMed DeBakey bearings were shown to be free of wear after 5 years, the contact region is a potential thrombosis hotspot. The Jarvik Heart^® was shown to have good haemocompatibility, with low haemolysis and no evidence of thromboembolic events, however, a ring of clot still formed on the front bearing ¹³. Hydrodynamic bearings remove most of this contact and are found in the Jarvik pediatric VAD ⁸⁸ which is under development. This pump consists of a spindle with two impeller blades, which is supported by an inflow and an outflow tripod when there is no flow. However, when the impeller spins the hydrodynamic lift forces generated between the spinning impeller and the tripod tips are enough to support the impeller ⁸⁹. Hydrodynamic bearings must be carefully designed to provide enough force to support an impeller, when this is not possible magnets can be used. The INCOR^® pump, which was first implanted clinically in 2002 ⁹⁰, is an example of a magnetically levitated axial flow device. The magnetic suspension is active in the axial direction and passive in the radial and uses 0.6 W of the 3–4 W energy consumed by the pump. Details of axial VADs for which CFD studies have been executed are given in the appendix (Table 2).

Table 2.

Details of axial pumps studied with CFD

Pump name	References	Impeller Radius (mm) r	Flow rate (l/min)		Pressure (mmHg)		Speed (rpm)		Clearance (mm)	${\mathit{MaxRe}}_{in}=\frac{vd}{\upsilon }$	${\mathit{MaxRe}}_{\mathit{imp}}=\frac{2r^2\omega }{\upsilon }$
			Optimum	Maximum (Q)	Optimum	Maximum	Optimum	Maximum
Adult pumps
Impella (2001)	59 81	<3.2		5.2			30000	32500	0.1	5,517	20,910
Impella (2006)	61	<2	2.4	2.7	50		45000	50000	0.075	4,297	12,566
Nanyang Technological University	41	7.8	5.14	8.5	100	120	11000	12000	0.12		45,872
Streamliner	184 187	9.5	6	15	140	260	7000	9000			51,035
FuWai	57 58	8.75	6	8	110	150	8000	9000	0.1	2,829	43,295
Xian Jiaotong	40	7.9	5	7	100	150	12000	13000	0.5	2,228	50,977
Virginia LEV-VAD	50 51 52	10	6	10	100	160	6000	8000	0.25	4,390	50,265
Pediatric pumps
Virginia Pediatric PVAD/PVAD2	11 53	7	1.5	3	72	95	8000	9000			27,709
Virginia Pediatric PVAD3	54 56	5.6	1.5	3	70	95	8000	9000	0.25	2,009	17,734
Virginia Pediatric PVAD4	55	5.6	1.5	4	70	95	7000	8000	0.2–0.4	2,680	15,763

3.3 Pulsatile Flow Blood Pumps

While pulsatile pumps have disadvantages in terms of the more complicated designs and durability of the moving components, they clearly do a better job at reproducing physiological blood flow. Blood flow generated by continuous flow pumps is pulsatile to some degree, since the pump is used in parallel with the left ventricle, but the degree of pulsatility depends on the health of the heart. The benefits of pulsatility are still in debate ⁹¹, but studies of cardiopulmonary bypass have shown that cerebral, renal and myocardial blood flows recover better, endothelial damage and systemic inflammation are reduced and mortality is lower when perfusion is pulsatile ⁹². It has been suggested that during chronic cardiac support, pulsatile flow improves the velocity of cells in the capillaries and increases the number of perfused capillaries, and systemic inflammation is lower ⁹².

There are many limitations of traditional positive displacement pulsatile pumps. Their large size makes them difficult to implant, while their thick percutaneous drivelines and noisy operation makes them uncomfortable to wear. Other complications include bleeding, infections and thrombo-embolic events. These factors lead to the current opinion that the use of positive displacement pumps is being discontinued in favour of rotary pumps. The development of small rotary pumps which can produce pulsatile flow by varying their speed ⁷⁵ may remove the main advantage of positive displacement pumps.

In contrast with continuous flow ventricular assist devices there have been very few CFD studies of pulsatile flow pumps. This is because there are many issues associated with pulsatile pumps which are significant simulation problems in themselves. The flow is unsteady, and with Reynolds number varying from 0 to about 3300 it is likely to be transitional, with turbulence generated during flow deceleration; additional turbulence is generated by the valves, even at modest inlet Reynolds numbers. The flow is driven by a flexible sac, which introduces moving boundaries where the precise motion is unknown and may differ for different cycles. And, the motion of the valves is fundamentally a fluid-structure interaction, between the valve, and the shear-thinning, viscoelastic fluid.

Details of pulsatile VADs for which CFD studies have been executed are given in the appendix (Table 3). The difficulty in calculating the flow in pulsatile pumps has resulted in a large literature on experimental measurement of the flow fields and blood damage ⁹³ while in vivo experience is reviewed in reference ¹⁰.

Table 3.

Details of pulsatile pumps studied with CFD

Pump name	References	Volume (ml) V	Chamber diameter (mm) D	Chamber thickness (mm)	Mitral valve diameter/inlet (mm) d	Aortic valve/outlet diameter (mm)	Steady calculation flow rate (l/min) Qs	Unsteady calculation		${\mathit{StRe}}_{in}=\frac{v_{s}d}{\upsilon }$	${\mathit{MaxRe}}_{in}=\frac{v_{p}d}{\upsilon }$
								Mean flow (l/min)	Peak flow (l/min) Qp
Penn State 50cc	62 132	50	63.5	18.8	23	21	5.0	3.5	12.0	1384	3321
Hokkaido Tokai	99	65	90	12	18	18	5.0			1789

3.4 Meshing Scheme

Mesh densities and schemes will obviously depend on the specific pump geometry. The total number of cells used to mesh a whole pump ranges from about 0.1 M to 3 M. In general more cells are required when using unstructured tetrahedral meshes than when structured hexahedral meshes are used. Differences in software appear to influence the types of meshes chosen, since some types of software allow for straightforward generation of hexahedral meshes while with others it is more difficult ⁴⁸.

Mesh independence studies are a vital part of CFD work since they show the extent to which the results depend on the mesh parameters and quantify the error associated with spatial discretization. However, in general there are few studies in which complete mesh refinement analyses have been reported. Where the results of a study are given, they are sometimes ambiguous, with simple statements of the percentage error compared to a finer mesh. Without the densities of the two meshes these statements give the reader no information about how well converged the solution is, since by making a mesh which is only a little finer it is obviously possible to achieve a tiny percentage difference between the two solutions ^{94, 95}.

Many commercial CFD software packages come with automatic mesh generation software, but these packages usually only create tetrahedral or hybrid cells, and require a lot of user manipulation of the grid. There are, however, some commercial mesh generation packages specifically for turbomachinery which can generate meshes for the blade region of a blood pump. Typically in turbomachinery applications it is necessary to generate a mesh around the blades (O-grid) which is fine in the direction perpendicular to the blade to capture the high pressure gradients. The mesh between the blades (H-grid) does not need to be so fine; the spacing is graded such that the cell size is small near the blades and largest midway between them. In the PVAD3 ⁵⁴ these two methods for hexahedral grid generation in the impeller region were compared. The result was that cells were less skewed, with larger minimum skew angles and larger aspect ratios, when the grid was created by meshing between two blades, rather than around a single blade. This shows how the type of mesh must be chosen to best suit the geometry. An automatic mesh generation program, specifically for rotary pumps, was developed by Wu et al ⁶⁰. This is based on the elliptic method and generates multiblock structured grids with high quality hexahedral cells and boundary orthogonality. While commercial mesh generation software usually takes the pump geometry in the form of surfaces from CAD software, Wu et al ⁶⁰ use parameterized geometry constructed from curves. When the underlying pump geometry is adjusted the mesh can be automatically updated to suit the new geometry.

In our own studies of the UltraMag ⁹⁶ centrifugal pumps we found a hybrid mesh to be a good compromise between the inherent difficulty in meshing complicated geometries with structured meshes, and the benefits of having structured meshes in suitable regions, in terms of reduced skewness and independent control of the mesh density in each direction. In the Ultramag ⁹⁶ the mesh structure was found to influence the fluid dynamics calculated in the gap region. Taylor vortices which should have been present according to the Taylor number ⁹⁷ were only found with a hexahedral mesh, and not with a tetrahedral mesh.

4. Solution of flow in a moving domain

All pumps involve moving parts, although the number of moving parts in continuous flow devices has been reduced to just the impeller. In general an impeller has 6 degrees of freedom: translation and rotation about the three Cartesian axes. Depending on the specific pump these will be limited or controlled by bearings, magnetic forces and hydrodynamic forces, so that the motion is basically limited to rotation of the impeller about its axis.

There are two methods for calculating the flow through pumps which have rotating impellers: Multiple Reference Frame (MRF) and Sliding Mesh. The MRF method is an approximation of the impeller motion in which two regions are defined moving relative to each other with a constant velocity. Steady state conditions are assumed and transient effects cannot be modelled. The sliding mesh explicitly models the relative motion of the two fluid regions, with the mesh position updated at each time step. This method is more accurate than the MRF approach, but also more computationally intense.

Most CFD studies of centrifugal pumps used multiple reference frames, however pumps which have been modelled using sliding meshes include Kyoto-NTN ³⁸, HeartQuest CF4 ⁴⁸, HeartMate III ³⁶ and EVAHEART ⁹⁸. One study compared the use of sliding meshes with MRFs in the HeartQuest CF4 ⁴⁷. Using the MRF method the steady state pressure rise was 100 mmHg (with flow rate 6 l/min and speed 2500 rpm) whereas the pressure rise predicted by the sliding mesh approach oscillated with the passing of each blade, giving a maximum difference of 15 mmHg from the value obtained with the MRF approach.

The majority of studies on axial pumps also use the MRF approach. Pumps which have been modelled using the slide mesh approach include Nanyang Technological University’s pump ⁴¹ and the Virginia LEV-VAD ⁵⁰. Song et al ⁵⁰ performed both steady and transient simulations on the Virginia LEV-VAD and showed that the pressure rise throughout the cardiac cycle varied from 80 to 180 mmHg.

The accuracy to which the MRF solution approximates that from a sliding mesh varies with the degree of rotor stator interaction. With the continuing increase in computer power it is likely that more calculations in the future will use the sliding mesh approach; this will enable more realistic boundary conditions, specifically flow and pressure pulsatility, to be modelled.

Pulsatile pumps involve more moving parts than rotary pumps and the number of issues involved in simulating pulsatile flow pumps has required simplification of the problem. A moving flexible diaphragm drives the flow and hence is the most important, but also the most difficult part to simulate. Simplification of the problem included: not moving the diaphragm at all, and instead using a velocity boundary condition on the fixed wall ^{62, 99}; assuming the diaphragm is rigid, with a prescribed shape (for example hemisphere) and undergoes prescribed simple motion (for example sinusoidal) ¹⁰⁰. The flexible diaphragm motion has also been modelled using a fluid structure interaction with a mixed Lagrangian-Eulerian model ¹⁰¹. The valves are another issue of fluid-structure interaction which seem to have been omitted by most authors, who assume instead that the blood can flow freely into or out of the chamber. An alternative approach is to make the viscosity of blood in the region of the closed valve become very high (increased by 10⁴) so that the velocity in that area reduces to approximately zero ⁶². Not all authors have investigated the flow over the full cardiac cycle, in a comparison of different pump designs one study used steady state analysis for calculations on the filling and ejecting phases separately ⁹⁹.

5. Turbulence

Turbulence, or the cascade of vortices taking energy from the mean flow down to the Kolmogorov scale and dissipating it as heat, effects everything about the flow properties: from estimates of pressure head which are one of the most basic predictions a pump designer needs to make, through to estimates of shear stress, which is important in predicting thrombosis and other forms of blood damage. It is therefore vital to know the flow regime that the pump is operating in, and how to model it.

VADs operate in the transitional to low Reynolds number, Re, turbulence range, depending on the specific device. This makes them difficult because traditional turbulence models have been developed for traditional engineering requirements, which means high Re flows. The choice, for researchers to date, has been to use one of these traditional models for turbulence, or to treat the flow as laminar. These turbulence models are only truly valid if a distinct, generally turbulent, boundary layer exists close to the wall and turbulent flow is fully developed away from the wall. At the same time, laminar solutions, with sufficiently fine meshes, are better for resolving the boundary layer if viscous forces are dominating the turbulent fluctuation.

Many CFD studies of centrifugal pumps have used the standard k-ε turbulence model ^{44, 45, 47, 37, 49}. This is a two equation RANS model, in which the solution of two transport equations allows both the turbulent velocity and length scales to be independently determined. The two equations model the transport of turbulent kinetic energy, k, and its dissipation rate, ε. The model was derived semi empirically and while the transport equation for k is derived from the exact equation, the transport equation for ε is obtained by physical reasoning. It is a popular turbulence model for industrial applications due to its robustness, computational economy and reasonable accuracy for a wide range of flows. However, the assumptions in the derivation are that flow is fully turbulent and the effects of molecular viscosity are negligible, so it is really only valid for high Re turbulent flows ¹⁰². In addition it has several known weaknesses, for example: under prediction of the reattachment length in turbulent flow past a backward facing step, a symmetric mean velocity profile rather than an asymmetric one in rotating channel flow, and over prediction of the growth rate of turbulent kinetic energy ¹⁰³.

The Wilcox k-ω model, another two equation RANS model, uses the specific dissipation rate, ω, which can also be thought of as the ratio of ε to k, as the second variable rather than the dissipation rate, ε. The k-ω model provides improved solutions over the k-ε model for low Re flows, boundary layers and separated flows ¹⁰⁴. Meanwhile the Menter SST k-ω model is a hybrid model which uses the k-ε model in the fully turbulent region far from the wall and a transformation from the k-ε to the k-ω model in the near wall region ²³.

5.1 Centrifugal Pumps

Details from the literature on centrifugal pumps which have been studied using CFD are given in the appendix (Table 1), along with calculations of Reynolds numbers based on inlet and impeller parameters. Maximum Re for the inlet, MaxRe_in, for the adult sized pumps is around 6600–7000, and so is well above the critical Re for transition from laminar to turbulent flow in a pipe, which is usually taken to be 2300 ¹⁰⁵. This corresponds with the transitional to low Re turbulence regime, below the levels of turbulence typically involved in other engineering applications. The maximum Re based on the impeller parameters, MaxRe_imp, is in the range 77000–155000. Since this is not pipe flow the transition to turbulence occurs at a different Re which is conventionally taken to be of the order 10⁶, ^{106, 107}. This puts these centrifugal blood pumps well into the laminar regime. The two paediatric centrifugal pumps ^{39, 42} have MaxRe_in of 3000–4000 and MaxRe_imp of 42000–64000 so again their inlet Reynolds number puts them above the critical Reynolds number while the impeller Reynolds number is well below the threshold.

Then, the use of a laminar solver might be justifiable and several groups have used laminar solutions ^{108, 39}, either for this reason or for reasons of economy, since utilizing turbulence models involves solving more equations and therefore increases the computational demands. Indeed laminar flow solutions do appear to predict the pressure rise reasonably well. Two studies investigated the calculated pressure rise in pumps obtained using laminar flow and compared the calculated with measured pressure rises. Reported errors were up to about 13 mmHg (10 %) in both the CentriMag^® Pediatric ³⁹ and the HeartMate III ³⁶ pumps. The turbulence models which have been used for centrifugal pumps are: standard k-ε, k-ε with enhanced wall treatment, and SST k-ω. The uses of these models are discussed in turn below.

Of those groups using the standard k-ε, several have compared the calculated pressure rise with experimental measurements. In the HeartQuest CF3 ⁴⁵ the pressure rise was over predicted by around 30–60 mmHg (25–70 %) while in the Kyoto-NTN there was an under prediction of around 10 mmHg (8.3 %)³⁸. In the HeartQuest CF3 the flow was calculated using both a laminar and k-ε turbulence model, and the resulting velocity field was compared with PIV measurements ^{43, 109}. At 1500 rpm and 5 l min⁻¹ the velocities obtained with the k-ε model showed much better agreement with the experiments than those with the laminar model. The radial velocity profiles were compared and k-ε prediction was similar in shape, with a small peak radial velocity error (+0.04 m/s) and the same amount of reverse flow at the rotor wall. The k-ε profile was however more skewed than the measured profile. In contrast the laminar predicted profile was extremely skewed and showed a huge region of reverse flow at the rotor wall and a large error (+0.28 m s⁻¹) in the peak radial velocity. k-ε predictions at the higher speed (2000 rpm and 6 l min⁻¹) show worse agreement (error in peak radial velocity −0.25 m s⁻¹) and laminar results are not given. Using quantitative oil streaking ¹¹⁰ shear stresses on the pump casing (2500 rpm, 6 l min⁻¹) were found to agree with the CFD results to within 10–15 %.

A standard k-ε model with enhanced wall treatment was used in calculations of flow in the Kyoto-NTN ³⁸. Comparison of calculated velocities with velocities measured in a scaled up model pump showed qualitative agreement; however, numerical comparisons have not been given. For the Nikkiso HPM-15 extensive experimental studies have been performed ^{103, 111} but the limited data published for the earlier CFD studies ^{49, 112} makes comparison difficult. Calculations were carried out using the standard k-ε model with a logarithmic wall function. At 2500 rpm, and with radial-impeller gap width of 3 mm, the maximum shear stress on the casing was measured as 450 Pa ¹⁰³ and the maximum shear stress in the fluid was 180 Pa ¹¹¹. In comparison simulated shear stresses were 696 Pa ¹¹² on the casing and 203 Pa ¹¹² (or 215 Pa ⁴⁹) in the fluid. With a narrower gap (0.5 mm) maximum shear stress in the fluid was measured as 330 Pa ¹¹¹ and calculated as 585 Pa ¹¹² (or 1160 Pa ⁴⁹).

The SST k-ω model was used to compute the flow in the TinyPump ⁴² and in comparisons of the calculated and measured pressure rise there was an under prediction of around 4 to 25 mmHg (5 –21 %). There have been very few studies comparing different turbulence models for use in centrifugal pumps. Calculations of velocity magnitude in the HeartQuest CF4 ⁴⁶ using a standard k-ε model with log-law wall functions were compared with calculations using a k-ω model for both the near and far from wall regions. Two different meshes were used, in one the first near wall mesh node was located at y⁺ = 11, which is at the edge of the viscous sublayer. This enabled the far wall region to be modelled using k-ε while the viscous sublayer was modelled by assuming a logarithmic function. In the second mesh the first near wall mesh node was located at y⁺<2 which ensured there were several nodes within the viscous sublayer, thus enabling the k-ω model to be used in both near and far wall regions. The predictions of both models were compared with PIV measurements on three cross-sectional planes. Better agreement was seen for the k-ω model, especially around the blades.

5.2 Axial Pumps

With slightly lower flow rates on average, as compared with the centrifugal pumps, MaxRe_in for the adult axial pumps is in the range 2,200–5,500 (Table 2) meaning that while some are above the critical Re for turbulence some are just below. MaxRe_imp is 43,000–51,000 for all except the Impella pump which is 13,000–20,000, and thus the impeller Re is very much below the threshold of 10⁶. Despite this none of the studies reviewed here used a laminar solution. Apel et al ⁵⁹ discuss in detail laminar versus turbulent modelling and based on flat plate theory, concluded that the flow in the pump should be laminar, however the diffuser downstream of the pump results in high vorticity, flow separation and turbulence generation and they consequently use a turbulence model. The turbulence models which have been used for axial blood pumps are: standard k-ε, k-ε with logarithmic wall function and low Re k-ε. The uses of these models are discussed below.

The standard k-ε model has been used for computing the flow in several pumps including Xi’an Jiaotong University’s pump ⁴⁰, Nanyang Technological University’s pump ⁴¹, the Virginia LEV-VAD ⁵¹, the Virginia PVAD (versions 1–4) ^{53, 11, 56, 55} and the Impella (2001) ⁵⁹. Of these several investigations compared pressure rises with measurements: the largest error in the Virginia LEV-VAD was around 10 mmHg (10 % over) ⁵¹, in the PVAD2 the largest error was around 15 mmHg (13 % under) ¹¹ and in the Impella (2001) the error was up to 24 mmHg (30 % under).

The k-ε model with a logarithmic wall function has been used by several groups including the Virgina PVAD3 ⁵⁴, Virgina LEV-VAD ⁵², and the FuWai pump ⁵⁷. Errors in the pressure rise were up to 20 mmHg (18 %) for the Virginia LEV-VAD ⁵², 10 mmHg for the PVAD3 (30 %) ⁵⁴,.

The flow in the Impella pump was simulated using a low-Reynolds number k-ε model ⁶¹. Simulated axial velocity profiles at many axial locations, and at 0 and 90° circumferential locations, were compared with profiles measured using DPIV. Both qualitative and quantitative comparisons were good in most regions, especially in the axial tip region and one diameter downstream of the impeller but poorest agreement was seen directly in front of the impinging blades where the measured profiles were fairly uniform across the passage, but calculated profiles contained fast flow in the centre and reverse flow at the walls. They attribute these differences to the problems of using PIV at such high transverse speeds.

There are no full studies comparing different turbulence models reported in the literature, however Throckmorton and Untaroiu ⁵⁵ stated that in a comparison of k-ε, k-ω and SST k-ω, the k-ε results agreed best with experimental measurements of bulk hydraulic properties. So far this review has focussed primarily on the pure engineering aspects of CFD use in VAD development. The next sections discuss more biologically motivated modelling.

6. Hydraulic Analysis

Hydraulic analyses are the primary use of CFD in VAD development, and calculation of the pressure head is usually first. Comparison of the calculated H-Q curve with experimental results is commonly used to validate the calculations: results at the nominal operating condition are generally within 5 % of the experimental values while those for other operating conditions are usually accurate to around 10 % ^{11, 36, 38, 39, 42, 51}.

Hydraulic efficiency, η, relates hydraulic energy to the shaft power with the following equation:

$$\eta =\frac{q\mathrm{\Delta }p}{M\omega }$$

where q is the flow rate, Δp the difference between the inlet and outlet pressures, M the torque and ω the angular speed. Typical efficiencies for blood pumps are in the range 20 – 30 % ^{113, 59, 114, 57, 51}. A VAD is required to be used over a range of operating conditions depending on patient needs so ideally the efficiency should vary minimally with operating condition ⁵⁹. As the gap between the blade tip and the outer housing is reduced pressure head and efficiency usually increase. However, Wu et al ¹¹⁴ found that reducing the tip clearance below a threshold value produced no increase in efficiency.

The reduction in efficiency with tip clearance is due to tip leakage flow: flow escaping backwards around the blade, through the clearance gap ⁴¹. This can be assessed using CFD by summing the component of the flow in the direction opposite to that of the blade rotation over the clearance gap. This leakage flow is found to decrease as the gap size is reduced ^{114, 45}.

The fluid forces on the impeller can be calculated by integrating over its surface area and this information can be used to determine the requirements of the bearing ^{53, 51}. This is particularly important for mag-lev impellers which do not support such high loads as traditional bearings. Also a mag-lev impeller can move within the magnetic field so it is important to ensure it does not move enough to touch the outer housing. In the case of hydrodynamic bearings the forces on the impeller are even more critical. Bertram et al ¹¹⁵ calculated the force on the impeller of the VentrAssist and compared this with gravity and magnetic forces to find the height at which the impeller sat above the base.

7. Blood Damage

VADs have saved or extended the lives of thousands of patients with heart disease ¹¹⁶ and with improvements in technology, along with the increasing prevalence of cardiovascular disease ² the number is likely to increase. However, the use of VADs is not without risks; while clinical complications vary among devices, they all produce unphysiological conditions in the circulatory system, which leads to a whole range of complications including inflammation, infection and thromboembolism ¹⁵. The alteration of normal blood function can take the form of: damage to erythrocytes (haemolysis) or alteration of their mechanical properties ^{117, 118}, activation of platelets ¹¹⁹ and leukocytes ¹²⁰, increased concentrations of inflammatory mediators and complement activation ¹²¹, as well as thromboembolism ¹⁶ and device thrombosis. While the introduction of newer VAD designs has reduced surgical morbidity, compared with that associated with the early pulsatile VAD designs, and reduced haemolysis, the risk of thrombosis remains high. Thrombosis can lead to cerebral microembolization ¹⁷ and neurological events ¹⁸, including transitory ischemic attacks and strokes ¹⁹, heart attacks and impairment of kidney and liver function ²⁰.

Haemolysis is the most well studied aspect of mechanically induced blood damage and is defined as the release of haemoglobin into the plasma due to mechanical compromise of the erythrocyte membrane. Haemolysis occurs when the product of, the shear stress acting on the cell and the time of the exposure to that shear stress, exceeds a critical threshold ¹²². RBCs are shaped like biconcave discs, a design which gives them a large surface to volume ratio, and in stagnant conditions they aggregate into rouleaux. As they are subjected to increasing shear stresses their behaviour changes until at a high enough level their membrane is forced to stretch ^{123, 124}. The mechanism for the release of haemoglobin may be by complete rupture of the cell ¹²⁵ or through pores appearing in the visco-elastic cell membrane during high stress ¹²⁶. If the shear stress is then removed the RBC returns to its biconcave disc shape (relaxation constant 100–300 ms ¹²⁷). Older RBCs have more viscous, stiffer membranes and a smaller surface area ¹²⁸. The amount of damage done by shear stress is thought to depend on the current level of damage and damage accumulates over the lifetime of the cells. When they are sufficiently damaged they are removed from the circulation by the spleen.

Platelets are the prominent cells involved in both physiological haemostasis and pathological thrombosis ¹²⁹ with platelet hyper-reactivity and circulating activated platelets associated with many cardiovascular, infectious, metabolic and auto-immune disorders. Platelets become activated when exposed to chemical agonists, such as ADP, thrombin, thromboxane A2 and serotonin, and mechanical shear stress ¹³⁰. There are two main theories for the precise mechanism by which mechanical shearing activates platelets: either, shear stress affects platelets directly via von Willebrand factor (vWf) binding to platelet GPIbα receptor, or, shear stress causes mechanical lysis of stored agonists from platelets and erythrocytes which then activate the platelets ¹³¹.

Once activated platelets accumulate, coagulate and adhere to the highly thrombogenic surfaces of medical devices. Blood clotting has long been known to involve three factors, Virchow’s triad: the nature of the surface, the condition of the blood and the local flow conditions. Slow, stagnant or recirculating flow and low shear stresses promote thrombosis ^{132, 30}.

7.1 Haemolysis

A model for haemolysis, which can be applied to all devices is desirable for VAD design. Many groups have attempted to calculate haemolysis in various blood wetted devices. The most widely used model is that of Giersiepen et al ¹³³ who developed a power law function for the damage fraction, D, based on in vitro haemolysis data obtained by Wurzinger et al ¹³⁴ in a Couette system in which human RBC suspension was exposed to defined shear stresses, τ, for defined times, t:

$$D={Ct}^{\alpha }{\tau }^{\beta }$$ 4

Giersierpen et al’s model ¹³³ has been used by many investigators, although some of them have replaced the constants, C, α, β, which are thought to overestimate the haemolysis. Paul et al ¹³⁵ found much lower haemolysis at comparable shear stress, exposure time conditions. Giersiepen’s power law is only strictly valid for constant shear stress over a given time and authors have formulated different approaches to extrapolating the results to the types of varying shear stress field found in medical devices.

The power law equation has been implemented in CFD calculations using post processing techniques in Eulerian and Lagrangian coordinates, as well as by solving transport equations for D. In the Eulerian approach a damage index is integrated over all the cells in the numerical space, for example Garon and Farinas ¹³⁶ use:

$$D={\left[\frac{1}{Q}\underset{V}{\int }{C}^{1/\alpha }{\tau }^{\beta }dV\right]}^{\alpha }$$ 5

where Q is the flow rate and V the volume. Garon and Farinas ¹³⁶ compared their numerical predictions with published haemolysis data for cannulae ¹³⁷ and with their own measurements in VADs and found good agreement. Arvand et al ¹³⁸ also used an Eulerian approach but incorporated pressure head and a high stress fraction and found their constants experimentally. This simple Eulerian approach is the easiest to implement but cannot account for the shear stress history of the cells, cannot show the distribution of haemolysis production and fails to account for differing residence times in different regions of the flow field.

In the Lagrangian formulation the damage index is integrated along tracer particle streaklines ¹³⁹ or post processed pathlines ^{140, 141, 142, 143}. After solving the governing flow equations, pathlines are calculated starting from the flow inlet using forward Euler integration. The lines are then discretized and the total damage calculated by summing the individual damage portions. Different authors have used various damage functions, for example Mitoh et al ¹³⁹ and Yano et al ¹⁴⁰, based their model on Bludszuweit’s idea ¹⁴⁴ of linear damage accumulation and defined the damage for a section i of the pathline as:

$$D_i=D_{i-1}+(1-D_{i-1}){{C\tau }_i}^{\beta }\mathrm{\Delta }{t_i}^{\alpha }$$ 6

Several authors ^{143, 145, 55, 137} define the infinitesimal damage simply using a mini power law:

$$dD={C\tau }^{\beta }{dt}^{\alpha }$$ 7

and integrate along the streamline. The temporal derivative has also been suggested as an infinitesimal damage ¹⁴⁶:

$$dD=C\alpha {\tau }^{\beta }{t}^{\alpha -1}dt$$ 8

and this does at least predict the same total blood damage under uniform shear stress as the power law equation. Grigioni et al ^{146, 147} showed that the mini power law form of the infinitesimal damage did not reproduce the power law result for the total damage under constant shear stress, and that while the temporal derivative does reproduce the total damage given by the power law equation, the infinitesimal damage in the temporal derivative form does not depend on the damage history. They formulate a new infinitesimal damage based on the idea of a mechanical dose, and show that it depends not only on the current shear stress and exposure time but also on the shear stress-exposure time history:

$$dD=C\alpha {\left(\underset{t_0}{\overset{t}{\int }}\tau {(\epsilon )}^{\beta /\alpha }d\epsilon +D(t_0)\right)}^{\alpha -1}\tau {(t)}^{\beta /\alpha }dt$$ 9

Goubergrits and Affeld ^{148, 149} also developed a similar infinitesimal damage accounting for damage history although theirs was formulated in a different way.

The Infinitesimal damage (ΔD) and total damage (D) functions described above were calculated by us for different shear stress histories and are compared in Figure 5.

Figure 5.

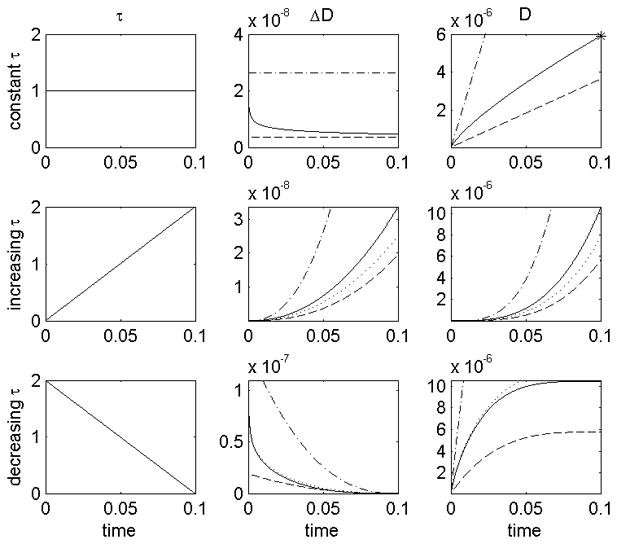
A comparison of infinitesimal damage (ΔD) and total damage (D) for different shear stress histories (top τ = constant, middle τ = increasing, bottom τ = decreasing). Damage models: mini power law (.-.-) ¹⁴³, ¹⁴⁵,⁵⁵, ¹³⁷, temporal derivative (…), Mitoh et al ¹³⁹ and Yano et al ¹⁴⁰ (- -), Grigioni et al (−) ¹⁴⁶. Power law equation for total damage after constant shear stress (*). It can be seen that: both the temporal derivative and Grigioni’s equation predict the same total damage as the power law equation after a constant shear stress; but that using the temporal derivative, the infinitesimal damage at t=0.05 is the same for all three shear stress histories.

Arora et al ^{142, 141} developed a strain based model of haemolysis based on the knowledge that haemolysis is related to the straining of the RBC. They define a morphology tensor for the RBC which accounts for the shape change due to the shear rate, included are viscoelastic deformation, tank-treading motion of the membrane and the areal strain limit. They then calculate the strain along pathlines and this allows the calculation of the haemolysis.

The Lagrangian pathline approach has had some success in predicting haemolysis ^{139, 140, 141}, however, obtaining pathlines has computational problems at near zero velocities and in recirculation regions, and does not necessarily take account of the entire flow field. Also, not all formulations take account of the damage history. The solution of a scalar transport equation has been suggested as a way to account for the whole Eulerian domain and, by appropriate selection of a source term, also include the damage history of the cells ¹⁴⁹. Our group used this method to calculate haemolysis in the UltraMag pump ⁹⁶.

7.2 Platelet Activation

Device induced platelet activation leads to blood clots and requires patients to take anti-coagulation medications which can in turn lead to bleeding. Minimising mechanical platelet activation would reduce the risk of clot formation and require lower doses of anti-coagulation medication. To this end it is important to understand the relationship between shear stress, exposure time and platelet activation. Platelet activation has been modelled assuming a haemolysis type power law equation ¹⁴⁹, an infinitesimal damage based on Grigioni et al’s ¹⁴⁶ haemolysis model ¹⁵⁰ and using a transcendental equation ¹⁵¹:

$$\stackrel{.}{D}(t)={\left(\frac{\tau }{{\tau }_0}\right)}^r\frac{1}{{(1-D(t))}^k}$$ 10

where k is negative to give a positive first derivative and therefore ensure damage always accumulates.

In addition to shear stress platelets are activated by chemical agonists such adenosine diphosphate (ADP) and thrombin. This chemical activation should not be treated separately from shear activation, since agonist production by platelets is dependent on the activation state, and so functions as a positive feedback mechanism.

7.3 Thrombosis and Embolisation

Clotting within the device compromises its efficiency and can lead to device failure while embolization of clots from the device can cause neurological events and strokes, amongst other problems. Continuum models for platelet aggregation which include chemical activation have been formulated by Fogelson et al ^{152, 153, 154, 155}, Sorensen et al ^{156, 157} and Goodman et al ¹⁵⁸ and these models are fundamentally similar. A convection-diffusion-reaction equation is solved for each of the species involved: resting, and activated platelets, platelet released agonists (such as ADP), platelet synthesized agonists (such as thrombin and thromboxane A₂), and prothrombin and antithrombin III which interact with thrombin. Platelet-platelet and platelet-surface adhesion are modelled via specified surface flux boundary conditions such that as the number of adhered platelets increases and the available free surface area decreases the probability of surface adhesion decreases. Surface activation can be included ^{156, 157}, or alternatively shear activation of adhered cells may be modelled ¹⁵⁸. Red blood cell enhanced platelet and large molecule diffusion can be incorporated either by specifying a diffusion constant, which is proportional to the wall shear rate ^{156, 157}, or by allowing the diffusion constant to vary with the local shear stress ¹⁵⁸.. The unknown parameters such as platelet adhesion rates and platelet diffusivity were found by fitting to experimental data from the literature or by performing experiments in straight tubes. Sorensen et al ¹⁵⁷ tested their model by comparison with experimental results from the literature and platelet deposition was in good agreement with one anticoagulant (but not another). One of the main limitations of their model is that it does not account for mechanical interactions between the flow and the thrombus.

The model by Fogelson et al ^{152, 153, 154, 155} uses an elastic link function to describe the inter-platelet bonds and their evolution, and predicts a phase transition which can be interpreted as platelet aggregation. A forcing term ensures fluid flows around the formed thrombus, and the model can predict embolization. They used their model to show how clot development in atherosclerosis depends on plaque rupture site. Goodman et al ¹⁵⁸ incorporate thrombus growth in their model using a simpler approach: when the volume of adhered platelets within a mesh element exceeds the volume of that element, the element becomes thrombus. The viscosity is increased 100,000 times, the boundary geometry is updated and the surface flux conditions are applied at the new boundary. Fluid forces on the growing thrombus are then tracked and the entire thrombus embolizes (and is removed from the grid) when the forces exceed a given characteristic adhesion strength. Their model was validated with experiments in constricted tubes. Video microscopy was used to measure formation, growth and embolization of thrombi, while scanning electron microscopy was used to measure adhered platelets. Good agreement was found for the location and quantity of adherent platelets, as well as for thrombus growth rates and embolization frequency.

Models featuring individual cells may capture the complex interactions involved in platelet aggregation. Fogelson’s micro scale approach ¹⁵³ can model a collection of individual platelets and their interactions with the surrounding fluid, each other and the vessel walls. They use an immersed boundary method to simulate the passage of the Lagrangian platelet models through an Eulerian grid of the flow domain. Each platelet has a membrane with properties influencing the platelet’s deformation. Blyth and Pozrikidis ¹⁵⁹ modelled a single platelet adhering to a surface using a boundary-element method with adhesion bond dynamics. Xu et al ¹⁶⁰ have developed a thrombosis model which uses convection-diffusion-reaction equations for the biochemistry of the plasma with a discrete cellular Potts model of the thrombus involving platelets and RBCs.

Currently these cellular models are unsuitable for studying platelet activation and adhesion in real devices since they are computationally too demanding. There are a few examples of platelet activation models applied to medical devices ¹⁵¹ but none specifically applied to VADs. The complexity of the modelling required, combined with solving the three full dimensional flow in a VAD is a challenge yet to be solved.

8. Interaction with the Cardiovascular System

A VAD operates as part of the cardiovascular system and the two interact in numerous ways: from biochemical issues such as emboli induced by the device which go on to cause problems elsewhere in the body, to mechanical ones such as the flow and pressure within the device. These interactions complicate numerical modelling and have therefore only recently begun to be taken into account. Progress in this direction could lead to more accurate predictions of device performance in vivo, as well as predictions of the effect of the device on the body.

The mechanical interaction between a VAD and the native cardiovascular system is complicated: both the device and the failing native heart pump in parallel, the continuous flow from the device increases the steady flow component to the circulatory system, while the pulsatility of the flow from the native heart results in a pulsatile component in the flow through the mechanical device ¹⁶¹.

Usually flow simulations for continuous flow VADs are performed under steady flow conditions, and devices are optimized based on these steady flow results. However, it has been shown that the rate of change of flow rate influences the flow field. In particular, deceleration destabilizes the flow field promoting separation while acceleration stabilizes the flow ¹⁶². For a device operating with constant speed it might be logical to assume that the pressure head follows a single speed line from the H-Q curve, oscillating along the line as the flow rate changes during the cardiac cycle. However, this is not the case. The inertia of the blood results in hysteresis and therefore a closed loop in H-Q space ^{162, 50, 47}. Some groups have looked at the effects of flow pulsatility ⁴⁷, but since the calculations are far more computationally expensive, these studies are in the minority. A further obstacle to pulsatile flow calculations is to determine the inlet and outlet boundary conditions. In steady flow calculations the inlet boundary is usually set to a specific steady velocity profile and the outlet boundary is fixed at a uniform, steady pressure. The actual unsteady boundary conditions will be dependent on the nature of the flow from the native heart and the pressure in the aorta, both of which are the result of the interaction of the native cardiovascular system and the device.

While 3D CFD fluid-structure interaction (FSI) models of limited parts of the assisted vasculature are beginning to emerge ¹⁶³, studying the effects of the device on the whole CV system, and vice versa, using 3D CFD would be an immense task and instead simpler models are used. For the vascular system electrical circuit analogue models (sometimes called lumped, or distributed, parameter models) have been developed. These models exploit an analogy between fluid flow through a compliant pipe network, and electrical circuits ¹⁶⁴. The fluid flow, pressure and tube compliance correspond respectively to current, voltage and capacitance in the electrical circuit. The extent of the vasculature required depends on the use of the model: when investigating the device effects on the heart, most of the vasculature can be combined into a lumped parameter model. An alternative to circuit analogue models is to solve the 1D flow equations for a distributed, compliant network.

Most studies to date model the LV with a time varying elastance, E(t), to describe the pressure-volume, p-V, relationship in the LV ¹⁶⁵:

$$p(t)=E(t)·(V(t)-V_0)$$ 11

The elastance curve is independent of cardiac load and only changes when the basic contractile function of the heart changes, for example due to drugs or disease, and normalization results in a general curve which is typical for a species. However, the time varying elastance has been found to change dramatically when the heart is assisted with a positive displacement pump due to extreme loading conditions which vary rapidly ¹⁶⁶. There is also a change in the elastance with continuous flow rotary pumps: the end diastolic volume decreases and the maximum pressure increase ¹⁶⁶ which is possibly due to damage to the heart tissue in the presence of the device. An alternative model is the one-fibre model which relates single sarcomere fibre stress and strain to ventricular pressure and volume using the ratio of cavity volume to wall volume ¹⁶⁷. This model was extended by Cox et al ¹⁶⁸ to include a baroreflex model.

Continuous flow rotary devices have a theoretical steady state pressure head given by ^{169, 170}:

$$H=\frac{u}{g}\left(u-\frac{Q}{A}cot\beta \right)$$ 12

where H is Euler’s pressure head, u is the speed of the blade tips, Q is the flow through the pump, A is the effective discharge area and β is the blade angle at discharge. This is a quadratic function of speed and a linear function of flow. However, for the purpose of studying the system–device interaction the unsteady properties of the pump are essential. Including a term to account for flow acceleration, and also incorporating viscous effects, results in an equation for the pressure head of the following form ^{169, 171}:

$$H(t)=A\omega {(t)}^2-aQ(t)-bQ{(t)}^2-L\frac{dQ(t)}{dt}$$ 13

Combining the models of the heart, vasculature and VAD as described above results in a model of the whole assisted circulation. Such models have a variety of uses, for example: calculating the rotational speed required to both maintain adequate cardiac output and avoid left ventricular collapse ^{172, 173}; calculating a time dependent speed such that the pump produces pulsatile flow ¹⁷⁴; estimating the aortic pressure in the assisted circulation ¹⁷⁵; and to study the effects of a failing blood pump with backflow on the left ventricle and aortic flow ¹⁷¹.

9. Blood Rheology

Blood is generally assumed to be a Newtonian fluid in VAD calculations, since shear rates found in blood pumps are generally high, and above 100 s⁻¹ the viscosity of blood is constant. However, there are some reports that the shear thinning property effects pump characteristics at low rotational speeds and low flow rates. The pressure rise generated at low flow rate and low speeds is lower with the shear thinning fluid than with a Newtonian fluid ^{176, 177}. The shear thinning viscous properties of blood have been modelled using the Casson, Carreau, power-law – shear models ¹⁷⁸ and the visco-elastic properties ¹⁷⁹ can be modelled with Maxwell type or Olroyd-B type models ^{180, 181}. Use of these non-Newtonian models of blood rheology may lead to better predictions of the continuum properties of the flow in VADs.

Imaging of RBCs in the blade tip clearance region of a VAD showed that as the gap width was reduced the concentration of RBCs in the gap decreased, suggesting a mechanism whereby cells are excluded from the gap ¹⁸². Modelling this type of effect will require consideration of the blood rheology at the microscale, but is important from a blood damage perspective; if the cells are not flowing into the gap region then they are not being subjected to the high shear stresses found there.

10. Design Optimization

While CFD is often used to examine the flow fields in the pump, shear stresses on the casing or the blades, or to estimate blood damage parameters such as haemolysis, the question of how best to use this information remains. From a clinical perspective assessments of blood damage potential can be useful in choosing one pump over another for an individual patient, based on that patient’s systemic requirements and results for several different pumps. However, pump designers want to know how best to use the CFD results to improve the designs of their pumps. This is often done using a sophisticated trial and error approach. A designer examines the results and uses them, along with their own experience, to make a judgement on how best to improve the design. Often they will perform calculations on a range of designs before selecting one to continue with, or adapt further. Equations for designing specific pump components are available in the literature, for example discharge triangles or variation in pressure head with specific speed ¹⁷⁰, and pump designs can be based on this information. However, it is often not clear how components will interact until they are tested. This testing can be done with CFD which accelerates the sophisticated trial and error process. There are numerous reports in the literature of these kinds of design improvement studies and just some of the ideas will be given here.

The impeller is one fundamental part of a pump but its optimum design is not necessarily intuitive since it has multiple parameters which affect the overall performance of a pump. CFD can be used for selecting the best design parameters. Arvand et al ¹⁸³ calculated the flow through their mixed-flow pump with three impellers, differing in shape and presence of washout holes, and compared the following characteristics: pressure rise, efficiency, washout and leakage flow rates, torque and haemolysis. By ranking the impellers for each characteristic they could see which performed best in most categories. The impeller chosen gave the largest pressure rise, highest efficiency, lowest tip leakage flow and the lowest haemolysis, although this impeller performed only second best in terms of washout flow and torque. Curtas et al ⁴⁸ found that blade curvature had a small effect on pump performance, with a straighter impeller creating a larger pressure head than evenly swept blades, but with a lower efficiency. Inlet and outlet angles both influenced the pump efficiency. Zhang et al ⁵⁸ found flow recirculation in their newly designed axial flow pump and increased the blade expansion angle in increments from 0 to 20° until the recirculation was eliminated. Three different versions of the impeller for the Levitronix PediVAS ³⁹ were simulated in order to assess the effects of longer blade tips on performance. The longer tips were found to increase the pressure head by around 50 %. In the Impella axial flow pump, Triep et al ⁶¹ investigated the effect of the length of the axial tip on the pump’s efficiency. Pumps with magnetically levitated impellers always have a narrow gap which separates the impeller from the pump housing. This gap is a secondary flow channel, and with high shear rates, and potentially long residence times, the region can be a blood damage hot spot. As such there have been many studies related to improving the parameters of the clearance gap. Anderson et al ⁴⁴ studied flow in the clearance gap of the HeartQuest pump and showed that reducing the gap width from 0.76 to 0.25 mm increased the pump efficiency by reducing the flow through the clearance gaps. However, the shear rates necessarily increase which is undesirable. They highlight the presence of the Ekman layer, a thin layer adjacent to the rotating impeller casing, in which there is a force due to friction on the rotating surface of the impeller opposing the radial pressure gradient. The Ekman layer traps blood in the clearance gap increasing exposure to the high shear stress. Miyazoe et al ⁴⁹ showed that reducing the clearance gap in the Nikkiso HPM-15 from 3.0 to 0.5 mm increased the shear stress 5 fold.

The above studies are examples of CFD based design improvement. A step above design improvement is CFD based design optimization ¹⁸⁴. This requires coupling a CFD solver with a parameter optimization method ³³ so that the flow field is solved for the initial design, and then, based on the values for efficiency, shear stress, recirculation or whatever the designers feel is important, the parameters for the pump are automatically adjusted. The flow field is then recalculated, if the results are improved, the changes are implemented, or if the results are still not good enough more changes will be automatically made. The whole process is iterative; only finishing when the design is optimized in terms of the specified objective performances. CFD based design optimization has been used in the development of, amongst others, axial flow pumps ¹⁸⁴ and centrifugal pumps ⁶⁰, as well a blood shearing instrument ¹⁸⁵.

11. Validation

CFD is a powerful tool which has already reduced the time required to develop a new blood pump and has the potential to further increase development speed with the implementation of design optimization codes. Future development of blood damage models should enable simulation of haemolysis, platelet activation and thrombosis, thereby reducing the requirement for in vitro blood studies. However, it is easy to perform calculations but the variety of results which can be obtained with incorrect inputs is huge ¹⁸⁶ and without confidence in the results CFD studies are of very limited value. Validation is the process of determining the degree to which a model is an accurate representation of the real world, and quantifies the uncertainty ²³. A simulation is considered to be validated if the differences between its results and experimental data are small and if the uncertainties in the experimental results are also small ²³.

Although extensive validation studies have been performed for industrial type pumps, these operate with different flow conditions and so the validation results do not necessarily provide useful information about CFD used in blood pumps. The different size, speeds, flow rates and working fluid mean that validation studies should be performed specifically for blood pumps. Validation is usually performed in vitro and most commonly uses the noninvasive optical techniques of flow visualization ^{74, 36, 187, 100}, for qualitative information, and particle image velocimetry ^{43, 109, 46, 111, 59, 61, 62} or laser Doppler anemometry ^{188, 100} for quantitative measurements. Another noninvasive technique which can be used to measure the wall shear stress is oil drop streaking ^{110, 187}. Hot film anemometry is an invasive technique which can also be used for studying in vitro flow and gives a high temporal resolution ^{189, 37, 103}. Predictions of fluid forces can be validated by comparison with measurements of forces on the impeller ^{51, 52, 54, 11, 56}. Many groups compare their CFD predictions of the pressure head produced by the pump with the measured values to give a bulk flow parameter for validation. While this does not show that flow field details are being correctly predicted, it does give some assurance and is a first step towards validation. Magnetic resonance imaging (MRI) has also been used to investigate the flow field in a pulsatile VAD ¹⁹⁰, and as in vivo imaging tool MRI has the possibility of being used to look at VADs in vivo, although currently the majority of devices are not MRI compatible.

There have been a large number of comparisons of computational with experimental results for specific pumps, however, while acknowledging a few notable exceptions, including transient versus steady flow ⁴⁷ and k-ε versus k-ω turbulence models ⁴⁶, there is still a lack of published work on the differences due to different numerical methods.

12. Future Directions

From reviewing the current literature a number of trends become apparent for the future direction of research into VAD development using CFD.

12.1 Types of Pumps

One of the biggest limitations of VADs is their invasiveness, which makes them very uncomfortable, and their bulkiness, which prevents them being fitted in smaller patients. Smaller devices are currently being developed but some of these are only suitable for partial support. An area where CFD can be applied is the design and optimisation of less invasive pumps. Another area of VAD design which is ripe for development is pulsatile pumps. Compared to rotating pumps far less is known about flow calculations in pulsatile pumps and models of these could really aid understanding of their complicated flows.

12.2 Turbulence

While current simulations appear to predict pressure head curves to within 10 % of the experimental values, and the available PIV studies do show reasonable agreement, more work is needed to determine which turbulence models are the best to use in different devices. Flow through various devices should be calculated using all of the turbulence models available. From detailed comparisons of experimental and computational results the errors involved with using the different models could be determined and the best turbulence models for predicting flow in these types of devices should become clear. Newer turbulence models designed to simulate transition to turbulence, such as the k-kl-ω model ¹⁹¹ may yield more accurate predictions.

The amount of computing power available, mesh size and number of equations determines the length of time calculations take. Steady state calculations discussed in this article, of flow through whole VADs, take around 10 – 12 hours on single Pentium 3 850 MHz or 4 3.0 GHz processors ^{57, 138}. A 2.83 GHz quad core with 32 GB memory can solve steady state turbulent flow for a mesh with 3 million elements in around 12 to 24 hours. The solution time for unsteady transient calculations is typically much longer, but depends on how many time steps are required. As computing power continues to increase Large Eddy Simulations, which have already been used for arterial blood flows, could be utilised. In the future Direct Numerical Simulation may be possible, at least for sections of the device or for validating the use of turbulence models.

12.3 Blood damage

The major obstacle in the path to increased patient use of VADs is blood damage. While haemolysis is no longer the largest blood damage issue, a universal model for haemolysis, which can be used in all devices, is still greatly desirable for evaluating pump designs. Thrombosis and emboli are currently major clinical challenges and the development of modelling approaches to predict these phenomena is vital. Current models for thrombosis consist of too many equations to implement in simulations of whole devices. However, if an approach can be found to apply their predictions to simulations the value of CFD to VAD development will be significantly increased. This will likely necessitate the use of multiscale approaches ¹⁹² which can model the nanoscopic molecular events in the context of the macroscopic device.

12.4 Cardiovascular system – Device Interaction

Interactions between the cardiovascular system and the VAD affect device performance and will likely influence the optimised pump design. Therefore models of devices should be incorporated into models of the whole cardiovascular system in order to more accurately predict flow in the device in vivo. The pulsatile nature of the flow can be studied and effects such as the destabilization, and possible turbulence generation, during flow deceleration could be investigated. In vivo conditions involve a lot of uncertainty since flow and pressure waves vary depending on exercise conditions and even beat to beat. Novel methods ¹⁹³ could be used to account for these uncertain conditions in optimising the pump design. Combined models will also enable modelling of the effects of the device on the cardiovascular system, such as changes in pressure-flow waveforms, changes in local flow patterns and predictions of where emboli go.

12.5 Blood Rheology

Most current VAD calculations assume a Newtonian viscosity for blood. However, as calculations become more realistic so to should the models of blood rheology. Improved continuum models, as well as discrete models will be useful.

12.6 Validation

More validation studies are needed to build confidence in the use of CFD for VADs. In particular detailed visualization studies in a range of different devices should be performed and compared with the computational results. Establishing a database of experimental results which could act as test cases for groups wishing to validate their computational methods would be useful. In addition to optical imaging measurements of velocity, which are invaluable for assessing CFD predictions, measurements of blood damage characteristics are also required for validating blood damage models.

13. Conclusion

Cardiovascular disease, and heart failure specifically, are increasingly prevalent in today’s world and the improvement of treatments will help save lives. VADs are already in use clinically but have the potential to benefit many more patients if their current shortcomings can be eliminated. CFD is an invaluable tool in the development of VADs, enabling new designs to be tested rapidly and undesirable flow characteristics eliminated in successive versions before prototypes are manufactured. CFD is used for predicting pressure-flow characteristics and efficiency curves, revealing the detailed flow field to help eliminate regions of recirculation or stagnation and for calculating fluid dynamic forces. When combined with models of blood damage CFD has been used for predicting haemolysis and platelet activation by VADs. When combined with shape optimization algorithms it can be used in design optimization.

In summary, this article has discussed the current state of CFD applied to VADs and shown the variety of uses and benefits of calculations in terms of increasing the speed of device development. A number of areas for future research have also been identified.

Figure 2.

An axial flow VAD placed directly into the LV and inset showing the Jarvik 2000.

Figure 3.

A small axial VAD implanted through the aortic valve and insert showing the Impella.

Figure 4.

A positive displacement VAD placed extracorporeally and inset showing the Thoratec PVAD^™.

Appendix: Pump Characteristics

The following tables (Table 1, Table 2, and Table 3) report details of pumps from CFD studies in the literature. Maximum Reynolds numbers have been calculated based on the data given in the papers and using υ = μ/ρ, with μ=0.0035 kg m⁻¹ s⁻¹ and ρ=1050kg m⁻³, ω is the maximum rotational speed in rad s⁻¹ and v is the mean velocity at the inlet calculated from the flow rate using v = Q/π(d/2)² . For rotary pumps, both the maximum inlet Reynolds number, MaxRe_in, and the maximum Reynolds number for the impeller region, MaxRe_imp, have been calculated.