Solving structure in the CP29 light harvesting complex with polarization-phased 2D electronic spectroscopy

Abstract

The CP29 light harvesting complex from green plants is a pigment-protein complex believed to collect, conduct, and quench electronic excitation energy in photosynthesis. We have spectroscopically determined the relative angle between electronic transition dipole moments of its chlorophyll excitation energy transfer pairs in their local protein environments without relying on simulations or an X-ray crystal structure. To do so, we measure a basis set of polarized 2D electronic spectra and isolate their absorptive components on account of the tensor relation between the light polarization sequences used to obtain them. This broadly applicable advance further enhances the acuity of polarized 2D electronic spectroscopy and provides a general means to initiate or feed back on the structural modeling of electronically-coupled chromophores in condensed phase systems, tightening the inferred relations between the spatial and electronic landscapes of ultrafast energy flow. We also discuss the pigment composition of CP29 in the context of light harvesting, energy channeling, and photoprotection within photosystem II.

Understanding the underlying principles that give rise to the exceptional efficiency of light harvesting in photosynthesis is key to the development of artificial solar energy collection. It is equally compelling from a fundamental standpoint on account of nature’s unique and elegant solution to solar energy funneling that employs ultrafast electronic excitation energy transfer (EET). Nevertheless, the very features that make photosynthetic light harvesting so effective commensurately ensure that it remains challenging to study. A complete understanding of the phenomenon is predicated on determining why a configuration of chlorophyll (Chl) pigments within a protein give rise to efficient EET. Measuring this dynamic process must be done with femtosecond time resolution and involves deciphering a spectrally congested electronically-coupled system of chromophores only angstroms apart in a protein solvent bath. Contributions to what is known have arisen from a confluence of ultrafast spectroscopic techniques, high-resolution spatial structure determination via X-ray crystallography, and active development of condensed phase modeling (1–3). That building structure-function relationships requires understanding energy flow with elusive subnanometer precision underscores the necessity for tracking energy spectrally and mapping the results back onto spatial structure, in spite of the challenges associated with assigning often congested spectral features to individual chlorophyll excitations.

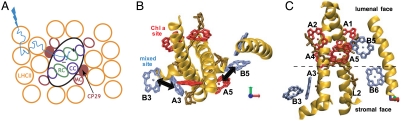
The CP29 light harvesting complex is purported to play multiple roles beyond solar energy collection in the photosystem II supercomplex (PSII) of plants. CP29 is one of three highly homologous pigment-protein complexes (PPCs) found adjacent to the reaction center core of PSII, where charge separation initiates energy transduction (Fig. 1A). These PPCs, so-called minor complexes, are thought to act as channels for excitation energy from an array of the major light harvesting complex, LHCII, to the core’s reaction centers (4). The minor complexes are also putative sites for nonphotochemical quenching (5), the harmless dissipation of excess chlorophyll excitations as heat in high light conditions to prevent radical oxidative damage. The current structural model for CP29 (6, 7) is based on moderate sequence homology with LHCII, whose structure has been solved at high resolution (8, 9). Ultimately, we would like to refine this homology model to more deeply understand CP29’s versatility in function, especially by achieving an alternative means to determine structure.

Fig. 1.

Models for PSII and CP29. (A) PSII and its light harvesting antenna. LHCII (orange) surrounds the minor complexes (MC, red), which surround the PSII core (black). Charge separation can be initiated in the reaction center (RC, green) once excitation energy is channeled through a core complex (purple). (B and C) CP29 homology model in two orientations, based on X-ray crystal structure of LHCII (PDB ID 1RWT). Eight Chl binding sites are shown, compared to 14 in LHCII: those in red bind Chl a specifically, while the mixed sites in blue can bind either Chl a or b. The primary carotenoid binding sites are also shown (brown). (B) The main sites considered in this work are labeled according to the homology model notation. Black arrows indicate the energy transfer pairs discussed in the text. (C) This orientation shows the segregation of chlorophylls to lumenal and stromal layers. Coordinate arrows (red, green, and blue) are drawn relative to (B).

Here, we present an advance in polarized 2D electronic spectroscopy that enables structural information about CP29 to be extracted directly from electronic data. Coherent 2D spectra (10–12) present the third order nonlinear optical response of a system as a function of both excitation and emission energies by iteratively interrogating the sample with a sequence of ultrafast light pulses while varying their relative delays. Correlations between resonant transitions in the sample are mapped over the entire laser pulse bandwidth. Some of the most salient features of all 2D spectra are cross-peaks, signals that expose correlations between differing excitation and emission energies. These cross-peaks are direct indicators of coupling between chromophores and of EET dynamics in systems with multiple interconnected excited states.

Polarized 2D spectroscopy (13) involves rotating the light pulse polarizations with respect to one another in order to enhance or suppress various distinct signal contributions that may not be generally discernible on account of their spectral overlap. Various polarization sequences have been proposed and implemented in order to parse 2D spectra (13–20). For example, suppression of the diagonal peaks of the Fenna-Matthews-Olson (FMO) pigment-protein complex was demonstrated, enabling a closer look at the remaining, often overpowered, cross-peaks (18). In ref. 19, two sequences that respectively enhanced and suppressed a particular EET cross-peak in FMO, were compared to simulated coupled-dimer spectra in order to determine the projection angle between the excitonic dipoles involved.

Obtaining quantitative information directly from polarized 2D spectroscopy requires a direct and quantitative comparison of different polarized spectra, which is only possible if they can be properly normalized with respect to the same reference. This condition is important not only for the signal amplitude but also critically for the complex phase. For example, spectrally resolved pump-probe measurements, which typically accompany conventional 2D data collection in order to properly phase the signal, cannot be employed when the first or last two light pulse polarizations are not parallel. Without being able to isolate the absorptive component of the signal from the dispersive component, peak positions and shapes are obscured, and the measurements are no longer sensitive to sign changes induced by the polarization sequence.

It is worth underscoring that the recent efforts to generate structural models using polarized 2D electronic spectroscopy have required the combination of experimental data and extensive theoretical modeling. A more direct means to relate polarized 2D signals to structural information could circumvent some of these difficulties. Though resolving structure alone is not sufficient to identify which chlorophylls are responsible for which spectral features or dynamics, for cases such as CP29 and also multiple membrane proteins that still elude crystallization efforts, our ability to understand structure-function relationships is handicapped. In the present case of CP29, the ability to accurately model system dynamics would facilitate discerning specific energy flow pathways and would enable a deeper understanding of its role and dissipation mechanism in nonphotochemical quenching.

By measuring a finite set of polarized 2D spectra, we show how it is possible to obtain quantitative structural information about relative chlorophyll transition dipole moment angles in CP29 without supplementary modeling, and also how our scheme yields a normalized set of spectra that can subsequently be used as a basis set to generate additional spectra representing the signals of arbitrary polarization sequences. This development opens up the ability to address outstanding questions about structure-function relationships in elusive electronically-coupled systems such as CP29.

Results and Discussion

Based on multiple optical spectroscopies and on its at least partial likeness to LHCII, the homology model for CP29 (6, 7) predicts a spatial structure illustrated in Fig. 1 B and C. There are on average six Chl a and two Chl b molecules per CP29, though a total of four out of eight pigment binding sites are not specific and can host either of the two pigments. This so-called “mixed binding” implies that CP29 can exist with 16 different permutations of chlorophyll pigment composition. Nevertheless, such variability must have a minimal effect on the protein complex function in PSII. Namely, while the interchangeability of Chl b and Chl a pigments in four of the binding sites will enhance the spectral coverage of light harvesting, it must not prevent nonphotochemical quenching or the channeling of energy through itself to the PSII core.

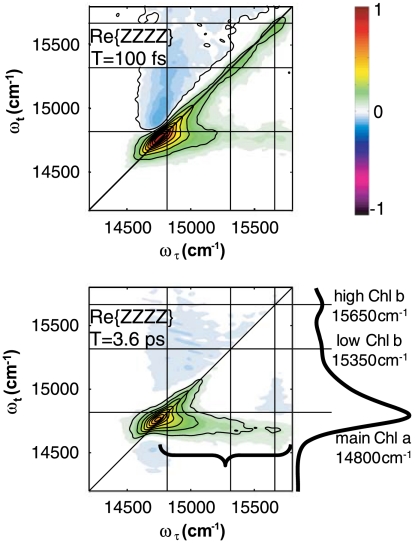
Measured absorptive parallel-polarized (ZZZZ) 2D spectra of the S₀ → S₁ chlorophyll electronic transitions in CP29 at 77 K are shown at T = 100 fs and 3.6 ps in Fig. 2. Overlaid horizontal and vertical lines indicate the energies of the main features of the sample’s linear absorption, which is also shown. In both the linear and nonlinear spectra presented, there is a single Chl a band peaked at 14,800 cm^-1 (676 nm) and two much weaker, resolved Chl b peaks at 15,350 and 15,650 cm^-1 (650 and 637 nm). The Chl a transitions provide the oscillator strength necessary to visualize EET from the Chl b states.

Fig. 2.

Absorptive ZZZZ 2D electronic spectra of CP29 at 77 K. Horizontal and vertical lines indicate the locations of the main Chl S₀ → S₁ transitions from the linear absorption spectrum adjacent to the T = 3.6 ps plot. The black brace highlights the cross-peak band indicating energy transfer to Chl a states. The T = 100 fs time point is scaled to its own maximum; for ease of comparison, the T = 3.6 ps spectrum is scaled to 3× the maximum of the 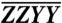plot in Fig. 3.

Concentrating first on the diagonal features of the plots, indicated by black diagonal lines, the bulk of the ZZZZ signal appears in the Chl a region of the spectrum (14,600 cm^-1–15,200 cm^-1), though the Chl b diagonal peaks around 15,350 cm^-1 and 15,650 cm^-1 are still clearly visible at 100 fs. After 3.6 ps in the system evolution, population has mostly decayed from the two Chl b peaks, yet the excitations have been transferred to Chl a excited states, as is manifested by a protracted cross-peak feature below the diagonal centered around ω_t = 14,750 cm^-1 (black brace). Despite the rather continuous nature of this feature, polarization-sensitive techniques can be used to discern different cross-peaks within it, ultimately leading to the determination of the relative dipole angles between coupled donor and acceptor pigments involved in distinct Chl b to Chl a energy transfer processes.

In fact, according to the homology model, Chl b to Chl a energy transfer takes advantage of the pigments with the strongest predicted electronic couplings in CP29’s Chl network by nearly an order of magnitude (∼150 cm^-1 compared to ∼30 cm^-1). These strongest couplings are indicated by the black arrows in Fig. 1B. According to previous assignments (7, 21) and measured ZZZZ spectra, the Chl b to Chl a energy transfer by 3.6 ps is dominated by EET within two distinct Chl heterodimers: The signal at (ω_τ = 15,350 cm^-1, ω_t = 14,750 cm^-1) results predominantly from B₅ → A₅ EET when the mixed site, B₅, is occupied by Chl b. The signal around (15,650 cm^-1, 14,750 cm^-1) results from EET between the two mixed sites, A₃ and B₃. There are two possible permutations of heterodimer pigment composition that will contribute in this latter case and also contribute to implications discussed below.

Polarization-Phased 2D Electronic Spectra.

We have developed the means to perform the complex normalization of polarized spectra based on the following tenets: The strength of a single third order signal contribution in nonlinear spectroscopy is described by a response function according to a perturbative formalism (22). The dependence of the response function on the transition dipole moments and electric field polarizations involved in the four light-matter interactions is consolidated in the orientational factor, a fourth-rank polarization tensor , where the average is over an isotropic distribution of molecular orientations. Here, {ijkl} index the x, y, and z components of the lab frame laser polarizations in inverse order of occurrence, and {αβγδ} index the normalized transition dipole moments in the molecular frame (13, 14).

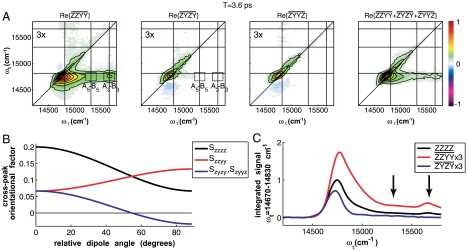
The normalized and phased absorptive (real) components of a set of three experimentally obtained polarized basis spectra at T = 3.6 ps, 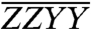, , 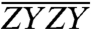and 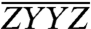, are shown in Fig. 3A. As a confirmation of the complex normalization described in the Materials and Methods, the sum of the three polarized spectra is also presented and agrees with the original ZZZZ spectrum in Fig. 2 to within a residual error smaller than the measurement noise floor. The color scaling and contour values are the same for all three polarized spectra, referenced to the maximum value of 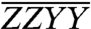. The two “cross-polarized” spectra, 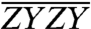and 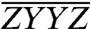, are virtually identical because any excited state coherences that would manifest themselves differently in these two spectra decay before 3.6 ps.

Fig. 3.

Polarization-phased 2D electronic spectroscopy. (A) Phased and normalized basis set polarized spectra and their sum. Boxed regions indicate the A₅–B₅ (stippled) and A₃–B₃ (dot-dashed) cross-peaks. Basis set spectra are all scaled to the maximum of the 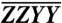plot, which exceeds the other maxima on account of the overlap between diagonal and enhanced cross-peak features. The absolute scale of the sum spectrum, , is 3× greater in keeping with the relative strengths of the orientational factors. (B) Orientational factors corresponding to energy transfer cross-peaks for the four polarization sequences used. (C) Integrated traces from the 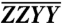, , and ZZZZ plots to quantitatively demonstrate the variation of the spectra along ω_τ over the cross-peak band. Arrows indicate the cross-peak regions of interest.

On account of orientational averaging, S_ijkl can be expressed in terms of the relative angles between relevant transition dipole moments. Thus, the energy transfer cross-peak orientational factors corresponding to their respective spectra are plotted together in Fig. 3B as a function of relative dipole angle, θ, between donor and acceptor. The orientational factors are symmetric about θ = 90°, i.e., S_ijkl(θ) = S_ijkl(180°-θ). 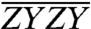As is predicted from these orientational factors’ analytic expressions, while the diagonal (θ = 0°) features of all three polarized spectra are of similar amplitude, the cross-peaks are enhanced for and suppressed in and 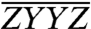. Upon careful consideration, in the 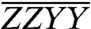spectrum, the relative enhancement of the A₃–B₃ cross-peak (dash-dotted box) exceeds that of the B₅–A₅ cross-peak (stippled box). Likewise, in the 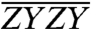spectrum, the relative suppression of the A₃–B₃ cross-peak exceeds that of the B₅–A₅ cross-peak. These modulations are evident quantitatively in the integrated traces in Fig. 3C.

Generating Supplementary Polarized 2D Electronic Spectra by Spectral Arithmetic.

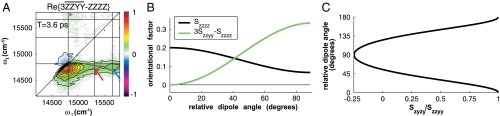
Arithmetic performed with the basis set of spectra provides further contrast between the two cross-peak features. As an illustration, consider the linear combination, 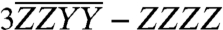(15). Because we have solved the problem of normalizing spectra with respect to one another, it is possible to construct this combination out of basis spectra. The according spectrum, constructed out of those presented in Fig. 3, is shown in Fig. 4A alongside the orientational factor (Fig. 4B). The most salient feature of the latter is that it vanishes at θ = 0°, indicating that diagonal peaks, for which all four interactions occur with the same transition dipole moment, must also vanish. This feature is confirmed by the absence of signal strength along the diagonal of the spectrum. The orientational factor dependence can also be used to corroborate the assignment of the Chl b → a cross-peaks. The higher energy A₃–B₃ cross-peak (blue arrow) is stronger than the lower energy A₅–B₅ cross-peak (red arrow) in this combination spectrum, in contrast to the corresponding ZZZZ spectrum in Fig. 2. Because the orientational factor increases monotonically between θ = 0° and 90°, this indicates that the A₃–B₃ cross-peak must involve a pair of transition dipole moments that are closer to being perpendicular. This observation reinforces that the higher energy cross-peak belongs to the A₃–B₃ dimer and that the lower energy one belongs to the A₅–B₅ dimer: According to the homology model, the relative site dipole angles for the A₃–B₃ and A₅–B₅ dimers are 74° and 158°, respectively. Note here that, for heterodimers, the site basis (uncoupled) and exciton eigenbasis (coupled) dipole angles should be virtually identical because the energy gap between the Chl a and b sites is sufficiently large compared to the electronic coupling to localize the excitons on the individual sites. Thus, in this case, the energy transfer cross-peaks provide a direct link to the spatial, in addition to electronic, structure of CP29.

Fig. 4.

Arithmetic with polarization-phased 2D electronic spectra. (A) The combination yields a cross-peak specific spectrum, which eliminates diagonal signals and emphasizes the A₃–B₃ cross-peak (blue arrow) over the B₅–A₅ cross-peak (red arrow). (B) Cross-peak orientational factors illustrate how the relative amplitudes of the cross-peaks in (A) and Fig. 2 differ. (C) Relative dipole angle dependence on the ratio S_zyzy/S_zzyy for a population transfer cross-peak.

Relative Transition Dipole Moment Angle Determination.

As a result of our normalization, the angles between energy transfer transition dipole moment pairs may furthermore be estimated directly from the normalized spectra in Fig. 3, provided that the orientational contribution to a cross-peak’s overall signal can be isolated. The orientational factor is the only factor that differentiates spectra taken with different polarization sequences. 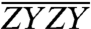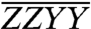Thus, so long as the cross-peak being examined is spectrally well isolated, like the Chl b to Chl a energy transfer cross-peaks of CP29, the ratio of the and spectra at the cross-peak location can be directly compared to the ratio of orientational factors, S_zyzy/S_zzyy. For cross-peaks due to population transfer, 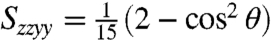and 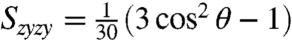(13). Therefore, 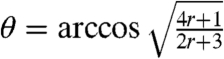, where we have substituted the ratio of properly normalized spectra at the cross-peak location, 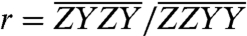, for the ratio of corresponding orientational factors. Thus, the angles (θ) obtained from the two spectrally isolated Chl b to Chl a population transfer cross-peaks in the spectra were determined by measuring the signal amplitude of the indicated regions of interest in Fig. 3A encompassing the cross-peak. For the A₃–B₃ cross-peak we obtain a value of 53° or 127° and for the A₅–B₅ cross-peak, additionally subtracting the tails of adjacent peaks, we determine the angle to be either 42° or 138°. The estimated error resulting from peak amplitude offsets and noise is ± 5°, as described in the SI Text.

The ambiguity in the angle determination is on account of the symmetry of the orientational factors about θ = 90°, as depicted in Fig. 4C. However, this ambiguity can be removed upon comparison to the angles predicted by the homology model. By selecting 53° and 138° respectively, deviation between measured and predicted values is kept to ∼20° in each case. For A₅–B₅, the angle is also close to the value of 116° obtained by linear dichroism on pigment deletion CP29 mutants (23). Thus, our findings indicate that the homology model captures the essential features of energy transfer in CP29 reasonably well, yet also indicate potential for improvement. The discrepancy could arise from multiple levels of uncertainty: Insofar as the homology model is concerned, the use of a surrogate protein crystal structure can only be expected to approximately represent the conformation of CP29 and the orientation of chlorophyll pigments relative to the protein. Furthermore, the angle of the transition dipole moments of chlorophyll pigments in specific protein environments cannot be expected to be identical to that determined from measurements in bulk solution. With respect to our measurements, we estimate that the precision of our reported technique for determining the relative dipole angles depends on the measurement sensitivity, the quality of the normalization achieved, and the steepness of the ratio r as a function of angle θ. However, our measurement uncertainty of ± 5° is less than the discrepancy between measured and predicted values of the angles. Thus, our findings can be fed back into the model in order to refine its ability to predict energy transfer dynamics, and the technique provides a general means to infer transition dipole moment orientation in local solvent environments through exclusive use of experimental data.

Implications for Light Harvesting in PSII.

Together, LHCII and the minor complexes, CP29, CP26, and CP24 comprise the antenna of PSII (Fig. 1A). Though these PPCs are all derived from the Lhcb protein family, the variations in amino acid sequence facilitate a broad range of function to maximize the efficiency of multiple light harvesting complexes together directing energy toward the reaction center. The light harvesting complexes must both collect light energy and pass it on to neighboring PPCs. In particular, it is significant that, by comparison to LHCII, CP29 (and other minor complexes) have significant pigment binding site deletions, and their mixed sites are predominantly located at the periphery of the protein structure (Fig. 1 B and C). To maintain robustness of function in spite of the mixed sites, we infer that these pigments must primarily serve to enhance energy collection, leaving the role of reliable connectivity with adjacent proteins to the Chl a pigments that are specifically bound.

It is also important to consider the orientation of the Lhcb proteins in the thylakoid membrane, which functions as the barrier to enable the buildup of a proton gradient to ultimately drive ATP synthesis (24) and trigger nonphotochemical quenching (25). We further note that the majority of binding site deletions in CP29 occur near the stromal (outer) surface of the protein as opposed to the lumenal surface (Fig. 1C), and that each of the three stromal binding sites is a mixed site. These observations suggest that another means to promote efficient collection and conduction of light energy is to maintain parallel stromal and lumenal chlorophyll networks. Energy transfer throughout PSII localized to one or the other of these networks may be most favorable, however the redundancy of these two layers and the weaker couplings between them may help to avoid bottlenecks or traps in both inter and intracomplex EET potentially arising from the interchangeability in the mixed sites.

As a point of reference, the lowest energy, or putative “exit,” site of LHCII comprises excitons delocalized over three Chl a sites on its lumenal surface (26, 27). This discussion also suggests that the lumenal level of CP29 is more active and potentially reliable in conveying energy toward the reaction center core, both on account of the number of pigments that it hosts and because most of its binding sites are specific to Chl a. This concentration of dedicated Chl a sites, and the fact that charge separation in the reaction center is also initiated near the lumen, underscores the importance of the lumenal layer of pigments in multiple, adjacent Lhcb proteins.

Consider now the dimers on which we have focused our analysis in the context of the overall pigment configuration within PSII. As illustrated in Fig. 1, because of its central location on the lumenal surface of CP29, we infer that the A₅–B₅ dimer either acts as a primary acceptor of excitation energy from LHCII or as a primary donor of energy to the PSII core. [The absolute orientation of CP29 within PSII has not been directly visualized, though cryoelectron microscopy on PSII combined with modeling based on available constituent crystal structures suggests that A₅ is adjacent to the PSII core (28)]. By contrast, the A₃–B₃ dimer on the stromal surface may serve to accept energy from pigments on LHCII’s stromal surface but is likely part of a pathway of secondary importance. Furthermore, in light of CP29’s importance in intercomplex EET, it is important to note that the determined relative angles between transition dipole moments within each of the A₃–B₃ and A₅–B₅ pigment pairs are intermediate between being parallel and perpendicular. A parallel arrangement would compromise coupling to other transition dipole moments with significant orthogonally oriented components both within CP29 and in neighboring PPCs. A perpendicular arrangement within either of the dimers would render intradimer coupling negligible, preventing rapid EET from Chl b to Chl a states. By striking a balance between intradimer coupling and coupling to external pigments, CP29 is able to effectively harvest light and transmit excitations.

Last, the notion that the A₅–B₅ dimer lies along a main energy flow trajectory between LHCII and the PSII core seems very reasonable, as together with the adjacent L₂ carotenoid binding site (Fig. 1C), it is a putative location for nonphotochemical quenching via charge transfer (5). This configuration strategically locates these pigments to readily intercept the flow of excitation energy en route to an already-occupied reaction center.

Conclusions

CP29 is critical to efficient light harvesting, energy conduction, and regulation in higher plants. As for many electronically coupled chromophore systems, our understanding of how its structure and composition determine its functionality is limited not only by spectral congestion and difficulties associated with performing high-resolution X-ray crystallography, but also because spatial and spectral resolution are not sufficient to infer the correspondence between space and energy nor the emergent condensed phase dynamics. We have developed a means to isolate the absorptive components of polarized 2D electronic spectra by taking advantage of well known properties of fourth-rank tensors in isotropic media. In addition to solving the phasing problem inherent to arbitrary polarization sequences, we have also provided a way to generate any polarized 2D spectrum using a finite set of basis spectra. The strategy is highly suitable to enhancing our understanding of CP29, in particular because it enables us to extract structural information directly from electronic spectra, irrespective of the absence of crystallographic data, and to correlate it with spectral properties and dynamics. Focusing on the Chl b to Chl a energy transfer cross-peaks, which are spectrally well isolated on account of the 2D spectroscopy, we have obtained values for the relative angles of the transition dipole moments in the native protein environment.

By examining pigment composition, we have also inferred much about the roles of particular EET dimers in CP29. Whereas the A₃–B₃ dimer may be responsible for light harvesting alone, the A₅–B₅ dimer may also play important roles in interPPC energy channeling and in nonphotochemical quenching. The particular angles determined between transition dipole moments in both cases illustrate how these pigments must interact with one another and with pigments in adjacent PPCs. Furthermore, the means by which CP29 is capable of quenching excitations in addition to collecting and conveying them is not completely understood. Should this function be in part tuned by structural changes in the protein, our direct measurements of structural parameters may provide a means for detecting such effects.

Materials and Methods

Sample Preparation.

Recombinant CP29 was prepared according to ref. 29. The Lhcb4 gene from Zea mays was overexpressed in Escherichia coli and reconstituted with a pigment mixture of Chl and carotenoids (Chl a/b ratio of 3.5; Chl/carotenoid ratio of 3 with carotenoids lutein, zeaxanthin, and neoxanthin in a 1∶1∶1 ratio) by undergoing a series of freeze-thaw cycles and purification by ultracentrifugation on sucrose density gradients and ionic exchange affinity columns. The measured pigment composition per protein was a Chl a/b ratio of 5.87∶2.13 with a carotenoid composition, L∶N∶Z, of .95∶.15∶.91. The sample was concentrated, mixed 25∶75 vol/vol with glycerol, and cooled in a 200 μm-path length quartz cell to 77 K, yielding a peak optical density of 0.2 at 676 nm.

Data Collection.

Using a beamsplitter and a transmissive grating, the output pulse of a home-built noncollinear optical parametric amplifier is split into four identical pulses in a box geometry that are ultimately focused to a ∼70 μm spot on the sample. Each pulse contains 5 nJ spread over a bandwidth of 90 nm, centered at 660 nm. The pulse spectrum amplitude was maintained to within ± 8% over the Chl a and b bands investigated. The delay between pulses 1 and 2, the coherence time τ, is precisely controlled by pairs of translating glass wedges in each of these two beams. Dynamics are observed by varying the waiting time T between pulses 2 and 3. The resulting four-wave mixing signal in the 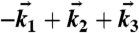wave vector phase-matching direction is dispersed at a spectrometer and is heterodyne-detected on a CCD using an attenuated pulse 4 as a local oscillator (LO). The coherence time is sampled from -528 fs to +528 fs in 5.5 fs steps, and the resulting interferograms are combined and Fourier transformed in τ in order to generate a 2D spectrum for a particular waiting time. Spectra are plotted as a function of excitation frequency ω_τ and emission frequency ω_t, conjugate variables to the coherence time τ and the rephasing time t (the delay between pulse 3 and the arrival of the signal). See ref. 30 for further details. For all of the data presented in this work, a broadband half-wave retarder (Meadowlark) is inserted into each of the four beam paths in order to adjust the relative polarization of the pulses. For each polarization sequence, the retarders are rotated and their tilt is readjusted to reoptimize the spatial overlap of all four pulses on the sample. In addition to measuring polarized spectra (see below) a spectrum for which all of the light pulse fields are parallel is measured and phased by fitting to spectrally resolved pump-probe data according to the projection slice theorem (11). The phasing removes the arbitrariness in phase between each of the phase-locked pulse pairs (1–2 and 3–4) and ensures that the absorptive (real) contribution to the spectrum may be isolated. Zeroth and first order phase terms, e^{iϕ₀+iω_tΔt}, were used in the fit, where ϕ₀ represents an overall phase and Δt is a few femtosecond correction to the measured time delay between pulse 3 and the LO (∼1 ps).

Recording, Phasing, and Normalizing Basis Set Spectra.

The strategy developed here to study EET in CP29 resolves normalization issues by recording the polarized 2D spectra associated with the only three independent polarization tensor components for an isotropic system: S_zzyy, S_zyzy, and S_zyyz. We determine the appropriate complex normalization coefficients for each of these spectra by fitting the three spectra’s sum to the phased parallel 2D spectrum using the tensor relation that relates the orthonormal basis set sequences to one another,

[1]

We denote the raw, complex-valued spectra by ZZYY, ZYZY, and ZYYZ and their respective complex coefficients that must be determined as C_ZZYY, C_ZYZY, and C_ZYYZ so that Eq. 1 is satisfied at all coordinates (ω_τ,ω_t) by

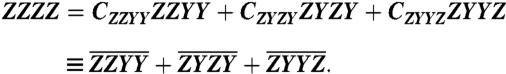[2]

The optimal coefficients are determined by obtaining the sum of the least-squares fits of the real (absorptive) and imaginary (dispersive) parts of Eq. 2 in quadrature, thus maximizing the number of features and constraints used in the fit and utilizing all available information within a desired 2D region of interest. The form used for each complex coefficient is (L + iM) × e^iω_tN, {L,M,N}∈ℜ, where N affords a higher order phase adjustment, analogous to that used in the phasing of ZZZZ. At each iteration, the least-squares fit to Eq. 2 is initiated several hundred times for a given coefficient, e.g., C_ZZYY, with randomly generated L, M, N values that fall within a particular range about the previous iteration’s optimal least-squares parameters. When treating longer waiting times that should be devoid of excitonic coherence effects, the 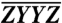and spectra should be identical, imposing an additional constraint. Thus, the fit to the 3.6 ps spectra used here can be further simplified. Once the relative amplitude and phase of the measured, polarized orthonormal basis spectra are known, they may be combined with different weightings in order to generate any arbitrary polarized spectrum (13, 15, 16, 31) or, as we also demonstrate, compared to determine relative pigment transition dipole moment orientation.