Grazer cues induce stealth behavior in marine dinoflagellates

Abstract

Chain formation is common among phytoplankton organisms but the underlying reasons and consequences are poorly understood. Here we show that chain formation is strongly impaired by waterborne cues from copepod grazers in the dinoflagellate Alexandrium tamarense. Chains of Alexandrium cells exposed to copepod cues responded by splitting into single cells or shorter chains. Motion analysis revealed significantly lower swimming velocities for single cells compared with chains, with two- to fivefold higher simulated predator encounter rates for two- and four-cell chains, respectively. In addition, the few remaining two-cell chains in grazed treatments were swimming at approximately half the speed of two-cell chains in treatments without grazers, which reduced encounter rates with grazers to values similar to that of single cells. Chain length plasticity and swimming behavior constitute unique mechanisms to reduce encounters with grazers. We argue that dinoflagellates can regulate the balance between motility and predator avoidance by adjusting chain length. The high predator encounter rate for motile chains may have contributed to the low prevalence of chain formation in motile phytoplankton compared with in nonmotile phytoplankton where chain formation is more common.

Oceanic primary producers contribute ~50% of the global carbon dioxide fixation and have profound effects on biogeochemical cycles (1), yet our understanding of their functional morphology is still rudimentary. As an example, chain formation is common mainly among nonmotile groups of marine phytoplankton, e.g., diatoms and cyanobacteria, but less common in motile groups like dinoflagellates. The ultimate reasons for chain formation are poorly understood and several alternative explanations have been proposed (2). Chains and colonies have been suggested to provide lower sinking rates, allowing nonmotile phytoplankters to remain in surface waters, although this result has little theoretical and experimental support (3). Size changes dramatically with chain and colony formation, allowing both motile and nonmotile phytoplankton organisms to enter size-limited grazer refuges. For example, a large Phaeocystis colony has a diameter of >10² times the diameter of a single cell. With the exception of parasites and pathogens, pelagic consumers are typically not able to feed on such a large size range of prey (4). Thus, it is likely that size selective grazing contributed to the evolution of size and colony formation in phytoplankton organisms (5). This relationship is further supported by the ability of Phaeocystis globosa and Scenedesmus subspicatus to sense and respond to grazer presence by forming colonies larger than the capture size of the inducing grazer (6, 7) or by breaking up colonies into sizes too small to be retained (8). Moreover, chain length correlates to growth rate in some diatoms and dinoflagellates (9, 10), suggesting that chain length may also depend on growth conditions. Finally, chains of dinoflagellates typically swim 40–60% faster than single cells, which has been suggested to enhance their ability to migrate vertically to collect nutrients at depth and harvest light at the surface (11) and to maintain depth in the face of turbulence (12–14).

Increased size and swimming velocity associated with chain formation, however, also leads to higher encounter rates with predators, and organisms must balance resource acquisition with the risk of predation (15). The encounter rate between a swimming dinoflagellate and an ambush-feeding predator scales with the swimming velocity and the square of the distance at which the cells can be perceived and attacked (16). Thus, chain formation is likely to result in an increased encounter rate with grazers, both due to the higher swimming velocity and due to an increased detection distance caused by increased hydrodynamic signal of larger and faster units (17).

Here we demonstrate in incubation experiments and through measurements of swimming velocities that a chain-forming motile dinoflagellate, Alexandrium tamarense, reduces its chain length and swimming velocity in response to waterborne grazer cues and that this response implies a substantially reduced risk of being eaten by a zooplankton grazer.

Results

Effect of Grazers on Chain Length.

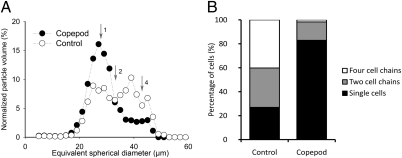
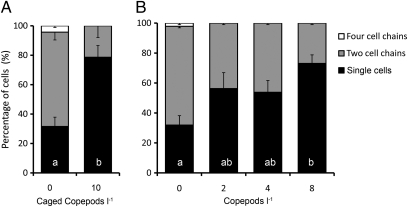
A. tamarense exposed to copepod grazers responded by splitting up chains into single cells and had a significantly lower proportion of cells in chains (P < 0.05) relative to that of control cultures (Fig. 1). Four-cell chains were common in the ungrazed treatment but observed only once in the grazed treatment. The concentration of cells (solitary or in chains) was reduced by <15% in the grazed treatment, showing that the reduction in chain length was not the result of grazing. This result was confirmed by a similar response in chain length in experiments where phytoplankton was exposed to copepods placed in plankton mesh (15-μm) cages (Fig. 2A) and demonstrates that the response was triggered by waterborne cues from the copepod grazers and not from physical contact with grazers. Alexandrium cultures exposed to copepod densities ranging from zero to eight copepods per liter revealed a density-dependent response with the highest proportion of single cells observed together with the highest number of grazers (Fig. 2B), corresponding to the upper range of naturally occurring copepod densities.

Fig. 1.

(A) Size distribution histograms of A. tamarense cultures grown with (solid symbols) and without copepod grazers (open symbols). The larger size of control cells is mainly caused by the higher prevalence of two- and four-cell chains compared with grazed treatments. The equivalent spherical diameters of one-, two-, and four-cell units are indicated by the numbered arrows. (B) The relative abundance of single cells and two- and four-cell chains from video observations of the same experiment.

Fig. 2.

(A and B) Fraction of cells as single cells and two- and four-cell chains. (A) Control Alexandrium cultures and cultures exposed to waterborne cues from caged copepods. Bars denote mean values of four replicates ± SE of mean. Letters denote statistically different groups based on Student's t test (P < 0.05). (B) Alexandrium cultures exposed to zero, two, four, or eight copepods per liter without cages. Bars show mean values of three replicates and error bars show SE of mean. Letters denote statistically homogenous subsets according to the Student-Newman-Keuls post hoc procedure (P < 0.05).

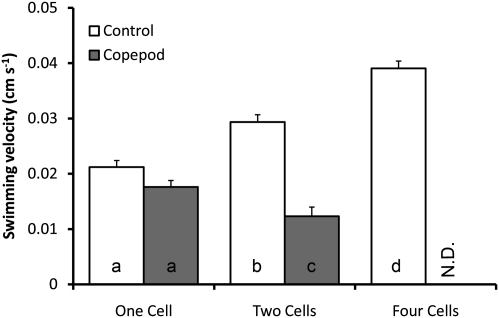
Motion analysis revealed higher swimming speed for chains in control treatments. Four-cell chains swam close to twice as fast as single cells and 33% faster than two-cell chains. Further, in grazed treatments, two-cell chains swam significantly slower compared with two-cell chains in control treatments (P < 0.05) and even slower than single cells in control containers (P < 0.05, Fig. 3 and Table 1), whereas single cells were swimming at a similar speed compared with control single cells (P = 0.10).

Fig. 3.

Swimming velocity of single cells and two- and four-cell chains in grazed and control treatments. Only one single four-cell chain was observed in the grazed treatment, and it is not included in the analysis (shown as N.D. in the graph). Bars show mean values + SE of mean based on the number of observations (Table 1). Letters indicate statistically homogenous subsets according to the Student-Newman-Keuls post hoc procedure (P < 0.05).

Table 1.

Motion analysis results from single cells and chains in control and grazed treatments

Treatment	Length, cells	ESD, μm	Velocity, μm·s−1, mean ± SE	Observations, tracks	Decorrelation time, τ, s, mean ± SE
Control	1	28	212 ± 12	23	1.3 ± 0.01
	2	34	294 ± 13	23	1.1 ± 0.02
	4	44	391 ± 13	24	2.0 ± 0.04
Grazed	1	28	176 ± 12	23	1.2 ± 0.02
	2	34	123 ± 17	7	1.7 ± 0.03
	4	44	—	—	—

Four-cell chains were observed only once in the grazed treatment and are not included.

The directional persistence of swimming cells, quantified by the decorrelation timescale (τ), was comparable between treatments (Table 1) and showed no consistent pattern between grazed and nongrazed treatments.

Discussion

The present study shows a unique mechanism for chain-forming motile cells to reduce their encounter rate with grazers. By separating chains into single cells, Alexandrium cells instantly reduce the risk of encountering consumers due to the lower velocity and reduced hydrodynamical signal generated by single cells. Reduction in predator encounters by chain-length plasticity in motile cells is different from previous reports of grazer-induced colony size plasticity (6–8) as these rely on creating a mismatch between the food retention size spectrum of the grazer rather than reducing the encounter rate with consumers. In contrast, both single cells and chains of A. tamarense are within the optimal prey size range of the copepod grazer used here (18).

We may calculate the effect on predator encounter rate by reduced chain-length and swimming velocity by noting that the volumetric encounter rate (clearance) between predators and Alexandrium cells (Eq. 1) is governed by the swimming velocities (v) of predator and prey and the reaction distance (R) at which A. tamarense cells or chains can be detected and attacked (16, 19):

v_prey is given from the motion analysis (Table 1). Rheotactic predators perceive motile prey by the hydrodynamic signal that the swimming prey generates, and the signal strength is proportional to the imposed fluid velocity (20). The reaction distance (R) can be approximated by describing the self-propelled cell as a dipole, for which the imposed fluid velocity scales with the prey velocity and size squared and attenuates with the distance squared (17, 21, 22). Hence, to first order

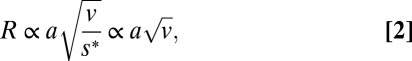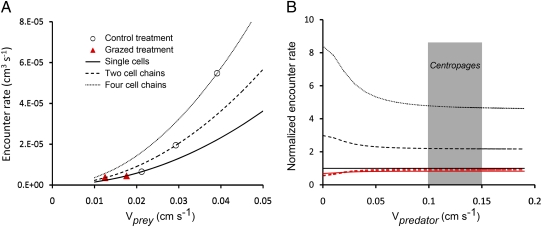
where a is the equivalent spherical radius (ESR) of the cell or chain and v is the swimming velocity. s* is the fluid velocity threshold signal strength for prey detection. Quantifying organism size by ESR does not account for the different shapes of chains and single cells and could potentially overestimate the reaction distance. However, Lewis and coworkers (13) showed that drag calculated from ESR deviated <3% from the drag calculated from Stimson and Jefrey's (23) analytical solutions for the motion of two attached spheres in viscous fluid, suggesting that ESR can be used as an approximation for our purpose. If we initially consider the simplest case of an ambush-feeding predator (v_predator = 0), the relative reaction distances and experimentally determined swimming velocities and size for single cells and chains result in 8.4 and 3.0 times higher volumetric encounter rates for four- and two-cell chains compared with single cells (Eq. 1 and Fig. 4A). Even the few two-cell chains in the grazed treatments are cleared at a rate comparable to single cells in control treatment because their larger size is compensated by their lower swimming velocity (Fig. 4). Two-cell chains were, however, scarce in the grazed treatment and it is possible that they represent recently divided cells that had not yet had time to regain speed after division or to part into single cells, rather than a behavioral response to copepod cues.

Fig. 4.

(A) Effect of chain formation and swimming speed on encounter rate (maximal clearance) with an ambush predator (v_predator = 0, Eq. 1). Values for single cells and chains from the ungrazed control (open circles) and the grazed treatment (red triangles) are shown. (B) The effect of predator velocity on encounter rates for single cells and chains (Eq. 1) from control (black) and grazed (red) treatments normalized to the encounter rate of single cells in the control treatment for comparison. The difference in encounter rate is highest for ambush predators where v_predator = 0 and decreases with increasing predator velocity toward the difference solely driven by the difference in reaction distance, i.e., 2.2 and 4.6 times higher for two- and four-cell chains, respectively, compared with single cells. Typical swimming velocities for the copepod predator used here are indicated by the shaded box labeled Centropages (45).

If we instead consider a moving predator, dinoflagellate velocity will become less important as predator velocity increase and the difference in encounter rate will approach the difference solely driven by the longer reaction distances (R) to chains, i.e., 2.2 and 4.6 times higher for two- and four-cell chains, respectively (Eq. 1 and Fig. 4B). This reasoning holds for rheotactic predators detecting prey by hydrodynamical signals. For grazers using chemical prey detection, such as many copepods (24), the reaction distance will also increase with chain length, simply because more cells leak more chemical signals. For moving and nonmoving cells the enhancement is proportional to the leakage rate and, hence to the number of cells in the chain (25, 26). For grazers with a feeding current the effect may be of similar magnitude, although the exact effect is difficult to predict. Volumetric encounter rates may thus increase by a factor of up to 4² in four-cell chains compared with single cells (Eq. 1). The density dependence experiment (Fig. 2B) suggests that the response is well tuned to the naturally occurring densities of copepod grazers and that the proportion of single cells depends directly on the density of copepods grazers. It is possible that the reactions would have been more pronounced if the dinoflagellates were introduced to water already tainted by copepods because copepod cues would not have to build up during the first part of the experiments. If copepods are removed, the dinoflagellates need time to undergo one to two divisions to recover chain length as chains are formed by daughter cells staying attached after division.

The observed swimming velocities for single cells and chains in the control treatment are in good agreement with previous observations of swimming behavior in chain-forming dinoflagellates. Fraga and coworkers (12) reported a 50–60% increase in swimming velocity for four-cell chains compared with single cells for Alexandrium affine and Gymnodinium catenatum, slightly less than the 84% observed here. Lewis and coworkers (13) found 45% higher swimming velocity for two-cell chains of A. tamarense compared with single cells, similar to the 38% observed in the present study.

Whereas the above considerations suggest that there are fitness benefits associated with reduced swimming velocity (lower predation risk), one may ask what the costs and benefits of elevated swimming speeds are in predator-free environments. The energetic cost of swimming at low Reynolds numbers is generally low (27) and the higher swimming velocity of chains may result mainly from the changed ratio between propulsion and drag forces (12). The difference in velocity between single cells and chains is actually less than predicted from propulsion to drag force calculations (12), suggesting that the higher velocity of chains comes for free or even at a reduced cost. Sperms from the wood mouse similarly gain higher path velocity by forming cooperative “trains” (28). Cells in chains may, however, experience increased competition from adjacent cells when nutrients are limiting. Assuming self-propelled spherical cells, using observed swimming velocities and cell chain sizes, and applying the numerical advection-diffusion model of Langlois et al. (26), we find that the specific transport-limited nutrient uptake may decrease by 13% in two-cell chains and by 45% in four-cell chains relative to solitary cells. The reduced nutrient uptake of cells in chains is relaxed because chains are elongated, whereas solitary cells are near spherical. In a patchy environment, however, most of the nutrient uptake may occur while cells are inside nutrient patches and nutrient uptake is not transport limited. A. tamarense cells perform nocturnal vertical migrations at speeds of up to 2 m·h⁻¹ and an amplitude of ~10 m to retrieve nutrients from depth (29), a strategy that appears critical to the survival of many dinoflagellates in nutrient-limited environments (11). On the basis of the swimming speeds from the current experiment, single cells would not be able to complete such migrations in 24 h, whereas chains would, provided that they are able to maintain directional swimming during migrations. The benefits of vertical migration have been calculated to greatly exceed the costs (30), suggesting that there is a trade-off between nutrient acquisition and grazer avoidance in chain-forming dinoflagellates and that the dinoflagellates can use grazer-induced chain-length plasticity to adjust the balance between the two. Experimental evidence that chains actually benefit from their higher velocity is, however, still lacking.

Grazing pressure on phytoplankton is extremely high (31) and large motile cells have to compensate for their motility-dependent higher encounter rates with grazers. They can do so either by higher growth rates, which is typically not the case for large dinoflagellates (32), or by avoiding grazers by other means. Escape responses is one such mechanism that occurs among motile dinoflagellates (33). The production of poisonous secondary metabolites appears particularly common among large chain-forming dinoflagellates (35–38), and the compounds have been associated with negative or feeding-deterrent effects on copepod grazers, although the underlying mechanism for this result is not clear (39, 40). The current study has demonstrated another mechanism to counteract grazers, i.e., chain splitting in response to the presence of grazers. These observations all conform to the “apparent plant hypothesis,” originally put forward to explain the allocation of resources to defense in terrestrial plants (41). According to its predictions, plants that are apparent in time and space are more likely to attract herbivores and should be better defended compared with less apparent plants. The higher encounter rate of large dinoflagellates and chain-forming species in particular renders them apparent to grazers and suggests that this encounter rate might have contributed to the evolution of predator avoidance strategies and toxin production in large and/or chain-forming dinoflagellates.

The grazer-induced breakup of chains into single cells allows chain-forming dinoflagellates to enter a “stealth mode” in response to grazer cues and reduce encounter rates severalfold. Grazer-induced chain length plasticity constitutes a unique mechanism for motile chain-forming phytoplankton to adjust their encounter rates with grazers to the prevailing grazing pressure. The almost double velocity of four-cell chains compared with single cells suggests that there may be a trade-off between motility and predator avoidance in chain-forming dinoflagellates and that balance between the two can be adjusted through grazer-induced chain length plasticity. A higher encounter rate of chains constitutes a strong obstacle for the evolution of chain formation in motile phytoplankton cells that is likely to have contributed to the low prevalence of chain formation in motile phytoplankton organisms.

Materials and Methods

Organisms and Conditions.

Two strains of A. tamarense [nos. 1 and 3, University of Gothenburg (Gothenburg, Sweden) Marine Culture collection–GUMACC isolated on the Swedish west coast in 2008 were used. A. tamarense cultures typically contain a mixture of single cells and two- and four-cell chains. Cultures were reared in K medium (34) at 16 C°, ~100 fmol m⁻²·s⁻¹, and 16:8 h light:dark cycles. Experiments were performed in the same conditions but in diluted (K/10) medium to avoid artifacts from extreme nutrient concentrations (42).

Conditioning of Cultures for Motion Analysis.

A well-mixed culture of A. tamarense no. 1 was divided between two glass flasks, 100 mL each. One of the flasks received a single adult of Centropages typicus, hereafter referred to as the grazed treatment, whereas the other was kept as a control. After 5 d, the size distribution of Alexandrium with and without grazers was determined (Multisizer III; Beckman and Coulter). The size distributions of single cells and two- and four-cell chains overlap, and the frequency of cells present in different chain lengths was obtained from the video recordings (described below) by counting the number of one-, two-, and four-cell units in the focal plane until >200 cells had been assigned from each treatment. The equivalent spherical radius used to calculate reaction distance in encounter rate models was extracted from Coulter Counter volume estimates of single cells.

Cage Experiment.

To test whether the increase in single cells in grazer-exposed cultures was caused by physical interactions with grazers or whether it was triggered by chemical cues from the copepods, we deployed caged copepods in 100-mL glass flasks. Flasks received 70 mL A. tamarense no. 3 culture (608 ± 18 cells·mL⁻¹) and cages 30 mL A. tamarense no. 3 culture (control) or 30 mL A. tamarense no. 3 together with a single adult C. typicus (copepod). The caged copepods and the responding Alexandrium cells in the flasks were separated by a 15-μm heat-sealed plankton mesh, which confined Alexandrium cells and copepods to their original compartments, but allowed dissolved cues to move freely between compartments. To facilitate the water exchange between the inside and the outside of cages, and thereby the exposure to copepod cues, the cages were gently lifted up and down three to five times a day in all treatments. After 6 d, a 1-mL sample was gently transferred to multidish wells, and the distribution between single cells and chains was determined as described above.

Density Experiment.

Triplicate bottles containing 500 mL A. tamarense no. 3, 247 ± 4 cells·mL⁻¹ (mean ± SE), were supplied with zero, one, two, or four adult Centropages to mimic naturally occurring densities of copepod grazers. After 7 d of incubation 2.5-mL samples were gently transferred to multidishes and the distribution between single cells and chains was determined for >100 cells per replicate.

Motion Analysis.

Video recordings were performed in a temperature-controlled room at 16 °C and with light from fluorescent tubes in the ceiling. The conditioned Alexandrium no. 1 cells were transferred into 50-mL cell culture flasks (Nunc) and left in the thermo-constant room for at least 2 h before experiments. A light-emitting diode was placed on the opposite side of the aquarium to provide maximum contrast. The diode was positioned in the focal point of a Fresnel lens (diameter 16 cm), creating parallel (collimated) light beams through the experimental aquarium. Video recordings were obtained with a monochrome analog CCD video camera (Minitron MTV-1802CD; Minitron Enterprise Co.) fitted with a 105-mm mikro nikkor lense, resulting in a vertical view field of ~9 × 5 mm. Video recordings were extracted into image stacks, inverted, and contrast enhanced (VirtualDub). The swimming behavior of dinoflagellates was analyzed using a MatLab algorithm that returned the positions, velocity, and net and gross displacement over time for individual cells or chains every 0.12 or 0.24 s. Trajectories averaged 14 ± 6.5 s (mean ± SD) in length. Convection was slow compared with the swimming velocity of Alexandrium cells, and tracks of single cells and chains from each treatment were obtained from the same video sequences, assuming that any contribution of convection would cancel out in the comparison between chains and single cells. Four-cell chains were observed only once in the grazed treatment recording and therefore not included in motion analysis. 3D swimming speeds were calculated by multiplying by , thus assuming that the cells on average were swimming istotopically in all directions. Highly convoluted swimming patterns may reduce encounter rates significantly (43). To control for any major changes in the rate of change of direction we estimated the decorrelation timescale (τ) as a measure of directional persistence from curve fits to Taylor's formula for diffusion by continuous movement (44) to plots of root mean square displacement over time (t):

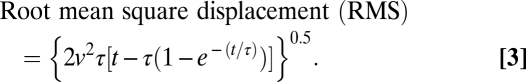Statistical Analysis.

The proportion of cells present in chains in grazed and nongrazed treatments for motion analysis was compared with a χ²-test using the control distribution as the expected frequency. The percentage of cells present in chains in the cage experiment was compared with Student's t test for two samples assuming equal variances. A single-factor ANOVA was used to evaluate the effect of grazer density. The effect of chain formation and grazer presence on swimming velocity was compared using a two-factor ANOVA, with the factors “grazer presence” (two levels: present and absent) and chain formation (three levels: single cells, two-cell chains, and four-cell chains) as fixed factors. The average velocity from each trajectory was used in the analysis. The Student–Newman–Keuls post hoc procedure was used to identify statistically homogenous subsets when ANOVA indicated significant effects.