Evaluation of a wave-vector-frequency-domain method for nonlinear wave propagation

Abstract

A wave-vector-frequency-domain method is presented to describe one-directional forward or backward acoustic wave propagation in a nonlinear homogeneous medium. Starting from a frequency-domain representation of the second-order nonlinear acoustic wave equation, an implicit solution for the nonlinear term is proposed by employing the Green’s function. Its approximation, which is more suitable for numerical implementation, is used. An error study is carried out to test the efficiency of the model by comparing the results with the Fubini solution. It is shown that the error grows as the propagation distance and step-size increase. However, for the specific case tested, even at a step size as large as one wavelength, sufficient accuracy for plane-wave propagation is observed. A two-dimensional steered transducer problem is explored to verify the nonlinear acoustic field directional independence of the model. A three-dimensional single-element transducer problem is solved to verify the forward model by comparing it with an existing nonlinear wave propagation code. Finally, backward-projection behavior is examined. The sound field over a plane in an absorptive medium is backward projected to the source and compared with the initial field, where good agreement is observed.

INTRODUCTION

Planar-projection methods calculate an acoustic field at arbitrary points in space or time, given the field distribution at some initial plane.1^,2 Such methods use a transfer function, or a series of transfer functions, that operate in Fourier space. These approaches are computationally advantageous compared to space–time methods,3 as they represent the wave equation in the form of an ordinary differential equation (ODE) as opposed to its partial differential (PDE) form in space–time. If the medium is linear and homogeneous, the ODE will have a known solution,1 and a projection to any new plane requires only a single operation. In heterogeneous media, an exact solution cannot be described. However, the reduction of the wave equation from a PDE to an ODE still represents a significant numeric simplification as well as relatively straightforward implementation.4 For instance, planar projection has been applied to multi-layer media and is able to account for refraction and single reflections.5

While most planar approaches are linear, nonlinear techniques have been investigated and utilized. Christopher and Parker5 performed projections by a modified angular spectrum approach (ASA) using applications of Burgers equation in the time domain. Subsequently, a variety of Burgers equation-modified ASA simulations have been reported.4^,6 ASA solutions of the Westervelt equation7^,8 have also been studied.9 While commonly used modeling approaches apply the KZK (Khokhlov–Zabolotskaya–Kuznetsov) equation10^,11 to solve for the nonlinear sound field, the Westervelt equation can potentially be more accurate in determining the field, since it does not rely on a parabolic approximation.12^,13 In general, ASA-based approaches solving the Westervelt equation can be computationally appealing especially when parabolic approximation breaks, and the frequency and angular spectrums are narrow. For example, in weakly nonlinear continuous wave cases, frequency space can be reduced to as little as the fundamental frequency and the second harmonic, and they are projected separately.14^,15 Additionally, pre-selection of a reduced region of k-space can allow a specific portion of a propagating field—typically the forward propagating wave—to be studied.

While most available forward nonlinear wave approaches assume the main nonlinear distortion in the direction normal to the source plane,5^,6 only a few works in the literature have proposed methods that are “omni-directional” in terms of the nonlinear acoustic field.16 This ability to consider nonlinear distortion in a direction other than normal to the source plane is especially advantageous when a strongly focused or steered transducer is to be modeled. The approach introduced in this paper embraces this ability as it essentially avoids using a plane-wave solution. More importantly, it will be demonstrated that in the frequency-domain representation of the Westervelt equation, convolutions in the vector space emerge. This is essential, as it automatically considers the interaction of all waves propagating in every direction, which is a novel point in this paper. This may prove particularly useful for strongly focused sources or sources with sharp edges, i.e., with broadband spatial spectrum.

The frequency-domain formulation also allows straightforward treatment of general dispersion cases,17^,18 which can have complicated representation in the space–time domain.19, 20, 21 Variations in the time-domain approach center on efficient methods to model the solutions.22, 23, 24, 25 On the other hand, the general case of anomalous dispersion can be handled with relative ease in wave-vector space.26 A relevant medical example of anomalous dispersion is trabecular bone. In contrast to most biologic tissues, phase velocity in trabecular bone tends to decrease with frequency.27 The present work indicates how the nonlinear frequency-domain wave equation can be further transformed into the wave-vector-frequency domain, where it has a known solution. It will be shown that this solution can be used for planar projection and is valid under arbitrary dispersion conditions.

The present study also considers yet another potential advantage of the method: The ability to propagate a nonlinear signal backward toward the source in absorptive media. In this manner a field measured away from a transducer could be used to predict field behavior closer to the radiator. Alternatively, a desired field could be synthetically generated and then projected backward to provide information on the requirement of the radiational and dimensional requirements of the source. The process requires the time history of a sound field over a given spatial plane as well the acoustic properties of the propagation medium. Successfully implemented, this approach could provide data to predict the acoustic field, including harmonic and low frequency portions of the signal at any point in space.

To demonstrate the approach, we develop a general algorithm, which is then used to model the specific case of the Westervelt equation. This algorithm is first verified by comparing results with analytic solutions for a plane wave. Meanwhile, a method for more efficient implementation is considered by maximizing the algorithm step size. We test whether propagation steps in the order of the fundamental wavelength are possible, as opposed to the 10–20 steps per wavelength required in finite-difference time-domain or finite element methods.3 The optimal step size for a given problem is found by a study that measures error as a function of step size and propagation distance. A two-dimensional (2-D) steered transducer is then studied to demonstrate the directional independence of this approach when calculating the nonlinear acoustic field. Furthermore, a three-dimensional (3-D) focused transducer problem is studied for verification of the forward model. The present method is compared with an existing nonlinear angular spectrum wave propagation code28 for the case of a Gaussian-modulated sinusoidal pulse. Finally, the accuracy of the algorithm is tested by implementing the backward model in absorptive media, and it is shown that the backward projected field agrees well with the initial signal.

THEORY

Field calculations will be performed using a propagation algorithm that operates in both the temporal and spatial frequency domains. Although a number of temporal frequency-domain nonlinear algorithms have been reported,17^,18 the present approach is unique in that it also solves the nonlinear term in the spatial frequency domain. In this way, the interaction of waves in all directions (all wave vectors) are included automatically in the solution, not only in one direction of propagation k_z as in previously used KZK or one-direction Westervelt equation models,5^,6 which is expected to be advantageous for strongly focused transducers or sources with broadband spatial spectra.

Although the frequency-domain equation is more general, it is instructive to start with the time-domain Westervelt equation in a homogeneous medium for the purpose of comparison. The equation assumes a thermo-viscous medium and is given by

$${\nabla }^{2}p(\mathbf{r},t)-\frac{1}{c_0^2}\frac{{\partial }^2}{\partial t^2}p(\mathbf{r},t)+\frac{\delta }{c_0^4}\frac{{\partial }^3}{\partial t^3}p(\mathbf{r},t)+\frac{\beta }{{\rho }_0{c}_0^4}\frac{{\partial }^2}{\partial t^2}{p}^2(\mathbf{r},t)=0$$ (1)

where p is the sound pressure, c₀ is the sound speed, δ is the sound diffusivity, β is the nonlinearity coefficient, and ρ₀ is the ambient density. We note that the solution to the Westervelt equation describes an approximation of quasi-plane waves, and is valid for directional sound beams once the propagation distance becomes much larger than a wavelength.11

By Fourier solution of the temporal dimension, as well as the Cartesian x- and y-dimensions, Eq. 1 is transformed from a PDE to an ODE,29

$$\frac{{\partial }^2}{\partial z^2}P(k_x,k_y,z,\omega )+K^{2}P(k_x,k_y,z,\omega )-\frac{\beta {\omega }^2}{{\rho }_0{c}_0^4}P(k_x,k_y,z,\omega )\otimes P(k_x,k_y,z,\omega )=0,$$ (2)

where

$$P(k_x,k_y,z,\omega )={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }p(\mathbf{r},t)e^{-i(k_{x}x+k_{y}y-\omega t)}dxdydt,$$ (3)

$$\begin{array}{l}P(k_x,k_y,z,\omega )\otimes P(k_x,k_y,z,\omega )\\ ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P(k_x\prime ,k_y\prime ,z,\omega \prime )P(k_x-k_x\prime ,k_y-k_y\prime ,z,\omega -\omega \prime )d{k}_x\prime d{k}_y\prime d\omega \prime ,\end{array}$$ (4)

$$K^2=\frac{{\omega }^2}{c_0^2}-k_x^2-k_y^2-i\frac{\delta {\omega }^3}{c_0^4}$$ (5)

and ω is the angular frequency, k_x and k_y are the wave numbers, and the convolution in Eq. 2 is with respect to k_x, k_y, and ω. K is defined as $k=+\sqrt{\left(k^2\right)}$ for ω < 0 and $k=+\sqrt{\left(k^2\right)}$ for ω > 0. As noted above, although Eq. 2 was derived from the Westervelt equation, in fact it is much more general, since the dispersion relation, i.e., Eq. 5, can readily be replaced by an arbitrary relation. The 3-D auto-convolution resulting from the nonlinear term in Eq. 1 serves the role of temporal frequency mixing, transferring energy both into and out of the higher components of the frequency spectrum. It also transfers energy between spatial frequencies, so that the interaction between wave propagation in different directions is accounted. Although calculation of this convolution is the most computationally demanding part of the present algorithm, it nevertheless could be made relatively efficient using fast Fourier transforms in combination with an optimization strategy.16 Presently, however, only the fast Fourier transforms are used to accelerate the convolution.

The solution of Eq. 2 can be derived by using the one-dimensional (1-D) Green’s function30 and is written as (derivations can be found in Appendix A)

$$\begin{array}{l}P(z)=P(0)e^{iKz}+\frac{M{e}^{-iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)-\\ \frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime +\frac{M{e}^{iKz}}{2iK}\left[\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime -\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \right].\end{array}$$ (6)

where

$$M=\frac{\beta {\omega }^2}{{\rho }_0{c}_0^4}\text{and}F\left(P(z\prime )\right)=P(k_x,k_y,z\prime ,\omega )\otimes P(k_x,k_y,z\prime ,\omega ).$$

This solution is implicit because of the unknown function F inside the integral. It is also not suitable for numerical implementation because of the integral from z to +∞. However, it will be shown below that, at least for a weakly nonlinear case,

$$\begin{array}{l}\left|\frac{M{e}^{-iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)-\frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime -\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \right|\\ \\ =\left|\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime \right|,\end{array}$$ (7)

so that Eq. 6 can be simplified to

$$P(z)=P(0)e^{iKz}+\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime .$$ (8)

This approximated solution, i.e., Eq. 8, will be used throughout the paper. Numerical results presented below will demonstrate that this approximation is valid even in strongly nonlinear cases.

To further simplify the problem, validation is performed for a continuous wave, which can more readily be verified against other methods. However, this procedure generalizes to transient cases. Moreover, though only results at the second harmonic are shown here, similar equations can be derived for any harmonic. A third harmonic example is shown in Appendix B. The advantage of considering a weakly nonlinear case is that it allows P(z^′) at the fundamental frequency to be substituted by its linear representation P(0)exp(iKz^′), while introducing only negligible errors. To proceed, it is assumed that the attenuation is larger than zero [im(K) > 0, so the integration to +∞ converges] but is sufficiently small so that it can be neglected in the derivation below for simplification. For the second harmonics, the left hand side of Eq. 7 reads

$$\begin{array}{l}\frac{M_2{e}^{-i{K}_{2}z}}{2i{K}_2}\underset{z}{\overset{+\infty }{\int }}{e}^{i{K}_{2}z\prime }F\left(P(z\prime )\right)dz\prime -\frac{M_2{e}^{i{K}_{2}z}}{2i{K}_2}\underset{z}{\overset{+\infty }{\int }}{e}^{i{K}_{2}z\prime }F\left(P(z\prime )\right)dz\prime -\frac{M_2{e}^{i{K}_{2}z}}{2i{K}_2}\underset{0}{\overset{z}{\int }}{e}^{i{K}_{2}z\prime }F\left(P(z\prime )\right)dz\prime \\ \approx \frac{M_2(e^{-i{K}_{2}z}-e^{i{K}_{2}z})}{2i{K}_2}\int P(0,\tilde{K}\prime )P(0,K\prime -\tilde{K}\prime )\underset{z}{\overset{+\infty }{\int }}{e}^{i(K_a+K_b+K_2)z\prime }dz\prime d\tilde{K}\prime \\ -\frac{M_2{e}^{i{K}_{2}z}}{2i{K}_2}\int P(0,\tilde{K}\prime )P(0,K\prime -\tilde{K}\prime )\underset{0}{\overset{z}{\int }}{e}^{i(K_a+K_b+K_2)z\prime }dz\prime d{\tilde{K}}^{\prime }\\ =\frac{M_2{e}^{i{K}_{2}z}}{2K_2}\int \frac{e^{i(K_a+K_b-K_2)z}-1}{K_a+K_b+K_2}P(0,\tilde{K}\prime )P(0,K\prime -\tilde{K}\prime )d\tilde{K}\prime \end{array}$$ (9)

where

$$\begin{array}{l}{K}_a=\sqrt{{\left(\frac{{\omega }_1}{c_0}\right)}^2-{\left|{\tilde{K}}^{\prime }\right|}^2},K_b=\sqrt{{\left(\frac{{\omega }_1}{c_0}\right)}^2-{\left|K\prime -{\tilde{K}}^{\prime }\right|}^2},\\ K_2=\sqrt{{\left(\frac{{\omega }_2}{c_0}\right)}^2-{\left|K\prime \right|}^2},M_2=\frac{\beta {\omega }_2^2}{{\rho }_0{c}_0^4},\end{array}$$ (10)

and ω₁ and ω₂ are the negative angular frequencies for the fundamental and second harmonics, respectively. Similarly, the right hand side of Eq. 7 yields

$$\begin{array}{l}\frac{M_2{e}^{i{K}_{2}z}}{2i{K}_2}\left[\underset{0}{\overset{z}{\int }}{e}^{-i{K}_{2}z\prime }F\left(P(z\prime )\right)dz\prime \right]\\ \approx -\frac{M_2{e}^{i{K}_{2}z}}{2K_2}\int \frac{e^{i(K_a+K_b-K_2)z}-1}{(K_a+K_b-K_2)}P(0,\tilde{K}\prime )P(0,K\prime -\tilde{K}\prime )d\tilde{K}\prime .\end{array}$$ (11)

The total solution for the second harmonic [Eq. 9 + Eq. 11] is

$$P(z)=\frac{4\beta k_1^2}{{\rho }_0{c}_0^2}\int \frac{e^{i(K_a+K_b)z}-e^{i{K}_{2}z}}{K_2^2-{(K_a+K_b)}^2}P(0,\tilde{K}\prime )P(0,K\prime -\tilde{K}\prime )d\tilde{K}\prime ,$$ (12)

where $k_1=\frac{{\omega }_1}{c_0}$

It is noted that this solution differs from the solution in Ref. 14 by a factor of $\frac{1}{2}$. This is because presently both negative and positive frequencies are used, so the energy is split into half to both frequencies, and this factor of $\frac{1}{2}$ produces a factor of $\frac{1}{4}$ inside the integral of Eq. 12, i.e., $P(0,\tilde{K}\prime )P(0,K\prime -\tilde{K}\prime )$ In addition, the above section only discusses the case where the angular frequency is ω₂. For the total solution, which includes the amplitude at −ω₂, the solution has to be multiplied by 2. This results in a final correction factor of $\frac{1}{4}\times 2=\frac{1}{2}$, and Eq. 12 recovers the solution in Ref. 14.

Considering a 1-D case, it is more straightforward to see that Eq. 7 holds, because Eq. 9 reduces to 0 while Eq. 11 does not. This 1-D case is in fact a good approximation to a highly directional 3-D case. For a more general 3-D problem, the validity of Eq. 7 is not as obvious, but it can be recognized that the difference between Eqs. 9, 11 comes primarily from (K_a + K_b + K₂) and (K_a + K_b − K₂) in the denominators. For cases tested in this study, the former is typically much larger than the latter in directions where the wave energy is significant, making Eq. 7 a good approximation. That is, since the energy in the direction of K₂ ≈ 0, i.e., parallel to the source plane, is negligible, the error introduce by this approximation is reasonably small. However, the validity of Eq. 7 becomes questionable when the energy along a direction nearly parallel to the source plane is not weak, e.g., a point source.

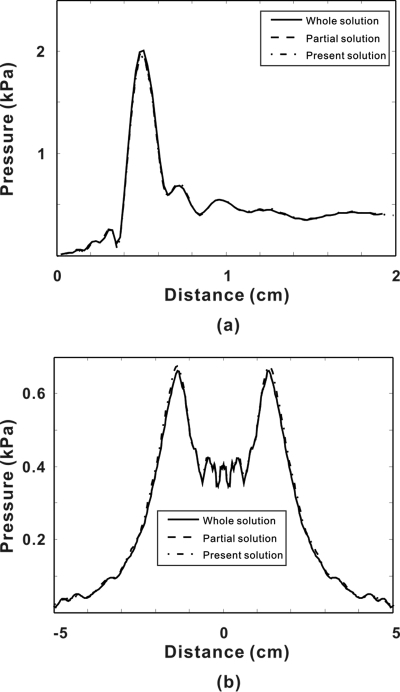
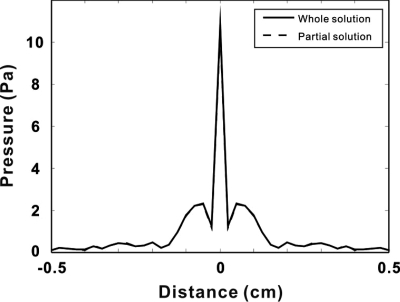
A 2-D example was first implemented to verify that under a more general situation Eq. 7 still holds. Details of the algorithm will be discussed in Sec. 3. A strongly focused transducer with a size of 20mm and a focus length of 5mm was considered. The fundamental frequency was 1MHz. The signal source amplitude was 100kPa. Attenuation was assumed negligible. Sound speed in the medium was 1500m∕s, the density was 1000kg∕m³, and the nonlinearity coefficient was 3.5. Figure 1a shows the results along the axis for Eqs. 11, 12, where the whole solution denotes Eq. 12 [the sum of Eqs. 11, 9] and the partial solution denotes Eq. 11. Figure 1b shows the results along the lateral dimension at a distance of 1.9cm from the source. Equation 8 was also implemented and can be found in Fig. 1 shown as the present solution. Good agreement found between the whole solution and the partial solution indicates the validity of Eq. 7. Closer scrutinization reveals that the error decreases exponentially with distance z. These comparisons also verify the present method for a strongly focused transducer which might be incorrectly analyzed by a method that does not consider the interaction between waves in different angles and presumes nonlinear distortion mainly in the z axis.

Figure 1.

The sound pressure amplitude of the second harmonic (a) along the axis for different solutions and (b) along the lateral dimension for different solutions.

For more strongly nonlinear cases, the situation becomes considerably more complex. It is expected by considering higher order approximation using the perturbation method, explicit format can be obtained for the function F, and Eq. 7 can be evaluated. A systematic study is not pursued here but is expected to be reported in a future paper. Nevertheless, a simple example will be demonstrated in this paper.

A moderately nonlinear 1-D problem is now considered, where the continuous wave is again used for excitation. For a 1-D case, attenuation must be taken into account as it restricts the harmonic components reasonably small so that the moderate nonlinearity assumption is valid. For the fundamental frequency, the right hand side of Eq. 7 becomes

$$\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime =e^{i{k}_{1}z}\frac{2M_1}{2i{k}_1}\underset{0}{\overset{z}{\int }}{e}^{-i{k}_{1}z\prime }P(z\prime ,-{\omega }_1)P(z\prime ,{\omega }_2)dz\prime$$ (13)

where

$$M_1=\frac{\beta {\omega }_1^2}{{\rho }_0{c}_0^4}.$$

Substituting the weak nonlinear approximation for the second harmonics, which can be easily obtained following the above procedure,

$$P(z\prime ,{\omega }_2)=\frac{4\beta k_1^2}{{\rho }_0{c}_0^2}\frac{e^{2i{k}_1^{\prime }z\prime }-e^{i{k}_2^{\prime }z\prime }}{k_2^{\prime 2}-4k_1^{\prime 2}}{P}^2(0,{\omega }_1),$$ (14)

where

$$k_1^{\prime }=\sqrt{{(\frac{{\omega }_1}{c_0})}^2-i\frac{\delta {\omega }_1^3}{c_0}},k_2^{\prime }=\sqrt{{(\frac{{\omega }_2}{c_0})}^2-i\frac{\delta {\omega }_2^3}{c_0^4}},$$

into Eq. 13 will only result in a higher order error [linear projection for the fundamental frequency is also used to represent P(z′,−ω₁)] and leads to

$$\frac{4\beta k_1^2{M}_1}{{\rho }_0{c}_0^2{k}_1^{\prime }}\frac{(k_1^{\prime }-k_1^{\prime \prime })e^{i(k_2^{\prime }-k_1^{\prime \prime })z}-(k_2^{\prime }-k_1^{\prime }-k_1^{\prime \prime })e^{i(2k_1^{\prime }-k_1^{\prime \prime })z}-(2k_1^{\prime }-k_2^{\prime })e^{i{k}_1^{\prime }z}}{(k_1^{\prime }-k_1^{\prime \prime })(k_2^{\prime }-k_1^{\prime }-k_1^{\prime \prime })(k_2^{\prime 2}-4k_1^{\prime 2})}{P}^3(0,{\omega }_1),$$ (15)

where $k_1^{\prime \prime }=\sqrt{{\left(\frac{{\omega }_1}{c_0}\right)}^2+i\frac{\delta {\omega }_1^3}{c_0^4}}$

On the other hand, in the same fashion, the left hand side of Eq. 7 reduces to

$$\begin{array}{l}\frac{M{e}^{-iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime -\frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime -\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \\ =-\frac{4\beta k_1^2{M}_1}{{\rho }_0{c}_0^2{k}_1^{\prime }}\frac{(3k_1^{\prime }-k_1^{\prime \prime })e^{i(k_2^{\prime }-k_1^{\prime \prime })z}-(k_2^{\prime }+k_1^{\prime }-k_1^{\prime \prime })e^{i(2k_1^{\prime }-k_1^{\prime \prime })z}-(2k_1^{\prime }-k_2^{\prime })e^{i{k}_1^{\prime }z}}{(3k_1^{\prime }-k_1^{\prime \prime })(k_2^{\prime }+k_1^{\prime }-k_1^{\prime \prime })(k_2^{\prime 2}-4k_1^{\prime 2})}{P}^3(0,{\omega }_1).\end{array}$$ (16)

Although not presented here, straightforward numerical verification shows that the absolute value of Eq. 15 rapidly becomes much larger than Eq. 16 as z increases, again confirming the validity of Eq. 7.

The total solution for the fundamental frequency can be then written as

$$P(0,{\omega }_1)e^{i{k}_1^{\prime }z}+\frac{4\beta k_1^2{M}_1}{{\rho }_0{c}_0^2{k}_1^{\prime }}\frac{(k_1^{\prime }-k_1^{\prime \prime })e^{i(k_2^{\prime }-k_1^{\prime \prime })z}-(k_2^{\prime }-k_1^{\prime }-k_1^{\prime \prime })e^{i(2k_1^{\prime }-k_1^{\prime \prime })z}-(2k_1^{\prime }-k_2^{\prime })e^{i{k}_1^{\prime }z}}{(k_1^{\prime }-k_1^{\prime \prime })(k_2^{\prime }-k_1^{\prime }-k_1^{\prime \prime })(k_2^{\prime 2}-4k_1^{\prime 2})}{P}^3(0,{\omega }_1),$$ (17)

which has been compared with the numerical solution of the Burgers equation11 with an error less than 1% for a moderately nonlinear case, considering a plane wave generated by a mono-frequency source with a frequency of 5MHz and peak amplitude of 6.4MPa, propagating in a medium with a speed of sound 1500m∕s, nonlinearity coefficient 3.5, diffusivity 8 × 10⁻⁴. This represents a moderately nonlinear problem, where the shock-formation distance is slightly smaller than the absorption length (2c₀³∕δω²). Comparing Eq. 17 with its weakly nonlinear approximation $P(0,{\omega }_1)e^{i{k}_1^{\prime }z}$ the maximum error has been found to be around +10% (“+” indicates the weakly nonlinear approximation overestimates the value, vice versa for “−”) across z = 0 to ∞. This error actually converges at a certain distance, as the second harmonic again becomes much smaller than the fundamental once again making the weakly nonlinear approximation valid. Substituting Eq. 17 into Eq. 6 leads to the solution at the second harmonic for a moderately nonlinear problem. Numerically evaluating the right hand side of Eq. 7 reveals that the weakly nonlinear approximation gives a maximum error of about +23% while also +23% for the left hand side. These two errors also grow at a similar rate and eventually converge at a certain distance, indicating that the error of evaluating their quotient will be smaller than +23%. In this specific case, the maximum error is −8%.

Next, a 3-D moderately nonlinear problem is considered. Although the final solution will be different, it is assumed that the error of evaluating the quotient on the left and right hand sides of Eq. 7 using the weakly nonlinear approximation is also in the order of ±10%. It has already been shown that Eq. 7 is valid using the weakly nonlinear approximation, therefore, the left hand side of Eq. 7 should still be much smaller than the right hand side even considering the error of this magnitude.

Considering a potential physical explanation of why

$$\left|\frac{M{e}^{-iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)-\frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \right|\ll \left|\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime \right|,$$ (18)

it is noted that the integrals represent contributions from the inhomogeneous term in Eq. 2, which can also be viewed as contributions from virtual sources.11 Since only the forward wave propagation is considered, the virtual sources exist between 0 and z. Therefore, the integrals from z to +∞ should be zero, or at least negligible. The integral

$$\left|\underset{z}{\overset{+\infty }{\int }}\frac{M{e}^{iKz}}{2iK}\times \underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \right|$$

is also very small compared with

$$|\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime |$$

For all the simulations carried out in this study, keeping the integral

$$\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime$$

in the solution introduces negligible differences. This becomes more clear considering a 1-D propagation problem: Suppose a wave is projected in a lossless medium for a small distance dz, so that the linear projection is still valid, we have

$$\begin{array}{l}\underset{0}{\overset{dz}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \\ \approx \underset{0}{\overset{dz}{\int }}{e}^{iKz\prime }\int P(\omega -{\omega }^{\prime },0){\mathrm{e}}^{i(K-K)ź}P({\omega }^{\prime },0)e^{iK\prime z\prime }d{\omega }^{\prime }dz\prime \\ =e^{iKdz}dz\frac{\sin (Kdz)}{Kdz}\int P(\omega -{\omega }^{\prime },0)P({\omega }^{\prime },0)d{\omega }^{\prime }\end{array}$$ (19)

where K′ = ω′∕c.

In a similar fashion, we have

$$\underset{0}{\overset{dz}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime =dz\int P(\omega -{\omega }^{\prime },0)P({\omega }^{\prime },0)d{\omega }^{\prime }$$ (20)

The absolute values of Eqs. 19, 20 differ by a factor of sin(Kdz)∕Kdz. Although the decay rate is slower than exponential, this sinc function decays from 1 to an infinitesimal number with increasing Kdz. For very small distances z, |sin(Kdz)∕Kdz| is close to 1; however, previous derivations suggest that

$$\frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)-\frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )dz\prime \right)$$

and

$$-\frac{M{e}^{iKz}}{2iK}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime$$

approximately cancel for small z, again resulting in a small value.

After finding the approximated solution in Eq. 8, the transform of the pressure can then be solved numerically in increments of Δz, to form the field over space. For example, we have31

$$\begin{array}{l}\underset{0}{\overset{\Delta z}{\int }}{e}^{iKz}F\left(P(z)\right)dz\approx F\left(P(0)\right)\times \Delta z,\\ \underset{0}{\overset{2\Delta z}{\int }}{e}^{iKz}F\left(P(z)\right)dz\approx F\left(P(0)\right)\times \Delta z+e^{iK\Delta z}F\left(P(\Delta z)\right)\times \Delta \mathrm{z.}\\ ...\mathrm{.}\end{array}$$ (21)

The integral is approximated by the Riemann sum. Although this approximation has a relatively large truncation error compared with higher order integrals, it is very robust and is expected to work well with a large step size for weakly nonlinear problems. This approximation, which evaluates integrals by the left-hand point rule for Riemann sums, in fact greatly resembles a first-order version of the impulse method for stiff ODEs.32 In both our methods and the impulse method, the propagator of the linear part of the differential equation is used to evolve both the nonlinear term and the initial condition over a large step. This algorithm can be contrasted with the first-order forward Euler, first-order symplectic Euler (leapfrog), second-order velocity verlet, and fourth-order Runge–Kutta explicit scheme for this type of ODE,31 where the step size usually has to be extremely small (in the order of 1∕K) for stable integrations.

Since the implicit analytic solution for the frequency-domain Westervelt equation is available [i.e., Eq. 8], it is now possible to also backward propagate waves by simply replacing z by −z in Eq. 8,2

$$P(k_x,k_y,-z,\omega )=P(k_x,k_y,0,\omega )e^{-iKz}-\frac{\beta {\omega }^2}{2i{\rho }_0{c}_0^{4}K}{e}^{-iKz}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(-z\prime )\right)dz\prime ,$$ (22)

as Eq. 2 is invariant with respect to the spatial dimension [i.e., if P(k_x,k_y,z,ω) is a solution to Eq. 2, P(k_x,k_y,−z,ω) is also a solution]. In contrast, it is noted that the frequency dimension is not invariant, which is a sufficient condition to indicate that the equation is not time invariant. We note that the acoustic time-reversal method is essentially based on the fact that the lossless acoustic wave equation is time invariant,33, 34, 35 i.e., if p(r,t) is a solution to the wave equation, then p(r,−t) is also a solution. This fundamental property does not hold in lossy media, resulting mathematically from the fact that the attenuation term is not an even-order derivative. On the other hand, in Eq. 2, space reversal is valid in the dimension z, even though time reversal does not hold. Application of the time-reversal method and the present backward-projection method are quite different, however, as time reversal is generally realized by temporal phase conjugation of a received signal followed by retransmission, whereas the present method sends the signal back to the source numerically using Eq. 22. It is possible, however, to numerically implement time reversal in a lossy medium by reversing the absorption coefficient.36 In this case, the present algorithm still has advantage over the time-reversal method in terms of sound field reconstruction in a nonlinear medium. Basically, the backward-projection algorithm has all the advantages of the forward model. For example, the backward projection can be easily implemented for arbitrary dispersions. The step size can be relatively large for weakly nonlinear problems. The backward projection also considers interaction of waves in different directions, which is not possible in most time-domain methods. An additional advantage of working in the frequency domain becomes apparent for cases involving a highly absorptive medium: While numerical noise tends to build up exponentially during backward projection, the algorithm can be easily combined with a frequency-domain filter to eliminate or reduce such noise, whereas in the time-domain, filtering is typically more complex and time-consuming.

NUMERICAL SIMULATIONS

Algorithm

An algorithm was developed to perform the discrete approximation of Eq. 8, using the approximation given by Eq. 21. An initial dataset p(x,y,z₀,t) was provided, representing the signal time history over the x-y plane at z = z₀ in front of the source. Values were expressed as a grid of n_x × n_y × n_t points, representing the two spatial planes and time, respectively. The values of n_x and n_y were set to be odd numbers so that the center point is in the middle. The discrete spatial coordinates were

$$\begin{array}{l}x=m\times dx,m=-n_x∕2+1∕2,\mathrm{...},n_x∕2-1∕2,\\ y=n\times dy,n=-n_y∕2+1∕2,\mathrm{...},n_y∕2-1∕2\end{array}$$ (23)

The numbers n_x, n_y, and n_t were determined on a case-by-case basis. Since a Fourier summation results in a periodic function, spectral methods inherently have a wrap-around problem (an outgoing wave enters one boundary and exits from the opposite boundary).37 Therefore, n_x and n_y must be sufficiently large especially in the far field, where more of the wave spreads into boundary. To minimize this effect, solutions near the boundary could be tapered to zero, but was not done in this study. In the present study, the maximum n_x and n_y used was 121. The number n_t was chosen to be slightly larger than T∕dt, where T is the time length of the excitation signal.

Temporal resolution was set by the Nyquist rate $\Delta t=\frac{1}{2f_{\max }}$, where the maximum frequency was set at the highest harmonic to be tracked plus the bandwidth of the initial signal. Spatial resolution requirements were set by the spatial cutoff, giving $\Delta x=\Delta y=\frac{c_0}{2f_{\max }}$. However, spatial resolution can be decreased without losing too much accuracy under special cases where pressure is concentrated in directions along the axis of propagation and the nonlinearity involved is not very strong. In this study, a spatial resolution of $\Delta x=\Delta y=\frac{c_0}{2f_c}=\lambda ∕2$ was used for the 3-D problem, where f_c is the fundamental frequency and λ is the wavelength at the fundamental frequency.

A potential disadvantage of the frequency-domain approach is the need to calculate the convolution integral at each iteration of the algorithm, thus offsetting some of the computational advantage of the method. This operation becomes more time intensive as the relevant bandwidth increases. To reduce processing time, selective sampling of k-space can be incorporated. If the signal is propagating approximately along the spatial z axis, the filter generally will be a low pass filter. In this study, the selective sampling of k-space is, however, not applied, as the computational times involved for all the case tested are reasonably short. Nevertheless, a low pass filter applied the constraint that spatial frequencies must be $<\frac{{\omega }^2}{c_0^2}$ i.e., evanescent waves were neglected. In addition, this filter served the purpose of eliminating numeric explosion from exponentially increasing round-off error during back-projection.

Verification

Error study

This section concentrates on error introduced as a function of the projection step size Δz, as formulated by Eq. 21.

One motivation for developing the method was its potential ability to take relatively large steps between the projection planes, Δz. It was expected that for weakly nonlinear cases, large steps relative to a wavelength could be used without producing large error in the calculation. To test the tradeoffs between step size and accuracy, we performed a series of simulations to look at error as a function of propagation distance and step size. We incrementally changed the propagation distance measured in the shock-formation distance σ (0.88σ, 0.44σ,…,0.0138σ) and dz (σ∕256, σ∕128,…,σ∕16) independently, while dt was kept with 32 harmonics being considered. The temporal resolution was chosen to be relatively high because the under-sampling of time-domain should be eliminated as it might influence the accuracy of the solution when changing the step-size dz.

Since an analytic solution for plane nonlinear wave propagation is available, it was chosen for this error study. To propagate a plane wave, the sound pressure distribution on the whole initial surface was uniform, and a sinusoidal burst of ten circles was used as the initial signal. For the excitation, the frequency was 5MHz and the initial pressure amplitude was 5MPa. For the medium, the nonlinearity coefficient was 3.5 and the speed of sound was 1500m∕s. The Fubini solution11 to the Burgers equation was used, which is valid up to the shock-formation distance σ in a lossless media.

To quantify the error, we calculated the time-domain L2 error of the present model versus the corresponding exact analytic solution (Fubini solution). The time-domain L2 error is defined as37

$$\epsilon =\frac{\Vert p_{\text{num}}(t)-p_{\text{exact}}(t)\Vert }{\Vert p_{\text{exact}}(t)\Vert },$$ (24)

where ‖p(t)‖ is the L2 norm of the time-domain signal p(t).

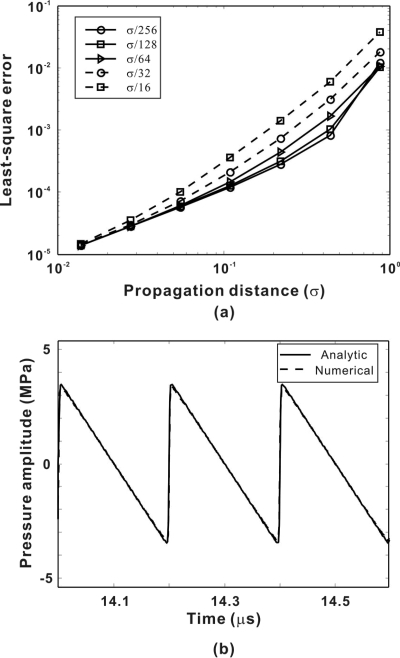
Examination of error as a function of the control variables, as plotted in Fig. 2a, indicated that error increased as the propagation distance increased. This trend was expected due to increased nonlinearity of the signal, thus causing an eventual breakdown in the band-limited assumptions of the present model. For relatively strong nonlinear cases (z > 0.4σ), the error did not increase significantly as the step size changed from σ∕256 to σ∕128, but the error did increase significantly when the step size was changed from σ∕64 to σ∕16. Overall, results indicated that, for a weakly nonlinear problem, a step size of dz = σ∕16 (equivalent to λ in this specific case) was still able to provide good accuracy (L2 error smaller than 0.001) while maintaining computational efficiency [less than 1 s for plane-wave simulation on a personal laptop: Dual-core 2.00GHz processors and 3GB of random access memory (RAM)], provided that the temporal resolution was sufficiently fine. Even for a strongly nonlinear case (z = 0.88σ), the error generated by using a step size = σ∕16 may be considered tolerable relative to the error typically introduced in experimental measurement. In contrast, the finite element method,3 which solves the time-domain nonlinear wave equation using a predictor∕multi-corrector algorithm in combination with standard time-stepping procedures, requires up to 80 elements per wavelength to obtain the Fubini solution. It is noted that the projection size determined here is based on plane-wave propagation in homogeneous media. For accurate results in cases containing diffraction, the step size must be reduced. However, as long as the regime is not at, or near, the shock-formation distance, a standard step size of σ∕64 is sufficient.

Figure 2.

(a) Curves of errors for the present method showing the L2 error for forward projection step size and propagation distance measured in shock-formation distance σ. (b) Comparison between the present method and analytic solution for one-dimensional nonlinear wave propagation at 3.3σ.

Therefore, the method proposed here has the advantage that the z-step for calculating the nonlinear term can be much larger than in the conventional time–space derivative scheme, where fast changes of the wave profile must be accounted for, and the z-step must be a small portion of the shock-formation distance. Here, fast changes are included in the phase exponential coefficient, similar to the KZK or Burgers equation, where they are accounted by operating in the retarded time variable. That is why in the limiting case of linear propagation the step can be arbitrary.

Lastly, to demonstrate the validity of Eq. 8 near or beyond the shock distance, an example was considered that compares the numerical method with the Fay solution to the Burgers equation,11 which is devised to provide an accurate solution when the propagation distance is larger than 3σ and the diffusivity is small. In the present study, a distance of 3.3σ and diffusivity of 2 × 10⁻⁵ was selected. Δz was chosen to be σ∕512, and the temporal resolution dt was increased to 1∕(256f_c) so that 128 harmonics were considered. The very fine temporal resolution was chosen because shock wave has a spectrum that converges slowly toward high frequencies and need more harmonics to represent the wave front. Figure 2b shows the comparison, and the agreement is good. The L2 error is 0.02.

Note that the present frequency-domain model is inherently most practically applicable to non-shockwave problems where only a limited number of harmonics need to be considered. Although still valid for cases of stronger nonlinearity, the computational advantage is diminished. To better apply the present model to shock wave propagation while maintaining efficiency, a limited-harmonic nonlinear algorithm could be used, e.g., limiting the steepness of the shockfronts by artificially increasing the attenuation.5 However, further development of this technique is beyond the scope of this work and not further discussed here.

Directional independence

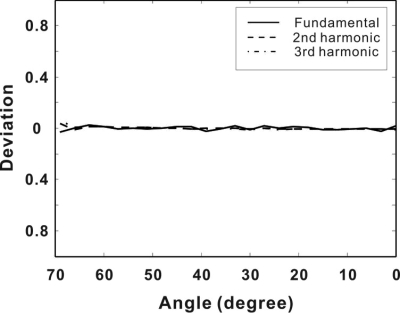
To test the directional independence of the nonlinear field solution, a 2-D steered transducer problem was explored. A 1 MHz fundamental frequency of continuous wave signal with amplitude of 1 MPa was used to excite a 15 cm continuous line array. The sound speed was set to 1500m∕s, the density to 1000kg∕m³, and the nonlinearity coefficient to 3.5. No attenuation was considered. The size of the transducer was much larger than the fundamental wavelength, so that the sound field along the center of the beam was nearly planar within a certain distance. The time step for the spectral method was set to be 1∕(64f_c). The spatial step dz and dx were set to 1∕8λ. Ideally, for different steering angles (different phase distributions on the transducer), the field along each beam-path should be identical for points equidistant from the center of the transducer. Figure 3 shows the deviation of results at the first three frequencies to their mean values with changing steering angles. The results were obtained at a distance of 39mm to the center of the source. The steering angle changes from 0° to 70° (angle with respect to the z axis). A larger angle was not used due to the large computational domain it requires. The maximum deviation is below 5%, confirming the directional independence of the current method.

Figure 3.

Deviation of results at the first three frequencies to their mean values for a steering transducer as a function of the steering angle.

Comparison with ASA code

Next, the model was applied to a more complex 3-D scenario. For comparison, we simulated identical initial fields in the forward direction both using the present algorithm and an established nonlinear code. For this purpose, an open code software package designed to simulate ultrasound wave propagation (Abersim)28 was used. This package was developed at the Department of Circulation and Medical Imaging at the Norwegian University of Science and Technology (NTNU), and deals with the diffraction, nonlinearity, and attenuation using an operator splitting approach. Similar to the present algorithm, the diffraction term is solved using the angular spectrum approach. However, this algorithm only projects sound in the forward direction. Nonlinearity is only accounted for a wave traveling parallel to the z axis, since a plane-wave assumption is made, in the term accounting for nonlinearity, the sound pressure p is only a function of z and t.38 In addition, attenuation in the algorithm is considered to obey a power law and is realized by a convolution. In contrast, in the present algorithm, the dependence of attenuation on frequency is arbitrary, and can be easily implemented without requiring convolution.

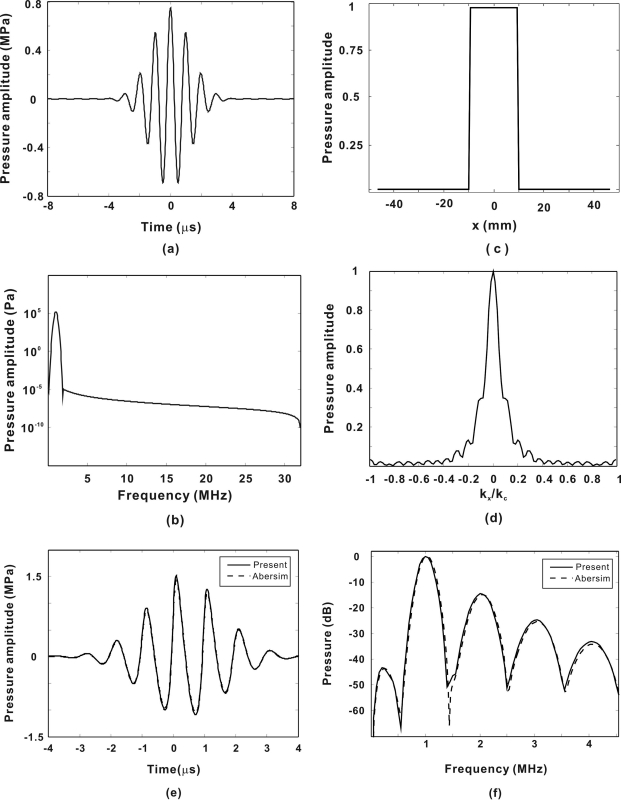
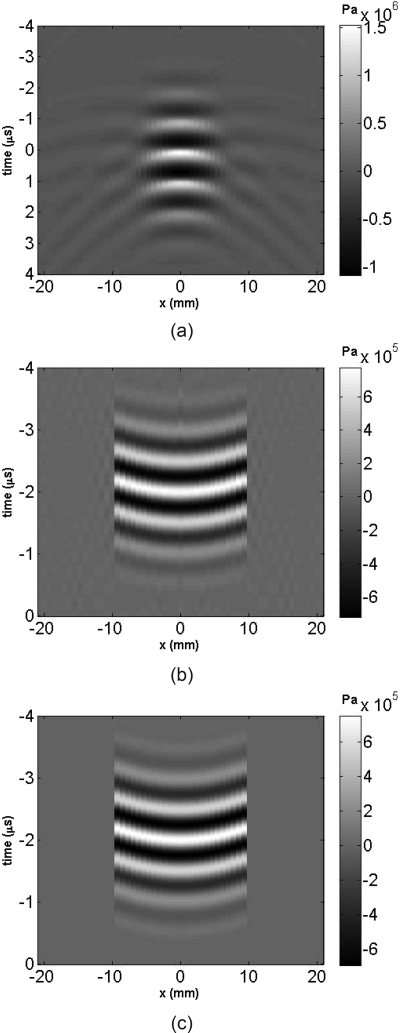
For testing, a 3-D example was addressed. The configuration simulated a concave circular transducer (single element) with an aperture radius of 10mm and a 75mm focal distance. The delay time used to create the focus was calculated by (d−d₀)∕c₀, where d is the distance from a point on the transducer to the focus and d₀ is the distance from the center of the transducer to the focus. The initial time-domain signal was Gaussian-shaped. The center frequency was 1 MHz, the fractional bandwidth was 0.3, and the initial peak pressure was 0.75 MPa. The excitation signal can be found in Fig. 4a, its spectrum can also be found in Fig. 4b. Figure 4c shows the spatial distribution for the fundamental frequency component along the x axis. It is noted that the distribution seems uniform as would be expected, since the time delay only changes the phase not the magnitude of the pressure. Figure 4d shows the spatial spectrum again for the fundamental frequency (k_c = 2πf_c∕c₀). For the fundamental frequency, k_x∕k_c ranges from −1 to 1, which represents the full range of possible propagation directions. Likewise for the sub-harmonic frequency, the range is expected to be from −2 to 2. It is well known that the spatial spectrum larger than 1 or smaller than −1 represents evanescent waves, therefore they will be filtered out in the current algorithm. For higher harmonics, the range is narrower than from −1 to 1, which does not cover the full range, but the error introduced is expected to be small because there is more directivity at higher harmonics.

Figure 4.

(a) Initial pressure in the center of the transducer for the three-dimensional simulation (1025 grid points). (b) Waveform spectrum of the initial pressure in the center of the transducer (32 harmonics). (c) Spatial distribution for the fundamental frequency component along the x axis (121 grid points). (d) Spatial spectrum for the fundamental frequency. (e) Time-domain comparison between the present method and Abersim at the focus (z = 75mm) for three-dimensional nonlinear wave propagation from a single-element circular transducer in muscle tissue. (f) Frequency-domain comparison (first four harmonics).

Human muscle was modeled by setting the sound speed to 1549.9m∕s, the density to 1060kg∕m³, the nonlinear parameter to β 3.9, and the attenuation to obey the power law as α(f) = a × f^b, where a was 0.52dB∕cm and b was 1.1.39 The temporal resolution in Abersim was set to 1∕(512f_c), as the Abersim simulation results converge well at this temporal resolution. Noticeable numerical damping was observed in Abersim at larger time steps. This was potentially due to Abersim’s use of the method of characteristics,9^,38 which can cause interpolation error when solving the nonlinear term. It was previously reported that “good results are obtained using a temporal grid of 10–15 samples per period at the highest harmonic frequency that should be accurately computed.”9 The time step for the present spectral method was set to be 1∕(64f_c) at which the result converges. It is noted that numerical damping has not been observed in the present model for large time steps. The spatial step, dz, in the present algorithm was set to 1∕4λ, while in Abersim a sub-cycling step given by Δz = c₀∕2πf_c was used. The sound diffusivity δ was calculated through the equation α = δω²∕2c₀³, where α is the attenuation coefficient.11 The dispersion obeys the Kramers–Kronig relations and is written as21

$$\frac{1}{c_w}=\frac{1}{c_0}+a\tan (\frac{\pi b}{2})\left({\left|\omega \right|}^{b-1}-{\left|{\omega }_0\right|}^{b-1}\right)$$ (25)

Prior to simulating nonlinear media, both the present code and Abersim were tested for linear cases (β = 0) with and without attenuation. The two approaches were found to have excellent agreement. To save space, the linear results are not presented here.

Time-domain solutions at the focus [Fig. 4e] as well as the frequency-domain solution for the first four harmonics [Fig. 4f] both indicate good agreement between the two methods. The time-domain L2 error was not estimated because different temporal resolutions were used.

The total calculation time of the present approach for this 3-D wave propagation problem is less than 15 min when implemented using MATLAB, on a XP 64-bit operating system. The hardware consisted of four dual-core 2.67GHz Xeon processors, and 24GB of RAM. The matrix size of the pressure p is 121 × 121 × 1025. Therefore, the present approach captures the whole solution of the Westervelt equation in a computationally efficient manner.

Backward projection

A key advantage of the present approach is the ability to propagate a nonlinear signal both toward and away from the source. Thus, a signal could be recorded at a given distance from the source, and then back-projected to give information about the signal near a transducer face, assuming the propagating field is contained within the measurement plane, z₀. As discussed in Sec. 2, this property can be contrasted with time reversal methods, which are violated in the presence of the absorption term.33 We demonstrate this ability by projecting the forward-propagated signals from a transducer backward to the source location, where they are compared with the original signal.

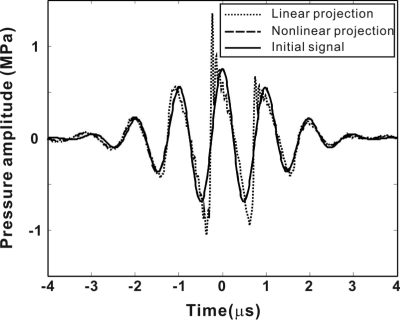
Two cases were tested for nonlinear wave propagation in different acoustic media. In the first case, the forward projected sound field was obtained from the example in Sec. 3 B 3 at the focal plane z = 75mm, where the simulated acoustic medium was human muscle. For the backward projection, the time step was 1∕(64f_c) and step-size dz was $\frac{1}{4}$ wavelength at the center frequency. The time history of the obtained signal along the x axis (y = 0, z = 75 mm) is provided in Fig. 5a. This signal was backward projected to the z = 0 plane as shown in Fig. 5b. The initial signal at z = 0 mm is shown in Fig. 5c. The L2 error was 0.09. More detailed comparison is shown for a point in the center of the transducer in the time-domain (Fig. 6). For reference, the linear backward projection (β = 0) is also implemented and plotted. It can be seen that in a nonlinear acoustic medium, the linear backward projection is inaccurate. Consequently, use of such linear methods to characterize a field in a nonlinear medium can be expected to lead to erroneous results. Accordingly, the L2 error for the linear backward projection was 0.27, significantly larger than the error for nonlinear projection. While a comprehensive study is not presented here, this error is expected to increase as nonlinearity increases.

Figure 5.

(a) Three-dimensional forward-projected signal at the focus plane (z = 75mm, y = 0mm). (b) Three-dimensional backward-projected signal at the source position (z = 0mm, y = 0mm). (c) Initial signal at the source position (z = 0mm, y = 0mm). The medium is human muscle.

Figure 6.

Comparison of the nonlinear backward-projected signal, linear backward-projected signal, and initial signal on the center of the transducer. The medium is human muscle.

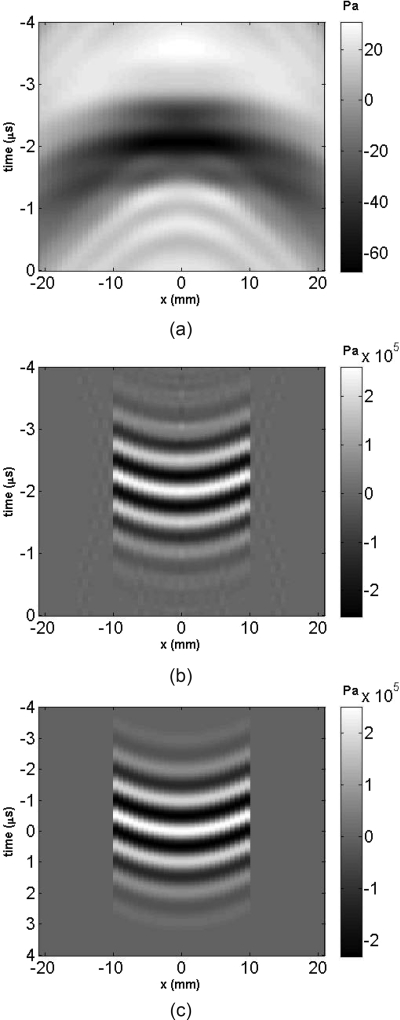
The second scenario considered a dispersion relation described by the frequency-dependent phase velocity given as c = 1525 − 2.5 × 10⁻⁵f(Hz). The attenuation was given as α(f) = 13.3 × f^1.09 + 0.05 (dB∕cm). The velocity26 and attenuation40 were within the range that may be found, for example, in human cancellous bone. To apply the present theorem, it is assumed that the ultrasound is nearly normally incident upon the bone surface, such that only longitudinal waves are generated, and the Westervelt equation might be a good approximation.41 The density was assumed to be 1850 kg∕m³.27 The nonlinearity coefficient β was 72.42 The forward projected sound field was obtained from a concave circular transducer with an aperture radius of 10mm and a focus distance of 60mm. The excitation signal was the same in Fig. 4a except that the peak amplitude was reduced to 0.25MPa. For both the forward and backward projections, the time step was 1∕(32f_c) and step-size dz was $\frac{1}{4}$ wavelength.

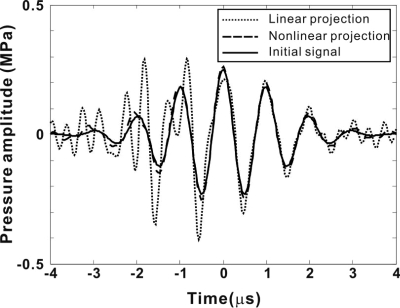
In comparison with the first case simulating muscle, the attenuation in the second case was significantly enhanced and was modeled by a nonlinear power fit. The nonlinear coefficient was also increased. For these reasons, a specific low pass frequency-domain filter was applied to the backward projection. The need for the filter came from the approximation that the attenuation obeys the same law for the whole frequency range. This assumption was made to simplify the numerical simulation. Therefore, in our simulation, the attenuation was extremely large at a very high frequency. This introduced an issue for the backward projection, as the attenuation term amplified the signal exponentially during the backward projection, and a small numerical noise at a very high frequency relative to the frequency content of the signal quickly led toward infinity. The cut-off frequency of a low-pass filter in such situations, however, is commonly determined based on the spectral analysis of the relevant sound field. In this case, spectral analysis showed that the signal was extremely small after the third harmonic (3MHz). Therefore, the cut-off frequency was set at 3MHz. Once again, the forward projected field at the focal plane (z = 60 mm) was initially generated. The time history of the obtained signal along the x axis (y = 0, z = 60 mm) is shown in Fig. 7a. This signal was backward projected to the z = 0 plane as shown in Fig. 7b. The initial signal at z = 0 mm is shown in Fig. 7c. The L2 error was 0.1. The linear projection was again also implemented and the L2 error was 0.37. A detailed comparison of sound pressure of a point in the center of the transducer is shown in Fig. 8. Overall, the wave reconstructions demonstrate the potential of the present method to accurately backward project a signal in a nonlinear medium.

Figure 7.

(a) Three-dimensional forward-projected signal at the focus plane (z = 60mm, y = 0mm). (b) Three-dimensional backward-projected signal at the source position (z = 0mm, y = 0mm). (c) Initial signal at the source position (z = 0mm, y = 0mm). The medium is human cancellous bone.

Figure 8.

Comparison of the nonlinear backward-projected signal, linear backward-projected signal, and initial signal on the center of the transducer. The medium is human cancellous bone.

SUMMARY AND CONCLUSION

The present nonlinear wave-vector-frequency-domain representation of the Westervelt equation has been shown to yield an implicit analytic solution. Its original form is not suitable for numerical implementation; therefore, its approximation was found and numerically solved. In the approach, diffraction is calculated through the solution to the homogenous frequency-domain Westervelt equation, while the nonlinearity is calculated by the particular solution through a Green’s function. Comparisons between the present method and other well-established methods, including analytic solutions, validate the accuracy and efficiency of the approach. Moreover, the analytic solution of the present method permits projection of acoustic waves from an initial measurement plane to distances closer to the source. This backward-projection technique was also verified numerically.

This study suggests that, similar to its linear counterpart, measurement of time and spatially resolved pressure across a single plane could provide data to characterize an entire field, including nonlinear induction of both harmonic and sub-harmonic wave components. A single plane also has the potential to characterize the radiative behavior of its source.2 This could be particularly useful in the case of high power transducers, where the source itself commonly radiates higher harmonics of the fundamental. In this case, the back-projection could serve to separate source signals from medium-dependent acoustic nonlinear effects.

The present examples are simulated using ideal conditions. It is expected that in the absorptive case, appreciable signal strength will be required for accurate back projection, with the precise requisite signal-to-noise ratio as a function of the desired accuracy. Planar projection is shown to be valid under arbitrary dispersion conditions for both forward and backward propagation. This could prove particularly useful under conditions of anomalous dispersion, and provides a straightforward and computationally efficient method for predicting behavior in dispersive media. Although the current algorithm was limited only to homogeneous situations, the method is expected to be applicable under more general conditions.43

Appendix A

This appendix derives the solution to Eq. 2. It is convenient to move the nonlinear term in Eq. 2 to the right hand side of the equation, where it may now be viewed as a “source function” for the equation, albeit one that is only known over a given initial plane at z₀. In this representation an implicit solution to Eq. 2 may be expressed in terms of an integral equation using the 1-D Green’s function30

$$G(z,z\prime )=\frac{-i}{2K}(e^{iK\left|z-z\prime \right|}-e^{iK\left|z+z\prime \right|}),0\le z,z\prime <\infty$$ (A1)

and the known homogeneous solution.

The general solution can be written as

$$\begin{array}{l}P(z)=A{e}^{iKz}+B{e}^{-iKz}+\frac{\beta {\omega }^2}{2i{\rho }_0{c}_0{}^{4}K}[\underset{0}{\overset{z}{\int }}\left(e^{iK(z-z’)}-e^{iK(z+z’)}\right)F\left(P(z’)\right)dz’\\ +\underset{z}{\overset{+\infty }{\int }}\left(e^{-iK(z-z’)}-e^{iK(z+z’)}\right)F\left(P(z’)\right)dz’]\\ =A{e}^{iKz}+B{e}^{-iKz}+\frac{\beta {\omega }^2}{2i{\rho }_0{c}_0{}^{4}K}[\underset{0}{\overset{z}{\int }}\left(e^{iK(z-z’)}-e^{iK(z+z’)}\right)F\left(P(z’)\right)dz’-\\ -\underset{0}{\overset{z}{\int }}\left(e^{-iK(z-z’)}-e^{iK(z+z’)}\right)F\left(P(z’)\right)dz’+\underset{0}{\overset{+\infty }{\int }}\left(e^{-iK(z-z’)}-e^{iK(z+z’)}\right)F\left(P(z’)\right)dz’]\\ =A{e}^{iKz}+B{e}^{-iKz}+\frac{\beta {\omega }^2}{2i{\rho }_0{c}_0{}^{4}K}[\underset{0}{\overset{z}{\int }}\left(e^{iK(z-z’)}-e^{iK(z-z’)}\right)F\left(P(z’)\right)dz’\\ +\underset{0}{\overset{+\infty }{\int }}\left(e^{-iK(z-z’)}-e^{iK(z+z’)}\right)F\left(P(z’)\right)dz’]\\ =A{e}^{iKz}+B{e}^{-iKz}-\frac{\beta {\omega }^2}{2i{\rho }_0{c}_0{}^{4}K}\left[e^{-iKz}\underset{0}{\overset{z}{\int }}{e}^{iKz’}F\left(P(z’)\right)dz’-e^{iKz}\underset{0}{\overset{z}{\int }}{e}^{-iKz’}F\left(P(z’)\right)dz’\right]\\ +\frac{\beta {\omega }^2(e^{-iKz}-e^{iKz})}{2i{\rho }_0{c}_0{}^{4}K}\underset{0}{\overset{+\infty }{\int }}{e}^{iKz’}F\left(P(z’)\right)dz’\end{array}$$ (A2)

where

$$F\left(P(z\prime )\right)=P(k_x,k_y,z\prime ,\omega )\otimes P(k_x,k_y,z\prime ,\omega ).$$ (A3)

Since $\underset{0}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime$ is a constant with respect to z, it merges into A and B, which leads to

$$P(z)=A{e}^{iKz}+B{e}^{-iKz}-\frac{\beta {\omega }^2}{2i{\rho }_0{c}_0^{4}K}\left[e^{-iKz}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime -e^{iKz}\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime \right].$$ (A4)

The task now is to determine A and B, which need boundary conditions. Applying the initial condition at the source plane leads to A = P(0) − B. Imposing the well-known Sommerfeld radiation condition

$$\underset{z\to \infty }{\lim }(\frac{dP}{dz}-iKP)=0$$ (A5)

yields

$$B=\frac{M}{2iK}\underset{0}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime$$ (A6)

where $M=\beta {\omega }^2∕{\rho }_0{c}_0^4.$

The final solution can be now written as

$$\begin{array}{l}P(z)=P(0)e^{iKz}+\frac{M{e}^{-iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)-\\ \frac{M{e}^{iKz}}{2iK}\underset{z}{\overset{+\infty }{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime +\frac{M{e}^{iKz}}{2iK}\left[\underset{0}{\overset{z}{\int }}{e}^{-iKz\prime }F\left(P(z\prime )\right)dz\prime -\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \right].\end{array}$$ (A7)

APPENDIX B

This appendix discusses the third harmonics generated by a continuous wave source under the weakly nonlinear approximation. For the third harmonics, the right hand side of Eq. 7 reads

$$\begin{array}{l}\frac{M_3{e}^{i{K}_{2}z}}{2i{K}_3}\underset{0}{\overset{z}{\int }}{e}^{-i{K}_{3}z\prime }F\left(P(z\prime )\right)dz\prime \\ =\frac{2M_3{e}^{i{K}_{2}z}}{2i{K}_3}\underset{0}{\overset{z}{\int }}\int e^{-i{K}_{3}z\prime }{P}_{{\omega }_1}(z,K\prime -\tilde{K}\prime )P_{{\omega }_2}(z,\tilde{K}\prime )dz\prime d\tilde{K}\prime \end{array}$$ (B1)

where

$$M_3=\frac{\beta {\omega }_3^2}{{\rho }_0{c}_0^4},$$

P_ω1 and P_ω2 are pressures at ω₁ and ω₂, respectively.

Substituting Eq. 12 into Eq. B1, we have

$$\begin{array}{l}\frac{2M_3{e}^{i{K}_{3}z}}{2i{K}_3}\underset{0}{\overset{z}{\int }}\int e^{-i{K}_{3}z\prime }{P}_{{\omega }_1}(z,K\prime -\tilde{K}\prime )P_{{\omega }_2}(z,\tilde{K}\prime )dz\prime d\tilde{K}\prime \\ =\frac{M_3{e}^{i{K}_{3}z}}{i{K}_3}\frac{4\beta k_1^2}{{\rho }_0{c}_0^2}\underset{0}{\overset{z}{\int }}\int e^{-i{K}_{3}z\prime }P(0,K\prime -\tilde{K}\prime )e^{i{K}_{b}z\prime }\int \frac{e^{i(K_a^{\prime 2}+K_b^{\prime 2})z}-e^{i{K}_2^{\prime }z}}{K_2^{\prime 2}-{(K_a^{\prime }+K_b^{\prime })}^2}P(0,\tilde{K}\prime \prime )P(0,\tilde{K}\prime -\tilde{K}\prime \prime )d\tilde{K}\prime \prime d\tilde{K}\prime dz\prime \\ =\frac{M_3{e}^{i{K}_{3}z}}{i{K}_3}\frac{4\beta k_1^2}{{\rho }_0{c}_0^2}\int \int \underset{0}{\overset{z}{\int }}{e}^{i(K_b-K_3)z\prime }\frac{e^{i(K_a^{\prime 2}+K_b^{\prime 2})z\prime }-e^{i{K}_2^{\prime }z\prime }}{K_2^{\prime 2}-{(K_a^{\prime }+K_b^{\prime })}^2}P(0,K\prime -\tilde{K}\prime )P(0,\tilde{K}\prime \prime )P(0,\tilde{K}\prime -\tilde{K}\prime \prime )dz\prime d\tilde{K}\prime \prime d\tilde{K}\prime \\ =-\frac{M_3}{K_3}\frac{4\beta k_1^2}{{\rho }_0{c}_0^2}\times \\ \iint \frac{(K_2^{\prime }-K_3+K_b)e^{i(K_a^{\prime }+K_b^{\prime }+K_b)z}}{(K_a^{\prime }+K_b^{\prime }-K_3+K_b)(K_2^{\prime }-K_3+K_b)\left[K_2^{\prime 2}-{(K_a^{\prime }+K_b^{\prime })}^2\right]}P(0,K\prime -\tilde{K}\prime )P(0,\tilde{K}\prime \prime )P(0,\tilde{K}\prime -\tilde{K}\prime \prime )d\tilde{K}\prime \prime d\tilde{K}\prime \\ +\frac{-(K_a^{\prime }+K_b^{\prime }-K_3+K_b)e^{i(K_2^{\prime }+K_b)z}+(K_a^{\prime }+K_b^{\prime }-K_2^{\prime })e^{i{K}_{3}z}}{(K_a^{\prime }+K_b^{\prime }-K_3+K_b)(K_2^{\prime }-K_3+K_b)\left[K_2^{\prime 2}-{(K_a^{\prime }+K_b^{\prime })}^2\right]}P(0,K\prime -\tilde{K}\prime )P(0,\tilde{K}\prime \prime )P(0,\tilde{K}\prime -\tilde{K}\prime \prime )d\tilde{K}\prime \prime d\tilde{K}\prime \end{array}$$ (B2)

where

$$\begin{array}{l}{K}_a^{\prime }=\sqrt{{\left(\frac{{\omega }_1}{c_0}\right)}^2-{\left|\tilde{K}\prime \prime \right|}^2},K_b^{\prime }=\sqrt{{\left(\frac{{\omega }_1}{c_0}\right)}^2-{\left|\tilde{K}\prime -\tilde{K}″\right|}^2},\\ K_b=\sqrt{{\left(\frac{{\omega }_1}{c_0}\right)}^2-{\left|K\prime -\tilde{K}\prime \right|}^2},K_2^{\prime }=\sqrt{{\left(\frac{{\omega }_2}{c_0}\right)}^2-{\left|\tilde{K}\prime \right|}^2},\\ K_3=\sqrt{{\left(\frac{{\omega }_3}{c_0}\right)}^2-{\left|K\prime \right|}^2}.\end{array}$$

Similarly, we have for the left hand side of Eq. 7

$$\begin{array}{l}\frac{M_2{e}^{-i{K}_{2}z}}{2i{K}_2}\underset{z}{\overset{+\infty }{\int }}{e}^{i{K}_{2}z\prime }F\left(P(z\prime )\right)dz\prime -\frac{M_2{e}^{i{K}_{2}z}}{2i{K}_2}\underset{z}{\overset{+\infty }{\int }}{e}^{i{K}_{2}z\prime }F\left(P(z\prime )\right)dz\prime -\frac{M_2{e}^{i{K}_{2}z}}{2i{K}_2}\underset{0}{\overset{z}{\int }}{e}^{iKz\prime }F\left(P(z\prime )\right)dz\prime \\ =-\frac{M_3}{K_3}\frac{4\beta k_1^2}{{\rho }_0{c}_0^2}\times \\ \iint \frac{(K_a^{\prime }+K_b^{\prime }+K_3+K_b)e^{i(K_2^{\prime }+K_b)z}}{(K_a^{\prime }+K_b^{\prime }+K_3+K_b)(K_2^{\prime }+K_3+K_b)\left[K_2^{\prime 2}-{(K_a^{\prime }+K_b^{\prime })}^2\right]}P(0,K\prime -\tilde{K}\prime )P(0,\tilde{K}\prime \prime )P(0,\tilde{K}\prime -\tilde{K}\prime \prime )d\tilde{K}\prime \prime d\tilde{K}\prime \\ -\frac{(K_2^{\prime }+K_3+K_b)e^{i(K_a^{\prime }+K_b^{\prime }+K_b)z}+(K_a^{\prime }+K_b^{\prime }-K_2^{\prime })e^{i{K}_{3}z}}{(K_a^{\prime }+K_b^{\prime }+K_3+K_b)(K_2^{\prime }+K_3+K_b)\left[K_2^{\prime 2}-{(K_a^{\prime }+K_b^{\prime })}^2\right]}P(0,K\prime -\tilde{K}\prime )P(0,\tilde{K}\prime \prime )P(0,\tilde{K}\prime -\tilde{K}\prime \prime )d\tilde{K}\prime \prime d\tilde{K}\prime \end{array}$$ (B3)

Although it is not mathematically obvious that Eq. 7 holds for the third harmonics, for the 1-D case, Eq. B3 reduces to zero while Eq. B2 does not. The 2-D example used in Sec. 2 is again used for the verification of Eq. 7. The details of the configuration of this 2-D problem can be found in Sec. 2. Figure 9 illustrates the results along the lateral dimension at a distance of 1.9cm from the source, for partial solution [Eq. B2] and complete solution [Eq. B2 + Eq. B3]. It can be observed that these two results are indistinguishable.

Figure 9.

The sound pressure amplitude of the third harmonic along the lateral dimension for different solutions.