Abstract
Different source-related factors can lead to vocal fold instabilities and bifurcations referred to as voice breaks. Nonlinear coupling in phonation suggests that changes in acoustic loading can also be responsible for this unstable behavior. However, no in vivo visualization of tissue motion during these acoustically induced instabilities has been reported. Simultaneous recordings of laryngeal high-speed videoendoscopy, acoustics, aerodynamics, electroglottography, and neck skin acceleration are obtained from a participant consistently exhibiting voice breaks during pitch glide maneuvers. Results suggest that acoustically induced and source-induced instabilities can be distinguished at the tissue level. Differences in vibratory patterns are described through kymography and phonovibrography; measures of glottal area, open∕speed quotient, and amplitude∕phase asymmetry; and empirical orthogonal function decomposition. Acoustically induced tissue instabilities appear abruptly and exhibit irregular vocal fold motion after the bifurcation point, whereas source-induced ones show a smoother transition. These observations are also reflected in the acoustic and acceleration signals. Added aperiodicity is observed after the acoustically induced break, and harmonic changes appear prior to the bifurcation for the source-induced break. Both types of breaks appear to be subcritical bifurcations due to the presence of hysteresis and amplitude changes after the frequency jumps. These results are consistent with previous studies and the nonlinear source-filter coupling theory.
INTRODUCTION
Voice instabilities and bifurcations, also referred to as voice breaks, have been a longstanding topic of interest in speech science. Even though these singularities are encountered in different circumstances, including the male voice at puberty (e.g., Harries et al., 1997), singing (e.g., Titze, 2004; Titze and Worley, 2009), and voice pathologies (e.g., Curry, 1949), they are not completely understood. Numerous studies have illustrated that different mechanisms can contribute to the production of voice breaks, where these instabilities are triggered by a multi-dimensional parameter space that includes vocal fold properties and their acoustic interaction with the vocal tract and subglottal system. Particular interest is given in this study to bifurcations produced by the addition of strong source-filter interactions, as recently examined in the nonlinear source-filter coupling theory (Titze, 2008) and numerical simulations (Titze, 2008; Titze and Worley, 2009; Tokuda et al., 2010). Supporting evidence that this acoustic phenomenon takes place in actual human speech was based on the relation between the fundamental frequency where these voice breaks occurred and the formant frequencies of the vocal tract and subglottal system through simple sound recordings (Titze et al., 2008; Tokuda et al., 2010). However, in vivo visualizations of vocal fold tissue motion have not been attempted during acoustically induced instabilities, for which validation of the phenomenon in human subjects is the subject of the current work.
The goal of this study was to explore the effects of acoustic coupling on tissue dynamics with human subjects. Numerical and experimental evidence from previous studies led to the hypothesis that strong acoustic coupling would introduce additional driving forces that would visibly affect the vocal fold tissue motion, a phenomenon that could be observed in vivo in human subjects. Bifurcations where less significant acoustic interaction is present were expected to exhibit visible differences in the unstable tissue motion with respect to the previous case. It was expected that these differences would be more evident by selecting vocal exercises that maximize and minimize the source-filter coupling. Furthermore, it was hypothesized that adding acoustic interaction in a region where bifurcations can occur naturally (as in register transitions regions) would facilitate their occurrence. Verification of these hypotheses would validate, in part, nonlinear coupling theory (Titze, 2008) and support the description of source-filter interactions based on lumped representations of the system.
Particular emphasis was given to documenting and analyzing the unstable motion of the vocal folds via recordings of laryngeal high-speed videoendoscopy (HSV). It was also desired to obtain estimates of the complete system behavior through simultaneous recordings of the glottal behavior, flow aerodynamics, and acoustic pressure. This ambitious experimental design severely limited the numbers of subjects able to follow the vocal tasks and exhibit the desired set of bifurcations at the tissue level. Thus, the current project is presented as a case study intended to serve as a reference for future investigations. The study extends previous efforts by Švec et al. (2008), in which register transitions and bifurcations where explored via videokymography, strobolaryngoscopy, and sound spectrography, and by Neubauer et al. (2001), in which spatio-temporal analysis was applied to laryngeal HSV recordings of irregular vibrations in subjects with vocal pathologies.
VOICE BIFURCATIONS
Irregular vocal fold vibration and voice bifurcations are generally considered to be produced by desynchronization between vibratory modes (Berry et al., 1994; Berry et al., 1996; Neubauer et al., 2001), strong asymmetries between left and right vocal folds and∕or excessively high subglottal pressure (Steinecke and Herzel, 1995; Jiang et al., 2001), changes in vocal fold tension (Švec et al., 1999; Miller et al., 2002; Tokuda et al., 2007), chaotic behavior near limit cycles between registers (Tokuda et al., 2008), and nonlinear acoustic coupling (Mergell and Herzel, 1997; Hatzikirou et al., 2006; Zhang et al., 2006b; Titze et al., 2008; Titze, 2008).
Titze et al. (2008) first proposed differentiating the origins of “source-induced” and “acoustically induced” voice bifurcations. This classification was adopted in this study, noting that it is unlikely that the two factors can be truly separated. Even though it is likely that a combination of components contributes to unstable behavior, it is considered that “source” or “acoustic” factors may be more dominant in certain cases, as previously noted by Titze et al. (2008).
Source-induced bifurcations
Observations of unintentional register transitions have been consistently reported in the frequency range of 150–200 Hz in males and 300–350 Hz in both males and females (Titze, 2000). Different studies have suggested that instabilities may occur given a physiologic limit in the maximum active stress in the thyroarytenoid (TA) muscle, which controls the medial surface shape of the glottis and thus its main modes of vibration (Švec et al., 1999; Titze, 2000; Miller et al., 2002). In this context, a bifurcation explanation from the theory of nonlinear dynamics was proposed to justify jumps occurred when there was a gradual tension transition and even when glottal parameters were held constant (Berry et al., 1996). Under this view, frequency jumps exhibiting amplitude differences and hysteresis are classified as subcritical bifurcations, and frequency jumps exhibiting smooth transitions with no hysteresis are termed as supracritical bifurcations (Tokuda et al., 2008; Tokuda et al., 2010). A number of studies have suggested that irregular vibration and voice bifurcations can also be produced by desynchronization between vibratory modes. This was initially discovered by analyzing pathological voices with nonlinear dynamic methods (Herzel et al., 1994) and later verified using empirical orthogonal functions (EOFs; also referred to as empirical eigenfunctions) from node displacement in a finite element model (Berry et al., 1994), spatio-temporal analysis of in vivo HSV (Neubauer et al., 2001), and a study of the medial surface dynamics in a physical rubber model of the vocal folds (Berry et al., 2006). Other studies have suggested alternative explanations, ranging from left–right (LR) asymmetry (Steinecke and Herzel, 1995), high subglottal pressure (Jiang et al., 2001), coexisting limit cycles (Tokuda et al., 2007; Tokuda et al., 2008), and the presence of a vocal membrane (Mergell et al., 1999).
A recent study by Echternach et al. (2010) investigated the open quotient during register transitions for untrained male subjects. Recordings of high-speed video using a rigid endoscope during upward pitch glides (between 110 and 440 Hz) were obtained. Even though the subjects intended to utter a vowel ∕i∕ to keep an open back cavity, the insertion of the rigid endoscope forced the vocal tract into a neutral configuration closer to a vowel ∕ae∕ with a first formant higher than 500 Hz. Thus, these recordings could not exhibit pitch and formant crossings and the bifurcations observed corresponded to source-induced ones.
Acoustically induced bifurcations
Early excised larynx studies acknowledged that involuntary register transitions were related to tracheal resonances (van den Berg, 1957, 1968). Further experiments with both excised larynx and artificial vocal folds have confirmed a noticeable influence of the subglottal and supraglottal resonances on the vocal fold dynamics (Austin and Titze, 1997; Alipour et al., 2001; Zhang et al., 2006a,b; Drechsel and Thomson, 2008). Numerical models have also served to explore the effect of acoustic coupling on voice bifurcations. Using a two-mass model with a one-tube resonator, bifurcations and instabilities for weak asymmetries were found (Mergell and Herzel, 1997). Correlation between bifurcations and supraglottal resonances were found when using a lumped mass model with a straight tube extension (Hatzikirou et al., 2006). Similar behavior was observed using more descriptive source models, the subglottal system, and wave propagation schemes (Titze, 2008; Tokuda et al., 2010).
Evidence of source-filter interaction leading to bifurcations has been reported in human subjects, as seen in register transitions in singers (Miller and Schutte, 2005), voice breaks in normal and pathological cases (Curry, 1949), and particularly in dynamic vocal exercises (Titze et al., 2008). Although some correlations between vocal tract resonances were observed in human subject recordings (Švec et al., 1999), such effects were considered minor with respect to that of tension control and not explored in depth. In recordings of different vocal gestures (Titze et al., 2008), the vocal exercise exhibiting most of the instabilities was found to be pitch (F0) glides at a soft loudness while producing a sustained vowel that has a low first formant frequency (F1), such as in vowels ∕i∕ and ∕u∕. Although voice bifurcations could include different phenomena such as frequency jumps, deterministic chaos, aphonation, and subharmonics, crossings between F0 and F1 in this vocal exercise primarily yielded frequency jumps. The fact that these voice breaks were more evident in male subjects with no vocal training suggested that muscle control and familiarity with unstable regions can overcome the bifurcations.
These observations were summarized in the nonlinear source-filter coupling theory of Titze (2008), where the combined sub- and supraglottal tract reactance was suggested to affect both airflow and vocal fold tissue motion. Although the term “nonlinear” could be omitted, as source-filter interactions in speech are always nonlinear, it was purposely used in this study for consistency with Titze (2008).
A previous attempt to explain voice breaks at low frequency (e.g., at 150 Hz) was based on constructive and destructive interference between subglottal formants and vocal fold movement. It was suggested that maximum amplitude and minimum amplitude can occur at pitch crossing with specific ratios of the first subglottal formant frequency (Titze, 1988a). A modest amount of support of these predictions was evidenced by means of excised canine larynx experiments (Austin and Titze, 1997), where the low consistency among different larynges was deemed to confound the results of the experiment. Although it has been further established that the subglottal tract can hinder vocal fold vibration (Zhang et al., 2006b; Zañartu et al., 2007; Titze, 2008), the idea of instabilities at entrainments lower than the first subglottal resonance does not completely fit with the current nonlinear theory (Titze, 2008) and thus has not been further explored.
METHODS
The vocal exercises and classification proposed by Titze et al. (2008) were followed so that acoustically induced bifurcations could be distinguished and contrasted with source-induced ones using pitch glide gestures. It was desired to obtain estimates of the complete system behavior for each dynamic vocal task exhibiting bifurcations. Thus, simultaneous recordings describing glottal behavior, flow aerodynamics, and acoustic pressures were obtained. A particular emphasis was put on documenting and analyzing the unstable motion of the vocal folds by means of digital high-speed video and image processing.
Experimental setup
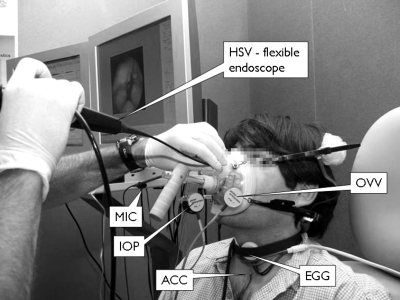
Three types of experimental configurations were used for different purposes. Setup 1 allowed for simultaneous measurements of laryngeal HSV, radiated acoustic pressure (MIC), neck skin acceleration (ACC), electroglottography (EGG), and oral volume velocity (OVV). This configuration captured HSV with a flexible endoscope, which not only allowed for aerodynamic assessment but also a normal articulation for the participant. A representation of this configuration is illustrated in Fig. 1. Setup 2 used HSV with a rigid endoscope, which provided higher HSV image quality and spatio-temporal resolution but did not allow for aerodynamic assessment and limited the degree of articulation for the participant. Synchronous measurements of ACC, EGG, and MIC were also used in this configuration. Setup 3 did not include HSV and only consisted of synchronous recordings of ACC, EGG, and MIC signals. All recordings were obtained in an acoustically treated room at the Center for Laryngeal Surgery and Voice Rehabilitation at the Massachusetts General Hospital.
Figure 1.
High-speed video measurement and data acquisition system. Setup 1: complete system and flexible endoscopy through a modified CV mask are shown. Real time data visualization is displayed for convenience of the clinician and system operator.
HSV recordings were acquired using a Phantom version 7.3 high-speed video color camera (Vision Research, Inc.) and a Phantom version 7.1 high-speed video monochromatic camera (Vision Research, Inc.). A C-mount lens adapter with adjustable focal length (KayPENTAX) was placed between the image sensor and the corresponding endoscope: A 70° transoral endoscope (JEDMED) was used for rigid endoscopy and a transnasal fiberscope (model FNL-10RP3; KayPENTAX) for flexible endoscopy. HSV data were recorded at 4000 or 10000 images per second depending upon lighting conditions with maximum integration time and a spatial resolution of 320 horizontal × 480 vertical pixels to capture an approximately 2 cm2 target area. The camera’s on-board memory buffer restricted the recording time to less than 12 s at the lowest desired resolution (4000 images per second). The light source contained a short-arc xenon lamp rated at 300 W (KayPENTAX). The fan-cooled housing produced a collimated beam of light with a color temperature of over 6000 K. Three glass infrared (two dichroic and one absorbing) filters blocked infrared light to reduce thermal energy buildup during endoscopy.
The MIC signal was recorded using a head-mounted, high-quality condenser microphone (model MKE104; Sennheiser electronic GmbH & Co. KG) with a cardioid pattern, offering directional sensitivity and a wideband frequency response. The microphone was situated approximately 4 cm from the lips at a 45° azimuthal offset. The microphone’s gain circuitry (model 302 Dual Microphone Preamplifier; Symetrix, Inc.) offered a low-noise, low-distortion preconditioning.
The ACC signal was obtained using a light-weight accelerometer (model BU-7135; Knowles) housed in a 1-in. diameter silicone disk. The accelerometer was preamplified with a custom-made preamplifier (Cheyne et al., 2003) and was attached to the suprasternal notch (∼5 cm below the glottis) to obtain indirect estimates of the subglottal pressure. This accelerometer at this location was essentially unaffected by sound radiated from the subject’s mouth (air-borne corrupting components), even with loud vocal intention (Zañartu et al., 2009).
An EGG signal was used to provide estimates of glottal contact. The EGG electrodes (model EL-2; Glottal Enterprises) were attached to the neck without interfering with the accelerometer placed at the suprasternal notch. The EGG electrodes were connected to a signal conditioner (model EG2-PC; Glottal Enterprises).
Simultaneous measurements of OVV required modifying the standard circumferentially vented (CV) mask (model MA-1L; Glottal Enterprises) to allow for adequate placement of the flexible endoscope with sufficient mobility while maintaining a proper seal (Kobler et al., 1998). The CV mask was also modified so it could be self-supported around the subject’s head and could hold the OVV sensor (model PT-series; Glottal Enterprises), an intraoral pressure (IOP) sensor (not analyzed in these experiments), and the MIC sensor. An electronics unit (model MS-100A2; Glottal Enterprises) provided signal conditioning and gain circuitry for the OVV sensor prior to digitizing. Figure 1 displays the modified CV mask along with other sensors used during the recordings.
Normalized values are presented in this study for comparison with the uncalibrated HSV units. All analog signals were passed through additional signal conditioning and gain circuitry (CyberAmp model 380; Danaher, Corp.) with anti-aliasing low-pass filters set with a 3-dB cutoff frequency of 30 kHz and later digitized at a 120 kHz sampling rate, 16-bit quantization, and a ±10 V dynamic range by a digital acquisition board (6259 M series; National Instruments).
Time synchronization of the HSV data and the digitized signals was critical for enabling correlations among them and synchronous representations. The hardware clock division and data acquisition settings were controlled by MIDAS DA software (Xcitex Corporation). Alignment of the HSV data and the other signals was accomplished by recording an analog signal from the camera that precisely indicated the time of the last recorded image. To compensate for the larynx-to-microphone acoustic propagation time, the microphone signal was shifted by 600 μs (17 cm vocal tract length plus 4 cm lip-to-microphone distance), the OVV signal by 500 μs (17 cm vocal tract), and the ACC signal by 125 μs (5 cm distance from the glottis), all into the past relative to the HSV data. Time delays caused by circuitry (model MS-100A2; Glottal Enterprises) required an additional 100 μs shift into the past for the OVV signal.
Subject selection and protocol
Setup 1 was initially tested on eight normal adult subjects uttering simple vocal tasks. Only three of these subjects (two male and one female, the latter with vocal training) completed the more complex protocol required to yield vocal instabilities. Although all three subjects exhibited some type of vocal instability, only one male was able to consistently produce both source-induced and acoustically induced voice breaks that were clearly observable in the tissue motion. The other two subjects exhibited the following behaviors: (1) The male subject exhibited only a source-induced frequency jump and (2) the female subject only exhibited one minor acoustically induced instability observable as a subharmonic in the microphone signal that was not observable at the tissue level. Thus, these two cases were discarded to focus on a case study that more clearly illustrated both nonlinear phenomena. The selected subject was a 34 yr old male subject with no vocal training and no history of vocal pathology.
Instabilities occurring when F0 was located within the bandwidth of F1 (sub or supra) were labeled as acoustically induced breaks, whereas those occurring when F0 was outside of this frequency range were labeled as source-induced breaks (Titze et al., 2008). To maximize the likelihood of these events, two different vowels were elicited at soft loudness levels: A close front unrounded vowel ∕i∕ (where F0–F1 crossings are more likely to occur) and a near-open front unrounded vowel ∕ae∕ (where F0–F1 crossings are less likely to occur). Vowel ∕ae∕ is produced naturally when trying to utter a vowel ∕i∕ while a rigid endoscope is in place. Both vowels were uttered as upward and downward pitch glides limited by the subject’s vocal range and endoscopic procedure, with no reference tones used.
Video and data processing
Data and video was processed to yield qualitative observations and quantitative analysis. Six glottal measures (four direct HSV measures and two EOF measures) obtained from HSV post-processing were used. The main considerations used in this processing are discussed in this section.
HSV-based measures depended on accurate extraction of vocal fold tissue motion from the time-varying glottal contour. All frames were cropped and rotated such that the glottal midline was oriented vertically. Glottal area and glottal contours were obtained using threshold-based edge detection. It was found that alternative methods of image segmentation, such as texture analysis by Ma and Manjunath (2000), watershed transformations by Osma-Ruiz et al. (2008), and Canny edge detection by Canny (1986), were not robust to the many variations that occurred in the images obtained, including errant shadowing, arytenoid hooding, and mucus reflections.
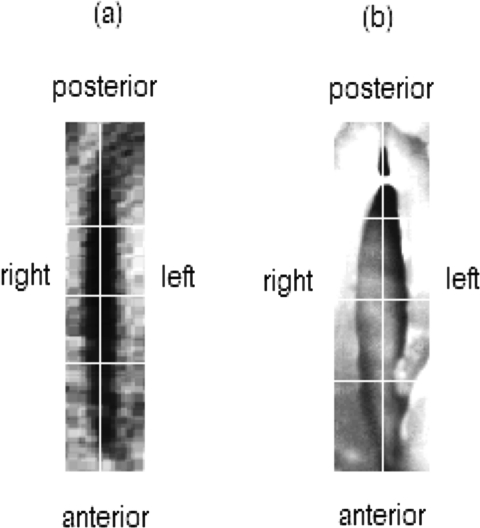
Vocal fold tissue motion was measured by tracking the medio-lateral motion of the left and right vocal fold edges closest to the glottal midline (see Fig. 2). Semiautomatic algorithms generated glottal contours, glottal area (Ag), digital kymograms (DKGs), and phonovibrograms (PVGs) to extract vibratory patterns and different glottal measures. DKGs were obtained from three selected cross sections representing the anterior–posterior (AP) glottal axis, as shown in Fig. 2.
Figure 2.
Endoscopic view obtained with (a) flexible endoscope and (b) rigid endoscope. White horizontal lines indicate the locations of the three selected DKGs. The white vertical line indicates the glottal midline.
Four quantitative HSV-based measures of glottal behavior were computed before and after the voice breaks for two selected DKGs across the AP glottal axis (middle and posterior) where no artifacts in the edge detection were present. The four selected HSV measures were open quotient (OQ; ratio between open phase duration and period), speed quotient (SQ; ratio between opening and closing phase durations), LR amplitude asymmetry (AA; ratio between amplitude difference and total amplitudes), and LR phase asymmetry (PA; ratio of the time difference between the maximum lateral displacements of the left and right vocal folds and the open phase duration). These measures have been used to study soft, normal, and loud voice (Holmberg et al., 1988), register transitions (Echternach et al., 2010), and normal and pathological cases (Švec et al., 2007; Bonilha et al., 2008; Mehta et al., 2010).
PVGs, spatio-temporal plots constructed from lateral displacement waveforms of the vocal folds, were generated (Lohscheller et al., 2008). The color scheme was simplified into a grayscale representation since no displacement across the glottal midline was observed. PVGs were obtained from the left and right glottal edge contour for each time step, encompassing no less than 30 cross sections for each vocal fold.
An EOF analysis was performed over a range of 25–50 ms immediately before and after the voice breaks, following the decomposition described by Neubauer et al. (2001). The EOF decomposition used the same glottal edge contour as for the PVG and provided quantitative insights into the modal behaviors exhibited by the vocal fold tissue. Any artifact (e.g., mucus or edge detection artifacts) was discarded to improve the PVG and EOF computation.
Two objective measures were extracted from the EOF decomposition: The relative weights and entropy measure, both calculated before and after the break for each vowel. The relative weights of the EOF depicted the contribution of different empirical modes of vibration and the information entropy measure (referred as Stot following the notation from Neubauer et al., 2001) represented the spatial irregularity and broadness of the mode distribution.
Center frequencies and bandwidths of the supraglottal and subglottal resonances were computed from the MIC and ACC signals, respectively. The covariance method of linear prediction was used to estimate the pole distributions within the closed phased portion of the vocal fold cycle. The closed phase was determined using the derivative of the electroglottogram (dEGG) (Childers and Chieteuk, 1995). A 50 ms separation from the break point was taken into account to ensure some stability in the signal.
Spectral representations were also included to match representations used in previous studies dealing with register changes and acoustic interaction (Švec et al., 2008; Titze et al., 2008). Thus, spectrograms used a Hamming window of 30 ms duration with 8192 frequency resolution points and 90% overlap for a dynamic range of 60 dB.
RESULTS
Subject screening
A summary of all vocal tasks that yielded some type of voice instability for the subject in this case study is presented in Table TABLE I.. Three types of instabilities were observed: Pitch jumps, pitch fluctuations, and aphonic segments. Pitch jumps were found to be the most frequent and the most easily repeatable instability and can also be related to bifurcations. For those instabilities labeled with F0–F1 crossings (sub- and supra-), the pitch was observed to have sudden changes before and after the unstable zones, matching the observations in Titze et al. (2008).
Table 1.
Pitch glides exhibiting voice instabilities for case study subject. Instances with HSV are denoted by (*) and (**), where the latter were used for post-processing. The experimental setup used for each recording is stated. Notation: F0 is the fundamental frequency either before or after the instability, F1 and F2 are the vocal tract formant frequencies, and F1sub and F2sub are the frequencies of subglottal resonances. The labeling for F0–F1 crossings was defined when the pitch was within the bandwidth of the first vocal tract formant (labeled as “supra”), the first subglottal resonance (labeled as “sub”), or outside of them (labeled as “no”).
| Vowel | Experimental setup | Pitch glide | F1 (Hz) | F2 (Hz) | F1sub (Hz) | F2sub (Hz) | F0 before (Hz) | F0 after (Hz) | Voice break | F0–F1 crossing |
|---|---|---|---|---|---|---|---|---|---|---|
| ∕i∕ | 3 | Up | 335 | 2491 | 555 | 1300 | 335 | 293 | Aphonic | Supra |
| ∕i∕ | 3 | Up | 357 | 2370 | 498 | 1335 | 442 | 420 | Aphonic | Sub |
| ∕i∕ | 3 | Down | 350 | 2356 | 477 | 1413 | 201 | 116 | Jump | No |
| ∕i∕ | 3 | Up | 328 | 2604 | 491 | 1371 | 335 | 442 | Jump | Supra |
| ∕i∕ | 3 | Down | 286 | 2498 | 513 | 1447 | 293 | 158 | Jump | Supra |
| ∕i∕ | 3 | Up | 335 | 2398 | 484 | 1342 | 137 | 236 | Jump | No |
| ∕i∕ | 3 | Down | 350 | 2342 | 569 | 1484 | 513 | 413 | Aphonic | Sub |
| ∕i∕ | 3 | Down | 321 | 2363 | 562 | 1420 | 293 | 165 | Jump | Supra |
| ∕i∕* | 1 | Down | 327 | 2254 | 543 | 1435 | 342 | 307 | Dip | Supra |
| ∕i∕** | 1 | Down | 327 | 2254 | 549 | 1274 | 305 | 190 | Jump | Supra |
| ∕ae∕ | 3 | Up | 697 | 1229 | 513 | 1427 | 420 | 399 | Aphonic | Sub |
| ∕ae∕ | 3 | Down | 654 | 1179 | 555 | 1406 | 498 | 456 | Aphonic | Sub |
| ∕ae∕ | 3 | Down | 647 | 1172 | 527 | 1484 | 239 | 130 | Jump | No |
| ∕ae∕ | 3 | Up | 718 | 1208 | 569 | 1399 | 151 | 279 | Jump | No |
| ∕ae∕* | 2 | Up | 661 | 1413 | 576 | 1243 | 172 | 307 | Jump | No |
| ∕ae∕* | 2 | Up | 583 | 1442 | 491 | 1271 | 158 | 286 | Jump | No |
| ∕ae∕* | 2 | Up | 619 | 1392 | 669 | 1541 | 172 | 314 | Jump | No |
| ∕ae∕** | 2 | Up | 551 | 1343 | 495 | 1363 | 159 | 325 | Jump | No |
The primary interest of this investigation is on bifurcations, for which the focus is placed on the frequency jump instabilities from Table TABLE I.. For vowel ∕ae∕, bifurcations were more easily observed in the ascending pitch glides, and only one instance exhibited a bifurcation in the descending pitch glide. Vowel ∕i∕ exhibited the inverse pattern, i.e., the most repeatable bifurcations were on the descending pitch glide and only once a bifurcation was observed in the ascending glide. The average and standard deviations for the fundamental frequency before and after the bifurcations for these cases is summarized in Table TABLE II.. In both vowels, a more consistent behavior was present on the onset of the bifurcation, and hysteresis was observed. This last observation is less well supported since certain gestures needed to describe hysteresis were only observed once. The fact that the subject was less prone to exhibit instabilities for different conditions may be associated to his familiarity with certain gestures or an effect of the acoustic coupling.
Table 2.
Frequency jumps in Table TABLE I. indicating bifurcations, where average (mean) and standard deviation (SD) of fundamental frequency (F0) are taken across all setups. Dashes under SD mean that only one instance was observed for the case. Hysteresis in F0 is observed with respect to the direction of the pitch glide.
| Vowel | Pitch glide | F0 before | F0 after | ||
|---|---|---|---|---|---|
| Mean (Hz) | SD (Hz) | Mean (Hz) | SD (Hz) | ||
| ∕ae∕ | Up | 164 | 9 | 304 | 22 |
| ∕ae∕ | Down | 239 | — | 130 | — |
| ∕i∕ | Up | 137 | — | 236 | — |
| ∕i∕ | Down | 274 | 8 | 158 | 19 |
For the subsequent analyses, the main focus is on the gestures that were more consistent, i.e., the descending pitch glide for vowel ∕i∕ and ascending pitch glide with a vowel ∕ae∕. These two cases also allow for comparing the presence or lack of F0–F1 crossings, regardless of the pitch glide direction. The selected HSV recordings within these cases (denoted by ** in Table TABLE I.) were within the expected ranges with respect to other experimental configurations, thus ruling out the possible effects of the CV mask and endoscope on the unstable behavior. These two recordings described transitions between chest and falsetto registers and were analyzed in detail in the following sections.
Spectrographic observations
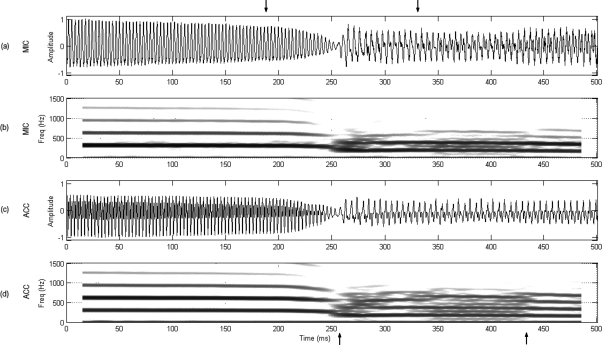
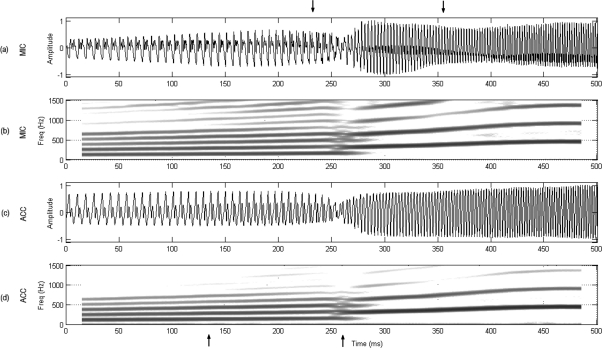
Spectrographic and temporal representations of 500 ms around the voice breaks for both MIC and ACC signals are presented for both vowels under consideration in Figs. 3 and 4. It can be seen in Fig. 3 that vowel ∕i∕ exhibited no transitional changes before the break, i.e., both signals suddenly jumped from one vibratory pattern to another with a short, less periodic region immediately after the break that produced higher inter-harmonic noise (between the lower arrows). Subsequent sections evaluate if this aperiodic component is also present in the tissue motion. Contrasting these observations, Fig. 4 shows that vowel ∕ae∕ exhibited a gradual change in the harmonic composition before the break, where the second and higher harmonic components (also noted as ripple in the temporal representations) was increasing in amplitude (between the lower arrows) up to the point of the voice break. This second harmonic component became the fundamental frequency after the bifurcation.
Figure 3.
Acoustically induced bifurcation. Downward pitch glide for vowel ∕i∕ using setup 1: (a) normalized microphone signal, (b) microphone spectrogram, (c) normalized accelerometer signal, and (d) accelerometer spectrogram. Upper arrows bound the register transition section to be further analyzed in Fig. 7. Lower arrows bound a less periodic region in the signals after the bifurcation point.
Figure 4.
Source-induced bifurcation. Upward pitch glide for vowel ∕ae∕ using setup 2: (a) normalized microphone signal, (b) microphone spectrogram, (c) normalized accelerometer signal, and (d) accelerometer spectrogram. Upper arrows bound the register transition section to be further analyzed in Fig. 8. Lower arrows bound a region with increased harmonic amplitude prior to the bifurcation point.
HSV sequences
A series of HSV sequences spanning a 30 ms window around the bifurcation point is presented for each vowel. The sequence for vowel ∕i∕ is displayed in Fig. 5 and has a time span of 10 ms per row. A few cycles before and after the break are observed in the first and last row, respectively, whereas the transition between the two registers is depicted in the second row. Differences between the vibratory patterns before and after the break were observed. Before the break, the glottis opened and closed uniformly along the AP direction. After the break, a posterior opening with shorter duration, higher degree of skewing and asymmetry, and reduced amplitude was observed. In addition, the transition between these two modes had a distinct feature toward the end of the second row, where a much larger glottal excursion was observed right before the beginning of the chest register. Furthermore, the interval between this marked pulse and the one before exhibited incomplete closure with PA in the lateral displacement observed as parallel LR tissue motion. However, this last feature can be better observed through continuous spatio-temporal plots in the subsequent section.
Figure 5.
Snapshot sequence of voice break for vowel ∕i∕. Time is represented from left to right and spans 10 ms per row with a 250 μs period between subsequent frames. The middle row depicts the register transition. The time interval in this HSV sequence is also shown in Fig. 7.
A downsampled HSV sequence for vowel ∕ae∕ is presented in Fig. 6, displaying 10 ms per row. A few cycles before and after the break are shown in the first and last row, and the main transition between them is depicted in the second row. In contrast with vowel ∕i∕, no significant differences between the vibratory patterns were observed before and after the break. The glottis did not exhibit AP differences in excursion, opening, or closing times.
Figure 6.
Snapshot sequence of voice break for vowel ∕ae∕. Time is represented from left to right and spans 10 ms per row with a downsampled 400 μs period between subsequent frames for visualization purposes. The middle row primarily depicts the register transition. The time interval in this HSV sequence is also shown in Fig. 8.
HSV recordings by the same subject during modal speech and sustained pitch exhibited similar differences in the AP direction between the same two vowels. Thus, some differences observed for vowel ∕i∕ in chest register may be introduced by either differences in laryngeal configuration or by acoustic coupling effects due to the much lower first formant present in that case. In addition, direct observation of the complete laryngeal view in the HSV depicted a noticeable displacement of the arytenoid cartilage before and after the voice break in vowel ∕ae∕, movement that was not observed for vowel ∕i∕.
Synchronous spatio-temporal observations
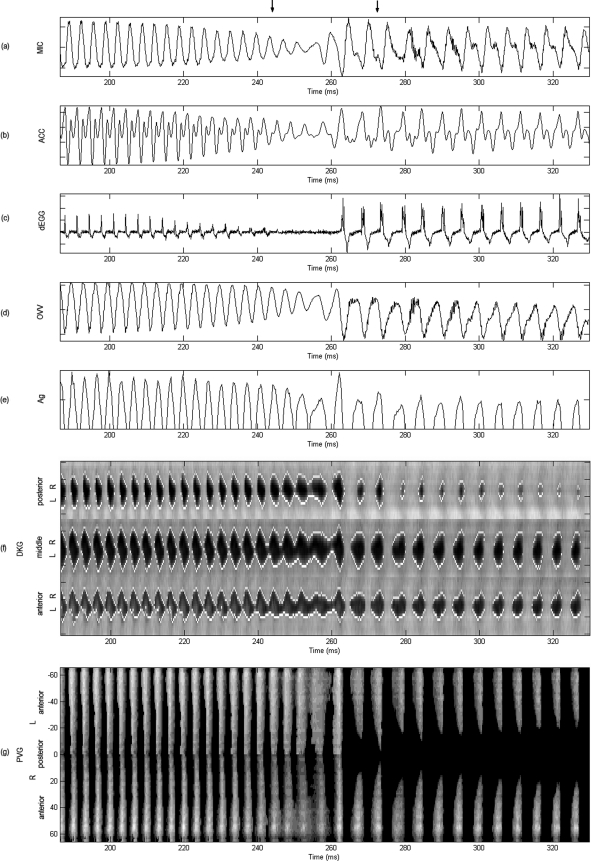
Figure 7 presents the set of synchronous plots for vowel ∕i∕ and corresponds to the interval between upper arrows in Fig. 3. In addition, the transition between the two registers shown between arrows in Fig. 7 corresponds to the HSV sequences of Fig. 5. As in Fig. 3, a noticeable difference was observed in the signal structure for the MIC and ACC signals before and after the break. The dEGG signal was weak before the break, nonexistent during it, and very strong and with multiple contact points after it. This indicated the nature of the collision forces at the glottis and the lack of contact during the break. This pattern was correlated with the high-frequency ripples observed in the MIC and OVV signals at the same time. Since no mucus was observed in the HSV, this rather aperiodic component was suspected to be a product of the tissue motion in that region. Quantitative assessment is presented in subsequent sections to evaluate this hypothesis. The no-contact region observed in the dEGG was also observed as a low frequency drift in the OVV signal in the same region. The last cycle before the sudden register transition exhibits the largest peak observed in Ag. Given its transient nature, this feature does not appear to be related to voluntary amplitude control. In addition, important Ag properties changed after the bifurcation, including its amplitude, shape, skewing, and closed∕open phase durations.
Figure 7.
Acoustically induced bifurcation. Synchronous plots for vowel ∕i∕ selected from the interval indicated in Fig. 3: (a) microphone, (b) accelerometer, (c) derivative of electroglottograph, (d) oral volume velocity, (e) glottal area, (f) anterior, middle, and posterior kymograms, and (g) phonovibrogram. All signals normalized. The normalized PVG grayscale indicates maximum amplitude in white. Upper arrows bound the bifurcation region shown in the HSV sequence of Fig. 5. Reduced vocal fold contact, parallel vocal fold motion, and increased glottal excursion followed by a sudden register transition are observed in this region. Most signals exhibit an aperiodic component after the bifurcation.
The DKGs from Fig. 7, exhibited significant changes in the oscillatory behavior before and after the break, as well as in the AP direction. Before the break, all three DKGs exhibited excursions of comparable amplitudes with an opening time similar to the closing time. However, after the break, the DKGs had different lateral displacement amplitudes and shapes. The posterior DKG differed from the other two DKGs in that its lateral displacement waveforms had a round shape with smaller amplitude. The anterior and middle DKGs had longer opening and shorter closing portions, which explained the skewing of Ag. Interestingly, the break portion exhibited incomplete closure and LR PA, the latter seen as parallel tissue motion and best observed in the middle and anterior kymograms of Fig. 7 at ∼255 ms.
The PVG in Fig. 7 further elucidated vibratory patterns of the vocal folds. Before the break, symmetric behavior was observed between the left and right vocal folds and along the AP direction, where the entire glottal edge opened simultaneously. The break exhibited LR asymmetries and a constant opening that ended in an abrupt closure around 265 ms. After this point, an AP difference was observed in the oscillation, where the anterior ends exhibited most of the lateral excursion. The slightly skewed pulses indicated that glottal opening and closure did not occur at the same time along the AP axis. In addition, the regions with maximal excursion (brighter regions) deviated toward the right (in time) with respect to the pulses before the break. This tissue motion indicated abrupt glottal closure that produced the skewing of the Ag and was hypothesized to yield the aperiodic components observed in MIC and OVV signals after the break.
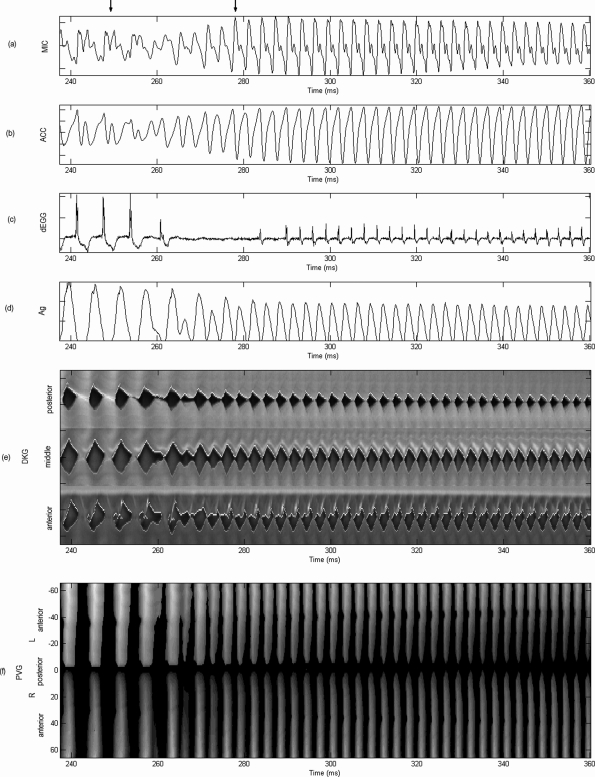
A different scenario is observed for the synchronous plots of vowel ∕ae∕ in Fig. 8, which corresponds to the interval shown between the upper arrows of Fig. 4. As before, the register transition portion shown between arrows in Fig. 8 corresponds to the HSV sequences of Fig. 6. The MIC and ACC signals exhibited a more stable behavior before and after the break and a much smoother transition between the two registers. Similar type of transitions were observed by Echternach et al. (2010) for source-induced register jumps. As expected, the dEGG indicated that the contact in the chest register was stronger than in the falsetto register. The Ag illustrated how a glottal pulse was increasingly appearing during the break, joining both oscillatory regimes smoothly. Although amplitude differences were observed after the bifurcation, the pulse shape of Ag was generally maintained.
Figure 8.
Source-induced bifurcation. Synchronous plots for vowel ∕ae∕ selected from the interval indicated in Fig. 4: (a) microphone, (b) accelerometer, (c) derivative of electroglottograph, (d) glottal area, (e) anterior, middle, and posterior kymograms, and (f) phonovibrogram. All signals normalized. The PVG grayscale indicates maximum amplitude in white. Upper arrows bound the bifurcation region shown in the HSV sequence of Fig. 6. Reduced vocal fold contact and transitional appearance of an additional glottal pulse are observed in this region.
The spatio-temporal plots in Fig. 8 show a much simpler structure compared with vowel ∕i∕, exhibiting AP uniformity and LR symmetry before and after the break. Both DKGs and PVG illustrated that an additional harmonic pulse was smoothly introduced before the voice break, anticipating the second vibratory pattern.
HSV-based measures
Table TABLE III. presents the four selected HSV-based measures of glottal behavior, each one computed for the chest and falsetto registers and both vowels.
Table 3.
HSV measures taken from two DKGs representing middle and posterior tissue motion during chest and falsetto registers. Average (mean) and standard deviation (SD) are obtained from 25 to 50 ms HSV samples for each case. The chest register in vowel ∕i∕ exhibits the largest SDs with respect to the mean values for all measures.
| HSV-based measures from AP DKGs | Vowel ∕i∕ | Vowel ∕ae∕ | ||
|---|---|---|---|---|
| Middle (%) | Posterior (%) | Middle (%) | Posterior (%) | |
| Mean ± SD | Mean ± SD | Mean ± SD | Mean ± SD | |
| OQ (f) | 83.3 ± 2.9 | 61.3 ± 2.2 | 91.0 ± 1.7 | 78.0 ± 3.7 |
| OQ (c) | 53.1 ± 5.3 | 35.3 ± 15.5 | 71.8 ± 1.8 | 54.5 ± 0.6 |
| SQ (f) | 84.0 ± 11.3 | 53.9 ± 16.7 | 66.3 ± 6.1 | 58.0 ± 7.1 |
| SQ (c) | 189.9 ± 40.7 | 119.6 ± 59.9 | 93.8 ± 8.8 | 48.9 ± 4.9 |
| AA (f) | 10.1 ± 7.4 | 18.3 ± 6.3 | 2.7 ± 2.8 | 7.1 ± 4.1 |
| AA (c) | −4.0 ± 6.2 | −7.6 ± 18.8 | −19.2 ± 7.0 | −22.7 ± 6.4 |
| PA (f) | 14.0 ± 2.2 | 14.3 ± 2.8 | 3.5 ± 1.8 | 0.8 ± 0.9 |
| PA (c) | 6.8 ± 3.6 | 5.0 ± 2.5 | 0.4 ± 0.6 | 4.5 ± 1.7 |
Notation: (f) = falsetto register, (c) = chest register.
A reduction in OQ in the chest register was observed for both vowels as the closed portion gets larger in this case. This expected behavior is in agreement with the observations made by Echternach et al. (2010). Even though comparable differences were observed in OQ for both vowels and registers, a shorter OQ was obtained in the chest registers in the posterior end of vowel ∕i∕, illustrating the different AP behavior between the two vowels.
Similarly, SQ increases due to the reduction of the closing phase (i.e., Ag skewing to the right). A greater change in the SQ was observed for vowel ∕i∕ in the chest register. AP differences are shown in this vowel since the posterior end had a more symmetric shape (SQ closer to 100%). Vowel ∕ae∕ shows less significant changes and rather maintains its SQ for both registers. This is due to the minor changes that the Ag and DKGs exhibited between the two registers for this vowel.
The asymmetry measures (AA and PA) were useful to identify differences between LR sides that were not obvious by simple observation of the spatio-temporal plots. Both measures of LR asymmetry were within the normal range for both vowels (Bonilha et al., 2008; Mehta et al., 2010). Comparable changes in polarity were observed in AA in both vowels between registers, indicating that the left vocal fold had a slightly larger displacement in the falsetto register. Differences between the registers were more noticeable in the posterior DKGs in both vowels, although larger AP differences were observed for vowel ∕i∕. In addition, PA was uniformly low along the AP direction and also exhibited larger changes for vowel ∕i∕.
It was observed that the chest register in vowel ∕i∕ exhibited the largest variance with respect to the mean values for all HSV measures, thus indicating a more irregular tissue motion. This finding is in agreement with the irregularities observed for the chest register in Figs. 3 and 7. Further insights into the regularity of the motion are explored in the subsequent section.
EOF decomposition
EOF decomposition was used to assess if the larger variance in the glottal measures and aperiodic components in multiple signals observed for the chest register of vowel ∕i∕, immediately after the bifurcation, indicated an abnormal∕irregular modal decomposition. EOF analysis of each vowel was performed for both falsetto and chest registers and for both left and right vocal folds. Comparisons were made between the two registers for each vowel, thus minimizing the uncertainty introduced by contrasting different recordings.
The cumulative sum of the first five most dominant relative EOF weights for the two vowels, each register, and left and right vocal folds is presented in Table TABLE IV.. As suggested by Neubauer et al. (2001), when the total cumulative surpasses 97%, sufficient precision can be obtained in the reconstruction of the vibratory pattern. Although, this ad hoc threshold is not based on the physiology, it has been used in prior work to evaluate irregular vibration (Neubauer et al., 2001) and is in agreement with the energy levels from subsequent studies showing that the main patterns of glottal dynamics are concentrated in the first two modes of vibration in normal phonation (Berry et al., 1996; Zhang et al., 2006a). Thus, the values above the threshold are highlighted in Table TABLE IV. to emphasize the number of modes needed to mainly compose the glottal dynamics.
Table 4.
Cumulative sum of the first five relative EOF weights for each vowel both before and after the voice breaks. The first values above a 97% threshold are underlined to define the number of significant modes needed for the reconstruction. Stot is the information entropy representing irregularity and broadness of the mode distribution for each case. The chest register in vowel ∕i∕ exhibits the broadest distribution and largest number of significant modes.
| EOF index | Vowel ∕i∕ | Vowel ∕ae∕ | ||||||
|---|---|---|---|---|---|---|---|---|
| Left | Right | Left | Right | |||||
| Falsetto (%) | Chest (%) | Falsetto (%) | Chest (%) | Falsetto (%) | Chest (%) | Falsetto (%) | Chest (%) | |
| 1 | 91.4 | 91.6 | 93.6 | 90.4 | 95.8 | 96.7 | 96.3 | 96.6 |
| 2 | 96.6 | 95.0 | 95.9 | 95.7 | 97.7 | 98.4 | 98.0 | 98.2 |
| 3 | 97.5 | 96.4 | 97.1 | 96.9 | 98.4 | 98.8 | 98.6 | 99.1 |
| 4 | 97.8 | 97.2 | 97.7 | 97.7 | 98.8 | 99.1 | 98.8 | 99.2 |
| 5 | 98.1 | 97.7 | 98.1 | 98.1 | 99.1 | 99.3 | 99.0 | 99.3 |
| Stot | 0.19 | 0.21 | 0.17 | 0.21 | 0.11 | 0.09 | 0.11 | 0.09 |
The chest register of vowel ∕i∕ had a broader distribution when compared with falsetto for the same vowel, as seen in the higher information entropy and number of modes needed for the decomposition. This difference between registers was not observed for vowel ∕ae∕, where the information entropy was lower for the chest register and the first two modes appeared to capture the essential glottal dynamics for both registers, matching results reported in previous studies (Neubauer et al., 2001; Berry et al., 1996; Zhang et al., 2006a).
The fact that more than two modes were needed to meet the 97% threshold in vowel ∕i∕ does not imply that there is an underlying pathological condition. In fact, this behavior is expected to be a consequence of the AP asymmetry and more irregular tissue vibration observed for vowel ∕i∕, which is in agreement with observations from previous sections.
DISCUSSION
The aim of these experiments was to compare voice breaks occurring with and without strong acoustic coupling, as that observed during F0–F1 crossings. A comprehensive set of measurements was performed as a case study of an adult male with no history of vocal pathology. The subject exhibited consistent behavior for two desired vocal gestures: A descending pitch glide of a vowel ∕i∕ and an ascending pitch glide of a vowel ∕ae∕. Given that for vowel ∕i∕ there was F0–F1 (vocal tract) crossing, such a break is labeled as acoustically induced, whereas that of vowel ∕ae∕ with no F0–F1 crossing is considered source induced. The most consistent unstable behavior for the vowel gestures was found to be during jumps in the fundamental frequency that were associated with register transitions.
The differences observed between cases labeled as source-induced and acoustically induced bifurcations support the hypothesis that acoustic coupling can introduce visual differences in tissue motion. Acoustically induced bifurcations were not anticipated by any detectable change in the acoustic, aerodynamic, or glottal behavior prior to the frequency jump. Furthermore, it was observed as a sudden tissue instability that exhibited incomplete glottal closure and significant PA (parallel LR vocal fold motion), followed by a large vocal fold excursion after which the fundamental frequency jumped to a different register. These observations were best seen in DKGs and Ag’s. All measured signals exhibited irregularities and aperiodic components immediately after the acoustically induced bifurcation that lasted ∼200 ms. Simultaneously, irregular tissue motion was detected in the vocal fold kinematics during this interval, as evidenced by larger variances in glottal measures and broader modal distributions. AP differences were observed from digital kymography and phonovibrography after the break as well. In addition, the presence of strong acoustic coupling appeared to facilitate register transitions, as the frequency jumps occurred earlier (i.e., at higher frequencies during the descending pitch glide and vice versa) when strong coupling was present.
In contrast, source-induced bifurcations showed a smoother transition between registers and a more regular and symmetric behavior before and after the bifurcation, matching the general behavior observed by Echternach et al. (2010). Acoustic and glottal dynamics components exhibited transitional changes prior to the bifurcation point. These changes were best seen in the acoustic signals as harmonic changes and added ripples, spanning more than 100 ms prior to the frequency jump. These changes are expected to be related to an observed arytenoid displacement that was only detected for this case. These observations link the source-induced case with gradual changes in vocal fold tension, which is in agreement with previous studies where smooth changes in tension triggered jumps to a higher mode of vibration, particularly when the oscillation was near coexisting limit cycles (Herzel et al., 1994; Berry et al., 1994; Berry et al., 2006; Tokuda et al., 2007, 2008). Thus, this voice break appeared to better match these source-induced factors and not a destructive interference with subharmonic ratios of the subglottal resonances (Titze, 1988b; Austin and Titze, 1997).
Further investigations with a larger pool of subjects are needed to better support all these findings. For instance, it is unclear if AP differences in the acoustically induced case were introduced by the coupling effect or by a particular laryngeal configuration. It is possible that these differences are associated to the laryngeal configuration for vowel ∕i∕ but suppressed by the stronger source-filter coupling before the bifurcation. Additional research is needed to verify this explanation. Nevertheless, the initial observations for both types of bifurcations support the nonlinear source-filter coupling theory (Titze, 2008) and its principles where the acoustic coupling was described based on impedance representations.
Since bifurcations occurring near F0–F1 crossings appear to exhibit different behavior and tissue motion, the results of these experiments support the naming scheme proposed by Titze et al. (2008). However, further investigations will need to test the robustness of this classification since in many instances bifurcations can be observed in ranges where it is difficult to establish if they occurred within the formant bandwidth. An alternative classification scheme might be obtained by investigating the hysteresis of the bifurcation and utilizing the distinction between supercritical bifurcations (smooth transitions) and subcritical bifurcations (amplitude jumps with hysteresis) (Tokuda et al., 2010). The results of the experiments in this study illustrate that both designated source-induced and acoustically induced cases exhibited hysteresis and amplitude differences before and after the breaks, for which they would classify as subcritical bifurcations. This finding is in agreement with previous numerical simulations with and without acoustic interaction (Tokuda et al., 2010). However, a rigorous analysis of the hysteresis was not possible to achieve in our experiments since the subject tended to exhibit bifurcations in only one of the pitch glide directions for each vowel. This behavior may be related to the subject’s ability to compensate the instabilities in one direction more than in other for certain vowels, a laryngeal configuration that affects the bifurcation for each vowel, the effects of the source-filter coupling, or a combination of these factors. This tendency was also observed in some cases in previous studies (Titze et al., 2008). Thus, it appears difficult to attain a controlled hysteresis analysis in human subjects’ recordings that involve bifurcations during pitch glides and different vowels.
It is noteworthy to comment on the difficulties associated with subject recruitment in these experiments. As noted by Titze et al. (2008), only a reduced percentage of the subjects were able to achieve the desired voice breaks, even for a simple scheme that did not include endoscopy. This finding, along with the more complex experimental setup conditions (including the need to attain full glottal exposure), imposed a challenge for the subjects to accomplish the vocal tasks and exhibit the desired instabilities. Similar challenges were observed in the study by Švec et al. (2008), in which only a single untrained subject was able to accomplish the desired task. Low yield in subject pools appear to be intrinsic to experiments where participants are expected to produce complex vocal tasks with relatively invasive sensors employed. Although expanding the current efforts on the effects of acoustic coupling on tissue dynamics is planned, subject recruitment is expected to continue being a practical limitation. This issue also questions the applicability of pitch glide maneuvers as part of routine clinical assessment of vocal function, at least when it includes simultaneous observations of laryngeal dynamics.
CONCLUSIONS
This study introduced a comprehensive analysis of vocal fold tissue motion and related measurements during acoustically induced and source-induced unstable oscillations, aiming to further explore the theory of nonlinear coupling in phonation proposed by Titze (2008). Simultaneous recordings were used, including flexible and rigid laryngeal HSV, ACC, OVV, EGG, and MIC for different vocal gestures. Instabilities were labeled as acoustically induced when F0–F1 crossings were observed and, conversely, source-induced when not. The high-speed video recordings analyzed in this paper are believed to be the first fully documented in vivo visualizations of acoustically induced instabilities.
The results of this study suggest that differences between the two types of voice instabilities can be observed through laryngeal HSV. At the tissue level, acoustically induced vocal fold instabilities appeared to be more abrupt and exhibited LR PA observed as parallel wall motion, whereas source-induced instabilities showed a smoother transition between oscillatory modes. Irregularities after the bifurcation were detected in the acoustic, aerodynamic, and glottal dynamic behavior. It appears that strong acoustic coupling affects the tissue motion near a resistive vocal tract impedance regime, affecting its regularity and possibly suppressing AP differences that are associated to laryngeal configurations. The results also suggest that strong acoustic interaction can facilitate register transitions by adding an additional acoustic loading effect near transitional zones. Both types of breaks exhibited hysteresis and some degree of amplitude changes after the breaks which would link them to subcritical bifurcations. However, a rigorous hysteresis analysis was not possible as the subject tended to exhibit voice breaks in one of the pitch glide directions more than the other. Nevertheless, these results are in agreement with previous studies and support nonlinear source-filter coupling theory and descriptions of acoustic coupling in term of lumped impedances. Future numerical and experimental studies are needed to corroborate the observations in this case study.
ACKNOWLEDGMENTS
This work was supported by grants from the NIH National Institute on Deafness and Other Communication Disorders (Grant Nos. T32 DC00038 and R01 DC007640), the Institute of Laryngology and Voice Restoration, and the National Science Foundation (NSF, Grant No. CBET-0828903). The contents of this work are solely the responsibility of the authors and do not necessarily represent the official views of the NIH or the NSF.
Portions of this work were presented at the 157th meeting of the Acoustical Society of America in Portland, OR, in May 2009.
References
- Alipour, F., Montequin, D., and Tayama, N. (2001). “Aerodynamic profiles of a hemilarynx with a vocal tract,” Ann. Otol. Rhinol. Laryngol. 110, 550–555. [DOI] [PubMed] [Google Scholar]
- Austin, S. F., and Titze, I. R. (1997). “The effect of subglottal resonance upon vocal fold vibration,” J. Voice 11, 391–402. 10.1016/S0892-1997(97)80034-3 [DOI] [PubMed] [Google Scholar]
- Berry, D. A., Herzel, H., Titze, I. R., and Krischer, K. (1994). “Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions,” J. Acoust. Soc. Am. 95, 3595–3604. 10.1121/1.409875 [DOI] [PubMed] [Google Scholar]
- Berry, D. A., Herzel, H., Titze, I. R., and Story, B. H. (1996). “Bifurcations in excised larynx experiments,” J. Voice 10, 129–138. 10.1016/S0892-1997(96)80039-7 [DOI] [PubMed] [Google Scholar]
- Berry, D. A., Zhang, Z., and Neubauer, J. (2006). “Mechanisms of irregular vibration in a physical model of the vocal folds,” J. Acoust. Soc. Am. 120, EL36–EL42. 10.1121/1.2234519 [DOI] [PubMed] [Google Scholar]
- Bonilha, H. S., Deliyski, D. D., and Gerlach, T. T. (2008). “Phase asymmetries in normophonic speakers: Visual judgments and objective findings,” Am. J. Speech Lang. Pathol. 17, 367–376. 10.1044/1058-0360(2008/07-0059) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canny, J. F. (1986). “A computational approach to edge detection,” IEEE Trans. Pattern. Anal. Mach. Intell. 8, 679–698. 10.1109/TPAMI.1986.4767851 [DOI] [PubMed] [Google Scholar]
- Cheyne, H. A., Hanson, H. M., Genereux, R. P., Stevens, K. N., and Hillman, R. E. (2003). “Development and testing of a portable vocal accumulator,” J. Speech Lang. Hear. Res. 46, 1457–1467. 10.1044/1092-4388(2003/113) [DOI] [PubMed] [Google Scholar]
- Childers, D., and Chieteuk, A. (1995). “Modeling the glottal volume-velocity waveform for three voice types,” J. Acoust. Soc. Am. 97, 505–519. 10.1121/1.412276 [DOI] [PubMed] [Google Scholar]
- Curry, E. (1949). “Voice breaks and pathological larynx conditions,” J. Speech Disord. 14, 356–358. [DOI] [PubMed] [Google Scholar]
- Drechsel, J. S., and Thomson, S. L. (2008). “Influence of supraglottal structures on the glottal jet exiting a two-layer synthetic, self-oscillating vocal fold model,” J. Acoust. Soc. Am. 123, 4434–4445. 10.1121/1.2897040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Echternach, M., Dippold, S., Sundberg, J., Arndt, S., Zander, M. F., and Richter, B. (2010). “High-speed imaging and electroglottography measurements of the open quotient in untrained male voices’ register transitions,” J. Voice. 24(6), 644–650. 10.1016/j.jvoice.2009.05.003 [DOI] [PubMed] [Google Scholar]
- Harries, M. L. L., Walker, J. M., Williams, D. M., Hawkins, S., and Hughes, I. A. (1997). “Changes in the male voice at puberty,” Arch. Dis. Child. 77, 445–447. 10.1136/adc.77.5.445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatzikirou, H., Fitch, W. T., and Herzel, H. (2006). “Voice instabilities due to source-tract interactions,” Acta Acust. Acust. 92, 468–475. [Google Scholar]
- Herzel, H., Berry, D., Titze, I. R., and Saleh, M. (1994). “Analysis of vocal disorders with methods from nonlinear dynamics,” J. Speech Hear. Res. 37, 1008–1019. [DOI] [PubMed] [Google Scholar]
- Holmberg, E. B., Hillman, R. E., and Perkell, J. S. (1988). “Glottal airflow and transglottal air pressure measurements for male and female speakers in soft, normal, and loud voice,” J. Acoust. Soc. Am. 84, 511–529. 10.1121/1.396829 [DOI] [PubMed] [Google Scholar]
- Jiang, J. J., Zhang, Y., and Stern, J. (2001). “Modeling of chaotic vibrations in symmetric vocal folds,” J. Acoust. Soc. Am. 110, 2120–2128. 10.1121/1.1395596 [DOI] [PubMed] [Google Scholar]
- Kobler, J. B., Hillman, R. E., Zeitels, S. M., and Kuo, J. (1998). “Assessment of vocal function using simultaneous aerodynamic and calibrated videostroboscopic measures,” Ann. Otol. Rhinol. Laryngol. 107, 477–485. [DOI] [PubMed] [Google Scholar]
- Lohscheller, J., Eysholdt, U., Toy, H., and Döllinger, M. (2008). “Phonovibrography: Mapping high-speed movies of vocal fold vibrations into 2-D diagrams for visualizing and analyzing the underlying laryngeal dynamics,” IEEE Trans. Med. Imaging 27, 300–309. 10.1109/TMI.2007.903690 [DOI] [PubMed] [Google Scholar]
- Ma, W. Y., and Manjunath, B. S. (2000). “EdgeFlow: A technique for boundary detection and image segmentation,” IEEE Trans. Image Process. 9, 1375–1388. 10.1109/83.855433 [DOI] [PubMed] [Google Scholar]
- Mehta, D. D., Deliyski, D. D., Zeitels, S. M., Quatieri, T. F., and Hillman, R. E. (2010). “Voice production mechanisms following phonosurgical treatment of early glottic cancer,” Ann. Otol. Rhinol. Laryngol. 119, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mergell, P., Fitch, W. T., and Herzel, H. (1999). “Modeling the role of nonhuman vocal membranes in phonation,” J. Acoust. Soc. Am. 105, 2020–2028. 10.1121/1.426735 [DOI] [PubMed] [Google Scholar]
- Mergell, P., and Herzel, H. (1997). “Modelling biphonation—The role of the vocal tract,” Speech Commun. 22, 141–154. 10.1016/S0167-6393(97)00016-2 [DOI] [Google Scholar]
- Miller, D. G., and Schutte, H. K. (2005). “‘Mixing’ the registers: Glottal source or vocal tract?” Folia Phoniatr. Logop. 57, 278–291. 10.1159/000087081 [DOI] [PubMed] [Google Scholar]
- Miller, D. G., Švec, J. G., and Schutte, H. K. (2002). “Measurement of characteristic leap interval between chest and falsetto registers,” J. Voice 16, 8–19. 10.1016/S0892-1997(02)00066-8 [DOI] [PubMed] [Google Scholar]
- Neubauer, J., Mergell, P., Eysholdt, U., and Herzel, H. (2001). “Spatio-temporal analysis of irregular vocal fold oscillations: Biphonation due to desynchronization of spatial modes,” J. Acoust. Soc. Am. 110, 3179–3192. 10.1121/1.1406498 [DOI] [PubMed] [Google Scholar]
- Osma-Ruiz, V., Godino-Llorente, J. I., Saenz-Lechon, N., and Fraile, R. (2008). “Segmentation of the glottal space from laryngeal images using the watershed transform,” Comput. Med. Imaging Graph. 32, 193–201. 10.1016/j.compmedimag.2007.12.003 [DOI] [PubMed] [Google Scholar]
- Steinecke, I., and Herzel, H. (1995). “Bifurcations in an asymmetric vocal-fold model,” J. Acoust. Soc. Am. 97, 1874–1884. 10.1121/1.412061 [DOI] [PubMed] [Google Scholar]
- Švec, J. G., Schutte, H. K., and Miller, D. G. (1999). “On pitch jumps between chest and falsetto registers in voice: Data from living and excised human larynges,” J. Acoust. Soc. Am. 106, 1523–1531. 10.1121/1.427149 [DOI] [PubMed] [Google Scholar]
- Švec, J. G., Šram, F., and Schutte, H. K. (2007). “Videokymography in voice disorders: What to look for?” Ann. Otol. Rhinol. Laryngol. 116, 172–180. [DOI] [PubMed] [Google Scholar]
- Švec, J. G., Sundberg, J., and Hertegård, S. (2008). “Three registers in an untrained female singer analyzed by videokymography, strobolaryngoscopy and sound spectrography,” J. Acoust. Soc. Am. 123, 347–353. 10.1121/1.2804939 [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (1988a). “A framework for the study of vocal registers,” J. Voice 2, 183–194. 10.1016/S0892-1997(88)80075-4 [DOI] [Google Scholar]
- Titze, I. R. (1988b). “The physics of small-amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 83, 1536–1552. 10.1121/1.395910 [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2000). Principles of Voice Production (National Center for Voice and Speech, Iowa City, IA: ), pp. 293–301. [Google Scholar]
- Titze, I. R. (2004). “A theoretical study of F0-F1 interaction with application to resonant speaking and singing voice,” J. Voice 18, 292–298. 10.1016/j.jvoice.2003.12.010 [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2008). “Nonlinear source-filter coupling in phonation: Theory,” J. Acoust. Soc. Am. 123, 2733–2749. 10.1121/1.2832337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titze, I. R., Riede, T., and Popolo, P. (2008). “Nonlinear source-filter coupling in phonation: Vocal exercises,” J. Acoust. Soc. Am. 123, 1902–1915. 10.1121/1.2832339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titze, I. R., and Worley, A. S. (2009). “Modeling source-filter interaction in belting and high-pitched operatic male singing,” J. Acoust. Soc. Am. 126, 1530–1540. 10.1121/1.3160296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokuda, I. T., Horáček, J., Švec, J. G., and Herzel, H. (2007). “Comparison of biomechanical modeling of register transitions and voice instabilities with excised larynx experiments,” J. Acoust. Soc. Am. 122, 519–531. 10.1121/1.2741210 [DOI] [PubMed] [Google Scholar]
- Tokuda, I. T., Horáček, J., Švec, J. G., and Herzel, H. (2008). “Bifurcations and chaos in register transitions of excised larynx experiments,” Chaos 18, 013102. 10.1063/1.2825295 [DOI] [PubMed] [Google Scholar]
- Tokuda, I. T., Zemke, M., Kob, M., and Herzel, H. (2010). “Biomechanical modeling of register transitions and the role of vocal tract resonators,” J. Acoust. Soc. Am. 127, 1528–1536. 10.1121/1.3299201 [DOI] [PubMed] [Google Scholar]
- van den Berg, J. (1957). “Subglottal pressures and vibration of vocal folds,” Folia Phoniatr. 9, 6571. [PubMed] [Google Scholar]
- van den Berg, J. (1968). “Register problems,” Ann. N.Y. Acad. Sci. 155, 129–134. 10.1111/j.1749-6632.1968.tb56756.x [DOI] [PubMed] [Google Scholar]
- Zañartu, M., Ho, J. C., Kraman, S. S., Pasterkamp, H., Huber, J. E., and Wodicka, G. R. (2009). “Air-borne and tissue-borne sensitivities of acoustic sensors used on the skin surface,” IEEE Trans. Biomed. Eng. 56, 443–451. [DOI] [PubMed] [Google Scholar]
- Zañartu, M., Mongeau, L., and Wodicka, G. R. (2007). “Influence of acoustic loading on an effective single mass model of the vocal folds,” J. Acoust. Soc. Am. 121, 1119–1129. 10.1121/1.2409491 [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2006a). “Aerodynamically and acoustically driven modes of vibration in a physical model of the vocal folds,” J. Acoust. Soc. Am. 120, 2841–2849. 10.1121/1.2354025 [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2006b). “The influence of subglottal acoustics on laboratory models of phonation,” J. Acoust. Soc. Am. 120, 1558–1569. 10.1121/1.2225682 [DOI] [PubMed] [Google Scholar]