The article by Loram et al. (2011) in a recent issue of The Journal of Physiology addresses three questions about the human control of an inverted pendulum or, more generally, an unstable load: (1) Is continuous control necessary? (2) Is intermittent control effective? (3) Is intermittent control physiological? The given answers (one ‘no’ and two ‘yeses’) are supported, in a convincing way, by experimental and theoretical arguments, thus providing sound arguments for the idea that intermittent control by ‘gentle taps’ is firmly in the human repertoire of basic motor skills for mastering unstable loads.
However, the dualism between continuous and intermittent control tells only part of the story. Both paradigms are indeed characterized by positional feedback via neural processes but this is not the only relevant mechanism available to the brain for solving stabilization tasks: a feasible alternative is provided by the intrinsic elastic properties of the human muscles (including tendons and ligaments), i.e. a zero-delay, positional feedback mechanism, with a gain that can be modulated by means of coactivation of antagonistic muscles.
Unstable tasks are characterized by an instability parameter that can be interpreted as a negative stiffness, e.g. the rate of growth of the gravity toppling torque at the ankle joint of a standing human. If joint stiffness is larger than such ‘critical’ value, then asymptotic stabilization of the load is provided by the intrinsic elastic properties, without any need for neural positional feedback. We may use the ‘brute force’ label for this stabilization strategy in order to emphasize that critical stiffness requires a high degree of muscle activation and thus a large effort. On the other hand, this mechanism has a large frequency band because the feedback delay is null.
In contrast, if intrinsic feedback is too weak or even null (as in the target article), then positional feedback, typically in the form of a sequence of control bursts (‘gentle taps’), becomes the only available mechanism, with a rather low effort level but with a limited operational bandwidth due to the large feedback delay.
Examples of both mechanisms, in the ‘pure’ form, can be found in the literature: the target article is an example of ‘pure intermittent positional strategy’; the stabilization of a robot-generated divergent force-field (DF) (Burdet et al. 2001) is an example of ‘pure stiffness strategy’. Human upright standing is an example of a hybrid strategy because the ankle stiffness in quiet standing is only about 70% of the critical level (Casadio et al. 2005) and the missing, crucial control action is provided by intermittent stabilization commands.
A number of questions then come to mind: Could people, in principle, apply a stiffness strategy in upright standing or an intermittent strategy in the compensation of a divergent field? How do they choose one strategy or the other? The negative answer to the first question is justified by the experimental finding (Loram et al. 2007) that ankle stiffness is dominated by the soft, linear Achilles tendon: this rules out the possibility of modulating stiffness by muscle coactivation. In this case, ‘brute force’ would not work and thus the human brain is forced to add some ‘gentle taps’ to the control of the standing posture. In contrast, the subjects recruited by Burdet et al. (2001) in the DF experiments do not exhibit any hint of applying the ‘gentle taps’ strategy but consistently manage to learn the coactivation patterns that provide the optimal impedance ellipse for the task. Why is it? The answer can be found by considering the band-limited characteristic of neural positional feedback and the fact that the falling time constant (see note), which can be evaluated from the parameters of the experimental setup, is below 100 ms, too short for a successful ‘gentle taps’ stabilization. On the contrary, the falling time constant of the target article is 916 ms, which is quite compatible with the frequency band of an intermittent mechanism. Humans indeed can manage to solve the pole balancing task for a pole length as short as about 30 cm, which corresponds to a time constant of about 175 ms.
In summary, humans appear to able to adopt either the ‘gentle taps’ or the ‘brute force’ strategy in different situations but the experimental conditions of most studies, as the ones considered above, do not give the subjects the chance of a choice. An exception is a recent preliminary study with an experimental set-up specifically designed in order to give the subjects the possibility to choose one strategy or the other (Saha & Morasso, 2010). In this study subjects operate a bimanual, elastic manipuladum in order to carry out reaching movements in a saddle-like unstable field; the elastic linkages of the manipulandum are non-linear (the length-tension curve is quadratic) and this allows the subjects to affect the stiffness ellipse by controlling the distance between the two terminals. The results show that subjects do not choose the same strategy but split into two groups of approximately equal size: one group spreads apart the two hands, up to the point where critical stiffness is reached, and the other group keeps the two hands close to each other and keeps balance by gentle taps. It appears then that people rank in a different manner the pros and cons of the two stabilization strategies: asymptotic stability and high effort level of ‘brute force’vs. bounded stability and low effort level of ‘gentle taps’.
Note
Second order unstable loads can be characterized by a differential equation of the following type: 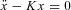 . This applies to the inverted pendulum, the virtual load of the target article, the divergent force field paradigm, etc. and the parameter K is determined by the design of the experimental set-up. The equation has two real poles of opposite sign:
. This applies to the inverted pendulum, the virtual load of the target article, the divergent force field paradigm, etc. and the parameter K is determined by the design of the experimental set-up. The equation has two real poles of opposite sign: 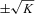 . The positive pole is the one that determines the unstable behaviour: starting from the equilibrium point
. The positive pole is the one that determines the unstable behaviour: starting from the equilibrium point 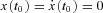 , any arbitrarily small disturbance will trigger a ‘fall’, i.e. an exponentially growing deviation from the equilibrium position x(t) ∝et/τ, where the ‘falling time constant’τ is equal to
, any arbitrarily small disturbance will trigger a ‘fall’, i.e. an exponentially growing deviation from the equilibrium position x(t) ∝et/τ, where the ‘falling time constant’τ is equal to 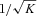 .
.
References
- Burdet E, Osu R, Franklin DW, Milner TE, Kawato M. Nature. 2001;414:446–449. doi: 10.1038/35106566. [DOI] [PubMed] [Google Scholar]
- Casadio M, Morasso P, Sanguineti V. Gait Posture. 2005;21:410–424. doi: 10.1016/j.gaitpost.2004.05.005. [DOI] [PubMed] [Google Scholar]
- Loram ID, Gollee H, Lakie M, Gawthrop PJ. J Physiol. 2011;589:307–324. doi: 10.1113/jphysiol.2010.194712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loram I, Maganaris C, Lakie M. J Physiol. 2007;582:677–692. doi: 10.1113/jphysiol.2007.140053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saha D, Morasso P. Viareggio: 2010. Bimanual control of an unstable task: stiffness versus intermittent control strategy. Proceedings of IEEE RO-MAN2010 September 12–15. [Google Scholar]


