Integrin Organization: Linking Adhesion Ligand Nanopatterns with Altered Cell Responses

Abstract

Integrin receptors bind to adhesion ligand (e.g. arginine-glycine-aspartic acid or RGD containing peptides) on extracellular matrix and organize into high-density complexes which mediate many cell behaviors. Biomaterials with RGD nanopatterned into multivalent “islands” (∼30-70 nm diameter) have been shown to alter cell responses, although the length scale of pattern features is orders of magnitude smaller than adhesion complexes. In this work, we employ together for the first time an extensive data set on osteoblast responses as a function of ligand nanopatterns, a computational model of integrin binding to ligand nanopatterns, and new measures of integrin organization on the cell surface. We quantify, at multiple length scales, integrin organization generated in silico as a function of RGD nanopattern parameters. We develop a correlative model relating these measures of in silico integrin organization and in vitro MC3T3 preosteoblast cell responses as functions of the same RGD nanopatterns: cell spreading correlates with the number of bound integrins, focal adhesion kinase (FAK) phosphorylation correlates with small, homogeneously distributed clusters of integrins, and osteogenic differentiation correlates with large, heterogeneously distributed integrin clusters. These findings highlight the significance of engineering biomaterials at the nanolevel and suggest new approaches to understanding the mechanisms linking integrin organization to cell responses.

Introduction

Integrins, the primary family of receptors responsible for cell adhesion to surrounding extracellular matrix (ECM) molecules, are known to mediate many key cellular processes. Interactions between integrins and their ligands can be described as a multi-step process leading to the formation of adhesion complexes. Integrin organization is initialized by the formation of submicroscopic integrin clusters (∼3 to 4 integrins/cluster), many of which together organize into “nascent adhesions” (Wiseman et al., 2004) within about 15 minutes of cell-surface contact (Gallant et al., 2005). Nascent adhesions recruit cytoskeleton proteins (e.g. vinculin, actin) and signaling molecules (e.g. paxillin, focal adhesion kinase or FAK) and with time form mature adhesion complexes, the most stable of which are focal adhesions (Petit and Thiery, 2000). It is the recruitment of signaling molecules and cytoskeleton proteins to sites of integrin organization within the cell membrane that result in the local mechanical and chemical changes required to turn a nascent adhesion into a mature adhesion complex (Miyamoto et al., 1995; Bershadsky et al., 2006; Gallant and Garcia, 2006; Critchley 2004). Integrin-mediated signaling within adhesion complexes is known to control critical cell behaviors, including proliferation, differentiation and apoptosis (Cowles et al., 2000; Danen and Yamada, 2001; Davey et al., 1999, Franceschi et al., 2003; Takeuchi et al., 1997; Chen et al., 1997).

Yet little is understood about which aspects of integrin organization (e.g. the number of integrins per submicroscopic cluster or the distribution of submicroscopic clusters) are likely to promote the downstream chemical and mechanical conditions that elicit particular cellular responses. In this work, we employ together for the first time an extensive data set on osteoblast responses as a function of ligand nanopatterns, a computational model of integrin binding to ligand nanopatterns, and measures of molecular organization developed in the field of colloid sciences. This combination allows us to ask a novel and important question: are there features of integrin organization that are highly correlated with three different cell responses – cell spreading, focal adhesion kinase (FAK) phosphorylation, and osteogenic differentiation – and, if so, what are those features?

We focus on the length scale of integrin organization. At the molecular scale, organization of integrins into nascent adhesions appears to be driven by multiple integrin actions: lateral diffusion within the cell membrane, binding to and dissociation from adhesion ligand presented on an underlying surface and clustering (Harbers and Healy, 2005; Petri et al., 2006; Kato and Mrksich, 2004; Arnaout, 2002; Miyamoto et al., 1995). This clustering is caused in part by integrin dimerization (Yauch et al., 1997; Li et al., 2004; Humphries, 2004; Vitte et al., 2004; Brinkerhoff et al., 2004; Brinkerhoff and Linderman, 2005). Integrin clustering at the resolution of single integrins cannot be measured with current experimental techniques, but computational models have been developed to simulate integrin clustering at the molecular scale (Brinkerhoff and Linderman, 2005; Irvine et al., 2002) and have been validated by comparison with some measurable aspects of cell adhesion, including the average size of a submicroscopic cluster as reported by Wiseman et al. (2004). These models simulate integrin binding and clustering arising in the presence of adhesion ligand but without any cytoskeletal or signaling molecules; it is not known whether such models are sufficient to predict ensuing cell behavior.

Considerable efforts by many groups have been devoted to developing model ECMs and biomaterials that modulate integrin binding in order to manipulate cell responses, by varying the type and bulk density of adhesion ligand and by nanopatterning an adhesion ligand (e.g. Huang et al. 2009; Irvine, et al., 2001; Harbers and Healy, 2005; Petrie et al., 2006; Alsberg et al., 2001; Yang et al., 2005; Cutler and Garcia, 2003; Reyes and Garcia, 2004; Stephansson et al., 2002; Liu and Tirrell 2008). Nanopatterning the adhesion ligand arginine-glycine-aspartic acid (RGD) into multivalent “islands” has been shown to alter critical cell responses including cell adhesion, migration, signaling (i.e. autophosphorylation of FAK—pFAK Y397 (Alberts et al., 2002; Guan, 1997), and differentiation (Lee et al., 2004; Maheshwari et al., 2000; Koo et al., 2002). We recently demonstrated an effect of RGD nanopatterns on cell spreading, FAK phosphorylation, and osteogenic differentation by MC3T3 preosteoblast cells (Comisar et al., 2007), using statistical analyses to determine which pattern parameters significantly affect each cell response. While this experimental work examines the widest range of RGD nanopatterns and the largest number of cell responses to date, the relationship between cell responses and integrin organization remains unknown and is our focus here.

The length scale of the RGD pattern features (10s to 100s of nanometers) suggests that the mechanism by which patterns influence cells is at the sub-adhesion complex level. If an adhesion complex is considered a “long” length scale (∼ micron), then sub-adhesion integrin organization can be at intermediate lengths (∼50 to ∼500 nm) or at short lengths on the order of a few integrins (<50 nm—a single integrin is 10 nm in diameter (Erb et al., 1997; Nermut et al., 1988)). Here, we propose a novel approach to describing integrin organization that captures both integrin binding and clustering at short and intermediate length scales. We develop a method to quantify the complex stochastic patterns of integrin organization associated with integrin binding by using measures of particle organization borrowed from the field of colloid sciences. Model-generated “snapshots” of integrin organization within nascent adhesions bear a striking similarity to confocal microscope images taken of colloidal gels (Dibble et al., 2006). Colloids are suspensions of micron-sized particles in a support phase in which short range particle interactions create long range order through a process called gelation (Varadan and Solomon, 2003). Similarly, cell adhesion occurs when local interactions at the nanometer scale (i.e. integrin-ligand binding and integrin-integrin dimerization) create highly organized micron-scale adhesion complexes. Weak colloidal gels contain large clusters of particles that are heterogeneously distributed throughout the gel, while strong gels contain small clusters of particles that are homogeneously distributed throughout the gel. These differences in particle organization lead to significant structural differences between weak and strong gels. Here, we propose that differences in integrin organization generated by different RGD nanopattern parameters could similarly be responsible for the effect of RGD nanopatterns on altered cell responses. To test this, we develop a correlative model to link measures of integrin organization as a function of RGD nanopatterns in silico with a previously published data set (Comisar et al., 2007) that reported in vitro cell responses as functions of the same RGD nanopatterns. This correlative model quantifies which differences in integrin organization correlate with particular cell responses, allowing us both to develop testable hypotheses regarding underlying biological mechanism(s) and propose directions for future scaffold design.

Methods

Parameters characterizing a nanopatterned surface

The methods to create RGD nanopatterned biomaterials containing multivalent RGD islands involve random mixing of RGD-coupled polymer chains with blank polymer molecules. First, a number of RGD molecules are covalently coupled to a single polymer molecule. These RGD-coupled polymer molecules are referred to as islands. The number of RGDs per polymer molecule is referred to in experimental work as the degree of substitution (d.o.s.). Because not all RGDs are likely to be available for binding (some will be found at integrin-inaccessible locations in the polymer (Comisar et al., 2006)), the number of ligands in an island actually available for binding will be referred to in this work as RGDs/island (≤d.o.s.). A fraction of RGD-coupled islands (fraction coupled, or F.C.) are randomly mixed with blank polymer molecules to space the islands within the polymer. As an example, Fig. 1 shows two different RGD nanopatterns with the same RGD bulk density (proportional to the product of RGDs/island and F.C.). When RGDs/island is low (Fig. 1b), the intra-island RGD spacing is higher than when RGDs/island is high (Fig. 1a). When F.C. is low (Fig. 1a), there are fewer islands on the surface and the islands are on average farther apart compared to when F.C. is high (Fig. 1b).

Figure 1. RGD nanopatterned polymer.

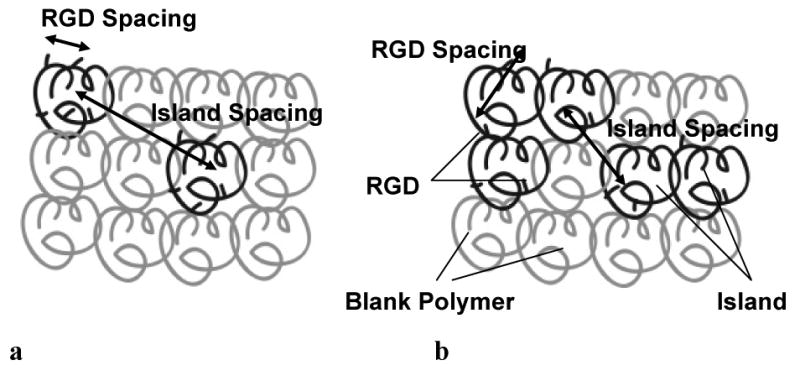
(a) 5 RGDs/island; F.C.=2/12 (b) 2 RGDs/island; F.C.=5/12. Both (a) and (b) have the same RGD bulk density (RGD/unit area).

Integrin Binding/Clustering Model

Integrin binding and clustering during cell adhesion to an RGD-containing surface were simulated using a Monte Carlo (stochastic) model adapted and updated from Brinkerhoff and Linderman (2005). Briefly, adhesion ligand was placed on a 2-D “adhesive surface” lattice. A second “cell membrane” lattice containing integrin receptors was created overlaying the adhesion ligand lattice. Integrins on the cell membrane were permitted to diffuse laterally, bind to and dissociate from ligand, and dimerize with and dissociate from other integrins (Supplementary Fig. 1). The probabilities of these events were related to the relevant kinetic rate constants, for which physiological values were estimated from the literature (see below). An integrin density of 1000 integrins per square micron, close to the measured integrin density within nascent adhesions, was used (Wiseman et al., 2004). Model results are consistent with the data of (Wiseman et al., 2004), who report submicroscopic integrin clusters of 3-4 integrins (data not shown).

In this work, the algorithm for creating the adhesion ligand lattice was modified to reflect RGD nanopatterns used in the experimental work (Comisar et al., 2007). Results from simulations of island location (Lee et al., 2004) and RGD location within islands (Comisar et al., 2006) were used. The polymer properties (i.e. alginate stiffness, chain molecular weight, and polymer weight/volume) as reported in Comisar et al. (2007) were used to calculate the number of chains that would be located within the 1.5 by 1.5 micron adhesion surface lattice simulated. The centers of mass of the chains were arranged in a hexagonal close-pack array (i.e. on the vertices of a triangular lattice). A fraction of the chains (F.C.) were randomly selected to be RGD-coupled (i.e. “islands”). RGDs were randomly laid down within one island radius of the center of mass of the island. Island radius was equal to the radius of gyration of an alginate chain as previously reported (Comisar et al., 2006) and was 34.5 nm for the polymer used in the experimental work. The number of RGDs/island was equal to the degree of substitution (d.o.s.) × accessibility, where accessibility was the estimated fraction of RGDs available for integrin binding. All model results in this work are reported in terms of RGDs/island, while experimental data referenced from previous work reported d.o.s.

Simulations were performed with five values of F.C. (0.1, 0.2, 0.3, 0.5 and 0.7) and eight values of RGDs/island (1, 2, 3, 5, 6, 9, 10, and 15) for a total of 40 different RGD nanopatterns. The values of F.C. corresponded to those used in the experimental work; RGDs/island corresponded to experimental values of d.o.s. (5, 15, 25) for a range of values of RGD accessibility. Estimates of 20% to 40% accessibility have been reported based on alginate simulations (Comisar et al., 2006), while experimental work (Kong et al., 2006) suggests that accessibility is likely significantly higher than 20%. Therefore, an accessibility of 40% was chosen for analyzing cell spreading and FAK phosphorylation data; similar conclusions can be drawn with accessibilities ranging from ∼30% to ∼50% (data not shown). Because osteocalcin data were collected using cells seeded in liquid alginate prior to crosslinking, which may allow a greater accessibility than for cells seeded onto pre-crosslinked alginate (the procedure used for collection of spreading and FAK data) (Kong et al., 2006), an accessibility of 55% was chosen in analyzing the osteocalcin data; similar conclusions can be drawn with accessibilities ranging from ∼50% to ∼100%.

Simulations were run until steady state was reached. Thus the model generated steady state “snapshots” of the cell membrane lattice; snapshots at three time points (to account for stochastic fluctuations) were saved for later analysis. These snapshots contained the x and y coordinates and the state (bound/unbound and dimerized/undimerized) of each integrin receptor.

Simulation parameter values

The rates at which molecules “find” each other by diffusion (just prior to binding) are not set but are the result of our simulations. However, we still need to estimate the intrinsic rate constants for the interaction of two molecules already close to each other. The dissociation of RGD from α_IIbβ₃ integrins has been measured as k_unbind = 0.2-22 s^-1 (Lee and Marchant, 2001; Goldsmith et al. 2000). The association constant k_bind for RGD binding can be estimated from k_unbind/K_D^2d where K_D^2d, the two-dimensional equilibrium dissociation constant (because RGD and integrin are both confined to surfaces) can be estimated from 4/3*R_encK_D^3d (Ward and Hammer 1994; Bell 1978). R_enc is the encounter radius of ∼ 0.1 nm (Lee and Marchant, 2001). With the three-dimensional equilibrium dissociation constant K_D^3d in the range of 10^-7-10^-6 M (Pierschbacher and Ruoslahiti, 1984), k_bind is estimated to be on the order of 10^-8 – 10^-5 cm²/s (using Avogodro's number to convert to more typical units for two-dimensional reactions).

Considering dimerization of integrins, the diffusion-limited rate constant k₊ can be used to estimate a value of k_mono, although k₊ is not used in simulations (which track diffusion explicitly). k₊ can be estimated from 2πD/ln(b/R_enc) where D is the translational diffusion coefficient (∼ 10^-11-10^-10 cm²/s), b is half the mean distance between integrins (∼ 20 nm) and R_enc is the encounter radius between two integrin monomers (∼ 2.5 nm), giving an estimated value of k+ in the range of 3×10^-11 cm²/s – 3×10^-10 cm²/s; more accurately the units are (#/cm²)^-1s^-1 (Brinkerhoff and Linderman 2005; Lauffenburger and Linderman 1993). One can convert this to more typical units by multiplying the two-dimensional rate constant by an estimated membrane thickness h (∼ 10 nm) and using Avogadro's number to get a range for k₊ of 2 × 10⁴ M^-1s^-1 – 2 × 10⁵ M^-1s^-1. The rate constant k_mono is estimated as K_D* k₊, where K_D is the equilibrium diffusion coefficient for integrin dimerization in solution, 0.0001-0.01 M (Li et al. 2001). Thus k_mono is on the order of 2 s^-1 to 2000 s^-1. A rough estimate for k_dimer of ∼ 10⁵ s^-1 can be made by considering how molecules might rotate to achieve the correct alignment for binding (Woolf and Linderman, 2003).

Probabilities of these reactions for use in simulations can be derived from the rate constants according to

$$P_{\mathit{\text{rxn}}}=1-\text{exp}(-k\Delta t)\approx k\Delta t$$ (1)

where k is the relevant reaction rate constant and Δt is the iteration time step (Rowley 1994). (The second order rate constant k_bind must first be divided by an estimate of the encounter area, ∼ R²_enc). For the simulations presented in the main body of the paper, parameter values used were chosen from within the ranges above: k_unbind = 1 s^-1, k_bind = 10^-7 cm²/s, k_mono = 100 s^-1, k_dimer = 10⁵ s^-1. The iteration time step Δt = 10^-6 s. Broader ranges for the parameter values were also explored and results are described in the supplement.

For a single particle exhibiting Brownian diffusion on a triangular lattice, the probability of moving at least one lattice spacing l in one iteration time step is

$$P_{\mathit{\text{move}}}=1-\text{exp}(\frac{-6\Delta \mathit{\text{tD}}}{l^2})\approx \frac{6\Delta \mathit{\text{tD}}}{l^2}$$ (2)

Integrin Organization Analysis

Although multiple methods were explored to quantify integrin organization in simulations, three measures exhibiting the closest correlation with experimental data are reported here: integrins bound, contact number, and bound number density fluctuation (BNDF).

Integrins Bound

The mean number of integrins bound to ligand was calculated and reported as a function of the RGD nanopattern parameters input into the simulation.

Contact Number

Contact number¹, a measure of short range (<50 nm) integrin clustering, is equal to the average number of integrins within a specified cut-off radius of a selected integrin, averaged across all integrins (Dibble et al., 2006; Varadan and Solomon, 2003). For colloids, the interaction distance between particles (corresponding to our cut-off radius) can be calculated based on the first minimum in the pair-correlation function. Because it is not obvious what the maximum distance between integrins still considered to be part of the same sub-microscopic cluster should be, multiple distances (cut-off radii of 18, 27, and 36 nm) that approximately corresponded to the length scale of submicroscopic integrin clusters were tested.

Bound Number Density Fluctuation (BNDF)

BNDF is a measure of intermediate length scale (∼50 to 500 nm) integrin organization (i.e. clustering and binding), and quantifies the distribution of clusters of bound integrins (Dibble et al., 2006; Varadan and Solomon, 2003). The higher the BNDF, the more heterogeneously the clusters are distributed throughout a system; a lower limit of zero corresponds to maximum homogeneity. To calculate BNDF, the model-generated cell membrane lattice was divided into a grid with boxes of side length L. The number of bound integrins in each box, N, was counted, and BNDF was computed by:

$$\mathit{\text{BNDF}}=(<N^{\mathit{2}}>-<N{>}^{\mathit{2}})/N$$ (1)

This was repeated for L= 50 nm to 500 nm. (For L<50 nm, the number of boxes is much greater than the number of integrins, resulting in loss of informational value of the measure. For L>500nm, the number of boxes approaches one in which case BNDF is always zero.) BNDF was plotted against r/L where r was the radius of an integrin (4.5 nm). The area under the curve (AUC) was calculated using the midpoint rule to geometrically integrate each curve from L=50 to 500 to give a measure of heterogeneity across the entire intermediate length scale.

Data binning

Because of small local fluctuations in the measures of integrin organization (an artifact of the method used to calculate contact number and BNDF), and significant noise in the experimental data, correlations between in silico integrin organization and experimental data on cell responses were more apparent when noise was reduced through binning. Experimental data were binned into two (cell spreading) or three (FAK phosphorylation and osteocalcin) levels. The upper and lower limits of each bin were selected so that both the mean and the standard error of as many conditions as possible fell entirely within a given bin. Similarly, each measure of integrin organization was binned into three levels: high, medium, and low. The boundaries between levels were assessed based on how rapidly changes in integrin organization occurred given a small change in RGD nanopattern parameters.

Comparison of Simulation and Experimental Data

Multiple methods were tested for finding correlations between integrin patterns and experimental data. For example, a quantitative approach (multiple linear regression) was initially applied to model the relationship between integrin organization and cell responses; both transformed (e.g. log transformed) and untransformed variables were tested. However, the significant experimental noise and variability in the data set as well as the small number of experimental conditions compared to the large number of potential measures of integrin organization made this approach unfeasible. Because the data used (Comisar et al., 2007) represents the largest, most complete data set to date, a different approach was needed.

Correlations between experimentally measured cell responses and model-generated measures of integrin organization were determined both graphically and by computing conditional probabilities. To assess correlations between integrin organization and cell responses, the discretized experimental data were overlaid onto plots of each measure of integrin organization as a function of F.C. and RGDs/island. To quantify these correlations, conditional probabilities were calculated as described in Walpole et al. (1998):

$$P(Y|X)=P(Y\cap X)/P(X)$$ (2)

where Y is the level of experimentally measured cell response, and X is the level of the measure of integrin organization. Because there were only fifteen experimental conditions, some discrete levels of X or Y contained only one or two data points, thus reducing the information value of the probability calculation. In such situations, levels were combined as appropriate (e.g. medium and low levels of integrins bound were combined) and the conditional probability recalculated. Although conditional probabilities for every combination of cell response and measure of integrin organization were calculated, only correlations with P(Y|X)>0.8 were considered significant enough to report.

Results

Snapshots of integrin organization as a function of ligand nanopattern

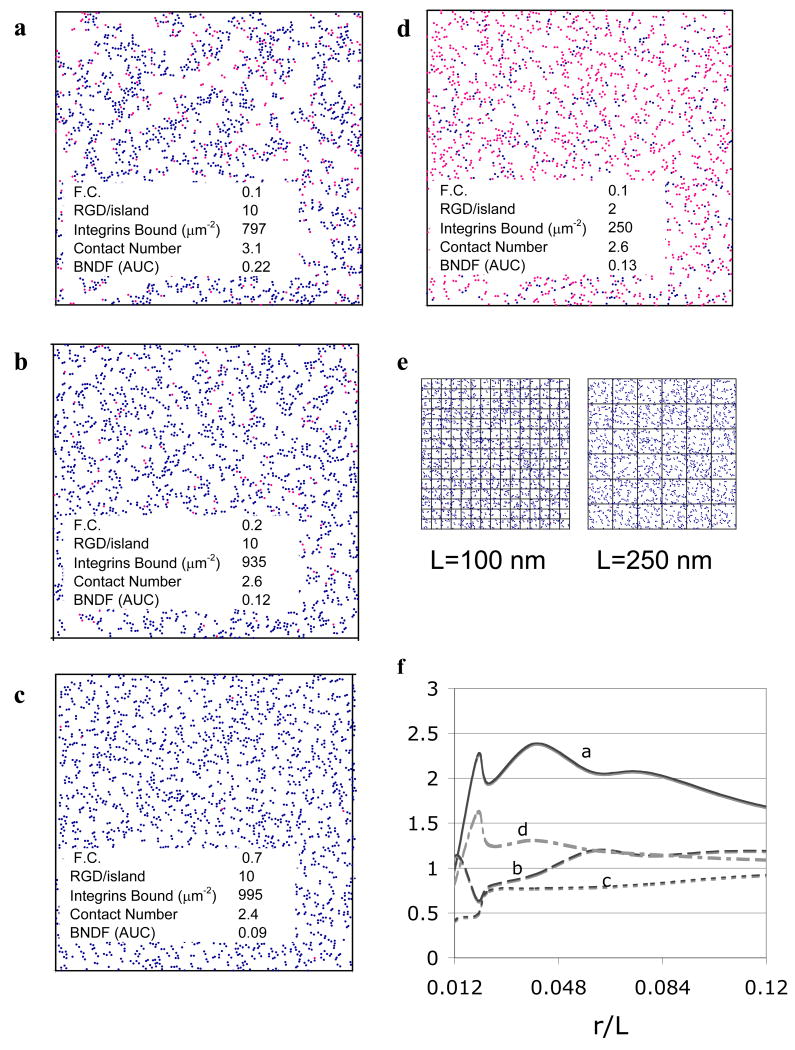
Different ligand nanopatterns produce strikingly different patterns of integrin organization, as shown in the model-generated “snapshots” of Fig. 2. RGD nanopatterning influenced both the number of integrins bound and the short-range organization of integrins into clusters (<50 nm length scale—approximately the size of RGD islands), as expected. In addition, different RGD nanopatterns resulted in distinct differences in integrin organization at intermediate (50-500 nm) length scales. Both F.C. and RGDs/island affected integrin organization at both sub-adhesion complex length scales. The number of integrins bound increases with F.C. and RGDs/island. At intermediate to high numbers of RGDs/island, low values of F.C. result in large, heterogeneously distributed integrin clusters (Fig. 2a). As F.C. increases, clusters become smaller and more homogeneously distributed (Fig. 2b,c). When the number of RGDs/island is small, however, integrins organize into small, more homogeneously distributed clusters even at low values of F.C. (Fig. 2d).

Figure 2. Model-generated integrin organization.

a-d) The (x,y) coordinates and binding status of each integrin on the simulated membrane lattice were plotted for one steady state simulation time step (● unbound, ● bound). Figures depict the entire simulated membrane (1.5 × 1.5 μm²) for input values of F.C. and RGDs/island shown. Simulation outputs of integrins bound, contact number, and BNDF (AUC) are listed. e) To calculate BNDF, the cell membrane lattices were divided into boxes of length L. The number N of bound integrins in each box was counted and BNDF calculated per Eqn. (1). f) BNDF versus r/L (r = 4.5 nm, the radius of an integrin) calculated from the images in a-d are shown.

Quantitative measures of integrin organization as a function of ligand nanopattern

The striking qualitative differences in integrin organization that can be seen in Fig. 2 (ad) suggest that there may be ways to quantify integrin organization in searching for correlations between integrin organization and experimentally measured changes in cell behavior. A large number of potential measures of integrin organization were examined; three measures were adopted for the final correlative model based on both the strength of their correlation with experimentally measured cell behavior and their biological relevance. Integrins bound quantifies the number of total integrins bound to ligand. Contact number quantifies the short-range organization of integrins into clusters (<50 nm length scale) by counting the average number of integrins within a 27 nm cut-off radius of a selected integrin². BNDF characterizes the distribution of clusters of bound integrins across the adhesive complex at an intermediate length scale (∼50 to 500 nm). Fig. 2e shows grids of length L laid over the integrin organization from Fig. 2c; calculation is per Eqn. (1). BNDF as a function of r/L (r is the radius of an integrin, L is the size of a box of the grid) is shown in Fig. 2f with L ranging from 50 to 500 nm. The RGD nanopattern F.C.=0.1 and 10 RGDs/island (Fig. 2a) generated the most heterogeneous integrin organization at intermediate length scales. Peaks in the curves of Fig. 2f reflect the length scale of maximum heterogeneity and approximately correspond to the diameter of a cluster of integrins and the size of the voids between clusters (large clusters of integrins separated by large voids can be seen in Fig. 2a), while a lack of peaks at any of these length scales indicates small clusters of integrins (<50 nm diameter—as in Fig. 2c). The area under the curve (AUC) of BNDF versus r/L was calculated and used as the measure of BNDF in this work.³

All three measures of integrin organization (integrins bound, contact number, and BNDF) were calculated for a range of ligand nanopatterns. The number of integrins bound was a direct function both of RGDs/island and F.C. BNDF and contact number were particularly interesting in their strong relationship to the number and spacing of islands (i.e. F.C.). Low BNDF and contact number resulted when F.C. was high (>0.3) regardless of the number of RGDs/island because the large number of closely spaced islands nucleated many submicroscopic integrin clusters. The maximum size that each of these submicroscopic integrin clusters could reach was limited by the total number of integrins (for >5 RGDs/island—Fig. 2c) or by the total number of ligands when RGDs/island was small (i.e. <5).

In contrast, when F.C. was low (<0.3), the small number of islands nucleated a small number of submicroscopic integrin clusters. When RGDs/island was small (i.e. <5 RGDs/island—Fig. 2d), BNDF and contact number were also small. However, when RGDs/island was high (i.e. >5 RGDs/island—Fig. 2a), each submicroscopic integrin cluster grew quite large. Because the stochastic placement of islands resulted in a small fraction of islands grouped together even at low values of F.C. (Lee et al., 2004), the size of some integrin clusters increased even above the number of RGDs/island. This resulted in a high level of heterogeneity and high contact number. Significantly, simulations with uniformly spaced islands separated by blank alginate did not exhibit this increase in BNDF and contact number at low values of F.C. (data not shown), suggesting that patterning ligands via the random mixing of blank and RGD-coupled polymers (the method simulated here) versus the uniform spacing possible with nanolithography may give different results despite similar values of island diameter, F.C. and RGDs/island (recently seen in the experimental work of Huang et al., 2009).

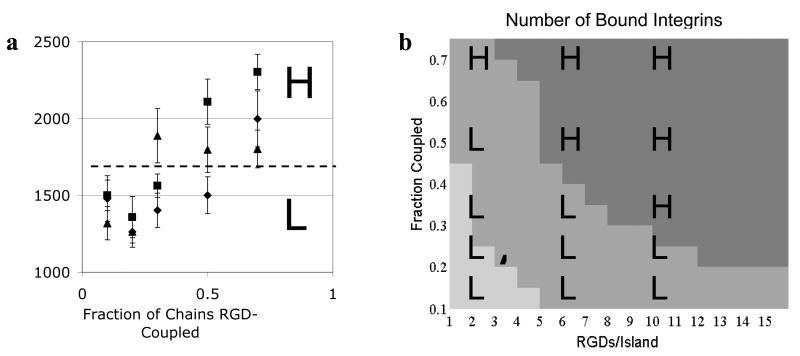
Cell spreading correlates with the total number of integrins bound

We next attempted to develop a correlative model to relate measures of in silico integrin organization with experimentally determined cell responses. We recently reported that cell spreading (as quantified by cell area) in MC3T3 preosteoblast cells on RGD nanopatterned alginate hydrogels is a function of F.C., RGDs/island and the interaction of these two pattern parameters (i.e. related to RGD bulk density) (Comisar et al., 2007). Spreading occurred at two statistically significant levels, high (H) and low (L), and this notation is overlaid on the data (Fig. 3a). Spreading increased with F.C.; however, higher levels of spreading were achieved at lower values of F.C. when RGDs/island was increased. Of the three measures of integrin organization described here and calculated for our simulations, only integrins bound was also a strong function of F.C., RGDs/island and RGD bulk density (Fig. 3b; shades of gray denote high (darkest), medium, and low numbers of bound integrins). The number of bound integrins increased with both F.C. and RGDs/island, though for very low values of F.C. and RGDs/island (bottom left corner of plot corresponding to low RGD bulk density), the number of integrins bound was limited by RGD bulk density. For very high values of F.C. and RGDs/island (upper right corner of plot, corresponding to very high RGD bulk densities), the number of integrins bound was limited by the total number of integrins. When not limited by RGD bulk density or integrin number, the number of integrins bound was increased by organization of integrins into multivalent islands as compared to RGD distributed randomly across a surface (data not shown).

Figure 3. Cell spreading correlates with number of integrins bound (#/μm²).

a) Cell area (μm²) plotted as a function of the fraction of alginate chains RGD-coupled (F.C.) and RGDs/island (◆2, ■ 6, ▲ 10) as reported in Comisar et al. (2007). Experimental data were binned into high (H) or low (L) cell area. b) Model prediction of the number of bound integrins as a function of RGD nanopattern. Simulation data was binned into ■high (≥950/ μm²), ■ medium (500 to 950/μm²), or ■ low (<500/μm²) values of bound integrins. See also Supplementary Fig. 2.

The spreading data were laid over the simulation results for integrins bound (Fig. 3b and Supplementary Fig. 2). There is a strong correlation between the number of integrins bound and cell area, as seen by the high levels of spreading (H) falling nearly exclusively in the darkest gray region (>950 integrins bound/μm²) while low levels of cell spreading (L) fall in the medium to light gray region (<950 integrins bound/μm²). This correlation was quantified using conditional probabilities (Eqn. (2)). When the number of integrins bound was high (>950/μm²), cell area was also high with 100% probability (n=5; n is the number of conditions at that level of integrins bound). When the number of integrins bound was medium to low (<950 per square micron), cell area was low with 90% probability (n=10).

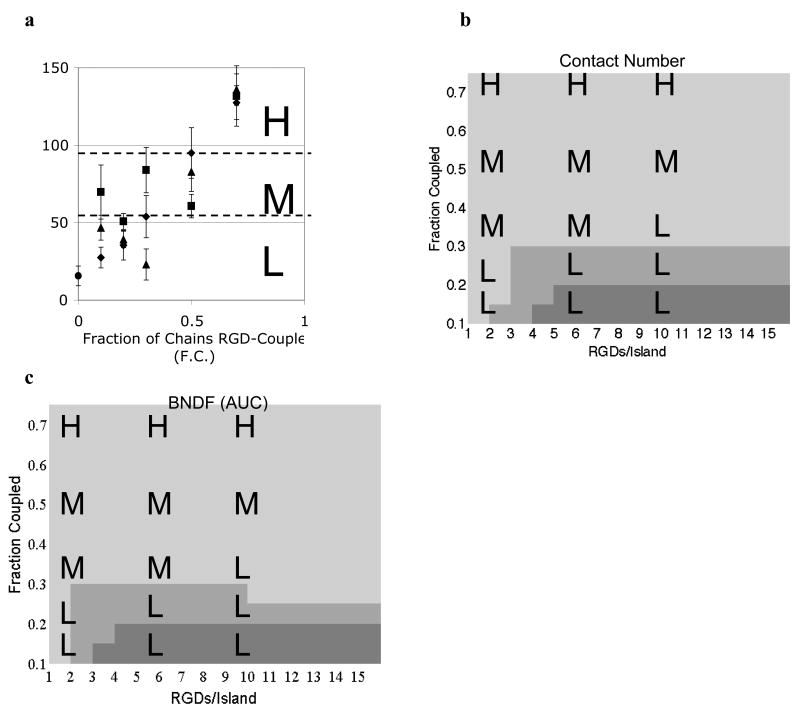
Focal adhesion kinase phosphorylation inversely correlates with both contact number and bound number density fluctuation

In MC3T3 preosteoblast cells seeded on RGD nanopatterned alginate hydrogels, phosphorylation of FAK at Y397 was a function of both F.C. and the interaction between F.C. and RGDs/island (i.e. related to RGD bulk density) (Comisar et al., 2007). FAK phosphorylation data (normalized by DNA content) were discretized as high (H), medium (M), or low (L) to capture the gradual increase in FAK phosphorylation levels as a function of F.C. (Fig. 4a). In simulations, both contact number (Fig. 4b) and BNDF (AUC) (Fig. 4c) were strong functions of F.C. (i.e. the number and spacing of islands), though RGDs/island also had an effect at low RGD bulk densities (<5 RGDs/island and F.C.<0.3). The lightest regions of Figs. 4b and 4c (low contact number and BNDF (AUC), respectively) correspond to Fig. 2c in which small clusters of integrins were distributed homogeneously across the membrane lattice, while the dark gray regions of Figs. 4b and c correspond to Fig. 2a in which large clusters of integrins were distributed heterogeneously. The medium gray regions of Figs. 4b and c correspond to Figs. 2b and d and reflect a transition between homogeneous and heterogeneous systems with intermediate to small clusters of integrins.

Figure 4. pFAK Y397 inversely correlates with contact number and BNDF.

a) pFAK Y397 (ng/mg DNA) plotted as a function of the fraction of alginate chains RGD-coupled (F.C.) and RGDs/island (◆2, ■ 6, ▲ 10, and ● blank alginate) as reported in Comisar et al. (2007). Experimental data were binned into high (H), medium (M), and low (L) levels of FAK phosphorylation. b) Model prediction of the contact number (cutoff radius of 27 nm) as a function of RGD nanopattern. Simulation data were binned into ■high (≥2.76), ■ medium (2.56 to 2.76), and ■ low (<2.56) values of the contact number. c) Model prediction of BNDF (AUC) as a function of RGD nanopattern. Simulation data were binned into ■high (≥0.17), ■ medium (0.12 to 0.17), and ■ low (<0.12) values of BNDF.

The FAK phosphorylation experimental data shown in Fig. 4a were laid over the simulation results for contact number (Fig. 4b) and BNDF (Fig. 4c). Medium to high levels of FAK phosphorylation (H and M) correspond closely to low levels (lightest gray) of contact number (<2.5) and BNDF (AUC) (<0.12), while low levels of FAK phosphorylation (L) correspond to medium to high (medium to darkest gray) levels of contact number (>2.5) and BNDF (AUC) (>0.12). In other words, small clusters of integrins homogeneously distributed correlate with elevated levels of FAK phosphorylation. When contact number was medium to high (>2.5), FAK phosphorylation was low with 100% probability (n=5), while a low contact number resulted in medium to high levels of FAK phosphorylation with 80% probability (n=10). When BNDF (AUC) was medium to high (>0.12), FAK phosphorylation was low with an 88% probability (n=7), while low BNDF (AUC) correlated with medium to high levels of FAK phosphorylation with an 86% probability (n=8). Although the number of integrins bound did not correlate with FAK phosphorylation for the RGD nanopatterns studied, the experimental data indicate that the lowest levels of FAK phosphorylation occurred on blank alginate (Comisar et al., 2007). Therefore, there is likely a minimum number of bound receptors required for increased FAK phosphorylation.

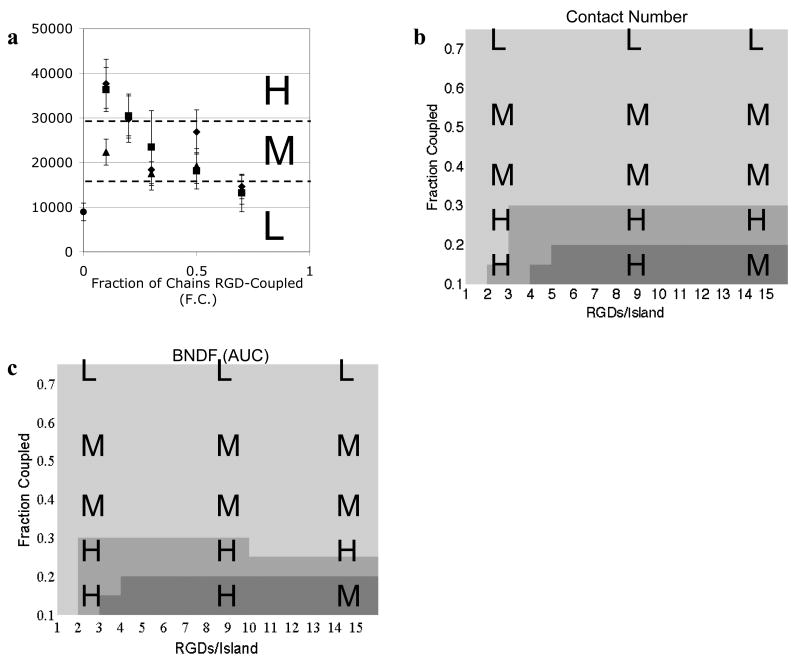
Osteogenic differentiation correlates with both contact number and bound number density fluctuation

In MC3T3 preosteoblast cells seeded on RGD nanopatterned alginate gels, osteocalcin secretion, a marker of osteogenic differentiation, was a function only of F.C. (Comisar et al., 2007). In contrast to cell spreading and FAK Y397 phosphorylation, osteocalcin secretion decreased as F.C. increased. Osteocalcin data (normalized by DNA content) were discretized into high (H), medium (M) or low (L) to capture the gradual decrease in osteocalcin secretion as a function of F.C. (Fig. 5a). As described above, both contact number (Fig. 5b) and BNDF (AUC) (Fig. 5c) were strong functions of F.C., though RGDs/island also had an effect at low RGD bulk densities.

Figure 5. Osteogenic differentiation correlates with contact number and BNDF.

a) Osteocalcin secretion (ng/mg DNA) plotted as a function of the fraction of alginate chains RGD-coupled (F.C.) and RGDs/island (◆3,■9, ▲ 15 and ● blank alginate) as reported in Comisar et al. (2007). Experimental data were binned into high (H), medium (M), and low (L) levels of osteocalcin secretion. b) Model prediction of the contact number (cut-off radius of 27 nm) as a function RGD nanopattern. Simulation data were binned into ■high (≥2.76), ■ medium (2.56 to 2.76), and ■ low (<2.56) values of the contact number. c) Model prediction of BNDF (AUC) as a function of RGD nanopattern. Simulation data were binned into ■high (≥0.17), ■ medium (0.12 to 0.17), and ■ low (<0.12) values of BNDF.

The experimental osteocalcin data from Fig. 5a were laid over the simulation results for contact number (Fig. 5b) and BNDF (AUC) (Fig. 5c) There is a strong correlation between medium to high levels of contact number (>2.5) and BNDF (AUC) (>0.12) and high levels of osteocalcin (H), and between low levels of contact number (<2.5) and BNDF (AUC) (<0.12) and low to medium levels of osteocalcin (L and M). In other words, large, heterogeneously distributed clusters of integrins correlate with increased osteogenic differentiation. When contact number was medium to high, osteocalcin was high with 83% probability (n=6), while a low contact number resulted in medium to low levels of osteocalcin with 100% probability (n=9). When BNDF (AUC) was medium to high (>0.12), osteocalcin was high with 80% probability (n=5), while low BNDF (AUC) correlated with medium to low levels of osteocalcin with 90% probability (n=10). As with FAK phosphorylation, the lowest levels of osteocalcin were reported on blank alginate (Comisar et al., 2007). Therefore, although the number of integrins bound did not correlate with osteocalcin secretion at the RGD conditions studied, there is likely a minimum number of bound receptors required for increased differentiation.

Predicting the Impact of Different Cell/Scaffold Systems

The correlations uncovered in this work between integrin organization and cell responses to RGD nanopatterns as well as simulations run with varied input parameters (e.g. higher or lower numbers of integrins) allow our model to be useful in predicting what effect changes in scaffold system or cell type would likely have on cell responses to RGD nanopatterns (Supplementary Table 1). For example, decreasing the integrin density by two thirds or decreasing ligand-integrin affinity (via k_bind) by two orders of magnitude led, not surprisingly, to a significant reduction in the number of bound integrins. These changes also resulted in a reduction in the effect of ligand nanopattern parameters on contact number and BNDF. This indicates the importance of engineering a scaffold system to promote a minimum number of bound integrins in order to control cell behavior through ligand nanopatterning. A minimum number of bound integrins was also found, experimentally, to be required for organization of integrins into adhesion complexes (Gallant et al., 2005). As a second example, simulations with higher integrin-ligand affinity resulted in lower BNDF overall (e.g. a more homogeneous integrin distribution), a small increase in integrins bound, and a decrease in contact number for high numbers of RGDs/island and F.C.>0.1. Based on the correlations found in this manuscript, then, selection of a ligand context resulting in higher ligand affinity (e.g. cyclic RGD in place of GGGGRGDSP) would likely result in a reduction in MC3T3 osteogenic differentiation and an increase in FAK phosphorylation, particularly for high numbers of ligands/island. FAK phosphorylation may then drive focal adhesion formation; an increase in the number of focal adhesions when RGD affinity is increased by varying the ligand context has been reported (Lehenkari and Horton, 1999).

Discussion

The variable space in engineering biomaterials at the nanoscale is enormous. In order to effectively develop better materials to control cell fate through altered adhesion, we must understand the mechanisms linking adhesion ligand nanopatterns, integrin organization and altered cell responses. The range of length and timescales involved as well as a lack of experimental techniques has hampered the effort to understand these mechanisms both experimentally and theoretically. Experiments have linked adhesion ligand (i.e. RGD) nanopatterns with altered cell responses, and computational models in the absence of experiments have linked RGD nanopatterns to altered integrin clustering (Brinkerhoff and Linderman, 2005; Lee et al., 2004; Comisar et al., 2007). Yet no work to date has related specific aspects of integrin organization arising from particular ligand nanopatterns with the altered cell responses arising from those nanopatterns; this is a critical step in identifying how ligand nanopatterns trigger specific cell responses.

That RGD pattern features, with length scales on the order of 10s to 100s of nanometers, influence cell behavior is surprising because adhesion complexes known to play an important role in controlling cell behaviors are much larger (several microns in diameter and containing perhaps thousands of integrins (Wiseman et al., 2004; Goffin et al., 2006)). Thus we suggest that the mechanism by which the effects occur is at the sub-adhesion complex level. Here we introduce new measures of integrin organization and find that those measures can predict with greater than 80% accuracy the long-term effect of adhesion ligand nanopatterns on cell responses. High levels of cell spreading were best predicted by high numbers of bound integrins, while high levels of FAK Y397 phosphorylation correlated with small, homogeneously distributed clusters of integrins. Osteogenic differentiation was higher on RGD nanopatterns that produced large, heterogeneously distributed integrin clusters.

This work demonstrates a compelling link between short (<50 nm) and intermediate (50 – 500 nm) range integrin organization and the eventual signaling and anchoring capacity of adhesive complexes, suggesting future directions for research into mechanism. One possible mechanism involves impaired accessibility of signaling molecules. Large, dense clusters of integrins (high contact number and BNDF) may result in dense clusters of signaling molecules, sterically hindering access to these molecules by kinases and downstream signaling molecules. Conversely, small, well-dispersed clusters of integrins (low contact number and BNDF) may optimize the accessibility of signaling molecules. Molecular simulations could be used to examine the length scale of optimal accessibility of various signaling molecules. One molecule that would be important to examine is paxillin, the earliest intracellular protein known to organize around submicroscopic integrin clusters (Wiseman et al., 2004). Paxillin serves as a docking site for FAK (Zaidel-Bar et al., 2007). In addition, the phosphorylation state of paxillin has been shown to regulate whether a nascent adhesion matures into a focal or fibrillar adhesion (Zaidel-Bar et al., 2007). Alternatively, local depletion of signaling molecules, rather than impaired accessibility of signaling molecules, may occur when integrins are organized into large, dense clusters as compared to smaller, more widely dispersed clusters. Over-expression of molecules such as paxillin or FAK might be used to test this hypothesis.

Finally, while perhaps less straightforward to test, the analogy with colloidal gels exploited in our analysis is intriguing. Weak colloidal gels, like the integrin organization that fosters osteogenic differentiation, contain large and heterogeneously distributed clusters of particles (Dibble et al., 2006). Strong colloidal gels, like the integrin organization associated with FAK phosphorylation, contain small and homogeously distributed clusters of particles. One could hypothesize that the ‘strong gel’ state of the cell could produce a more mechanically stable cytoskeleton than the ‘weak gel’ state, with implications for cell signaling.

By providing insight into the effect of adhesion ligand presentation on cell responses, our work can be used to suggest directions for engineering tissue culture scaffolds. For example, in order for cells to respond to adhesion ligand nanopatterns, a significant number of integrins must be bound to adhesion ligand. The total number of integrins and/or the fraction of integrins able to bind a particular ligand may vary significantly depending on cell type or condition (e.g. differentiation state) (Petrie et al., 2006; Gilbert et al., 2003; Bennett et al., 2001), while the affinity of a particular integrin for adhesion ligand is dependent on ligand peptide sequence (e.g. RGD versus GFOGER from collagen I (Reyes and Garcia, 2004)) as well as the protein context of the ligand sequence (e.g. cyclic vs. linear RGD hexapeptide (Kato and Mrksich, 2004)). Our model predicts that when small numbers of integrins are bound, RGD nanopatterns no longer affect cell responses. Experimental work has shown that a cell type expressing lower levels of the α_vβ₃ integrin primarily responsible for adhesion to RGD (Petrie et al., 2006) were not affected by RGD nanopatterns to the same degree as MC3T3 cells (Hsiong et al., 2007; Kong et al., 2007). However, when these cells were allowed to differentiate for several days prior to seeding, resulting in higher α_vβ₃ integrin expression, their response to RGD nanopattern parameters more closely mimicked the MC3T3 cell response. These results indicate that knowing a cell's integrin profile in order to select an adhesion ligand to which a significant number of integrins can bind is of critical importance in designing scaffold systems to direct cell fate through altered cell adhesion.

Selection of island diameter is also an important consideration in scaffold design. Island diameter affects integrin organization in two ways: first, by determining total number and spacing of islands for a particular value of F.C., and second, by determining the spacing between RGDs on an island (RGD spacing) at a given number of RGDs/island. The nanopatterning method used here involving random mixing of RGD-coupled and blank polymer yields local fluctuations in the density of islands which results in some groups of more than one island separated by large spaces of blank alginate (Comisar et al., 2006) These randomly formed groups of islands and groups of blank alginate chains promote the formation of large, heterogeneously distributed integrin clusters for low values of F.C., even when island diameter is large enough that on average, neighboring islands overlap. Uniform methods, however, must ensure that the number of islands and island diameter are selected so that the spacing between islands is greater than the intra-island RGD spacing. Otherwise, the patterns are obscured (i.e. equivalent to single RGDs randomly placed across the surface), resulting in an overall reduction in bound integrins for a given RGD bulk density and an overall reduction in BNDF and contact number. RGD spacing, affected by island diameter, can be used to control the number of integrins bound. Brinkerhoff and Linderman (2005) report that integrin binding is maximized with an RGD spacing between 10 nm (the diameter of an integrin) and ∼18 nm (the maximum center to center distance between two integrins able to dimerize). If larger islands are used with the appropriate number of RGDs/island for an approximately 10-18 nm RGD spacing, increased cell spreading at low values of F.C. (i.e. high heterogeneity) can be achieved. Such a scaffold could simultaneously optimize cell adhesion and osteogenic differentiation.

Criticism of random mixing patterning methods has been made because the island spacing is not precisely controlled (Arnold et al., 2004; Christman et al., 2006; Mrksich, 2002). However, this work suggests that because BNDF and contact number, neither of which are sensitive to small fluctuations in island spacing, correlate most closely with FAK phosphorylation and osteogenic differentiation, uniform patterning methods would be unlikely to confer significant advantage in controlling cell responses compared to random mixing methods. This work also indicates the importance of choosing a patterning method with flexibility in the number of RGDs/island. Given low F.C., multivalent RGD presentation results in formation of large, heterogeneously distributed integrin clusters and is associated with increased osteogenic differentiation in the MC3T3 cells studied. Other studies using RGD nanopatterned substrates have also found an advantage in controlling migration and adhesion force through multivalent RGD presentation compared to single RGD (Maheshwari et al., 2000; Koo et al., 2002). Currently, uniform patterning methods are limited to single RGDs per island (Arnold et al., 2004; Cavalcanti-Adam et al., 2006).

There are clearly aspects of the experimental data that cannot be captured in this work. Likely, further chemical and mechanical changes initiated after integrin clustering play a role. This work focuses on the organization of integrins within nascent adhesions from the smallest and earliest unit of organization--submicroscopic clusters (10s of nanometers)--up to, but not including, the recruitment of cytoskeleton proteins and the resulting mechanical forces which drive maturation of adhesion complexes (several microns). Additionally, the adhesive surface simulated was inflexible, not an accurate representation of hydrogels. Kong et al. (2005), for example, have demonstrated a significant effect of substrate stiffness on cell response to RGD density. Consideration of both cellular mechanics and material compliance would be valuable additions to the model used in this work (Gallant and Garcia, 2006; Shemesh et al., 2005; Gov, 2006; Nicolas et al., 2004; Nicolas and Safran, 2006; Marklein and Burdick 2010). Yet despite the simplicity of our model and the complexity of the cellular events, we were able to predict high vs. low levels of cell spreading, FAK phosphorylation, and osteogenic differentiation with a high degree of accuracy by examining integrin binding and clustering. Given current lack of knowledge and experimental limitations, these simple correlations can be critical in suggesting directions for improvements in nanopatterning of adhesion ligand within biomaterials in order to direct cell fate.