Ex-vivo ultrasound attenuation coefficient for human cervical and uterine tissue from 5 – 10 MHz

Abstract

Attenuation estimation and imaging in the cervix has been utilized to evaluate the onset of cervical ripening during pregnancy. This feature has also been utilized for the acoustic characterization of leiomyomas and myometrial tissue. In this paper, we present direct narrowband substitution measurement values of the variation in the ultrasonic attenuation coefficient in ex vivo human uterine and cervical tissue, in the 5–10 MHz frequency range. At 5 MHz, the attenuation coefficient values are similar for the different orientations of uterine tissue with values of 4.1 – 4.2 dB/cm, 5.1 dB/cm for the leiomyoma, and 6.3 dB/cm for the cervix. As the frequency increases, the attenuation coefficient values increase and are also spread out, with a value of approximately 12.6 dB/cm for the uterus (both parallel and perpendicular), 16.0 for the leiomyoma, and 26.8 dB/cm for the cervix at 10 MHz. The attenuation coefficient measured increases monotonically over the frequency range measured following a power law.

INTRODUCTION

Several investigators have utilized variations in ultrasonic properties such as the propagation speed (1–4) and attenuation (2–14) to differentiate between normal and diseased tissue. Bamber and Hill (15) measured the ultrasonic attenuation and propagation speed in bovine and human soft tissues in the temperature range from 5 – 65 °C, while Worthington and Sherar (16) measured these properties in the porcine kidney. Both groups measured the attenuation using a broadband (transducer bandwidth of 50% or greater) substitution method. Literature results on the variation of the ultrasonic propagation speed and attenuation coefficients in human and animal tissues have been summarized in Wells(17), Goss (18), and Duck (19).

One of the most common reasons for ultrasound imaging of the pelvis remains dysfunctional uterine bleeding (20–21). Common causes include the presence of leiomyomas or fibroids (22–24), adenomyosis (20), endometrial polyps,, endometrial cancer, endometrial hyperplasia among other conditions. However, conventional ultrasound imaging cannot reliably differentiate myometrial abnormalities such as adenomyosis and leiomyomas, or endometrial abnormalities such as hyperplasia, polyps, and cancer (21, 25). Measurement of the stiffness (26–29) and acoustic (30–35) properties of the cervix and uterus and associated pathologies may provide important insights on ability to differentiate between tissue types.

Pre-term labor and birth is associated with about 12 percent of all pregnancies in the United States. Ultrasound measurements of the cervical length have been utilized to determine the risk for pre-term labor (36–37). Previous work has also indicated that ultrasound scattering may be related to the organization and density of collagen in the cervix. McFarlin et al. (33) report that with a progress in pregnancy in rats the collagen content of the cervix increases, however, the fibrils become more disorganized thereby increasing the spacing between the fibrils. They reported on the variation of quantitative ultrasound (QUS) parameters namely the scatterer diameter and acoustic concentration during pregnancy, with the scatterer diameter remaining within the standard deviation however the acoustic concentration decreased significantly (−130 to −141 dB/mm³ over days 15–21) as the cervix ripened. This result was also corroborated by Feltovich et al, (38) who reported an increased spacing (from a mean spacing of 20 nm to 30 nm ± 2nm) between the fibrils with progress in pregnancy while their diameter (from about 53 to 58 nm ± 3nm standard error of the mean) remained unchanged. Bigelow et al. (34) hypothesized that as the spacing between the collagen fibrils increases the ultrasonic attenuation of the cervix would decrease, since the surrounding tissue is filled with water and other enzymes. Quantitative ultrasound imaging techniques that utilize attenuation estimates have the potential to detect changes in the cervical microstructure that occur during pregnancy. During cervical ripening, the collagen fibers are not as organized altering the stiffness of the cervix and a reduction in the attenuation slope is expected (30). Studies have also shown that the amount of collagen in the cervix is lower for women with cervical insufficiency (39).

Keshavarzi et al. (32) present the only peer-reviewed report on measurement of the attenuation coefficient in fresh human uterine fibroid and myometrial tissue before and after high-intensity focused ultrasound treatment in the 1–3 MHz frequency range. Their results indicate a linear increase in the attenuation coefficient of both the fibroids and myometrial tissue with frequency, with the attenuation increasing after high-intensity focused ultrasound treatments, from 0.9 to 2.2 and 1.8 to 3.9 dB/cm, respectively, for fibroids and 0.5 to 1.6 and 1.7 to 3.3 dB/cm, respectively, for myometrium. The increase in attenuation coefficient as reported is due possibly to the loss of fluid from the tissue and the presence of gas or vapor bubbles in the high intensity focused ultrasound region.

In this paper, we present the ultrasonic attenuation coefficient in ex vivo human uterine and cervical tissue, in the 5–10 MHz frequency range, where the attenuation coefficient increases monotonically following a power law. The attenuation coefficient was measured using a narrowband substitution technique.

MATERIALS AND METHODS

Uterine and cervical tissue samples from 24 women ranging in age from 31 to 79 years (mean age 50.4 ± 10.8 years) were used to determine their ultrasound attenuation coefficient in the 5–10 MHz range. Tissue samples were obtained from the Department of Pathology in accordance with a protocol approved by the University of Wisconsin’s Institutional Review Board (IRB). Each patient had been diagnosed with a pathology necessitating a complete hysterectomy, requiring removal of the entire uterus and cervix. All surgical procedures were performed at the University of Wisconsin hospitals and clinics in Madison, Wisconsin. Following surgical resection, the entire organ was transferred to the Surgical Pathology facility. Rectangular specimens approximately 25 mm on a side and approximately 5 mm thick were excised from the uterine and cervical walls by a pathologist and placed in saline to be transported to our laboratory for acoustic and tissue stiffness measurements (28–29).

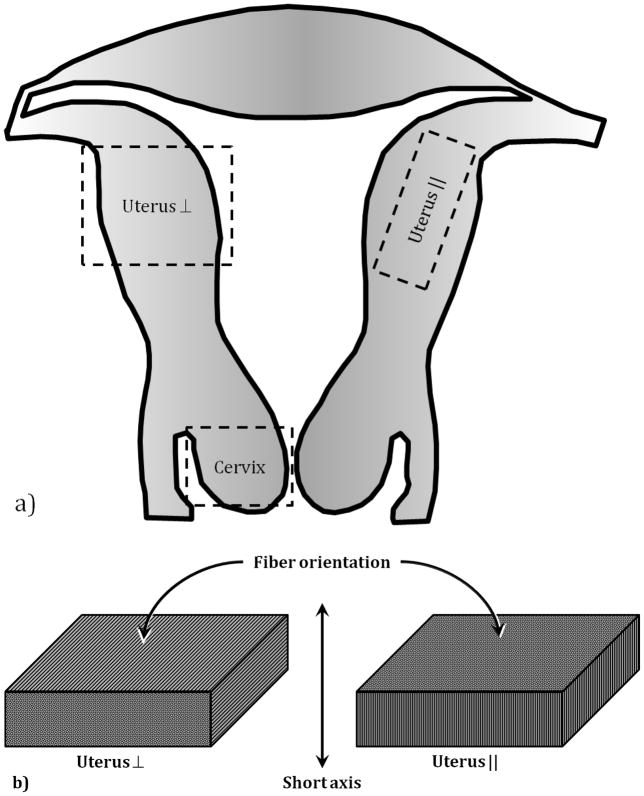
Samples were tested typically within two hours of the organ being transferred to the Surgical Pathology facility. The time delay was due to the availability of the pathologist to prepare samples, and for transporting the samples from the surgical pathology facility to our laboratory where the experiments were conducted. The specimens were kept immersed in saline in a refrigerator and allowed to come to room temperature prior to testing. All physical dimensions were measured four times using a pair of dial calipers, and the results averaged. From each patient, a part of the cervix and two orthogonally oriented sections of the uterine wall were obtained. In the uterine samples, the muscle fibers generally ran either perpendicular or parallel to the short axis of the sample. These orientations are denoted here by the terms uterus ⊥ and uterus ||, respectively. This was not done with the cervical tissue due to the limited amounts of material that could be obtained from an intact cervix. However, the fibers in the cervical tissue sample generally ran perpendicular to the short axis of the sample. Leiomyoma or uterine fibroid tissues were also obtained whenever available. The leiomyomas had no distinct fiber orientation. Figure 1a is a schematic of the uterus showing the locations from which each sample was obtained, and figure 1b indicates the fiber orientation with respect to the sample’s short axis. Table 1 summarizes the number of samples tested by component. The difference in the number of samples for each component is due to viability of the tissue, as determined by the pathologist. For example, in the case of one patient, no normal uterine tissue was obtained due to the profusion of leiomyomas. However, that case did provide a viable cervical tissue sample.

Figure 1.

Schematic diagram of the uterus (a). The labeled boxes indicate the approximate location of the tissue samples, along with the Fiber orientation (b) of the uterine tissue samples.

Table 1.

Summary of specimens obtained

Component	Number of samples tested
Cervix	20
Uterus ⊥	19
Uterus ||	14
Leiomyoma	6

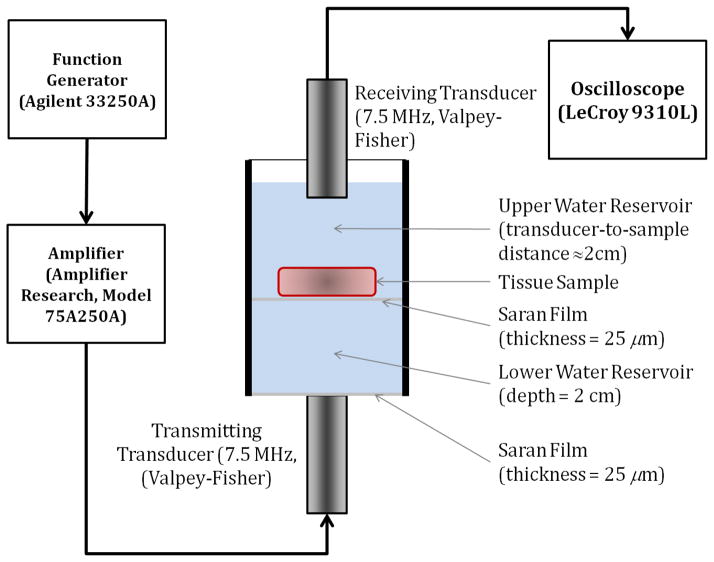
Ultrasonic attenuation of the tissue samples were measured in the frequency range 5–10 MHz using commercially available unfocused single element transducers with a 7.5 MHz center frequency with a −6 dB bandwidth of 6.348 MHz or 85% bandwidth and element diameter of 0.125 mm (Valpey Fisher corporation, MA, USA). Two identical transducers were utilized for the through transmission measurements to ensure that they posses similar point spread functions. Ultrasound frequencies in this range are frequently used for real-time clinical imaging of uterine and cervical abnormalities. Figure 2 shows a schematic diagram of the apparatus used for the narrowband substitution measurements. The testing chamber was an acrylic cylinder, filled with room temperature de-ionized water in two reservoirs. The upper reservoir held the sample and the receiving transducer was immersed in the water bath in the upper reservoir. A Saran film (thickness 25 μm) separated the two reservoirs. The lower reservoir with a depth of 2 cm held only water, and it ensured that the sample would always remain beyond the near-field region of the transmitting transducer. The bottom was sealed off with Saran film, underneath which the transmitting transducer was situated. Ultrasound gel was used to couple the transmitting transducer to the Saran film.

Figure 2.

Schematic diagram of the measurement apparatus.

A narrowband through transmission substitution technique (40)was utilized to measure the attenuation coefficient of the tissue sample. We measure the reduction in signal amplitude with and without the sample present in the acoustic path between the transmitting and receiving transducers. A sinusoidal signal burst in the desired frequency range with a 20-cycle duration was first obtained using a function generator Agilent 3325OA (Santa Clara, CA, USA)). This signal was amplified using a commercially available signal amplifier (Model 75A250A, Amplifier Research, PA, USA) before being transmitted through the transducer. After propagating through the water only, or the water and sample path, the reference and attenuated signal was picked up by the receiving transducer and sent it to the oscilloscope (LeCroy 9310L) for display and subsequent measurement. Measurement of the time-shift for sound speed measurements was performed at the center of the signal burst to avoid ambiguities due to signal loss due to attenuation, along with the reduction in signal amplitude for attenuation measurements.

Measurements were made on the water path without the sample before and after measuring the signal with the sample present. The sample itself was measured five times in different locations in order to obtain independent measurements. Given these inputs, the attenuation coefficient is determined by measuring the amplitude of the ultrasonic wave according to

$$\alpha [\text{dB}/\text{cm}]=\frac{20}{d}{log}_{10}\left(\frac{V_0}{V_1}\right),$$ (1)

where V₀ and V₁ are the peak-to-peak voltages of the signal received at the oscilloscope of the attenuated ultrasonic wave through the water path and the sample, respectively, and d is the path thickness.

In order to obtain accurate measurements of the attenuation coefficient, the acoustic transmission properties of the Saran layers have to be considered (41). Both the entrance and exit transmission coefficients for propagation though the Saran layers for the bottom reservoir are used to obtain the correction factor. Equations (1–3) in Wear et al. (41) describe the correction procedure for transmission though the Saran layer. Data for the frequency-dependent attenuation was acquired by varying the transmit center frequency using the function generator and reading the resulting change in voltage response directly off the oscilloscope display.

RESULTS AND DISCUSSION

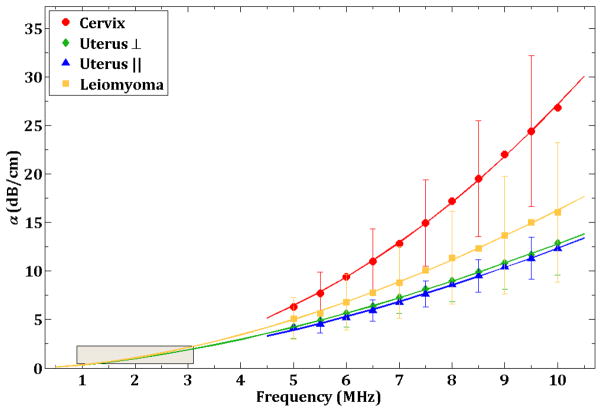
The frequency dependence of the ultrasonic attenuation coefficient for the three tissue types is shown in Figure 3. The data points are the mean observations and the error bars represent one standard deviation from the mean. Not all error bars are displayed for each tissue type in order to avoid cluttering the figure. The plotted lines are computed using least squares fitting of the data to the equation

Figure 3.

Ultrasonic attenuation coefficient (dB/cm) values of various tissue types in the 5 – 10 MHz frequency range. The data points are the mean value at each frequency and the error bars represent one standard deviation from the mean. The curves for each sample represent the least squares fit for each tissue type. The gray box in the lower left corner indicates the location of the results reported in Keshavarzi. The curves for uterus and leiomyoma have been extrapolated down to 1 MHz to show the implied agreement with Keshavarzi’s results.

$$\alpha (f)={Af}^n,$$ (2)

where values for A, n, and the goodness-of-fit measure r², for each component are shown in Table 2. The curves for the leiomyoma and uterus ⊥ have been extrapolated down to 1–3 MHz in order to compare with Keshavarzi et al. (32) results. The box indicates the location of Keshavarzi’s (32) data and it is encouraging to note that the extrapolated curves present a qualitative agreement in the trend of the results.

Table 2.

Coefficients and goodness of fit measure by tissue type

Tissue	A	n	r2
Cervix	0.2267	2.0780	0.9995
Uterus ⊥	0.3202	1.6016	0.9995
Uterus ||	0.2730	1.6559	0.9987
Leiomyoma	0.3246	1.7003	0.9983

At 5 MHz, the values for alpha are relatively close to each other, from 4.1–4.2 dB/cm for the uterus, 5.1 for the leiomyoma, and 6.3 for the cervix. This corresponds to a mean difference (relative to the cervix) of about 1.7 dB/cm. As the frequency increases, the values spread rapidly, with a value of approximately 12.6 dB/cm for the uterus at 10 MHz, 16.0 for the leiomyoma, and 26.8 dB/cm for the cervix, resulting in a mean difference of about 12.5 dB/cm.

There is a small separation between the two uterus curves, suggesting that fiber orientation influences ultrasound attenuation. However, the true separation may not be clear, given the size of the error bars.

The increase in cervical attenuation with increasing frequency when compared to that of the uterus is likely due to the tissue composition. According to Winkler and Rath (1999), the cervix consists mainly of collagen (70% Type I, 30% Type III, and a small amount of Type IV). It is only 5–10% smooth muscle. The uterus, on the other hand consists mainly of smooth muscle. The increased attenuation in the fibroid compared to normal uterine tissue (15 dB/cm vs. 8 db/cm at 7.5 MHz)is possibly due to the increased disorder in fiber orientation, leading to higher extinction/scattering of the propagating ultrasound waves.

SUMMARY

The results in this paper present ultrasonic attenuation coefficient variations in ex vivo human uterine and cervical tissue using a transmit center frequency of 7.5 MHz. The results show that in the 5–10 MHz range, the attenuation coefficient increases monotonically, and follow a power law. The results extend the knowledge acquired previously by other researchers in a lower frequency range. Quantitative measurement of the attenuation may also help in the development of noninvasive ultrasound based approaches for the characterization of uterine and cervical microstructure.

Research Highlights.

We present direct narrowband substitution measurement values of the variation in the ultrasonic attenuation coefficient in ex vivo human uterine and cervical tissue, in the 5–10 MHz frequency range. The attenuation coefficient measured increases monotonically over the frequency range measured following a power law.