Measurement of mechanical tractions exerted by cells within three-dimensional matrices

Abstract

Quantitative measurements of cell-generated forces have heretofore required that cells be cultured on two-dimensional substrates. We describe a technique to quantitatively measure three-dimensional traction forces exerted by cells fully encapsulated within well-defined elastic hydrogel matrices. We apply this approach to measure tractions from a variety of cell types and contexts, and reveal patterns of force generation attributable to morphologically distinct regions of cells as they extend into the surrounding matrix.

Cells are constantly probing, pushing and pulling on the surrounding extracellular matrix (ECM). These cell-generated forces drive cell migration and tissue morphogenesis and maintain the intrinsic mechanical tone of tissues^{1, 2}. Such forces not only guide mechanical and structural events, but also trigger signaling pathways that promote functions ranging from proliferation to stem cell differentiation^{3, 4}. Therefore, precise measurements of the spatial and temporal nature of these forces are essential to understanding when and where mechanical events come to play in both physiological and pathological settings.

Methods employing planar elastic surfaces or arrays of flexible cantilevers have mapped, with subcellular resolution, the forces that cells generate against their substrates^{1, 5–7}. However, many processes are altered when cells are removed from native three-dimensional (3D) environments and cultured on two-dimensional (2D) substrates. At a structural level, cells encapsulated within a 3D matrix exhibit dramatically different morphology, cytoskeletal organization, and focal adhesion structure from those on 2D substrates⁸. Even the initial means by which cells attach and spread against a 2D substrate are quite different from the invasive process required for cells to extend inside a 3D matrix. These differences suggest that dimensionality alone may significantly impact how cellular forces are generated and transduced into biochemical or structural changes. Yet, although the mechanical properties of 3D ECMs and the cellular forces generated therein have been shown to regulate many cellular functions⁹, the quantitative measurement of cellular forces within a 3D context has yet to be demonstrated.

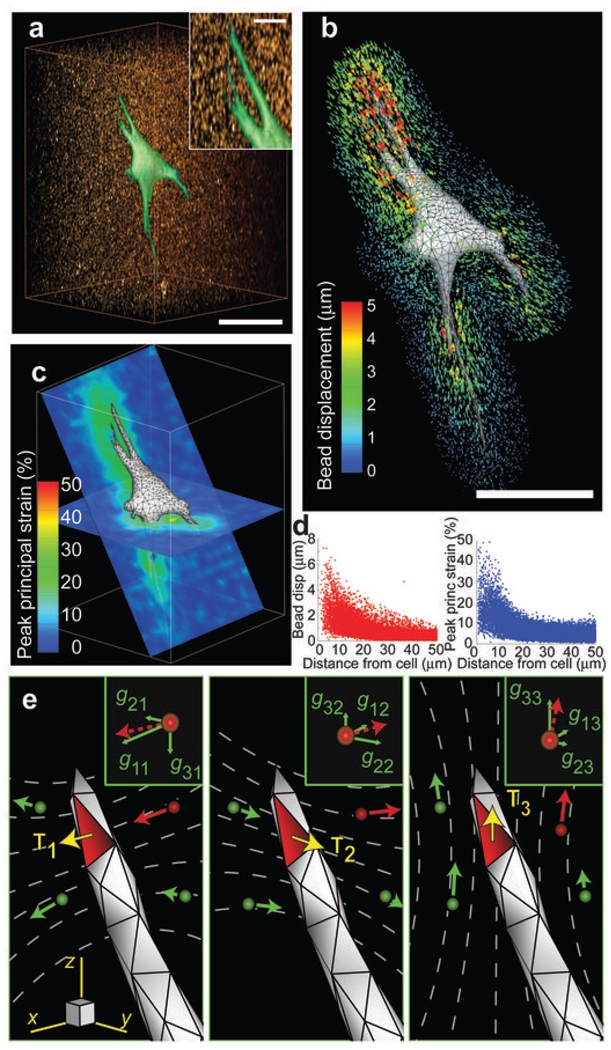
Here, we quantitatively measure the traction stresses (force per area), hereafter tractions, exerted by cells embedded within a hydrogel matrix. GFP-expressing fibroblasts were encapsulated within mechanically well-defined polyethylene glycol (PEG) hydrogels that incorporate proteolytically degradable domains in the polymer backbone and pendant adhesive ligands¹⁰. The incorporation of adhesive and degradable domains permits the cells to invade, spread, and adopt physiologically relevant morphologies (Fig. 1a and Supplementary Movie 1). The hydrogels used in this study had a Young’s modulus of 600 to 1,000 Pa (Supplementary Fig. 1), a range similar to commonly used ECMs such as reconstituted collagen or Matrigel and to in vivo tissues such as mammary and brain tissue^{11, 12}. Cells in 3D PEG gels deformed the surrounding matrix, which was visualized by tracking the displacements of 60,000–80,000 fluorescent beads in the vicinity of each cell (Fig. 1b, Supplementary Fig. 2, Supplementary Note 1 and Supplementary Movie 2). Bead displacements were determined relative to a reference, stress-free, state of the gel after lysing the cell with detergent (Supplementary Movie 3). We typically observed deformations of 20–30% peak principal strain in much of the surrounding hydrogel (Fig. 1c, d). The largest strains, up to 50%, occurred in the vicinity of long slender extensions, which is consistent with observations of strong forces exerted by these regions on 2D substrates¹³. Because the mechanics of the PEG hydrogels showed no substantial dependence on strain or frequency (Supplementary Fig. 1), we used linear elasticity theory and the finite element method to determine the cellular tractions that would give rise to the measured bead displacements. Briefly, we generated a finite element mesh of the hydrogel surrounding the cell from confocal images. A discretized Green’s function was constructed by applying unit tractions to each facet on the surface of the cell mesh and solving the finite element equations to calculate the induced bead displacements (Fig. 1e). Standard regularization methods for ill-posed, over-determined linear systems of equations were then used to compute the tractions exerted by the cell (Supplementary Note 2). The time required for the calculation of a single data set is approximately 4.5 hours using readily available computational equipment. However, this can be reduced dramatically by using a simplified finite element mesh of the cell and hydrogel. These lower resolution datasets still capture the fundamental character of higher resolution measurements (Supplementary Fig. 3).

Figure 1.

Cell-induced hydrogel deformations and construction of a discretized Green’s function. (a) Volume rendering of a GFP-expressing NIH 3T3 fibroblast (green) spreading into a 3D hydrogel containing fluorescent beads (red). Scale bar = 50 µm, 10 µm (inset). (b) Surface mesh of the cell. Scale bar = 50 µm. Bead displacement trajectories are mapped and color coded by magnitude. (c) 2D slices through the volume showing the magnitude of the peak principal strain in the hydrogel surrounding the cell. (d) Plots of bead displacements and hydrogel strain as a function of distance from the cell surface. (e) Schematic outlining the use of the finite element method to reconstruct the Green’s function. Surface traction (T), applied to the highlighted facet, induces displacements of the surrounding beads (g_ij,, inset). When repeated over all facets and beads, these relationships describe a discretized Green’s function that can be used to calculate the tractions applied by the cell (Supplementary Note 2). The subscript indices of T and g represent the Cartesian components of the bead displacement in direction i in response of an applied surface traction in direction j.

We used simulated traction fields to validate the approach and to characterize its spatial resolution (Supplementary Fig. 4). Experimental noise from the bead displacements was measured from cell-free regions of the hydrogel before and after detergent treatment, and surface discretization noise was measured from multiple discretizations of the same cells. These datasets then were superimposed onto the displacements generated by simulated loadings prior to traction reconstruction. In this setting, the percent of traction recovered was proportional to the magnitude and characteristic length of the simulated loadings (defined as the average period of spatial oscillation). For all cases, the presence of noise reduced recovery accuracy by approximately 20–30%. Despite these limitations, the recovered tractions still captured the essential periodic features of even the most spatially complex simulated loadings with characteristic lengths of spatial variation down to 10 µm.

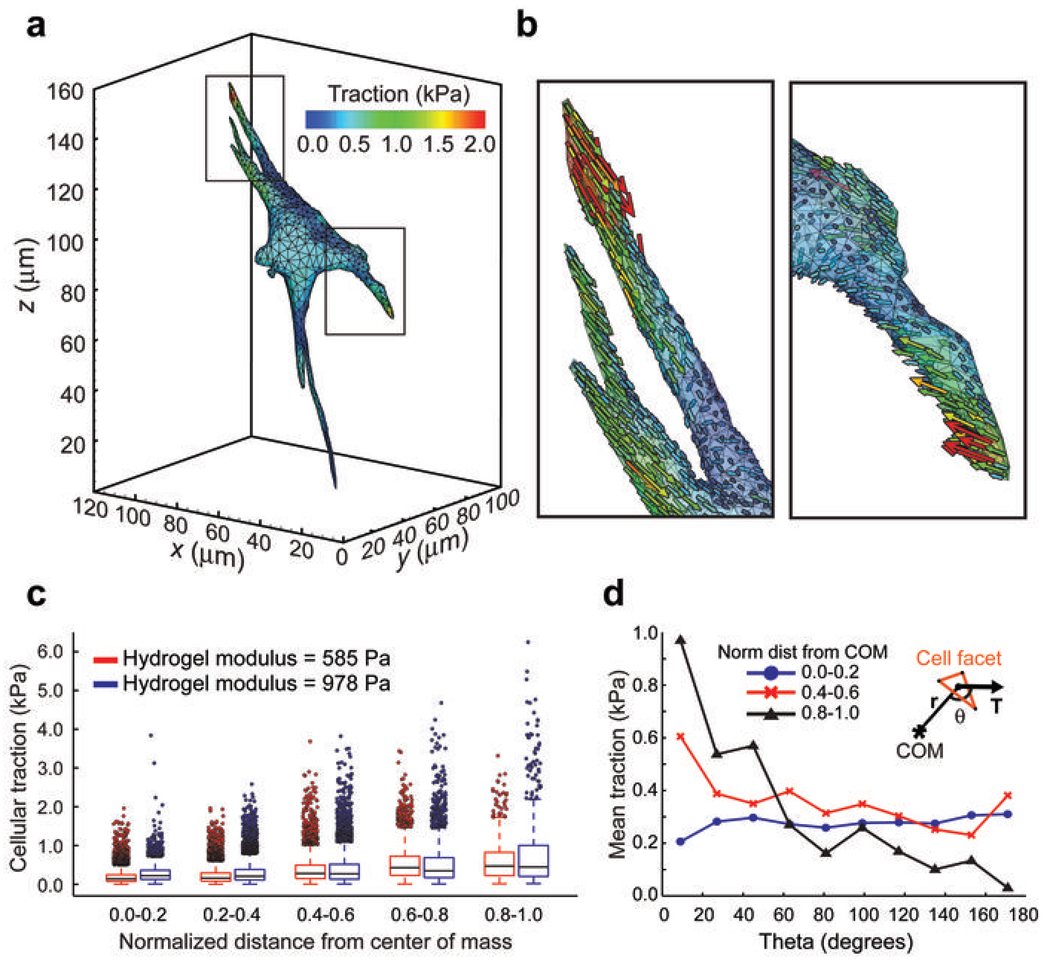
We next calculated the tractions from live cells encapsulated within 3D hydrogels and found that cells exerted tractions in the range of 100–5000 Pa, with strong forces located predominantly near the tips of long slender extensions (Fig. 2a, b and Supplementary Movie 4). For all measurements, forces were in static equilibrium with a typical error of approximately 1–5% of the total force applied by the cell. Further analysis revealed that these tractions were minimally impacted by possible variations in local hydrogel mechanics or by uncertainty in the measured bead displacements (Supplementary Figs. 5- and 6). Previous measurements of cellular forces on 2D surfaces have generally been limited to shear loadings, although recent studies have measured small forces exerted normal to the planar surface as well^{14, 15}. However, it is unclear whether these relationships might be altered for cells inside a 3D matrix. Here, we found that cells encapsulated within a 3D matrix predominantly exerted shear tractions; although, small normal tractions were also present near the cell body. To determine if patterns of force might be associated with specific regions of cells, we quantified the magnitude and angle of tractions with respect to the center of mass of the cell. Generally, tractions increased as a function of distance from the center of mass (Fig. 2c). Interestingly, cells encapsulated in hydrogels with a Young’s modulus of ~1,000 Pa generated stronger tractions than those in ~600 Pa hydrogels. However, the observed differences in tractions were not due to an overall increase in total cellular contractility, as measured by the net contractile moment (Supplementary Fig. 7), but rather, were most apparent in strong inward tractions near the tips of long slender extensions (Fig. 2c). This reveals a local and non-linear reinforcement of cellular contractility in response to substrate rigidity and suggests that such regions may be hubs for force-mediated mechanotransduction in 3D settings. The cell bodies showed no bias in traction angle; however, strong tractions became progressively aligned back toward the center of mass in more well spread regions of the cell (for example near the tips of long slender extensions) (Fig. 2d). In general, these patterns of force were reflected in multiple cell types, but could be altered by cell-cell proximity or culture as a multicellular aggregate. Neighboring 3T3 cells preferentially extended away from each other, whereas proliferating multicellular tumor spheroids exerted outward normal tractions on the matrix (Supplementary Figs. 8- and 9).

Figure 2.

Measurement of tractions exerted by live cells. (a) Contour plot of the tractions (magnitude) exerted by the cell. (b) Magnified sections outlined in a showing the individual traction vectors on each facet. (c) Plot of the traction magnitudes as a function of the normalized distance from the center of mass (COM) of the cell. This normalized distance is approximately 1 for the most spread regions (such as tips of long slender extensions) and approximately 0 for the central cell body. (d) Mean traction at a given angle for cells encapsulated in 978 ± 228 Pa hydrogels. The angle (θ) was computed between the traction vector (T) and the position vector (r) of the cell facet with respect to the center of mass of the cell (inset). Plots shown are for least spread (0.0–0.2), moderately spread (0.4–0.6) and most spread (0.8–1.0) regions of cells. Data from c and d are from n = 12 cells from each condition.

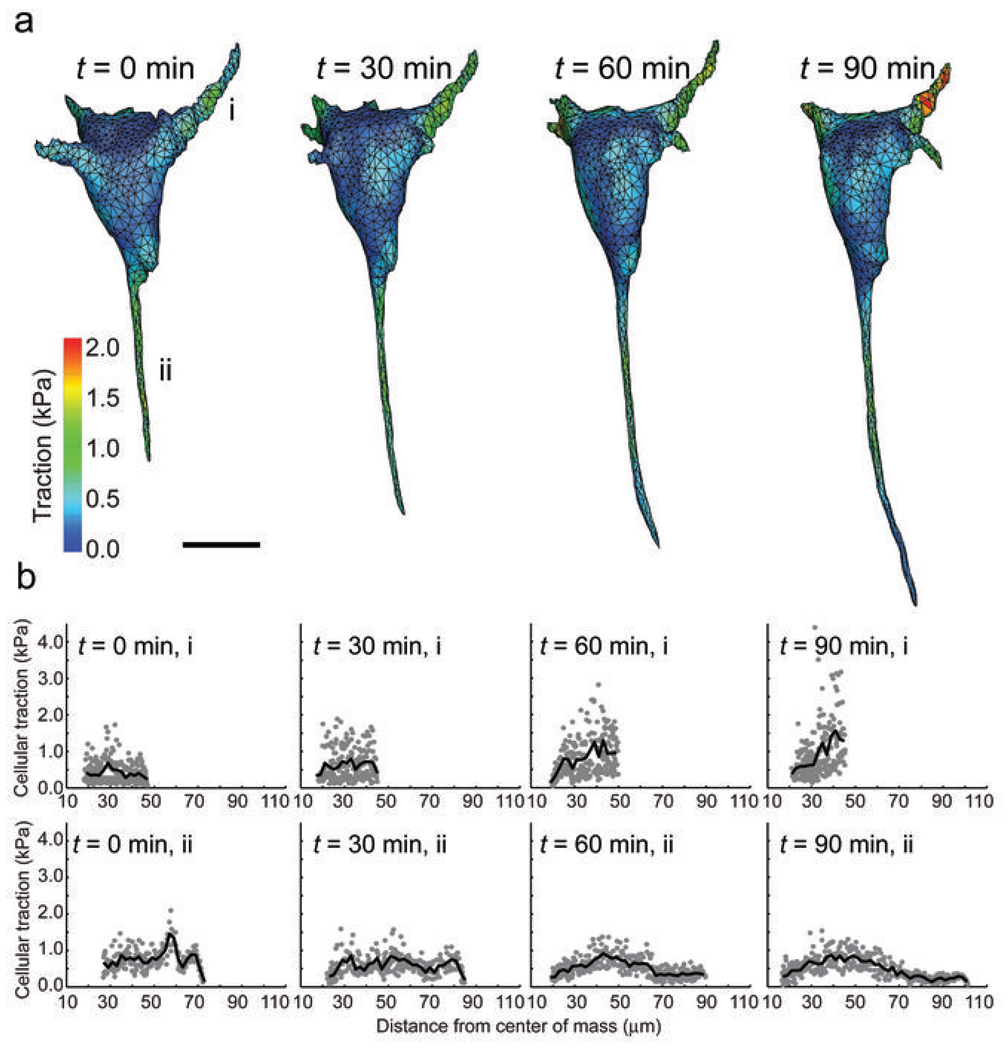
Upon closer inspection, we found a subset of extensions that displayed strong tractions several microns behind the leading tip, while the tractions at the tip itself were substantially lower. As such traction profiles are similar to those observed behind the leading edge of a lamellipodia for a migrating cell on a 2D substrate¹, we hypothesized that such regions may represent invading or growing cellular extensions in 3D. To test this possibility, we measured the tractions from time-lapse images of cells as they invaded into the surrounding hydrogel (Fig. 3a). Indeed, tractions at the tips of growing extensions were notably lower than the strong tractions exerted by proximal regions of the same extension (Fig. 3b and Supplementary Fig. 10). However, we did not observe normal forces pushing into the ECM in these extensions, which suggests that a local inhibition of myosin generated contractility allows tip advancement. Moreover, we also detected strong tractions from small extensions on the cell face opposite the invading extensions. Such stable extensions exhibited very different force distributions than the growing extensions, often lacking the characteristic drop in force near the leading edge, and may correspond to an anterior-posterior polarity axis formed in the cell.

Figure 3.

Measurement of dynamic tractions exerted by spreading cells. (a) Contour plot of the tractions (magnitude) exerted by a cell as it invades into the surrounding hydrogel. Stabile and invading extensions are labeled i and ii, respectively. Scale bar = 20 µm. (b) Tractions exerted by extensions labeled in a as a function of distance from the center of mass of the cell.

Together, these data suggest that cells in 3D matrices probe the surrounding ECM primarily through strong inward tractions near the tips of long slender extensions. Importantly, we demonstrate that this technique is generalizable to different cell types, cell-cell interactions and even to multicellular tumor structures where both tumor growth and invasion have been previously shown to be mechanoresponsive¹¹. Because the synthetic hydrogels used in this study are of similar elastic moduli to in vivo tissues^{11, 12} and can support a wide range of cellular functions¹⁶, we anticipate that this approach will enable investigations into the role of cellular forces in a variety of biological settings.