Challenges in Quantifying Multisensory Integration: Alternative Criteria, Models, and Inverse Effectiveness

Abstract

Single neuron studies provide one foundation for understanding many facets of multisensory integration. These studies have used a variety of criteria for identifying and quantifying multisensory integration. While a number of techniques have been used, there lacks an explicit discussion of the assumptions, criteria, and analytical methods traditionally used to define the principles of multisensory integration. This was not problematic when the field was small, but with rapid growth a number of alternative techniques and models have been introduced, each with its own criteria and sets of implicit assumptions to define and characterize what is thought to be the same phenomenon. The potential for misconception prompted this reexamination of traditional approaches in order to clarify their underlying assumptions and analytic techniques. The objective is to review the traditional quantitative methods advanced in the study of single-neuron physiology in order to appreciate the process of multisensory integration and its impact.

Multisensory Integration

One of the fastest growing fields in the neurosciences is the study of multisensory integration, a field attracting researchers from a host of disciplines, all sharing an interest in how the integration of information across the senses changes behavior and perception. The diversity of articles in this special issue of Experimental Brain Research is testament to its broad implications. Although this field differs from that of classical unisensory research by exploring how the different senses interact rather than how they function individually, it shares many of its theoretical assumptions and analytic techniques. The bases for these assumptions and the quantitative approaches used to measure multisensory integration are issues of importance in the current context.

There is an implicit assumption in the field that the brain alters its reactions to external events when it integrates information across the senses in a manner that reflects the concordance of the information transmitted by the individual sensory channels (Stein and Meredith 1993). The most obvious examples are cases in which, multisensory integration yields a response that is different from the response to the individual modality-specific cues. Consequently, identifying and quantifying the effects of multisensory integration requires a comparison between the multisensory response and the response evoked by a single modality-specific stimulus (typically the most effective). In some cases it is also practical to compare the multisensory response to different models of information fusion; for example, models in which the unisensory responses are summed, or “optimal” models which represent the response predicted by the best combination of the unisensory inputs (Patton et al. 2002; Ernst and Banks 2002; Deneve and Pouget 2004; Alais and Burr 2004). As in classical sensory research, it is common to conduct more than one analysis on a dataset in order to answer multiple experimental questions.

Here we focus on the utility of the quantitative frameworks that have been used for assessing the impact of multisensory integration on the responses of single neurons and the behaviors that result in the context of possible alternatives to these approaches. While we specifically restrict our examination to studies of single neurons, mostly within the superior colliculus (SC), and the orientation behaviors it mediates, we would be remiss without mentioning the growing literature that examines issues of multisensory processing using population techniques, such as fMRI and evoked response potentials (Calvert et al. 2001; Schroeder 2001; Foxe and Schroeder 2005; Lakatos et al. 2007; Beauchamp, 2005; Driver and Noesselt 2008). This work has provided some tremendous insight into our understanding of multisensory integration, but is beyond the scope of the current review. The aim is to understand how one can best appreciate the impact of multisensory integration in single neurons under different experimental conditions by choosing appropriate analytic approaches.

The Criterion for Multisensory Integration

Systematic studies of single neurons in the deep layers of the cat superior colliculus (SC) have provided a wealth of information describing multisensory integration. Initial studies revealed that many single neurons could be activated by stimulation of more than one sense (visual, auditory, or somatosensory). Each possible modality convergence pattern has been noted among the population of SC neurons, and they were defined as “multisensory” because they either generated responses to stimuli from more than a single sense, or their response to a stimulus in one sensory modality could be altered by the presence of a stimulus from another. A review of this early literature can be found in the volume by Stein and Meredith (1993).

The Initial Problem

There was no a priori reason to believe that because a neuron responded to multiple sensory modalities, its response to a combination of cross-modal stimuli would bear any particular relationship to the responses elicited by the modality-specific stimuli in isolation (i.e., it could be larger, smaller, or no different). At the time of the early physiology studies in the 1980’s, it was considered possible that these neurons only represented a common route by which independent inputs from a variety of senses could gain access to the same motor apparatus in generating behavior (e.g., possibly employing a “winner-take-all” algorithm). The researchers reasoned that, if this were true, the response to a combination of stimuli might have been no different than the response to a single stimulus. A similar outcome was expected if the SC treated combinations of cross-modal stimuli as belonging to different events (i.e., as if they were not mutually informative), and consequently selected to respond to one or the other stimulus (likely the most salient). In this case a single neuron might be multisensory but fail to “integrate” signals across the senses. Whether or not multisensory neurons would respond to a combination of cross-modal cues as if they were mutually informative and, in doing so, react to them differently than they would to the most effective of them individually was an open question, and became the basis for how integration was initially defined. However, this problem was certainly not unique in neurophysiology, and was not substantively different from efforts that involved determining whether any sensory neuron can detect a change in any stimulus parameter (e.g., intensity, contrast, velocity, frequency, etc.). Indeed, there is a long history of such examinations in both sensory physiology and psychophysics.

The Solution

The selected criterion for multisensory integration was the same as that used in sensory physiology and psychophysics to identify any stimulus-dependent effect: a statistically significant change in the response. In studies of neurophysiology, the mean number of impulses evoked by the cross-modal stimulus complex (e.g., visual-auditory) was compared to the mean number evoked by the most effective of its individual component stimuli (visual or auditory) (Meredith and Stein 1983). In other words, this test determined if there was any benefit or detriment, in terms of the magnitude of the response, associated with adding information from a second sensory modality from the perspective of the individual neuron (or the brain).

Using this criterion it became apparent that many neurons integrated their multiple sensory inputs because their multisensory responses were either greater or less than the unisensory referent. In some cases neurons that usually responded to only a single stimulus modality (e.g., vision-sensitive neurons) were shown to be multisensory when the addition of a stimulus from another sensory modality (e.g., auditory or somatosensory) reliably changed the response. The operations involved in identifying multisensory integration were later expanded to evaluate the general category of computation engaged, and are illustrated in Figure 1.

Fig. 1.

A schematic of the standard method for identifying and evaluating the computations underlying multisensory integration. First, the mean multisensory response magnitude is compared, using a statistical criterion, to the largest of the mean unisensory responses (gray diamond). If the multisensory response is significantly larger, multisensory enhancement is identified (green, top). If the multisensory response is significantly smaller, multisensory depression is identified (yellow, bottom). If multisensory enhancement is identified, the computation can be further subdivided into superadditive, additive, or subadditive enhancement by comparing the multisensory response to the predicted sum of the unisensory responses. Bar graphs provide examples of the response magnitudes evoked by cross-modal stimuli presented individually (S₁, S₂) and in combination (S₁S₂) for each computational mode. If multisensory depression is identified, the computation engaged can be further subdivided into superminimal, minimal, or subminimal depression by comparing the multisensory response to the smallest of the unisensory responses. Bar graph conventions are the same as above.

It was also apparent that being responsive to multiple sensory modalities does not guarantee that a neuron integrates its multiple sensory inputs. Indeed, as will be discussed below, some multisensory neurons do not implement multisensory integration at all, and some do so only in certain circumstances. Nevertheless, based on the large numbers of SC neurons studied, it appears that under normal conditions the vast majority of multisensory neurons are capable of integrating the information they receive via their different sensory channels (see Stein and Stanford 2008 for a recent review). The most commonly studied form of multisensory integration is “multisensory enhancement,” wherein cross-modal cues that are closely aligned in space and time elicit significantly more impulses than does the most effective of these individual component stimuli (see also Meredith and Stein 1996; Kadunce et al. 1997, King and Palmer 1985). Often, however, the same neurons show “multisensory depression” (fewer impulses than elicited by the most effective component stimulus) in response to cross-modal stimuli that are disparate (generally in space) (see again Meredith and Stein 1996; Kadunce et al. 1997; Jiang and Stein 2003).

The statistical approach used to identify multisensory integration at the neurophysiological level was equally applicable to behavioral data, and the same logic was used in its application: the presence of multisensory integration was operationally verified when the behavioral response obtained was significantly different from the response to a single modality-specific stimulus. Initial studies focused on changes in detection and/or localization performance induced by cross-modal sensory cues. Studies in cats revealed striking behavioral-physiological parallels in the principles of multisensory integration (see Stein et al. 1988; Stein et al. 1989; Wilkinson et al. 1996; Jiang et al. 2002; Burnett et al. 2004; Burnett et al. 2007). The same cross-modal stimulus configurations that enhance (or degrade) physiological responses in SC neurons enhance (or degrade) overt orientation and localization performance. The presumptive reason for this consistency is that these behavioral effects of multisensory integration are driven, in large part, by changes in the neural activity evoked in the SC by the initiating event. If that is true, then any experimental interventions that compromise the ability of SC neurons to engage in multisensory integration (of which there are a number) should also compromise multisensory integration as observed in overt orientation and localization behavior. Perhaps not surprisingly, this has also been shown to be the case in a variety of circumstances.

Evidence of Nonlinearity

The SC neurons that integrate cross-modal information receive unisensory inputs from association cortex (Wallace and Stein 1994). These cortical inputs match the sensory convergence patterns achieved by other inputs to the same SC neuron (Wallace et al. 1992; Jiang et al. 2001; Alvarado et al. 2007a), allowing that neuron to integrate its modality specific inputs (Stein 2005). Any disruption of those inputs alters multisensory integration in SC neurons. For example, temporarily depriving multisensory SC neurons of influences from association cortex, by cryogenic blockage, renders them unable to engage multisensory integration according to the aforementioned statistical criterion, although they continue to respond to different sensory inputs (see Wallace and Stein 1994; Jiang et al. 2001). This may indicate that these inputs are active in the subthreshold phase preceding the onset of the physiological response, when their impact is not yet directly observable at the extracellular level (see Rowland and Stein 2007). It also compromises multisensory integration in overt orientation and localization behavior, but not the animal’s ability to respond to the individual modality-specific stimuli (Wilkinson et al. 1996; Jiang et al. 2002). Similar physiological and behavioral results are evident when animals are reared in environments devoid of particular multisensory experiences; for example, by rearing animals in the dark so that they have no visual-nonvisual experience (Wallace and Stein 1997; Wallace et al. 2004; Carriere et al. 2007). These results suggest that the underlying circuit engages a fundamentally nonlinear computation, because the deletion of certain inputs does not affect the unisensory and multisensory responses in an equivalent manner.

The field has expanded dramatically since the earliest of these studies to include a host of physiological, behavioral and perceptual measures in a number of different species, many of which rest on similar conceptual models. Thus, some of the assumptions and constraints in the assessment of multisensory integration at the level of the single neuron are worth re-examining here. First among these is the use of the criterion to determine whether a neuron has engaged in multisensory integration. Although the traditional criterion has been effective, it is not the only possible criterion.

An Alternative Criterion: The Additive Model

An alternative criterion that has been used for identifying multisensory enhancement is one in which the multisensory response must be greater than the sum of the two (or more) unisensory responses (Populin and Yin 2002). The use of the term ‘multisensory enhancement’ in this context is not the equivalent of ‘multisensory enhancement’ as it was defined earlier (see above), in which the enhancement need only be significantly greater than the most effective component response and could be subadditive, additive or superadditive. This has been the source of some confusion. We believe that the use of the summed unisensory responses (the “additive model”) is a powerful tool when examining the underlying computation engaged during multisensory integration. However, as the criterion for identifying multisensory enhancement it is not only confusing, but faces substantial theoretical and empirical challenges that are not faced by the traditional definition.

First, there is no compelling reason to believe that a sum of the modality-specific component responses would not be an appropriate product of multisensory enhancement. For example, an additive combination of cross-modal inputs in some cases yields a prediction of optimal multisensory integration (Pouget et al. 2002). Thus, in circumstances in which the neural circuit may actually be engaged in optimal multisensory enhancement, but does not achieve superadditivity, the use of the additive model as the criterion for enhancement would lead one to conclude that no multisensory enhancement had taken place. Second, any response larger than the largest unisensory response, but less than the sum of the responses, might be misinterpreted as reflecting some sort of response depression. Because the obtained response in this circumstance could still be much larger than the largest unisensory response, it seems misguided to think of the underlying computation here as somehow reflecting a mutually suppressive interaction. Finally, in the circumstance in which the brain is presented with two stimuli from different senses but perceives them as belonging to separate events (i.e., they are not "integrated" according to the common definition of the word), and responds to one or the other, one would not expect to find a response consistent with the additive prediction because such a result would indicate that the neuron responded to both inputs. These circumstances argue against the use of the additive model as a criterion for identifying multisensory enhancement.

Perhaps even more compelling than these theoretical issues, however, are the empirical results of the experimental studies described earlier. They demonstrate that multisensory responses do not always deviate in magnitude from the largest unisensory response. This capacity for multisensory integration does not appear in multisensory neurons until late in development. Furthermore, the magnitude of the response of SC neurons to multiple visual stimuli presented within the receptive field is often equivalent to its response to one alone (Alvarado et al. 2007b; Stanford and Stein 2007). This suggests that a “maximizing” computation (as would result from a “winner-take-all” algorithm) is often a default computation in the SC circuit that is only subordinated in the case of multisensory integration, presumably because of the inputs from cortex. These results provide a strong empirical rationale for using the traditional criterion, because it already uses the most effective unisensory component response as its referent.

It should be recognized, however, that these reasons for preferring the traditional criterion are predicated on the assumption that the responses that are obtained represent the activity level of a single unit (neuron in physiology, or individual in behavior). In the case of fMRI, ERP, MEG, and multi-unit recordings, this assumption does not hold, and researchers were faced with a different problem. In these preparations, the recorded response may reflect a pooling (e.g., through voltage summation (Logothetis and Pfeuffer 2004)) of the activity from multiple unisensory sources. An additive model was used in these cases as a more “conservative” criterion for multisensory integration in order to obviate this possibility (Calvert et al. 2000; Calvert 2001; Calvert et al. 2001). Because it was recognized that this criterion increased the likelihood of rejecting multisensory integration when it did occur (Laurienti et al. 2005), some have attempted to avoid this difficulty by tailoring experimental designs to permit unequivocal interpretation with respect to the traditional benchmark of the largest unisensory response (e.g., using multiple stimulus efficacies, (see Stevenson et al. 2007))

Do Multisensory Neurons Have A Default Computational Mode?

The answer to the above query is “no”. One important consideration in the interpretation of multisensory responses collected from a population of neurons is that the population profile reflects not only the intrinsic properties of individual neurons, but importantly also reflects the specific stimuli with which they were evaluated. Thus, studies designed to evaluate multisensory integration across the dynamic range of neurons often yield populations of enhancement centered on an additive computation (e.g., Perrault et al., 2004; Stanford et al., 2005; Alvarado et al., 2007). This result does not indicate that additivity is the default computation; but rather that it is more common when neurons are presented with stimuli whose efficacies are approximately at the midpoint of their dynamic ranges (Stanford and Stein 2007). Thus, for example, if the same neurons were tested with minimally-effective stimuli exclusively, one would draw completely different conclusions about the relative incidence of superadditive versus additive computations. Indeed, one could theoretically use stimuli that would provide an overwhelming proportion of superadditive responses. In fact, even responses that are robust overall (and thus likely to be additive or subadditive) very often show evidence of superadditive computation at their onset when activity is weakest (Rowland and Stein 2007). It is, perhaps, this initial portion of a multisensory response that has the greatest impact on behavior (Rowland et al., 2007).

Quantifying the Magnitude of Multisensory Enhancement

Neural responses that meet the traditional criterion for multisensory enhancement (Figure 1) can exceed the most vigorous unisensory responses by vastly different amounts. There is a great deal of variance in these observations across different neurons and stimulus configurations. Traditionally, the magnitude of multisensory integration (i.e., enhancement and depression) is calculated as the percent difference in the mean number of stimulus-driven action potentials evoked by a cross-modal stimulus (i.e., the “response”) and that evoked by the most effective modality-specific stimulus component (spontaneous activity is always subtracted; for a similar baseline canceling approach used in fMRI and ERP studies, see Miller and D’Esposito 2005 and Bonath et al. 2007). In other words, the difference (in number of action potentials) between the multisensory and strongest unisensory response magnitudes is normalized by the magnitude of the strongest unisensory response. As a result, the magnitude of enhancement or depression depends in large part on the magnitude of the unisensory response on which they are based. For example, an increase of 2 impulses from 2 (strongest unisensory) to 4 (multisensory) represents 100% enhancement whereas the same 2 impulse increment from 10 to 12 would correspond to a 20% enhancement according to the formula:

$$\mathit{\text{MSI}}=\frac{(\mathit{\text{CM}}-{\mathit{\text{SM}}}_{\text{max}})}{{\mathit{\text{SM}}}_{\text{max}}}\times 100,$$

where MSI is the multisensory index, or the proportionate change in the neuron’s response, CM is the mean number of impulses in response to the cross-modal stimulus, and SM_max is the mean number of impulses in response to the most effective (modality-specific) component stimulus (see Meredith and Stein 1983).

In physiology, the expression of multisensory enhancement as a proportion of the strongest unisensory response is intuitive given that the means and variances of sensory responses are frequently in proportion to one another (Khanna and Teich 1989; Teich et al. 1997; Holt et al. 1996; Softky and Koch 1993). Thus, a change in mean response magnitude from 2 to 4 impulses (100%) represents a more significant shift statistically than a change from 10 to 12 impulses (20%). Assuming a Fano factor of 1 (i.e., exploiting the common neural model of a Poisson process, see Figure 3), the first change would represent a shift equal to the variance of the distribution, the second change would represent a change of 1/5 the variance (although the validity of assuming a Poisson process is a consideration in data analysis, see below). Given a simple rate coding scheme it is reasonable to expect that the impact of adding input from a second modality to any process that depends on such activity (e.g., stimulus detection, orienting movement) would scale in an analogously proportionate manner. In behavior, the premise that the impact of adding a second modality should be judged relative to the efficacy of the reference modality is logically consistent with empirical findings of perceptual psychophysics. Within a sense, the relationship between stimulus energy and a just noticeable difference (JND) in sensation often follows either a logarithmic or power relationship, such that the increment in stimulus energy needed to produce an equal increment or equal proportion of change in sensation is a constant proportion of the baseline stimulus level. Thus, at higher stimulus levels, larger intensity increments are required to achieve the same impact. Viewed another way, a uniform increment in stimulus energy has a proportionately smaller perceptual impact as the overall stimulus energy increases. The multisensory circumstance is analogous to stimulus manipulations producing changes in effectiveness within a single sensory modality. Here, the addition of a stimulus from a second modality alters the detection, perceived intensity, and/or likelihood of responding to a stimulus in the first modality, and does so in a manner proportional to its original effectiveness (e.g., Sumby and Pollack 1954; Stein et al. 1996; Lovelace et al. 2003; Gillmeister and Eimer 2007; Odgaard et al. 2003; Arieh and Marks 2008).

Figure 3.

Three response relationships among populations of SC neurons that are relevant to the principle of inverse effectiveness. The data were taken from (Stanford et al., 2005), and each dot represents a sample from a different stimulus or neuron. Left: A correlation exists between the estimated response variance and the response magnitude across the population, with the line of unity (solid black) providing the predicted relationship for a Poisson process. Although the data are roughly consistent with this model, the Poisson model does more poorly at high response magnitudes where the model’s assumptions become less well justified. Center: There is a tight correlation (r²=0.87) between the magnitudes of the multisensory and the best unisensory responses and the inset shows a log-log plot of this trend. Right: A characteristic example of “inverse effectiveness” showing a negative trend between MSI and the magnitude of the best unisensory response (inset shows the log-log plot). MSI = multisensory index; Imp. = impulses.

Another proportionate method that is commonly employed is the contrast index, defined below

$$\text{Contrast}=(\text{CM}-{\text{SM}}_{\text{max}})/(\text{CM}+{\text{SM}}_{\text{max}})$$

The principle difference between this metric and MSI is that the contrast includes the cross-modal response magnitude in the denominator. An advantage to this measure is that it is defined even in circumstances where a neuron or animal might only respond to the multisensory stimulus (i.e., the unisensory stimulus is below threshold). The disadvantage is that it compresses the values to a range between −1 and 1, and thus very different values of enhancement can appear more similar.

An Alternate Quantification: Raw Response Differences

An alternative approach to the use of a proportionate measure in quantifying multisensory integration would be to use the raw differences in the multisensory and strongest unisensory responses (Ghazanfar et al. 2005; Holmes 2007). This alternative is less appealing from a signal analysis perspective because it does not always restrict the calculation in an appropriate manner given the statistics of the system under study. It seems less appropriate to say that a change from an expected response of 2 impulses to 4 impulses is equivalent to a change from 10 impulses to 12 impulses if, in the first case the unisensory response would almost never (on an individual trial) contain 4 impulses, while in the second case the unisensory response (on an individual trial) would often contain 12 impulses. Of course, the traditional measure does not provide a full accounting of the statistics either, but as shorthand for the amount of multisensory enhancement evident in a particular condition it appears superior to this alternative.

One reason for promoting this alternative may be that, at the very lowest levels of physiological responsiveness, one might be dealing with mean response magnitudes that fall below 1 impulse. Consequently, reports of mean impulse counts changing from 0.2 impulses to 0.8 impulses might be perceived as representing insignificant changes because the numbers themselves are so small, especially because neurons modeled as binary processes clearly cannot generate 1/5 of an impulse. However, it must be remembered that response magnitude calculations reflect an average of the impulses elicited across trials. When responses are near threshold, individual trials typically contain no impulses or only a few impulses. Thus, a reported response magnitude of 0.2 impulses per trial is often obtained from a neuron that responds on 20% of the trials, while a magnitude of 0.8 impulses per trial often indicates responses on 80% of the trials. When response magnitudes are viewed in these terms, the MSI reported using the traditional measure reasserts its validity, because although a change of 0.6 impulses seems to be an odd and unfamiliar concept, a change in reliability of 60% is not. Furthermore, if one extends this logic to a large population of multisensory neurons responding synchronously to the event, these concepts seem especially relevant given the role of the SC in the detection and localization of events that are often near threshold.

The Principle of Inverse Effectiveness

Early studies of multisensory integration sought ways to relate the magnitude of a multisensory response to different properties of the stimuli used or to the unisensory responses they elicited. One consistent heuristic for multisensory enhancement that was discovered was that those modality-specific stimuli which evoked stronger responses when presented in isolation typically elicited lower magnitudes of multisensory enhancement (as indicated by the MSI) when presented in combination (figure 2). For multisensory depression, the situation was opposite: the weaker the modality-specific stimulus, the more negative the MSI (e.g., Jiang and Stein 2003). Thus, these two forms of inverse effectiveness follow different trends and must be thought about independently. They are also initiated by different stimulus conditions in the SC: enhancement via cross-modal cues in concordance and depression via cross-modal cues in disparity (see also Kadunce et al. 1997; Meredith and Stein 1996). This “rule of thumb” was described as the “principle of inverse effectiveness” (Meredith and Stein 1986).

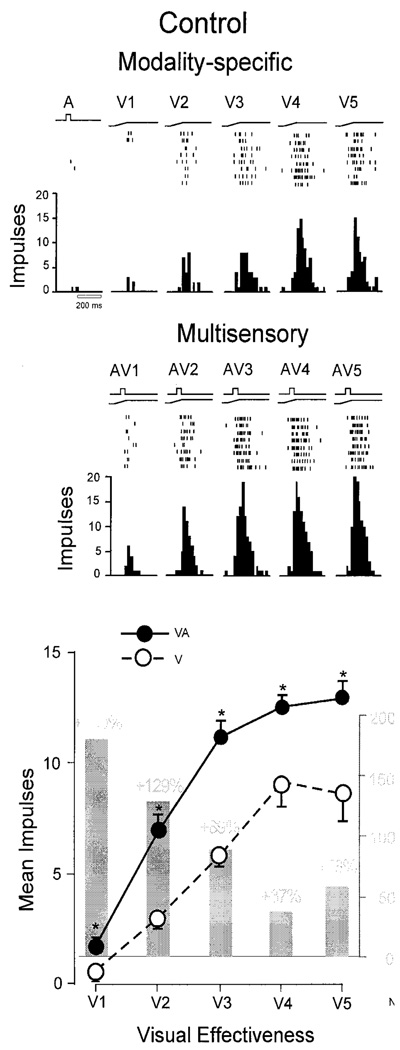
Figure 2.

Inverse effectiveness in a single SC neuron. Top: Impulse rasters and histograms for of the response of an SC neuron to auditory (A) and visual stimuli of 5 intensities (V1–V5) presented alone. Middle: Impulse rasters and histograms showing the response of the neuron to co-presentation of an auditory stimulus (which alone generated no substantial response) with each of the visual stimuli. As intensity is increased, the multisensory response becomes more robust. Bottom: Larger unisensory visual responses correlate with larger multisensory responses. Note that the multisensory and unisensory responses appear to saturate at different maximum levels and that there is a significant amount of overlap in the ranges of the unisensory and multisensory response magnitudes. MSI (%) is shown by the gray histograms, and decreases as the unisensory response magnitude increases. Taken from Jiang et al. 2001.

The principle was then explored in individual neurons by manipulating the efficacy of the modality-specific stimuli (e.g., by changing their physical characteristics) and measuring the multisensory product yielded by their combination (Meredith and Stein 1986; Kadunce et al. 1997; Wallace and Stein 1997; Jiang et al. 2001; Stanford et al. 2005; Perrault, Jr. et al. 2005; Alvarado et al. 2007a; Alvarado et al. 2007b). This was most often done in examinations of multisensory enhancement. In the vast majority of cases the unisensory and multisensory response magnitudes were tightly correlated, and MSI decreased when stimulus effectiveness levels increased. The fact that the unisensory and multisensory responses were correlated indicated that the SC functioned as a principled mechanistic system; that is, when unisensory responses were weak, multisensory responses were also weak, and when unisensory responses were strong, multisensory responses were also strong (i.e., response magnitudes were not random). The fact that there was also an inverse relationship between multisensory enhancement and unisensory efficacy suggested that multisensory integration in the SC conformed to a simple mechanistic principle: as the information provided by an individual unisensory channel increased, the amount of “error” that was resolved by adding information from a less-informative source (and thus the proportional benefit) decreased (e.g., see Patton et al. 2002).

This principle of inverse effectiveness was shown to accurately describe data trends within individual neurons tested with different stimuli (e.g., Meredith and Stein 1986), across populations of neurons (e.g., Stanford et al., 2005; Alvarado et al., 2007a, but see below), and also within the time course of an individual multisensory response (see Rowland et al. 2007b). Indeed, there is a wealth of data using this principle to describe the empirical results obtained in a wide variety of experiments in multisensory integration (Stein and Meredith 1990; Peck 1996; Wallace et al. 1996; Wallace et al. 1998; Stanford et al. 2005; Perrault, Jr. et al. 2005; Rach and Diederich 2006; Bolognini et al. 2007; Lippert et al. 2007; Rowland et al. 2007b; Wang et al. 2008; Hecht et al. 2008b; Hecht et al. 2008a). In other circumstances, the principle of inverse effectiveness has been used to calibrate comparisons across experimental conditions in which the unisensory response efficacies were not the same (e.g., for behavioral responses at different locations in space) (Gingras et al. 2009). Given that unisensory response magnitudes can never be made identical, observations that similar behavioral population do or do not follow nearly identical trends of inverse effectiveness (i.e., conform to the same trend line) are useful in determining to what degree observed differences in response enhancement are due to different unisensory response magnitudes. In addition, recent network models describing multisensory processes generate outputs consistent with empirical observations of inverse effectiveness (Anastasio et al. 2000; Patton et al. 2002; Anastasio and Patton 2003; Rowland et al. 2007a; Ursino et al. 2008; Magosso et al. 2008; Ma and Pouget 2008; Hecht et al. 2008b; Hecht et al. 2008a).

It is important to note that some observations appear to deviate from the principle of inverse effectiveness (Ross et al. 2007). In these circumstances, increasing the effectiveness of the unisensory stimulus did not decrease multisensory enhancement, but rather, increased it within a local range. In such cases, the principle of inverse effectiveness allows the discovery of particular combinations of cross-modal stimulus parameters that may have an unexpected impact; for example, those that may cause sensory signals to be bound across modalities more efficaciously. Indeed, it is quite expected (given the evidence cited above) that there are particular configurations of stimuli that, based on experience, will generate multisensory enhancements that do not follow the expected trend of inverse effectiveness. Thus, close attention should be given to such examples as they may provide insights to the impact of higher order influences on this process. However, as described below, one must exercise significant caution in such instances.

Using the Concept of Inverse Effectiveness

The first step in approaching any dataset is, of course, to determine whether there appears to be a trend that requires description. Inverse effectiveness is not omnipresent in multisensory neural datasets. It is driven by the presence of multisensory integration and disrupting this process in the SC by, for example, deactivating cortex, also eliminates the trend of inverse effectiveness that described it. Similarly, during early neonatal stages when the multisensory integration capability has not yet developed there is no inverse trend describing MSI and unisensory responses, additionally, unisensory integration (e.g., visual-visual, auditory-auditory, etc.) in the SC yields no reliable significant enhancement and no inverse trend.

The utility of the principle of inverse effectiveness is that it is a succinct description of how the system operates. However, there are likely to be substantial differences in the actual trend lines describing the relationship between the multisensory and unisensory responses in different circumstances (neurons, structures, stimulus features, etc.). Because inverse effectiveness is based on a measure of proportionate change, any deviations from it would require a substantial alteration in the raw magnitude of the multisensory response and, as noted above, would be cause for closer scrutiny to determine its basis.

But some caution must be exercised when an inverse trend is noted. Indeed, some questions were raised at the recent International Multisensory Research Forum regarding the possibility that the trend might be evident even in random datasets (Holmes 2008). Thus, it should be noted that not all inverse trends are consistent with the principle of inverse effectiveness. First, it should be noted that the initial observations of inverse effectiveness were made in the context of individual neurons, and the best approach is to analyze its trends within a single unit (neuron or subject), because differences across neurons or subjects can obscure the relevant trends. Secondly, although the inverse relationship between multisensory enhancement and unisensory efficacy is typically interpreted as evidence for inverse effectiveness, it should be kept in mind that the underlying model should only be inferred when there is a correlation between the unisensory and multisensory responses and the data are consistent with the principle itself. In the absence of a unisensory-multisensory correlation, there is no guarantee that the system under study functions in principled fashion. This is because the observed variance can be attributed to random changes or sampling noise, and would reduce confidence that the observed relationships reveal how an underlying mechanistic system is operating. In this case the observations would be of little utility. Although this correlation was present in the original physiological studies of the SC (Figure 3), it might not always be true in every dataset, and it can be instructive to consider why the correlation is necessary by examining several theoretical and transformations of real datasets.

In the first dataset, we assume that the sensory responses themselves are purely random (as if SC responses were not principled) and that the multisensory and the most effective unisensory responses are sampled from the same distribution. In this circumstance there is no actual multisensory enhancement, and the only deviations of the unisensory and multisensory responses are due to noise. Because these random numbers are taken to represent actual mean responses, but have no associated trial-by-trial variance, no statistical calculations regarding enhancement or depression are possible. However, despite the oddity of this construct, it can be informative because a negative trend relating MSI to unisensory efficacy is apparent (black symbols, Figure 4, left). Yet, it would still not reflect the principle of inverse effectiveness because, 1) the trend crosses MSI=0 approximately halfway through the range, and 2) increasing unisensory efficacy past this point leads to greater depression, the opposite of what one would predict based on the original principle. The global trend of these random numbers is clearly inconsistent with inverse effectiveness, and the global trend is what is being evaluated in this thought experiment.

Figure 4.

Inverse effectiveness is not a ubiquitous feature of datasets. Three randomized datasets are presented, each showing similar effects. For each case, the panel on top shows a scatter plot of multisensory responses and the maximum unisensory response to observe correlations, and in the bottom panel, MSI is plotted against the maximum unisensory response to examine any relationship between MSI and unisensory efficacy. Note that the bottom plots use a quasi-log scale for the ordinate: logarithmic (base 10) in the range above 10 and below −10, but linear between −10 and 10, to emphasize the area of interest. Left: Results of a simulation in which two unisensory responses and one multisensory response are generated from identical distributions. This procedure is repeated 20,000 times. Note the absence of a correlation between the two variables, a consequence of their randomness. Grey symbols represent MSI calculated from each sample in the top panel. Black dots show the mean MSI within each 0.1 wide bin of the abscissa. Note that though the trend of black points has a negative slope, it a) crosses MSI=0 halfway through the range and b) continues to become more negative with increasing values of the maximum unisensory response. This means that by increasing unisensory effectiveness, the multisensory interaction transitions from enhancement to depression, which is inconsistent with inverse effectiveness, and, in the negative range, shows the opposite of the predicted trend for inverse effectiveness. Center: Results of a simulation in which the mean values of unisensory and multisensory responses from a real dataset (same as Fig. 3) are “scrambled”. This procedure is repeated 20,000 times. Note that statistics are possible in this dataset (the standard deviations associated with the means are used), and multisensory responses that are significantly different from maximum “unisensory” responses (top), and the associated MSI (bottom) are depicted in red and the others in green (two-tailed t-test, alpha= <0.05). All other conventions are the same as in the left figure. This dataset shows the same trend as the purely random numbers, with one additional caveat: most (approximately 95%) of the multisensory response values are not significant; that is, they show neither multisensory enhancement nor depression. As before, the trend line of means crosses MSI=0 about halfway through the range and continue to become even more negative, which is inconsistent with inverse effectiveness. Right: Results of a simulation in which the trial-by-trial impulse counts from the a real dataset (same as Figure 3) are randomly sampled 30 times each to simulate two unisensory responses and one multisensory response. This is repeated 202,000 times. All other conventions are the same as the center plot. The outcome is that there is no correlation and almost no significant differences between the maximum unisensory and multisensory responses (top). In addition, almost no data points show significant enhancement (bottom), a few show significant multisensory depression (bottom), and the negative trend line relating MSI to unisensory response efficacy again crosses zero. These plots illustrate that the results of random numbers or randomizing real datasets yields products inconsistent with the principle of inverse effectiveness.

A second dataset is based on a manipulation of empirical observations (the data are taken from Figure 3). Here the mean visual and auditory responses are “scrambled” (randomly assigned) and randomly paired with actual multisensory responses. The same trend is evident (Figure 4, center), but incorporating the original response variances reveals that the overwhelming proportion of points (>97.5%) fail to show significant enhancement or depression (shown in green, Fig 4, middle), and thus, as above, fail to achieve the criterion required for evaluating whether the principle applies. Finally, if the real data are “scrambled” on a trial-by-trial basis (n=30) from a common distribution of response magnitudes measured on each trial, and then averaged to produce a mean, the same result is obtained. However, when the data are randomized in this fashion, almost none of the multisensory responses show significant enhancement (green, Figure 4, right), so there is no need for further description. Real data are special and arbitrary transformations or random datasets don’t provide results consistent with the principle.

A potentially more interesting dataset is one in which the distributions of multisensory and most effective unisensory response magnitudes do not overlap, but there is no correlation between them. In other words, there is multisensory enhancement in every sample (and thus, the responses are not really random), but there is no underlying computational model by which the unisensory inputs are integrated: their pairings with the multisensory responses are randomly determined. This dataset also yields an inverse relationship between MSI and unisensory efficacy and the dataset is not subject to many of the problems addressed above: the distributions do not overlap, there is no multisensory depression, the trend line does not cross zero, and all points can, in theory, be significant.

If inverse effectiveness were used in a purely descriptive manner, then it would be correct to say that this principle was present in this dataset. However, because there is no actual relationship between the unisensory and multisensory responses, and thus no real underlying computational model, this conclusion would be unsatisfactory. This possibility points to the fact that, for practical use, if one wants to infer an underlying principled system of multisensory integration; one should not only identify a negative relationship between MSI and unisensory efficacy, but also a significant correlation between the unisensory and multisensory responses. Statistical criteria can be used in both cases: we recommend an F-test for the former, and a regression analysis (.e.g., type II regression) for the latter, although the actual statistical methods should depend on the shapes of the underlying distributions. The F-test also provides a method for identifying significant deviations from an inverse effectiveness trend: it allows one to determine whether the addition of a factor(s) to account for an apparent deviation from the trend (such as that discussed in the example earlier), is in reality a better (statistically significant) accounting of the data given the additional degrees of freedom that it represents. In this same vein, the principle of inverse effectiveness may only apply within a specific range in a given dataset, and these methods can be used to determine its applicability across the whole or parts of the dataset. One must depend on the insight and expertise of individual investigators to use methods like this to determine whether any point(s) that appear to violate this descriptive trend are of likely significance.

However, there is an additional consideration in using this approach. While an F-test is sufficient to determine an inverse relationship between MSI and unisensory efficacy at the level of the population, it assumes by default that the variables of interest themselves are deterministic and that any deviation in the sample from the anticipated trend is due to noise. These assumptions may not hold in every circumstance, and a more complete analysis of inverse effectiveness requires analysis of the trends evident within single individuals or neurons, which we illustrate here in the context of the SC.

Inverse effectiveness in the SC

Although inverse effectiveness was originally noted in individual SC neurons, and has been used most often to explain their individual trends, it has become common practice to plot inverse effectiveness as a trend that exists across the population. When doing so, however, it is important to note a number of possible issues. For example, in a given population of experimental samples, there can be a great deal of variance in the response properties of different neurons. Thus, small samples, or samples composed of neurons with very different response properties, may provide a group profile that does not reflect the properties of its individual components.

Furthermore, although MSI is typically reported as a deterministic variable, in reality its value represents the expected average of a distribution whose shape depends on the shapes of the distributions of the multisensory and unisensory responses from which it is computed. Statistical evaluation of the trend of MSI with respect to the unisensory response efficacy can account for this factor graphically by attaching errors bars to the MSI prediction (Figure 5). There are several methods that can be used to determine the expected shape of the MSI distribution for any particular pairing of unisensory and multisensory responses. The critical computation is in estimating the standard error associated with the mean unisensory and multisensory responses. Unless one can confidently assume an underlying model of impulse generation (e.g., a Poisson model) is equally accurate in all ranges, we recommend an empirical bootstrapping procedure by which the actual data are sampled (with replacement) a number of times equal to the number of trials in the experiment, then averaged to form a single data point representing one possible mean outcome. The accuracy of the bootstrapping procedure can be verified by comparing the cumulative distributions of the bootstrapped samples to those in the actual data (Figure 5, top). This procedure can be repeated many times (e.g., 10,000) to generate a great number of possible mean outcomes for the unisensory and multisensory responses. The theoretical distributions of multisensory and unisensory mean outcomes can then be randomly matched and MSI computed for each pairing. Provided these simulations are of sufficient quantity, this analysis produces a distribution of the MSI values expected for each level of efficacy. It is then possible to verify that these distributions change significantly in a negative direction over the range of sampled values using standard statistical techniques.

Figure 5.

Identifying significantly negative trend lines between MSI and maximum unisensory magnitude in a single SC neuron in which a large range of unisensory response magnitudes were collected (from Perrault et al., 2005). Top: In order to model the error associated with the estimates of the mean unisensory and multisensory responses, an empirical bootstrapping procedure is performed in which 20 samples of trial-by-trial impulse counts are selected (with replacement) for the purposes of averaging. The concordance of the selected trial-by-trial impulse counts with the actual data can be seen by the close match between then dotted and dashed lines for each of the unisensory (left) and multisensory (right) cumulative frequency distributions for this neuron. Bottom: The left figure illustrates the good correlation between mean unisensory and multisensory response magnitudes. Error bars indicate the standard error of the mean computed from the actual impulse counts. The right figure illustrates the relationship between median MSI (the MSI distribution rarely approximates a normal distribution) and the maximum unisensory response magnitude, showing a clearly negative trend. The error bars indicate the range accounting for 68% of the distribution of the data.

Concluding Remarks

A number of issues regarding multisensory integration have been explored here. In each case, the alternatives and caveats associated with each technique have been reviewed in order to clarify these issues for the broader community interested in multisensory integration. Of primary interest has been an examination of the traditional approach to the analysis of multisensory integration at the level of the single neuron in the SC and the behaviors that are linked to those responses. Many of these techniques, and their underlying assumptions, have been transferred from fields of classical sensory research (in which the senses are studied in isolation) and are based on sound computational models of information fusion.

Within this framework, multisensory integration is operationally identified as a statistical difference between the responses elicited by a cross-modal stimulus complex and the largest response evoked by one of its constituent modality-specific stimuli. The value of this definition has been discussed in the context of other possible definitions, and other possible analytical approaches. The conclusion is that multiple measures should be applied to provide a more complete perspective of any dataset. Once multisensory integration has been identified, it is often illuminating to apply additional measures in order to classify the computational mode that has been engaged in its implementation.

A significant point of discussion has also been that both indices of multisensory integration (enhancement and depression) are best described in terms of the proportional difference between the multisensory and strongest unisensory responses. A natural consequence of examining the relationship between these responses by varying the effectiveness of the stimuli being integrated has been the discovery of the principle of inverse effectiveness: an inverse trend between multisensory enhancement and the magnitude of the associated unisensory responses. More attention should be given to deviations from this expected trend because they may represent special cases for consideration, and reflect the impact of processes that are, as yet, poorly understood.

The present discussion has been constrained to issues that relate specifically to multisensory integration at the level of the single neuron and the level of the whole animal in behavioral performance. However, as the field of multisensory integration matures, researchers should continue to evaluate the theoretical assumptions, models, and analytical techniques that can be used to further our understanding of this capacity regardless of the specific experimental techniques that are employed in its study. It is without doubt that, as in other fields, the statistical techniques currently used to assess this capacity can be improved and made more useful. However, in making these improvements, it is advisable to take into account the insights underlying the frameworks and techniques traditionally used in identifying and quantifying multisensory integration at the neuronal level that have been derived from sensory physiology, as well as their successes in describing the behavioral and perceptual impact of this process. Going forward, we should be especially mindful to respect existing definitions (e.g., MSI) as we strive toward a standardized multisensory terminology that promotes transparency across the wide array of multisensory disciplines.