Abstract
A model of adaptation and visual coding was used to simulate how color appearance might vary among individuals that differ only in their sensitivity to wavelength. Color responses to images were calculated for cone receptors with spectral sensitivities specific to the individual, and in postreceptoral mechanisms tuned to different combinations of the cones. Adaptation was assumed to normalize sensitivity within each cone and postreceptoral channel so that the average response to an ensemble of scenes equaled the mean response in channels defined for the reference observer. Image colors were then rendered from the adapted channels' outputs. The transformed images provide an illustration of the variations in color appearance that could be attributed to differences in spectral sensitivity in otherwise identical observers adapted to identical worlds, and examples of these predictions are shown for both normal variation (e.g. in lens and macular pigment) and color deficiencies (anomalous trichromacy). The simulations highlight the role that known processes of adaptation may play in compensating color appearance for variations in sensitivity both within and across observers, and provide a novel tool for visualizing the perceptual consequences of any variation in visual sensitivity including changes associated with development or disease.
Keywords: adaptation, anomalous trichromacy, color appearance, color vision, lens pigment, macular pigment
Introduction
Individuals vary widely in their sensitivity to wavelength, yet these differences often fail to predict judgments of color appearance. For example, the stimuli that observers describe as white or a particular hue cannot be accounted for by normal variations in spectral sensitivity (Webster et al., 2000) or in the ratio of different cone types (Brainard et al., 2000), and are largely unaffected by the large changes in sensitivity that accompany aging (e.g. because of increasing lens brunescence) (Schefrin and Werner, 1990; Werner and Schefrin, 1993). Similarly, within a single observer there is little change in achromatic loci between the fovea and nearby periphery despite the spatial variations in sensitivity imposed by macular pigment screening (Beer et al., 2005; Webster and Leonard, 2008; Webster et al., 2010). Such results suggest that many aspects of color appearance may be compensated for the spectral sensitivity limits of the observer.
One process that is likely to contribute importantly to this compensation is visual adaptation. Adaptation is thought to adjust the sensitivity of visual mechanisms in order to match their responses to the range of their inputs, and consequently also balances the range of responses across mechanisms (Barlow, 1990; Atick et al., 1993). This tends to counteract and thus correct for variations in the stimulus, an adjustment that underlies some aspects of color constancy. For example, in a world with less light we become more sensitive, so that the perceived lightness of the world tends to remain stable. In the same way, adaptation can also lead to perceptual constancy when it is the perceiver who varies. In an observer who sees light less well, adaptation may scale up their responses so that they are again matched to the level of stimulation. As a result, the appearance of the world may tend to remain stable even though the sensitivity of the observer changes over time or retinal location, and may also tend to remain stable across observers who have intrinsically different sensitivity limits (Webster et al., 2005).
In this study we explored the consequences of adaptation for understanding how much color appearance should vary in observers with different spectral sensitivity limits, owing to differences in the density of screening pigments or in the action spectra of the cones. Previously we developed an algorithm for simulating the changes in color appearance that might occur when the same observer is adapted to different environments (McDermott et al., 2008; Juricevic and Webster, 2009). As the gamut of colors changes across different scenes, adaptation to these changes predicts substantial changes in color coding within the individual. Images simulating these changes thus provide a way of visualizing how much our perception might vary because of variation in the world. Here we simulate the converse case of adapting different individuals to the same world, thus providing a novel method for characterizing the perceptual consequences of normal sensitivity changes or color deficiencies. Of course these simulations – like all previous attempts to characterize how the world might appear to observers with different visual systems – cannot predict the actual subjective experience of the observer. Instead, our aim is to show the changes in color appearance that could be attributed to a change only in spectral sensitivity, and differ from previous simulations by explicitly modeling the effects of adaptation on the predicted appearance changes. The simulations emphasize the importance of incorporating adaptation into portrayals of how visual appearance may vary because of individual differences in spectral sensitivity, and in particular show that as a result of adaptation even observers with markedly different spectral sensitivity limits could in principle experience color in very similar ways.
Methods
We used a simple two-stage model of color coding in which light was initially detected by the L, M, and S cones and then recoded into channels that linearly combined the cone signals to respond to different combinations of luminance and chromatic contrast. The model is described in detail in previous reports (McDermott et al., 2008; Juricevic and Webster, 2009). Here we note that the standard observer was based on the Smith and Pokorny fundamentals (Smith and Pokorny, 1975). The post-receptoral channels consisted of 26 unipolar mechanisms tuned to directions at 45° intervals within a version of the Derrington, Krauskopf and Lennie color space (Derrington et al., 1984), scaled to roughly equate sensitivity along the three cardinal axes. The number of mechanisms is not critical to the present simulations since contrast changes are minor with changes in the lens and macular pigment, and primarily affect the axis defined by comparisons between the longer wavelength pigments for anomalous trichromats. We have therefore simulated only the contrast changes that result along the cardinal axes. Colors in the output images were given by the vector sum of the channel responses along the nominal LvsM, SvsLM, and achromatic axes of the color space. The model assumes that the same colors are experienced in different environments – or here in different observers – when the same triplet of summed responses is generated. This obviously will not capture many potential factors affecting color appearance, but isolates the contribution of sensitivity variations to appearance in observers who otherwise respond to and interpret colors in equivalent ways. In particular, the model again makes no predictions about individual differences in color appearance – which are pronounced (Webster et al., 2000) – but does predict the extent to which these should arise from differences only in spectral sensitivity. Further, it should be emphasized that the model is designed to predict the consequences of theoretically complete and thus very long-term states of adaptation, and thus would not predict the consequences of short-term exposures to changes in the environment or the observer. In particular, the images we illustrate simulate how color appearance is predicted to change with a change in visual sensitivity assuming the two extreme cases of either no adaptation or complete adaptation.
Adaptation was modeled as multiplicative gain changes occurring independently within each cone and postreceptoral channel. The gains were scaled so that the mean response of each mechanism to a set of images equaled the mean response of the ‘same’ mechanism in a standard observer. This rule incorporates the assumption that each channel is adapting to center its response range relative to the ambient range of stimuli and assumes that this sensitivity level corresponds to the responses that would be obtained under reference viewing conditions. In simulating adaptation to different environments we chose a single environment as the reference stimulus distribution. In the present work the reference was instead the responses of our standard observer. Multiplicative gain changes are consistent with von Kries adaptation in the cones, but contrast adaptation effects tend to show weaker response changes at high contrasts than predicted by simple scaling (Georgeson, 1985; Webster and Mollon, 1994), and many second-site adjustments in chromatic pathways are instead additive (e.g. Shevell, 2003). Again our model therefore does not simulate contrast changes measured over short time scales, but may more accurately reflect the pattern of response changes that occur over long time scales, and is consistent with theoretical assumptions of how channels at all visual levels should maximize their capacity.
In our previous work, simulating adaptation of the standard observer to different image sets could be done colorimetrically (i.e. directly from the chromaticity and luminance of pixels in the images). In the present study we instead had to make assumptions about the spectra of the color signals. The adaptation level defining the white point was set relative to an equal energy spectrum (Illuminant E). For colors in the image we converted the RGB values to the phosphor spectra consistent with our CRT monitor, and then calculated the responses to these spectra in individuals with different cone spectral sensitivities. As a result our images show how images might appear to different observers on a CRT display and not how these observers might perceive the original scenes.
For each observer, the average contrast seen by each channel was calculated for a set of calibrated images of natural outdoor scenes (Webster et al., 2007). The ratio of these responses to the standard observer response was then used to scale the channel outputs before rendering the image. The images shown are based on adaptation to a single environment (Sierras in summer), but are characteristic of the pattern we found for different environments.
Results
Lens aging
As noted, the density of the lens pigment increases steadily with age and thus progressively screens more of the short wavelength light reaching the receptors, yet judgments of color appearance remain largely stable across the lifespan (Werner and Schefrin, 1993). We simulated the changes in appearance that should occur if the cones and postreceptoral channels simply rescale their sensitivities to match the changes in excitation that result from the changes in lens screening. Age-related changes in lens pigment density were based on the model of Pokorny et al. (1987).
Figure 1 shows the color differences predicted between two observers who differ only in the amount of lens pigment (i.e. in observers who have identical visual systems and visual responses except for the difference in lens screening). The top image provides an example of a natural image, while the palette below is a rendering of the Munsell palette used in the World Color Survey to sample color naming across different language groups (Kay et al., 1997). The palette thus provides an illustration of the extent to which focal color choices might be expected to vary between individuals or populations, if the only difference between the observers is in the density of lens pigment.
Figure 1.
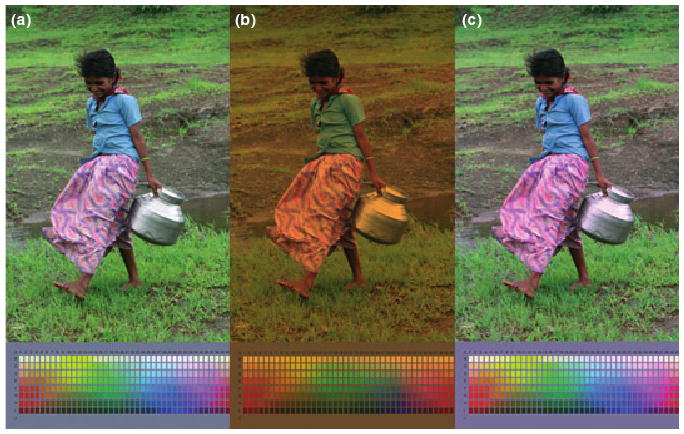
Changes in color appearance predicted by increasing lens pigment density. (a) The original image, as seen by a reference observer assumed to have lens density characteristic of a 12-yr old. (b) The same image filtered through a lens characteristic of an average 72-yr old. (c) The filtered image as it would appear to the same visual system but with the cones adapted to the change in the average incident spectrum. Palettes below the images show the predicted changes in the Munsell array from the World Color Survey.
In Figure 1a, the original unadapted image was chosen arbitrarily to correspond to a reference observer with the average lens pigment density of a 12-year old. In Figure 1b, the colors are instead shown as they would appear through the lens of an average 72-year old. That is, this image directly shows the effect of the lens screening and is how the colors would appear if there were no adaptation to the change in the lens. Figure 1c shows the image after scaling the cone sensitivities to equate the mean responses across the two observers, an adjustment that is again consistent with von Kries adaptation. This removes most (but not all) of the color differences introduced by the lens pigment change. Because the cone scaling removes most of the effects of the lens change, the responses of postreceptoral channels are only weakly affected by the density difference, and thus including an additional stage of contrast adaptation has little effect on the predicted image colors, and is not shown. (However, note that other types of lens change, such as the development of cataracts, may strongly reduce contrast in the retinal image and would thus be predicted to produce large changes in contrast adaptation, an effect which is observed experimentally (Kwon et al., 2009)).
The simulations illustrate two important features of how color appearance might change with changes in lens screening. The first is the strong degree to which simple von Kries-like adaptation preserves color constancy despite changes in lens density within or between observers. Lindsey and Brown (2002) noted an intriguing geographical correspondence between languages that lack a basic color term for blue and the level of ambient UV-B light, and proposed that this could occur if increased lens brunescense owing to UV-B exposure led to a loss of sensitivity to blue. This can be readily seen in the image filtered through the lens (Figure 1b), where the blue blouse becomes green. However, Hardy et al. (2005) found that older and younger observers who vary in lens pigment density nevertheless use color names including blue in similar ways to describe spectra, and our adapted image is consistent with their conclusion that this could be because chromatic adaptation would work to counteract the losses in spectral sensitivity (Figure 1c).
The second feature is that the adaptation we modeled does not lead to complete color constancy. For example, more saturated colors in the adapted images take on subtly yet distinctively different hues from the original image. The reason that von Kries adaptation does not undo all of the effects of the spectral screening of the lens is the same reason that it cannot discount all of the effects of a change in illumination – the spectral changes in the color signal bias the cone ratios in different ways for different spectra, and thus cannot be compensated by rescaling each cone type independently (Worthey and Brill, 1986). Moreover, these differences are not corrected by the known pattern of changes produced by contrast adaptation (Webster and Mollon, 1995). Thus the simulations suggest that if real observers show greater constancy then there must be additional, unknown forms of compensation that correct for the changes in spectral sensitivity.
Macular pigment
The second example we consider is macular screening, which like the lens pigment reduces the incident light at shorter wavelengths. The density of macular pigment peaks at the central fovea and falls rapidly with eccentricity, so that there is negligible screening beyond a few degrees eccentricity (Snodderly et al., 1984). Photoreceptors in the periphery are consequently exposed to much higher levels of short wavelength light. Figure 2 shows the predicted differences in color appearance between the fovea and near periphery, assuming a peak density of 0.5 in the fovea and 0 in the periphery. Not surprisingly, the peripheral image should appear much bluer if there is no compensation (Figure 2b). However, adapting the cones to the average spectral difference at the two loci is again sufficient to largely (though, as with a lens change, not completely) preserve color constancy within the observer (Figure 2c). Moreover, because of this, once the cones are rescaled there is again relatively little change in contrast response and thus relatively little effect of contrast adaptation in the rendered image (not shown). These effects are consistent with studies which have found nearly complete compensation for the white point within the central visual field (Beer et al., 2005; Webster and Leonard, 2008). Studies using the technique of hue cancellation have instead observed compensation only within the S cones (Hibino, 1992; Stringham and Hammond, 2007). However, Figure 2d shows how the image should appear in the periphery if only the S cones adapt to the spectral change from macular screening. The predicted green tint in the image is again inconsistent with the phenomenal impression of color or with the lack of measureable changes in the achromatic loci between the fovea and near periphery (Webster et al., 2010).
Figure 2.

Changes in color appearance predicted by decreasing the macular pigment density. (a) the original image, as seen by a reference observer assuming a peak density of 0.5 in the central fovea. (b) The same image as seen without macular screening, characterizing the incident light in the periphery. (c) The appearance of the peripheral image assuming the cones in the periphery are adapted to the average spectrum they are exposed to. (d) The appearance of the peripheral image if only the S cones are adapted to the changes in macular screening.
Anomalous trichromacy
In the final example, we simulated the color changes predicted for deuteranomalous or protanomalous observers (or specifically, the changes in color appearance that would be predicted in a model observer that adapts and responds in the same way as a reference observer but with a different photopigment complement). These differ from the examples for inert screening pigments because they now include very large changes in contrast as well as changes in the mean cone excitation. Protanomalous observers were created by replacing the L cone with a version of the M photopigment shifted 6 nm toward longer wavelengths, while for the deuteranomalous we instead replaced the M cone with a version of the L cone pigment shifted 6 nm to shorter wavelengths. The shifts preserved the shape of the pigment spectra on a log wavenumber axis. Responses in the anomalous observers were then calculated assuming that the visual system treated the anomalous cone as equivalent to the missing cone.
Figures 3 and 4 illustrate the resulting appearance changes. Scaling the cones so that their average response to the image equals the average response of the reference observer is predicted to equate achromatic percepts between the normal and anomalous individuals (Figures 3b and 4b). The images remain deficient in contrast along the color axes characterizing their deficiency, and the von Kries-scaled images thus provide an illustration of the color directions affected by their anomalous cone spectra. Yet this image is unlikely to capture what the world might look like to them, for the channels encoding these contrasts should again in theory adjust their gain to match the range of signals they see (Macleod, 2003; Bosten et al., 2005). The righthand panels show the predicted image colors following this contrast adaptation (Figures 3c and 4c). Both forms of anomalous trichromacy primarily affect the contrast along their “LvsM” dimension and thus the contrast changes primarily rescale the range of colors along this axis.
Figure 3.

Changes in color appearance predicted for a protanomalous observer. (a) The original image as seen by the reference normal trichromat. (b) The image as seen by a protanomalous observer assuming adaptation only in the cones to match the average spectrum. (c) The image assuming perceived contrasts are rescaled within mechanisms tuned to the individual's cardinal axes.
Figure 4.

Same as Figure 3 but for a deuteranomalous observer.
The images following contrast adaptation (Figures 3c and 4c) predict that these anomalous observers – with very impoverished sensitivity to the contrast provided by comparing their longwave cones – could nevertheless experience the world to be largely as colorful as it is for normal trichromats. Can this be a plausible visualization of the effects of their color deficiency on color appearance? The answer is that it may only approximate the experience of some individuals because the deficiency may be manifest in very different ways. MacLeod (2003) noted that a gain adjustment like contrast adaptation could effectively compensate for the reduced difference signal in the cones, and could leave the anomalous trichromat with color discrimination rivaling normals if the gain occurs before the site of limiting noise. This is consistent with some observers and with the finding that discrimination in anomalous trichromats is not always correlated with the severity of the deficiency (Macleod, 2003). Our simulation might thus realistically capture the “normal” gamut of color appearance in such observers despite the fact that they would behave very differently in a task like color matching.
Alternatively, if the noise is prior to the gain change, then adaptation will boost the signal and the noise. Such observers may show reduced sensitivity while phenomenally the world might still appear perceptually balanced in color. In that case our simulations may help to visualize the average nature of their color experience but would not capture the indeterminacy of their percepts. One way to implement this might be to construct a set of images with colors that randomly vary over a range that would remain indistinguishable to the anomalous observer. For example, Figure 5 shows simulations of the Munsell palette for the protanomalous observer in Figure 3, for the case in which noise is introduced prior to the gain change. For this illustration Gaussian noise was added to vary the mean color of each chip in the palette, with a standard deviation chosen so that the noise was near threshold for a normal trichromat (top left). The remaining panels show three examples of the palettes as modeled for the protanomalous observer. In this case both the signal and the noise are amplified to produce large random variations that are readily visible to the trichromat but should be roughly metameric for the modeled color deficient observer. Yet importantly, the average perceptual gamut of colors remains comparable for both the normal and anomalous observer.
Figure 5.

Simulations of color appearance changes for the protanomalous observer for the case where noise precedes the contrast gain changes. Noise was added to the palette so that it was near threshold for a normal trichromat (top left panel). The remaining panels show palettes with different noise samples processed through the modeled protanomalous observer. This amplifies both the reduced signal and the noise, which is evident as random variations in the palette colors to the trichromat but should appear as largely indistinguishable variations to the anomalous observer.
Finally, our simulations would not predict appearance judgments in individuals where the mechanism responses are not recalibrated through a process like adaptation. For example, Regan and Mollon (1997) found in a perceptual grouping task that the salience of S-cone contrasts was higher than LvsM contrasts for most, though not all, anomalous trichromats compared to normals. If this salience measure correlates with perceived contrast then it raises the question of why many color deficient observers may not show the patterns of color appearance predicted by known forms of color adaptation.
Discussion
Many previous studies have simulated color vision in observers with varying spectral sensitivities, including differences among human observers or across species (e.g. Vienot et al., 1995; Teller, 1997; Vorobyev et al., 2001; Rowe and Jacobs, 2004). Here we have argued that adaptation is an important factor to consider in predicting how much color appearance should vary among observers who may have different sensitivities but are likely to be adapted in similar ways and to similar visual worlds. The importance of receptoral adaptation has also been noted by Vorobyev et al. (2001) for simulating color appearance in different animal visual systems.
Incorporating the principle of adaptation differs from the common approach of filtering the images for the changes in sensitivity that arise from changes in spectral or spatial sensitivity, and then rendering the filtered images as they would be seen by a normal observer (Teller, 1997). Such images provide a powerful depiction of the potential effects of changes in color or spatial contrast sensitivity. Yet they may overestimate the changes in appearance, for these observers are also very likely to adapt in ways that should work to discount appearances for their sensitivity limits. In fact something like this is necessary to account for color appearance in any observer, for we see white in a world through eyes that always have a biased spectral sensitivity, and see the world as perceptually balanced in color and brightness even though the cone contrasts available to signal luminance or chromatic differences are very different because of the overlapping sensitivities of the cones (Chaparro et al., 1993).
Clearly, in the extreme, adaptation cannot recover information that is lost. For example, to the extent that dichromats completely lose one dimension of color coding, there is little need to posit a role of adaptation along the missing dimension (Vienot et al., 1995). Yet even dichromats can show residual trichromacy because of retinal or receptoral inhomogenieties (Smith and Pokorny, 1977; Nagy and Boynton, 1979; Neitz et al., 1999) and can use a repertoire of color names similar to trichromats to describe colors (Wachtler et al., 2004). Mechanisms that could support these capacities by comparing variants of their single longer wave cone type could reasonably be expected to adapt to match their responses to the range of their inputs, and thus could again generate impressions that tend toward a perceptually balanced world. Similarly, anomalous trichromats might adapt to their restricted range of cone signals so that postreceptoral mechanisms exploit the full range of their responses (Regan and Mollon, 1997; Macleod, 2003; Bosten et al., 2005).
However, as noted, as the sensitivity losses become more pronounced it becomes increasingly important to consider how noise influences differences in perceptual experience. In particular, as we illustrated in Figure 5, noise introduced prior to the sites of adaptation should lead to color anomalous observers with correspondingly indeterminate percepts even if their perceptual gamut rivals color normals. For such observers it is difficult if not impossible to simulate for a color normal the color experience of the color deficient – since the normal trichromat can resolve both the signals and noise that the anomalous observer cannot. However, the effects of adaptation nevertheless remain important in considering how color appearance is likely to be normalized in these observers. Specifically, it seems likely that the images in Figures 3 and 4 that incorporate well-established processes of adaptation that are appropriate to the observer, will provide a better simulation of the perceived colorfulness of the images than simulations that instead show the reduced cone contrasts relative to the adapted state of the color normal observer.
There are many other aspects of color appearance that our model does not simulate and which it cannot predict. For example, individuals differ in the stimulus that appears white to them or in the spectra that appear as unique hues. Part of these differences could reflect individual differences in the states of adaptation (e.g. observers might see white differently if they are adapted to a different average color in the world (Webster and Leonard, 2008)). Yet differences in color naming also reflect cognitive and cultural factors or learning (e.g. to associate certain colors with certain characteristics of the environment (Mollon, 2006)). Our model is also obviously wrong in assuming that the visual system of different observers is identical beyond the site of transduction and that the neural signals for color are labeled in the same way; and similarly, is unrealistic in treating the color of each pixel independently. For example, the simulation does not include possible appearance changes owing to factors like color induction which depend on spatial interactions between image regions. We caution again that we are not attempting to simulate what any individual actually experiences, but only how much appearance would be expected to change owing to a change only in spectral sensitivity. Such simulations remain useful because they can illustrate the range of effects that could be attributable to simple forms of color adaptation. If observers with different spectral sensitivities show more inter-observer constancy than predicted from the types of low-level adaptation we have considered, then this points to the role of additional forms of sensitivity compensation which may yet be identified (Webster et al., 2010). Alternatively, if observers show less compensation, then this suggests that there may be additional factors which influence the degree or type of adaptation.
While we have considered only color appearance, the principle of adapting images to simulate the effects of a sensitivity change on visual appearance is a general one and could be applied to many perceptual dimensions, especially those dimensions which, like color, include a perceptual norm or a ‘gray level.’ A common prediction for these dimensions is that adaptation will adjust appearance so that the norm or perceptually neutral stimulus corresponds to the average stimulus the observer is exposed to (Webster and Leonard, 2008). For instance, the world may appear focused to different observers even if they have very different optical aberrations. Simulating these effects may provide a useful general method for visualizing how similar perceptions might be despite differences in visual sensitivity or how stable they might remain despite changes in sensitivity limits within an observer during normal development or with a progressive disease.
Acknowledgments
Supported by EY-10834.
References
- Atick JJ, Li Z, Redlich AN. What does post-adaptation color appearance reveal about cortical color representation? Vision Res. 1993;33:123–129. doi: 10.1016/0042-6989(93)90065-5. [DOI] [PubMed] [Google Scholar]
- Barlow HB. A theory about the functional role and synaptic mechanism of visual aftereffects. In: Blakemore C, editor. Visual Coding and Efficiency. Cambridge University Press; Cambridge: 1990. pp. 363–375. [Google Scholar]
- Beer D, Wortman J, Horwitz G, Macleod D. Compensation of white for macular filtering [Abstract] J Vis. 2005;5:282a. [Google Scholar]
- Bosten JM, Robinson JD, Jordan G, Mollon JD. Multidimensional scaling reveals a color dimension unique to ‘color-deficient’ observers. Curr Biol. 2005;15:R950–R952. doi: 10.1016/j.cub.2005.11.031. [DOI] [PubMed] [Google Scholar]
- Brainard DH, Roorda A, Yamauchi Y, Calderone JB, Metha A, Neitz M, Neitz J, Williams DR, Jacobs GH. Functional consequences of the relative numbers of L and M cones. J Opt Soc Am A. 2000;17:607–614. doi: 10.1364/josaa.17.000607. [DOI] [PubMed] [Google Scholar]
- Chaparro A, Stromeyer CF, Iii, Huang EP, Kronauer RE, Eskew RT., Jr Colour is what the eye sees best. Nature. 1993;361:348–350. doi: 10.1038/361348a0. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Krauskopf J, Lennie P. Chromatic mechanisms in lateral geniculate nucleus of macaque. J Physiol. 1984;357:241–265. doi: 10.1113/jphysiol.1984.sp015499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgeson MA. The effect of spatial adaptation on perceived contrast. Spat Vis. 1985;1:103–112. doi: 10.1163/156856885x00125. [DOI] [PubMed] [Google Scholar]
- Hardy JL, Frederick CM, Kay P, Werner JS. Color naming, lens aging, and grue: what the optics of the aging eye can teach us about color language. Psychol Sci. 2005;16:321–327. doi: 10.1111/j.0956-7976.2005.01534.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hibino H. Red-green and yellow-blue opponent-color responses as a function of retinal eccentricity. Vision Res. 1992;32:1955–1964. doi: 10.1016/0042-6989(92)90055-n. [DOI] [PubMed] [Google Scholar]
- Juricevic I, Webster MA. Variations in normal color vision. V. Simulations of adaptation to natural color environments. Vis Neurosci. 2009;26:133–145. doi: 10.1017/S0952523808080942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay P, Berlin B, Maffi L, Merrifield W. Color naming across languages. In: Hardin CL, Maffi L, editors. Color Categories in Thought and Language. Cambridge University Press; Cambridge: 1997. pp. 21–56. [Google Scholar]
- Kwon M, Legge GE, Fang F, Cheong AM, He S. Adaptive changes in visual cortex following prolonged contrast reduction. J Vis. 2009;9:20–21. doi: 10.1167/9.2.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindsey DT, Brown AM. Color naming and the phototoxic effects of sunlight on the eye. Psychol Sci. 2002;13:506–512. doi: 10.1111/1467-9280.00489. [DOI] [PubMed] [Google Scholar]
- MacLeod DIA. Colour discrimination, colour constancy, and natural scene statistics (The Verriest Lecture) In: Mollon JD, Pokorny J, Knoblauch K, editors. Normal and Defective Colour Vision. Oxford University Press; London: 2003. pp. 189–217. [Google Scholar]
- McDermott K, Juricevic I, Bebis G, Webster MA. Adapting images to observers. In: Rogowitz BE, Pappas TN, editors. Human Vision and Electronic Imaging XIII, SPIE Proceedings. Vol. 686. 2008. pp. OV1–OV10. [Google Scholar]
- Mollon JD. Monge (The Verriest Lecture) Vis Neurosci. 2006;23:297–309. doi: 10.1017/S0952523806233479. [DOI] [PubMed] [Google Scholar]
- Nagy AL, Boynton RM. Large-field color naming of dichromats with rods bleached. J Opt Soc Am. 1979;69:1259–1265. doi: 10.1364/josa.69.001259. [DOI] [PubMed] [Google Scholar]
- Neitz J, Neitz M, He JC, Shevell SK. Trichromatic color vision with only two spectrally distinct photopigments. Nat Neurosci. 1999;2:884–888. doi: 10.1038/13185. [DOI] [PubMed] [Google Scholar]
- Pokorny J, Smith VC, Lutze M. Aging of the human lens. Appl Optics. 1987;26:1437. doi: 10.1364/AO.26.001437. [DOI] [PubMed] [Google Scholar]
- Regan BC, Mollon JD. The relative salience of the cardinal axes of colour space in normal and anomalous trichromats. In: Cavonius CR, editor. Colour Vision Deficiencies. Dordrecht: Kluwer; 1997. pp. 261–270. [Google Scholar]
- Rowe MP, Jacobs GH. Cone pigment polymorphism in New World monkeys: are all pigments created equal? Vis Neurosci. 2004;21:217–222. doi: 10.1017/s0952523804213104. [DOI] [PubMed] [Google Scholar]
- Schefrin BE, Werner JS. Loci of spectral unique hues throughout the life span. J Opt Soc Am A. 1990;7:305–311. doi: 10.1364/josaa.7.000305. [DOI] [PubMed] [Google Scholar]
- Shevell SK. Color appearance. In: Shevell SK, editor. The Science of Color. Elsevier; Oxford: 2003. pp. 149–190. [Google Scholar]
- Smith VC, Pokorny J. Spectral sensitivity of the foveal cone photopigments between 400 and 500 nm. Vision Res. 1975;15:161–171. doi: 10.1016/0042-6989(75)90203-5. [DOI] [PubMed] [Google Scholar]
- Smith VC, Pokorny J. Large-field trichromacy in protanopes and deuteranopes. J Opt Soc Am. 1977;67:213–220. doi: 10.1364/josa.67.000213. [DOI] [PubMed] [Google Scholar]
- Snodderly DM, Auran JD, Delori FC. The macular pigment. II. Spatial distribution in primate retinas. Invest Ophthalmol Vis Sci. 1984;25:674–685. [PubMed] [Google Scholar]
- Stringham JM, Hammond BR., Jr Compensation for light loss due to filtering by macular pigment: relation to hue cancellation. Ophthalmic Physiol Opt. 2007;27:232–237. doi: 10.1111/j.1475-1313.2007.00462.x. [DOI] [PubMed] [Google Scholar]
- Teller DY. First glances: the vision of infants. the Friedenwald lecture. Invest Ophthalmol Vis Sci. 1997;38:2183–2203. [PubMed] [Google Scholar]
- Vienot F, Brettel H, Ott L, Ben M'barek A, Mollon JD. What do colour-blind people see? Nature. 1995;376:127–128. doi: 10.1038/376127a0. [DOI] [PubMed] [Google Scholar]
- Vorobyev M, Marshall J, Osorio D, Hempell De Ibarrra N, Menzel R. Colourful objects through animal eyes. Color Res Appl. 2001;26(suppl):S214–S217. [Google Scholar]
- Wachtler T, Dohrmann U, Hertel R. Modeling color percepts of dichromats. Vision Res. 2004;44:2843–2855. doi: 10.1016/j.visres.2004.06.016. [DOI] [PubMed] [Google Scholar]
- Webster MA, Leonard D. Adaptation and perceptual norms in color vision. J Opt Soc Am A. 2008;25:2817–2825. doi: 10.1364/josaa.25.002817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster MA, Mollon JD. The influence of contrast adaptation on color appearance. Vision Res. 1994;34:1993–2020. doi: 10.1016/0042-6989(94)90028-0. [DOI] [PubMed] [Google Scholar]
- Webster MA, Mollon JD. Colour constancy influenced by contrast adaptation. Nature. 1995;373:694–698. doi: 10.1038/373694a0. [DOI] [PubMed] [Google Scholar]
- Webster MA, Miyahara E, Malkoc G, Raker VE. Variations in normal color vision. II. Unique hues. J Opt Soc Am A. 2000;17:1545–1555. doi: 10.1364/josaa.17.001545. [DOI] [PubMed] [Google Scholar]
- Webster MA, Werner JS, Field DJ. Adaptation and the phenomenology of perception. In: Clifford C, Rhodes G, editors. Fitting the Mind to the World: Adaptation and Aftereffects in High-Level Vision, Advances in Visual Cognition Series. Vol. 2. Oxford University Press; Oxford: 2005. pp. 241–277. [Google Scholar]
- Webster MA, Mizokami Y, Webster SM. Seasonal variations in the color statistics of natural images. Network. 2007;18:213–233. doi: 10.1080/09548980701654405. [DOI] [PubMed] [Google Scholar]
- Webster MA, Halen K, Meyers AJ, Winkler P, Werner JS. Colour appearance and compensation in the near periphery. Proc Roy Soc B-Bio Sci. 2010;377:1817–1825. doi: 10.1098/rspb.2009.1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner JS, Schefrin BE. Loci of achromatic points throughout the life span. J Opt Soc Am A. 1993;10:1509–1516. doi: 10.1364/josaa.10.001509. [DOI] [PubMed] [Google Scholar]
- Worthey JA, Brill MH. Heuristic analysis of von Kries color constancy. J Opt Soc Am A. 1986;3:1708–1712. doi: 10.1364/josaa.3.001708. [DOI] [PubMed] [Google Scholar]


