Abstract
Although there are many imaging studies on traditional ROI-based amygdala volumetry, there are very few studies on modeling amygdala shape variations. This paper present a unified computational and statistical framework for modeling amygdala shape variations in a clinical population. The weighted spherical harmonic representation is used as to parameterize, to smooth out, and to normalize amygdala surfaces. The representation is subsequently used as an input for multivariate linear models accounting for nuisance covariates such as age and brain size difference using SurfStat package that completely avoids the complexity of specifying design matrices. The methodology has been applied for quantifying abnormal local amygdala shape variations in 22 high functioning autistic subjects.
Keywords: Amygdala, Spherical Harmonics, Fourier Analysis, Surface Flattening, Multivariate Linear Model, SurfStat
1. Introduction
Amygdala is an important brain substructure that has been implicated in abnormal functional impairment in autism (Dalton et al., 2005; Nacewicz et al., 2006; Rojas et al., 2000). Since structural abnormality might be the cause of the functional impairment, there have been many studies on amygdala volumetry. However, previous amygdala volumetry results have been inconsistent. Aylward et al. (1999) and Pierce et al. (2001) reported that amygdala volume was significantly smaller in the autistic subjects while Howard et al. (2000) and Sparks et al. (2002) reported larger volume. Haznedar et al. (2000) and Nacewicz et al. (2006) found no volume difference. Schumann et al. (2004) reported that age dependent amygdala volume difference in autistic children and indicated that the age dependency to be the cause of discrepancy. All these previous studies traced the amygdalae manually and by counting the number of voxels within the region of interest (ROI), the total volume of the amygdala was estimated. The limitation of the traditional ROI-based volumetry is that it can not determine if the volume difference is diffuse over the whole ROI or localized within specific regions of the ROI (Chung et al., 2001). We present a novel computational and statistical framework that enables localized amygdala shape characterization and able to overcome the limitation of the ROI-based volumetry.
1.1 Previous Shape Models
Although there are extensive literature on local cortical shape analysis (Chung et al., 2005; Fischl and Dale, 2000; Joshi et al., 1997; Taylor and Worsley, 2008; Thompson and Toga, 1996; Lerch and Evans, 2005; Luders et al., 2006; Miller et al., 2000), there are not many literature on amygdala shape analysis other than Cates et al. (2008), Qiu et al. (2008) and Khan et al. (1999) mainly due to the difficulty of segmenting amgydala. On the other hand, there are extensive literature on shape modeling other subcortical structures using various techniques.
The medial representation (Pizer et al., 1999) has been successfully applied to various subcortical structures including the cross sectional images of the corpus callosum (Joshi et al., 2002) and hippocampus/amygdala complex (Styner et al., 2003), and ventricle and brain stem (Pizer et al., 1999). In the medial representation, the binary object is represented using the finite number of atoms and links that connect the atoms together to form a skeletal representation of the object. The medial representation is mainly used with the principal component analysis type of approaches for shape classification and group comparison.
Unlike the medial representation, which is in a discrete representation, there is a continuous parametric approach called the spherical harmonic representation (Gerig et al., 2001; Gu et al., 2004; Kelemen et al., 1999; Shen et al., 2004). The spherical harmonic representation has been mainly used as a data reduction technique for compressing global shape features into a small number of coefficients. The main global geometric features are encoded in low degree coefficients while the noise will be in high degree spherical harmonics (Gu et al., 2004). The method has been used to model various subcortical structures such as ventricles (Gerig et al., 2001), hippocampi (Shen et al., 2004) and cortical surfaces (Chung et al., 2007). The spherical harmonics have global support. So the spherical harmonic coefficients contain only the global shape features and it is not possible to directly obtain local shape information from the coefficients only. However, it is still possible to obtain local shape information by evaluating the representation at each fixed point, which gives the smoothed version of the coordinates of surfaces. In this fashion, the spherical harmonic representation can be viewed as mesh smoothing (Chung et al., 2007). Instead of using the global basis of spherical harmonics, there have been attempts of using the local wavelet basis for parameterizing cortical surfaces (Nain et al., 2007; Yu et al., 2007).
Other shape modeling approaches include distance transforms (Leventon et al., 2000), deformation fields obtained by warping individual substructures to a template (Miller et al., 1997) and the particle-based method (Cates et al., 2008). A distance transform is a function that for each point in the image is equal to the distance from that point to the boundary of the object (Golland et al., 2001). The distance map approach has been applied in classifying a collection of hippocampi (Golland et al., 2001). The deformation fields based approach has been somewhat popular and has been applied to modeling whole 3D brain volume (Ashburner et al., 1998; Chung et al., 2001; Gaser et al., 1999), cortical surfaces (Chung et al., 2003; Thompson et al., 2000), hippocampus (Joshi et al., 1997), and cingulate gyrus (Csernansky et al., 2004). The particle-based method uses a nonparametric, dynamic particle system to simultaneously sample object surfaces and optimize correspondence point positions (Cates et al., 2008).
1.2 Available Computer Packages
Over the years, various neuroimage processing and analysis packages have been developed. The SPM (www.fil.ion.ucl.ac.uk/spm) and AFNI (afni.nimh.nih.gov) software packages have been mainly designed for the whole brain volume based processing and massive univariate linear model type of analyses. The traditional statistical inference is then used to test hypotheses about the parameters of the model parameters. The subsequent multiple comparisons problem is addressed using the random field theory or random simulations. Although SPM and AFNI are probably two most widely used analysis tools, their analysis pipelines are based on univariate general linear models and they do not have a routine for a multivariate analysis. Therefore, they do not have the subsequent routine for correcting multiple comparison corrections for the multivariate linear models as well.
There are also few surface based tools such as the surface mapper (SUMA) (Saad et al., 2004) and FreeSurfer (surfer.nmr.mgh.harvard.edu). SUMA is a collection of mainly cortical surface processing tools and does not have the support for multivariate linear models. The spherical harmonic modeling tool SPHARM-PDM (www.nitrc.org/projects/spharm-pdm) is also available (Styner et al., 2006). SPHARM-PDM supports for multivariate analysis of covariance (MANCOVA), which is a subset of the more general multivariate linear modeling framework.
For general multivariate linear modeling, one has to actually use statistical packages such as Splus (www.insightful.com), R (www.r-project.org) and SAS (www.sas.com). These statistical packages do not interface with imaging data easily so the additional processing step is needed to read and write imaging data within the software. Further these tools do not have the random field based multiple comparison correction procedures so the users are likely export analyzed statistics map to SPM or fMRISTAT (www.math.mcgill.ca/keith/fmristat) increasing the burden of additional processing steps.
1.3 Our Contributions
In this paper, we use the weighted spherical harmonic representation for parameterization, surface smoothing and surface registration in a unified Hilbert space framework. Chung et al. (2007) presented the underlying mathematical theory and a new iterative algorithm for estimating the coefficients of the representation for extremely large meshes such as cortical surfaces. Here we apply the method to real autism surface data in a truly multivariate fashion for the first time.
Our approach differs from the traditional spherical harmonic representation in many ways. Although the truncation of the series expansion in the spherical harmonic representation can be viewed as a form of smoothing, there is no direct equivalence to the full width at half maximum (FWHM) usually associated with kernel smoothing. So it is difficult to relate the unit of FWHM widely used in brain imaging to the degree of spherical harmonic representation. On the other hand, our new representation can easily relate to FWHM of smoothing kernel so we have a clear sense of how much smoothing we are performing before hand.
The traditional representation suffers from the Gibbs phenomenon (ringing artifacts) (Gelb, 1997) that usually happens in representing rapidly changing or discontinuous data with smooth periodic basis. Our new representation can substantially reduce the amount of Gibbs phenomenon by weighting the coefficients of the spherical harmonic expansion. The weighting has the effect of actually performing heat kernel smoothing, and thus reducing the ringing artifacts. We quantify the improved performance of our new representation in the both real and simulated data using for the first time.
Since the proposed new representation requires a smooth map from amygdala surfaces to a sphere, we have developed a new and very fast surface flattening technique based on the propagation of heat diffusion. By tracing the integral curve of heat gradient from a heat source (amygdala) to a heat sink (sphere), we can obtain the flattening map. Since solving an isotropic heat equation in a 3D image volume is fairly straightforward, our proposed method offers a much simpler numerical implementation than available surface flattening techniques such as conformal mappings (Angenent et al., 1999; Gu et al., 2004; Hurdal and Stephenson, 2004) quasi-isometric mappings (Timsari and Leahy, 2000) and area preserving mappings (Brechbuhler et al., 1995). The established spherical mapping is used to parameterize an amygdala surface using two angles associated with the unit sphere. The angles serve as coordinates for representing amygdala surfaces using the weighted linear combination of spherical harmonics. The tools containing the weighted spherical harmonic representation and the surface flattening algorithm can be found in www.stat.wisc.edu/∼mchung/research/amygdala. It should be pointed out that our representation and parameterization techniques are general enough to be applied to various brain structures such as hippocampus and caudate that are topologically equivalent to a sphere.
Based on the weighted spherical harmonic representation of amygdalae, various multivariate tests were performed to detect the group difference between autistic and control subjects. Most of multivariate shape models on coordinates and deformation vector fields have mainly used the Hotelling's T-sqaure as a test statistic (Cao and Worsley, 1999; Chung et al., 2001; Collins et al., 1998; Gaser et al., 1999; Joshi et al., 1997; Thompson et al., 1997). The Hotelling's T-sqaure statistic tests for the equality of vector means without accounting the additional covariates such as gender, brain size and age. Since the size of amygdala is dependent on brain size and possibly on age as well, there is a definite need for a model that is able to include these covariates explicitly. The proposed multivariate linear model does exactly this by generalizing the Hotelling's T-square framework to incorporate additional covariates.
In order to simplify the computational burden of setting up the proposed multivariate linear models, we have developed the SurfStat package (www.math.mcgill.ca/keith/surfstat). that offers a unified statistical analysis platform for various 2D surface mesh and 3D image volume data. The novelty of SurfStat is that there is no need to specify design matrices that tend to baffle researchers not familiar with contrasts and design matrices. SurfStat supersedes fMRISTAT, and contains all the statistical and multiple comparison correction routines.
2. Methods
2.1 Surface Parameterization
Once the binary segmentation ℳa of an object is obtained either manually or automatically, the marching cubes algorithm (Lorensen and Cline, 1987) was applied to obtain a triangle surface mesh ∂ℳa. The weighted spherical harmonic representation requires a smooth mapping from the surface mesh to a unit sphere S2 to establish a coordinate system. We have developed a new surface flattening algorithm based on heat diffusion.
We start with putting a larger sphere ℳs that encloses the binary object ℳa. Figure 2 shows an illustration with the binary segmentation of amygdala. The center of the sphere ℳs is taken as the average of the mesh coordinates of ∂ℳa, which forms the surface mass center. The radius of the sphere ℳs is taken in such a way that the shortest distance between the sphere to the binary object ℳa is fixed (5mm for amygdale). The final flattening map is definitely affected by the perturbation of the position of the sphere but since we are fixing it to be the mass center of surface for all amygdale, we do not need to worry about the perturbation effect.
Figure 2.
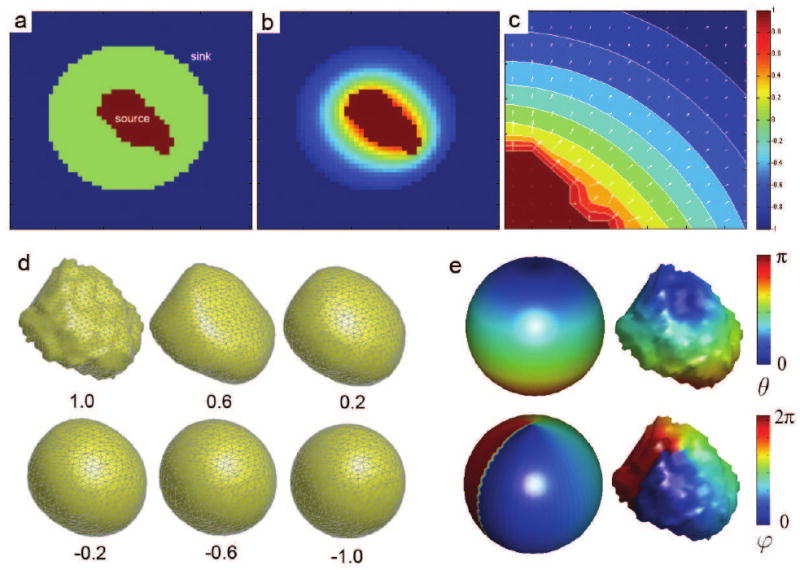
(a) The heat source (amygdala) is assigned value 1 while the heat sink is assigned the value -1. The diffusion equation is solved with these boundary condition. (b) After a sufficient number of iterations, the equilibrium state f(x,∞) is reached. (c) The gradient field ∇f(x,∞) shows the direction of heat propagation from the source to the sink. The integral curve of the gradient field is computed by connecting one level set to the next level sets of f(x,∞). (d) Amygala surface flattening is done by tracing the integral curve at each mesh vertex. The numbers c = 1.0, 0.6, ⋯ , −1.0 correspond to the level sets f(x,∞) = c. (e) Amygdala surface parameterization using the angles (θ, φ). The point θ = 0 corresponds to the north pole of a unit sphere.
The binary object ℳa is assigned the value 1 while the enclosing sphere is assigned the value -1, i.e.
| (1) |
for all σ ∈ [0, ∞). The parameter σ is the diffusion time. ℳa and ℳs serve as a heat source and a heat sink respectively. Then we solve isotropic diffusion
| (2) |
with the given boundary condition (1). Δ is the 3D Laplacian. When σ → ∞, the solution reaches the heat equilibrium state where the additional diffusion does not make any change in heat distribution. The heat equilibrium state is also obtained by letting and solving for the Laplace equation
| (3) |
with the same boundary condition. This will results in the equilibrium state denoted by f(x, σ = ∞). Once we obtained the equilibrium state, we trace the path from the heat source to the heat sink for every mesh vertices on the isosurface of ℳa using the gradient of the heat equilibrium ∇f(x,∞). Similar formulation called the Laplace equation method has been used in estimating cortical thickness bounded by outer and inner cortical surfaces by establishing correspondence between two surfaces by tracing the gradient of the equilibrium state (Yezzi and Prince, 2001; Jones et al., 2006; Lerch and Evans, 2005).
The heat gradients form vector fields originating at the heat source and ending at the heat sink (Figure 2). The integral curve of the gradient field at a mesh vertex p ∈ ∂ℳa establishes a smooth mapping from the mesh vertex to the sphere. The integral curve τ is obtained by solving a system of differential equations
with τ(t = 0) = p. The integral curve approach is a widely used formulation in tracking white matter fibers using diffusion tensors (Basser et al., 2000; Lazar et al., 2003). These methods rely on discretizing the differential equations using the Runge-Kutta method, which is computation intensive. However, we avoided the Runge-Kutta method and solved using the idea of the propagation of level sets. Instead of directly computing the gradient field ∇f(x,∞), we computed the level sets f(x,∞) = c of the equilibrium state corresponding to for varying c between -1 and 1. The integral curve is then obtained by finding the shortest path from one level set to the next level set and connecting them together in a piecewise fashion. This is done in an iterative fashion as shown in Figure 2, where five level sets corresponding to the values c = 0.6,0.2, −0.2, −0.6, −1.0 are used to flatten the amygdala surface. Once we obtained the spherical mapping, we can then project the angles (θ, φ) onto ∂ℳa and the two angles serve as the underlying parameterization for the weighted spherical harmonic representation.
For the proposed flattening method to work, the binary object has to be close to either star-shape or convex. For shapes with a more complex structure, the gradient lines that correspond to neighboring nodes on the surface will fall within one voxel in the volume, creating numerical singularities in mapping to the sphere. Other more complex mapping methods such as conformal mapping (Angenent et al., 1999; Gu et al., 2004; Hurdal and Stephenson, 2004) can avoid this problem but more numerically demanding. On the other hands, our approach is simpler and more computationally efficient because it works for a limited class of shapes.
2.2 Weighted Spherical Harmonic Representation
The parameterized amygdala surfaces, in terms of spherical angles θ, φ, are further expressed using the weighted spherical harmonic representation (Chung et al., 2007), which expresses surface coordinate functions as a weighted linear combination of spherical harmonics. The automatic degree selection procedure was also introduced in the previous work but for the completeness of our paper, the method is briefly explained in section 2.3.
The mesh coordinates for the object surface ∂ℳa are parameterized by the spherical angles Ω = (θ, φ) ∈ [0, π] ⊗ [0, 2π) as
The weighted spherical harmonic representation is given by
where
are the spherical harmonic coefficient vectors and Ylm are spherical harmonics of degree l and order m defined as
where and is the associated Legendre polynomial of order m (Deflection,). The associated Legendre polynomial is given by
The first few terms of the spherical harmonics are
The coefficients flm are estimated in a least squares fashion (Chung et al., 2007; Gerig et al., 2001; Shen et al., 2004).
Many previous imaging and shape modeling literature have used the complex-valued spherical harmonics (Bulow, 2004; Gerig et al., 2001; Gu et al., 2004; Shen et al., 2004), but we have only used real-valued spherical harmonics (Deflection,; Homeier and Steinborn, 1996) throughout the paper for the convenience in setting up a real-valued stochastic model. The relationship between the real- and complex-valued spherical harmonics is given in Blanco et al. (1997), and Homeier and Steinborn (1996). The complex-valued spherical harmonics can be transformed into real-valued spherical harmonics using an unitary transform.
In the subsequent multivariate linear modeling, some sort of surface smoothing is necessary before the random field theory based multiple comparison correction is performed. One important property of the weighted spherical harmonic representation is that the representation can be considered as kernel smoothing. On a unit sphere, the heat kernel is defined as
| (4) |
The heat kernel is symmetric and positive definite, and
The bandwidth σ controls the dispersion of the kernel weights. As σ → 0,
the Dirac-delta function. On the other hand, as σ → ∞,
Heat kernel smoothing of the coordinate function p is defined as
| (5) |
By substituting (4) into (5) and interchanging the integral with the summation, we have
| (6) |
which is the infinite dimensional weighted Spherical harmonic representation. Hence, the weighted Fourier representation can be considered as kernel smoothing and it inherits all the necessary properties of kernel smoothing.
2.3 Optimal Degree Selection
Since it is impractical to sum the representation to infinity, we need a rule for truncating the series expansion. Given the bandwidth σ of heat kernel, we automatically determine if increasing degree k has any effect on the goodness of the fit of the representation. In all spherical harmolnic literature (Gerig et al., 2004; Gerig et al., 2001; Gu et al., 2004; Shen and Chung, 2006; Shen et al., 2004), the truncation degree is simply selected based on a pre-specified error bound. On the other hand, our proposed statistical framework is based on a type-I error.
Although increasing the degree increases the goodness-of-fit of the representation, it also increases the number of coefficients to be estimated quadratically. It is necessary to find the optimal degree where the goodness-of-fit and the number of parameters balance out. Consider the k-th degree error model:
| (7) |
where ε is a zero mean Gaussian random field. We test if adding the k-th degree terms to the k − 1-th degree model is statistically significant by formally testing
This can be easily done using the F statistic 2k + 1 and n − (k + 1)2 degrees of freedom. At each degree, we compute the corresponding p-value and stop increasing the degree if it is smaller than pre-specified significance α = 0.01. For bandwidths σ = 0.01, 0.001, 0.0001, the approximate optimal degrees are 18, 42 and 78 respectively. In our study, we have used k = 42 degree representation corresponding to bandwidth σ = 0.001. The bandwidth 0.01 smoothes out too much local details while the bandwidth 0.0001 introduces too much voxel discretization error into the representation.
2.4 Reduction of Gibbs Phenomenon
The weighted spherical harmonic representation fixes the Gibbs phenomenon (ringing effects) associated with the traditional Fourier descriptors and spherical harmonic representation by weighting the series expansion with exponential weights (Chung et al., 2007). The exponential weights make the representation converge faster and reduces the amount of ringing artifacts. The Gibbs phenomenon often arises in Fourier series expansion of discrete data.
To numerically quantify the amount of overshoot, we define the overshoot as the maximum of L2 norm of the residual difference between the original and the reconstructed surface as
If surface coordinates are abruptly changing or their derivatives are discontinuous, the Gibbs phenomenon will severely distort the surface shape and the overshoot will never converge to zero.
We have reconstructed a cube and a left amygdala with various degree presentation and the bandwidth showing more ringing artifacts and overshoot in the traditional representation compared to the proposed weighted version. The exponentially decaying weights make the representation converge faster and reduce the Gibbs phenomenon significantly. Figure 3 shows the comparison of overshoots between the two representations. The plots display the amount of overshoot for the traditional representation (black) and the weighted version (red). The weighted spherical harmonic representation shows less amount of overshoot compared to the traditional technique.
Figure 3.
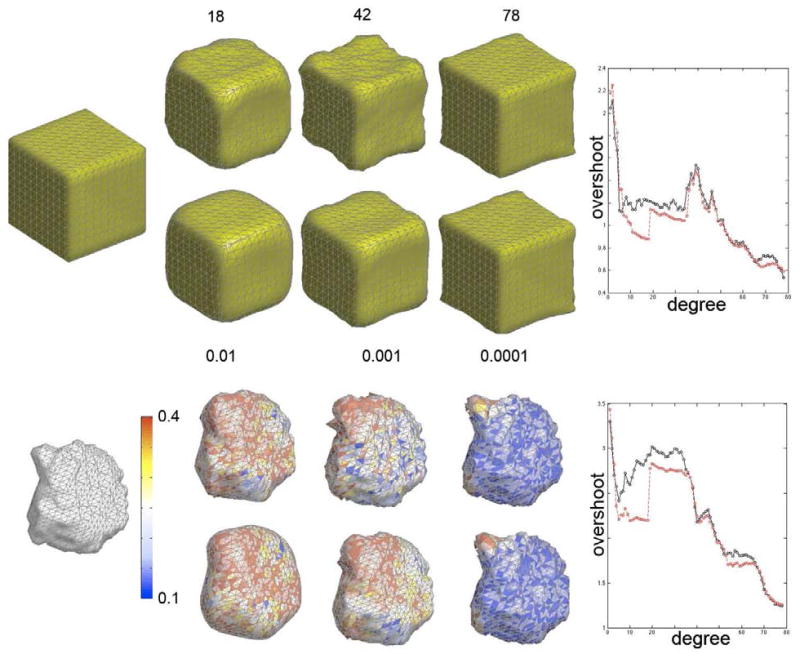
The first (third) row shows the significant Gibbs phenomenon in the spherical harmonic representation of a cube (left amygdala) for degrees k = 18, 42, 78. The second (fourth) row is the weighted spherical harmonic representation at the same degrees but with bandwidth σ = 0.01, 0.001, 0.0001 respectively. The color scale for amygdala is the absolute error between the original and reconstructed amygdale. In almost all degrees, the traditional spherical harmonic representation shows more prominent Gibbs phenomenon compared to the weighted version. The plots display the amount of overshoot for the traditional representation (black) vs. the weighted version (red).
2.5 Surface Normalization
MRIs were first reoriented manually to the pathological plane for the manual binary segmentation of amygdale (Convit et al., 1999). The images then further underwent a 6-parameter rigid-body alignment with manual landmarking (Nacewicz et al., 2006). The aligned left amygdale are displayed in Figure 4 showing an approximate initial alignment. The the proposed weighted spherical harmonic representations were then obtained. The additional alignment beyond the rigid-body alignment was done by matching the weighted spherical harmonic representations. Note we are not trying to match the original noisy surfaces but rather their smooth analytic representations. The correspondence is established by matching the coefficient of spherical harmonics at the same degree and order. This guarantees the sum of squares errors to be minimum in the following sense. Consider two surface coordinates p and q given by the representations
Figure 4.
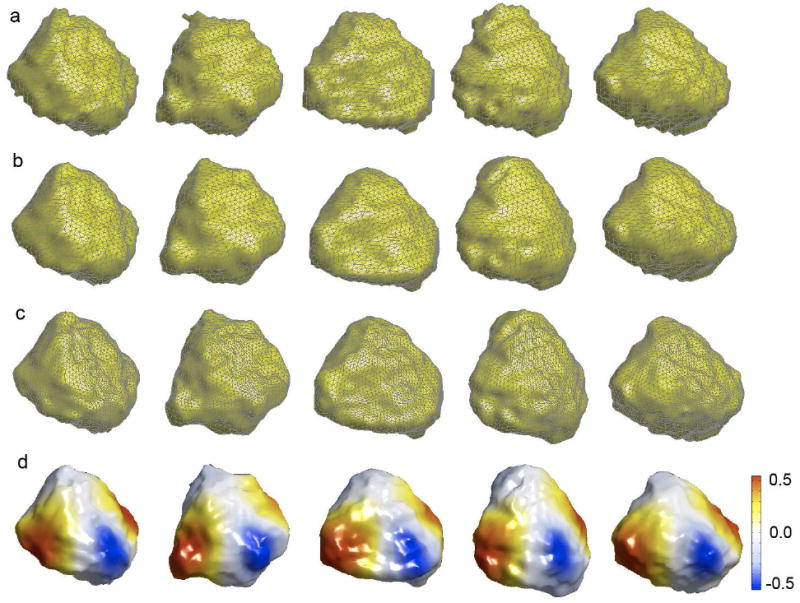
(a) Five representative left amygdala surfaces. (b) 42 degree weighted spherical harmonic representation. Surfaces have different mesh topology. (c) However, meshes can be resampled in such a way that all meshes have identical topology with exactly 2562 vertices and 5120 faces. Identically indexed mesh vertices correspond across different surfaces in the least squares fashion. (d) Spherical harmonic basis Y22 is projected on each amygdala to show surface correspondence. Note that the red colored left most corners more or less align properly.
and
where flm and glm are Fourier vectors. Suppose the surface p is deformed to p + d under the influence of the displacement vector field d. We wish to find d = (d1, d2, d3) that minimizes the discrepancy between p + d and q in the finite subspace ℋk, which is spanned by up to degree k spherical harmonics. The restriction of the search space to the finite subspace simplifies the computation as follows:
| (8) |
The proof is given in Chung et al. (2007). The optimal displacement in the least squares sense is obtained by simply taking the difference between two weighted spherical harmonic representation and matching coefficients of the same degree and order. (8) can be used to establish the correspondence across different meshes with different mesh topology, i.e. mesh connectivity. For instance, the first surface in Figure 4-(a) has 1270 vertices and 2536 faces while the second surface has 1302 vertices and 2600 faces. We establish correspondence between topologically different meshes by matching a specific point p(Ω0) in one surface to q(Ω0) in the other surface and it is optimal in the least squares fashion. Since the representation is continuously defined in any Ω ∈ [0, π] ⊗ [0, 2π), it is possible to resample surface meshes using a topologically different spherical mesh. We have uniformly sampled the unit sphere and constructed a spherical mesh with 2563 vertices and 5120 faces. This spherical mesh serves as a common mesh topology for all surfaces. After the resampling, all surfaces will have the identical mesh topology as the spherical mesh, and the identical vertex indices will correspond across different surfaces (Figure 4-(c)). This is also illustrated in Figure 4-(d), where the pattern of basis Y22 corresponds across different amygdale. A similar idea of uniform mesh topology has been previously used for establishing MNI cortical correspondence(Chung et al., 2003; Chung et al., 2005; MacDonald et al., 2000; Lerch and Evans, 2005; Taylor and Worsley, 2008; Worsley et al., 2004).
Denote the surface coordinates corresponding to the i-th surface as pi. Then we have the representation
| (9) |
There are total (k + 1)2 × 3 coefficients to be estimated. Assume there are total n surfaces, the average surface p̄ is given as
| (10) |
In our study, the average left and right amygdala templates are constructed by averaging the spherical harmonic coefficients of all 24 control subjects. The template surfaces serve as the reference coordinates for projecting the subsequent statistical parametric maps (Figure 7 and 8).
Figure 7.
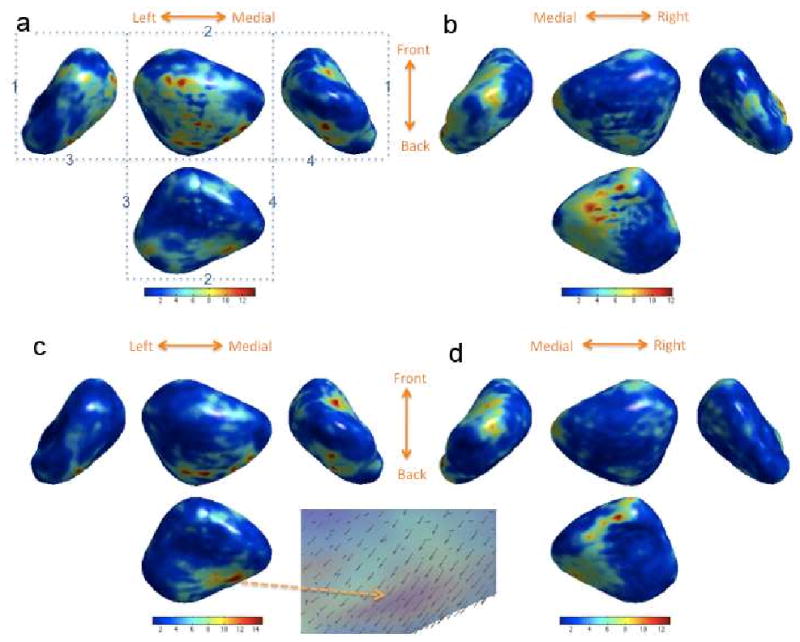
F statistic map of shape difference displayed on the average left amygdala (a) and right amygdala (b). We did not detect any significant difference at α = 0.01. The left amygdala (a) is displayed in such a way that, if we fold along the dotted lines and connect the identically numbered lines, we obtain the 3D view of the amygdala. The top middle rectangle corresponds to the axial view obtained by observing the amygdala from the top of the brain. (c) and (d) show the F statistic map of shape difference accounting for age and the total brain volume. The arrows in the enlarged area show the direction of shape difference (autism - control).
Figure 8.
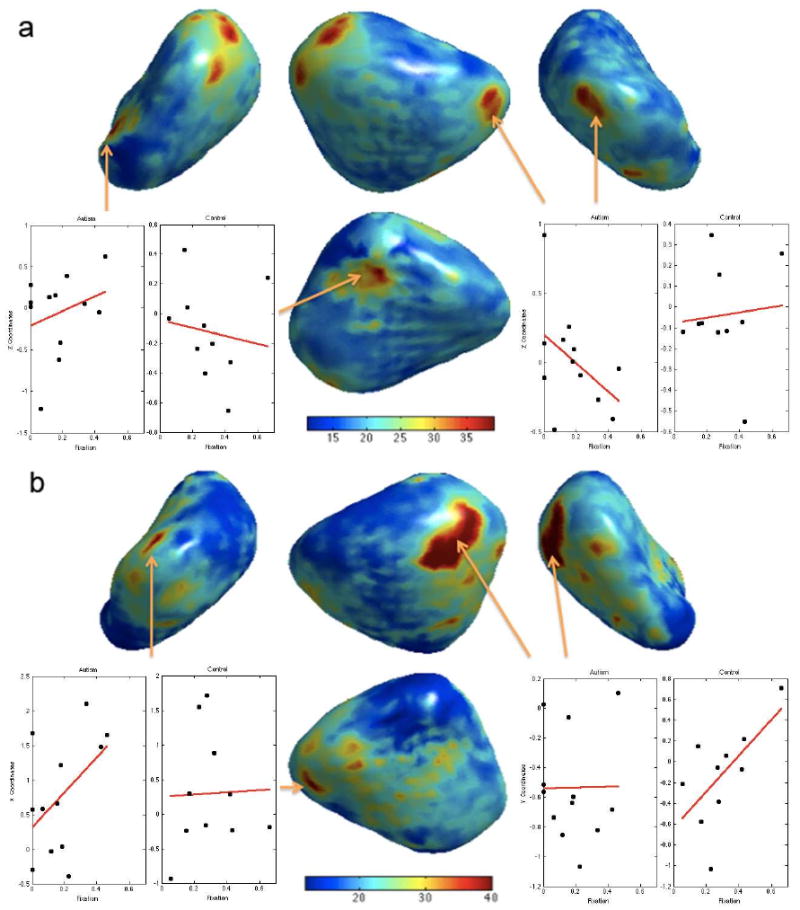
F statistic map of interaction between group and gaze fixation. Red regions show significant interaction for (a) left and (b) right amygdale. For better visualization, the color bar for the right amygdala (b) has been thresholded at 40 since the maximum F statistics at the largest cluster is 65.68 (p = 0.003). The scatter plots show the particular coordinate of the displacement vector from the average surface vs. gaze fixation. The red lines are regression lines.
Validation
The methodology is validated in simulated surfaces where the ground truth is exactly known. In order not to bias the result, we have used an intrinsic geometric method using the Laplace-Beltrami eigenfunctions as a way to simulate surfaces with the known ground truth (Lévy and Inria-Alice, 2006). For the surface coordinates p, we have the Laplace-Beltrami operator Δ and its eigenfunctions ψj satisfying
where
Then each surface can be represented as a linear combination of the Laplace-Beltrami eigenfunctions:
where fj = 〈p, ψj〉. Note that low degree coefficients represent global shape features and high degree coefficients represent high frequency local shape features. So by changing the high degree coefficients a bit, we can simulate new surfaces with similar global features but with the exact surface correspondence.
For the first simulated surface, we simply used the left amygdala surface of a randomly selected subject with 1000 basis ψj (Figure 5-(a)). Now if we reuse the first five coefficients fj while changing the remaining coefficients to gj, we can obtain the second simulated surface given by
Figure 5.
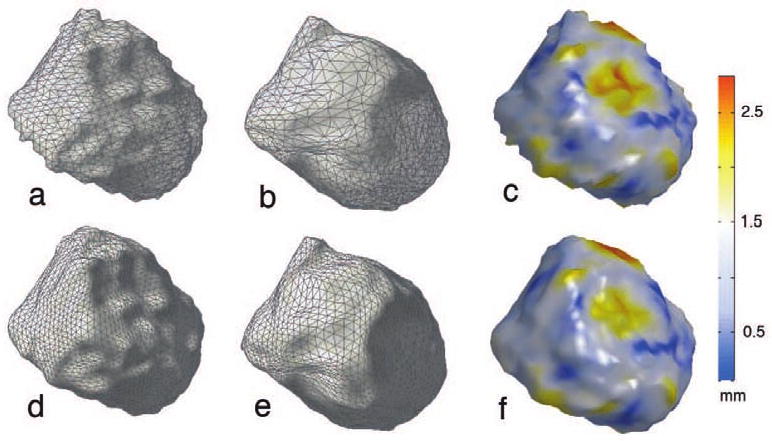
(a) (b) Simulated surfaces with the known displacement field between them. (c) The displacement in mm. (d) (e) Corresponding weighted spherical harmonic representation (f) The estimated displacement from the weighted spherical harmonic representations.
This is shown in Figure 5-(b) where the global shape is similar to (a) but local shape features differ substantially. The high degree coefficients gj were obtained from the remaining 45 amygdala surfaces to generate 45 simulated surfaces. This process generates one fixed surface which serves as a template and 45 matched surfaces with the known displacement fields. The simulated surface went through the proposed processing pipeline and the weighted spherical harmonic representations were computed. The displacement between the representations is given by the minimum distance (8). Figure 5-(f) shows the estimated displacement which shows smoother pattern than the ground truth. This is expected since the ground truth is the distance between noisy surfaces while the estimated displacement is the distance between smooth functional representations. However, the pattern of estimation does follow the pattern of the ground truth sufficiently well. In fact the mean relative error over each surface is 0.116 ± 0.011.
2.6 Multivariate Linear Models
Multivariate linear models (Anderson, 1984; Taylor and Worsley, 2008; Worsley et al., 2004) generalize widely used univariate general linear models (Worsley et al., 1996) by incorporating vector valued response and explanatory variables. The weighted spherical harmonic representation of surface coordinates will be taken as the response variable P. Consider the following multivariate linear model at each fixed (θ, φ)
| (11) |
where P = (p1′,p2′, ⋯, pn′)′ is the matrix of weighted spherical harmonic representation, X is the matrix of contrasted explanatory variables, and B is the matrix of unknown coefficients. Nuisance covariates are in the matrix Z and the corresponding coefficients are in the matrix G. The subscripts denote the dimension of matrices. The components of Gaussian random matrix U are zero mean and unit variance. Σ accounts for the covariance structure of coordinates. Then we are interested in testing the null hypothesis
For the reduced model corresponding to B = 0, the least squares estimator of G is given by
The residual sum of squares of the reduced model is
while that of the full model is
Note that Ĝ is different from Ĝ0 and estimated directly from the full model. By comparing how large the residual E is against the residual E0, we can determine the significance of coefficients B. However, since E and E0 are matrices, we take a function of eigenvalues of as a statistic. For instance, Lawley-Hotelling trace is given by the sum of eigenvalues while Roy's maximum root R is the largest eigenvalue. In the case there is only one eigenvalue, all these multivariate test statistics simplify to Hotelling's T-sqaure statistic. The Hotelling's T-square statistic has been widely used in modeling 3D coordinates and deformations in brain imaging (Cao and Worsley, 1999; Chung et al., 2001; Gaser et al., 1999; Joshi, 1998; Thompson et al., 1997). The random field theory for Hotelling's T-square statistic has been available for a while (Cao and Worsley, 1999). However, the random field theory for the Roy's maximum root has not been developed until recently (Taylor and Worsley, 2008; Worsley et al., 2004).
The inference for Roy's maximum root is based on the Roy's union-intersection principle (Roy, 1953), which simplifies the multivariate problem to a univariate linear model. Let us multiply an arbitrary constant vector ν3×1 on both sides of (11):
| (12) |
Obviously (12) is a usual univariate linear model with a Gaussian noise. For the univariate testing on Bν = 0, the inference is based on the F statistic with p and n − p − r degrees of freedom, denoted as Fν. Then Roy's maximum root statistic can be defined as R = maxν Fν. Now it is obvious that the usual random field theory can be applied in correcting for multiple comparisons. The only trick is to increase the search space, in which we take the supreme of the F random field, from the template surface to much higher dimension to account for maximizing over ν as well.
2.7 SurfStat
SurfStat package was developed to utilize a model formula and avoids the explicit use of design matrices and contrasts, which tend to be a hinderance to most end users not familiar with such concepts. SurtStat can import MNI (MacDonald et al., 2000), FreeSurfer (surfer.nmr.mgh.harvard.edu) based cortical mesh formats as well as other volumetric image data. The model formula approach is implemented in many statistics packages such as Splus (www.insightful.com) R (www.r-project.org) and SAS (www.sas.com). These statistics packages accept a linear model like
as the direct input for linear modeling avoiding the need to explicitly state the design matrix. P is a n × 3 matrix of coordinates of weighted spherical harmonic representation, Age is the age of subjects, Brain is the total brain volume of subject and Group is the categorical group variable (0=control, 1 = autism). This type of model formula has yet to be implemented in widely used SPM or AFNI packages.
2.8 Simulation Study
We have performed two simulation studies to determine if the proposed pipeline can detect a small artificial bump. A similar bump test was done in Yu et al. (2007) for testing the effectiveness of a spherical wavelet representation. In the first simulation, we have generated the binary mask of a sphere with radius 10mm. Then we obtained the weighted spherical harmonic representation (6) of the sphere with σ = 0.001 and degree k = 42. Taking the estimated coefficients flm as the ground truth, we simulated 20 spheres (group A) by putting noise N(flm, (flm/20)2) in the spherical harmonic coefficients. The standard deviation is taken as the 20th of the estimated coefficient. We have also given a bump of height 1.5mm to the sphere and simulated 20 bumped sphere (Figure 6 -(a)). Two groups of surfaces are fed into the multivariate linear model testing for the group effect. The T-statistic map is projected on the average of 40 simulated surfaces (Figure 6-(b)). Since the bump is so small with respect to the noise level, we did not detect any the bump (p = 0.35).
Figure 6.
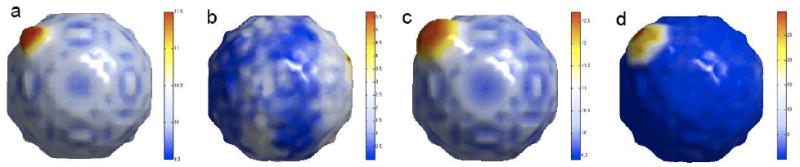
Simulation results. (a) small bump of height 1.5mm was added to a sphere of radius 10 mm. (b) T-statistic of comparing randomly simulated 20 spheres and 20 bumped spheres showing no group difference (p = 0.35). (c) small bump of height 3mm was added to a sphere of radius 10mm. (d) T-statistic of comparing randomly simulated 20 spheres and 20 bumped spheres showing significant group difference (p < 0.0003).
In the second simulation, we increased the height of the bump to 3mm (Figure 6-(c)) and repeated the first simulation. The resulting T-statistic map is projected on the average of 40 simulated surfaces (Figure 6-(d)). Unlike the first simulation study, we have detected the bump in yellow and red regions (p < 0.0003). These experiments demonstrate that the proposed framework works for detecting sufficiently large shape difference, and further demonstrate that what we detected in the real data is of sufficiently large shape difference. Otherwise, we simply wouldn't detect the signal in the first place.
3. Application: Amygdala Shape Modeling in Autism
3.1 Image and Data Acquisition
High resolution T1-weighted magnetic resonance images (MRI) were acquired with a GE SIGNA 3-Tesla scanner with a quadrature head coil with 240 × 240 mm field of view and 124 axial sections. Details on image acquisition parameters are given in Dalton et al. (2005) and Nacewicz et al. (2006). T2-weighted images were used to smooth out inhomogeneities in the inversion recovery-prepared images using FSL (www.fmrib.ox.ac.uk/fsl). Total 22 high functioning autistic and 24 normal control MRI were acquired. Subjects were all males aged between 8 and 25 years. The Autism Diagnostic Interview-Revised (Lord et al., 1994) was used for diagnoses by trained researchers K.M. Dalton and B.M. Nacewicz (Dalton et al., 2005).
MRIs were first reoriented to the pathological plane for optimal comparison with anatomical atlases (Convit et al., 1999). Image contrast was matched by alignment of white and gray matter peaks on intensity histograms. Manual segmentation was done by a trained expert B.M. Nacewicz who has been blind to the diagnoses (Nacewicz et al., 2006). The manual segmentation also involves refinement through plane-by-palne comparison with ex vivo atlas sections (Mai et al., 1997). The reliability of the manual segmentation protocol was validated by two raters on 10 amygdale resulting in interclass correlation of 0.95 and the spatial reliability (intersection over union) average of 0.84. Figure 1 shows the manual segmentation of an amygdala in three different cross sections. The amygdala (AMY) was traced in detail using various adjacent structures such as anterior commissure (AC), hippocampus (HIPP), inferior horn of lateral ventricle (IH), optic radiations (OR), optic tract (OT), temporal lobe white matter (TLWM) and tentorial notch (TN).
Figure 1.
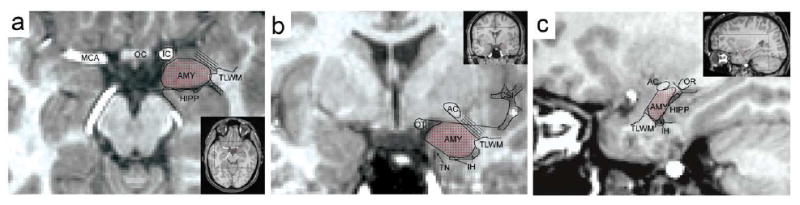
Amygdala manual segmentation at (a) axial (b) coronal and (c) midsagittal sections. The amygdala (AMY) was segmented using adjacent structures such as anterior commissure (AC), hippocampus (HIPP), inferior horn of lateral ventricle (IH), optic radiations (OR), optic tract (OT), temporal lobe white matter (TLWM) and tentorial notch (TN).
The total brain volume was also computed using an automated threshold-based connected voxel search method, and manually edited afterwards to ensure proper removal of CSF, skull, eye regions, brainstem and cerebellum using in-house software Spamalize (Oakes et al., 1999; Rusch et al., 2001; Nacewicz et al., 2006). The brain volumes are 1224±128 and 1230±161 cm3 for autistic and control subjects. The volume difference is not significant (p = 0.89).
A subset of subjects (10 controls and 12 autistic) went through a face emotion recognition task consisting of showing 40 standardized pictures of posed facial expressions (8 each of happy, angry and sad, and 16 neutral) (Dalton et al., 2005). Subjects were required to press a button distinguishing neutral from emotional faces. The faces were black and white pictures taken from the Karolinska Directed Emotional Faces set (Lundqvist et al., 1998). The faces were presented using E-Prime software (www.pstnet.com) allowing for the measurement of response time for each trial. iView system with a remote eye-tracking device (SensoMotoric Instruments, www.smivision.com) was used at the same time to measure gaze fixation duration on eyes and faces during the task. The system records eye movements as the gaze position of the pupil over a certain length of time along with the amount of time spent on any given fixation point. It has been hypothesized that subjects with autism should exhibit diminished eye fixation duration relative to face fixation duration. If there is no confusion, we will simply refer gaze fixation as the ratio of durations fixed on eyes over faces. Note that this is a unitless measure. Our study enables us to show that abnormal gaze fixation duration is correlated with amygdala shape in spatially localized regions.
3.2 Amygdala Volumetry
We have counted the number of voxels in amygdala segmentation and computed the volume of both left and right amygdale. The volumes for control subjects (n = 22) are left 1892 ± 173mm3, right 1883 ± 171mm3. The volumes for autistic subjects (n = 24) are left 1858 ± 182mm3, right 1862 ± 181mm3. The volume difference between the groups is not statistically significant based on the two sample t-test (p = 0.52 for left and 0.69 for right). The testing was done using SurfStat. Previous amygdala volumetry studies in autism have been inconsistent (Aylward et al., 1999; Haznedar et al., 2000; Nacewicz et al., 2006; Pierce et al., 2001; Schumann et al., 2004; Sparks et al., 2002). Aylward et al. (1999) and Pierce et al. (2001) reported that significantly smaller amygdala volume in the autistic subjects while Howard et al. (2000) and Sparks et al. (2002) reported larger volume. Haznedar et al. (2000) and Nacewicz et al. (2006) found no volume difference. These inconsistency might be due to the lack of control for brain size and age in statistical analysis (Schumann et al., 2004).
3.3 Local Shape Difference
From the amygdala volumetry result, it is still not clear if shape difference might be still present within amygdala. It is possible to have no volume difference while having significant shape difference. So we have performed multivariate linear modeling on the weighted spherical harmonic representation. We have tested the effect of group variable in the model
which resulted in the threshold of 26.99 at α = 0.1. On the other hand the maximum F statistic value is 13.55 (Figure 7 (a)). So we could not detect any shape difference in the left amygdala. For the right amygdala, the threshold is 26.64 which is far larger than the maximum F statistic value of 12.11. So again there is no statistically significant shape difference in the right amygdala.
We have also tested the effect of Group variable while accounting for age and the total brain volume in the SurfStat model form
| (13) |
The maximum F statistics are 14.77 (left) and 12.91 (right) while the threshold corresponding to the α = 0.1 is 14.58 (left) and 14.61 (right). Hence, we still did not detect group difference in the right amygdala (Figure 7-(d)) while there seems to be a bit weak group difference in the left amygdala (Figure 7-(c)). However, they did not pass the α = 0.01 test so our result is inconclusive. The enlarged area in Figure shows the average surface coordinate difference (autism - control) in the region of the maximum F value.
Head circumference and brain enlargement are linked to autism (Dementieva et al., 2005; Tager-Flusberg and Joseph, 2003) and thus the covariate Brain in the model (13) may introduce a scaling related effect that was originally not present in the data. However, we did not find significant brain volume difference between the groups (p = 0.89). The brain size difference does not significantly compound our result. From figure 8, we can see that the results between with and without covariating Brain are not much different (they are all statistically insignificant). Therefore, Brain in the model mostly accounts for subject-specific brain size difference rather than the group-specific brain size difference.
3.4 Brain and Behavior Association
Among total 46 subjects, 10 control and 12 autistic subjects went through face emotion recognition task and gaze fixation ( Fixation) was observed. The gaze fixation are 0.30±0.17 (control) and 0.18 ± 0.16 (autism). Note that these are unitless measures. Nacewicz et al. (2006) showed the gaze fixation duration correlate differently with amygdala volume between the two groups; however, it was not clear if the association difference is local or diffuse over all amygdala. So we have tested the significance of the interaction between Group and Fixation using multivariate linear models. The reduced model is
while the full model is
| (14) |
and we tested for the significance of the interaction Group*Fixation.
We have obtained regions of significant interaction in the both left (p < 0.05) and right (p < 0.02) lateral nuclei in amygdale (Figure 8). The largest cluster in the right amygdala shows highly significant interaction (max F = 65.68, p = 0.003). The color bar in Figure 8-(b) has been thresholded at 40 for better visualization. The scatter plots of the z-coordinate of the displacement vector field vs. Fixation are shown at the two most significant clusters in each amygdala. The red lines are linear regression lines. The significance of interaction implies difference in regression slopes between groups in a multivariate fashion. Note that there are three different slopes corresponding to x, y and z coordinates but due to the space limitation, we did not show other coordinates.
The total number of unknown parameters in our most complicated model (14) is 6×3 = 18 including the constant terms. This is a large number of parameters to estimate if (14) was a univariate linear model. However, in our multivariate setting, it is reasonable number of parameters since we are also tripling the number of measurements as well. Note that Roy's maximum root statistic is based on maximizing an F-statistic with 1 and n − 1 − 5 degrees of freedom. Since the number of subjects is n = 22 + 24, we have the sufficient degrees of freedom not to worry about the over-fitting problem. Unfortunately, practical power approximation for Roy's maximum root statistic does not exists although that of Lawley-Hotelling trace is available (Barton and Cramer, 1989; O'Brien and Muller, 1993) so the discussion of the parameter over-fitting is still an open statistical problem.
4. Discussion
Summary
The paper propose a unified multivariate linear modeling approach for a collection of binary neuroanatomical objects. The unified framework is applied to amygdala shape analysis in autism. The surfaces of the binary objects are flattened using a new technique based on heat diffusion. The coordinates of amygdala surfaces are smoothed and normalized using the weighted spherical harmonic representation. The multivariate linear models accounting for nuisance covariates are used using a newly developed SurfStat package.
Since surface data is inherently multivariate, traditionally Hotelling's T-square approach has been used on surface coordinates in a group comparison that can not account for nuisance covariates. On the other hand, the proposed multivariate linear model generalizes the Hotelling's T-square approach so that we can construct more complicated statistical models while accounting for additional covariates. The model formula based multivariate linear modeling tool SurfStat has been developed for this purpose and publicly available. We have applied the proposed methods to 22 autistic subjects to test if there is localized shape difference within an amygdala. We were able to localize regions, mainly in the right amygdala, that shows differential association of gaze fixation with anatomy between the groups.
Anatomical Findings
Many MRI-based volumetric studies have shown inconsistent results in determining if there are any abnormal amygdala volume difference (Aylward et al., 1999; Howard et al., 2000; Haznedar et al., 2000; Pierce et al., 2001; Schumann et al., 2004; Sparks et al., 2002; Nacewicz et al., 2006). These studies focus on the total volume difference of amygdala obtained from MRI and was unable to determine if the volume difference is locally focused within the subregions of amygdala or diffuse over all regions.
Although we did not detect statistically significant shape difference within amygdala at 0.01 level, we detected significant group difference of shape in relation to the gaze fixation duration mostly in the both lateral nuclei (largest clusters in Figure 8). The lateral nucleus receives information from the thalamus and cortex, and relay it to other subregions within the amygdala. Our finding is consistent with literature that reports that autistic subjects fail to activate the amygdala normally when processing emotional facial and eye expressions (Baron-Cohen et al., 1999; Critchley et al., 2000; Barnea-Goraly et al., 2004). There are two anatomical studies that additionally support our findings. A post-mortem study shows there are increased neuron-packing density of the medial, cortical and central nuclei, and medial and basal lateral nuclei of the amygdala in five autopsy cases (Courchesne, 1997). Further, reduced fractional anisotropy is found in the temporal lobes approaching the amygdala bilaterally in a diffusion tensor imaging study (Barnea-Goraly et al., 2004).
The inconsistent amygdala volumetry results seem to be caused by the local volume and shape difference of the lateral nuclei that may or may not contribute to the total volume of amygdala. Further diffusion tensor imaging studies on the white matter fiber tracts connecting the lateral nuclei would shed a light on the abnormal nature of lateral nucleus of the amygdala and its structural connection to other parts of the brain.
Methodological Limitations
There are few methodological limitations in our proposed study. Surface flattening is based on tracing the streamline of the gradient of heat equilibrium. The proposed flattening technique is simple enough to be applied to various binary objects. However, for the proposed flattening method to work, the binary object has to be close to star-shape or convex. Theoretically, the solution to the Laplacian equation is uniquely given and the heat gradient will never cross within the space between the inner and outer boundaries. However, for more complex structures like cortical surfaces, the gradient lines that correspond to neighboring nodes on the surface may fall within one voxel in the volume, creating overlapping nonsmooth mapping to the sphere. The overlapping problem can be avoided by subsampling the voxel grid in a much finer resolution but extending the method to cortical surfaces is left as a future study.
Although the proposed framework of diffusion-based flattening and the weighted spherical harmonic representation provide surface registration beyond the initial affine transformations, the accuracy is not high compared to other optimization based registration (Heimann et al., 2005; Meier and Fisher, 2002; Styner et al., 2003). It is likely that the optimization based methods will outperform our method. Although the comparative analysis against these methods is the beyond the scope of the current paper, the simulation study in section 2.5 demonstrates the proposed method provides sufficiently good accuracy (relative error of 0.116 ± 0.011).
Although the proposed weighted spherical harmonic approach streamlines various image processing tasks such as smoothing, representation and registration within a unified mathematical representation, we did not compare the performance with other available shape representation techniques such as the medial representation (Pizer et al., 1999) and wavelets (Yu et al., 2007). This is the beyond the scope of the current paper and requires an additional comparative study.
Acknowledgments
The authors with to thank Martin A. Styner of the Department of Psychiatry and Computer Science of the University of North Carolina at Chapel Hill and Shubing Wang of Merck for various discussion on spherical harmonics. This research is supported in part by grant 1UL1RR025011 from the Clinical and Translational Science Award (CTSA) program of the National Center for Research Resources, National Institutes of Health and WCU grant through the department of Brain and Cognitive Sciences at Seoul National University.
Appendix
We illustrate SurfStat package by showing the step-by-step command lines for multivariate linear models used in the study. The detailed description of the SurfStat package can be found in www.stat.uchicago.edu/∼worsley/surfstat. The SurfStat is a general purpose surface analysis package and it requires additional codes and for amygdala specific analysis. The additional codes can be found in www.stat.wisc.edu/∼mchung/research/amygdala.
Given an amygdala mesh surf, which is, for instance, given as a structured array of the form
-
surf =
-
vertices: [1270×3 double]
faces: [2536×3 double]
-
the amygdala flattening algorithm will generate the corresponding unit sphere mesh sphere that has identical topology as surf. The weighted spherical harmonic representation P with degree k = 42 and the bandwidth σ = 0.001 is computed from
> [P,coeff]=SPHARMsmooth(surf,sphere,42,0.001);
The coordinates of the weighted spherical harmonic representation have been read into an array of size 46 (subjects) × 2562 (vertices) × 3 (coordinates) P. Brain size ( brain), age ( age), group variable ( group) are read into 46 (subjects) × 1 vectors. The group categorical variable consists of strings ’ control’ and ’ autism’. We now convert these to terms that can be combined into a multivariate linear model as follows:
>Brain = term(brain);
>Age = term(age);
>Group = term (group);
>Group
autism control 0 1 0 1 1 0 1 0 . . . . . .
To test the effect of group, the linear model of the from P = 1 + Group is fitted by
>E = SurfStatLinMod(P,1 + Group, Avg);
where Avg is the average surface obtained from the weighted spherical harmonic representation.
We specify a group contrast and calculate the T-statistic:
>contrast = Group.autism - Group.control
-
contrast =
−1
−1
1
1
.
.
.
LM = SurfStatT(E, contrast);
LM.t gives the vector of 2562 T-statistic values for all mesh vertices. Instead of using the contrast and T-statistic, we can test the effect of group variable using the F-statistic as well:
>E0 = SurfStatLinMod(P,1);
>LM = SurfStatF(E,E0);
E0 contains the information about the sum of squared residual of the reduced model P = 1 in E0.SSE while E contains that of the full model P = 1 + Group. Based on the ratio of the sum of squared residuals, SurfStatF computes the F-statistics. To display the F-statistic value on top of the average surface, we use FigureOrigami(Avg, LM.t) which produces Figure 7.
We can determine the random field based thresholding corresponding to α = 0.01 level:
>resels = SurfStatResels(LM);
>stat_threshold(resels, length(LM.t),1,LM.df,0.01,[],[],[],LM.k)
-
peak_threshold =
26.9918
resels computes the resels of the random field and peak_threshold is the threshold corresponding to 0.1 level.
We can construct a more complicated model that includes the brain size and age as covariates:
>E0 = SurfStatLinMod(P,Age+Brain);
>E = SurfStatLinMod(P,Age+Brain+Group,Avg);
>LM = SurfStatF(E,E0);
LM.t contains the F-statistic of the significance of group variable while accounting for age and brain size. We can also test for interaction between gaze fixation Fixation and group variable:
>E0=SurfStatLinMod(P,Age+Brai +Group+Fixation);
>E=SurfStatLinMod(P,Age+Brain+Group+Fixation+Group*Fixation,Avg);
>LM=SurfStatF(E,E0);
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson T. An Introduction to Multivariate Statistical Analysis. 2nd Wiley; 1984. [Google Scholar]
- Angenent S, Hacker S, Tannenbaum A, Kikinis R. On the laplace-beltrami operator and brain surface flattening. IEEE Transactions on Medical Imaging. 1999;18:700–711. doi: 10.1109/42.796283. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Hutton C, Frackowiak RSJ, Johnsrude I, Price C, Friston KJ. Identifying global anatomical differences: deformation-based morphometry. Human Brain Mapping. 1998;6:348–357. doi: 10.1002/(SICI)1097-0193(1998)6:5/6<348::AID-HBM4>3.0.CO;2-P. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aylward E, Minshew N, Goldstein G, Honeycutt N, Augustine A, Yates K, Bartra P, Pearlson G. Mri volumes of amygdala and hippocampus in nonmentally retarded autistic adolescents and adults. Neurology. 1999;53:2145–2150. doi: 10.1212/wnl.53.9.2145. [DOI] [PubMed] [Google Scholar]
- Barnea-Goraly N, Kwon H, Menon V, Eliez S, Lotspeich L, Reiss A. White matter structure in autism: preliminary evidence from diffusion tensor imaging. Biological Psychiatry. 2004;55:323–326. doi: 10.1016/j.biopsych.2003.10.022. [DOI] [PubMed] [Google Scholar]
- Baron-Cohen S, Ring H, Wheelwright S, Bullmore E, Brammer M, Sim-mons A, Williams S. Social intelligence in the normal and autistic brain: An fMRI study. Eur J Neurosci. 1999;11:1891–1898. doi: 10.1046/j.1460-9568.1999.00621.x. [DOI] [PubMed] [Google Scholar]
- Barton C, Cramer E. Hypothesis testing in multivariate linear models with randomly missing data. Communications in Statistics-Simulation and Computation. 1989;18:875–895. [Google Scholar]
- Basser P, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo tractography using dt-mri data. Magnetic Resonance in Medicine. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Blanco M, Florez M, Bermejo M. Evaluation of the rotation matrices in the basis of real spherical harmonics. Journal of Molecular Structure: THEOCHEM. 1997;419:19–27. [Google Scholar]
- Brechbuhler C, Gerig G, Kubler O. Parametrization of closed surfaces for 3d shape description. Computer Vision and Image Understanding. 1995;61:154–170. [Google Scholar]
- Bulow T. Spherical diffusion for 3D surface smoothing. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004;26:1650–1654. doi: 10.1109/TPAMI.2004.129. [DOI] [PubMed] [Google Scholar]
- Cao J, Worsley KJ. The detection of local shape changes via the geometry of hotellings t2 fields. Annals of Statistics. 1999;27:925–942. [Google Scholar]
- Cates J, Fletcher P, Styner M, Hazlett H, Whitaker R. Particle-Based Shape Analysis of Multi-Object Complexes. Medical image computing and computer-assisted intervention: MICCAI… International Conference on Medical Image Computing and Computer-Assisted Intervention; 2008. pp. 477–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung M, Dalton KM, L S, Evans A, Davidson R. Weighted Fourier representation and its application to quantifying the amount of gray matter. IEEE Transactions on Medical Imaging. 2007;26:566–581. doi: 10.1109/TMI.2007.892519. [DOI] [PubMed] [Google Scholar]
- Chung M, Robbins S, Dalton KM, D R, A A, Evans A. Cortical thickness analysis in autism with heat kernel smoothing. NeuroImage. 2005;25:1256–1265. doi: 10.1016/j.neuroimage.2004.12.052. [DOI] [PubMed] [Google Scholar]
- Chung M, Worsley K, Paus T, Cherif D, Collins C, Giedd J, Rapoport J, Evans A. A unified statistical approach to deformation-based morphometry. NeuroImage. 2001;14:595–606. doi: 10.1006/nimg.2001.0862. [DOI] [PubMed] [Google Scholar]
- Chung M, Worsley K, Robbins S, Paus T, Taylor J, Giedd J, Rapoport J, Evans A. Deformation-based surface morphometry applied to gray matter deformation. NeuroImage. 2003;18:198–213. doi: 10.1016/s1053-8119(02)00017-4. [DOI] [PubMed] [Google Scholar]
- Collins DL, Paus T, Zijdenbos A, Worsley KJ, Blumenthal J, Giedd JN, Rapoport JL, Evans AC. Age related changes in the shape of temporal and frontal lobes: An mri study of children and adolescents. Soc Neurosci Abstr. 1998;24:304. [Google Scholar]
- Convit A, McHugh P, Wolf O, de Leon M, Bobinkski M, De Santi S, Roche A, Tsui W. Mri volume of the amygdala: a reliable method allowing separation from the hippocampal formation. Psychiatry Res. 1999;90:113–123. doi: 10.1016/s0925-4927(99)00007-4. [DOI] [PubMed] [Google Scholar]
- Courchesne E. Brainstem, cerebellar and limbic neuroanatomical abnormalities in autism. Current Opinion in Neurobiology. 1997;7:269–278. doi: 10.1016/s0959-4388(97)80016-5. [DOI] [PubMed] [Google Scholar]
- Critchley H, Daly E, Bullmore E, Williams S, T VA, Robert-son D, et al. The functional neuroanatomy of social behaviour: Changes in cerebral blood ow when people with autistic disorder pro- cess facial expressions. Brain. 2000;123:2203–2212. doi: 10.1093/brain/123.11.2203. [DOI] [PubMed] [Google Scholar]
- Csernansky J, Wang L, Joshi S, Tilak Ratnanather J, Miller M. Computational anatomy and neuropsychiatric disease: probabilistic assessment of variation and statistical inference of group difference, hemispheric asymmetry, and time-dependent change. NeuroImage. 2004;23:56–68. doi: 10.1016/j.neuroimage.2004.07.025. [DOI] [PubMed] [Google Scholar]
- Dalton K, Nacewicz B, Johnstone T, Schaefer H, Gernsbacher M, Goldsmith H, Alexander A, Davidson R. Gaze fixation and the neural circuitry of face processing in autism. Nature Neuroscience. 2005;8:519–526. doi: 10.1038/nn1421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dementieva Y, Vance D, Donnelly S, Elston L, Wolpert C, Ravan S, DeLong G, Abramson R, Wright H, Cuccaro M. Accelerated head growth in early development of individuals with autism. Pediatric neurology. 2005;32:102–108. doi: 10.1016/j.pediatrneurol.2004.08.005. [DOI] [PubMed] [Google Scholar]
- Fischl B, Dale A. Measuring the thickness of the human cerebral cortex from magnetic resonance images. PNAS. 2000;97:11050–11055. doi: 10.1073/pnas.200033797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaser C, Volz HP, Kiebel S, Riehemann S, Sauer H. Detecting structural changes in whole brain based on nonlinear deformationsapplication to schizophrenia research. NeuroImage. 1999;10:107–113. doi: 10.1006/nimg.1999.0458. [DOI] [PubMed] [Google Scholar]
- Gelb A. The resolution of the gibbs phenomenon for spherical harmonics. Mathematics of Computation. 1997;66:699–717. [Google Scholar]
- Gerig G, Styner M, Jones D, Weinberger D, Lieberman J. Shape analysis of brain ventricles using spharm. MMBIA. 2001:171–178. [Google Scholar]
- Gerig G, Styner M, Szekely G. Statistical shape models for segmentation and structural analysis. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 467–473. [Google Scholar]
- Golland P, Grimson W, Shenton M, Kikinis R. Deformation analysis for shape based classification. Lecture Notes in Computer Science. 2001:517–530. [Google Scholar]
- Gu X, Wang Y, Chan T, Thompson T, Yau S. Genus zero surface conformal mapping and its application to brain surface mapping. IEEE Transactions on Medical Imaging. 2004;23:1–10. doi: 10.1109/TMI.2004.831226. [DOI] [PubMed] [Google Scholar]
- Haznedar M, Buchsbaum M, Wei T, Hof P, Cartwright C, Bienstock CA, Hollander E. Limbic circuitry in patients with autism spectrum disorders studied with positron emission tomography and magnetic resonance imaging. American Journal of Psychiatry. 2000;157:1994–2001. doi: 10.1176/appi.ajp.157.12.1994. [DOI] [PubMed] [Google Scholar]
- Heimann T, Wolf I, Williams T, Meinzer H. 3D active shape models using gradient descent optimization of description length. Information Processing in Medical Imaging, Lecture Notes in Computer Science. 2005:566–577. doi: 10.1007/11505730_47. [DOI] [PubMed] [Google Scholar]
- Homeier H, Steinborn E. Some properties of the coupling coefficients of real spherical harmonics and their relation to Gaunt coefficients. Journal of Molecular Structure: THEOCHEM. 1996;368:31–37. [Google Scholar]
- Howard M, Cowell P, Boucher J, Broks P, Mayes A, Farrant A, Roberts N. Convergent neuroanatomical and behavioral evidence of an amygdala hypothesis of autism. NeuroReport. 2000;11:2931–2935. doi: 10.1097/00001756-200009110-00020. [DOI] [PubMed] [Google Scholar]
- Hurdal MK, Stephenson K. Cortical cartography using the discrete conformal approach of circle packings. NeuroImage. 2004;23:S119–S128. doi: 10.1016/j.neuroimage.2004.07.018. [DOI] [PubMed] [Google Scholar]
- Jones D, Catani M, Pierpaoli C, Reeves S, Shergill S, O'Sullivan M, Golesworthy P, McGuire P, Horsfield M, Simmons A, Williams S, Howard R. Age effects on diffusion tensor magnetic resonance imaging tractography measures of frontal cortex connections in schizophrenia. Human Brain Mapping. 2006;27:230–238. doi: 10.1002/hbm.20179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi S. Large Deformation Diffeomorphisms and Gaussian Random Fields for Statistical Characterization of Brain Sub-Manifolds 1998 [Google Scholar]
- Joshi S, Grenander U, Miller M. The geometry and shape of brain sub-manifolds. International Journal of Pattern Recognition and Artificial Intelligence: Special Issue on Processing of MR Images of the Human. 1997;11:1317–1343. [Google Scholar]
- Joshi S, Pizer S, Fletcher P, Yushkevich P, Thall A, Marron J. Multiscale deformable model segmentation and statistical shape analysis using medial descriptions. IEEE Transactions on Medical Imaging. 2002;21:538–550. doi: 10.1109/TMI.2002.1009389. [DOI] [PubMed] [Google Scholar]
- Kelemen A, Szekely G, Gerig G. Elastic model-based segmentation of 3-d neuroradiological data sets. IEEE Transactions on Medical Imaging. 1999;18:828–839. doi: 10.1109/42.811260. [DOI] [PubMed] [Google Scholar]
- Khan A, Chung M, Beg M. Robust atlas-based brain segmentation using multi-structure confidence-weighted registration. Lecture Notes on Computer Science. 1999;5762:549–557. doi: 10.1007/978-3-642-04271-3_67. [DOI] [PubMed] [Google Scholar]
- Lazar M, Weinstein D, Tsuruda J, Hasan K, Arfanakis K, Meyerand M, Badie B, Rowley H, Haughton V, Field A, Witwer B, Alexander A. White matter tractography using tensor deflection. Human Brain Mapping. 2003;18:306–321. doi: 10.1002/hbm.10102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerch JP, Evans A. Cortical thickness analysis examined through power analysis and a population simulation. NeuroImage. 2005;24:163–173. doi: 10.1016/j.neuroimage.2004.07.045. [DOI] [PubMed] [Google Scholar]
- Leventon M, Grimson W, Faugeras O. Statistical shape influence in geodesic active contours. IEEE Conference on Computer Vision and Pattern Recognition; 2000. [Google Scholar]
- Lévy B, Inria-Alice F. Laplace-beltrami eigenfunctions towards an algorithm that” understands” geometry. IEEE International Conference on Shape Modeling and Applications 2006. SMI 2006; 2006. pp. 13–13. [Google Scholar]
- Lord C, Rutter M, Couteur A. Autism diagnostic interviewrevised: a revised version of a diagnostic interview for caregivers of individuals with possible pervasive developmental disorders. J Autism Dev Disord. 1994:659–685. doi: 10.1007/BF02172145. [DOI] [PubMed] [Google Scholar]
- Lorensen W, Cline H. Marching cubes: A high resolution 3D surface construction algorithm. Proceedings of the 14th annual conference on Computer graphics and interactive techniques; 1987. pp. 163–169. [Google Scholar]
- Luders E, Thompson PM, Narr K, Toga A, Jancke L, Gaser C. A curvature-based approach to estimate local gyrification on the cortical surface. NeuroImage. 2006;29:1224–1230. doi: 10.1016/j.neuroimage.2005.08.049. [DOI] [PubMed] [Google Scholar]
- Lundqvist D, Flykt A, Ohman A. Karolinska Directed Emotional Faces. Department of Neurosciences, Karolinska Hospital; Stockholm, Sweden: 1998. [Google Scholar]
- MacDonald J, Kabani N, Avis D, Evans A. Automated 3-D extraction of inner and outer surfaces of cerebral cortex from mri. NeuroImage. 2000;12:340–356. doi: 10.1006/nimg.1999.0534. [DOI] [PubMed] [Google Scholar]
- Mai J, Assheuer J, Paxinos G. Atlas of the Human Brain. Academic Press; San Diego: 1997. [Google Scholar]
- Meier D, Fisher E. Parameter space warping: shape-based correspondence between morphologically different objects. IEEE Transactions on Medical Imaging. 2002;21:31–47. doi: 10.1109/42.981232. [DOI] [PubMed] [Google Scholar]
- Miller M, Banerjee A, Christensen G, Joshi S, Khaneja N, Grenander U, Matejic L. Statistical methods in computational anatomy. Statistical Methods in Medical Research. 1997;6:267–299. doi: 10.1177/096228029700600305. [DOI] [PubMed] [Google Scholar]
- Miller M, Massie A, Ratnanather J, Botteron K, Csernansky J. Bayesian construction of geometrically based cortical thickness metrics. NeuroImage. 2000;12:676–687. doi: 10.1006/nimg.2000.0666. [DOI] [PubMed] [Google Scholar]
- Nacewicz B, Dalton K, Johnstone T, Long M, McAuliff E, Oakes T, Alexander A, Davidson R. Amygdala volume and nonverbal social impairment in adolescent and adult males with autism. Arch Gen Psychiatry. 2006;63:1417–1428. doi: 10.1001/archpsyc.63.12.1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nain D, Styner M, Niethammer M, Levitt J, Shenton M, Gerig G, Bobick A, Tannenbaum A. Statistical shape analysis of brain structures using spherical wavelets. IEEE Symposium on Biomedical Imaging ISBI; 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oakes T, Koger J, Davidson R. Automated whole-brain segmentation. NeuroImage. 1999;9:237. [Google Scholar]
- O'Brien R, Muller K. Unified power analysis for t-tests through multivariate hypotheses. Applied analysis of variance in behavioral science. 1993:297–344. [Google Scholar]
- Pierce K, Muller RA, A J, Allen G, Courchesne E. Face processing occurs outside the fusiform ”face area” in autism: evidence from functional mri. Brain. 2001;124:2059–2073. doi: 10.1093/brain/124.10.2059. [DOI] [PubMed] [Google Scholar]
- Pizer S, Fritsch D, Yushkevich P, Johnson V, Chaney E. Segmentation, registration, and measurement of shape variation via image object shape. IEEE Transactions on Medical Imaging. 1999;18:851–865. doi: 10.1109/42.811263. [DOI] [PubMed] [Google Scholar]
- Qiu A, Miller M. Multi-structure network shape analysis via normal surface momentum maps. NeuroImage. 2008;42:1430–1438. doi: 10.1016/j.neuroimage.2008.04.257. [DOI] [PubMed] [Google Scholar]
- Rojas D, Smith J, Benkers T, Camou S, Reite M, Rogers S. Hippocampus and amygdala volumes in paretns of children with autistic disorder. The Canadian Journal of Statistics. 2000;28:225–240. doi: 10.1176/appi.ajp.161.11.2038. [DOI] [PubMed] [Google Scholar]
- Roy S. On a heuristic method of test construction and its use in multivariate analysis. Ann Math Statist. 1953;24:220–238. [Google Scholar]
- Rusch B, Abercrombie H, Oakes T, Schaefer S, Davidson R. Hippocampal morphometry in depressed patients and control subjects: relations to anxiety symptoms. Biological Psychiatry. 2001;50:960–964. doi: 10.1016/s0006-3223(01)01248-3. [DOI] [PubMed] [Google Scholar]
- Saad Z, Reynolds R, Argall B, Japee S, Cox R. Suma: an interface for surface-based intra-and inter-subject analysis with afni. IEEE International Symposium on Biomedical Imaging (ISBI); 2004. pp. 1510–1513. [Google Scholar]
- Schumann C, Hamstra J, Goodlin-Jones B, Lotspeich L, Kwon H, Buonocore M, Lammers C, Reiss A, Amaral D. The amygdala is enlarged in children but not adolescents with autism; the hippocampus is enlarged at all ages. Journal of Neuroscience. 2004;24:6392–6401. doi: 10.1523/JNEUROSCI.1297-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen L, Chung M. Large-scale modeling of parametric surfaces using spherical harmonics. Third International Symposium on 3D Data Processing, Visualization and Transmission (3DPVT).2006. [Google Scholar]
- Shen L, Ford J, Makedon F, Saykin A. surface-based approach for classification of 3d neuroanatomical structures. Intelligent Data Analysis. 2004;8:519–542. [Google Scholar]
- Sparks B, Friedman S, Shaw D, Aylward E, Echelard D, Artru A, Maravilla K, Giedd J, Munson J, Dawson G, Dager S. Brain structural abnormalities in young children with autism spectrum disorder. Neurology. 2002;59:184–192. doi: 10.1212/wnl.59.2.184. [DOI] [PubMed] [Google Scholar]
- Styner M, Gerig G, Joshi S, Pizer S. Automatic and robust computation of 3d medial models incorporating object variability. International Journal of Computer Vision. 2003;55:107–122. [Google Scholar]
- Styner M, Oguz I, Xu S, Brechbuhler C, Pantazis D, Levitt J, Shenton M, Gerig G. Framework for the statistical shape analysis of brain structures using spharm-pdm. Insight Journal, Special Edition on the Open Science Workshop at MICCAI. 2006 [PMC free article] [PubMed] [Google Scholar]
- Tager-Flusberg H, Joseph R. Identifying neurocognitive phenotypes in autism. Philosophical Transactions: Biological Sciences. 2003;358:303–314. doi: 10.1098/rstb.2002.1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J, Worsley K. Random fields of multivariate test statistics, with applications to shape analysis. Annals of Statistics. 2008 page in press. [Google Scholar]
- Thompson P, Giedd J, Woods R, MacDonald D, Evans A, Toga A. Growth patterns in the developing human brain detected using continuum-mechanical tensor mapping. Nature. 2000;404:190–193. doi: 10.1038/35004593. [DOI] [PubMed] [Google Scholar]
- Thompson P, Toga A. A surface-based technique for warping 3-dimensional images of the brain. IEEE Transactions on Medical Imaging. 1996;15 doi: 10.1109/42.511745. [DOI] [PubMed] [Google Scholar]
- Thompson PM, MacDonald D, Mega MS, Holmes CJ, Evans AC, Toga AW. Detection and mapping of abnormal brain structure with a probabilistic atlas of cortical surfaces. J Comput Assist Tomogr. 1997;21:567–581. doi: 10.1097/00004728-199707000-00008. [DOI] [PubMed] [Google Scholar]
- Timsari B, Leahy R. An optimization method for creating semi-isometric flat maps of the cerebral cortex. The Proceedings of SPIE, Medical Imaging 2000 [Google Scholar]
- Worsley K, Marrett S, Neelin P, Vandal A, Friston K, Evans A. A unified statistical approach for determining significant signals in images of cerebral activation. Human Brain Mapping. 1996;4:58–73. doi: 10.1002/(SICI)1097-0193(1996)4:1<58::AID-HBM4>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- Worsley K, Taylor J, Tomaiuolo F, Lerch J. Unified univariate and multivariate random field theory. NeuroImage. 2004;23:S189–195. doi: 10.1016/j.neuroimage.2004.07.026. [DOI] [PubMed] [Google Scholar]
- Yezzi A, Prince J. A PDE approach for measuring tissue thickness. IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR).2001. [Google Scholar]
- Yu P, Grant P, Qi Y, Han X, Segonne F, Pienaar R, Busa E, Pacheco J, Makris N, Buckner R, et al. Cortical Surface Shape Analysis Based on Spherical Wavelets. IEEE Transactions on Medical Imaging. 2007;26:582. doi: 10.1109/TMI.2007.892499. [DOI] [PMC free article] [PubMed] [Google Scholar]


