Abstract
It is well-known that population substructure may lead to confounding in case-control association studies. Here, we examined genetic structure in a large racially and ethnically diverse sample consisting of 5 ethnic groups of the Multiethnic Cohort study (African Americans, Japanese Americans, Latinos, European Americans and Native Hawaiians) using 2,509 SNPs distributed across the genome. Principal component analysis on 6,213 study participants, 18 Native Americans and 11 HapMap III populations revealed 4 important principal components (PCs): the first two separated Asians, Europeans and Africans, and the third and fourth corresponded to Native American and Native Hawaiian (Polynesian) ancestry, respectively. Individual ethnic composition derived from self-reported parental information matched well to genetic ancestry for Japanese and European Americans. STRUCTURE-estimated individual ancestral proportions for African Americans and Latinos are consistent with previous reports. We quantified the East Asian (mean 27%), European (mean 27%) and Polynesian (mean 46%) ancestral proportions for the first time, to our knowledge, for Native Hawaiians. Simulations based on realistic settings of case-control studies nested in the Multiethnic Cohort found that the effect of population stratification was modest and readily corrected by adjusting for race/ethnicity or by adjusting for top PCs derived from all SNPs or from ancestry informative markers; the power of these approaches was similar when averaged across causal variants simulated based on allele frequencies of the 2,509 genotyped markers. The bias may be large in case-only analysis of gene by gene interactions but it can be corrected by top PCs derived from all SNPs.
Keywords: AIMs, African American, Native Hawaiian, Latino, admixture, principal component analysis
Introduction
Population stratification is a special form of confounding in genetic association studies. It refers to the distortion of the relationship between a genotype of interest and disease status caused by the existence of undetected genetic structure (Lander and Schork 1994). If the study population consists of subpopulations that have both different disease rates and different marker allele frequencies, the proportions of cases and controls sampled from each subpopulation will tend to differ, as will the allele or genotype frequency between cases and controls at any locus at which the subpopulations differ, even though there is no such difference within each subpopulation (Marchini et al. 2004). Such spurious associations can also occur when cases and controls are sampled from the same admixed population in which the proportions of ancestry from different sources vary widely between individuals (e.g. African Americans). Stratification may lead to either a false positive signal of a null marker or a masking of a true causal variant. The impact of stratification in population-based association studies has been discussed extensively (Thomas and Witte 2002; Wacholder et al. 2002). A series of methods have been developed to correct for this type of bias and they generally use one of the two approaches, i.e., either by adjusting for estimated ancestries (e.g. Pritchard et al. 2000) or ancestry-related principal components (Price et al. 2006), or by adjusting for a single factor that captures the average effect of confounding as in the genomic control (GC) method (Devlin and Roeder 1999). All methods rely on the availability of genotypes for a relatively large number of null markers.
The extent of population structure should be evaluated individually for each actual study, as it may depend upon study-specific factors, such as geographical location of recruitment sites, sample size, method of matching, racial/ethnic composition of the participants and response rates across racial groups. For example, inconsistent results have been reported with respect to the correspondence between genetic clusters and commonly used racial/ethnic categories — poor correspondence in Wilson et al. 2001 as opposed to nearly perfect correspondence in Tang et al. 2005.
The Multiethnic Cohort (MEC) Study is a large population-based cohort study comprised primarily of five racial/ethnic groups (African Americans, Japanese Americans, Latinos, European Americans and Native Hawaiians) recruited from Hawaii and California (Kolonel et al. 2000). Because of the diverse ethnic/cultural environment in both areas, the MEC data are unique resource for addressing questions related to population stratification in U.S. studies. In particular, Native Hawaiians are a recently admixed population whose genetic substructure has not been studied in detail, to our knowledge. Hawaiian history dates back more than 1500 years, when Polynesians from the Marquesas Islands first arrived, with successive waves coming from other islands (notably Tahiti) until the 13th or 14th centuries (Beechert 1985). The first documented European contact with Hawaii came in 1778 when Captain James Cook re-discovered the Hawaiian Islands. In the early 20th century, the sugar and pineapple industry fueled Hawaii's economy, bringing an influx of East Asian and Portuguese immigrants (Nordyke 1989). The current self-identified Hawaiians are believed to be admixed among Polynesian, European and Asian ancestries.
In this paper, we examined the correspondence between self-reported ethnicity and genetic ancestry in the five MEC ethnic groups, quantified ancestral contributions from different sources for known admixed groups (African Americans, Latinos and Native Hawaiians) and evaluated three commonly-used methods in correcting for ancestry differences in genetic association studies of cancer that include all 5 MEC groups, namely, GC, adjustment for self-reported race and adjustment for principal components derived from all SNPs and from different sets of ancestry informative markers.
Subjects and Methods
The MEC genetic study of prostate cancer
The MEC is a large cohort study designed to provide prospective data on cancer as it relates to lifestyle and other exposures hypothesized to alter cancer risk. The cohort was assembled in 1993-1996 and is composed of over 215,000 men and women who completed a self-administered questionnaire at entry, with information on demographics (including race/ethnicity), medical history, family history, diet, medication and physical activity. To maximize the range of exposures, participants spanned all socio-economic levels from five ethnic groups: African Americans (AA), Japanese Americans (JA), Latinos (LA), Whites/European Americans (WA) and Native Hawaiians (HA). Individuals with mixed ancestry were assigned to one ethnic group according to the following priority ranking: AA, HA, LA, JA, WA and other (see Supplementary Materials for details on race/ethnicity definition). Incident cancer diagnoses in the MEC were identified by record linkage to the California Cancer Registry, the Los Angeles County Cancer Surveillance Program and the Hawaii Cancer Registry. Controls were randomly selected from the pool of subjects without cancer and who provided a biospecimen for genotyping, and were frequency-matched to cases on gender and age at cohort entry (in 5-year intervals) within each ethnic group (Haiman et al. 2007). Sample collection and all other procedures were approved by the institutional review boards at the University of Hawaii and the University of Southern California. Additional details of the data collection methods are provided in Kolonel et al. 2000.
Subjects and genotypes
The current SNP data were generated in the replication phase of a genome-wide association study on prostate cancer (Yeager et al. 2009). For validation purposes, genotype data for unrelated HapMap samples from 11 populations were included (the International HapMap Consortium 2007). These are 1) Asians: 79 Han Chinese in Beijing, China (CHB), 70 Chinese in Metropolitan Denver, Colorado (CHD), 83 Japanese in Tokyo, Japan (JPT), 2) Africans: 83 Luhya in Webuye, Kenya (LWK), 140 Maasai in Kinyawa, Kenya (MKK), 107 Yoruba in Ibadan, Nigeria (YRI), 3) Europeans: 108 Utah residents with Northern and Western European ancestry (CEU), 76 Toscans in Italy (TSI), 4) 43 persons with African ancestry in the southwest U.S. (ASW), 5) 83 Gujarati Indians in Houston, Texas (GIH), and 6) 41 persons of Mexican ancestry in Los Angeles, California (MEX). We also included genotype data on Native Americans (10 unrelated Mayans and 8 unrelated Pima Indians) from the Human Genome Diversity Project (HGDP) (Jakobsson et al. 2008).
Altogether 3,869 autosomal SNPs were genotyped in both the MEC prostate cancer study and the HapMap project (Phase 3, release #26). Included in the analysis were 6,213 MEC subjects with >95% genotype success rates: 1,533 AA (772 cases, 761 controls), 1,493 JA (750 cases, 743 controls), 1,435 LA (715 cases, 720 controls), 1,472 WA (739 cases, 733 controls) and 280 HA (141 cases, 139 controls). SNPs were excluded if 1) the genotype call rate was <95% in any of the HapMap or MEC populations and 2) genotype frequencies deviated from Hardy-Weinberg equilibrium (HWE) in unaffected MEC Japanese or Whites (p-value < 0.0001 from χ2 goodness-of-fit test). We did not perform the HWE test in MEC AA, LA and HA, since the relatively recent admixture in these populations might lead to distortion of the signal. From the 3,591 SNPs that passed the above criteria, we selected 3,041 SNPs by 1) randomly dropping one SNP if two SNPs are within 2kb of each other and 2) dropping SNPs that are in strong correlation with at least one other SNP (Pearson correlation r2 > 0.85). Used in the final analysis were 2,509 SNPs that also passed quality control in the HGDP and are on the Illumina 610-quad SNP panel (for compatibility with our ongoing genome-wide association studies). The median inter-marker distance was 787 kb (interquartile range 99.4 kb – 1.65 Mb).
Principal component analysis (PCA)
We performed PCA using a similar strategy as in (Price et al. 2006) but with slight modifications. A standardized genotype matrix A = (aij) was formed by calculating each element aij as , where gij = 0, 1 or 2 is the genotype of individual i at locus j (i = 1, …, n, j = 1, …, m) and pj is the estimated allele frequency at locus j. The eigen function of the R software package was used to obtain eigenvectors of the covariance matrix of SNPs (dimension m × m, calculated with R function cov using non-missing genotypes) — this matrix is equivalent up to a constant to A′A in the absence of missing genotypes. The first L principal components (PCs) were obtained by transforming A with the eigenvectors v1, v2, …, vL corresponding to the L largest eigenvalues. For a subject i with mic non-missing genotypes, the lth PC element is given by , where vjl is the jth element of vl and the sum is over the non-missing genotypes. The top few PCs that retain most of data variability are useful in cluster analysis (Jolliffe 2002). In the presence of population structure, PCs contain important ancestry information and can be used to correct for population stratification (Price et al. 2006).
Self-reported ancestry proportion and outliers in the MEC
MEC participants reported ethnic backgrounds for both parents separately. Multiple ethnicities were allowed but no ancestral proportion (e.g. 25, 50%) was requested. Among all the 6,213 subjects, only 33 had missing information on one or both parents. To explore the usefulness of the questionnaire data on parental ethnicity, we derived “self-reported” ancestral proportions for MEC subjects, assuming equal admixture if multiple ethnicities were reported for a parent. For example, if a MEC participant reported one parent of (European/White + African) ancestry and one parent of (European/White + Asian) ancestry, we interpreted each parent as 50% European and the participant as 50% European. In reality, both parents could be from >0 to <100% European and so could the MEC participant. However the derived ancestral proportion may serve as a reasonable “guess” of the true value. Five categories for each ancestry were defined: 100, 75 to <100, 50 to <75, 25 to <50% and other (<25% ancestry or missing parental information). We then evaluated the correspondence between the derived ancestry categories and the clustering membership on PC plots. Subjects whose self-reported ethnicity did not conform to the cluster membership were identified as “outliers” by setting up boundary lines based on visual inspection.
Ancestry Informative Markers and individual admixture
A small set of Ancestry Informative Markers (AIMs), i.e., markers with high allele frequency differences between continental/geographical groupings, are known for maximally retaining ancestry information when large-scale genotyping is either unrealistic or undesirable. The purposes of selecting AIMs here are 1) to save computation time when using STRUCTURE to estimate individual admixture, and 2) to explore the number of AIMs necessary in MEC studies to define outliers and to correct for stratification. Previously-defined AIMs panels cannot be applied due to little overlap with the current 2509 SNPs. For details on the selection of AIMs, see Supplementary Materials. Briefly, AIMs were selected for separating 1) HapMap Asians, Africans and Europeans (P1-CONT AIMs), 2) Native Americans, HapMap Africans and Europeans (P2-LAT AIMs), and 3) HapMap Asians, Europeans and the MEC HA who reported two Hawaiian-only parents (P3-HAW AIMs). Different sizes of AIMs sets were selected and their performance (ability of separating populations and accuracy in defining outlier status) was evaluated with PC plots.
Individual ancestral proportions for MEC AA, LA and HA were estimated with the Bayesian Markov Chain Monte Carlo (MCMC) clustering algorithm implemented in STRUCTURE 2.3.1 (Hubisz et al. 2009; Pritchard et al. 2000) using 200 P1-CONT, 200 P2-LAT and 400 P3-HAW AIMs, respectively. These AIMs were found to be sufficient for good separation of relevant ancestral populations (see Supplementary Materials). Ancestral populations were included in the STRUCTURE procedure to increase the accuracy of admixture estimation. These populations are: CEU and YRI for MEC AA, CEU, YRI and HGDP Native Americans for MEC LA, and CEU and JPT for MEC HA. Outliers in AA and LA were excluded from ancestry estimation. STRUCTURE was run under the admixture and independent allele frequency model (constant λ = 1.0), using population sampling location as prior information to facilitate clustering (Hubisz et al. 2009). The MCMC scheme was run with 200,000 burn-ins and 200,000 iterations after burn-in for different numbers (K) of subpopulations (K = 2 to 4 for AA and K = 3 to 5 for HA and LA). Several independent simulations were performed to monitor model convergence.
The relationship between individual ancestry estimates and the top PCs were assessed with linear regression. For MEC HA, we also assessed the agreement between STRUCTURE-derived and self-reported Native Hawaiian ancestry with Spearman's correlation and the weighted kappa coefficient.
Population stratification in case-control studies nested in the MEC
Simulations were performed to evaluate the extent of bias and the performance of various methods to control for bias in realistic MEC-based case-control association studies (in Supplementary Materials, a worst-case scenario of stratification in case-control studies—case-only analyses of gene by gene interactions—in MEC studies, was also simulated). We assumed equal numbers of cases and controls within each ethnic/racial group since in MEC studies controls are usually frequency-matched to cases on self-reported ethnicity, age and sex. Loosely speaking, when other factors are fixed, population stratification is caused by the different case fractions across subpopulations. In MEC studies, case fractions across the 5 ethnic groups are affected by disease rate in each ethnic group in the general population, the MEC cohort size in each group relative to the general population and the questionnaire response rate and biospecimen (blood, mouthwash, or saliva from which DNA could be extracted) collection rate in each ethnic group.
To avoid dealing with the above factors, we turned to empirical sample sizes from the current MEC case-accrual to generate realistic data. Prostate cancer is the most common cancer in the MEC biorepository and we did not find much evidence of stratification from the current analysis (Figure S12). Breast cancer, the second most common cancer, has been analyzed in association studies and stratification did not seem a problem either (Haiman et al. 2008). We thus focused on 8 other cancer types (colorectal, lung, lymphoma, stomach, endometrial, kidney, leukemia and bladder) for which there are at least 200 cases with biospecimen. The sample sizes and case fractions across ethnic groups are shown in Table S1 (Supplementary Materials).
Equal numbers of cases and controls along with 2,509 genotypes were sampled randomly from the prostate cancer data within each ethnic group to approximate the empirical sample sizes and case fractions for all 5 groups. The assumption here was that the genetic structure in future studies would be similar to that in the current study. Since no genotype was related to disease, all markers were “null”. We compared the distributions of the p-values obtained from testing associations between the null markers and disease status using logistic regression with the following adjustment strategies: 1) no adjustment, 2) adjustment for self-reported race categories, 3) adjustment for race categories and five ordered levels of self-reported ancestry proportion within each race (100, 75 to <100, 50 to <75, 25 to <50% and other), and 4) adjustment for the first 4 or the first 10 PCs from PCA of all 6,213 MEC subjects based on 2,509 SNPs, and based on 300 and 200 P3-HAW AIMs, and 200, 100 and 50 P1-CONT AIMs. GC was also applied, in which the over-dispersion parameter λ was estimated as the mean of the χ2 statistics among all SNPs or among AIMs in unadjusted models (no adjustment was made if λ < 1, following Bacanu et al. 2000).
We also simulated “causal” variants in order to compare the power of the different adjustment methods. For each cancer type or each setting of sample size and case fractions, null markers were simulated as before and were used to calculate PCs and to estimate λ in the GC method (assuming that causal variants are a small proportion among genotyped markers and ignoring them has little effect on these quantities). Independently from the null markers, 2,509 causal variants were simulated based on allele frequencies at each of the genotyped locus. Within each ethnic group — note that the numbers of cases and controls are fixed — genotypes AA, AB and BB of the causal SNP in controls were simulated from the density {(1−p)2, 2p(1−p), p2}, where B is the risk allele and p is the allele frequency of B estimated using controls in the prostate cancer study in that ethnic group. Let p0 be the risk allele frequency in the simulated control population with 5 ethnic groups. The relative risk, r, of a causal variant was calculated such that the power at significance level α is 90% for a study with the same sample size and the same p0 in the control population, but without structure. We adjusted α to be 0.01 or 0.05 for each cancer type to ensure that r was less than 3. This approach allowed us to estimate the empirical power of each method as the proportion of significant tests among all causal variants, even though the causal SNPs had different allele frequencies. With r chosen, genotypes AA, AB and BB in cases were generated from a density function that is proportional to { , , }, where b = log(r) and a = log(T) and T is baseline disease risk 0.0001, i.e., we assumed a rare disease and a log-additive risk model. We used a fixed T because the genotype distribution is insensitive to T under the rare disease assumption. Since the sample sizes and case fractions approximated those in future MEC studies, and since the genotypes of the causal variants were simulated based on empirical allele frequencies in each ethnic group, this simulation reflected stratification in realistic MEC studies. We analyzed all causal variants using the methods described above.
All analyses were performed with R 2.9 unless otherwise noted.
Results
Self-reported ethnic composition in the MEC
Ethnic composition for the MEC participants was derived using self-reported parental information (Table 1). The majority of the Japanese Americans (JA), European Americans (WA), Latinos (LA) and African Americans (AA) (98.6%, 94.5%, 90.0% and 90.9%, respectively) reported two parents of one ethnic background that was the same as their own, although LA and AA are each considered an admixed group. In contrast, only 33 (11.8%) of the 280 MEC Native Hawaiians (HA) reported 2 parents of only Hawaiian ancestry, the others were mixed mostly with Asian and European contributions — 81 (28.9%) were of ≥50% European ancestry and 72 (25.7%) were of ≥50% Asian ancestry and these two groups do not overlap. Results of HA are presented separately from the other four groups because of the more complex self-reported admixture in this group.
Table 1.
Distribution of self-reported ancestry proportion among MEC prostate cancer study participants in the 5 ethnic groups
| African Americans | Native Hawaiians | Japanese | Latinos | European Americans | |
|---|---|---|---|---|---|
| 100% | 1393 (90.9) | 33 (11.8) | 1472 (98.6) | 1292 (90.0) | 1391 (94.5) |
| 75% to <100% | 35 (2.3) | 31 (11.1) | 0 | 27 (1.9) | 23 (1.6) |
| 50% to <75% | 72 (4.6) | 105 (37.5) | 21 (1.4) | 99 (6.9) | 42 (2.8) |
| 25% to <50% | 21 (1.4) | 96 (34.2) | 0 | 10 (0.7) | 4 (0.3) |
| <25% and other | 12 (0.8) | 15 (5.4) | 0 | 7 (0.5) | 12 (0.8) |
Numbers shown are counts (percentages). Self-reported ancestry proportion was calculated from parental information assuming equal ancestry contribution if multiple ethnicities were reported for an individual. For African Americans and Latinos, ancestry proportion refers to the proportion of being black and Latino/Hispanics, respectively.
Genetic clusters and outliers
PCA was applied to HapMap, MEC and HGDP Native American subjects based on the 2,509 SNPs that were genotyped in all groups. The top 5 principal components (PCs) sequentially accounted for 7.24%, 4.98%, 1.10%, 0.38%, and 0.23% of the total variation and the remaining principal components each accounted for 0.19% to 0.22%, suggesting the first 4 PCs retain most of the information. Indeed no ethnicity-related pattern was observed in plots of other PCs. In MEC subjects, none of the top 4 PCs was differentially distributed between prostate cancer cases and controls in any racial group (all p > 0.09, Wilcoxon rank-sum test), so cases and controls were pooled in all analyses.
HGDP Native Americans and HapMap samples
Clustering of the HapMap populations and the Native Americans (Figure S1, Supplementary Materials) shows that the 3 major continental groups (Europeans, Asians and Africans) are well separated based on PC1 and PC2. Minor within-group variation can be observed for the Europeans and Asians, in contrast to the more pronounced variation among the African populations YRI, LWK and MKK. Native Americans form one distinct cluster between the Europeans and East Asians. PC3 seems to be a Native American-specific component — Native Americans and MEX all have larger PC3 values than other groups, although the PC3 values for MEX are smaller than those for most Native Americans. One ASW subject has a PC3 value comparable to MEX, suggesting certain Native American descent.
MEC non-Hawaiians
Clustering of the MEC AA, JA, LA and WA groups (Figure 1) shows similar patterns to those observed in clustering of the Native Americans and HapMap populations. Except for a few outliers, the MEC JA and WA form distinctive clusters and their average genetic composition is most similar to their HapMap counterparts. MEC AA show a wide range of European ancestry and MEC LA vary greatly with respect to the amount of European and Native American ancestry. US-born and non-US born MEC LA have similar distribution for PC1 to PC4 (results not shown). We identified “outliers” whose self-reported race did not match the clustering membership for MEC JA, WA, AA and LA. Outlier status matched well with the genetic composition derived from self-reported parental information in JA and WA but not in AA and LA (see Supplementary Materials for details).
Figure 1.
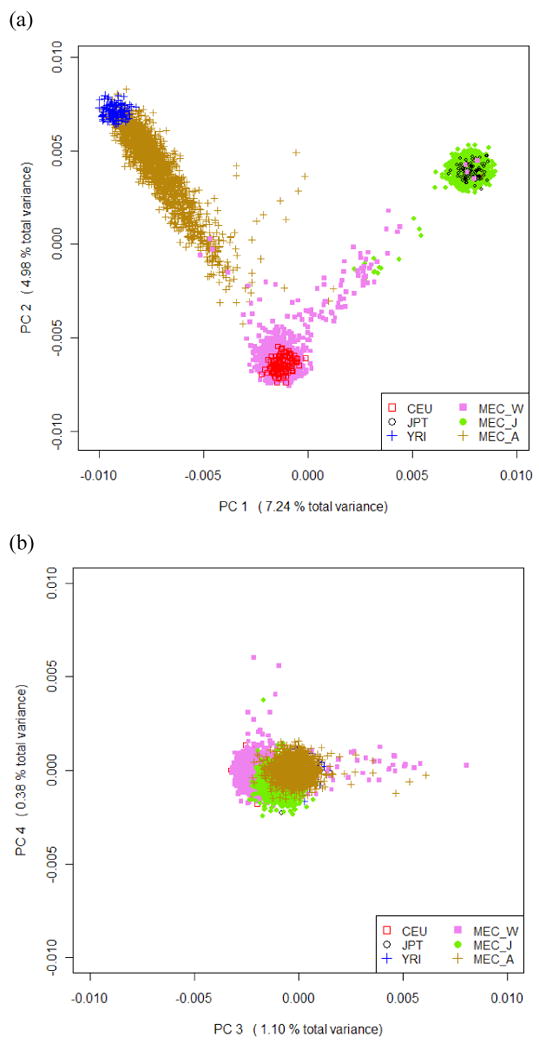
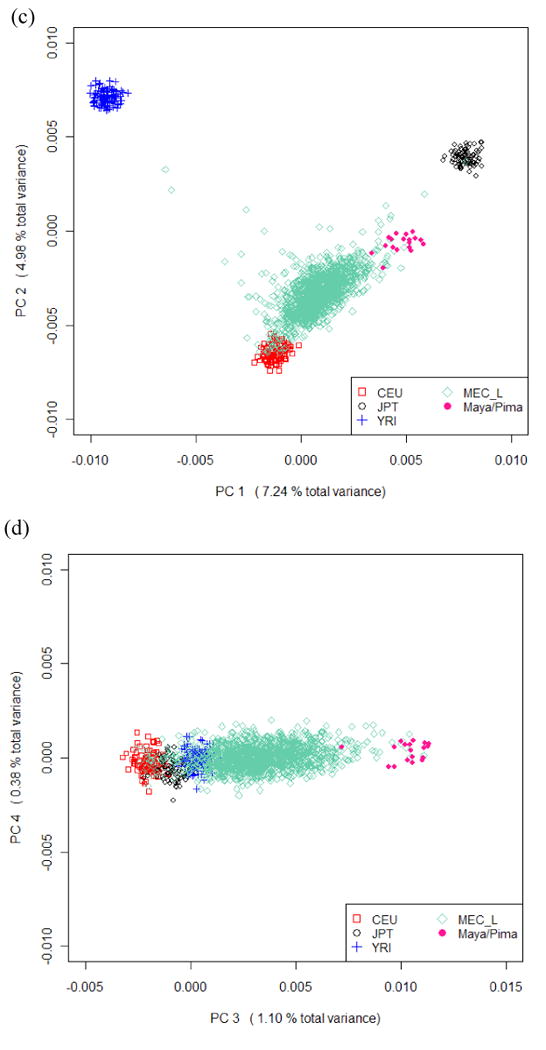
Clustering of MEC Whites/European Americans (MEC_W), Japanese (MEC_J), African Americans (MEC_A) and Latinos (MEC_L) along with HapMap CEU, YRI, JPT and HGDP Native Americans (Maya/Pima) based on the top 4 PCs obtained from PCA of all subjects. (a)(c) Plot of the 1st and 2nd PCs (b)(d) Plot of the 3rd and 4th PCs.
MEC Native Hawaiians
MEC HA can be divided into 5 non-overlapping groups according to self-reported proportion of ancestry: subjects with 100% Hawaiian (H) ancestry (i.e. the H2H group, n = 33), subjects with 75% to <100% H ancestry (n = 31), subjects with ≥50% White ancestry (n = 81), subjects with ≥50% Asian ancestry (n = 72) and subjects mixed otherwise (n = 35 for the category of 50% to <75% H plus n = 28 for <50% H). The first two groups look similar based on the 4 PCs (Figure 2 a, b) and can be grouped together as Hawaiians with ≥75% H, representing a relatively “more Hawaiian” population. These Hawaiians (≥75% H) can easily be separated from the Europeans (CEU) based on PC1 or PC2. However, only the fourth PC separates them from Asians (JPT). In fact PC4 alone can be used to separate the ≥75% Hawaiians from all other populations; therefore, it likely matches to the unique Native Hawaiian (Polynesian) ancestry. Most Hawaiians (90.4%) have higher values of PC4 than CEU or JPT.
Figure 2.
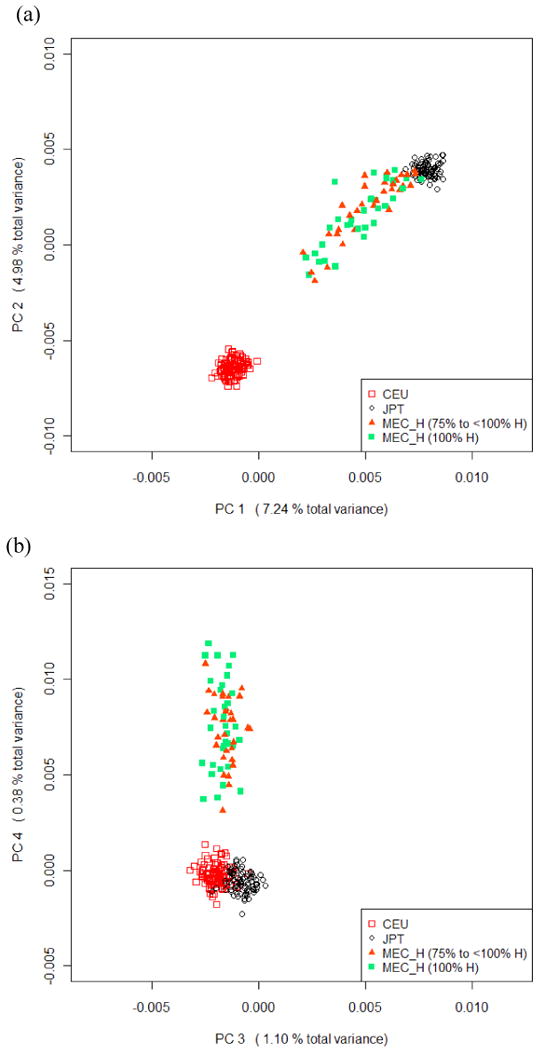
Clustering of the MEC Hawaiians (MEC_H) along with HapMap CEU and JPT based on the top 4 PCs obtained from PCA of all subjects. (a)(b) MEC_H self-reported to be ≥75% Hawaiian (c)(d) All MEC_H. Hawaiian (H) ancestry was estimated from parent information (assuming equal admixture if multiple ethnicities were reported).
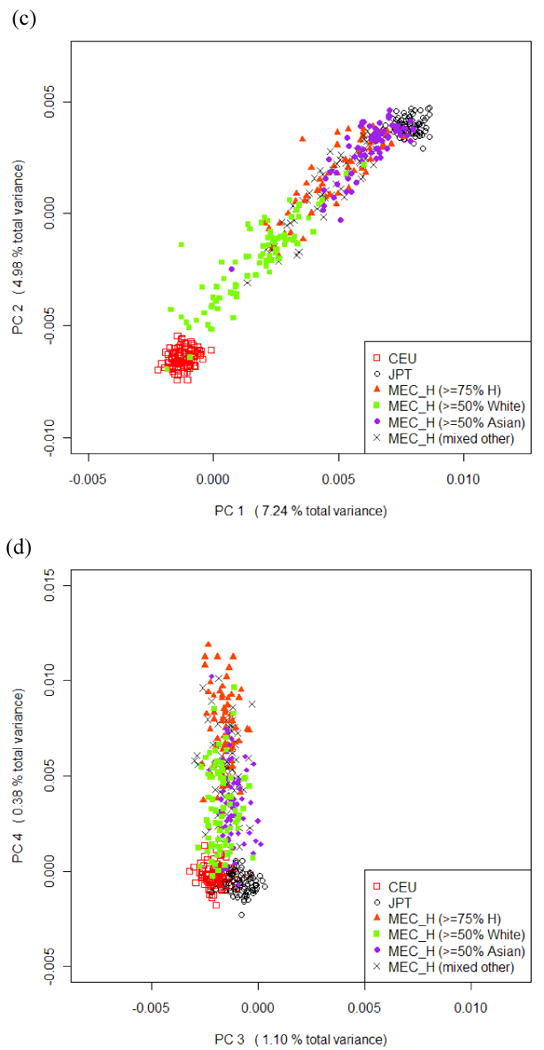
The 4 HA groups defined on self-reported ancestry proportions overlap with each other on the scale of all the top 4 PCs, forming a continuous “band” on clustering plots (Figure 2 c, d). A notable pattern is that HA with ≥50% Asian ancestry and with ≥50% White ancestry are located more closely to the Asian and European clusters (compared to the ≥75% H subjects), respectively, suggesting that the estimated ancestral proportions reflect the true proportions to a great extent, although individually they may not match perfectly. For example, the two Hawaiians who located inside the CEU cluster (Figure 2 c) reported their parents as “1 Hawaiian 1 White” and “1 (Hawaiian + White) 1 White”. These plots are consistent with the theory that self-identified Native Hawaiians are admixed with both Asian and European elements. Analysis using Hawaiians only or Hawaiians together with JPT and CEU showed similar patterns as discussed above (see Supplementary Materials).
AIMs and individual admixture
We briefly summarize the performance of the different sets of AIMs (details are in Supplementary Materials). For separating HapMap Asians, Europeans and Africans, 50 P1-CONT (Figure S7) or P2-LAT AIMs are adequate, although further experiments suggested as few as 25 AIMs are enough to distinguish YRI, CEU and JPT. For separating the 3 counterpart populations in the MEC (JA, AA and WA) where admixture/outliers are present, 100 P1-CONT or P2-LAT AIMs produced acceptable separation. However, even with 200 P1-CONT AIMs, outlier status does not match perfectly with those detected with all SNPs, i.e. not all previously-defined outliers are extreme points (Figure S8). For the purpose of separating Native Americans from the 3 major continental groups, P2-LAT AIMs performed slightly better than P1-CONT AIMs and 100 P2-AIMs can achieve the goal (Figure S9). For distinguishing Hawaiians with ≥75% H ancestry from other populations, especially East Asians, up to 200 P1-CONT or P2-LAT AIMs are not sufficient and 300 P3-HAW AIMs are needed (Figure S10). These 300 P3-HAW AIMs can effectively distinguish among the HapMap Asians, Europeans, Africans and HGDP Native Americans as well (Figure S11).
STRUCTURE 2.3.1 was used to infer individual ancestry proportions for MEC AA (excluding 31 outliers), LA (excluding 16 outliers) and HA along with their ancestral populations. Several independent runs yielded similar data likelihood and individual ancestry estimates. The likelihood favored the models with 2 populations in analysis of AA (together with CEU and YRI) and 3 populations in analysis of LA (with CEU, YRI and Native Americans) and HA (with CEU and JPT). Individual admixture estimation was based on the favored numbers of populations.
The average European and African ancestry among the MEC AA is estimated to be 24% (range 4 – 65%, interquartile range 14 – 31%) and 76% (range 35 – 96%, interquartile range 69 – 86%), respectively. Individual STRUCTURE-estimated European ancestry is most significantly related to PC2. The partial r2 between European ancestry and PC2, PC1, PC3 is 0.886, 0.021, 0.001, respectively (p < 0.0001). PC4 is not related to European ancestry (p > 0.05).
Among MEC LA, the mean Native American ancestry is estimated to be 38% (range 7.5 – 85%, interquartile range 30 – 46%) and the mean European ancestry is 59% (range 14 – 91%, interquartile range 51 – 67%). African ancestral contribution in this group is quite small (mean 3%, range 0.4 - 20%, interquartile range 1.6 – 3.7%). Native American and European ancestry are most significantly related to PC3. The partial r2 between Native American ancestry and PC3, PC1, PC2, PC4 is 0.846, 0.030, 0.003, 0.0009, respectively (p = 0.002 for PC4, p < 0.0001 for others).
For MEC HA, the mean East Asian, European and Native Hawaiian (Polynesian) ancestry is 27% (range 1.5 – 95%, interquartile range 8.6 – 43%), 27% (range 0.4 – 97%, interquartile range 3.1 – 45%) and 46% (range 1.5 – 98%, interquartile range 29 – 61%), respectively. No ancestry source is significantly related to PC3 (p > 0.05). European ancestry is most related to PC2, and also to PC4 and PC1 (partial r2 = 0.963, 0.011, 0.009, respectively, all p < 0.0001). Native Hawaiian ancestry is most related to PC4, also to PC2 (partial r2 = 0.924 and 0.006, both p < 0.0001), supporting that the fourth PC is a Hawaiian-specific component.
The average STRUCTURE-estimated Hawaiian ancestry is 74% (range: 31 – 98%, interquartile range: 56 – 86%) among H2H and is 70% (range: 37 –97%, interquartile range: 60 – 79%) among Hawaiians self-reported to be of 75% to <100% H, which is probably why these two groups look similar on clustering plots. The ordered 4 levels of STRUCTURE-derived Native Hawaiian ancestry (≥75%, 50% to <75%, 25% to <50%, <25%) agree well with those estimated from self-reported parent information — the weighted kappa coefficient is 0.42 (95% CI 0.35 – 0.48). Spearman correlation between STRUCTURE-estimated and self-report H ancestry (4 levels) is 0.71 (p = 2×10-44).
Population stratification in future MEC studies
We simulated realistic MEC case-control studies and compared the distributions of the p-values obtained from analyzing null markers with the various methods. Only modest bias was present in all eight simulated studies (or eight settings of sample size and case fractions). As an example, Figure 3 shows the p value distribution in a simulated colorectal cancer study with 2,000 cases (25% AA, 27% LA, 28% JA, 16% WA and 4% HA) and 2,000 controls. The degree of bias was modest towards the null — fewer associations than expected were observed. Adjusting for race/ethnicity categories, or race/ethnicity categories plus self-reported ancestry proportions, or adjusting for the top 4 or top 10 PCs from all SNPs or from ≥100 P1-CONT AIMs (sometimes 50 P1-CONT AIMs) was sufficient in correcting the bias. No bias was detected using GC (i.e. all λ's < 1) therefore no GC adjustment was made. In all simulations, no association was significant after Bonferroni correction (all p's > 0.05/2509). In Supplementary Materials, we showed that the p-values from case-only analysis of gene by gene interactions were extremely different from the expected uniform distribution, reflecting the fact that this simulation resembled a worst-case scenario of population stratification in case-control studies. Among all methods, only adjusting for top PCs from all 2,509 SNPs restored the p-value distribution to roughly uniform.
Figure 3.
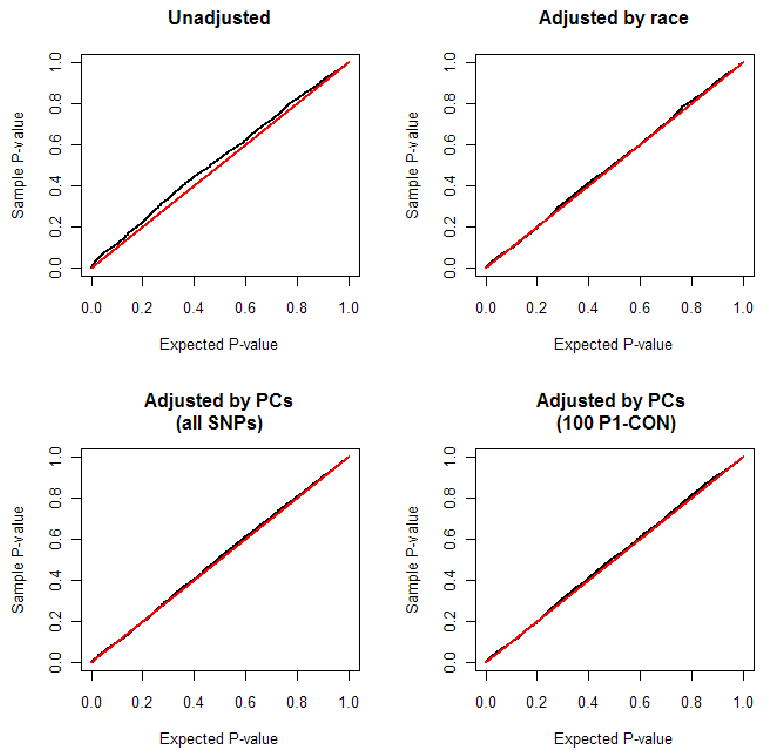
Distribution of the p-values obtained from association tests between 2509 null SNPs and disease status in a simulated MEC colorectal cancer study with 2000 cases and 2000 controls (see text for case fractions in the 5 ethnic groups). The shown distributions are from models with no adjustment and with adjustment for race categories, for the first 4 PCs from all SNPs and from 100 P1-CONT AIMs (selected to separate Asians, Africans and Europeans). The diagonal line represents the expected uniform distribution.
We also compared the power of the different strategies in analyzing causal SNPs with simulated MEC case-control data. GC adjustment was rarely made due to small λ's (< 1.0). In all simulations, the power from the unadjusted tests was about 4-7% lower than the nominal level 90% and also lower than that from the adjusted tests, consistent with the previous observation that the bias here was towards the null. Adjustment for self-reported race categories, or race plus self-reported ancestry proportions or PCs from all SNPs or from different AIMs sets yielded similar power (from 87% to 89%). Table 2 shows power comparisons in 4 out of the 8 simulated studies. Adjusting for race categories resulted in slightly higher (≤1% difference) power than adjusting for PCs. Moreover, adjusting for the top 10 PCs resulted in little loss of power compared to adjusting for only the 4 most important PCs.
Table 2.
Empirical power of various adjustment strategies in analyzing 2509 causal variants (each designed to achieve 90% power in an unstructured study) in four simulated MEC case-control cancer studies with all 5 ethnic groups
| Cancer type | Total number of cases1 | α | Odds ratio range2 | Unadjusted | Adjusted for race3 | Adjusted for 4 PCs | Adjusted for 10 PCs | ||
|---|---|---|---|---|---|---|---|---|---|
| all SNPs | 100 P1-CONT4 | all SNPs | 100 P1-CONT | ||||||
| Colorectal | 2000 | 0.01 | 1.19-1.48 | 0.825 | 0.876 | 0.872 | 0.870 | 0.872 | 0.871 |
| Lung | 600 | 0.01 | 1.37-1.98 | 0.828 | 0.881 | 0.872 | 0.872 | 0.873 | 0.872 |
| Lymphoma | 300 | 0.05 | 1.46-2.22 | 0.846 | 0.881 | 0.877 | 0.874 | 0.875 | 0.874 |
| Leukemia | 200 | 0.05 | 1.59-2.54 | 0.857 | 0.891 | 0.884 | 0.877 | 0.879 | 0.880 |
Equal number of cases and controls within each ethnic group was assumed. See Table S1 for case fractions across ethnic groups.
The range of odds ratios among the simulated causal variants. For each causal variant, odds ratio was calculated to ensure 90% power at significance level α for an unstructured study with the same sample size.
Race/ethnicity categories were used.
P1-CONT markers were selected to separate Asians, Europeans and Africans.
Discussion
Whether population stratification is a threat to the validity of case-control association studies has been under debate. In our experiments, we simulated realistic case-control studies nested in a multiethnic cohort consisting of five ethnic groups (African Americans, Japanese, Caucasians, Latinos and Native Hawaiians), with sample sizes and case distributions approximated from the true parameters in the MEC biorepository. Our results indicated that the extent of bias is likely to be modest and that adjusting for the common race/ethnicity categories or PCs from as few as 100 AIMs can adequately control for the bias. The low level of bias was consistent with previous predictions (Wacholder et al. 2002) and probably resulted from one of the strengths of the MEC study, i.e. MEC subjects of the same ethnicity were mostly sampled from the same geographic location and that the cases and controls in MEC-based studies are usually frequency-matched on race/ethnicity. When controls and cases are sampled from different geographic locations, population stratification may occur even though study subjects are of the same ethnicity (for example, see Plenge et al. 2007). One limitation in our experiment was that we did not directly address the extent of bias in genome-wide association studies (GWAS); however, the concern of population stratification in GWAS stems from the large sample sizes used in such studies to obtain high statistical power, since the power is equally high for detecting false associations generated by stratification. The sample size in our simulated colorectal cancer study was fairly large (4,000 individuals. a size that is comparable to most current GWAS studies).
The power of the PCA approach (Patterson et al. 2006; Price et al. 2006) in correcting for stratification has been demonstrated in numerous reports. In Supplementary Materials, we also showed that even the severe population stratification in case-only analysis of gene by gene interactions can be corrected by the top PCs based on 2,509 SNPs. One issue about the PCA approach is that there has been no consensus on how to determine the best number of PCs to use. The Tracy-Widom test (Patterson et al. 2006), as well as a complex permutation procedure (Yu et al. 2008), have been proposed. For data with a few thousand SNPs, we found it easy to determine the number of important PCs by simply looking for the “elbow point” in a scree plot (Jolliffe 2002), i.e., where the ordered (descending) eigenvalues start to take almost constant values, then choosing the PCs corresponding to the eigenvalues before the “elbow point”. In MEC studies with 5 ethnic groups, 4 PCs turned out to be important and the PCs matched meaningfully with genetic ancestry — part of the reason may be that the ancestral populations such as Native Americans and HapMap Africans were included in the PCA procedure.
Regardless of this issue, our simulations showed that including more PCs (up to 10) than the important ones in regression models did not reduce study power, although this result may not be generalized to other studies. Yu et al. (2008) demonstrated that unnecessary adjustment of population substructure (even one PC) could lead to a significant loss in power in extreme situations. Our simulations also showed that controlling for self-report ethnicity or the top PCs in MEC studies yielded similar average power across causal variants with different allele frequencies. GC adjustment was not made here because all estimated λ's were <1 (Bacanu et al. 2000); however, a more detailed comparison of the power between the GC and the PCA approach favored the latter (Zhang et al. 2008).
STRUCTURE-derived individual genetic ancestries in MEC AA, LA and HA are highly correlated with the most important PCs, as expected. Estimates of admixture proportions in the MEC AA and LA are consistent with other reports on U.S. studies. The average European ancestry in MEC AA (mostly from Los Angeles) is 24% (range 4 – 65%), compared to the ∼20% estimation from other US studies (Fejerman et al. 2009; Reiner et al. 2005). Slight variation in European admixture in AA across clinical sites/states has been observed before. For example, European admixture was estimated at 19% for samples from New York City (Fejerman et al. 2009), 17.0% for samples collected from Winston-Salem, NC and 23.9% for those from Pittsburgh, PA (Reiner et al. 2005). For MEC LA, the European ancestry (average 59%, range 14 – 91%) and African ancestry (average 3%, range 0.4 - 20%) are in line with other reports on U.S. Latinos. For example, Hispanics in San Luis Valley, Colorado, were estimated on average to have 61.6% European and 5.6% African components (Bonilla et al. 2004). In comparison, a study on 6 Mestizo populations from Mexico also revealed low African ancestry in Latinos/Mexicans, although the average European contribution was 0.42 ± 0.16, lower than that in US studies (Silva-Zolezzi et al. 2009).
Admixture estimation in Native Hawaiians based on genetic data has not been reported before, to our knowledge. Our results showed that the MEC HA have a great deal of East Asian and European ancestry. The mean East Asian, European and Native Hawaiian ancestry is 27% (range 1.5 – 95%), 27% (range 0.4 – 97%) and 46% (range 1.5 – 98%), respectively. Categorized Hawaiian ancestry proportions derived from self-reported parental information statistically significantly match those from STRUCTURE estimates. However, MEC HA who reported two Hawaiian parents (H2H) were estimated to be 74% H on average, similar to the average (70% H) among those self-reported to be of 75% to <100% H (i.e. HA with 1 Hawaiian parent and 1 mixed parent with Hawaiian and one non-Hawaiian ancestry). Admixture estimation in Hawaiians may be improved by inclusion of the ancestral Polynesian population and using them to select AIMs for use in STRUCTURE. The proportion of MEC HA of ≥75% H (STRUCTURE-derived) was estimated to be 13%, similar to the proportion observed in a cross-sectional survey where self-reported Hawaiian blood quantum (i.e. 25%, 50%, etc) was recorded (Grandinetti et al. 2002).
AIMs are useful in situations where large-scale genotyping is impossible, e.g. in the follow-up phase of a GWAS. A previous report examined the performance of 128 AIMs and various subsets of these AIMs in separating populations from major continents (Kosoy et al. 2009). Our results are consistent with theirs. The unique MEC HA population provides an opportunity to explore the number of AIMs needed to separate the Hawaiian (Polynesian) component from East Asian or European ancestry. According to our experiments, up to 300 AIMs may be needed. We recognize that the number of AIMs may be reduced if a larger pool of SNPs (e.g. from genome-wide SNP arrays) is available or the Polynesians rather than the MEC H2H subjects are used in AIMs selection.
The MEC consists of three recently admixed populations: AA, LA and HA. Admixture mapping takes advantage of long-range haplotypes generated by a relatively small number of recombination events in such populations to find chromosomal regions containing disease-causing variants that are distributed differentially among parental populations (Hoggart et al. 2003; McKeigue 1997; Patterson et al. 2004). A key advantage of this approach over GWAS is that it requires 200-500 times fewer markers (Patterson et al. 2004). Application of admixture mapping in AAs has led to discovery of susceptibility regions for multiple sclerosis and prostate cancer (Freedman et al. 2006; Reich et al. 2005). Admixture mapping for obesity and Type 2 diabetes has also been conducted in African Americans or Latinos (Martinez-Marignac et al. 2007; Zhu and Cooper 2007). Although several hundred AIMs allow for accurate estimation of individual admixture, several thousand AIMs are required for definition of chromosomal ancestry across the genome. Multiple panels of AIMs have been defined for admixture mapping in African Americans (Smith et al. 2004; Tian et al. 2006) and Hispanics/Latinos (Mao et al. 2007; Price et al. 2007). In contrast, no such AIMs panel has been reported for Native Hawaiians. Compared to East Asians and Caucasians, Native Hawaiians have higher rates of obesity (Albright et al. 2008) and breast and lung cancer (Hawaii Cancer Facts and Figures http://hawaii.gov/health/statistics/brfss/other-reports/cancer2003-04.pdf). The relationship between the risk disparity and the difference in distributions of environmental/genetic factors is worth studying. Defining more informative AIMs for Hawaiians and deriving more accurate ancestry estimates should enhance research in this area.
In summary, we analyzed the genetic structure of a Multiethnic population of African Americans, Japanese Americans, European Americans, Latinos and Native Hawaiians using PCA based on 2,509 autosomal SNPs and estimated the different sources of ancestry for the three admixed groups. The bias in realistic MEC case-control cancer studies was estimated to be modest and readily correctable by adjusting for race/ethnicity categories or top PCs based on 2,509 SNPs or 100 AIMs. Finally, the power of these adjustment methods was found to be similar in our simulation studies.
Supplementary Material
Acknowledgments
We thank the researchers and participants of the Multiethnic Cohort study. We also thank Dr. David Van Den Berg, Loreall Pooled and Xin Sheng for their technical assistance in genotyping as well as Dr. Gary Chen and Christian Caberto for help in genotype pre-processing and data management. This work was supported by grants from the National Institutes of Health (R37CA54281, P01CA33619, R01CA63464, and U01CA98758).
Footnotes
The authors declare that they have no conflict of interest.
References
- Albright CL, Steffen AD, Wilkens LR, Henderson BE, Kolonel LN. The prevalence of obesity in ethnic admixture adults. Obesity. 2008;16:1138–1143. doi: 10.1038/oby.2008.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacanu SA, Devlin B, Roeder K. The power of genomic control. Am J Hum Genet. 2000;66:1933–1945. doi: 10.1086/302929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beechert ED. Working in Hawaii: A Labor History. University of Hawaii Press; Honolulu: 1985. [Google Scholar]
- Bonilla C, Parra EJ, Pfaff CL, Dios S, Marshall JA, Hamman RF, Ferrell RE, Hoggart CL, McKeigue PM, Shriver MD. Admixture in the Hispanics of the San Luis Valley, Colorado, and its implications for complex trait gene mapping. Ann Hum Genet. 2004;68:139–153. doi: 10.1046/j.1529-8817.2003.00084.x. [DOI] [PubMed] [Google Scholar]
- Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- Fejerman L, Haiman CA, Reich D, Tandon A, Deo RC, John EM, Ingles SA, Ambrosone CB, Bovbjerg DH, Jandorf LH, Davis W, Ciupak G, Whittemore AS, Press MF, Ursin G, Bernstein L, Huntsman S, Henderson BE, Ziv E, Freedman ML. An admixture scan in 1,484 African American women with breast cancer. Cancer Epidemiol Biomarkers Prev. 2009;18:3110–3117. doi: 10.1158/1055-9965.EPI-09-0464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman ML, Haiman CA, Patterson N, McDonald GJ, Tandon A, Waliszewska A, Penney K, Steen RG, Ardlie K, John EM, Oakley-Girvan I, Whittemore AS, Cooney KA, Ingles SA, Altshuler D, Henderson BE, Reich D. Admixture mapping identifies 8q24 as a prostate cancer risk locus in African-American men. Proc Natl Acad Sci U S A. 2006;103:14068–14073. doi: 10.1073/pnas.0605832103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grandinetti A, Keawe'aimoku Kaholokula J, Chang HK, Chen R, Rodriguez BL, Melish JS, Curb JD. Relationship between plasma glucose concentrations and Native Hawaiian Ancestry: The Native Hawaiian Health Research Project. Int J Obes. 2002;26:778–782. doi: 10.1038/sj.ijo.0802000. [DOI] [PubMed] [Google Scholar]
- Haiman CA, Patterson N, Freedman ML, Myers SR, Pike MC, Waliszewska A, Neubauer J, Tandon A, Schirmer C, McDonald GJ, Greenway SC, Stram DO, Le Marchand L, Kolonel LN, Frasco M, Wong D, Pooler LC, Ardlie K, Oakley-Girvan I, Whittemore AS, Cooney KA, John EM, Ingles SA, Altshuler D, Henderson BE, Reich D. Multiple regions within 8q24 independently affect risk for prostate cancer. Nat Genet. 2007;39:638–644. doi: 10.1038/ng2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haiman CA, Hsu C, de Bakker PIW, Frasco M, Sheng X, Van Den Berg D, Casagrande JT, Kolonel LN, Le Marchand L, Hankinson SE, Han J, Dunning AM, Pooley KA, Freedman ML, Hunter DJ, Wu AH, Stram DO, Henderson BE. Comprehensive association testing of common genetic variation in DNA repair pathway genes in relationship with breast cancer risk in multiple populations. Hum Mol Genet. 2008;17:825–834. doi: 10.1093/hmg/ddm354. [DOI] [PubMed] [Google Scholar]
- Hoggart CJ, Parra EJ, Shriver MD, Bonilla C, Kittles RA, Clayton DG, McKeigue PM. Control of confounding of genetic associations in stratified populations. Am J Hum Genet. 2003;72:1492–1504. doi: 10.1086/375613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Mol Ecol Resour. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsson M, Scholz SW, Scheet P, Gibbs JR, VanLiere JM, Fung HC, Szpiech ZA, Degnan JH, Wang K, Guerreiro R, Bras JM, Schymick JC, Hernandez DG, Traynor BJ, Simon-Sanchez J, Matarin M, Britton A, van de Leemput J, Rafferty I, Bucan M, Cann HM, Hardy JA, Rosenberg NA, Singleton AB. Genotype, haplotype and copy-number variation in worldwide human populations. Nature. 2008;451:998–1003. doi: 10.1038/nature06742. [DOI] [PubMed] [Google Scholar]
- Jolliffe IT. Principal component analysis. 2. Springer-Verlag; New York: 2002. [Google Scholar]
- Kolonel LN, Henderson BE, Hankin JH, Nomura AM, Wilkens LR, Pike MC, Stram DO, Monroe KR, Earle ME, Nagamine FS. A multiethnic cohort in Hawaii and Los Angeles: baseline characteristics. Am J Epidemiol. 2000;151:346–357. doi: 10.1093/oxfordjournals.aje.a010213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosoy R, Nassir R, Tian C, White PA, Butler LM, Silva G, Kittles R, Alarcon-Riquelme ME, Gregersen PK, Belmont JW, De La Vega FM, Seldin MF. Ancestry informative marker sets for determining continental origin and admixture proportions in common populations in America. Hum Mutat. 2009;30:69–78. doi: 10.1002/humu.20822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Schork NJ. Genetic dissection of complex traits. Science. 1994;265:2037–2048. doi: 10.1126/science.8091226. [DOI] [PubMed] [Google Scholar]
- Mao X, Bigham AW, Mei R, Gutierrez G, Weiss KM, Brutsaert TD, Leon-Velarde F, Moore LG, Vargas E, McKeigue PM, Shriver MD, Parra EJ. A genomewide admixture mapping panel for Hispanic/Latino populations. Am J Hum Genet. 2007;80:1171–1178. doi: 10.1086/518564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Cardon LR, Phillips MS, Donnelly P. The effects of human population structure on large genetic association studies. Nat Genet. 2004;36:512–517. doi: 10.1038/ng1337. [DOI] [PubMed] [Google Scholar]
- Martinez-Marignac VL, Valladares A, Cameron E, Chan A, Perera A, Globus-Goldberg R, Wacher N, Kumate J, McKeigue P, O'Donnell D, Shriver MD, Cruz M, Parra EJ. Admixture in Mexico City: implications for admixture mapping of type 2 diabetes genetic risk factors. Hum Genet. 2007;120:807–819. doi: 10.1007/s00439-006-0273-3. [DOI] [PubMed] [Google Scholar]
- McKeigue PM. Mapping genes underlying ethnic differences in disease risk by linkage disequilibrium in recently admixed populations. Am J Hum Genet. 1997;60:188–196. [PMC free article] [PubMed] [Google Scholar]
- Nordyke EC. The Peopling of Hawaii. University Press of Hawaii; Honolulu: 1989. [Google Scholar]
- Patterson N, Hattangadi N, Lane B, Lohmueller KE, Hafler DA, Oksenberg JR, Hauser SL, Smith MW, O'Brien SJ, Altshuler D, Daly MJ, Reich D. Methods for high-density admixture mapping of disease genes. Am J Hum Genet. 2004;74:979–1000. doi: 10.1086/420871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS Genet. 2006;2:2074–2093. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plenge RM, Seielstad M, Padyukov L, Lee AT, Remmers EF, Ding B, Liew A, Khalili H, Chandrasekaran A, Davies LR, Li W, Tan AK, Bonnard C, Ong RT, Thalamuthu A, Pettersson S, Liu C, Tian C, Chen WV, Carulli JP, Beckman EM, Altshuler D, Alfredsson L, Criswell LA, Amos CI, Seldin MF, Kastner DL, Klareskog L, Gregersen PK. TRAF1-C5 as a risk locus for rheumatoid arthritis--a genomewide study. N Engl J Med. 2007;357:1199–1209. doi: 10.1056/NEJMoa073491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson N, Yu F, Cox DR, Waliszewska A, McDonald GJ, Tandon A, Schirmer C, Neubauer J, Bedoya G, Duque C, Villegas A, Bortolini MC, Salzano FM, Gallo C, Mazzotti G, Tello-Ruiz M, Riba L, Aguilar-Salinas CA, Canizales-Quinteros S, Menjivar M, Klitz W, Henderson B, Haiman CA, Winkler C, Tusie-Luna T, Ruiz-Linares A, Reich D. A genomewide admixture map for Latino populations. Am J Hum Genet. 2007;80:1024–1036. doi: 10.1086/518313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich D, Patterson N, De Jager PL, McDonald GJ, Waliszewska A, Tandon A, Lincoln RR, DeLoa C, Fruhan SA, Cabre P, Bera O, Semana G, Kelly MA, Francis DA, Ardlie K, Khan O, Cree BA, Hauser SL, Oksenberg JR, Hafler DA. A whole-genome admixture scan finds a candidate locus for multiple sclerosis susceptibility. Nat Genet. 2005;37:1113–1118. doi: 10.1038/ng1646. [DOI] [PubMed] [Google Scholar]
- Reiner AP, Ziv E, Lind DL, Nievergelt CM, Schork NJ, Cummings SR, Phong A, Burchard EG, Harris TB, Psaty BM, Kwok P. Population structure, admixture and aging-related phenotypes in African American adults: the cardiovascular health study. Am J Hum Genet. 2005;76:463–477. doi: 10.1086/428654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva-Zolezzi I, Hidalgo-Miranda A, Estrada-Gil J, Fernandez-Lopez JC, Uribe-Figueroa L, Contreras A, Balam-Ortiz E, del Bosque-Plata L, Velazquez-Fernandez D, Lara C, Goya R, Hernandez-Lemus E, Davila C, Barrientos E, March S, Jimenez-Sanchez G. Analysis of genomic diversity in Mexican Mestizo populations to develop genomic medicine in Mexico. Proc Natl Acad Sci U S A. 2009;106:8611–8616. doi: 10.1073/pnas.0903045106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MW, Patterson N, Lautenberger JA, Truelove AL, McDonald GJ, Waliszewska A, Kessing BD, Malasky MJ, Scafe C, Le E, De Jager PL, Mignault AA, Yi Z, De The G, Essex M, Sankale JL, Moore JH, Poku K, Phair JP, Goedert JJ, Vlahov D, Williams SM, Tishkoff SA, Winkler CA, De La Vega FM, Woodage T, Sninsky JJ, Hafler DA, Altshuler D, Gilbert DA, O'Brien SJ, Reich D. A high-density admixture map for disease gene discovery in african americans. Am J Hum Genet. 2004;74:1001–1013. doi: 10.1086/420856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang H, Quertermous T, Rodriguez B, Kardia SL, Zhu X, Brown A, Pankow JS, Province MA, Hunt SC, Boerwinkle E, Schork NJ, Risch NJ. Genetic structure, self-identified race/ethnicity, and confounding in case-control association studies. Am J Hum Genet. 2005;76:268–275. doi: 10.1086/427888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International HapMap Consortium A second generation human haplotype map of over 3.1 million SNPs. Nature. 2007;449:851–861. doi: 10.1038/nature06258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas DC, Witte JS. Point: population stratification: a problem for case-control studies of candidate-gene associations? Cancer Epidemiol Biomarkers Prev. 2002;11:505–512. [PubMed] [Google Scholar]
- Tian C, Hinds DA, Shigeta R, Kittles R, Ballinger DG, Seldin MF. A genomewide single-nucleotide-polymorphism panel with high ancestry information for African American admixture mapping. Am J Hum Genet. 2006;79:640–649. doi: 10.1086/507954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wacholder S, Rothman N, Caporaso N. Counterpoint: bias from population stratification is not a major threat to the validity of conclusions from epidemiological studies of common polymorphisms and cancer. Cancer Epidemiol Biomarkers Prev. 2002;11:512–520. [PubMed] [Google Scholar]
- Wilson JF, Weale ME, Smith AC, Gratrix F, Fletcher B, Thomas MG, Bradman N, Goldstein DB. Population genetic structure of variable drug response. Nat Genet. 2001;29:265–269. doi: 10.1038/ng761. [DOI] [PubMed] [Google Scholar]
- Yeager M, Chatterjee N, Ciampa J, Jacobs KB, Gonzalez-Bosquet J, Hayes RB, Kraft P, Wacholder S, Orr N, Berndt S, Yu K, Hutchinson A, Wang Z, Amundadottir L, Feigelson HS, Thun MJ, Diver WR, Albanes D, Virtamo J, Weinstein S, Schumacher FR, Cancel-Tassin G, Cussenot O, Valeri A, Andriole GL, Crawford ED, Haiman CA, Henderson B, Kolonel L, Le Marchand L, Siddiq A, Riboli E, Key TJ, Kaaks R, Isaacs W, Isaacs S, Wiley KE, Gronberg H, Wiklund F, Stattin P, Xu J, Zheng SL, Sun J, Vatten LJ, Hveem K, Kumle M, Tucker M, Gerhard DS, Hoover RN, Fraumeni JF, Jr, Hunter DJ, Thomas G, Chanock SJ. Identification of a new prostate cancer susceptibility locus on chromosome 8q24. Nat Genet. 2009;41:1055–1057. doi: 10.1038/ng.444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu K, Wang Z, Li Q, Wacholder S, Hunter DJ, Hoover RN, Chanock S, Thomas G. Population substructure and control selection in genome-wide association studies. PLoS ONE. 2008;3:e2551. doi: 10.1371/journal.pone.0002551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang F, Wang Y, Deng HW. Comparison of population-based association study methods correcting for population stratification. PLoS One. 2008;3:e3392. doi: 10.1371/journal.pone.0003392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Cooper RS. Admixture mapping provides evidence of association of the VNN1 gene with hypertension. PLoS One. 2007;2:e1244. doi: 10.1371/journal.pone.0001244. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


