Phase-Contrast Velocimetry with Simultaneous Fat/Water Separation

Abstract

Phase-contrast MRI can provide high-resolution angiographic velocity images, especially in conjunction with non-Cartesian k-space sampling. However, acquisitions can be sensitive to errors from artifacts from main magnetic field inhomogeneities and chemical shift from fat. Particularly in body imaging, fat content can cause degraded image quality, create errors in the velocity measurements, and prevent the use of self-calibrated amplitude of static field heterogeneity corrections. To reduce the influence of fat and facilitate self-calibrated amplitude of static field heterogeneity corrections, a combination of chemical shift imaging with phase-contrast velocimetry with nonlinear least-squares estimation of velocity, fat, and water signals is proposed. A chemical shift and first-moment symmetric dual-echo sequence is proposed to minimize the scan time penalty, and initial investigations are performed in phantoms and volunteers that show reduced influence from fat in velocity images.

Phase-contrast (PC) velocimetry MRI can be utilized to provide both quantitative velocity and anatomic information. Velocity information is of particular interest as it can be processed to yield diagnostic measures not generally available from standard contrast developed from spin relaxation. In vascular imaging, PC velocity data can be utilized to determine abnormal flow rates (1–3), determine vessel wall compliance (4), and observe abnormal flow dynamics (5–7). Additionally, velocity data can be processed to determine hemodynamic parameters such as wall shear stress (8–10) and relative pressure (11, 12). Accurate quantification of velocity fields and parameters derived from those fields often requires images that simultaneously have high temporal and spatial resolution, which is difficult to achieve due to the scan time increase from multiple measurements required for velocity encoding.

Stronger, faster imaging gradients can be utilized to provide limited acceleration to PC examinations. However, the acceleration comes at the cost of increased eddy-current artifacts, reduced signal-to-noise ratio (SNR), and reduced data collection efficiency. Improved acquisition efficiency at high bandwidth can be gained by going to non-Cartesian PC sampling patterns such as spiral (13), echo-planar imaging (14), or multiecho radial (15). These acquisitions can be used to maintain a similar readout gradient duration as a lower bandwidth Cartesian acquisition, whose length is ultimately limited by T₂* decay, and simultaneously covering more k-space per unit time. These techniques open up the possibility of clinical applications of PC that would not be generally practical, such as real-time two-dimensional PC (16, 17). Additionally, these trajectories often facilitate short echo times (TEs) and have reduced sensitivity to distortions caused by flow.

However, the utilization of PC in areas with significant fat signal can be challenging. In imaging the coronary arteries, hepatic vasculature, and venous system outside the head, chemical shift artifacts can cause fat signal to interfere with neighboring water signal, reducing the accuracy of velocity measurements within those voxels. These errors arise near fat-water boundaries, reducing the accuracy of quantitative vessel wall parameters, such as wall shear stress, and hindering the visualization of small vessels. This is especially true when PC is used in conjunction with non-Cartesian trajectories at high field and high spatial resolution. Unfortunately, limited options are available for reliable fat suppression with PC. Traditional fat-suppression pulses may increase specific absorption rate (SAR), may reduce data collection time, and are sensitive to off-resonance effects caused by heterogeneity of the main magnetic field. Selective water excitation using spectral spatial pulses has been utilized for fat suppression in PC (18). However, in addition to amplitude of static field (B₀) field sensitivity, these pulses are sensitive to flow artifacts (19).

Chemical shift imaging (CSI) techniques, which acquire images at multiple TEs and utilize the complex signal to separate water and fat, are not sensitive to B₀ heterogeneity and can be utilized in conjunction with almost any imaging method, including PC velocimetry (20). Typically, these techniques come at the cost of a 3-fold increase in the number of measurements, which for interleaved velocity encoding also leads to a 3-fold decrease in the minimum temporal resolution, already hampered by the severalfold acquisition overhead of PC imaging. Additional SNR can be gained with the additional scan-time increase; however, optimal noise performance relies on the misalignment of fat and water phase at every echo (21). In PC imaging, phase is imparted to moving spins, leading to reduced noise performance in voxels with fat and water spins moving at different velocities. The 3-fold scan time increase and noise performance reduction are forced due to the separation of CSI from velocity encoding. To reduce the number of encodings and improve noise performance, we propose the combination of velocity and CSI (CSI-PC). This enables fat-water separation and chemical shift error reduction in PC with substantially fewer measurements. To reconstruct these images, we propose a nonlinear estimation that corrects for off-resonance distortions caused by main field heterogeneity and simultaneously provides fat/water separation for improved velocity measurement accuracy. Finally, we develop a highly efficient dual-echo acquisition that further reduces imaging penalties for fat-water separation and demonstrate its use for three-dimensional (3D) PC applications.

THEORY

Off-Resonance Artifacts in PC

Off-resonance precession causes a varying level of distortion, depending on the k-space trajectory. In single-echo Cartesian imaging, this generally results in a simple spatial shift in the direction of the readout gradient, which is proportional to the phase evolution during the readout gradient. In more complex trajectories, off-resonance can exhibit more significant distortion, leading to point spread functions that appear as signal dropouts and blurring (22). Off-resonance precession arises from both chemical shift and main field heterogeneity. Hence, in the paper, we use the term off-resonance to refer to both main field heterogeneity and chemical shift effects. In the presence of fat, the chemical shift of fat can cause its signal to interfere with the water signal. In PC velocimetry sequences, the fat signal is strong due to its relatively short T₁ and short pulse repetition time (TR) gradient echo sequences, which aggravates the effect.

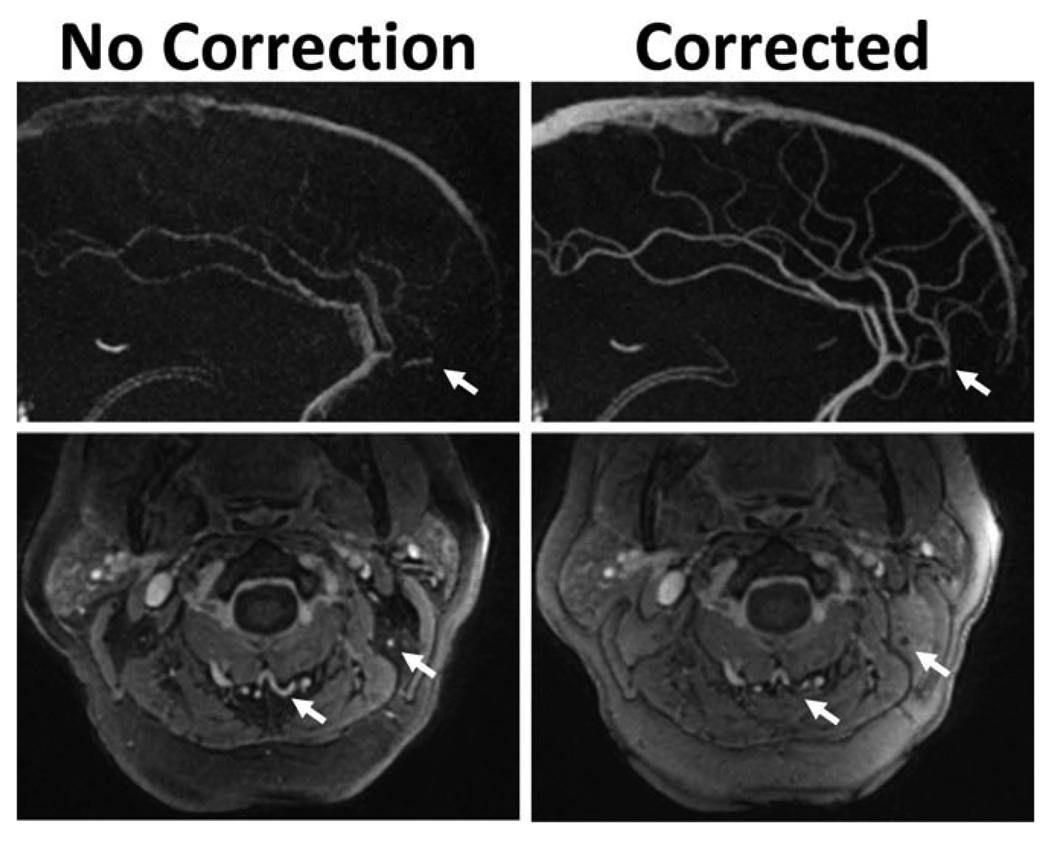
Chemical shifts can also disrupt self-calibrating B₀-heterogeneity measurements derived from multiecho data, where the time between echoes is arbitrarily assigned (15,23). Figure 1 shows an example dual-echo 3D radial PC images with and without self-calibrated off-resonance corrections. Intracranial sagittal maximum intensity projections show improved image quality with corrections. Simultaneously, if fat corrupts the field map, visualization of small vessels within the fat can be compromised, as shown in axial magnitude images obtained in the neck of an obese patient. This type of error is avoided if field maps are computed using separate sequences designed to minimize the phase errors from fat (24). However, this approach requires additional scan time and may require additional processing to correct misalignment of the image sets caused by patient motion.

FIG. 1.

Illustration of image artifacts due to errors in self-derived field map in the presence of interfering fatty tissues. Example dual-echo, 3D radial PC images with and without off-resonance map corrections. Intracranial sagittal maximum intensity projections (top) show improved image quality with off-resonance corrections. However, when fat interferes with estimation of the field map, small vessels within the fat (white arrows) can be removed by the off-resonance correction, as shown in axial magnitude images obtained in an obese patient (bottom). This is due to incoherent addition of the two echoes, when corrected at the fat off-resonance frequency.

Signal Model

Iterative nonlinear fat-water separation techniques, such as Iterative Decomposition of water and fat with Echo Asymmetry and Least-squares (IDEAL) (20,25), have previously been shown to be insensitive to B₀ heterogeniety. IDEAL assumes that the signal at any given voxel can be described by

$$S_n=({\mathrm{\rho }}_F{e}^{i({\mathrm{\phi }}_F+2\mathrm{\pi }\mathrm{\Delta }{\mathit{\text{ft}}}_n)}+{\mathrm{\rho }}_W{e}^{i{\mathrm{\phi }}_W})e^{i\mathrm{\psi }{t}_n},$$ [1]

where S_n is the measured signal, n is the measurement number, ρ_F and ρ_W are the signal intensity of fat and water, respectively, φ_F and φ_W are the phases of fat and water, respectively, t_n is the TE at measurement n, Δf is the fat chemical shift with respect to water, and ψ is the off-resonance from B₀ heterogeniety. IDEAL is fully compatible with PC imaging. In straightforward application of IDEAL with PC imaging (IDEAL-PC), three images at different TEs should be collected for each velocity-encoding direction since the water phase offset is assumed constant at each TE. This approach triples the scan time of standard PC experiment. To reduce the number of required measurement points, we propose to incorporate the phase evolution from velocity encoding direction into the signal model as an additional phase term:

$$S_n=({\mathrm{\rho }}_F{e}^{i({\mathrm{\phi }}_F+2\mathrm{\pi }\mathrm{\Delta }{\mathit{\text{ft}}}_n+\mathrm{\gamma }{\overrightarrow{M}}_n•{\overrightarrow{V}}_F)}+{\mathrm{\rho }}_W{e}^{i({\mathrm{\phi }}_W+\mathrm{\gamma }{\overrightarrow{M}}_n•{\overrightarrow{V}}_W)})e^{i\mathrm{\psi }{t}_n},$$ [2]

where M⃗_n is the first moment of the gradients at measurement n and V⃗_F, V⃗_W represent the velocity vectors of fat and water, respectively. This signal model assumes that the signal magnitude of fat and water must not be affected by the velocity encoding. Previously, we have used this assumption in magnitude-constrained reconstruction of PC data (26). This assumption holds if the diffusion and dephasing effects of each velocity encoding are similar. To ensure that this is true, velocity encoding should be performed using encoding schemes where the first moment magnitude is the same for all encodings (27). In most cases, this signal model can be further simplified by assuming fat to be static, reducing the model to:

$$S_n=({\mathrm{\rho }}_F{e}^{i({\mathrm{\phi }}_F+2\mathrm{\pi }\mathrm{\Delta }{\mathit{\text{ft}}}_n)}+{\mathrm{\rho }}_W{e}^{i({\mathrm{\phi }}_W+\mathrm{\gamma }{\overrightarrow{M}}_n•{\overrightarrow{V}}_W)})e^{i\mathrm{\psi }{t}_n}$$ [3]

This assumption requires the phase of fat to be independent of velocity encoding, which is generally not true for the raw data due to phase offsets from eddy currents and concomitant gradient errors. Thus, phase corrections for these offsets must be incorporated into the reconstruction or performed before any signal fitting is performed.

Simplified analysis allows intuitive estimation of benefits of the proposed CSI-PC approach compared to IDEAL-PC imaging. Equation 3 has only eight scalar unknowns for 3D velocity encoding (six phase, tw magnitude), reducing the number of required complex measurements to six. This number of measurements represents a 2-fold reduction compared to straightforward IDEAL-PC experiment, which requires 12 complex measurements. When the velocity of fat cannot be assumed to be constant, CSI-PC requires three extra velocity encodings, for a total of nine encodings. In this work, we have focused on the cases in which the velocity of fat can be assumed to be constant.

Reconstruction

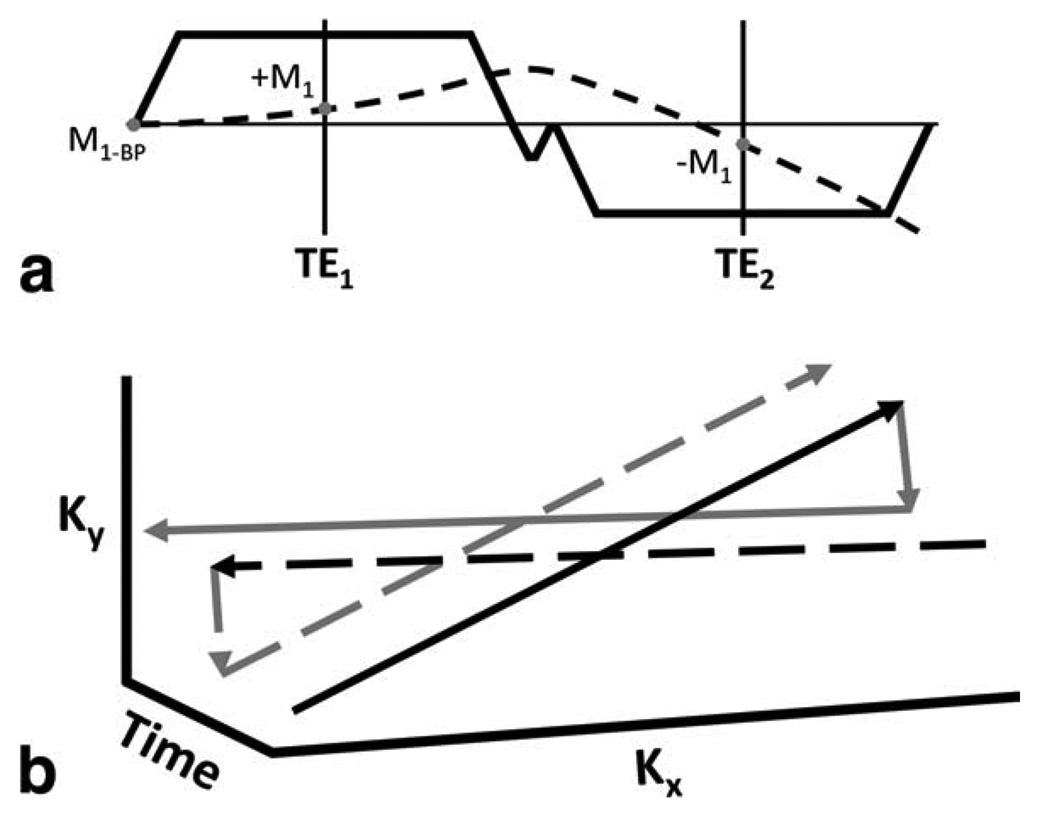
Theoretically, reconstruction of images subject to the combined fat/water signal model can be done directly from k-space data (26) to allow for more optimal utilization of the signal model. However, the scale of the nonlinear inverse problem may be prohibitively large for practical reconstruction. To simplify the reconstruction, we propose to perform k-space data inversion and nonlinear fitting in separate stages, as shown in Fig. 2. This is similar in nature to the k-space application of IDEAL (28). Complex images are first reconstructed from fully sampled k-space centers at a low resolution, using the standard Fourier transform or gridding operation. The low-resolution images are then fitted to the signal model on a per-coil basis, using the regularized Newton-Raphson nonlinear least-squares method (29) described in the Appendix. The nonlinear estimation procedure is identical to that used in IDEAL. However, we found that regularization is required in the proposed scheme due to the poor determination of the velocities when the water signal is small relative to the fat signal. While the procedure yields low-resolution estimates of all model parameters, only the field map is taken at the output. The remaining low-resolution parameters are used as initial values in the subsequent high-resolution fitting procedure. In multicoil cases, individual low resolution B₀ heterogeneity field-map images are combined using standard multicoil image combination (30,31). To create high-resolution complex images free of B₀ heterogeneity effects, we apply multifrequency reconstruction (22,32) of all k-space data, using the low-resolution field map estimate. With single-echo Cartesian sampling, the multifrequency reconstruction can be replaced with simple image-based demodulation to save computation time. As the resulting high-resolution images are demodulated with the field map, they can be fitted to the signal model without the B₀-heterogeneity term (factor e^iψt_n in Eq. 3). The result is high-resolution estimates of all other parameters for each coil. Again, multicoil images can be recombined in the usual fashion.

FIG. 2.

Diagram of the nonlinear reconstruction scheme utilized. k-space data are first reconstructed at low resolution and fit to the signal model, producing low-resolution estimates of the B₀ heterogeneity, water, fat, and velocity images. k-space data are then reconstructed at high-resolution, using the low-resolution field map for fitting. These high-resolution images are then fit to the signal model without B₀ heterogeneity off-resonance, producing high-resolution water, fat, and velocity images.

MATERIALS AND METHODS

Simulations

Initial simulations were performed to evaluate the performance of the nonlinear fitting algorithm and investigate the effects of fat on PC imaging with several trajectories. We performed signal-fitting simulations to establish the SNR efficiency and evaluate the influence of regularization on the convergence and estimation error. In Monte Carlo simulations, we created 100,000 realizations for 10 fat fractions evenly spaced from 0 to 100%, with a velocity value 65% of the prescribed velocity encoding. For each realization, we assigned random values to B₀ heterogeneity off-resonance and velocity direction, with B₀ heterogeneity off-resonance values ranging from −1.7 to 1.7 parts per million (ppm). This range of off-resonance values corresponds to half the off-resonance frequency of the main peak of fat (3.36 ppm) and reduces the likelihood of fat/water swapping. For each realization, we calculated signals for standard PC and CSI-PC and added the same independent gaussian noise to the real and imaginary channels (SNR = 25 relative to the water signal intensity). For CSI-PC, we utilized eight TEs with fat phase shifts equally spaced from 0 to 2π. For standard PC, we simulated with eight acquisitions at the same TE. Finally, we performed the velocity encoding using four-point balanced encoding repeated twice, once for the first four TEs and then again for the last four TEs.

The regularized Newton-Raphson nonlinear minimization (Appendix) was applied to find the solution. The regularization values ranged from 10⁻¹⁵ to 10⁻², with a factor of 10 between each value. We initialized fat and water signal magnitudes, with the average signal intensity and all phase terms to zero. For standard PC simulation, we utilized an approximation to least-squares solution to determine velocities (33). To compute the mean velocity bias due to reconstruction from the noisy signal, we calculated the velocity difference average:

$${\overrightarrow{V}}_{\mathit{\text{bias}}}=\frac{1}{N}{\Vert {\displaystyle \sum _{i=1}^N}({\overrightarrow{V}}_{\mathit{\text{measure}},i}-{\overrightarrow{V}}_{\mathit{\text{actual}}})\Vert }_2,$$ [4]

where N is the number of realizations, V⃗_actual is the known, input velocity, and V⃗_measure,i is the computed velocity from the ith realization of noisy signal. Additionally, we estimated the variance in the velocity:

$${\mathrm{\sigma }}_v^2=\frac{1}{N-1}{\displaystyle \sum _{i=1}^N}{\Vert {\overrightarrow{V}}_{\mathit{\text{measure}},i}-{\overrightarrow{V}}_{\mathit{\text{noise}}-\mathit{\text{free}}}\Vert }_2^2,$$ [5]

where V⃗_noise–free is the solution computed with no noise added. In the case of no estimation bias, V⃗_noise–free is identical to V⃗_actual. For CSI-PC examinations, the water noise signal average (NSA) was additionally computed:

$$\mathit{\text{NSA}}=\frac{{\mathrm{\sigma }}_s^2}{{\mathrm{\sigma }}_W^2},$$ [6]

where ${\mathrm{\sigma }}_{\mathrm{s}}^2$ is the variance in each measurement and ${\mathrm{\sigma }}_{\mathrm{W}}^2$ is the estimated variance of the water magnitude. It is optimal to have the NSA equal to the number of echoes, which would imply that the noise in the water image is as good as the signal averaging.

To demonstrate the efficacy of CSI-PC, simulations were performed using two-dimensional radial, spiral, and Cartesian trajectories with a 6.6-ms data acquisition window. Uniform density spiral trajectories utilized 12 interleaves and were designed with a time-optimal waveform design (34) using a max gradient 40 mT/m and max slew rate of 150 mT/m/sec. Radial images were acquired with a dual-echo radial trajectory (15), with 256 angles spaced evenly from 0 to 2π. All trajectories utilized the same velocity encoding and TEs utilized in nonlinear fitting simulations described above. A 7.9mm-diameter vessel with parabolic flow was simulated surrounded by fat with equivalent signal intensity extending 50mm from the center of the vessel. The off-resonance from B₀ heterogenity was set to be 30 Hz across the image volume. Image acquisition was simulated with 1.0 × 1.0mm² spatial resolution, with reconstruction performed at 0.25 × 0.25mm². Gaussian noise with a standard deviation equal to 0.05% of the maximum k-space value was added independently to the real and imaginary channels of the simulated data. Results were compared to a standard PC acquisition with identical parameters.

Dual-Echo Radial Trajectory

The combination of CSI and PC velocimetry proposed here requires consideration of both chemical shift and velocity encoding in the experimental design to obtain data that can be fit to the signal model. CSI requires acquisition of several datasets, each with a unique echo shift (and hence, image phase progression) to allow estimation of complex fat and water images, and field map. In turn, PC velocimetry requires a fixed TE between acquisitions, with a bipolar encoding gradient applied before each acquisition to provide velocity encoding in a given direction. Additionally, for CSI-PC, each data set must have the same artifacts from off-resonance (blurring, geometric distortions) and velocity (displacement artifacts, dephasing effects). The task of making the data sets consistent in such a way requires that the trajectories of each dataset be similar in k-t-space, with only a constant difference in the time of acquisition between any two data sets. In general, this would require that one TE be collected at each TR because the first moment at TE must be similar between the two echoes. This could be achieved with bipolar fly-back gradients; however, this leads to substantial increases in the achievable echo spacing and TEs. With a properly designed non-Cartesian trajectory, two echoes can be collected per TR. This requires that both echoes have similar phase evolution from velocity and off-resonance across any given line in k-space. To implement a time-efficient multiecho readout following the design criteria introduced above, we have developed a dual-echo radial trajectory that consists of a bipolar readout gradient that has a first-moment offset at each TE instead of the standard flow compensation offset of zero. The trajectory incorporates a small encoding gradient to sample different k-space lines within a single TR to avoid different off-resonance precession in the projections. To satisfy the conditions of CSI-PC, projections are repeated, as shown in Fig. 3, so that each repeated line in k-space has both the same first-moment offset at each TE and a constant time difference as a function of k-space (to avoid inconsistencies due to off-resonance effects). In this fashion, both sets of echoes have similar artifacts from first-moment offsets, T₂* decay, and off-resonance; however, since projections are repeated, sampling efficiency is reduced compared to previous applications of the trajectory (15). In the reconstruction, both the first and second echoes are assumed to have the same, constant first moment, which is set by the flow-encoding bipolar gradient.

FIG. 3.

Readout gradient (solid line) with corresponding first-moment trajectory (dashed line) for a flow-compensated line in k-space (a). The trajectory in k-t-space for two separate TRs (b). For visualization, a projection in the k_x-k_y plane is shown. Projections are repeated in separate TRs, as shown by solid and dashed lines, such that projections at the same angle have the same first-moment offset and trajectory in k-t-space. Black lines indicate the first echo and gray lines indicate the second echo.

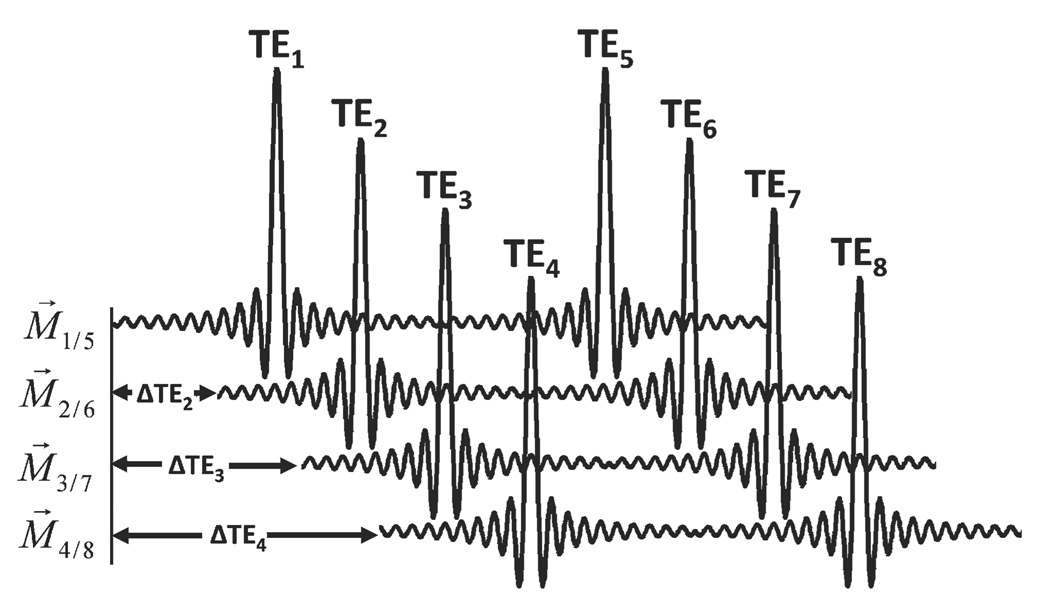
Since each of the two echoes in a given TR has similar flow encoding, at least four flow encodings must be performed to determine three velocity directions. Time encoding is incorporated using echo shifting, as shown in Fig. 4. Eight distinct echoes are collected, with times spaced evenly from a 0 to 2π shift of fat. Flow encoding is performed with balanced four-point encoding (27) to reduce magnitude differences between data sets. This scheme is easily incorporated into two-dimensional radial, hybrid 3D radial (i.e., two-dimensional radial with one-dimensional phase encoding) and fully 3D radial trajectories. In this work, we have incorporated it into time-averaged, gradient and radiofrequency spoiled, fully 3D radial sequence for evaluation

FIG. 4.

Echo shifting diagram for dual-echo radial imaging. M⃗. is the first moment for flow encoding at the given TE, i. For this sampling scheme, the effective first moment is the same between the 1st and 2nd echo, as noted. Images are acquired with echo shifts such that fat phase shifts from 0 to 2π are evenly sampled.

Phantom Experiments

All measurements were performed on clinical 3.0-T system (HD EXCITE TwinSpeed Signa; GE Healthcare, Waukesha, WI; whole-body mode gradients, slew rate: 80 mT/m/ms, max gradient strength: 23 mT/m) with an eight-channel phased-array coil used for acquisition (HD Cardiac; GE Healthcare). Reconstructions were performed offline using multithreaded C-code on a four-processor 64-bit Linux machine (Opteron 8356; AMD, Sunnyvale, CA). A dual-echo, time-averaged, radiofrequency and gradient spoiled 3D radial pulse sequence was modified to include echo shifting for PC CSI. To evaluate the separation of static fat and moving water, we designed two phantoms with a single tube flowing through a fluid bath. One of the phantoms had a fluid bath of peanut oil and the other had a fluid bath of doped water. Both phantoms used tubes of the same size and length with an inner diameter of 7.9mm, outer diameter of 8.6mm, and length of 40 cm. The phantoms were connected to a programmable computer-controlled pump (CompuFlow 1000 MR; Shelley Medical, London, Ontario, Canada). Data were acquired covering a 24 × 24 × 12 cm³ field of view with 0.9mm isotropic resolution, with pump set to constant flow at a rate of 10 mL/sec. Echoes were collected using a 310 Hz/pixel readout gradient amplitude, with the receiver sampling rate set to 976 Hz/pixel. This readout oversampling reduces artifacts from any structures outside the prescribed field of view, with only modest increases in reconstruction time due to the increased number of samples. The velocity encoding was set to 40 cm/sec. TEs were designed for even spacing between 0 and 2π fat shift, with the second echo shifted by an extra 2π due to gradient limitations. This resulted in TEs of 3.3, 3.5, 3.7, 4.1, 6.7, 6.9, 7.2, and 7.5 ms and a TR of 10.5 ms. A 15° flip angle was used in all cases, chosen based on empiric observations to minimize signal saturation. A total of 8000 projections per velocity encoding direction were collected, for a total scan time of 5 min 36 sec. Following the CSI-PC examination, a standard dual-echo fully 3D radial PC acquisition was performed with no TE shifting and unique projections collected at each of the two TEs. The standard PC had a shorter TR of 9.6 ms, for a total scan time of 5 min 4 sec. Both sequences incorporate gradient calibrations to correct for errors from trajectory deviations (15). All reconstructions were performed using an optimized gridding operation (35), with conjugate phase reconstruction performed using least-squares interpolations of seven evenly spaced frequencies (32). Concomitant gradient phase offsets were corrected prior to signal fitting (36). Signal fitting was performed with a λ of 10⁻⁶, as described in the Appendix.

Human Volunteers

To establish feasibility of CSI-PC in vivo, we obtained images in human volunteers, with institutional board approval and informed consent. Respiratory-gated examinations of the descending aorta and renal arteries were performed with the same imaging coil, TR, TEs, flip angle, number of projections, and reconstruction parameters as those used in the phantom experiments. The scan covered a field of view of 40 × 40 × 16 cm, with 1.25mm isotropic resolution. Respiratory gating doubled the scan time of both acquisitions to 11 min 12 sec in CSI-PC and 10 min 8 sec in standard PC. We visually evaluated the water and fat images to estimate the level of fat and water separation. Additionally, we created the angiographic images using the formula:

$$\mathit{\text{CD}}=\{\begin{array}{cc}\hfill M·\text{sin}(\frac{\mathrm{\pi }}{2}·|\overrightarrow{V}|/V_A)\hfill & \hfill \left|\overrightarrow{V}\right|<V_A\hfill \\ \hfill M\hfill & \hfill \text{otherwise}\hfill \end{array},$$ [7]

where CD is the angiographic image, V⃗ is the velocity as determined from phase processing, and V_A is an arbitrarily defined threshold velocity. We set M to the magnitude image for standard PC and to the water-only image for CSI-PC. This weighting scheme mimics complex difference processing (37) but allows images to be calculated from processed images. For all reconstructed images reported here, V_A was set to the velocity encoding of 40 cm/sec. These images were visually evaluated to determine depiction of the vasculature. Additional oblique reformats were performed of the velocity images to compare velocities measured with standard PC and CSI-PC.

RESULTS

Simulations

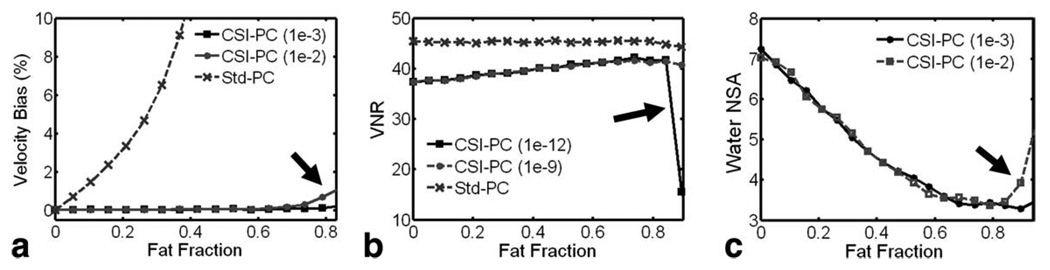
Figure 5 shows the results of Monte Carlo–based measurements of velocity bias, velocity-to-noise ratio, and water NSA as a function of fat fraction. Only regularization values of interest (i.e., start of bias or noise amplification) are shown. Small fat signal fractions lead to significant velocity bias in standard PC, while CSI-PC produces unbiased velocity values even at very high fat fractions. Since the fat signal is static and standard processing averages intravoxel velocities, the velocity bias in standard PC always reduces the magnitude of measured velocities. High regularization values (>10⁻³) lead to a velocity bias in CSI-PC at high fat fractions. The velocity-to-noise ratio produced by CSI fitting is dependent on the fat fraction and is consistently lower than that of standard PC. In voxels with no fat contribution, the velocity-to-noise ratio of CSI-PC is roughly 85% that of the dual-echo PC; however, this is still 22% better than a standard four-point, single-echo acquisition. As the fat-fraction increases, the velocity-to-noise ratio of CSI-PC increases; however, with regularization values less than 10⁻⁹, there is a substantial increase in velocity noise at high fat fractions. The water NSA is also dependent on the fat fraction and is significantly lower than standard PC, which has an NSA of 8. Regularization values above 10⁻³ also lead to a bias in the water signal estimate that reduces the noise estimate.

FIG. 5.

Monte Carlo–based measured of velocity bias (a), velocity-to-noise ratio (b), and water NSA (c) as a function of fat fraction. Only regularization values in which estimation bias begins, as denoted by arrows, are shown. Increasing fat fraction results in increasingly large errors in velocity values. CSI-PC velocity values are accurately estimated, except when very high regularization values (λ > 10e-3) are used for large fraction of fat (a). Compared to standard PC, the proposed acquisition scheme for CSI-PC exhibits a small increase in noise, with high regularization values increasing the noise for large fat quantity (b). With no fat, the NSA is close to the maximum of 8 but decreases with increasing fat-fraction (c). At high regularization the noise is reduced, due to bias in the measure (a,c).

Figure 6 shows simulated velocity images of simulated acquisitions with Cartesian, single-echo radial, and interleaved spiral trajectories. In all cases, CSI-PC is able to reconstruct the parabolic flow pattern, while standard PC produces artifacts at the edge of the vessel. In Cartesian sampling, the fat signal is spatially shifted with respect to water signal, causing errors in the velocity measurements along one edge of the vessel. In radial sampling, there is a high level of radial symmetry, leading to uniform blurring at the edge of the vessel. Since relatively few shots are utilized to cover k-space with the spiral sampling trajectory, significant artifacts arise from off-resonance phase accrual. This sensitivity to off-resonance artifacts leads to substantial artifacts in the velocity images seen throughout the vessel.

FIG. 6.

Simulated 3-T images of a small vessel surrounded by fat of equal intensity, using spiral, Cartesian, and radial acquisitions, all with a 6.6-ms acquisition window. All trajectories show significant error from fat/water interference with standard PC, which is removed using CSI-PC.

Phantom

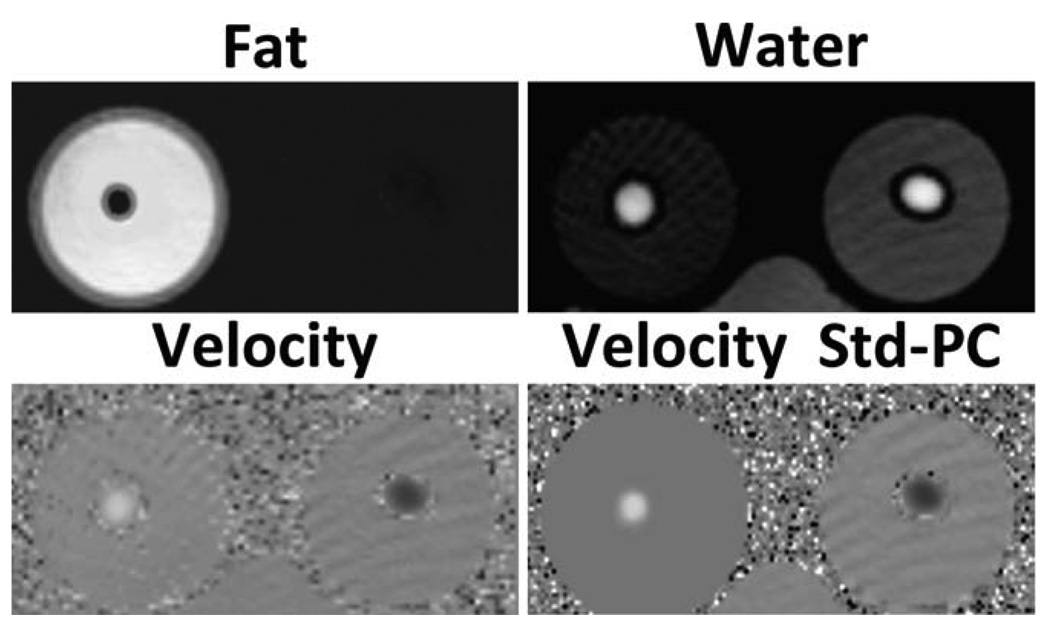
Figure 7 shows the representative phantom fat, water, B₀ heterogeneity field map, and through-plane velocity images. No masking was utilized for velocity images. The results demonstrate generally good separation of fat and water, but roughly 5% of the fat signal is put into the water signal. We attribute it to the incomplete modeling of the multiple frequency peaks of fat (38), which also leads to small differences in B₀ heterogeneity field map values. Field map images show minimal influence from fat, with relatively uniform signal behavior across the volume. Low-intensity streak artifacts are visible in velocity images. These artifacts are visible as bands of alternating velocity intensity and arise from the slow entry to steady state of a long T₁ static phantom placed within the field of view. Velocity noise is seen at the edge of the tubing due to the limited signal from the tubing wall, which, as the tubing wall was not modeled, is not seen in simulations. Figure 8 shows reformatted velocity profiles from the CSI-PC and standard PC sequences. In the fat phantom, the velocity is underestimated at the edges of the vessel, using standard PC. CSI-PC measures an identical profile to that measured with standard PC in the water phantom.

FIG. 7.

Example fat, water, through-plane CSI-PC velocity, and through-plane standard PC velocity images at the central slice of the phantom, using the radial trajectory. Near-complete separation of fat-water images is achieved, with some residual fat signal in the water, possibly due to incomplete characterization of the multiple fat peaks. Low-intensity streak artifacts are visible in areas of low signal intensity. These artifacts arise from the slow entry into steady state of a long T₁ phantom placed in the field of view. Additionally, the standard PC velocity images show artifacts at the edge of the tube that are not present in the CSI-PC velocity images.

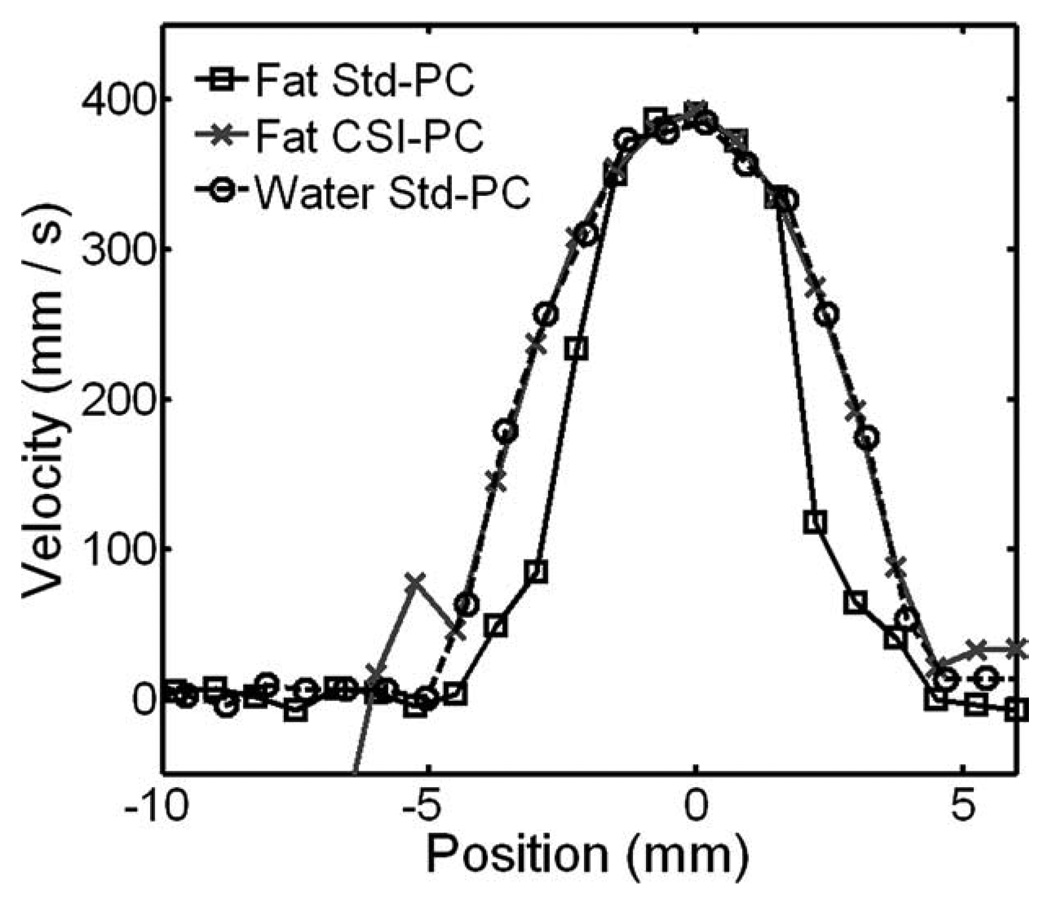
FIG. 8.

Velocity profiles obtained in the fat phantom and water phantom with the 3D radial sequence. Both methods show similar maximum velocity measurements in the center of the vessel, with good agreement with the expected maximum velocity of 40.8, using laminar pipe flow equations. Standard PC images acquired in fat (Fat Std-PC) show velocity bias at the edge of the vessel. At the same time, CSI-PC images (Fat CSI-PC) obtain profiles similar to those acquired in the reference water phantom (Water Std-PC).

Human Volunteers

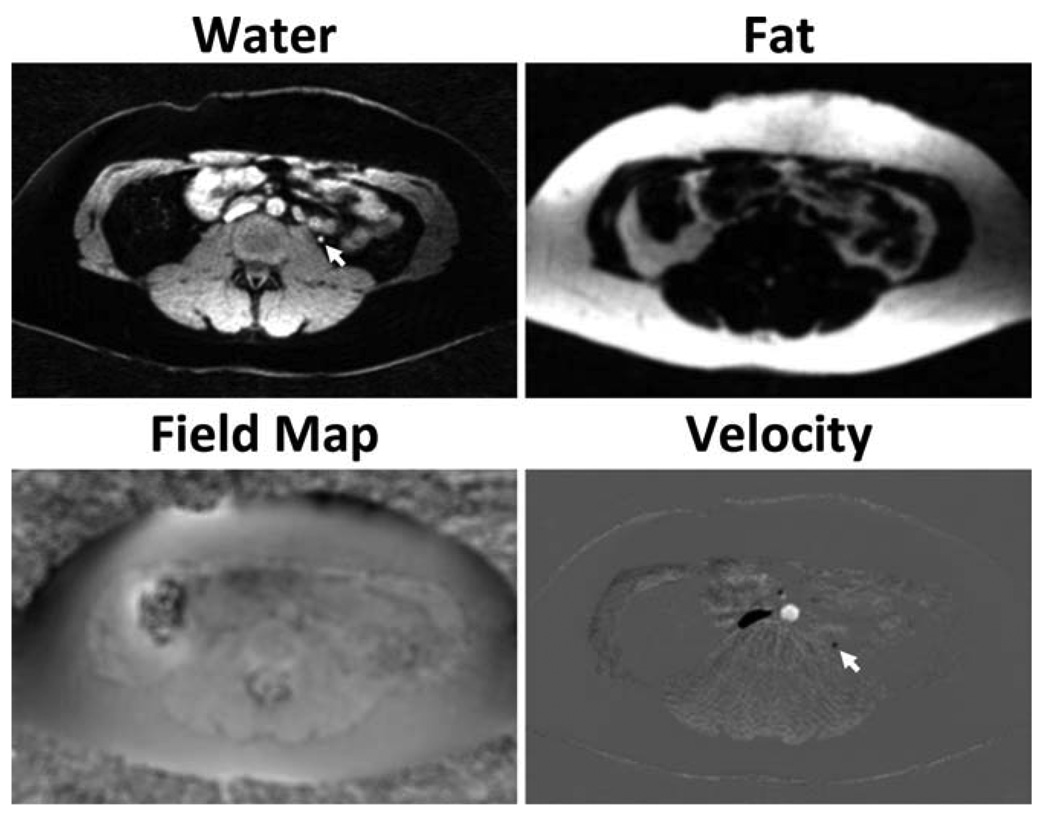
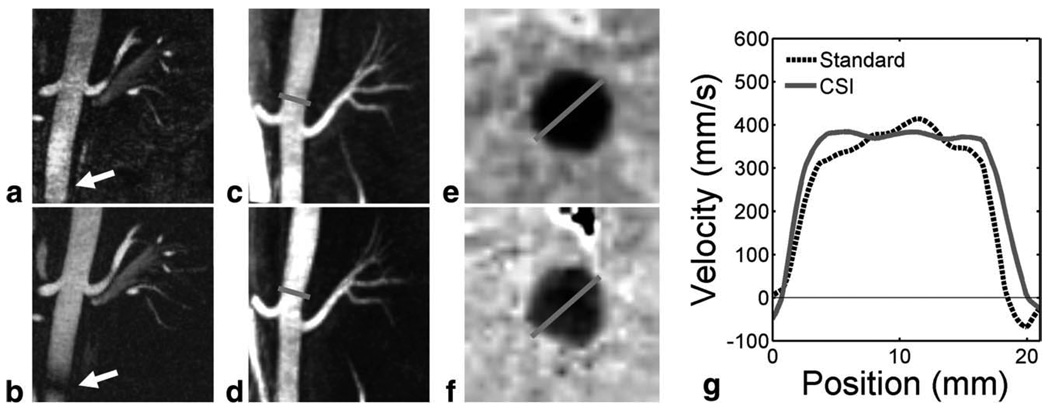
Figure 9 shows the representative source fat, water, and B₀ heterogeneity field map from standard PC and CSI-PC. For volunteers, the CSI-PC reconstruction took roughly 1 min per slice, with most time spent performing nonlinear signal fitting. Fat and water images demonstrate good suppression of interfering signals. Again, roughly 5% of the fat signal is misregistered into the water signal. Fat images show evident blurring from the radial trajectory. B₀ heterogeneity field map images show minimal influence from fat, with small differences due to inaccurate characterization of the fat off-resonance spectrum. Representative angiographic images derived from two volunteers are shown in Fig. 10a–d for standard PC and CSI-PC. Oblique reformats of images acquired in a normal volunteer (body mass index = 25 kg/m²) with CSI-PC (Fig. 10a) and CSI-PC (Fig. 10b) and show the SNR penalty incurred when utilizing CSI-PC. However, signal cancellation is seen in the descending aorta in standard PC that is not evident in CSI-PC. These errors are due to incoherent echo addition caused by B₀ heterogeneity. In a targeted maximum-intensity projection of an obese volunteer (body mass index = 40 kg/m²), similar apparent image quality is observed between CSI-PC (Fig. 10c) and standard PC (Fig. 10d). No artifacts were observed from Cardiac pulsatility due to the incoherent nature of such artifacts in the 3D radial sequence. From reformatted slices of the obese volunteer, differences in the through plane velocity can be observed similar to those observed in phantoms. The standard PC velocity profile appears to be narrower than the CSI-PC due to significant fat contribution.

FIG. 9.

Example axial images obtained in abdominal scans of a healthy volunteer, using the proposed CSI-PC procedure. Velocity images are masked by the water magnitude image for improved visualization. The results demonstrate excellent separation of fat and water. Field map images from CSI-PC show a minimal influence from fat, likely caused by inaccurate characterization of the multiple peaks of fat. This allows for B₀ heterogeneity corrections without losing small vessels embedded in fat (arrows).

FIG. 10.

Reformatted CSI-PC images (a) in a healthy volunteer show reduced apparent SNR and increase background signal compared to standard PC images in the same volunteer (b) because of half the acquisition time required for a full CSI-PC examination. CSI-PC images do not suffer from B₀ heterogeneity off-resonance artifacts in the inferior segment of the descending aorta (arrow). In contrast, targeted maximum-intensity-projection images of an obese volunteer (body mass index = 40 kg/m²) show similar image quality in CSI-PC (c) and standard PC (d). Gray lines mark the locations for two-dimensional through-plane velocity reformats of CSI-PC (e) and standard PC (f) in the obese volunteer. CSI-PC shows higher velocity at the vessel wall, highlighted in a one-dimensional profile of the standard and CSI velocities (g).

DISCUSSION

In this work, we have proposed the efficient combination of CSI and PC velocimetry for suppression of errors in velocity measures due to fat. Velocity errors caused by fat/water interference can be removed, with the proposed fat separation leading to more accurate velocity estimates. With this method, velocity measurements of vessels in the proximity of fat, such as the coronary arteries, descending aorta, and peripheral vessels, can be performed with improved accuracy.

The proposed CSI-PC approach has several advantages over standard techniques used to minimize fat-related errors in flow measurements. Unlike fat saturation or water-only excitation techniques, B₀ heterogeneity has minimal effect on fat separation in CSI-PC. Additionally, field maps derived from the fitting can be utilized for B₀ heterogeneity corrections. This is especially important with non-Cartesian trajectories that are often used for rapid acquisitions. Compared to a straightforward combination of PC velocimetry with fat/water separation approaches such as IDEAL, fitting can be performed with half the measurements. CSI-PC also has significantly more freedom in choosing the echo spacing and velocity encodings, which may lead to more optimal SNR performance. With the optimal IDEAL TEs, the fat phase is distributed at −π/6, π/2, and π7/6 with respect to water. In PC velocimetry, the phase offsets of fat and water can be significantly different from each other due to velocity encoding. Subsequently, the optimality of echo spacing in IDEAL-PC is not guaranteed for voxels consisting of fat and water components moving at different velocities. In the work, we used a heuristic CSI-PC acquisition scheme based on the combination of standard velocity encoding and constant spacing time sampling. Similar to work performed in optimizing echo spacing for IDEAL (21), future work is required to evaluate the echo spacing and velocity encoding scheme for CSI-PC. This analysis requires a noise analysis of all practical velocity encodings and TEs and selection of the optimal sampling scheme. Given performance improvements achieved in fat/water separation, substantial improvements in SNR may be achievable.

The improved accuracy of flow velocimetry and reduced image artifacts with multiecho radial CSI-PC comes at the expense of two times scan time increase when compared with standard multiecho radial PC. In this work, we have enforced the same imaging time for both CSI-PC and standard PC, thereby undersampling CSI-PC datasets by two times compared to standard radial PC and increasing aliasing (streaking) artifacts. This is apparent in the volunteer studies, where there is a significant increase in background signal level in subjects with little to no fat. In the undersampled radials presented, this reduction comes from both the increased pseudorandom artifacts and the SNR penalty of CSI-PC. The SNR penalty arises both from reduced acquisition time and noise amplification due to the model-fitting procedure. In obese volunteers, the removal of fat aliasing artifacts may lead to reduced background suppression, as seen in the portrayed obese volunteer. The noise amplification may be potentially reduced with optimized acquisition schemes. Accordingly, avoiding undersampling will increase apparent SNR. Due to the implied scan time penalty, CSI-PC may be less attractive in imaging situations when fat signal does not disrupt the velocity measurements and when a good shim can be achieved. When these conditions are met will be highly dependent on both the patient’s anatomy and the sequence utilized. Sequences with long readout gradients such as spiral and twisting radial line (TWIRL) (39) will be significantly more sensitive to fat interference compared to those with relatively short readout windows and hence may significantly benefit from the proposed method.

As with any model-based quantitative MRI technique, the accuracy of CSI-PC depends on completeness of a modeling equation, which may or may not be sufficient for calculations in different imaging situations. Magnitude differences from T₂* and velocity dephasing must be common to all measurements to make the model consistent with measurements. In CSI-PC, intravoxel dephasing differences are prevented by using balanced trajectories, which maintain the magnitude of the first moment between scans. In this work, T₂* decay has not been modeled in the signal model. Any T₂* decay will lead to errors in the velocity and fat/water values and may be the source of reduced background suppression in anatomic images. To minimize these errors, T₂* values can be incorporated into the signal model simply by treating the field heterogeneity as a complex term, in the manner similar to T₂* IDEAL imaging (40). This comes at the cost of increased noise in other measures.

In addition to the preservation of magnitude between encodings, phase evolution must be well described by the signal model. This forces phase-offsets terms from concomitant gradients and eddy currents to be corrected before fitting procedures or incorporation into the reconstruction. Concomitant fields are well described by the gradients and are relatively easily incorporated into reconstruction process (36,41); however, eddy-current terms are difficult to predict. These phase offsets only become problematic when fat is assumed to be static and the fat signal does not account for the phase terms from the bipolar. Potentially, this may lead to some percentage of fat being misclassified as moving water. However, the order of the effect is unknown at the moment and more investigations are required. Additionally, it has been shown recently that modeling fat as a single component may reduce the accuracy of fat/water separation (38), which may lead to less incomplete correction of flow velocity values. The method proposed here is readily extendable to handle multipeak fat spectrum to minimize the potential errors.

As most nonlinear methods, our approach does not guaranty the global convergence, which depends on initialization and the regularization parameters used. It was shown in a previous study that a local minimum can occur, which will lead to significant biases in the solution values (i.e., swap of fat and water signal) (42). For example, B₀ heterogeneity can cause a fat/water swap if signal fitting is initialized with a significantly different B₀ heterogeneity off-resonance than actually existed. Reasonable initialization values to the signal fitting routines help prevent these problems. Simple region growing can be used to initialize the B₀ heterogeneity off-resonance value to prevent this in most cases (42). The choice of regularization parameter controls the rate of convergence and in the extremes can influence the convergence value and noise performance. If the regularization value is small, fewer iterations are required and noise amplification can occur in fat and water values. For large regularization values, convergence will take more iterations and bias can exist in noisy data. From our experience, the reasonable choice of regularization parameter is in the range [10⁻³ to 10⁻⁹], which resulted in approximately 10 iterations until convergence.

The reconstruction scheme proposed in this paper is a compromise between accuracy in fitting and reconstruction time. In a more accurate reconstruction, velocity and fat/water signals x⃗ would be directly estimated from the data in a least-squares fashion

$$\overrightarrow{x}=\text{arg}\underset{\overrightarrow{x}}{\text{min}}{\Vert K-\mathit{\text{ES}}(\overrightarrow{x})\Vert }_2,$$ [8]

where K is the collected data, E is the Fourier and coil sensitivity encoding matrix, and S is the signal (Eq. 3). This signal estimation is similar to magnitude-constrained reconstruction for PC flow quantification (26). Additional regularization terms can be introduced to smooth the field map values or phase offsets (43). Unfortunately, this minimization procedure requires a much larger model-based nonlinear estimation, which will be potentially more time consuming, possibly prohibitively long for large 3D volumes. Additional work is required to examine the influence of more optimal reconstructions on imaging performance.

CONCLUSION

We have proposed a method to combine CSI with PC velocimetry. The combination of CSI with PC velocimetry reduces prevalence of fat and B₀ heterogeneity artifacts in velocity measurements and improves the accuracy of PC velocimetry in the presence of interfering fatty tissues. Our method allows two times reduction of scan time compared to the straightforward combination of CSI and PC approaches. We also have further minimized the scan time penalty, utilizing a novel design of dual-echo radial trajectory. The techniques may be implemented with other trajectories and are directly extendable to other PC gradient echo sequences.

APPENDIX

Regularized Newton-Raphson Fitting

The CSI-PC parameter vector x⃗ = [ρ_W ρ_F φ_W φ_F ψ V_x ν_y V_z] is sought as the result of minimization of the l₂-norm of the residual between data samples, D, and the CSI-PC signal function (Eq. 3) sampled with n measurement values, Ŝ(x⃗) = [S₁ (x⃗) … S_N (x⃗)]^T:

$$\overrightarrow{x}=\text{arg}\underset{\overrightarrow{x}}{\text{min}}\left({\Vert D-\widehat{S}(\overrightarrow{x})\Vert }_2\right)$$ [A1]

To solve this equation, we expand the signal function about x⃗₀ using a Taylor series:

$$\widehat{S}(\overrightarrow{x})=\widehat{S}({\overrightarrow{x}}_0)+\widehat{S}\prime ({\overrightarrow{x}}_0)\mathrm{\Delta }\overrightarrow{x}+\mathit{\text{H.O.T.}}$$ [A2]

Ignoring higher-order terms (H.O.T.), this yields

$$\widehat{S}(\overrightarrow{x})=\widehat{S}({\overrightarrow{x}}_0)+J\mathrm{\Delta }\overrightarrow{x}$$ [A3]

Here J is the Jacobian matrix, with elements given by:

$$\begin{array}{c}\hfill J={[S_1^{\prime }({\overrightarrow{x}}_0)\dots S_N^{\prime }({\overrightarrow{x}}_0)]}^T\hfill \\ \hfill S_i^{\prime }(\overrightarrow{x})=[\frac{\partial S_i(\overrightarrow{x})}{\partial {\mathrm{\rho }}_W}\dots \frac{\partial S_i(\overrightarrow{x})}{\mathrm{\partial }{V}_z}],i=1,\dots ,N\hfill \end{array}$$

Setting this equal to the acquired data D:

$$R=D-S({\overrightarrow{x}}_0)=J\mathrm{\Delta }\overrightarrow{x},$$ [A4]

where R is the residual. Solving for Δx⃗ requires handling the possible singularity of the matrix J. This situation is likely to arise when ρ_W is close to zero, so that Δ v becomes ill determined. Hence, regularization should primarily concern velocity terms. This is controlled by simple Tikhonov regularization (29) of the updates, using diagonal matrix I_v, where only the diagonal entries corresponding to velocity terms are set to 1. The solution is then

$$\mathrm{\Delta }\overrightarrow{x}={(J^{T}J+\mathrm{\lambda }{I}_v)}^{-1}{J}^{T}R,$$ [A5]

where λ is the regularization parameter (small number with respect to the values of J). Δx⃗ is treated as a search direction. The step γ in the descent direction is determined as the one minimizing the L2 norm of the residual:

$$\underset{\mathrm{\gamma }}{\text{min}}\left({\Vert D-\widehat{S}({\overrightarrow{x}}_0+\mathrm{\gamma }\mathrm{\Delta }\overrightarrow{x})\Vert }_2\right)$$ [A6]

γ can be found using Brent line search (29). In this approach, the norm in Eq. A6 is evaluated at discrete values of γ (e.g., 0, 0.5, 1), and a polynomial interpolation is applied to find the optimized step γ_opt (quadratic fit for three-point search). Once the step size is found, x⃗ is updated (x⃗₀ ← x⃗₀ + γ_optΔx⃗), and steps [A2]–[A6] are repeated until the l₂ -norm in Eq. A1 reaches the predefined tolerance value.