Abstract
Aims
U.S. college drinking data and a simple population model of alcohol consumption are used to explore the impact of social and contextual parameters on the distribution of light, moderate, and heavy drinkers. Light drinkers become moderate under social influence, moderate drinkers may change environments and become heavy drinkers. We estimate the drinking reproduction number, Rd, the average number of individual transitions from light to moderate drinking that result from the introduction of a moderate drinker in a population of light drinkers.
Methods
Ways of assessing and ranking progression of drinking risks and data-driven definitions of high- and low-risk drinking environments are introduced. Uncertainty and sensitivity analyses, via a novel statistical approach, are conducted to assess Rd variability and to analyze the role of context on drinking dynamics.
Results
Our estimates show Rd well above the critical value of 1. Rd estimates correlate positively with the proportion of time spent by moderate drinkers in high-risk drinking environments. Rd is most sensitive to variations in local social mixing contact rates within low-risk environments. The parameterized model with college data, suggests that high residence times of moderate drinkers in low-risk environments maintain heavy drinking.
Conclusions
With regard to alcohol consumption in US college students, drinking places, the connectivity (traffic) between drinking venues, and the strength of socialization in local environments are important determinants in transitions between light, moderate and heavy drinking as well as in long-term prediction of the drinking dynamics.
Keywords: Drinking reproduction number, drinking environments, social influence, college drinking, uncertainty and sensitivity analyses
INTRODUCTION
College student drinking within the U.S. provides an ideal setting for the controlled study of drinking dynamics, the process by which social structures produce change over time in drinking patterns. Students seek out heavy drinking environments and live in social environments where alcohol consumption is prevalent [1]. Hence, it is not surprising that their drinking rates positively correlate with measures of the availability of drinking places [2,3]. Observational studies of the relationship between interpersonal dynamics and drinking behavior have been carried out in bars, fraternity houses and other environments [1,4-7]. Ideally, such studies should be carried out within theoretical frameworks where the impact of context heterogeneity on drinking dynamics is assessed. Mathematical models of the dynamics of college drinking that acknowledge the existence of an adaptive dynamic drinking culture should be further developed [8]. Contagion models [9,10] have been used effectively in the study of the dynamics of social processes (see [11-18] for various examples) and in the alcohol field they have demonstrated that in populations where relapse rates are high, long-term drinking trends depend on treatment rates and on the current proportions of different drinking types [19]. Variations in the proportion of drinking time spent in heterogeneous drinking venues can also impact a population's drinking patterns [8].
Our goals here are primarily to show the usefulness of mathematical models and highlight the type of data sets that may be needed in the study of drinking dynamics. We examine the effect of residence times in distinct drinking environments and contextual mixing on college drinking patterns. Specifically, the distribution of the model's drinking reproduction number, Rd (the average number of individual transitions from light to moderate drinking that result from the introduction of a moderate drinker in a population of mostly light drinkers), is estimated. The variability of Rd is assessed using a range of parameters including the relative residence-times of drinkers in low- and high-risk environments, local social-influences of drinkers within specific environments, rates of progression of drinkers from the moderate to the heavy drinking state, and college drop-out and matriculation rates of the population.
A Mathematical Framework And Approach
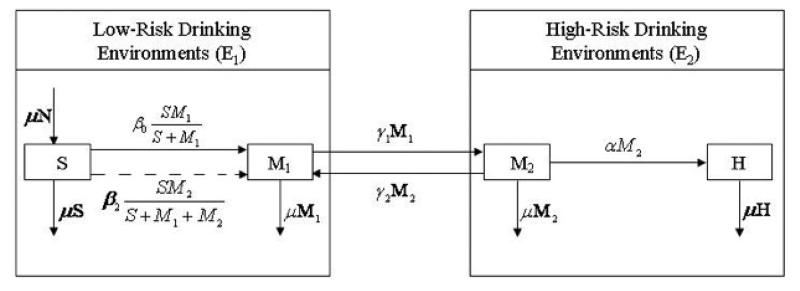
Drinkers are classified as “light” or “susceptibles” (S), “moderate” (M), and “heavy” (H) (see Figure 1 and [8]). Drinkers interact in “low-risk” (E1), “high-risk” (E2) or non-drinking environments. S- and H-drinkers primarily socialize in their preferred environments, outside E2 and E1, respectively. M-drinkers (divided into M1 and M2 classes) socialize in non-drinking environments and in E1 and E2, respectively. M-drinkers move between drinking environments at the per-capita rates γi (i = 1, 2), average residence times per environment of 1/γi (i = 1, 2). Light drinkers transition into the moderate class at a rate that depends on the strength and duration of M-drinkers' influence. Such simple parameter-scarce models have been extensively and successfully used in other disciplines (see for e.g., [20,21]).
Figure 1.
College Drinking Population Model with Three Types of Drinkers (light (S), Moderate (M1 and M2) and heavy (H)) and Two Distinct Drinking Environments (low-risk (E1) and high-risk (E2)). We use a dotted line to indicate that S-M2 influences happen outside the E1 and E2 drinking environments.
This simple model incorporates four major mechanisms: (1) local influence of M1 on S in E1, the strength measured by β0, that enables progression from S to M1; (2) progression of M2 to H at the rate α (1/α denoting the average time before an M-drinker becomes a heavy drinker); (3) relative residence times, function of 1/γ1 and 1/γ2, the average residence times of M-drinkers in the two distinct risk environments; and (4) the strength of influence of M2–drinkers on S-individuals, outside of the E1 and E2 environments, captured by β2. The college population is assumed constant (N). Therefore, the S-recruitment rate,μN (where μ is the per capita average departure rate), matches the total dropout and graduation rates of college drinkers.
We assume that students enter the college-drinking population as light drinkers as data on differential recruitment rates are unavailable. The dropout rate is assumed to be the same for all groups and may not be realistic for some college campuses. However, since our focus is on a typical US campus and since there are some studies that show no relationship of drinking to academic problems (see for e.g., [22-24]), there does not seem to be sufficient reason to build in an adjustment for differential dropout rates associated with drinking. Additional assumptions are:
Movement takes place only between E1 and E2;
Drinking status pre-determines the drinker's drinking venue-type;
Only moderate drinkers frequent E1 and E2;
Social influences are modeled via frequency dependent contacts between moderate and light drinkers in E1 or outside the drinking environments;
Moderate drinkers may (as a function of their residence time in E2) become H-drinkers;
The recovery and relapse are assumed to be negligible.
We arrive at the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
where N = S + M1 + M2 + H and M =M1 + M2.
Figure 1 highlights the rates of change per compartment captured by these equations while Table 1 collects the model parameter definitions. The basic reproductive number is given by the unit-less expression
| (5) |
denotes the proportion of the relative drinking time spent by M-drinkers in E2. Values of γ near 0 or 1 correspond to nearly “no movement” between E1 and E2 while γ = 0.5 models the most traffic. Rd greater than 1 leads to the establishment of heavy drinking while Rd less than 1 corresponds to the situation where the H and M classes cannot be sustained. This would not be the case in a model where recruitment brings students directly into the M- and H-classes. The college-drinking literature suggests comparatively fewer incoming M- and H-drinkers than their S-counterparts, so we ignore them. Rd=1 is the system's “change point” between maintenance and non-maintenance of the H- and M-drinkers over time and a condition Rd>1 reflects the current drinking situation (existence of high number of relatively stable heavy and moderate drinking population) in US. The effectiveness of interventions (medical or behavioral) are evaluated by the ability of the program to reduce Rd. Ideally, one would like to bring the system to the point where Rd<1, that is, below the change point. Previous analyses of the model support the hypothesis that the proportion of heavy drinkers is lower if E1 and E2 are weakly connected (γ is close to 0 or 1, see [8]), when Rd is above change point.
Table 1.
Definition of the parameters and their estimates for two values of y. Two definitions of high-risk settings are used to obtain two values of y.
| Para- meter |
Definition | Unit | Mean (Std.) |
Mean (Std.) |
|---|---|---|---|---|
| γ | Proportion of residence time of a moderate drinker in high-risk environments (Complement of this proportion will be their time in low-risk environments) |
No units | 0.28 (0.01) |
0.83 (0.02) |
| β 0 | Average number of “effective” influences (environment dependent) of one light drinker per unit time with moderate drinkers in low-risk environments |
Interactions per person per year |
0.71 (0.45) |
1.69 (1.08) |
| β 2 | Average number of “effective” influences (environment dependent) of one light drinker per unit time with moderate drinkers of high-risk environments mediated by moderate drinkers of low-risk environments |
Interactions per person per year |
2.20 (1.40) |
0.75 (0.47) |
| μ | Per capita arrival and departure rate for the system |
Per person per year |
0.27 (0.06) |
0.27 (0.06) |
| α | Per capita progression rate of moderate drinkers in high-risk environments to heavy drinking class (per capita linear transition rate) |
Per person per year |
0.51 (0.12) |
0.17 (0.04) |
| Rd | Average number of secondary conversions of light to moderate drinkers generated by the introduction of a typical” moderate drinker into a population of primarily light drinkers |
No units | 2.69 (0.16) |
2.14 (0.47) |
METHODS
The model uses the following three drinking categories: Light drinkers, those who drink at least once a month but do not consume more than 3 drinks at any one sitting; Moderate drinkers, those who drink at least once a month, consuming 3 to 5 drinks per sitting or drink at least once a week consuming no more than 3 drinks per sitting; and Heavy drinkers, those who drink 3 to 4 drinks at least once a week or consume 5 or more drinks at any one sitting at least once a month (see Engs et al. [25,26]). Data from national college-drinking studies ([25,26]) are used to assess the frequency distribution of drinkers by class-year. On the basis of these data, it was concluded that 64.2% of freshmen, 71.4% of sophomores, 76.1% of juniors and 80.6% of seniors fall into one of the three drinking classes (see Table 2). Additionally, we interpret the data as: 64.2% of college drinkers drink for four years, 7.2% for three years, 4.7% for only two years and 4.5% for only one year. This interpretation assumes no regression in drinking levels among the college students and is used to estimate the mean (3.63) and variance (0.69) of the parameter 1/μ (the average time a typical student remains a drinker while in college). Hence, an estimate for the mean of μ, college's dropout and matriculation rate, is 0.27 (= 1 / 3.63) with a variance of 0.0039 (Var (1/μ) = (0.69)2/(3.63)4; [27]).
Table 2.
Percentage of drinkers in four class-years along with their increase from previous class-year during academic year academic year 1993-94 (data source: Engs et al., 1997).
| Class Year |
Abstainers (%) |
Drinkers (Light+Moderate+Heavy) (%) |
% Increase In Drinkers From Previous Class Year |
|---|---|---|---|
|
Freshman N=3352 |
35.8 | 64.2 | |
|
Sophomore N=2883 |
28.6 | 71.4 | 7.2 |
|
Junior N=2973 |
23.9 | 76.1 | 4.7 |
|
Senior N=2527 |
19.4 | 80.6 | 4.5 |
The 2003-survey of 14 California and California State University campuses was used to define high- and low-risk college-drinking environments [28]. The relative rate of context-dependent alcohol-use or drinker residence times was used to introduce environment-specific risk definitions [29]. Students reported whether or not they had consumed alcohol since enrolling in college, drinking frequencies and quantities per sitting over the past four weeks or since the start of the semester, and the frequencies with which they consumed alcohol at different venues around campus (excluding their own homes).
For each drinking venue and drinking class, the number of times that alcohol was consumed over 4 weeks is reported in the Table 3 with utilization rates per drinker (venue visits per drinker type) in parentheses. This shows that drinking by all groups takes place at all venues and that each group has “preferred” venues. Heavy drinkers are found most often at off-campus parties. The second most frequented venue type by heavy drinkers is pubs, bars and restaurants, and the third most fraternity parties. 83.4% of moderate-drinker visits are to these three venue types (95% CI, 80.5% to 86.3%) but heavy drinkers are most likely to drink at residence halls, fraternity parties, and outdoors where moderate drinkers are found only 28.4% of the time (95% CI, 26.7% to 30.1%). Hence, the two definitions that we used for defining a high-risk setting were the places where heavy drinkers are most likely to be found and the places where heavy drinkers are most likely to drink.
Table 3.
Use of drinking venues by drinker class.
| Visits by all Drinkers in Class |
||||
|---|---|---|---|---|
| Drinking Venue | Light | Moderate | Heavy | Total Visits |
| Pubs, Bars, or Restaurants | 1815 | 3664 | 2925 | 8404 |
| (E2 by D1; E1 by D2) | (0.330) | (1.198) | (2.321) | (0.856) |
| Residence Halls | 643 | 1268 | 1302 | 3213 |
| (E1 by D1; E2 by D2) | (0.117) | (0.415) | (1.033) | (0.327) |
| Campus events | 142 | 321 | 307 | 770 |
| (E1 by D1; E1 by D2) | (0.026) | (0.105) | (0.244) | (0.078) |
| Off-Campus Parties | 3338 | 5891 | 5050 | 14279 |
| (E2 by D1; E1 by D2) | (0.607) | (1.926) | (4.008) | (1.455) |
| “Greek” Parties | 969 | 1950 | 1966 | 4885 |
| (E2 by D1; E2 by D2) | (0.176) | (0.638) | (1.560) | (0.498) |
| Outdoors | 300 | 698 | 761 | 1759 |
| (E1 by D1; E2 by D2) | (0.055) | (0.228) | (0.604) | (0.179) |
| Total | ||||
|
| ||||
| Number of Drinkers (%) | 5497 (56.0%) | 3058 (31.2%) | 1260 (12.8%) | 9815 |
| Number of Visits | 7207 | 13792 | 12321 | 33320 |
| (Visits per Drinker type) | (1.311) | (4.510) | (9.779) | (3.395)1 |
The table collects the results of the responses of the 9,815 drinkers surveyed. The number in parentheses indicate number of venue visits per drinker in drinking class. E1 and E2 represent low- and high-risk environments. We define high-risk setting as the place where either heavy drinkers are most likely to be found (D1) or where heavy drinkers are most likely to drink (D2). The paraenthesis under each venue shows whether that venue is low- or high-risk environment according to the two definitions (D1 and D2). For example, venue “Pubs, Bars or Resturants” is high-risk according to the first definition, D1, and low-risk according to the second definition, D2. “Campus events” and “Greek” parties always remain low- and high-risk, respectively.
The data in Table 3 provide estimates of the parameter γ, the proportion of time that moderate drinkers spend in E2. Hence, 28.4% and 83.4% of moderate-drinkers' drinking occasions (assumed proportional to the time spent by moderate drinkers at these places) are spent in high-risk environments. These estimates of γ (one per definition of high-risk setting) are of limited value since they are generated using regional data sets and we lack universally agreed definitions of high-risk. Thus, we carried out uncertainty and sensitivity analyses over a wide range of γ values (19 distributions). It was assumed that γ comes from uniform distributions with means of 0.05*k (k = 1…19) and variance 0.02. The results when γ is centered at 0.284, 0.5 or at 0.834 are highlighted throughout the text based on the data in Table 3.
Estimates of β0, β2, and α could not be found in the literature. Hence, a model-based approach and the data on the proportion of drinking types were used to estimate these. Specifically, the drinking proportions of S, M, and H individuals from data (represented by s*, m* and h*; Table 4) were paired with the model steady state equations to obtain these estimates. Steady state equation from Equation (4) generate the following estimate expression for α
| (6) |
where and . A linear relationship between β0 and β2 from the remaining steady state equations of the model provided a relation for all feasible values of γ, μ, α and class sizes. Interval bounds on β0 were generated using the sampled values of γ, μ, and α, the β0-β2 linear relation, and the non-negativity requirement on the parameter β0. The β0 bounds are used to define uniform distributions for β0. Estimates of β2 were obtained from the linear relationship linking β0 to β2 (see [30] for details).
Table 4.
Percentage of drinkers in three drinking-level classes from 1982 to 1991 (data source: Engs et al., 1994). Data have shown little variation from 1982 to 1991. The averages given in the last column are used as estimates of steady state number of the drinking classes.
| Years |
|||||
|---|---|---|---|---|---|
| Classes |
1982 (%) N=4324 |
1985 (%) N=3377 |
1988 (%) N=4232 |
1991 (%) N=3820 |
Average (%) |
| S | 24.0 | 23.9 | 25.3 | 26.8 | 25.00 |
| M | 51.2 | 51.0 | 48.5 | 45.9 | 49.15 |
| H | 24.8 | 25.1 | 26.2 | 27.3 | 25.85 |
Modified from Engs et al. (1992)---average over time included.
Uncertainty and Sensitivity Analyses
The uncertainty analyses were used to assess the variability in the empirical Rd distribution generated from the variability in parameter estimates. The sensitivity analyses assess the amount and type of change inherent in the model as captured by the terms that define Rd. If Rd is very sensitive to a particular parameter, then a perturbation of the conditions that connect the dynamics to such a parameter may prove useful in identifying policies that reduce college-drinking prevalence. Sensitivity and uncertainty analyses are common in the study of the role of variability in tipping point phenomena [31-33]. Reasonable distributions of β0, β2, γ, μ and α (see Table 1 for mean and standard deviation) were either assumed or obtained from the analyses. A uniform distribution was used for γ and a truncated (at 0; to ensure positivity) normal distribution for the parameter μ with its mean and variance as computed earlier (Figure 2). A random sample was taken from the distributions for γ (for each k=1 to 19) and μ. An estimate for α was obtained from substituting this random sample in Equation (6). The sample set, (γ, μ, α), was further used for obtaining estimates for β0, and β2 as mentioned earlier.
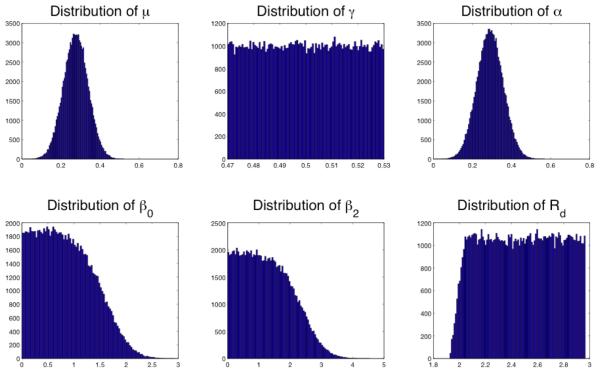
Figure 2.
Frequency distributions of the parameters including Rd when sampling γ from uniform distributions with mean 0.28. The overall shape of the distribution remains same for the cases when mean of γ-distribution was 0.50 and 0.83. Distributions were calculated from one of the 10 Monte-Carlo samples, each of size 105 sampled parameter values using approach described in the text. Horizontal axis has parameter values, and vertical axis represents frequencies in the graphs.
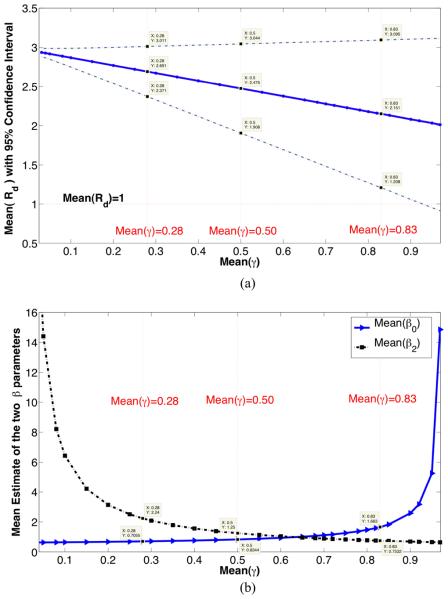
105 independent samples of the vector (β0, β2, μ, α, and γ) were generated using the above method via Monte Carlo sampling. An empirical frequency distribution for Rd as a function of the variability of the five parameters, using Equation (5), was derived from these samples. This entire sampling procedure was repeated 10 times for robustness. Table 1 collects the mean estimates. An empirical distribution (generated when γ was sampled from a uniform distribution with mean 0.28) of Rd and its parameters are shown in Figure 2. Figure 3(a) shows the Rd mean estimates and their variances as the assumed mean of γ varies from 0 to 1.
Figure 3.
Variation in estimates of parameters with change in distribution of γ.
Figure 3(a): Uncertainty in Rd when Mean(γ) is varied.
Figure 3(b): Variation in estimated values of β0 and β2 with change in γ estimates.
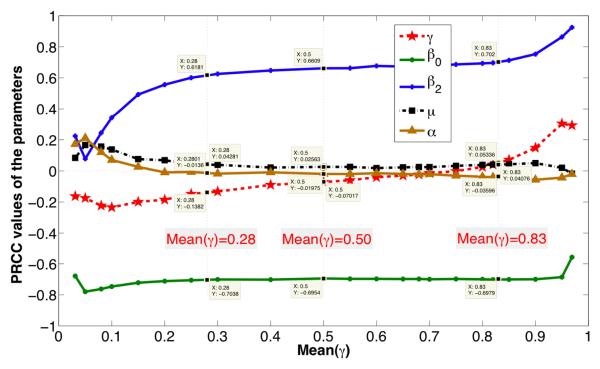
Partial rank correlation coefficients (PRCC) were calculated to estimate the size of correlations between values of Rd and the five model parameters across 105 random draws from the empirical distribution of Rd and its associated parameters. A large PRCC is indicative of high sensitivity to parameter estimates while a small PRCC reflects low sensitivity [34,35]. The PRCC of Rd with respect to each parameter was calculated using a sequence of regression models [30] and the results are shown in Figure 4 (with varying mean γ value). The signs of PRCC values determine whether a parameter is directly or inversely correlated with Rd.
Figure 4.
Sensitivity (measured by PRCC values) of the Rd with respect to its parameter when Mean(γ) is varied.
RESULTS
The results in Figure 3 and 4 were obtained under the assumption that the observed drinking levels are at steady state. These steady state drinking levels are computed using the data in Table 4. The estimates of β0, β2 and γ from our calculations are inter-related, that is, the same distribution of drinking patterns can be obtained by different combinations of β0, β2 and γ. Figure 3(b) shows that if the residence time of moderate drinkers in high-risk environments (γ) is high, then light drinkers are predominantly mixing with moderate drinkers in low-risk environments (β0 is high and β2 is low). If γ is low (i.e., moderate drinkers spend less time in high-risk environments) then light drinkers predominantly mix with M2-drinkers (β0 is low and β2 is high). Communities where moderate drinkers have higher average residence times in high-risk environments may insulate light drinkers from interactions with moderate drinkers. Communities where moderate drinkers have higher average residence times in low-risk environments may activate interactions between light and moderate drinkers. Over the broad range of γ this effect is rather subtle, but suggests that moderate drinkers spending more time in high-risk drinking environments will have less influence on light drinkers as light drinkers are less likely to be found in these environments by assumption. When γ is about 0.5, both β0 and β2 are low, that is, interactions between light and moderate drinkers will be relatively low in the presence of substantial movement of moderate drinkers between environments.
The mean estimate of the reproductive number is uniformly greater than 1.00 (but less than 3.00) for all values of γ (Figure 3a). The 95% CI for this measure drops below 1.00 only when γ > 0.90. The mean estimate of the reproductive number is greater than 2.00 for the two estimated values ofγ (Table 1). A large reproductive number means that the total rate of conversion to the heavy drinking state is high. The more time a moderate drinker spends in high-risk environments the less drinking-influence he/she will have on light drinkers, so Rd decreases with increasing values of γ. However, the variability in the Rd estimates increases with increases in γ. Highly connected (i.e., γ = 0.5) environments in which moderate drinkers shift back-and-forth from low-risk to high-risk environments give an Rd estimate of 2.4 (95% CI, 1.91 to 3.04). In fact, we see that if γ≤0.47, then the probability that Rd will lie between 2 and 3 is effectively 1.00. This probability is reduced to 0.5 as γ→1. That is, as moderate drinkers spend more time in high-risk environments the reproductive number for conversions of light drinkers to moderate state decreases towards 1.00.
Rd is most sensitive to changes in the social influence parameters β0 and β2. When γ≤0.81, β0 is most influential on Rd. However, when γ > 0.81, β2 becomes the most influential parameter (Figure 4). Whenever E1 and E2 are highly connected (i.e, γ=0.5), the ranking of the parameters in decreasing order of their sensitivities to Rd is β0 (−0.69), β2 (+0.66), γ (−0.07), μ (+0.02), and α (−0.01). When γ≤0.68 the residence time parameter (γ) is the next most crucial parameter after β0 and β2. γ remains influential even when γ>0.81, but its influence on Rd is direct (not inverse as is the case when γ≤0.68; Figure 4). The rate of progression of moderate drinkers to the heavy drinking class (α) and the arrival/departure rate of drinkers to/from the system (μ) are least important when it comes to assessing the variation of Rd for most γ values.
DISCUSSION
We studied the drinking reproduction number (Rd), which measures the average number of additional moderate drinkers generated by a moderate drinker when introduced into a population of mostly light drinkers. Rd turned out to be much greater than 1 over broad ranges of values of γ, the proportion of time spent by a moderate drinker in high-risk environments. For example, the near-exclusive use of high-risk venues by moderate drinkers (γ near 1) only seems to alter the dynamics of heavy drinking population, that is, the isolation of light drinkers from the influence of moderate drinkers is effective in reducing heavy drinkers in the population.
The strength of local social mixing and the movement of drinkers are more crucial to drinking dynamics than the progression rates to heavy drinking or the college dropout and matriculation rates. Assessment of the correlations between Rd and each of the model parameters show that the parameter associated with the local social interactions between moderate and light drinkers in low-risk drinking environment is inversely related to Rd. Specifically, the increased mobility of moderate drinkers between environments facilitates the establishment of heavy drinking communities in college populations, while drinking sustainability is driven by the strength of local mixing in low-risk environments and socialization among drinkers outside the drinking environments.
This simple model captures relevant real world processes and shows how relatively few assumptions can account for the development of heavy drinking behavior while providing useful insights on which effective and lasting interventions can be built. Specifically, the dynamic model presented here supports the use of environmental interventions that focus on high-risk settings in and around college campus. This work suggests that interventions aimed at altering observed patterns of socialization (e.g., through residence hall assignments or fraternity and sorority recruiting policies) hold particular promise. Indeed, there is some evidence that establishing substance-free housing for students is, in fact, tied to lower alcohol consumption [36,37].
In conclusion we should note some of the limiations of the model presented and possible directions for future research. First, our model took account of just two contrasting social contexts (incorporating both on- and off-campus venues) that cater to the college drinking population and we addressed how various enviornmental factors collectively affect drinking patterns. While such a model could serve as an example for studies of other questions such as between-campus differences, one would need data from specific settings to study any one particular campus. In the present study we simply used data from various sources and tried to draw conclusion about a “typical” campus. Indeed, one of the goals of this paper was to highlight the type of data sets that may be needed to estimate parameters of the dynamic model of the form used here. One substantive concern in this regard is the absence of adequate data on selection of drinking environments, the reciprocal relationships of selection on drinking itself, and social mixing and influences that take place among drinkers and non-drinkers in those locations.
Second, in the present simple form of the model, moderate drinkers retained their identity outside the drinking environments but the model still included the influence of high-risk moderate drinkers on light drinkers outside the high-risk environments. We did not consider explicitly the movement and transition of drinkers and non-drinkers in non-drinking environments. The need to introduce additional non-drinking environments in which these influences occur, perhaps between drinking and non-drinkers classes, should be tested in future models.
Finally, the model would be strengthened, were it to include parameters that quantify the average residence times of different types of drinkers, the progression rates from one form of drinking to another, the proportion of new recruits into each drinking class and the strength of social influences in different venues. However, these contextual aspects of college drinking are largely absent from the college drinking literature and hence we must use frameworks and definitions that can be connected to current data. In future we hope to carry out surveys to estimate these parameters for understanding college drinking dynamics using complex models of a similar type.
ACKNOWLEDGMENTS
This work has been mainly supported by NIAAA grant on Ecosystem Models of Alcohol-Related Behavior”, Contract No HHSN2S1200410012C, ADM; Contract No. No1AA410012, Prevention Research Center (PIRE) at Berkeley. It was also partially supported by National Science Foundation (Grant DMS-0441114), National Security Agency (Grant H98230-05-1-0097), The Alfred P. Sloan Foundation (through the ASU-Sloan National Pipeline Program in Mathematical Science), The Office of the Provost of Arizona State University and Los Alamos National Laboratory.
Footnotes
DECLARATIONS OF INTEREST
None.
References
- 1.Clapp JD, Lange JE, Min JW, Shillington A, Johnson M, Voas RB. Two studies examining environmental predictors of heavy drinking by college students. Prevention Science. 2003;4:99–108. doi: 10.1023/a:1022974215675. [DOI] [PubMed] [Google Scholar]
- 2.Chaloupka FJ, Wechsler H. Binge drinking in college: The impact of price availability and alcohol control policies. Contemporary Economic Policy. 1996;14:112–124. [Google Scholar]
- 3.Scribner R, Mason K, Theall K, Simonsen N, Schneider SK, Towvim LG, DeJong W. The contextual role of alcohol outlet density in college drinking. J Stud Alcohol Drugs. 2008;69:112–120. doi: 10.15288/jsad.2008.69.112. [DOI] [PubMed] [Google Scholar]
- 4.Gruenewald PJ. Why do alcohol outlets matter anyway? A look into the future. Addiction. 2008;103(10):1585–1587. doi: 10.1111/j.1360-0443.2008.02332.x. [DOI] [PubMed] [Google Scholar]
- 5.Clapp JD, Reed MB, Holmes BA, Lange JE, Voas RB. Drunk in public, drunk in private: the relationship between college students, drinking environments and alcohol consumption. American Journal of Drug and Alcohol Abuse. 2006;32:275–285. doi: 10.1080/00952990500481205. [DOI] [PubMed] [Google Scholar]
- 6.Demers A, Kairouz S, Adlaf E, Gliksman L, Newton-Taylor B, Marchand A. Multilevel analysis of situational drinking among Canadian undergraduates. Social Science and Medicine. 2002;55:415–424. doi: 10.1016/s0277-9536(01)00258-1. [DOI] [PubMed] [Google Scholar]
- 7.Harford TC, Wechsler H, Seiberg M. Attendance and alcohol use at parties and bars in college: a national survey of current drinkers. Journal of Studies on Alcohol. 2002;63:726–733. doi: 10.15288/jsa.2002.63.726. [DOI] [PubMed] [Google Scholar]
- 8.Mubayi A, Greenwood P, Castillo-Chavez C, Gruenewald P, Gorman DM. Impact of relative residence times in highly distinct environments on the distribution of heavy drinkers. Socio-Economic Planning Sciences. 2010;44(1):1–12. doi: 10.1016/j.seps.2009.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Anderson RM, May R. Infectious diseases of humans: dynamics and control. Oxford University Press; Oxford: 1991. [Google Scholar]
- 10.Brauer F, Castillo-Chavez C. Mathematical Models in Population Biology and Epidemiology (Applied Texts in Mathematics, 40) Springer-Verlag; New York: 2001. [Google Scholar]
- 11.Patten SB, Arboleda-Florez JA. Epidemic theory and group violence. Social Psychiatry and Psychiatric Epidemiology. 2004;39:853–856. doi: 10.1007/s00127-004-0867-9. [DOI] [PubMed] [Google Scholar]
- 12.Penzar D, Srbljinovic A. Dynamic modeling of ethnic conflicts. International Transactions in Operational Research. 2002;11:63–76. [Google Scholar]
- 13.Bettencourt LMA, Cintron-Arias A, Kaiser DI, Castillo-Chavez C. The power of a good idea: Quantitative modeleing of the spreaed of ideas from epidemiological models. Physica A. 2006;364:513–36. [Google Scholar]
- 14.Behrens DA, Caulkins JP, Tragler G, Haunschmied JL, Feichtinger G. A dynamic model of drug initiation: implications for treatment and drug control. Mathematical Biosciences. 1999;159:1–20. doi: 10.1016/s0025-5564(99)00016-4. [DOI] [PubMed] [Google Scholar]
- 15.Braun RJ, Wilson RA, Pelesko JA, Buchanan RB, Gleeson JP. Application of small-world network theory in alcohol epidemiology. Journal of Studies on Alcohol. 2006;67:591–599. doi: 10.15288/jsa.2006.67.591. [DOI] [PubMed] [Google Scholar]
- 16.Cintron-Arias A, Sanchez F, Wang X, Castillo-Chavez C, Gorman DM, Gruenewald PJ. The role of nonlinear relapse on contagion amongst drinking communities. In: Chowell, et al., editors. Mathematical and statistical estimation approaches in epidemiology. Springer; New York: 2008. pp. 343–60. [Google Scholar]
- 17.Caulkins JP, Reuter P. Illicit drug markets and economic irregularities. Socio-Economic Planning Sciences. 2006;40:1–14. [Google Scholar]
- 18.Hawkins RC, Hawkins CA. Dynamics of substance abuse: implications of chaos theory for clinical research. In: Chamberlain L, Butz M, editors. Clinical Chaos: a Therapist's Guide to Non-Linear Dynamics and Therapeutic Change. Brunner/Mazel; Philadelphia: 1998. pp. 89–101. [Google Scholar]
- 19.Sanchez F, Wang X, Castillo-Chavez C, Gorman DM, Gruenewald PG. Drinking as an epidemic: a simple mathematical model with recovery and relapse. In: Witkiewitz K, Marlatt GA, editors. Guide to Evidence-Based Relapse Prevention. Academic Press; New York: 2007. pp. 353–68. [Google Scholar]
- 20.Anderson RM, May RM. Epidemiological Parameters of HIV Transmission. Nature. 1988;333:514–522. doi: 10.1038/333514a0. [DOI] [PubMed] [Google Scholar]
- 21.Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: Virion clearance rate, infected cell lifespan, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 22.Powell LM, Williams J, Wechsler H. Study habits and the level of alcohol use among college students. Educ. Econ. 2004;12:135–149. [Google Scholar]
- 23.Wolaver AM. Effects of heavy drinking in college on study effort, grade point average, and major choice. Contemp. Econ. Policy. 2002;20:415–428. [Google Scholar]
- 24.Wood PK, Sher KJ, Erickson DJ, Debord KA. Predicting academic problems in college from freshman alcohol involvement. J. Stud. Alcohol. 1997;58:200–210. doi: 10.15288/jsa.1997.58.200. [DOI] [PubMed] [Google Scholar]
- 25.Engs RC, Hanson DJ. Boozing and brawling on campus: a national study of violent problems associated with drinking over the past decade. Journal of Criminal Justice. 1994;22(2):171–180. [Google Scholar]
- 26.Engs RC, Hanson DJ, Diebold B. The drinking patterns and problems of a national sample of college students, 1994: Implications for education. Journal of Alcohol and Drug Education. 1997 spring. [Google Scholar]
- 27.Casella G, Berger RL. Statistical Inference. 2nd ed. Duxbury press; 2002. [Google Scholar]
- 28.Paschall MJ, Saltz RF. Relationships between college settings and student alcohol use before, during, and after events: A multi-level study. Drug and Alcohol Review. 2007;26:639–648. doi: 10.1080/09595230701613601. [DOI] [PubMed] [Google Scholar]
- 29.Saltz R, Paschall MJ, McGaffigan RM, Nygaard P. Alcohol risk management in college settings: the Safer California Universities project. 2009 doi: 10.1016/j.amepre.2010.08.020. under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mubayi A. The role of environmental context in the dynamics and control of alcohol use. Arizona State University; Tempe: 2008. PhD dissertation. [Google Scholar]
- 31.Blower SM, Dowlatabadi H. Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model as a example. International Statistical Review. 1994;62:229–243. [Google Scholar]
- 32.Nuno M, Feng Z, Martcheva M, Castillo-Chavez C. Dynamics of two-strain with isolation and partial cross-immunity. SIAM J. Appl. Math. 2006;65(3):964–982. [Google Scholar]
- 33.Sanchez MA, Blower SM. Uncertainty and sensitivity analysis of the basic reproduction number: Tuberculosis as an example. American Journal of Epidemiology. 1997;145(12):1127–1137. doi: 10.1093/oxfordjournals.aje.a009076. [DOI] [PubMed] [Google Scholar]
- 34.Helton JC. Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal. Reliability Engineering and System Safety. 1993;42:327–367. [Google Scholar]
- 35.Saltelli A, Chan K, Scott M. Sensitivity analysis. John Wiley & Sons; Chichester: 2000. [Google Scholar]
- 36.Wechsler H, Lee JE, Nelson TF, Lee H. Drinking levels, alcohol problems and secondhand effects in substance-free college residences: Results of a national study. J. Stud. Alcohol. 2001;62:23–31. doi: 10.15288/jsa.2001.62.23. [DOI] [PubMed] [Google Scholar]
- 37.Wechsler H, Lee JE, Nelson TF, Kuo M. Underage college students' drinking behavior, access to alcohol, and the influence of deterrence policies: Findings from the Harvard School of Public Health College Alcohol Study. J. Amer. Coll. Hlth. 2002;50:223–236. doi: 10.1080/07448480209595714. [DOI] [PubMed] [Google Scholar]