Characterization of Proteins with Wide-angle X-ray Solution Scattering (WAXS)

Abstract

X-ray solution scattering in both the small-angle (SAXS) and wide-angle (WAXS) regimes is making an increasing impact on our understanding of biomolecular complexes. The accurate calculation of WAXS patterns from atomic coordinates has positioned the approach for rapid growth and integration with existing Structural Genomics efforts. WAXS data are sensitive to small structural changes in proteins; useful for calculation of the pair-distribution function at relatively high resolution; provides a means to characterize the breadth of the structural ensemble in solution; and can be used to identify proteins with similar folds. WAXS data are often used to test structural models, identify structural similarities and characterize structural changes. WAXS is highly complementary to crystallography and NMR. It holds great potential for the testing of structural models of proteins; identification of proteins that may exhibit novel folds; characterization of unfolded or natively disordered proteins; and detection of structural changes associated with protein function.

Introduction

X-ray solution scattering in both the small-angle (SAXS) and wide-angle (WAXS) regimes is making an increasing impact on our understanding of biomolecular complexes. Solution scattering is highly complementary to crystallography and NMR and is well positioned to address bottlenecks in structural genomics efforts and contribute to research in proteomics and systems biology (Hura et al., 2009). The SAXS regime is usually defined as extending to scattering angles that correspond to spacings of ~ 15–20 Å (q ~ 0.3Å⁻¹; where q is the momentum transfer, 4πsin(θ/2)/λ, and θ is the scattering angle). WAXS extends data present in the SAXS regime out to scattering angles comparable to those used in crystallographic studies (q ~ 2.5 Å⁻¹). This extension is not trivial, as intensity of scattering is 1–3 orders of magnitude weaker than in the SAXS regime. Furthermore at scattering angles beyond q ~ 1.0 Å⁻¹ contribution from solvent scattering is increasingly intense. For instance, solvent scattering from a 10 mg/ml solution of carbonmonoxy-hemoglobin is roughly 40% as intense as the SAXS data extrapolated to zero angle for this sample; whereas scattering from protein in this solution at q ~ 2 is 0.1–0.2 % that of the small angle scattering or 0.25 – 0.5% as intense as the solvent scattering on which it is superimposed. Although WAXS data is significantly weaker than SAXS data, it can be collected using less than 100 μl of solution with protein concentrations as low as 5 to 10 mg/ml in less than 10 seconds with the high fluxes routinely available at a synchrotron x-ray source.

SAXS is used for rapid determination of radius of gyration (Rg); low resolution molecular envelopes, and the pair-distribution function (Putnam et al., 2007; Forster et al., 2008). Rg provides insight into the molecular weight – and thereby the oligomerization state – of the protein in solution. Low-resolution ab initio shape determinations provide information about the oligomeric form and assembly of complexes (Chacon et al., 2000; Svergun et al., 2001; Takahashi, et al., 2003). The pair distribution function, essentially a histogram of the interatomic vector lengths, can provide insight into the relative placement of subunits and the nature of structural changes carried out during protein function or induced by ligand binding or changes in environment. Comparison with crystallographic structures greatly enhances the power of these methods which enables, for instance, identifying of disordered regions or studying the unfolding of proteins in solution (Tsutakawa et al., 2006).

Extraction of information from a WAXS pattern represents a different challenge. The information content of a solution scattering pattern is approximately linear in q meaning that WAXS data has, in principle, several times the amount of information contained in a SAXS pattern. However, direct calculation of high resolution structural features from WAXS data is precluded because the information required for a full three dimensional reconstruction of a structure increases as q³. Consequently, WAXS data is often used indirectly to test structural models, identify structural similarities and characterize structural changes. WAXS data is particularly sensitive to small structural changes in proteins (Tiede et al., 2002; Hirai et al., 2004; Fischetti et al., 2004b; Rodi et al; 2007); useful for calculation of the pair-distribution function at relatively high resolution; provides a means to characterize the breadth of the structural ensemble in solution (Tiede et al 2002; Makowski et al., 2008a); and can be used to identify proteins with similar folds (Hirai et al., 2002; Sokolova et al., 2003a; 2003b; Petoukhov and Svergun, 2005; Makowski et al., 2008b).

Use of WAXS in conjunction with crystallography and other structural methods is particularly effective due to the capability of calculating WAXS patterns from atomic coordinate sets. This makes it possible to use WAXS data to test detailed molecular models of a system. Furthermore, as we will see, use of an exhaustive data base of WAXS patterns may provide a basis for generating a limited set of possible folds for a protein on the basis of its WAXS pattern alone and will make possible identification of proteins that have a high probability of exhibiting a novel fold; providing information highly complementary to ongoing Structural Genomics efforts.

In this paper, the essentials of WAXS data collection and analysis are outlined and demonstrated for specific examples; and the potential impact of WAXS on structural genomics efforts is discussed.

Materials and Methods

Collection of WAXS Data

Wide-angle x-ray scattering (WAXS) data is most effectively collected at a synchrotron source providing a high intensity, highly collimated, monochromatic beam using a two-dimensional detector and automated sample handling robot. The data reported here were collected at the BioCAT undulator beam line (18ID) at the Advanced Photon Source (APS) (Fischetti et al., 2004a). The experimental layout has been previously described (Fischetti et al., 2004b). The sample cell consisted of a thin-walled quartz capillary (1 or 1.5 mm inside diameter) attached to a programmable pump adjusted to deliver continuous flow through the capillary during data collection, in order to limit x-ray exposure of any given protein to under 100 milliseconds as required to minimize radiation damage (Fischetti et al., 2003). The x-ray scattering pattern was recorded with a MAR165 2k x 2k CCD detector and specimen-to-detector distance was approximately 170 mm. In most cases, a data set consisted of a series of 1 second exposures including 5 from buffer, 5–10 from protein solution and 5 from the empty capillary. Exposures from sample and buffer were alternated to minimize the possible effects of drift in any experimental parameter. Incident beam flux was monitored using nitrogen gas filled ion chambers. Integrated beam flux during each exposure was used to scale scattering from protein solutions with scattering from buffer solutions. Collection of multiple independent data sets allowed calculation of standard deviation at each scattering angle, and error propagation formulae were used to calculate the effect of errors on the final estimate of scattering from protein.

Scattering Data Analysis

The two dimensional scattering patterns were integrated radially to one-dimensional scattering intensity profiles using the program Fit2D (Hammersley, 1997; 1998). Scattering from samples were separable into three components: that due to scattering from the protein (including associated hydration layer); the bulk solvent; and the capillary. Scattering from protein was estimated according to:

$${\text{I}}_{\text{prot}}={\text{I}}_{\text{obs}}-{\text{I}}_{\text{cap}}-(1-{\text{v}}_{\text{ex}}){\text{I}}_{\text{solvent}}$$ (1)

where I_obs was the measured scattering from the protein sample; I_cap the measured scattering from the empty capillary; v_ex is the proportion of the solution occupied by the protein (excluded volume), and I_solvent was estimated by

$${\text{I}}_{\text{solvent}}={\text{I}}_{\text{bkgd}}-{\text{I}}_{\text{cap}}$$ (2)

where I_bkgd is the measured scattering from the buffer-filled capillary. Scattering from empty capillary does not adequately reflect the scattering it contributes when the capillary is filled with buffer or protein solution, due to absorption of scattering by buffer and/or protein. This was accounted for by modeling the capillary scatter as

$${\text{I}}_{\text{cap}}={(\text{scale}\text{factor})}^{\ast }{\text{I}}_{\text{cap}}(\text{observed})+\text{constant}(\text{absorption}\text{correction})$$ (3)

The scale factor and constant were selected by empirically fitting the capillary scatter to the scatter from buffer-filled capillary in the scattering range q = 0.3 to 1.0 Å⁻¹ since scatter from buffer is negligible in this range (Makowski et al., 2008a).

An alternate measure of scattering from protein is the excess intensity calculated using

$${\text{I}}_{\text{excess}}={\text{I}}_{\text{obs}}-{\text{I}}_{\text{cap}}-{\text{I}}_{\text{solvent}}$$ (4)

In practice, this weighting of the solvent scattering results in the excess intensity being negative for q >2.0 (scattering from solvent is, in general, stronger than that from protein in this region). The advantages of I_excess are that (i) it results in a measure of intensity directly comparable to that generated using the program EXCESS (Park et al., 2009; see below); and (ii) experimental determination of excluded volume is not required, and errors due to inaccuracies in estimation of protein concentration are eliminated.

Calculation of Solution Scattering from Atomic Coordinates –Continuum Models

The development of a rapid method for calculating solution scattering patterns from atomic coordinates has been crucial to the evolution of SAXS into a method of widespread impact in structural biology. CRYSOL (Svergun et al., 1995), the most widely used of the software packages available for carrying out this calculation, has had very broad and important impact on the community. Along with the development of ab initio methods for shape determination (Chacon et al., 2000; Svergun et al., 2001), it has provided substantial impetus for the growth of SAXS in structural biology. A recent alternative approach that provides quick calculation of SAXS data from atomic coordinates using a coarse grained model of protein structure appears to provide an important alternative to CRYSOL for calculation of moderate angle scattering from large complexes (Yang et al., 2009).

At first glance, the calculation of solution scattering from a protein should be easily and accurately carried out using the Debye formula that expresses the scattered intensities as a weighted sum of all the inter-atomic vectors in the protein. That this does not provide an adequate estimate of scattering from a protein is due to the fact that the protein is immersed in solvent (e.g. Lattman, 1989). This introduces two additional considerations; the effect of the exclusion of water from the interior of the protein; and the effect of the solvation layer which has been shown by many investigators to have properties distinct from that of bulk water. When a continuum model of water is used, the volume from which water is excluded must be calculated and accounted for. This is often done using ‘dummy atoms’ centered at the positions of each atom of the protein and having a (negative) ‘weight’ proportional to the number of solvent electrons excluded by the atom (Fraser, Macrae and Suzuki, 1978). This approximation is adequate for the SAXS regime, but appears to introduce errors when used to calculate scattering at wider angles (Bardhan et al., 2009). The best approach to modeling excluded volume may be the cube method, introduced many years ago (Pavlov and Fedorov, 1983), but used sparingly because of the computational requirements. Recently, more efficient algorithms for its use along with ready access to greater computational power has motivated its re-consideration (Bardhan et al., 2009).

The solvation layer introduces further complications in the calculation of scattered intensity. The density of water in the immediate vicinity of a protein surface is greater than that of bulk by an amount that appears to depend on the chemical nature of the surface groups in the immediate vicinity. Estimates based on comparison of SAXS and small angle neutron scattering from proteins of known structure indicate that water in the first hydration layer has a density that, on average, is about 10% greater than that of bulk water (Svergun et al., 1998). Accounting for the effect of this layer is essential for accurate computation of solution scattering from proteins. In CRYSOL, the layer is modeled as uniform and of adjustable weight. This approach has been very successful for modeling SAXS data.

Although it has been adapted for use in WAXS, the computational assumptions used in CRYSOL appear inadequate for calculation of wide-angle scattering (Bardhan et al., 2009). The use of a continuum model of solvent does not lead to accurate calculation of WAXS scattering without the refinement of two free parameters; one relating to excluded volume and the other involving weighting of the solvation layer (Bardhan et al., 2009; Park et al., 2009). The optimum value of these parameters appears to depend on the nature of the protein surface and is, in general, different for each protein. Accurate calculation of solution scattering data beyond the SAXS regime requires consideration of the inhomogeneities of the solvation layer. Such a calculation may be done using a statistical approach to the distribution of water around different protein surface groups (J. Virtanen, T.R. Sosnick and K.K. Freed, personal communication), or it may use an explicit atomic representation of water (Park et al., 2009).

CRYSOL results in good agreement between calculated and observed WAXS scattering only when the parameters involved in defining the solvation layer and the excluded volume are allowed to vary. When this refinement is used, the agreement is often quite good. Interestingly, when differences in WAXS patterns are calculated using CRYSOL, they appear to correspond much more closely to experiment than the intensities themselves (Fischetti et al., 2004b). This observation provides confidence that differences among WAXS patterns calculated using CRYSOL will map onto differences obtained using experimental data when used to generate a representation of all possible WAXS patterns as demonstrated below.

Explicit Atom Representation of Water

A continuum description of water provides a reasonable model for the electron density distribution at ~ 50 Å resolution where the liquid has no apparent internal structure. Whether water can be treated as continuum at 10 Å resolution and beyond is less clear. Thus, it is not surprising that when the continuum-solvent representation is extended to the resolution of WAXS, significant and seemingly systematic discrepancies are found between the observed and calculated scattering patterns. Recently, a method has been developed for calculating WAXS patterns using an explicit atomic representation of water (Park et al., 2009), implemented in the program EXCESS. Starting with a set of atomic coordinates, a protein is computationally placed in a solvent ‘droplet’ ~ 7 Å larger than the protein in every direction. A short MD simulation is used to place solvation layer water molecules around the protein. Scattering from a set of protein-water structures are calculated and averaged, and from this average, the scattering from a comparable ensemble of pure solvent is subtracted, resulting in an estimate of I_excess precisely comparable to that obtained from experimental measurements using equation (4). The effect of excluded volume and solvation layer are implicitly contained in this formalism.

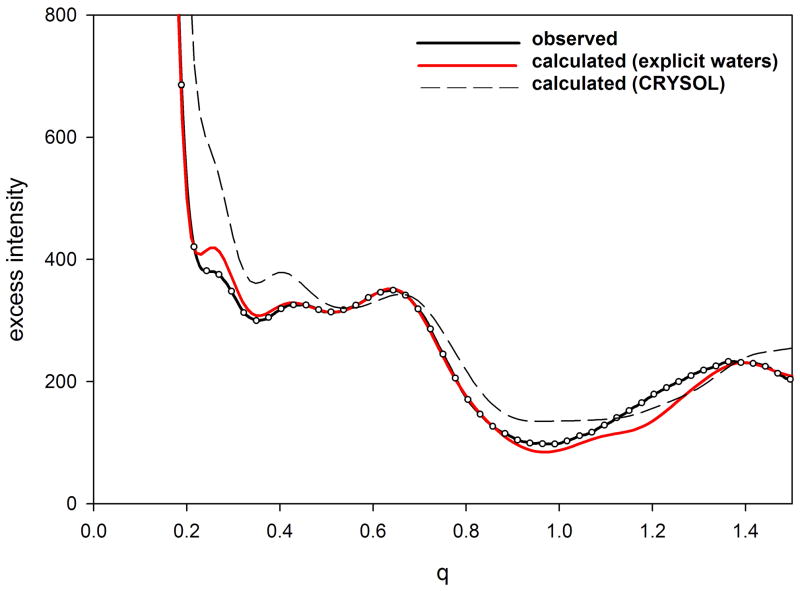
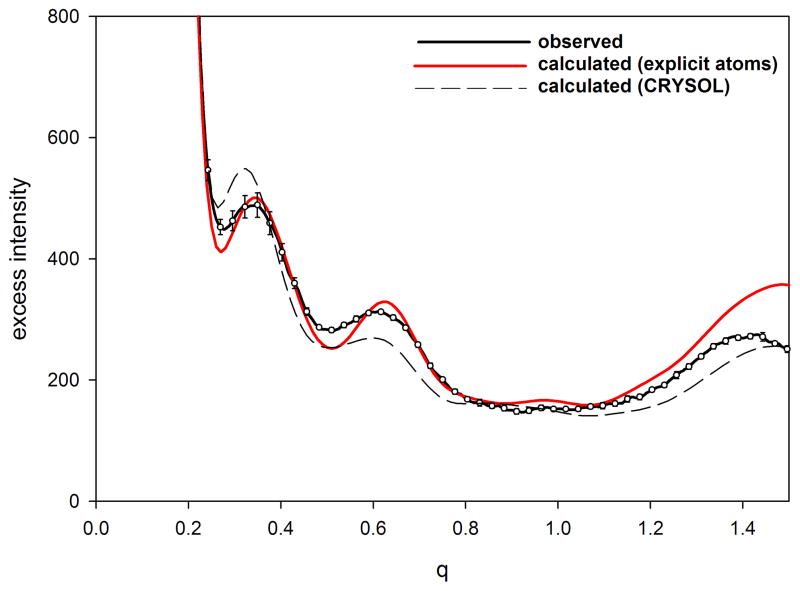
Use of this explicit water representation results in calculation of WAXS patterns that correspond very well with experiment (Park et al., 2009). in many cases, the calculated I_excess, falls within experimental errors out to a q > 1.0 Å⁻¹. At moderate angles (0.2 < q < 1.0 Å⁻¹), small discrepancies between calculated and observed take on a form expected to derive from fluctuations in the protein in solution (see figure 2; below). At wide angles (q >. 2.0 Å⁻¹), additional discrepancies appear to be due to errors in the scattering factor of water, issues that are being resolved in future updates of EXCESS. Current implementation of EXCESS is relatively computer intensive, with calculation of a WAXS pattern from a protein of moderate size requiring 12–24 hours of CPU time. More efficient algorithms for this calculation are under development.

Figure 2.

Comparison of observed and calculated I_excess from (a) equine myoglobin and (b) hen egg white lysozyme. Protein samples had a concentration of 20 mg/ml and a temperature of 20°C. Calculation was carried out with EXCESS using an explicit atomic representation of water (Park et al., 2009). Error bars represent the standard deviation of 10 exposures and cannot be seen in the data from myoglobin because they are smaller than the diameter of the circles representing the observations. To enhance representation of the error bars, only 10% of the measured intensities are plotted.

Results

Detection of Structural Changes due to Ligand Binding

The sensitivity of WAXS scattering to small changes in protein structure have led to its use in screening of functional binding of small molecule ligands to proteins (Rodi et al., 2007). The development of techniques to generate large libraries of target-focused probe chemicals coupled with the ever-increasing numbers of proteins entering screening programs via genome expression profiling, has intensified the need for novel rapid screening techniques that can pinpoint those molecules with biologically relevant properties. WAXS has proven effective (Fischetti et al, 2004; Rodi et al., 2007) for distinguishing between a functional binding event (that is accompanied by a change in protein structure) and non-functional binding (that generally does not alter the structure of the protein). The rationale for using WAXS to make this distinction is that any event that leads to a change in protein structure is likely to result in some modulation in protein function, whereas an event that does not alter protein structure is much less likely to alter function. WAXS has an advantage over other biophysical approaches in being sensitive to a very broad range of structural changes ranging from rigid-body rotation of domains, to hinge motions, closing of flaps, and the folding or unfolding of loops.

In most cases, the intensity change due to a ligand-binding-induced structural change is readily detectable. Figure 1 shows an example of WAXS patterns from a chemically synthesized HIV protease and the protease bound to the inhibitor MVT-101 bound (Torbeev and Kent, 2007). Error bars are standard deviations of 6 independently collected patterns. Increased uncertainties in the intensities at high q – evident in the figure - are due to subtraction of strong scattering from solvent at those spacings. The difference between the two curves at q = 0.4–0.5 Å⁻¹ is highly reproducible and 5–10 x greater than the standard errors. The reduced chi-square, χ_υ, (chi-square divided by the number of degrees of freedom) provides a reasonable measure of the similarity between the two curves and values greater than 1.0 indicate significant differences (Rodi et al., 2007). For the two curves in Figure 1, χ_υ = 1.44, indicating that the patterns are from solutions in which the proteins have distinctly different structures. It can be demonstrated that this intensity difference is due to the closing of the active site flaps in response to inhibitor binding.

Figure 1.

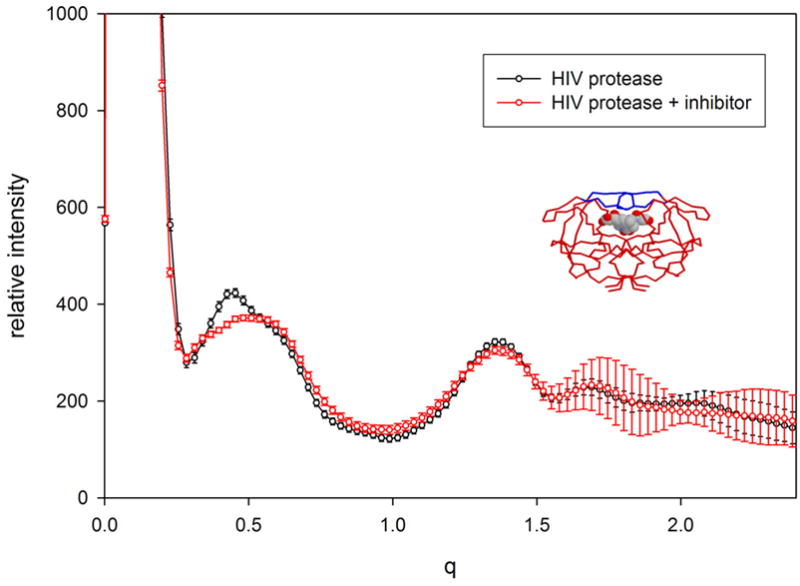
WAXS patterns from HIV protease (black) and HIV protease with the inhibitor MVT-101 bound (red). The differences between these two curves are statistically significant, being concentrated in the region q ~ 0.4 – 0.5, and reflecting the closing of the active site flaps in response to the binding of inhibitor. The inset is a rendering of the protease with the inhibitor represented as a space-filling model and the protein as a background tracing. In the apo form, the flaps (rendered blue in the inset) appear to exhibit substantial flexibility - movement that is required for entry of substrate (or inhibitor) into the active site. HIV protease was chemically synthesized and kindly provided by Vladimir Torbeev and Steve Kent (University of Chicago). Both samples had protein concentrations of 10 mg/ml. To enhance representation of the error bars, only 10% of the measured intensities are plotted.

Comparison of Calculated vs Observed WAXS Data

WAXS scattering from myoglobin and lysozyme as computed using an explicit atom representation of water (Park et al., 2009) are compare to observed patterns in Figure 2. The experiments were performed with 20 mg/ml solution of myoglobin and 25 mg/ml solution of lysozyme at 4 °C. For each protein, scattering intensities were measured seven times from the solution and four times from the pure buffer, from which the excess intensities and error bars were estimated. For both myoglobin and lysozyme there is excellent agreement between the simulated and observed data, except for some discrepancies beyond q = 1.2/Å. This level of agreement in the range of 0.05/Å < q < 1.2/Å, corresponding to length scales between 5 and 100 Å, is unprecedented and indicates that the atomistic-water method has correctly captured the nature of solvation around proteins that the previous continuum-water methods have missed. Error bars (standard deviation) for myoglobin are not visible in the plot because they are smaller than the diameter of symbols used to plot the measured intensities. The small deviation between calculated and observed at q ~0.25 Å⁻¹ may be due to structural fluctuations in the protein or small structural changes due to oxidation of the iron (data was collected from the met-form of myoglobin). Differences between calculated and observed intensities for lysozyme (figure 2b) are of the precise form expected from structural fluctuations (Makowski et al., 2008a).

Construction of ‘WAXS-space’

That WAXS data cannot be directly used to calculate the structure of a macromolecule or macromolecular complex makes development of indirect approaches essential. The knowledge-rich state of structural biology – partly generated through the structural genomics programs - makes the use of indirect approaches feasible. Our ability to accurately compute the WAXS patterns expected from a structure, combined with the availability of thousands of structures spanning the protein structure universe makes the construction of a ‘space’ of all possible WAXS patterns practical. Here we describe the construction and use of a pilot data base of WAXS patterns computed using CRYSOL. In spite of the shortcomings of CRYSOL for calculation of scattering patterns in the WAXS regime, as pointed out above, the differences between WAXS patterns calculated with CRYSOL appear to correspond well to observations (Fischetti et al., 2004b), implying that the structure of the space constructed from CRYSOL patterns will be analogous to that obtained using experimental data.

Although knowledge of the number of independent parameters defined by a WAXS pattern quantifies the information content (Makowski et al., 2008b), it provides little insight into how useful that information is in distinguishing between protein folds. The amount of information in a WAXS pattern that is relevant to distinguishing among protein structures can be estimated through the analysis of multiple WAXS patterns computed from crystallographic coordinates. To take this approach, we represent a WAXS pattern as a multi-dimensional vector with components that correspond to the intensities in the pattern. For instance, data extending to q = 1.2 Å⁻¹ sampled at intervals of 0.015 Å⁻¹ is equivalent to a vector in 80 dimensions. For virtually all proteins this constitutes oversampling (Shannon, 1949) as adjacent intensities sampled on this grid will not be independent. Nonetheless, this does not alter the results of the analysis, since the number of significant dimensions can be determined by a principal components analysis (PCA) that automatically discards redundant information (Lebart et al., 1984).

A data set suitable for PCA was constructed using 498 WAXS patterns calculated from atomic coordinates of domains selected to represent the broadest possible range of known folds (Hou et al., 2003). These small domains have typical characteristic dimensions of about ~35 Å which makes it appropriate to compare the information intrinsic to their distribution in WAXS-space with the results of a naïve sampling theorem calculation. A principal components analysis was carried out on the set of 498 vectors representing these WAXS patterns and corresponding eigenvectors and eigenvalues were obtained. The eigenvector corresponding to the largest eigenvalue represents the direction in WAXS-space that most completely distinguishes among the members of the set (in this case, the set of 498 WAXS patterns). Eigenvectors that correspond to small eigenvalues represent directions in this space that do not distinguish between patterns. The distribution of eigenvalues generated by this calculation implies an information content comparable to that obtained by a simple Shannon-type sampling analysis (Makowski et al., 2008b). This correspondence substantiates the analysis and suggests that all portions of a scattering pattern contribute to distinguishing among WAXS patterns from different proteins.

Distribution of Protein Folds in WAXS-space

The utility of WAXS patterns for characterization of protein folds is determined largely on the basis of the correlation between similarities in structure and proximity in WAXS space. The four major classes of protein structure (α; β; α/β and α+β) cluster well in WAXS space. Figure 3 exhibits the distribution of ~ 100 proteins representing these four classes according to their position along eigenvectors 2, 3 and 4. In this orientation of WAXS-space the α-proteins (red) are distributed to the right; the β-proteins (blue) to the upper left and the α/β proteins to the lower left. The α+β proteins (black) are largely at the interface of the three other classes. The segregation observed here is enhanced when additional dimensions are taken into account. This result provides some confidence that position in WAXS space can provide information about protein fold.

Figure 3.

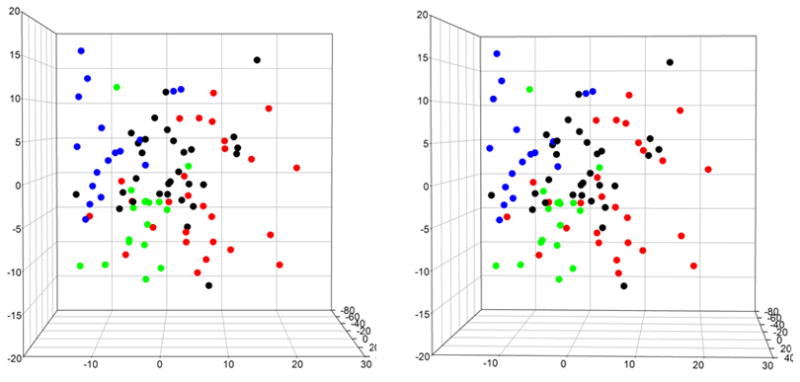
Stereo pair showing the distribution of α (red), β (blue), α/β (green) and α+β (black) proteins in WAXS space, projected onto the coordinates corresponding to the 2nd, 3rd and 4th most significant eigenvectors.

Disorder in proteins is increasingly recognized as both widespread and important for function. Since disorder will affect WAXS data, the position a protein holds in WAXS space will be affected by disorder. The degree to which disorder will influence the distribution of proteins in WAXS space has not been carefully examined. Small changes in intensity due to changes in the breadth of the structural ensemble have been observed (Makowski et al., 2008a). In the case of hemoglobin, for instance, these changes do not remove it from the region of WAXS space defined by the distribution of globins. Larger changes in intensity due to substantial change in disorder - as might occur in response to ligand binding - have the potential for moving a protein to an entirely new region of WAXS space. In the extreme case of scattering from completely denatured protein, scattering from all proteins looks very similar except for a radial scaling of the pattern due to differences in molecular weight.

Identification of Structural ‘Neighbors’ on the Basis of their WAXS Patterns

The concept of a protein fold is coming under increased scrutiny as more protein structures are generated, often introducing intermediate structures that are difficult to assign unambiguously to one fold or another, resulting in the blurring of boundaries between folds. The concept of ‘protein fold’ is thus becoming somewhat elusive (Honig, 2007); ‘There is no clear quantitative measure available as to how a fold should be defined’. Nevertheless, it is often clear that some proteins have ‘similar’ folds and others do not. A few examples may make this clearer.

The program DALI has been used extensively to generate a quatitative measure of the similarity or difference between two three-dimensional structures (Holm and Sander, 1995). This is often expressed as a Z-score. Generally, if a protein pair has a high Z-score as computed by DALI, they exhibit folds that are closely related to one another. In general, high Z-score correlate with co-localization in WAXS space (proteins have very similar WAXS patterns), implying that proteins that co-localize in WAXS space will have similar folds (Makowski et al., 2008b). How similar is ‘similar’, and what information can we extract from that similarity? Conversely, how dissimilar do two patterns have to be to provide evidence that they correspond to proteins with distinct folds?

Analysis of the distribution of the 498 domains, each representing a distinct fold, indicates that those proteins clustered together in WAXS space exhibit similar folds. For instance, 1hw1, a largely α-helical protein, has 6 neighbors within a distance of 10 (arbitrary) units in WAXS space. In Figure 4, the structures of 1hw1 and two of these nearest neighbors are rendered (the remaining 4 are also small, largely α-helical proteins). Although exhibiting distinct folds (as defined by Hou et al., 2003), these are all small, globular alpha helical proteins. Proteins giving rise to WAXS patterns that fall in this region of WAXS space are almost certain to exhibit a compact, largely α-helical fold.

Figure 4.

Clustering in WAXS space. Renderings of 1hw1 (left) and two of its nearest neighbors in WAXS space. These three domains are members of the 498 distinct domains chosen to represent all of fold space (Hou et al., 2003). Nonetheless, their structures are clearly related. Other proteins exhibiting WAXS patterns that place them in the region of WAXS space can be shown to have closely related folds.

Interestingly, oligomers appear to cluster with their constituent monomers in WAXS space. Hemoglobin, for instance, appears near myoglobin. This is not surprising, as an oligomer shares with the monomer all interatomic vectors confined to individual domains. The monomer lacks the longer, interdomain vectors, but in at least some cases, the intradomain vectors appear to dominate. The following example demonstrates the advantage of this property.

D-ribose binding protein was chosen arbitrarily to act as an ‘unknown’ to evaluate the information that could be generated from a comparison of its WAXS pattern with those in the Pilot Database. The PDB file 2DRI was used to calculate the corresponding WAXS pattern which was then compared to all WAXS patterns in the Pilot Database. The two patterns that most closely corresponded to the 2DRI pattern were those from 1trka3.pdb and 1pfka.pdb, the structures of which are show in Figure 5. Qualitatively, the structure of 1pfka (chain a of 1pfk) appears very similar to that of 2dri. 1trka (chain a of 1trk) appears to be made of two domains, at least one of which is quite similar in structure to 2dri. The CATH classification for both domains of 2DRI is a 3 layer (α−β−α) sandwich with a Rossman fold as is the case for 1pfk and for all domains of 1trk. It is a reflection of the nature of the information embedded in a WAXS pattern that a protein with different domain structure is a neighbor in WAXS space. In this particular case, the distribution of intra-domain vectors dominates the comparison. Given the similarities between these two nearest neighbors, one might reasonably conclude that there was a high probability that 2dri contains at least one Rossman fold. Given its molecular weight, the similar molecular weight of 1pfka and that of each domain of 1trka; one might further conclude that 2dri was most likely comprised of a pair of Rossman folds. From the similarities of the two nearest neighbors it would, at the very least, be safe to conclude that 2dri is unlikely to have a novel fold.

Figure 5.

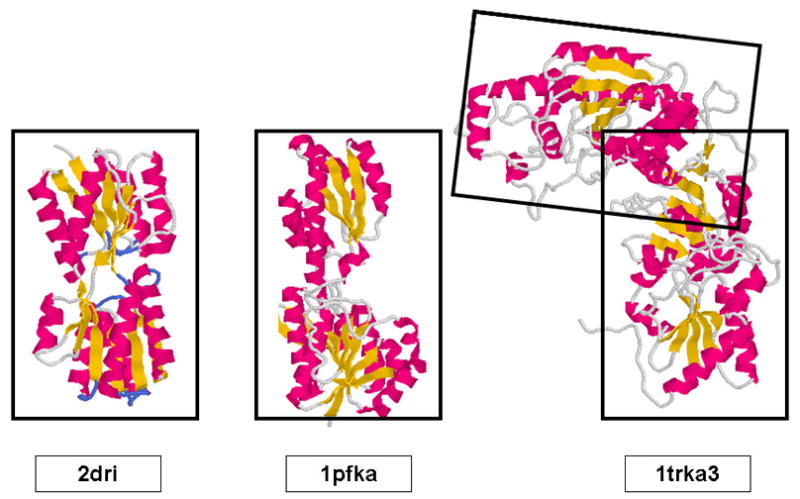
Comparison of the structure of 2dri with that of the A-chains of 1pfk and 1trk. Qualitatively, the structures of the domains of these three proteins appear to be very similar. 1trk consists of a pair of similar domains, each of which has similarities to 2dri.

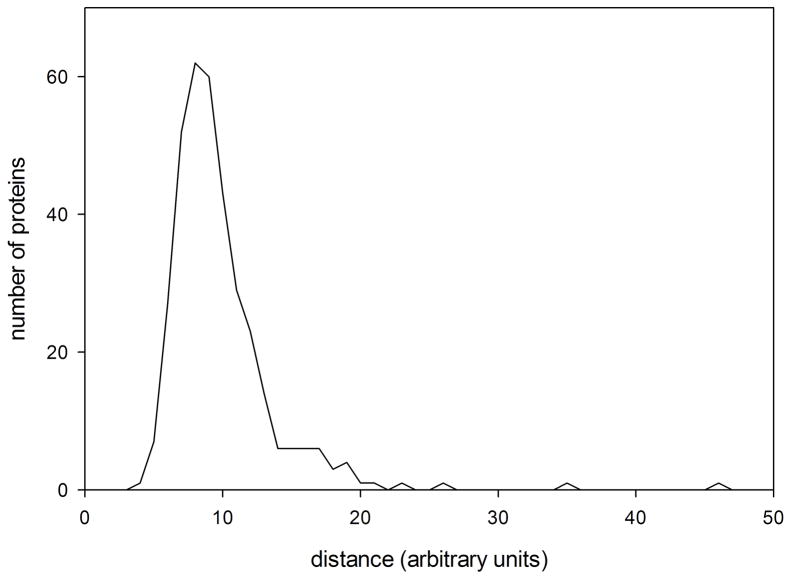
The histogram in Figure 6 represents the distribution of nearest neighbors among the 498 proteins exhibiting distinct folds and included in the Pilot Database. Recall that these 498 proteins were selected because they represent different folds. We refer to the peak position corresponding to the most likely nearest-neighbor distance between proteins with distinct folds as ΔW_f-f. If two proteins are separated by less than half ΔW_f-f in WAXS space, there is a high probability that they exhibit the same, or very closely related folds. If they are separated by more than ΔW_f-f, then there is a high probability that they exhibit different folds.

Figure 6.

Histogram of nearest neighbor distances between proteins representing different folds in the Pilot Database. On average, the nearest neighbors of proteins in this database are no more than 8–9 (arbitrary) units away. Proteins having the same folds are usually found closer to one another than that. Proteins more than 8–9 units from any protein of known structure may represent a novel fold.

Discussion

State of the Art

WAXS patterns from proteins, other macromolecules or macromolecular assemblies offers substantial promise as a source of structural and functional information that is difficult to obtain by other methods. It represents a technique complementary to crystallography and NMR that can provide information about protein structure and dynamics in solution under conditions not amenable to other techniques. Data collection at synchrotron sources has developed to the point where useful data can be collected from modest amounts of protein in a few seconds. Time-resolved studies are increasingly used to follow structural changes on the millisecond and faster time scales (Cammarata et al., 2008).

Analysis and interpretation of WAXS data are still evolving. Accurate calculation of scattered intensities from a set of atomic coordinates will be the keystone to these developments. For instance, the observation of intensity differences provides clear evidence of structural changes, but interpretation of these differences in terms of the form of structural change requires generation of structural models that can be tested by comparison with observations. Successful use of this information depends on reliable calculation of WAXS data from atomic coordinates. Generation of a computationally efficient, widely available version of EXCESS will provide substantial impetus to the use of WAXS data for a wide variety of applications.

Role in Molecular Dynamics

Molecular dynamics (MD) simulations have made substantial contributions to our understanding of protein motions and their range of application is rapidly expanding through the development of coarse graining and coordinated approaches involving both computation and experiment. MD provides an important adjunct to experimental approaches, enabling a richer interpretation of experimental data based on the detailed movements of specific structural elements in a protein (Lindorff-Larsen, et al., 2005). The time scales available to MD have been extended by coarse graining methods that employ simplified representations of a peptide (e.g. Trylska et al., 2007). The relatively short time frames accessible to all atom MD result in an insufficient sampling of the ensemble (Clarage et al., 1995). However, recently developed umbrella-sampling methods provide a more thorough view of the ensemble, generating a representative subset of structures valuable for computing WAXS patterns more accurately than possible with a single coordinate set (Lau and Roux, 2007). A current shortcoming of MD is the relative lack of experimental tests of the results. WAXS data can address this shortcoming through time resolved WAXS studies (e.g. Cammarat et al., 2008) or through characterization of the protein ensemble in solution (Makowski et al., 2008a). Although WAXS data has insufficient information to confirm all the quantities that can be derived from MD, they are capable of identifying aspects of the simulations that are not consistent with observation. The use of WAXS data to measure the range of motion exhibited by proteins in solution will provide important experimental tests of the results of MD simulations.

A functional state of a protein is not a single, rigid conformation, but rather an ensemble of structures or sub-states that are accessible to one another through relatively low-energy conformational transitions (e.g. Fraunfelder et al., 1991). A WAXS pattern reflects the structure of all proteins in the scattering volume, thereby including, implicitly, information about the ensemble. Comparison of an experimental WAXS pattern with that calculated from a single protein conformation – as in FIbure 2b - can provide explicit information about the spatial range of molecular motion in solution (Makowski, et al., 2008b).

Binding of a ligand shifts the relative abundance of different conformations, changing both the form and breadth of the ensemble and altering both the structural and dynamic properties of the protein. The form of the ensemble corresponding to a specific functional state anticipates the movements that are required to transition from one functional state to another (Vendruscolo and Dobson, 2006). For instance, the large-scale motions in substrate-free adenylate kinase preferentially follow pathways that create a configuration capable of proficient chemistry (Henzler-Wildman et al., 2007a; 2007b). Proteins have evolved low-energy pathways linking functionally important states and appear to undergo random fluctuations that preferentially explore them. The motions involved in transitions among the sub-states of an ensemble occur across multiple time scales. Fast, thermal motions of individual atoms take place on the pico- to nanosecond time scales. Large-scale conformational changes – slow concerted motions of larger structural elements that are often involved in functional activity - take place on the microsecond to millisecond time scale (e.g. Vendruscolo and Dobson, 2006). Slow conformational transitions appear to be facilitated by the high-frequency local fluctuations (McCammon et al., 1977; Henzler-Wildman et al, 2007a), explaining why regions that exhibit high crystallographic temperature factors or low order parameters in NMR experiments are frequently identified as being involved in functionally important conformational changes. Many conformational changes associated with function involve movement of relatively large substructures – domains, secondary structures or loops - and are thereby correspondingly slow. Measurement of the spatial extent of these motions is particularly pertinent to an understanding of protein function. The use of WAXS data to characterize the structural ensemble constitutes a direct experimental approach to the measurement of these motions.

Role in Drug Discovery

WAXS has potential for use as a routine screening tool for detection of functional interactions between proteins of therapeutic interest and small molecule ligands for the purposes of drug discovery and development. WAXS is a sensitive probe of structural change in proteins and can detect protein changes across all length scales relevant to protein-small molecule interactions (Fischetti et al., 2004b). It overcomes the shortcomings of many existing screening techniques. First, it does not require either the protein or the ligand to be immobilized, labeled or modified in any manner. Second, it detects structural changes, not binding per se. A binding event that causes no structural change is not likely to be functional. On the other hand, a binding event that causes a structural change in a protein has a high probability of altering the function of the protein in some way. Since WAXS detects structural changes rather than binding, it has a high probability of detecting those interactions that are functional. Third, it is an entirely generic assay. The process of screening is exactly the same no matter what the function of the protein under examination may be. This avoids the need to develop specific assays for every protein function to be examined. The process of lead discovery presents an early and significant bottleneck in the process of pharmaceutical drug design and slows the ultimate development of new therapeutic treatments. WAXS constitutes a new and powerful tool to impact this process.

Role in Structural Genomics

Structural Genomics efforts have had a substantial impact on our characterization of the universe of all protein structures (Baker and Sali, 2001). In spite of that, a large number of protein sequence families that have yet to be mapped onto structure space. Yan and Moult (2005) estimated that by the time 1000 microbial genomes have been sequenced we will have identified 250,000 protein families. ‘However, the vast majority of these families will be small, and it will be possible to obtain structural templates for 70–80% of protein domains with an achievable number of representative structures, by systematically sampling the larger families.’ Not surprisingly, the larger families are more likely to have structural coverage – although even for the large families, the probability of coverage is not greater than about 80%. The current release of Pfam (22.0) contains 9318 protein families (Finn et al., 2008). Nearly 40% of the largest 5000 families are not represented by solved structures. Characterization of these 1500–2000 families would have a huge impact on our vision of Protein Structure Space.

Given the persistent efforts of the Protein Structure Initiative Centers to impact these structurally-uncharacterized families, one can conclude that many of these will not soon be solved crystallographically or by NMR. This provides strong impetus for use of complementary methods for their characterization. A well organized SAXS pipeline can be used to determine size, shape and oligomeric state of the protein (Hura et al., 2009). Development of an extensive database of WAXS patterns that cover the known regions of structure space would provide a framework for assigning of possible folds for each of these unknown structures through the identification of neighbors in WAXS-space. This work would also identify those proteins with high probability of having a novel fold, thus providing specific targets worthy of increased effort.

The protein families not yet solved represent regions of sequence space that are far from any protein of known structure. Some of them will have structures very similar to those already known. Others will have completely novel folds. WAXS has the potential to be able to distinguish between these two possibilities as well as characterizing those proteins that fall between these two extremes. In some cases, it will be possible to identify ‘structural neighbors’ of the unknown protein- in other words, proteins with very similar folds. In other cases, it may be possible to identify the protein as natively unstructured. In almost all cases, some new information about the structure of an unknown protein can be generated. The effort per protein is relatively low. Less than a milligram of protein in an experiment that takes 1–2 minutes is adequate to collect WAXS data of sufficient quality to provide this information.

Conclusion

WAXS is a structural technique, highly complementary to crystallography and NMR, with great potential for the testing of structural models of proteins; identification of proteins that may exhibit novel folds; characterization of unfolded or natively disordered proteins; and detection of structural changes associated with protein function. The accurate calculation of WAXS patterns from atomic coordinates has positioned the approach for rapid growth and integration with existing Structural Genomics efforts.