Theoretical Models of Microvascular Oxygen Transport to Tissue

Abstract

To improve understanding of microvascular O₂ transport, theoretical modeling has been pursued for many years. The large number of studies in this area attests to the complexities (biochemical, structural, hemodynamic) involved. This article focuses on theoretical studies from the last two decades and, in particular, on models of O₂ transport to tissue by discrete microvessels. A brief discussion of intravascular O₂ transport is first given, highlighting the physiological importance of intravascular resistance to blood-tissue O₂ transfer. This is followed by a description of the Krogh tissue cylinder model of O₂ transport by a single capillary, which is shown to remain relevant in modified forms that relax many of the original biophysical assumptions. However, there are many geometric and hemodynamic complexities that require the consideration of microvascular arrays and networks. Multi-vessel models are discussed which have shown the physiological importance of heterogeneities in vessel spacing, O₂ supply, red blood cell flow path, as well as interactions between capillaries and arterioles. These realistic models require sophisticated methods for solving the governing partial differential equations, and a range of solution techniques are described. Finally, the issue of experimental validation of microvascular O₂ delivery models is discussed, and new directions in O₂ transport modeling are outlined.

Introduction

To support the energy requirements of vertebrate tissues, oxygen is transported from the lungs to individual cells via the circulatory system. This O₂ is primarily carried in the form of oxyhemoglobin, i.e., bound to the hemoglobin (Hb) molecules inside red blood cells (RBCs). The actual transfer of O₂ from RBCs to parenchymal cells, where it is utilized by mitochondria, is accomplished in the microcirculation. Therefore, it is crucial to understand the transport properties of the microvasculature in order to understand both normal physiological function and a number of diseases that involve the microcirculation. However, there are a number of complexities that make microvascular O₂ transport difficult to study, particularly when quantitative results are desired. The microvasculature has a very complicated three-dimensional spatial structure and a small scale (~1–100µm). Its structural complexity leads to heterogeneity in microvascular perfusion, and unique hemodynamic effects not seen in larger vessels (e.g., substantial variations in hematocrit) occur due to the fact that many vessel sizes are on the order of the RBC size. RBC perfusion heterogeneity in turn leads to heterogeneities in O₂ supply, tissue oxygenation, and O₂ consumption. These heterogeneities can have important physiological consequences (e.g., localized hypoxia), but since they are difficult to characterize experimentally (64), theoretical modeling has been used to study their effects. This theoretical work began with Krogh and Erlang (49), and was taken up again in the 1960s. The various aspects of steady-state and time-dependent O₂ transport that have been studied up to the late 1980s, from Hb-O₂ binding to whole-organ transport, were discussed very thoroughly by Popel (65). Here we mainly consider theoretical models of O₂ transport that have been used since that time and, in particular, concentrate on spatially distributed models at the level of single and multiple discrete microvessels. For the most part, compartmental models (e.g., (78)), models using continuous vessel descriptions (e.g., (71)), and models in artificial tissues (e.g., (82)) are not considered, and the focus is on tissue O₂ transport in skeletal muscle, heart, brain, and tumors. Both theoretical models and the results they were used to obtain are discussed.

This article begins with a brief discussion of intraerythrocyte and intravascular O₂ transport (see (65) and (34) for more details), including factors that determine intravascular resistance to blood-tissue O₂ transport. The original Krogh model of O₂ delivery by a single capillary is then presented and its main assumptions are listed. The importance of these is discussed; first in the context of single-vessel models (including time-dependent and multi-species cases), and then in terms of models that use multi-vessel arrays or networks and require sophisticated analytical or numerical solution techniques. Finally, experimental support for realistic modeling of microvascular O₂ transport and new directions in modeling are discussed.

Intraerythrocyte and Intravascular Transport Models

Red Blood Cells

Since most O₂ is carried in the blood bound to hemoglobin (Hb) inside red blood cells (RBCs), realistic modeling of microvascular O₂ transport requires a model of Hb-O₂ binding. This binding occurs in four steps, due to the fact that the Hb molecule has four O₂ binding sites (heme groups) that act cooperatively. A full description of the equilibrium binding (for models of Hb-O₂ binding kinetics, see (65)) therefore requires four experimental constants and is given by the Adair equation. However, the Adair equation cannot be inverted analytically, so the easily invertible Hill equation has been used in most theoretical models to describe fractional Hb-O₂ saturation (SO₂):

$$S(P)=\frac{P^n}{P^n+P_{50}^n}$$ (1)

(1)

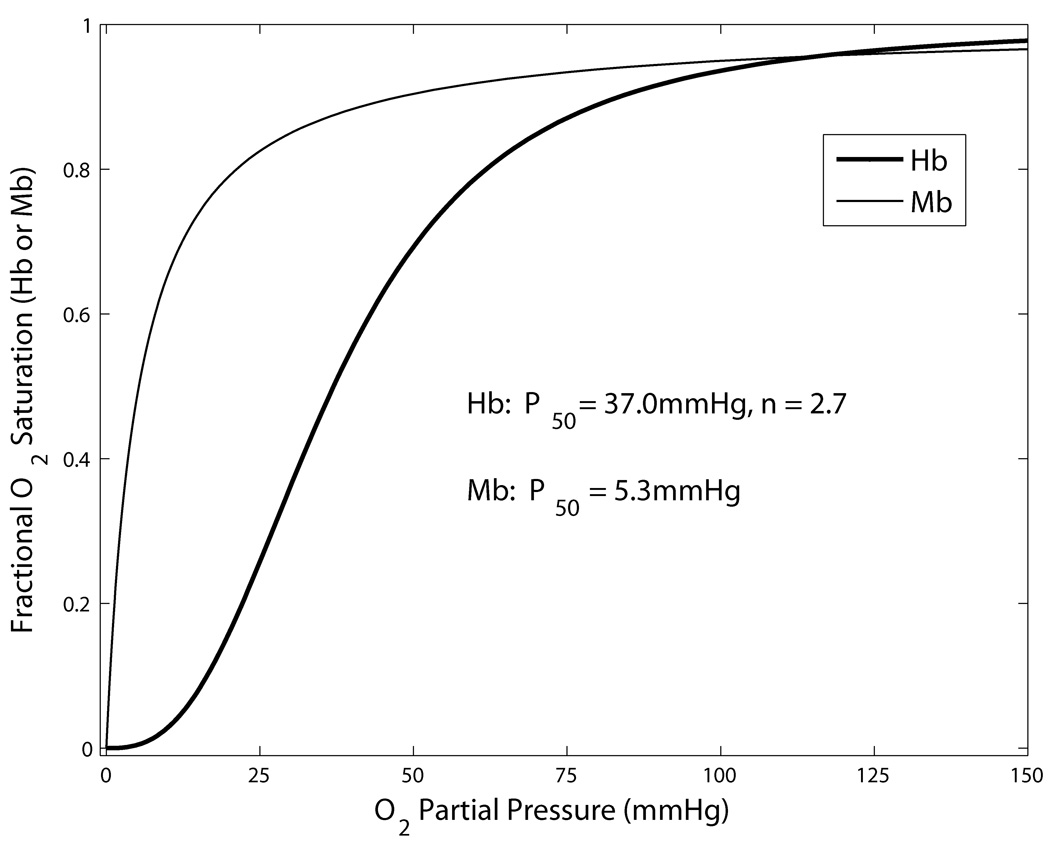
Here P is the local O₂ partial pressure (PO₂) inside the RBC, P₅₀ is the half-saturation PO₂ and n is the Hill exponent. P₅₀ and n are obtained by fitting the Hill equation to experimental data on the oxyhemoglobin dissociation curve, with typical values of P₅₀=29mmHg and n=2.2 for hamster (17) and P₅₀=37mmHg and n=2.7 for rat (15). The Hb-O₂ dissociation curve given by Eq. (1) is shown in Fig. 1. Although the Hill equation is only highly accurate in the SO₂ range of 20–80%, this has been deemed sufficient for most O₂ transport models, given the other approximations used. Note that the exact form of the dissociation curve (e.g., P₅₀ and n) varies with blood pH, CO₂ concentration, concentration of 2,3-diphosphoglycerate (DPG), and temperature. A useful model of this dependence was recently described (12); see appendix of (13) for errata.

Figure 1.

Equilibrium dissociation curves for fractional Hb-O₂ and Mb-O₂ binding as a function of PO₂. Parameter values shown are typical for rat blood.

The amount of Hb-bound O₂ at any point inside a RBC is given by C_Hb S, while the amounts of free or dissolved O₂ in the RBC and the plasma are given by α_RBC P_RBC and α_pl P_pl, respectively, where α_RBC and α_pl are O₂ solubilities and P_RBC and P_pl are PO₂ values. The total concentration of free and Hb-bound O₂ in a given blood sample is

$${\alpha }_{pl}{P}_{pl}\left(1-H\right)+{\alpha }_{RBC}{P}_{RBC}H+C_{Hb}SH$$ (2)

where P_pl and P_RBC are the average PO₂ values in the plasma and RBCs, H is the hematocrit, C_Hb is the O₂-binding capacity of RBC Hb solution, and S is the average SO₂ inside the RBCs. Note that here C_Hb is the product of the RBC hemoglobin concentration and the O₂ binding capacity of Hb. In addition to describing Hb-O₂ binding and blood O₂ concentration, understanding O₂ transport also requires modeling the diffusion of free and Hb-bound O₂ within the RBC and the transport of O₂ through the cell membrane. Theoretical work of this type has been performed in the past (see (65)); however, more recently RBC-plasma O₂ transport models have been incorporated into intravascular O₂ transport models, as described below.

Capillaries

In order to model O₂ transport from capillary blood to tissue, it is necessary to consider the properties of O₂ transport inside capillaries. Many models (including Krogh-Erlang) that have focused on O₂ transport in the tissue surrounding capillaries have failed to account for intracapillary O₂ gradients, which lead to an effective resistance to blood-tissue O₂ transport (34). To quantify capillary intravascular resistance (IVR), theoretical studies have been performed to determine the magnitude of this resistance and how it depends on various parameters such as capillary diameter and RBC velocity.

Following earlier work (see (34)), Federspiel and Popel (18) considered stationary spherical RBCs arranged in single file with a full description of diffusion of free and Hb-bound O₂ inside the RBCs, the kinetics of Hb-O₂ binding, and diffusion of O₂ in the surrounding plasma. Using a constant PO₂ at the capillary wall, it was shown that the mass transfer coefficient (MTC) or inverse resistance depends strongly on hematocrit (or the inverse of the RBC spacing) and also on capillary diameter relative to RBC size (clearance). The MTC was several times smaller for discrete RBCs than for a continuous Hb solution, and application to a capillary-tissue transport model implied IVR was 30–70% of the total resistance for O₂ transport from blood to tissue. A subsequent study (92) showed that RBC shape affects O₂ flux, with calculated MTC increasing by 26% as the RBC changed from its undeformed disc shape to parachute shape.

The capillary MTC is usually defined as the average flux of O₂ per unit area through the capillary wall divided by the average difference between intraerythrocyte PO₂ and wall PO₂:

$$k_{cap}=\frac{\langle j_{wall}\rangle }{\langle P_{cap}-P_{wall}\rangle }$$ (3)

The MTC can be expressed in dimensionless form as a Nusselt number:

$$Nu=\frac{\langle j_{wall}\rangle R_{cap}}{\langle P_{cap}-P_{wall}\rangle D_{pl}{\alpha }_{pl}}$$ (4)

where R_cap is the capillary radius, and D_pl and α_pl are the plasma O₂ diffusivity and solubility, respectively. Capillary diameter and RBC O₂ diffusivity and solubility can also be used to obtain Nu from k, and P_cap can be replaced with P*, the PO₂ based on the average RBC SO₂.

Groebe and Thews (31) used a finite-difference method to study O₂ transport from moving cylindrical RBCs (without plasma convection) in heavily working muscle for O₂ flux and PO₂ boundary conditions at the wall. Increased RBC spacing decreased overall capillary O₂ release but increased release by individual RBCs, and it was concluded that O₂ flux oscillations due to RBC movement did not significantly affect tissue O₂ delivery. Bos et al. (7) presented a model of intravascular O₂ transport that used point sources to represent discrete RBCs and a tissue cylinder surrounding the capillary with constant O₂ consumption and Mb facilitation. A “stroboscopic” method was used to follow equally spaced RBCs as they moved through a capillary at constant velocity. Although resistance due to plasma, capillary wall, and interstitium was not considered, the model allowed calculation of a PO₂ drop between the RBC center and the capillary wall and hence estimation of the effective PO₂ drop (extraction pressure, EP) between capillary and tissue due to intravascular gradients. EP was shown to vary from about 4–20mmHg as hematocrit decreased from 50-20% and to decrease slightly towards the venous end of the capillary. Bos et al. (6) studied transport from cylindrical RBCs with plasma and tissue layers using a finite-difference method. The results of the point-source model were generally confirmed, and behavior of EP was determined for a range of hematocrits and Peclet numbers (Pe=v_RBCl/D, where l is the RBC spacing and D is the plasma O₂ diffusivity). Over the same range of parameters, plasma convection only changed EP by approximately 10% or less.

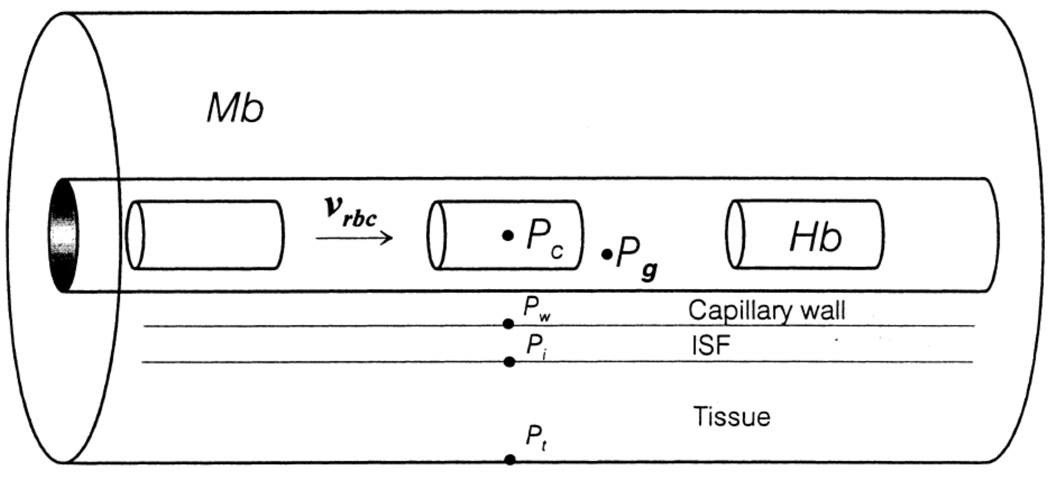
More recently, capillary MTCs for O₂ have been computed using models that include separate concentric layers surrounding the lumen to represent the capillary wall, interstitial space, and parenchymal tissue (Fig. 2). Using cylindrical RBCs, Eggleton et al. (14) calculated MTCs for hematocrits of 25–55% and showed only a weak dependence on RBC velocity and capillary radius. This work also demonstrated that assuming a constant wall PO₂, instead of using an actual model of O₂-consuming tissue, results in a significant overestimate of the MTC, as does using the Clark approximation (10) for RBC-plasma O₂ flux. A quadratic equation was given that closely fit the computed dependence of the MTC on hematocrit:

$${\mathrm{k}}_{\text{cap}}=1.21-4.38H+23.6H^2(\text{nl}{\mathrm{O}}_2{\mathrm{s}}^{-1}{\text{mmHg}}^{-1}{\text{cm}}^{-2})$$ (5)

Figure 2.

Axially symmetric geometry and cylindrical RBCs used to calculate capillary MTCs. Reprinted from Eggleton et al. (14) with permission.

However, it was not clear how accurate this equation would be for capillary hematocrits below 25%, as are often seen experimentally. A model similar to (14) but with the addition of plasma convection was used to compute MTCs (for capillary-tissue and RBC-plasma transport) when a Hb solution was present in the plasma (88). MTCs in this case depended on both hematocrit (in the range 20%-40%) and SO₂. Hb-O₂ binding kinetics had a relatively small effect (<20%) on MTCs for normal blood, but a much larger effect (~55%) in the presence of plasma Hb.

Arterioles and Venules

Since arterioles are also involved in blood-tissue diffusive O₂ transport, it is important to understand how they carry O₂ and release (or take up) O₂ to the surrounding tissue before including them in models of tissue O₂ delivery. As pointed out by Hellums et al. (34), there are two distinct size regimes of non-capillary microvessels that must be considered. In larger microvessels (20–100µm diameter), intravascular O₂ transport can be modeled using a continuum RBC distribution in the vessel core surrounded by a plasma layer. However, in smaller microvessels (8–15µm), it is believed that the actual distribution of RBCs in the lumen needs to be considered to accurately predict O₂ transport properties. No theoretical work has yet been done on this latter case, due to the geometric and computational complexities involved, and therefore only extrapolations from results for smaller and larger vessels are available.

For 20–100µm vessels, Nair et al. (59) developed a theoretical model of intravascular O₂ transport and validated it against experimental data. This model utilized assumed hematocrit and velocity distributions inside the vessel and a finite-element method to calculate steady-state O₂ transport in the RBC-rich core and plasma sleeve regions, which were coupled by assuming continuity of PO₂. This model included Hb-O₂ kinetics and transport between the RBCs and plasma in the core. A simplified model (60) assumed equilibrium Hb-O₂ binding and equilibrium between the plasma and RBC Hb in the core, and both models agreed well with O₂ saturation measurements in a 27µm artificial capillary. These models were used to calculate MTCs for diameters in the range 15–100µm. While MTCs generally depend only weakly on SO₂ in capillaries, they increase approximately linearly with SO₂ in arterioles, and the slope of this relation increases with increasing vessel diameter. Huang and Hellums (41) presented a model of coupled O₂/CO₂ transport inside a large microvessel. This model included many of the same properties as (60), but also contained a detailed description of the complex process of CO₂ transport and its effect on O₂ transport. It was shown that the two-phase nature of blood (plasma and RBCs) and deviations from local chemical equilibrium needed to be considered to accurately predict blood O₂ release accompanied by CO₂ uptake.

Page et al. (61) extended the model (59) to the case where a Hb solution was present in the plasma and included a new treatment of shear augmentation, which was more important than for the case without plasma Hb (particularly for O₂ uptake). This model was shown to agree with experimental data on O₂ release and uptake in a 25µm artificial capillary. An interesting result of this work was that blood containing RBCs and 30% Hb solution had the same O₂ transport capability as an Hb solution without RBCs having the same total Hb content. A similar model but with O₂ flux boundary conditions was recently presented by Cole et al. (11). While the above models of Hellums and co-workers were validated in terms of overall change in O₂ content, it was not possible to validate the details of intravascular transport of O₂, and the possible effects of the vascular wall, interstitial space, and surrounding tissue were not considered.

Note that, up to the present time, there have been a number of limitations on the degree to which microvascular O₂ transport (geometry, hemodynamics, O₂ concentration) could be studied experimentally. Although three-dimensional data is required, the length scales involved (<100µm) have been too small for in vivo imaging modalities such as magnetic resonance (MRI), x-ray tomography (CT), and ultrasound (US). Sectioning and electron microscopy of ex vivo tissue samples allow three-dimensional geometry to be obtained; however, microvessel O₂ supply rates (RBC supply rate and SO₂) cannot be obtained, and true in vivo geometry can be lost due to sample shrinkage or unphysiological vasodilation. Therefore, intravital videomicroscopy (43) has been the principal technique used, although it too has limitations in terms of the depth at which measurements can be made (typically <100µm), the amount of three-dimensional information that can be obtained, its temporal resolution (and hence maximum RBC velocity as well as minimum intravascular length scale), and its accuracy and spatial resolution in determining RBC SO₂ values (16) and plasma or tissue PO₂ values (26, 27). Experimental uncertainties in vessel-tissue geometry, intra- and perivascular O₂ distributions, and hemodynamics (e.g., RBC supply distributions), as well as in in vivo parameters such as maximal O₂ consumption rate and O₂ diffusivity, have motivated much of the theoretical modeling that has been performed on microvascular O₂ transport. This modeling has made possible investigation of fundamental biophysical effects that could not be studied experimentally, such as the role of plasma convection in capillary-tissue transport (6), and has proven very valuable in supplementing experimental data, such as in calculating three-dimensional tissue PO₂ distributions from measured capillary geometry and hemodynamics (23).

Single-Vessel (Tissue Cylinder) Transport Models

Standard Krogh Model

A natural way to begin studying blood-tissue O₂ transport is to consider a single blood vessel and its release of O₂ into the surrounding tissue. Inspired by the structure of skeletal muscle, with its parallel muscle fibers and capillaries, Krogh (49) originated the idea of representing the O₂ transport in an entire microvascular bed by a single capillary that supplies O₂ to the cylinder of tissue surrounding it. This axisymmetric (tissue cylinder) geometry, with a number of additional assumptions, is known as the Krogh model. The prediction of this model for tissue PO₂ was obtained by Krogh with the assistance of the mathematician Erlang, hence the result is known as the Krogh-Erlang solution. The additional assumptions of this model, some of which were not explicit at the time it was proposed, are:

1. Tissue O₂ consumption is constant and uniform

2. Tissue PO₂ at the capillary wall equals average capillary PO₂ (no IVR)

3. Tissue O₂ solubility and diffusivity are uniform

4. Axial (or longitudinal) diffusion of O₂ is not significant

5. All important microvascular O₂ transport phenomena are steady-state

6. All capillaries are parallel, unbranched, and equally spaced

7. All capillaries receive equal convective O₂ supply (RBC supply rate times entrance SO₂)

8. Capillaries are the only microvessels that play a role in O₂ transport to tissue

The above assumptions lead to the following reaction-diffusion problem for steady-state PO₂ in the tissue cylinder (P), given capillary PO₂ (P_cap):

$$\begin{array}{cc}D\alpha \frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial P}{\partial r}\right)=M_0& \text{with}\mathrm{P}={\mathrm{P}}_{\text{cap}}\text{at}\mathrm{r}={\mathrm{R}}_{\text{cap}}\text{and}\partial \mathrm{P}/\partial \mathrm{r}=0\text{at}\mathrm{r}={\mathrm{R}}_{\mathrm{t}}\end{array}$$ (6)

where r is the radial coordinate, D is the tissue O₂ diffusivity, α is the tissue O₂ solubility, M₀ is the tissue O₂ consumption rate, R_cap is the capillary radius, and R_t is the tissue radius. The Krogh diffusion coefficient is defined as K=Dα. The solution (Krogh-Erlang) to the above equation is:

$$P(r)=P_{cap}+\frac{M_0}{4D\alpha }\left(r^2-R_c^2\right)-\frac{M_0{R}_t^2}{2D\alpha }\text{ln}\frac{r}{R_{cap}}$$ (7)

Thus, given a small number of geometric (R_cap, R_t) and biophysical (D, α, M₀) parameters and P_cap at a given location, the Krogh model is able to predict the radial variation in tissue PO₂, including the minimum PO₂, which occurs at the outer edge of the tissue cylinder (r=R_t).

By supplementing the above model with a cross-sectionally averaged model of capillary O₂ transport, it is possible to predict the PO₂ in a capillary and its surrounding tissue. Neglecting O₂ dissolved in the plasma, intracapillary transport can be described by the following convection problem for capillary SO₂ (S), given capillary entrance SO₂ (S_a):

$$\pi R_c^{2}H{C}_{Hb}v\frac{\partial S}{\partial z}=-2\pi j(z)R_c\text{with}S=S_a\text{at}z=0$$ (8)

where H is capillary hematocrit, C_Hb is the O₂-binding capacity of the RBC Hb solution, v is RBC velocity, and j is O₂ flux per unit area leaving the capillary at axial location z. Since the Krogh model assumes constant O₂ consumption and no axial diffusion, the O₂ flux for all z is:

$$j(z)=-D\alpha {\frac{\partial P}{\partial r}|}_{R_c}=\frac{M_0}{2R_c}\left(R_t^2-R_c^2\right)$$ (9)

This result allows direct integration of the capillary transport equation to obtain the solution:

$$S(z)=S_a-\frac{M_0\left(R_t^2-R_c^2\right)}{H{C}_{Hb}v}z$$ (10)

Given an invertible form of the Hb-O₂ dissociation curve (e.g., the Hill equation), Eq. (10) gives P_cap(z)=P(S(z)) at each axial location, which can be used in the solution (7) for tissue PO₂. The minimum tissue PO₂ for the above capillary-tissue model occurs at z=L (capillary exit) and r=R_t (the “lethal corner”). Although its predictions for tissue PO₂ generally differ from experimental measurements, the Krogh model remains an important starting point for understanding O₂ transport to tissue. It represents the case of perfectly homogeneous O₂ transport, and for capillary transport with unidirectional flow gives the largest minimum tissue PO₂ and least tissue PO₂ heterogeneity (coefficient of variation or relative dispersion, =(standard deviation)/mean).

Modified Krogh Models

In an attempt to improve the physiological accuracy of the Krogh model, and to better match experiment, a number of modifications have been incorporated into the model. The most important modifications made while maintaining the Krogh geometry include (c.f. assumptions 1–5 above): variable (PO₂-dependent) tissue O₂ consumption, IVR to O₂ transport or a model of intravascular O₂ gradients, facilitated diffusion by tissue myoglobin (Mb), axial O₂ diffusion in the tissue, and time-dependent transport.

i. PO₂-Dependent O₂ Consumption

Experimentally, the local tissue O₂ consumption rate is found to be approximately constant for tissue PO₂ above a certain critical value, P_crit; below this value O₂ consumption drops off sharply to zero (possibly due to diffusion limitation of O₂ flux into mitochondria). Therefore, in order to study situations in which hypoxia is expected, a mathematical model of PO₂-dependent consumption is required. The most common model (Michaelis-Menten) uses first-order kinetics and gives the following equilibrium O₂ consumption rate:

$$M(P)=\frac{M_{0}P}{P+P_{crit}}$$ (11)

where P is the tissue PO₂ and M₀ is the maximum local O₂ consumption rate. The Michaelis-Menten model does not keep O₂ consumption strictly constant for P>P_crit, but gives a reasonable approximation to the actual behavior and is more convenient computationally than the zeroth-order (“on/off”) model. Although M₀ depends on the particular tissue and conditions being considered, P_crit is usually taken to be in the range 0.5–1.0 mmHg. Tissue O₂ consumption is often assumed to be uniform, but mitochondrial clustering has been considered in some models (28, 58).

ii. Intravascular O₂ Transport Resistance

As discussed above, the existence of intravascular PO₂ gradients implies a finite IVR to blood-tissue O₂ transport. In a number of models of O₂ transport to tissue (see above), intravascular O₂ transport is directly included. However, when this approach is not desirable (e.g., for network problems where the computational cost would be too high), MTCs computed separately can be included in the vessel-tissue transport problem. This is typically done by using a flux boundary condition on tissue PO₂ at the outer edge of the microvessel wall instead of the continuous PO₂ condition of the Krogh model:

$$-D\alpha \frac{\partial P_w}{\partial r}=j_{wall}\equiv k\left(P_{cap}-P_w\right)$$ (12)

where j_wall is the capillary-tissue O₂ flux, k is the MTC, P_w is the tissue PO₂ at the vessel wall, and P_cap is the cross-sectionally averaged intravascular PO₂.

iii. Mb Facilitation of O₂ Diffusion

The Mb molecule found in heart and striated muscle can bind and release O₂ in the same way as Hb, and its movement can enhance O₂ diffusion. Since Mb has only one heme group, there is no cooperativity of binding and the equilbrium Mb-O₂ dissociation curve is given by:

$$S_{Mb}(P)=\frac{P}{P+P_{Mb,50}}$$ (13)

where P_Mb,50 is the experimentally determined half-saturation value. Using Fick’s law, the flux of O₂ bound to Mb can be expressed as j_Mb02 =−D_Mb C_Mb ∇S_Mb, where D_Mb is the Mb diffusion coefficient (assumed the same for free and O₂-bound Mb) and C_Mb is the total O₂ binding capacity of tissue Mb. Expressing the total O₂ flux as j=−Dα∇P−D_MbC_Mb∇S_Mb and using the above expression for S_Mb(P), we obtain

$$j=-D\alpha \left(1+\frac{D_{Mb}{C}_{Mb}}{D\alpha }\frac{P_{Mb,50}}{{\left(P+P_{Mb,50}\right)}^2}\right)\nabla P$$ (14)

where the second term inside the parentheses represents the increase in the effective O₂ diffusion constant due to Mb facilitation. Since P_Mb,50 is relatively small (~2–5mmHg), this facilitation will only be significant at low PO₂ values, i.e., when the Mb-O₂ dissociation curve (Fig. 1) has a significant slope. The above expression for j can be used to obtain a steady-state equation for tissue O₂ diffusion and consumption by setting −∇·j=M, where M is the O₂ consumption rate. Mb gives tissue some resistance to localized hypoxia by increasing diffusion to low-PO₂ regions, and also plays a role in local O₂ storage and buffering. Mb diffusion appears to be isotropic in heart and skeletal muscle cells (62) with D_Mb≈8×10⁻⁷cm²/s in heart at 40°C (55).

iv. Axial O₂ Diffusion in the Tissue

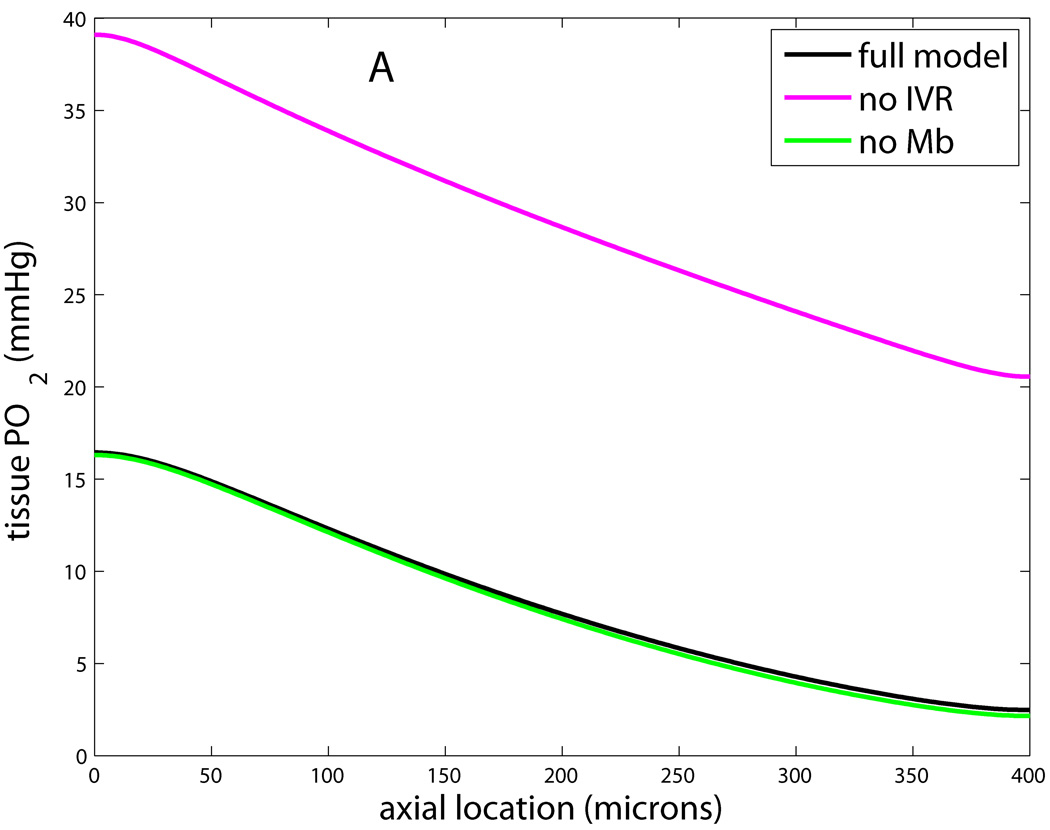
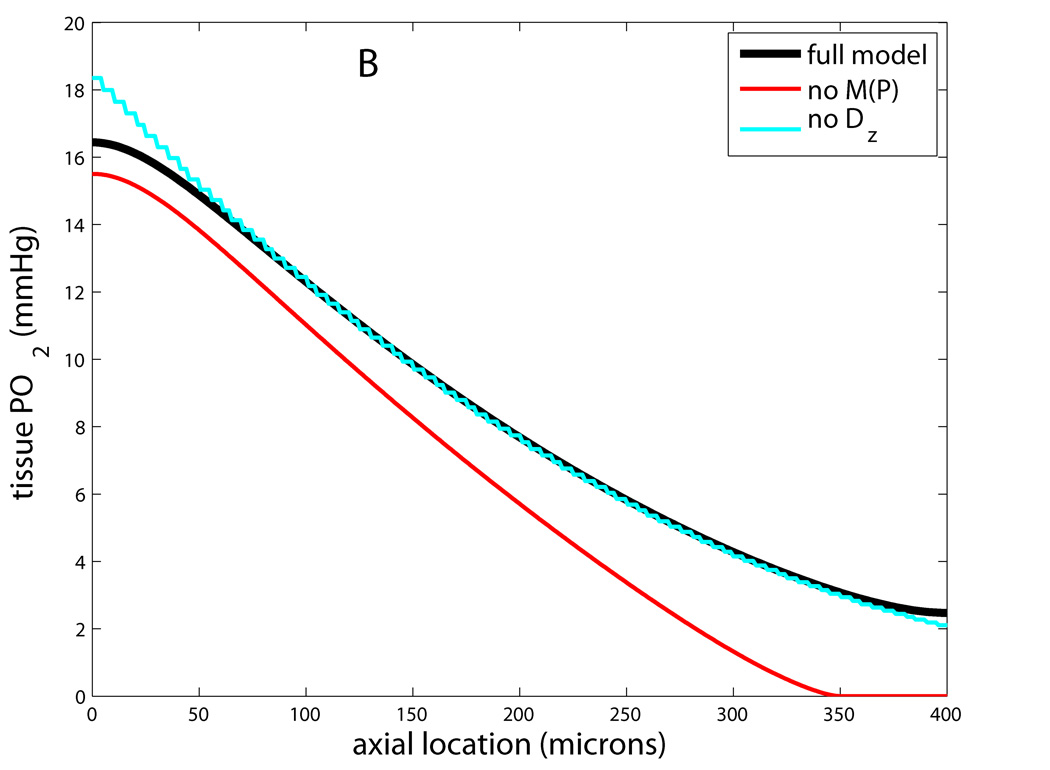
This feature has also been found to be important in modeling microvascular O₂ transport, because each slice of the tissue cylinder is not independent but can exchange O₂ with its neighbors. Axial diffusion inside flowing microvessels is less important due to the relatively greater effect of axial convection. This can be quantified with a Peclet number, Pe=vL/D, which represents the importance of transport by convection (proportional to blood or RBC velocity v) relative to transport by diffusion (proportional to D/L for diffusion coefficient D and length scale L). For a typical capillary RBC velocity of 200µm/s and length of 500µm, and a typical diffusivity of 4×10⁻⁵cm²/s, we have Pe=25. This number will be larger in arterioles and venules, and therefore axial diffusion can be neglected inside most flowing microvessels. Adding axial diffusion to the Krogh model simply requires an additional Dα ∂²P/∂z² term on the left-hand side of Eq. (3). Fig. 3 shows how neglecting each of the preceding four properties affects capillary and tissue PO₂ in the Krogh geometry.

Figure 3.

Effects of neglecting features i–iv in modified Krogh models. Shown is PO₂ at tissue edge (r=R_t) vs. axial location (z) for full model that includes Michaelis-Menten consumption, intravascular resistance, Mb facilitation, and axial diffusion in the tissue; and models that neglect one of these. A: Model without IVR has tissue PO₂ about 25mmHg higher than full model, while model without Mb has slightly lower PO₂ in lethal corner. B: Model with constant consumption has lower PO₂ at all locations and gives zero PO₂ for last 50µm, while model with no axial diffusion has higher PO₂ at arterial end and lower PO₂ at venous end.

v. Time-Dependent O₂ Transport

The convective O₂ supply to individual capillaries can vary considerably over time (e.g., due to upstream arteriolar vasomotion), and there are many problems of interest in which time-dependent O₂ transport is relevant (e.g., the onset of ischemia or exercise). Therefore, several studies have used time-dependent Krogh-type models. The necessary mathematical description involves the time-dependent forms of Eqs. (6) and (8), with appropriate initial and external boundary conditions, and a capillary-tissue interface condition as in Eq. (12). For example, with features i–iv above, tissue PO₂ can be described by

$$\frac{\partial P}{\partial t}={\left[1+\frac{C_{Mb}}{\alpha }\frac{d{S}_{Mb}}{dP}\right]}^{-1}\left\{D{\nabla }^{2}P-\frac{1}{\alpha }M(P)+\frac{1}{\alpha }{D}_{Mb}{C}_{Mb}\nabla \cdot \left(\frac{d{S}_{Mb}}{dP}\nabla P\right)\right\}$$ (15)

where ∇² includes both r and z derivatives. Capillary SO₂ can be described by

$$\frac{\partial S}{\partial t}=-{\left[H{C}_{Hb}+{\alpha }_b\frac{\partial P_b}{\partial S}\right]}^{-1}\left\{v_b\left(H_D{C}_{Hb}+{\alpha }_B\frac{\partial P_b}{\partial S}\right)\frac{\partial S}{\partial z}+\frac{2}{R}{j}_{wall}\right\}$$ (16)

where α_b and α_B are the volume- and flow-averaged blood O₂ solubilities, v_b is the average blood velocity, H_D is the discharge (flow-weighted) hematocrit, j_wall is the capillary wall flux per unit area given by Eq. (12), and P_b(S) is the average blood PO₂ given by the inverted form of Eq. (1). This model includes dissolved PO₂ in the blood and assumes that average plasma and RBC PO₂ at each axial location are approximately equal.

Schumacker and Samsel (73) used a Krogh model with PO₂-dependent consumption (constant above 1mmHg, zero below) to analyze O₂ delivery and tissue uptake. Using reduced hematocrit, capillary entrance SO₂, or RBC velocity to decrease tissue O₂ supply, they investigated the role of diffusion limitation in the supply dependency of tissue O₂ extraction. It was found that the critical O₂ supply (at which O₂ uptake begins to decrease) was the same for all three types of hypoxia as long as the tissue cylinder radius was less than 80µm (for the assumed O₂ consumption rate). However, this led to critical O₂ extraction ratios (O₂ uptake divided by O₂ supply) greater than 90%, whereas experimental values are in the 65–75% range. In order to match both the measured critical extraction ratios and the observed similarity between the three types of hypoxia, it was necessary to assume a 30% functional O₂ shunt. These results demonstrated the limitations of the Krogh model in trying to analyze situations in which transport heterogeneity is important. Using Krogh and Hill (uniform O₂ supply on exterior of tissue cylinder) models, Piiper and Scheid (63) performed a similar study and showed that if multiple size tissue cylinders were considered (simulated supply heterogeneity), diffusion limitation began at a lower O₂ supply than in a single cylinder with the same average diameter.

Lagerlund and Low (51) used a Krogh-type model with axial diffusion, Michaelis-Menten consumption, and no IVR to study steady-state O₂ transport in rat peripheral nerve tissue. They solved the steady-state equations using a finite-difference method and found better agreement with experiment for reduced O₂ supply than in a model with constant O₂ consumption and no axial diffusion. The above model was later extended to time-dependent transport (52). For exponential changes in capillary entrance PO₂, blood velocity, or maximum local O₂ consumption (M₀), they found tissue PO₂ changed either mono- or biexponentially in reaching a new steady state. The slower of the two possible time constants was <0.5 s⁻¹, implying minimal time lag in response of tissue PO₂ to the imposed O₂ supply alterations. Sharma and Jain (80) used a similar model but added terms representing the dynamics of RBC-plasma O₂ flux.

Fletcher and Schubert (19) used a Krogh-type model to show that measured PO₂ histograms in isolated perfused cat heart could be closely matched when axial diffusion was included in the tissue, but only if the diffusion coefficient was 7–10 times the accepted value. This result was not explained by adding tissue Mb (20), even though relatively high Mb concentration and diffusivity (3×10⁻⁶ cm²/s) were used. One interpretation of these results is that the Krogh geometry simply does not apply to the heart (see (4, 96), discussed below). Hudetz (42) studied O₂ transport in the cerebral cortex using the standard Krogh model but with a conical tissue cylinder that tapered toward the venous end of the capillary. This model did not consider IVR and could be solved analytically. Small increases in O₂ consumption (functional activation) required proportional increases in capillary O₂ supply (blood flow), but large increases in consumption required disproportionate supply increases. For moderate hypoxemia, the predicted increase in blood flow agreed with experimental measurements. Whiteley et al. (95) used a finite-element method to study steady-state O₂ transport from a single axisymmetric capillary. Blood was treated as homogeneous, O₂ consumption was constant, and tissue Mb was included. The main conclusions of this study were that axial diffusion should be included in the tissue and that Mb should be included when tissue PO₂ falls below 13mmHg (assuming P_50,Mb=2mmHg). Similar previous work using a homogeneous description of blood (33, 79) indicated that including Hb-O₂ kinetics lowers end-capillary plasma and tissue PO₂ compared to the equilibrium case, particularly for hypoxia and anemia.

McGuire and Secomb (57, 58) utilized a Krogh-type model that included IVR, tissue Mb, Michaelis-Menten consumption kinetics, and axial diffusion to study heavily working human skeletal muscle. Right-shifting of the Hb-O₂ dissociation curve (as observed during exercise) and mitochondrial clustering near the capillary were also considered. They showed that there is diffusion limitation and hypoxia in heavily working muscle (58) and predicted capillary densities based on their model and measured parameters (57) . The fact that measured capillary densities are much lower than those predicted suggested that biopsies in contracted muscle lead to underestimates of capillary density (because increased capillary tortuosity is not considered) and do not accurately reflect in vivo O₂ transport capacity. Note that heavily working muscle is the case for which the Krogh geometry remains most relevant, since capillary transport is most dominant and parallel capillaries have the least diffusive interaction (see (17, 74), discussed below).

Multi-Species Models

Krogh-type models have been used to study blood-tissue transport of substances other than O₂; however, here we are concerned principally with O₂ transport and therefore only discuss models in which transport of O₂ is coupled to that of another species. Transport of other species can be important as a means of studying O₂ transport (54) or because of the effect of O₂ on the other species (e.g., O₂-dependent production and consumption of NO (53, 84)). Other species can also affect O₂ transport itself; for example, by competing with O₂ for binding to Hb (as does CO), by shifting the Hb-O₂ saturation curve (as discussed below for CO₂), and by inhibiting mitochondrial O₂ consumption (as does NO (53)). Li et al. (54) used a Krogh-type model with four concentric layers (RBCs, plasma, interstitial fluid, and parenchymal cells) to study tracer kinetics of ¹⁵O-O₂ and ¹⁵O-water. This model considered axial but not radial gradients within each layer (or compartment), as well as exchange between the layers. The steady-state O₂ distribution was first calculated and then used to model coupled dynamics of labeled O₂ and water. By fitting model solutions to experimental tracer curves, this model can be used to estimate myocardial O₂ consumption.

Schacterle et al. (72) developed a simple steady-state model of O₂/CO₂ transport in arterioles surrounded by tissue containing a continuous distribution of capillaries. Blood was treated as homogeneous, and O₂ and CO₂ only interacted through explicit inclusion of the Bohr (CO₂-dependent shifting of Hb-O₂ dissociation curve) and Haldane (O₂-dependent shifting of the Hb-CO₂ dissociation curve) effects. For an arteriole with 22µm diameter and 1000µm length, results suggested that blood PCO₂ comes closer to equilibrium with surrounding tissue than does PO₂. In the study by Dash and Bassingthwaighte (13) a four-layer axially varying model (similar to (54)) was used to study coupled O₂/CO₂ transport between a capillary and the surrounding tissue. The model included bicarbonate and hydrogen ions, and both the Bohr and Haldane effects. This model should require less computation than models that resolve radial gradients and allows calculation of both steady-state and time-dependent transport over a wide range of physiological conditions. Although this model and that of Li et al. (54) did not include radial gradients, the MTCs used between regions could presumably be adjusted to approximate any given situation. The simulation code for this model is available at the Physiome Project website (www.physiome.org/Models/).

Kirkpatrick et al. (47) used a Krogh-type model to study O₂ and glucose transport in tumors. It was shown that glycolysis has only a minor effect on tumor hypoxia but that hypoxia is very sensitive to the O₂ consumption rate. It was also shown that using a distribution of tissue cylinder sizes increases the hypoxic fraction compared with using a single cylinder. Lamkin-Kennard et al. (53) modeled coupled O₂/NO transport in arteriolar cross-sections (no axial transport). Steady-state radial NO and O₂ transport in the lumen, plasma layer, endothelium, vascular wall, and surrounding tissue were simulated for different conditions. One of their principal findings was that increased tissue NO could increase O₂ delivery to more distant tissue regions due to its ability to reversibly inhibit O₂ consumption.

Multi-Vessel Transport Models

Parallel Capillary Models

The above modifications to the standard Krogh model do not consider O₂ diffusion between microvessels, which is believed to be important in many physiological situations. As a first step toward studying O₂ transport by realistic microvascular networks, and in particular to address Krogh model assumptions 6–8 above, parallel arrays of capillaries have been considered. Using data from the hamster cremaster muscle, Klitzman et al. (48) developed a model of steady-state O₂ transport that neglected IVR but included dissolved and Hb-bound O₂ in the blood and diffusion between capillaries (with concurrent blood flow) and tissue in planes perpendicular to the capillary axis. This model, with its square grid of 16 equally spaced capillaries, was solved by Popel et al. (66) using a finite-difference method to study the effect of heterogeneities in O₂ delivery on tissue PO₂ distributions. Using probability distributions to set the RBC supply rate and capillary inlet SO₂, and Michaelis-Menten consumption, it was shown that both mean and minimum tissue PO₂ decreased as the dispersion of these supply parameters increased.

Calculated tissue PO₂ distributions for rest and exercise (~4 times resting O₂ consumption and RBC supply rate) showed general agreement with PO₂ measurements using microelectrodes. Ellsworth et al. (17) used experimental data on the hamster cheek pouch retractor muscle and an extension of the model (66) to study heterogeneity in capillary RBC supply rate, entrance SO₂, and path length. For uniform path lengths, capillary SO₂ became more uniform towards the capillary exit in resting muscle but more heterogeneous in working muscle. However, path length variability resulted in more SO₂ heterogeneity and a closer match with experimental data for the resting case.

Groebe and Thews (32) considered three-dimensional O₂ transport in a single working muscle fiber surrounded by parallel capillaries with increased axial Mb diffusivity. Using an approximate analytical solution that included discrete RBCs inside the capillaries, they showed that a modified Krogh model (including IVR) gave good agreement with their three-dimensional model when the capillary-to-fiber ratio was close to 1, but that both the modified Krogh and Hill models disagreed considerably with their model when the capillary-to-fiber ratio was close to 2. Their model generally agreed with cryospectrophotometric measurements of PO₂ (based on Mb saturation) in working muscle available at the time (21). A simplified version of this model was later presented (29). Hoofd (35, 36) presented a steady-state model appropriate for O₂ transport by capillary arrays or networks having a preferential direction, as occurs in skeletal muscle. An analytical solution was first presented for tissue PO₂ in planes perpendicular to the capillaries, and then a numerical method was described for connecting successive planes to obtain the three-dimensional PO₂ distribution. This model included tissue Mb and allowed for variable O₂ consumption, and could be applied to both concurrent and countercurrent flow situations.

Application to dog gracilis muscle (37, 38) showed that accurately calculating tissue PO₂ distributions required the inclusion of realistic spacing of parallel capillaries. Since this spacing heterogeneity was not included in (32), much more narrow PO₂ distributions were obtained than in (37, 38). Although the model (32) gave good agreement with experimental measurements, these may have underestimated actual tissue PO₂ heterogeneity due to the fact that the spatial resolution was much lower than originally believed, i.e., 60µm vs. <4µm while the mean muscle fiber radius was 45µm (91) .

Salathe (69) presented a method for calculating the steady-state O₂ distribution due to an array of capillaries in the absence of IVR and variable O₂ consumption. The model used matching of average O₂ fluxes and concentrations between neighboring rectangular tissue domains surrounding each capillary to derive a system of ordinary differential equations (for capillary O₂) coupled to a system of algebraic equations (for average tissue domain boundary O₂). This model was later extended to include axial diffusion (70), as well as Mb facilitation and countercurrent flow (83). This model has been applied to arrays of 2–50 capillaries and seems to provide good accuracy (69) and computational efficiency for applicable problems.

Goldman et al. (23) used parallel arrays in a network transport model ((24), see below) to analyze experimental data on capillary hemodynamics and SO₂ in rat skeletal muscle during sepsis (15). Sepsis causes decreased functional capillary density (FCD) and had been found to increase O₂ extraction in capillaries that maintained flow. However, because hemodynamic and SO₂ data could not be obtained from capillaries with RBC velocities greater than 300µm/s, the overall effect of sepsis on tissue O₂ extraction could not be determined. By using a range of “fast-flow” velocities and adjusting the O₂ consumption rate (M₀) to match measured extraction ratios in “normal-flow” vessels, it was shown that consumption increased 2- to 4-fold in sepsis but that tissue hypoxia did not occur. In a subsequent study (22), the baseline model for O₂ transport during sepsis was considered for decreasing O₂ supply. It was shown that the pathological supply dependency seen in sepsis, which had previously been attributed to a defect in arteriolar flow regulation, could be partly explained by further decreases in FCD as flow decreased.

Another approach that has been used in parallel array models of O₂ transport, and which could also be applied to capillary networks, is the Williford-Bruley (W-B) “probabilistic deterministic” numerical method (8, 45). This technique uses time-dependent probability density functions in three spatial dimensions to evolve tissue O₂ distributions on a grid. However, it is not clear how features such as tissue Mb and IVR could be treated with the W-B method.

Capillary Network Models

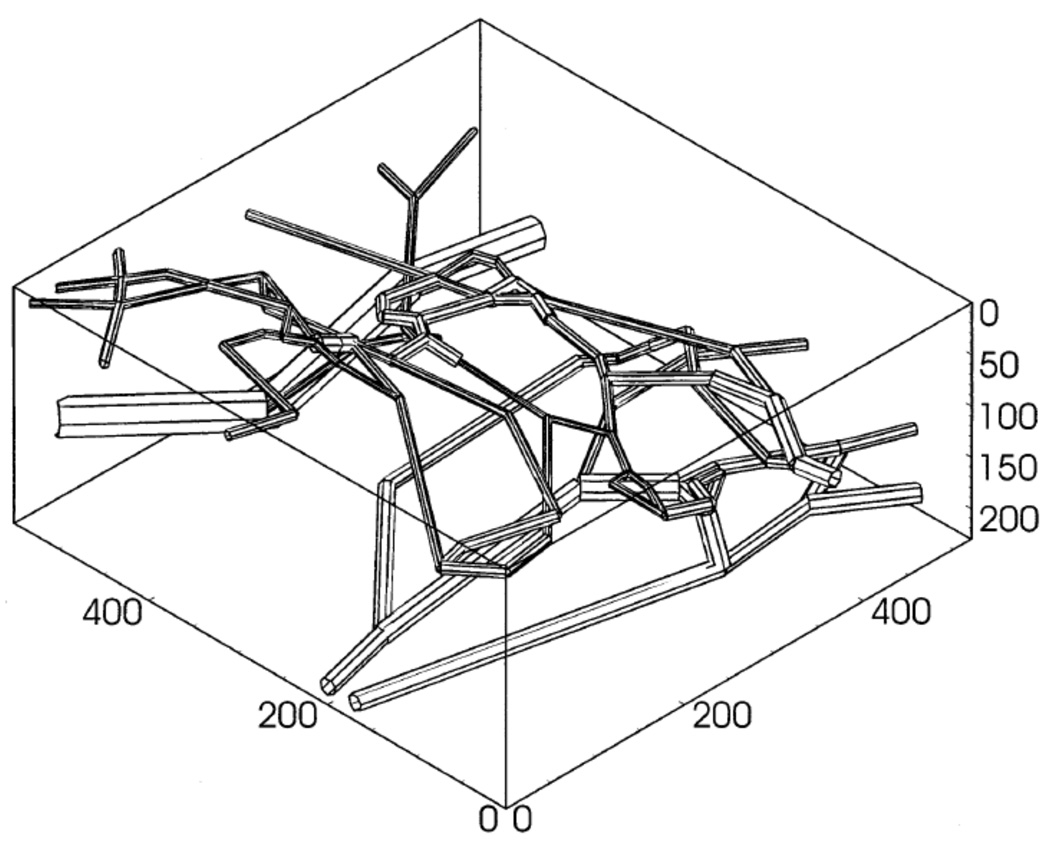
Hsu and Secomb (40) presented a steady-state model of O₂ transport in capillary networks and surrounding tissue based on the Green’s function method. This model included three-dimensional diffusion but not IVR or variable O₂ consumption. The solution method was computationally efficient because it reduced the three-dimensional problem for tissue PO₂ to the one-dimensional problem of finding appropriate source terms for each capillary segment. This model was extended to include variable O₂ consumption (using an iterative procedure) and used to study O₂ transport in mammary adenocarcinoma tumors (76). Using measured microvascular network geometry (Fig. 4) and blood flow, it was shown that O₂ transport was highly heterogeneous and as a result tissue hypoxia occurred at a lower O₂ consumption rate than predicted by the Krogh model for the same average microvessel density. A number of other factors in tumor oxygenation were studied using this model, including the effect of reduced Hb O₂ affinity (46). A version of this model has been used to study O₂ transport in the rat cerebral cortex, using three-dimensional networks reconstructed from micrographs of corrosion casts (75). The three-dimensional network model predicted much lower minimum tissue PO₂ than would an equivalent Krogh model and it was found that hypoxia due to large decreases in blood flow could be avoided by moderate decreases in the O₂ consumption rate. A review and extension of the above Green’s function method was given in (77).

Figure 4.

Geometry of microvascular network used to study O₂ transport in tumors. Reprinted from Kavanagh et al. (46) with permission.

Groebe (30) extended a previous parallel capillary model (32) to the case of three-dimensional O₂ transport from capillary networks. This steady-state model used an approximate analytical solution based on O₂ sources inside individual RBCs and constant O₂ consumption, and included IVR and Mb facilitation. The model was applied to a heavily working muscle fiber supplied by four capillaries and shown to agree with the previous single-fiber results.

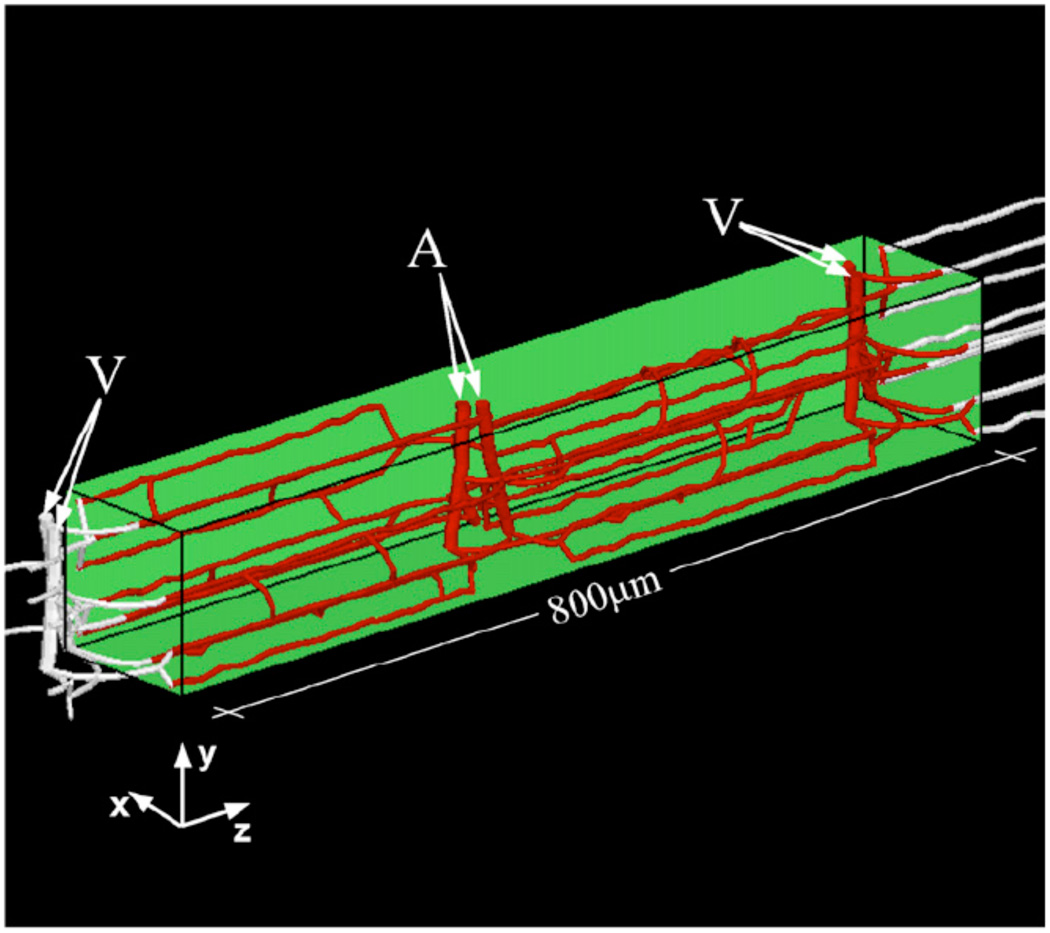
Goldman and Popel (24) presented a finite-difference based model that allowed study of O₂ transport by branching networks of microvessels; included three-dimensional diffusion, IVR, Mb facilitation, dissolved and Hb-bound O₂ in the blood; and could calculate steady-state or time-dependent solutions. This model, which also included a two-phase simulation of network blood flow (based on (68)), was used to study the effect of capillary network geometry on steady-state O₂ transport in the hamster cheek pouch retractor muscle. The arrangement of parallel capillaries induced by the underlying geometry of hexagonally packed muscle fibers was found to be important in reducing tissue PO₂ heterogeneity, as was countercurrent flow, and anastomoses between parallel capillaries were found to help maintain blood flow and tissue PO₂ when some parallel capillaries were blocked. The same model was used to study capillary network O₂ transport during oscillatory blood flow or vasomotion (25). A version of this model (using rat parameters) was applied to an expanded microvascular network consisting of 8 capillary modules with feeding arterioles and draining venules (microvascular units, MVUs, Fig. 5) to study the effect of angiogenesis on muscle oxygenation (44). Interestingly, the splitting mode of angiogenesis (increased parallel capillaries) produced the least hypoxia at high O₂ consumption, but also had the highest blood flow; for equal blood flow, the sprouting mode (increased anastomoses) gave the least hypoxia. This complex network model was extended to include plasma Hb (with corresponding RBC-plasma and capillary-tissue MTCs) and used in a combined theoretical/experimental study (87). This work showed that decreased Hb O₂ affinity (P₅₀) can increase diffusive shunting between microvessels and that microvascular structure can affect the Hb affinity needed to minimize tissue hypoxia.

Figure 5.

Geometry of a skeletal muscle microvascular unit containing two capillary networks with supplying arterioles and draining venules. Single and multiple MVUs have been considered in O₂ transport studies of angiogenesis (44) and Hb-based blood substitutes (87). Reprinted from Tsoukias et al. (87) with permission.

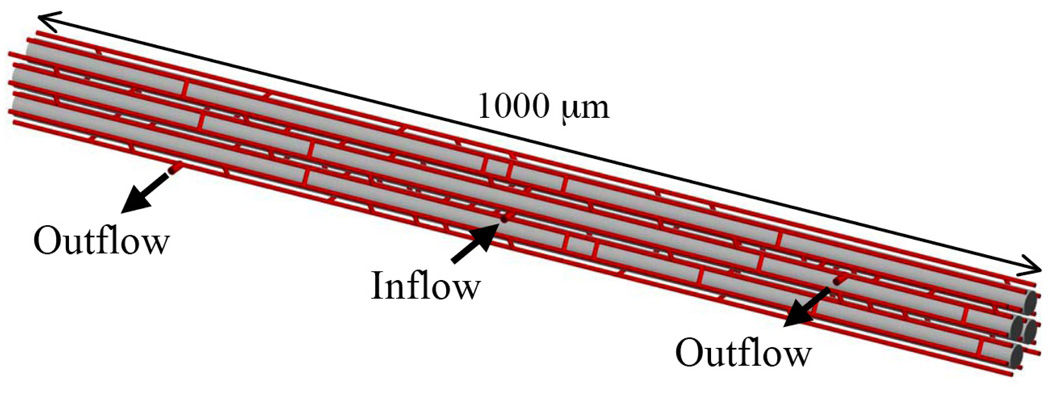
Wieringa et al. (96) presented a three-dimensional network model of steady-state O₂ transport in the heart that assumed constant O₂ consumption and was solved in two-dimensional layers by the finite-element method. Despite a number of simplifications (e.g., no diffusion between layers), this model showed the importance of intercapillary diffusion, particularly when flow direction and path length are heterogeneous, and results indicated that venous PO₂ is not a good indicator of actual tissue oxygenation. Beard and Bassingthwaighte (4) presented a network model of the heart that used 16 parallel capillaries on a hexagonal grid with 160 random cross-connections and included three-dimensional diffusion, Mb facilitation, and Michaelis-Menten consumption.

Using a finite-difference method, they showed that steady-state O₂ distributions were much more heterogeneous than a Krogh-type model would predict and that Mb could reduce tissue hypoxia but only for a modest range of consumption rates. The solution method was extended to an inhomogeneous finite-volume (IVol) method (2) that allowed arbitrary network geometry, time-dependent transport, and larger tissue grid spacing for more efficient numerical solution. The new method was applied to predict PO₂ distributions in perfused hearts based on optical spectroscopy data (5), using a network model as in (4) but with the interstitial space explicitly included (Fig. 6).

Figure 6.

Geometry of capillary network (red), muscle fibers (grey), and interstitial space (white) used to study O₂ transport in the heart. Reprinted from Beard et al. (5) with permission.

Capillary/Arteriole and Venule/Arteriole Interaction Models

To explore experimental data on longitudinal PO₂ gradients in arterioles (50) that suggested the O₂ permeability of blood-perfused tissue was much greater than expected (67), Weerappuli and Popel (94) developed a model of O₂ exchange between an arteriole or venule and surrounding capillary-perfused tissue (resting hamster cheek pouch retractor muscle). This model used a finite-difference method to solve the steady-state problem in the plane perpendicular to the arteriole with a continuous description of capillary O₂ transport (71). Results were obtained for 1^st and 4^th order arterioles with constant luminal PO₂ values of 37.7 and 31.6 mmHg, respectively, and a far-field tissue PO₂ of 20mmHg. Results for Sherwood number (Sh, dimensionless O₂ flux) vs. Pe showed increases up to ~Pe=30. There was a wake of increased tissue PO₂ on the downstream side of the arteriole and slightly greater flux from the larger arteriole. A venule with luminal PO₂ of 15mmHg had a similar but opposite effect on nearby tissue PO₂. Further work using this model (93) again suggested that the O₂ permeability in vivo must be 1–2 orders of magnitude greater than the in vitro value (i.e., the Krogh constant, K=Dα).

To address possible errors caused by using a continuous description of capillary O₂ transport, Hsu and Secomb (39) applied the Green’s function method to O₂ transport from a single arteriole perpendicular to a plane containing several parallel discrete capillaries. They found arteriolar O₂ flux of the same magnitude as (93), but with a slower increase as a function of Pe. Hence, the controversy over the actual magnitudes of arteriolar O₂ flux and in vivo O₂ permeability remained unresolved. Tsai et al. (86) proposed that extremely high arteriolar wall O₂ consumption (see discussion of their methods in (26)) was causing the discrepancy between theory and experiment, but an analysis of available data based on the O₂ diffusion and consumption properties of the wall (89) concluded that O₂ fluxes had been overestimated based on estimates of convective O₂ transport at upstream and downstream points.

Despite the above controversy, a version of the model (39) was used to investigate details of three-dimensional capillary-arteriole O₂ exchange in a block of tissue containing parallel capillaries crossed by two arterioles. This study (74) gave an indication of the roles that capillaries and arterioles play in O₂ transport under realistic conditions. For resting conditions, diffusive O₂ loss from arterioles was 86% of total consumption, but more than half this O₂ was taken up by capillaries and delivered to other locations. During exercise (10 times resting O₂ consumption and blood flow), the diffusive O₂ loss from arterioles was 32% of total consumption and only 5% of the total consumed O₂ diffused from arterioles into capillaries. Thus, arterioles supplied about 40% of consumed O₂ directly to tissue during rest and 27% during exercise.

Chen et al. (9) used a steady-state three-dimensional model to study coupled NO/O₂ transport in an arteriole/venule pair surrounded by capillary-perfused tissue, which was modeled as a porous medium that connected the larger vessels by both diffusion and convection. Capillaries facilitated the release of O₂ from the larger vessel pair to the surrounding tissue and greatly enhanced transport of NO from venule to arteriole. The finding of increased O₂ release might help explain the experimental finding of large arteriolar O₂ efflux (50, 67); however, this was measured in unbranched vessels whereas (9) included O₂ convection through the arteriolar wall.

Conclusions and Future Directions

From the many detailed theoretical studies performed over the last two decades, a number of important results on microvascular O₂ transport have emerged. The importance of biophysical properties (Krogh assumptions 1–5) was first evaluated, while later work examined the significance of geometric and hemodynamic properties of the microvasculature (assumptions 6–8). In particular, the effects of heterogeneities in capillary spacing, O₂ supply, flow direction, and path length, as well as the way in which arterioles and venules interact with capillaries and tissue, have only begun to be understood as more sophisticated models have been developed. There is still far from a complete understanding of how a particular functional microvascular structure (geometry, hemodynamics, inlet SO₂) determines tissue oxygenation and O₂ consumption. In addition, the effect of realistic temporal variations in O₂ supply on three-dimensional O₂ transport to tissue is largely unknown.

Although more efficient methods of including the effect of capillary-scale heterogeneities on organ-scale physiology are still needed, existing theoretical models are capable of investigating most outstanding details of structure-function relationships in microvascular O₂ transport. To support this work, detailed experimental data is needed to determine input parameters and thoroughly validate the models (which for the most part has never been done). Experimental methods have for some time been less developed than theoretical ones, as pointed out by Pittman (64); however, a combination of existing and emerging techniques (1, 26, 43, 81, 85, 90) shows promise for supporting further theoretical advances based on development and validation of realistic models of in vivo O₂ transport. One important area of current theoretical modeling of the microcirculation involves multi-scale models that couple details of O₂ transport to related biological processes (such as angiogenesis (56) and metabolism (3)) occurring at similar and smaller scales. Combined with more fundamental studies of microvascular O₂ transport, these multi-scale models should lead to a more complete picture of the synergy between tissue properties and functional characteristics of the microvasculature, and this could have dramatic implications both for maintenance of health and treatment of various diseases.

Figure 7.