Perceptual Grouping Affects Pitch Judgments Across Time and Frequency

Abstract

Pitch, the perceptual correlate of fundamental frequency (F0), plays an important role in speech, music and animal vocalizations. Changes in F0 over time help define musical melodies and speech prosody, while comparisons of simultaneous F0 are important for musical harmony, and for segregating competing sound sources. This study compared listeners’ ability to detect differences in F0 between pairs of sequential or simultaneous tones that were filtered into separate, non-overlapping spectral regions. The timbre differences induced by filtering led to poor F0 discrimination in the sequential, but not the simultaneous, conditions. Temporal overlap of the two tones was not sufficient to produce good performance; instead performance appeared to depend on the two tones being integrated into the same perceptual object. The results confirm the difficulty of comparing the pitches of sequential sounds with different timbres and suggest that, for simultaneous sounds, pitch differences may be detected through a decrease in perceptual fusion rather than an explicit coding and comparison of the underlying F0s.

Perceptual Grouping affects Pitch Judgments across Time and Frequency Pitch – the perceptual correlate of periodicity and fundamental frequency (F0) – is a salient characteristic of sound, which plays a role in speech, music, and the analysis of auditory scenes (McDermott & Oxenham, 2008; Plack & Oxenham, 2005). While some listeners can correctly identify the pitch of sounds in the absolute (Levitin & Rogers, 2005), for most listeners, and under most circumstances, differences and variations in pitch play a far more important role than does absolute pitch information. For instance, the perception of melody in music and prosody in speech relies in large part on the ability to extract pitch “contours,” i.e., pitch variations over time. Differences in pitch also play an important role in the perception of simultaneously presented sounds, as in polyphonic music or multi-talker environments (Carlyon & Gockel, 2008; Huron, 1989; Micheyl & Oxenham, 2009).

Most pitch models, based either on spectral information (e.g Goldstein, 1973; Terhardt, 1974; Wightman, 1973), temporal information (e.g. Licklider, 1951; Meddis & O’Mard, 2006; Srulovicz & Goldstein, 1983), or both (e.g. Shamma & Klein, 2000), have focused on correctly predicting the perception of the pitch of isolated sounds. In such models it is either implicitly or explicitly assumed that when a listener is comparing the pitches of two sounds, the pitch of each tone is first extracted, and then the two pitch estimates are compared. Several methods have been proposed for segregating the pitches of simultaneous sounds such that they can be compared. These methods include place-based template models, in which multiple harmonic templates can be activated by sound combinations (Duifhuis, Willems, & Sluyter, 1982; Scheffers, 1983); autocorrelation models, in which different periodicities are assumed to dominate in different frequency regions (as in competing vowels investigated by Meddis & Hewitt, 1992); cancellation models, in which one (dominant) set of harmonics, or periodicity, is cancelled from a spectral (Parsons, 1976), or temporal (de Cheveigné, 1993), representation of the mixture to facilitate the estimation of the second pitch present; and timing nets, which use a form of autocorrelation to separate multiplexed periodicities in their inputs (Cariani, 2001); for recent reviews, see de Cheveigné (2006) and Micheyl and Oxenham (2009). The assumption that comparing two pitches merely involves estimating each pitch, independent of other properties of the sounds (e.g., timbre) and of their relationship (e.g., relative timing), suggests that any sound that elicits a pitch can be compared to any other pitch-eliciting sound. However, there is evidence that under certain circumstances listeners have difficulty comparing pitches that are individually salient. For example, gross spectral differences – which produce salient timbre differences – between successively presented complex tones often lead to poorer pitch discrimination performance than is achieved when the tones have similar spectral envelopes and similar timbres (e.g. Micheyl & Oxenham, 2004; Moore & Glasberg, 1990; Warrier & Zatorre, 2004). Such effects of timbre on pitch perception accuracy have yet to be incorporated into any quantitative model of pitch perception.

Another important aspect of pitch perception, which existing pitch models do not address, relates to the effects of temporal relationships between the tones. In particular, these models do not make specific predictions as to whether sequential and simultaneous comparisons of sounds will result in similar or different pitch discrimination accuracy. Few empirical studies have directly addressed this question, and arguments can be made in either direction.

At least two lines of reasoning suggest that pitch discrimination accuracy should be worse when tones filtered into different spectral regions are presented simultaneously than when they are presented sequentially. The first involves an effect known as pitch discrimination interference (PDI). Several experiments have shown that the presence of a harmonic complex in one spectral region can interfere with the pitch perception of a simultaneous complex in another region (Gockel, Carlyon, & Moore, 2005; Gockel, Carlyon, & Plack, 2004, 2009; Krumbholz et al., 2005; Micheyl & Oxenham, 2007). Such interactions may result in poorer comparisons of the pitches of the two complexes. The second line of reasoning involves the potential role of attention. When comparing two simultaneous pitches, listeners may switch their attention between the two tones (Carlyon, Demany, & Semal, 1992). If a listener can only attend to one tone at a time, the analysis time assigned to each tone would be less than if tones of equal length had been presented sequentially.

However, arguments can also be made to predict the opposite pattern of results. Firstly, the simultaneous presentation of tones may provide listeners with alternate cues that are not available when the tones are presented sequentially. One such cue relates to beats of mistuned consonance (BMC), a beating percept produced by two sinusoids that form a slightly mistuned consonant interval, such as an octave (Plomp, 1967). The phenomenon of BMC can occur even if the tones are presented to opposite ears (Feeney, 1997), suggesting that the phenomenon is not solely cochlear in origin. Another cue that might play a role when the tones are presented simultaneously involves potential differences in perceived fusion between the two tone pairs. Common F0 is thought to be a strong perceptual grouping cue (e.g., Bregman, 1990). Therefore, when the simultaneous tones in the two spectral regions share the same F0, they are more likely to be heard as a single, perceptually fused, sound. In contrast, when the two tones have slightly different F0s, they may be less fused. Thus, listeners could perform an F0 comparison task with simultaneously presented tones by responding to the degree of perceived fusion rather than extracting one F0 from each spectral region and explicitly comparing them. A third potential reason why simultaneous presentation might lead to better performance is that memory constraints could limit performance when tones are presented sequentially. If the pitch of the first tone must be estimated and held in memory while the pitch estimate of the second tone is generated, the memory of the pitch estimate for the first tone may degrade over time (Clement, Demany, & Semal, 1999; Demany, Montandon, & Semal, 2005; Kinchla & Smyzer, 1967), making comparisons of pitch estimates between the two tones less accurate than when the tones are presented at the same time, in which case the pitch estimates may be generated simultaneously.

Despite the important potential implications of these conflicting predictions for pitch theories, no direct comparisons of sequential and simultaneous pitch discrimination have been made using equivalent pairs of complex tones. The most directly relevant study (Carlyon & Shackleton, 1994) concluded that listeners are as sensitive to F0 differences between simultaneous sounds and as they are to F0 differences between sequential sounds, so long as these sounds each produce a strong pitch percept when presented in isolation. Unfortunately, various factors complicate the interpretation of those results. In particular, the tones were filtered into the same spectral region – and thus had the same timbre – in the sequential conditions, but were filtered into non-overlapping spectral regions in the simultaneous conditions. In addition, the sequential conditions contained only two tones that were compared, whereas the simultaneous conditions contained fours tones – two pairs, one of which contained an F0 difference while the other did not. Thus, neither the methods nor the stimuli were conducive to a direct comparison of the simultaneous and sequential conditions, and the conclusions of this study have been challenged on multiple grounds (Gockel et al., 2004; Micheyl & Oxenham, 2005).

The aim of our first experiment was to test the conflicting predictions mentioned above by explicitly comparing listeners’ pitch discrimination performance when equivalent tones are presented simultaneously versus sequentially. The results show that listeners’ performance was significantly worse when the tones were presented sequentially than when they were presented simultaneously. The two subsequent experiments were designed to distinguish between likely causes of this difference in pitch discrimination performance. Overall, the results suggest that pitch comparisons can be very poor between sequential stimuli that differ widely in their spectral content, and that improved performance when the stimuli are presented simultaneously are mediated by changes in perceptual fusion rather than an explicit comparison of two F0s.

Experiment 1: Simultaneous vs. Sequential Presentation of Tones

Method

Stimuli

A schematic of the stimuli used in Experiment 1 is shown in Figure 1 (panels A and B). The basic stimuli were harmonic complex tones with a nominal F0 of 200 Hz, and with all components presented in sine (0°) starting phase at a level of 46 dB SPL per component before filtering. The complexes were presented in pairs, with one complex filtered into a low spectral region and one complex filtered into a high spectral region. The low-region complex was lowpass filtered using an 8^th-order Butterworth filter with a cutoff frequency of 700 Hz, to allow at least three audible harmonics within the passband. The high-region complex was bandpass filtered between 1150 and 3500 Hz, using a 6^th-order Butterworth highpass and 8^th-order Butterworth lowpass filter, respectively. These filters allowed some resolved harmonics to be included in the high complex for all F0s used in this experiment (e.g., A. J. M. Houtsma & J. Smurzynski, 1990). The lowest harmonic included in the high complex varied with the F0, but was always between the fifth and the seventh. Components that would have been attenuated more than 10 dB by the filtering were not generated. The duration of each complex was 400 ms, including 10-ms squared-cosine onset and offset ramps. Based on previous work (e.g. A. J. Houtsma & J. Smurzynski, 1990; Moore & Glasberg, 1990), we expected these parameters to yield good F0 discrimination within each region. This was confirmed in five of our participants, who returned after completing Experiment 1 for a brief control study identical to the Sequential condition of Experiment 1 except that both complexes in a pair were filtered into the same spectral region. All participants in this follow-up study were able to discriminate sequentially presented complexes (with both complexes in the same spectral region) with greater than 95% accuracy for F0 differences of one semitone (~6%) or more.

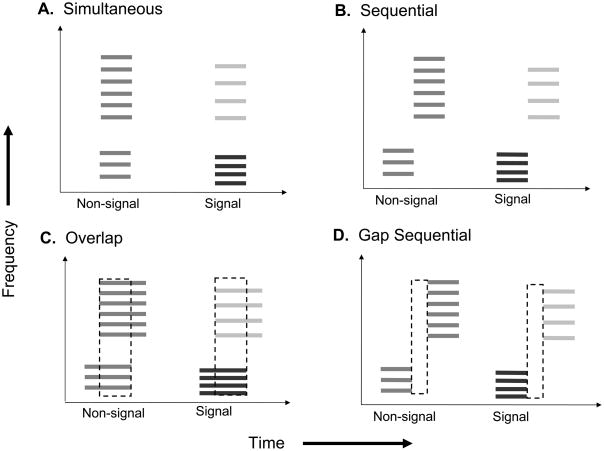
Figure 1.

Schematic diagram showing the conditions used in Experiments 1, 2, and 4. Participants listened to two pairs of spectrally segregated harmonic complexes and indicated the interval in which the F0s differed (signal interval). Increased spacing between lines and lighter shading indicate a higher F0. The Simultaneous (A) and Sequential (B) conditions are used in experiments 1, 2, and 4. The Gap (C) and Overlap (D) conditions are used in Experiment 2. The diagram is not to scale.

A broadband threshold equalizing noise (TEN) at 40 dB SPL per equivalent rectangular auditory bandwidth (ERB_N) (Moore, Huss, Vickers, Glasberg, & Alcantara, 2000) was played throughout each trial to further limit peripheral interactions between components in the two spectral regions, and to mask any potential distortion products generated by the stimuli. This level was selected based on pilot testing such that the level of each component of the complex tones was approximately 10 dB above masked threshold. The noise began 200 ms before the beginning of the first stimulus interval in a given trial and ended 200 ms after the end of the second stimulus interval

Procedure

Participants were seated in a double-walled sound attenuating booth. Sounds were generated digitally using Matlab (Mathworks, Natick, MA), converted to voltage using a 24-bit digital-to-analog Lynx L22 converter (LynxStudio, Costa Mesa, CA), and were presented monaurally via HD580 headphones (Sennheiser, Old Lyme, CT). Each trial consisted of two consecutive tone pairs, separated by an interstimulus interval of 500 ms. To limit participants’ ability to perform the task reliably based on F0 comparisons across pairs instead of within pairs, the nominal F0 of each pair was randomly and independently assigned from a rectangular distribution of ±3 semitones around 200 Hz (168–238 Hz). In one pair, the two complexes had the same F0, and in the other pair, the F0s of the two complexes differed by 0.5, 1, 2, or 4.5 semitones, mistuned symmetrically on a semitone scale around the nominal F0. For the mistuned pairs, the higher F0 was randomly assigned with equal probability to either the low or high spectral region. We refer to the case of the higher F0 in the higher spectral region as “positive mistuning,” and the higher F0 in the lower spectral region as “negative mistuning.” In the Simultaneous condition, the two complexes in a given pair had simultaneous onsets and offsets. In the Sequential condition the high complex began immediately after the low complex ended, with no gap or overlap between the complexes. The stimuli were presented in blocks of 50 trials, and within each block the mistuning was held constant. Participants identified the tone pair in which the F0s differed by pressing one of two buttons and were given visual feedback (“correct” or “wrong”) after each trial. Participants completed trials during a single two-hour session and were encouraged to take breaks during the session as needed. Breaks could occur after any 50-trial block.

Participants were presented with 13 blocks of each condition. The first five blocks were treated as practice, and involved mistunings of 6.5, 4.5, 2, 1, and 0.5 semitones. These blocks were followed by eight experimental blocks, including two blocks at each level of mistuning (0.5, 1, 2, and 4.5 semitones) in pseudorandom order, such that all levels were presented once before any level was presented again. Half of the participants completed the Sequential condition first, and the other half completed the Simultaneous condition first.

Participants

Twenty-eight participants (20 female) were recruited via flyers posted on campus in the psychology and music departments, and were paid for their participation. Their ages ranged from 18 to 56 (mean age 24 yr). Prior to testing, each listener’s hearing was screened. All participants but one had normal hearing, defined as pure-tone thresholds of 20 dB HL or lower at .5, 1, 2, 4, and 8 kHz. One listener had a pure-tone threshold of 25 dB HL at 8 kHz. This participant was not excluded because none of the stimuli in this experiment had components above 6 kHz. All but one listener had fewer than 4 hours prior experience with psychoacoustic experiments, and the amount of musical training among participants varied from no musical training to fifteen years of lessons on a musical instrument. Nine participants completed the conditions of experiment 2 before participating in the current experiment.

Results

Performance in Simultaneous and Sequential tasks was evaluated in terms of d′. Though proportions of correct responses (PCs) were measured in the experiment, there are at least two advantages to using d′, instead of the raw PCs for data analysis and interpretation purposes. Firstly, proportions are susceptible to floor and ceiling effects, and their variance usually varies with their mean, being largest near a mean of 0.5, and smallest as the mean PC approaches 1.0. These effects are alleviated by an appropriate transformation of the PC values into d′. Secondly, PCs measured in experiments involving a dual-pair design (Rousseau & Ennis, 2001), such as that used in this experiment, are not directly comparable to PCs measured in experiments using a different psychophysical paradigm, such as the more commonly used two-interval, two-alternative forced-choice (2I-2AFC) paradigm (see: Creelman & Macmillan, 1979; Micheyl, Kaernbach, & Demany, 2008; Micheyl & Messing, 2006; Micheyl & Oxenham, 2005; Noreen, 1981). In fact, direct comparisons of PCs between 2I-2AFC and dual-pair experiments can be quite misleading. For instance, whereas 76% correct corresponds to a d′ of 1 in the traditional 2I-2AFC paradigm (Macmillan & Creelman, 2005), the same PC corresponds to a d′ of 2.17 in the dual-pair paradigm with roving (Micheyl & Messing, 2006); to obtain a d′ of 2.17 in the 2I-2AFC paradigm, the participant would have to produce a PC of 94%. As this example shows, the same PC can signify a considerably higher sensitivity in a dual-pair experiment than in a 2I-2AFC experiment. Since we were ultimately interested in comparing our results with F0-discrimination data in the literature, which have usually been obtained using a 2I-2AFC paradigm, this provided another reason to use d′ instead of PC.

Values of d′ corresponding to measured PCs were calculated using the following equation (Micheyl & Messing, 2006):

$$d^{\prime }=2{\mathrm{\Phi }}^{-1}\left(0.5+\sqrt{PC/2-0.25}\right).$$ (1)

Where Φ⁻¹ denotes the inverse normal distribution function. As explained in previous publications (Micheyl et al., 2008; Micheyl & Messing, 2006; Micheyl & Oxenham, 2005), this calculation assumes equal-variance Gaussian observations (Green & Swets, 1966), and a “differencing” strategy (Carlyon, 1998; Noreen, 1981; Rousseau & Ennis, 2001). According to this strategy, participants first estimate the F0 of each complex within a pair, then compare the two resulting estimates, and finally select the pair in which the distance between the two F0 estimates is largest. When the relevant stimulus parameter (here, nominal F0) is roved over a wide range (relative to ΔF0) across trials, as was the case here, the differencing strategy corresponds to the optimal maximum-likelihood strategy; in other words, it is the best the observer can do. Thus, d′ values calculated using Equation 1 provide an upper bound on performance. To avoid problems due to proportions of correct responses occasionally being equal to 1, 0.5 (out of a possible 50) was added to each square of the hit/miss tables before the calculation of d′ (Hautus, 1995). Values of d′ were calculated for each individual in each condition and then averaged across individuals.

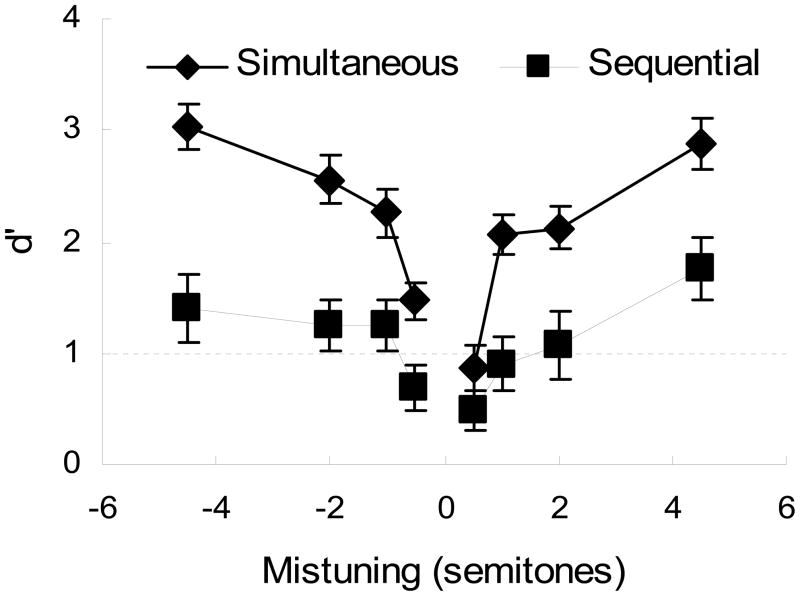
The results are shown in Figure 2. For the Simultaneous condition, the mean d′ values (averaged across listeners) ranged from 0.84 to 3.04. For the Sequential condition, mean d′ values ranged from 0.40 to 1.57. A three-way repeated-measures analysis of variance (RMANOVA) was performed with mistuning amount (0.5, 1, 2, 4.5 semitones), mistuning direction (positive or negative), and condition (Simultaneous or Sequential) as the within-subject factors, and task performance (d′) as the dependent variable. The Huynh-Feldt correction was used to compensate for a lack of sphericity when appropriate. The results showed a significant main effect of condition, F(1,27)=31.63, p<0.001, η_p²=.54, reflecting the observation that performance seemed better overall in the Simultaneous condition than in the Sequential condition. In both conditions, listeners predictably performed better as mistuning amount increased, F(3,81)=51.09, p<.001, η_p²=.70. The increase was steeper in the Simultaneous condition than in the Sequential condition, as reflected by an interaction between condition and mistuning amount, F(3,81)=3.33, p=.006, η_p²=.15. In addition, mistuning detection was slightly better when the high spectral region contained the lower F0 than when mistuning was in the opposite direction, F(1,27)=12.32, p=.002, η_p²=.31. Interactions between condition and mistuning direction F(1,27)=1.922, p=.177, η_p²=.07, between mistuning direction and amount F(3,81)=2.56, p=.078, η_p²=.09, and between all three factors F(3,81)=1.40, p=.253, η_p²=.05 were not significant.

Figure 2.

The averaged results of Experiment 1, comparing performance on a F0 difference detection task when tones are presented in the Simultaneous (diamonds) versus the Sequential (squares) conditions. Discrimination sensitivity (d′) is shown as a function of the F0 mistuning between two harmonic complexes in separate spectral regions.

To facilitate comparisons with earlier studies of F0 discrimination, in which results were reported in terms of difference limens for F0 (DLF0s), we also calculated “threshold ΔF0s”, in addition to d′ values. These threshold ΔF0s were determined as the F0 difference corresponding to a d′ of 1, based on interpolation of the mean psychometric functions fitted with logistic functions using a maximum-likelihood procedure implemented in Matlab (The Mathworks, Natick, MA). The interpolated threshold ΔF0s were roughly 1.5% for the Simultaneous condition and 3.5% for the Sequential condition. The difference in these estimated thresholds is consistent with the overall finding of poorer performance in the Sequential than in the Simultaneous condition. However, as more information is provided by the actual d′ values as a function of mistuning, in subsequent experiments we focus on the psychometric functions.

One possible explanation for performance differences in the Simultaneous and Sequential tasks relates to differences in musical training. At intake, our listeners indicated their years of musical training. We reran the RMANOVA with musical experience as a between-subjects factor. Listeners were divided into groups with no musical experience (n = 11), 1–9 years of experience (n = 11) or more than ten years of musical experience (n = 10). In this analysis, musical experience did not significantly affect performance F(2,29)=1.28, p=.29, η_p²=.081, nor did it interact significantly with any of the within-subjects factors. Thus, the duration of musical training does not seem to provide a reliable predictor of performance in these tasks.

Discussion

Participants reported finding the Sequential task more difficult than the Simultaneous task. This difference in perceived difficulty was reflected in their d′ scores and threshold ΔF0s. This difference in performance is consistent with the indirect inferences made by Micheyl and Oxenham (2005), who reanalyzed the data of Carlyon and Shackleton (1994) and found that the performance measured by these authors in their simultaneous F0 comparison task was better than would be predicted based on the performance that they measured in their sequential F0 comparison task. More generally, the finding that performance in a simultaneous F0 comparison task is not as expected based on performance in a sequential task is consistent with the possibility that the two tasks involve different mechanisms (Demany & Semal, 1992). We also note that performance in the Sequential condition (and in the Simultaneous condition at 4.5 semitones) is not accurate enough to rule out the possibility that listeners were performing the task by selecting the interval containing the most extreme F0, rather than comparing F0 across spectral regions (Dai & Micheyl, 2010).

The pattern of results suggests that pitch discrimination interference and attention switching do not limit performance in the Simultaneous condition; as discussed in the introduction, had either of these factors been a dominant factor, we might have expected performance in the Sequential condition to exceed that in the Simultaneous condition. Instead, we can focus on potential explanations that predict better performance in the Simultaneous than in the Sequential condition. One such explanation is that detecting a difference in F0 between two simultaneously presented sounds does not necessarily involve an explicit extraction of F0. As mentioned in the introduction, the potential cues for such detection include BMC and perceptual fusion: BMCs would only be present (if at all) when the complexes in the two spectral regions differed in F0; perceptual fusion of the two simultaneous complexes might be reduced through mistuning, so that detecting a mistuning between the two regions may involve perceiving a loss of fusion, rather than an explicit mistuning. Informal reports from the listeners indicated that the mistuned intervals in the Simultaneous conditions had a “dissonant” quality not present in the intervals in which the two tones had the same F0. This is consistent with both the BMC and perceptual fusion explanations described above.

Another explanation that is consistent with better performance in the Simultaneous condition involves a decline in the memory trace of the pitch estimate of the first tone before it can be compared with the second tone (e.g., Laming & Scheiwiller, 1985). However, the results from a more recent study suggest that a simple decay of pitch memory may not adequately explain the differences observed here. Demany, Montandon, and Semal (2005) found that frequency discrimination between two sequentially presented brief tones actually improved as the ISI between them increased from 0 to approximately 500 ms, and then deteriorated only for longer ISIs. The former effect could be related to a reduction in backward recognition masking as ISI increases beyond 0 ms (Massaro, 1975; Massaro & Idson, 1977). Based on this finding, the difficulty experienced by our participants in the Sequential condition could be because the tones are presented directly after one another, rather than because of a decay in the memory trace between the time of the first and second pitch estimates.

Experiment 2 was designed to test these various explanations further. If changes in perceptual fusion can explain performance in the Simultaneous condition, then performance in that condition should be affected by stimulus manipulations that affect the perceptual organization of the test sounds. If a lack of sufficient time to consolidate a pitch representation of the first sound in each interval can explain the poor performance in the Sequential task, then manipulating the gap between the stimuli within each interval should affect performance.

Experiment 2: Effects of Temporal Asynchrony or a Silent Gap

The main finding of Experiment 1 was that listeners were better able to detect an F0 difference between two spectrally non-overlapping harmonic complexes when the tones were presented simultaneously than when they were presented sequentially. We hypothesized that listeners may have been able to use a cue in the Simultaneous condition that was not available in the Sequential condition. The two cues discussed involve BMC and the degree of perceptual fusion. To distinguish between these two possible cues, we created a new condition (Overlap) in which the onsets of the two tones were asynchronous but the two tones overlapped temporally for the same duration as the tones in the Simultaneous condition of Experiment 1. The onset asynchrony should not affect BMC-related cues because the two complexes are still presented at the same time and so continue to interact. However, onset asynchrony is a segregation cue, so the asynchrony should disrupt perceived fusion (Bregman, 1990). Therefore, if the benefit of complexes being played simultaneously in Experiment 1 was due to their being grouped as a single auditory object (perceptually fused) when they shared a common F0, performance in the Overlap condition should be worse than in the Simultaneous condition because the two tones should form two separate objects regardless of whether they share the same F0. The longer tone durations in the Overlap condition should provide more information for any mechanism that estimates the F0 in each spectral region.

Aside from being poorer than in the Simultaneous condition, performance in the Sequential condition was surprisingly poor in absolute terms. Performance did not reach ceiling even at F0 differences of 4.5 semitones, or about 30%. This may be due to the fact that in the Sequential condition, the two tones were played immediately after one another. As mentioned earlier, Demany et al. (2005) found that frequency discrimination is non-monotonically related to the temporal gap between the tones. It may be that this non-monotonic behavior is particularly strong in conditions involving tones filtered into different spectral regions, which differ markedly in timbre. For such tones, pitch may need to be extracted and abstracted from timbre for each complex before it can be compared. This pitch-timbre separation process may increase processing time. To investigate whether listeners benefit from a gap between the tones, we generated a condition (Gap) that was identical to the Sequential condition of Experiment 1 except that a gap of 200 ms was inserted between the offset of the first tone and the onset of the second tone in each interval. If the memory trace of the first tone monotonically degrades after its offset, we would expect the gap to make performance worse. If, instead, listeners can use the extra 200 ms to better encode the pitch estimate of the first tone, this gap could improve performance, perhaps to the extent that it is unnecessary to postulate any additional mechanisms to explain the superior performance in the Simultaneous condition.

Method

A schematic of the stimuli presented in the four conditions of this experiment is shown in Figure 1. Complex tones as described for Experiment 1 were used in this experiment. The first two conditions were identical to the Simultaneous and Sequential conditions of Experiment 1 (Figure 1, A and B). In the third condition, termed the Overlap condition, the duration of each tone was 600 ms, and the onset of the second tone was delayed by 200 ms relative to the onset of the first tone, such that the two tones overlapped by 400 ms (Figure 1C). In order to make sure that participants were aware of the two possible ways of listening to the stimuli in that condition, the instructions mentioned that they could either listen to the two sounds as individual sounds or concentrate on the time when the two complexes overlapped. In the fourth condition, the Gap condition, 400-ms tones were presented such that the onset of the second tone was 600 ms after the onset of the first tone (Figure 1D). This created a 200-ms gap between the two complex tones. A duration of 200 ms was chosen to provide a clear gap between the tones in each interval, while keeping the total length of each trial down to 2.5 s. As in the Sequential condition, the first tone in both the Overlap and Gap conditions was filtered into the lower spectral region and the second was filtered into the higher spectral region.

The general procedure was the same as for Experiment 1. Fifteen participants who took part in Experiment 1 also completed the two additional conditions of Experiment 2. They completed the four conditions (two from Experiment 1 and two from Experiment 2) in counterbalanced order to avoid order effects. Three participants ran an earlier version of the Overlap condition, which had shorter tone durations. Because the data obtained in this condition are not directly comparable to those obtained using the final version of the Overlap condition, they were not included in the analyses described below. Participants completed the four conditions over two 2-h sessions on different days, such that two conditions were completed during each session.

Results

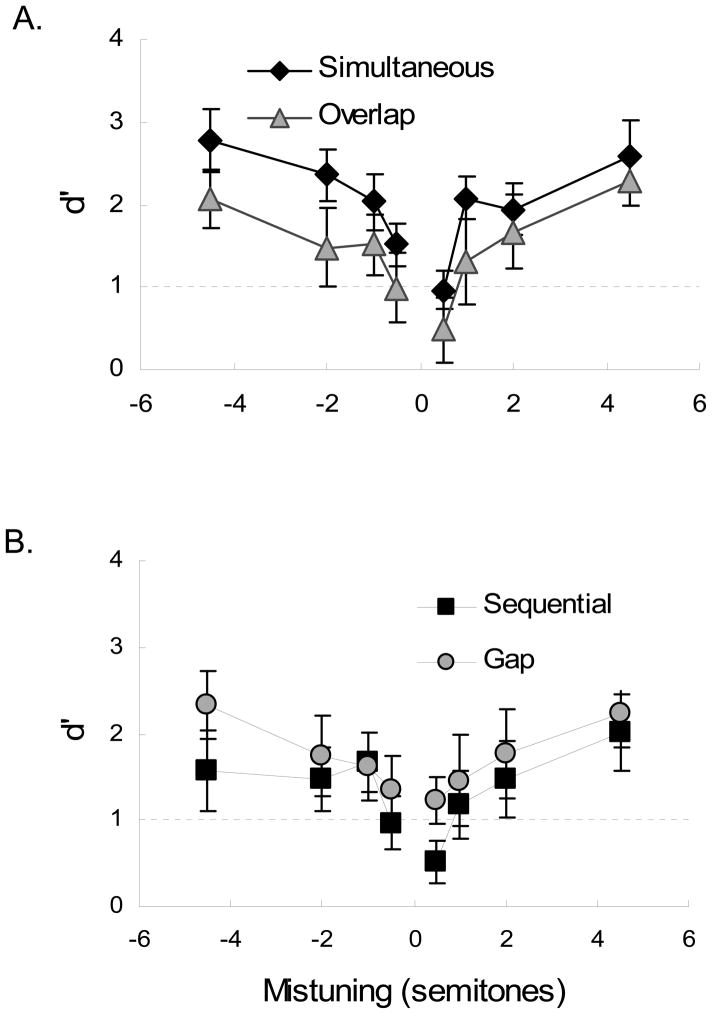
The results of Experiment 2 are shown in Figure 3. For all four conditions d′ values were calculated using the differencing strategy for 4IAX, as described in Experiment 1. Since all participants who participated in Experiment 2 also participated in Experiment 1, data from Experiment 1 for these participants are included in both the figure and in the analysis.

Figure 3.

The averaged results of Experiment 2. The panel on the left (A) shows performance in a concurrent F0 difference detection task between tones having synchronous (Simultaneous, filled diamonds) and asynchronous (Overlap, shaded triangles) onsets. The difference between the two conditions is significant. The panel on the right (B) shows performance in a serial F0 difference detection task between tones in which the second tone immediately followed the first (Sequential, filled squares) and one in which the second tone followed the first after a 200 ms gap (Gap, shaded circles). Performance was not significantly different in these conditions. In both panels discrimination sensitivity (d′) is shown as a function of F0 mistuning.

The data were analyzed using a three-way RMANOVA comparing Simultaneous and Sequential conditions across mistuning levels and directions. As in Experiment 1, significant main effects of condition, F(1,14)=6.89, p=.02, η_p²=.33, mistuning amount, F(3,42)=25.69, p<.001, η_p²=.65, and mistuning direction, F(1,14)=8.77, p=.01, η_p²=.39, were observed. Again, performance was better in the Simultaneous condition, for larger mistunings, and when F0 was lower in the higher spectral region than in the lower spectral region. However, due perhaps to the smaller sample size here than in Experiment 1, there was no longer a significant interaction between experimental condition and the degree of mistuning, F(3,42)=1.41, p=.25, η_p²=.09. The interaction between degree and direction of mistuning was significant F(3,42)=3.3, p=.04, η_p²=.19, but the interaction between condition and mistuning direction, F(1,14)=1.11, p=.31, η_p²=.07, and the three-way interaction, F(3,42)=2.24, p=.11, η_p²=.14, were not significant.

The most relevant comparisons in Experiment 2 are between the Simultaneous and Overlap conditions and between the Sequential and Gap conditions. A comparison of the Simultaneous and Overlap conditions indicates whether the onset asynchrony affects listeners’ ability to detect mistuning. For this comparison, a three-way RMANOVA was performed with condition, mistuning amount, and mistuning direction as the within-subject factors, and the d′ values from each subject in each condition as the dependent variable. The analysis showed significant main effects for condition, F(1,11)=4.94, p=.05, η_p²=.31, for mistuning amount, F(3,33)=53.14, p<.001, η_p²=.83, and for mistuning direction F(1,11)=6.251, p=.03, η_p²=.36. Performance was poorer in the Overlap condition than in the Simultaneous condition, increased with the amount of mistuning, and was larger for positive mistunings than for negative mistunings. No significant interaction effects were observed, condition × direction F(1,11)=2.45, p=.15, η_p²=.18; condition × mistuning amount F(3,33)=.187, p=.91, η_p²=.02; mistuning direction × amount F(3,33)=1.825, p=.16, η_p²=.14; mistuning amount × direction × condition F(3,332)=.69, p=.560, η_p²=.06.

A comparison of the Sequential and Gap conditions was made to help clarify the reason for poor performance in the Sequential condition. For this comparison, a three-way RMANOVA was performed with mistuning and presentation type as the within-subject factors, and the d′ values from each subject in each condition as the dependent variable. The results showed no significant main effect for condition, F(1,14)=2.52, p=.14, η_p²=.15, or mistuning direction, F(1,14)=.34, p=.57, η_p²=.02. The only significant effect was for the amount of mistuning, F(3,42)=10.11, p<.001, η_p²=.42. None of the interactions were significant, condition × mistuning direction, F(1,14)=.02, p=.90, η_p²=.001; condition × mistuning amount, F(3,42)=.935, p=.43, η_p²=.06; mistuning direction × amount, F(3,42)=1.12, p=.34, η_p²=.07; mistuning direction × amount × condition, F(3,42)=1.54, p=.22, η_p²=.10. Detailed inspection of Figure 3 reveals visible differences in average d′ between the Sequential and Gap conditions, particularly at the −4.5 and 0.5 semitone mistunings, and higher values of d′ in the Gap condition than in the Sequential condition in seven of the eight levels of mistuning. However, a binomial sign test on differences comparing individual performance in these two conditions failed to reject the null hypothesis, p = .26. Thus, we cannot conclude that the introduction of a 200-ms silent gap between tones significantly affected performance.

Discussion

A comparison of the Simultaneous and Overlap conditions showed poorer performance in the Overlap condition, despite the fact that that the Overlap condition provided participants with longer tones from which to make F0 judgments, and with the same duration of simultaneous presentation. Thus, if participants were able to make independent estimates of the two F0s, performance in the Overlap condition should have equaled or exceeded that in the Simultaneous condition. Also, listeners could have performed equally well in the Overlap and Simultaneous conditions by attending only to the portion of the Overlap stimulus in which both tones were presented. The results do not seem consistent with the hypothesis that listeners were using a BMC cue in the Simultaneous condition, since the onset difference should not affect the presence of BMCs. Instead, the results are consistent with the idea that listeners used the degree of perceived fusion as a cue to detect mistuning in the Simultaneous condition, and that the onset asynchrony produced perceptual segregation, making both the tuned and mistuned intervals sound segregated.

A comparison of the Sequential and Gap conditions did not yield a statistically significant difference. Since performance in the Gap condition was no worse than in the Sequential condition, there is little evidence that poor performance in the Sequential condition is due to a degraded memory trace, which would be further degraded by the 200-ms delay between the two complex tones. Similarly, the gap does not seem to have produced a strong benefit through greater time for encoding. Perhaps both effects counteracted each other to some degree. If this is so, it is possible that an even longer gap might have improved performance. A future study could subject this question to a parametric investigation. However it seems more likely that the poor performance in the Sequential condition of Experiment 1 was not due to the lack of a gap, but to the large spectral (and timbral) difference between the two tones in each interval.

Experiment 2a: Perceived Fusion of Simultaneous and Overlap conditions

The results from Experiments 1 and 2 are consistent with the idea that listeners perform better in the Simultaneous condition because they are able to differentiate between in-tune and out-of tune pairs by listening for changes in a fusion cue that varies with the amount of mistuning in the Simultaneous condition, but not in the other conditions. In this follow-up experiment we tested whether listeners are more likely to hear two spectrally segregated tones as a single (fused) tone when they have the same, or similar, F0 and when they are presented simultaneously, compared to when the tones are presented asynchronously and/or are mistuned.

Method

Twelve normal-hearing listeners who did not participate in Experiments 1 or 2 completed four blocks of trials. Data from one additional listener was excluded because her performance in overlap trials was at chance, so we could not be sure she understood the task. Listeners were recruited from subjects participating in other studies in our lab, and were compensated for their participation.

Each trial consisted of a single pair of tones, identical to the tones presented in the Simultaneous or Overlap conditions, with a background TEN at 40 dB SPL per equivalent rectangular auditory bandwidth (ERB_N). Each block included ten trials of each condition at 0, 1, and 4.5 semitones mistuning presented in random order. For each trial, listeners heard the tones and were instructed to indicate whether they heard one or two tones. No feedback was given.

Results

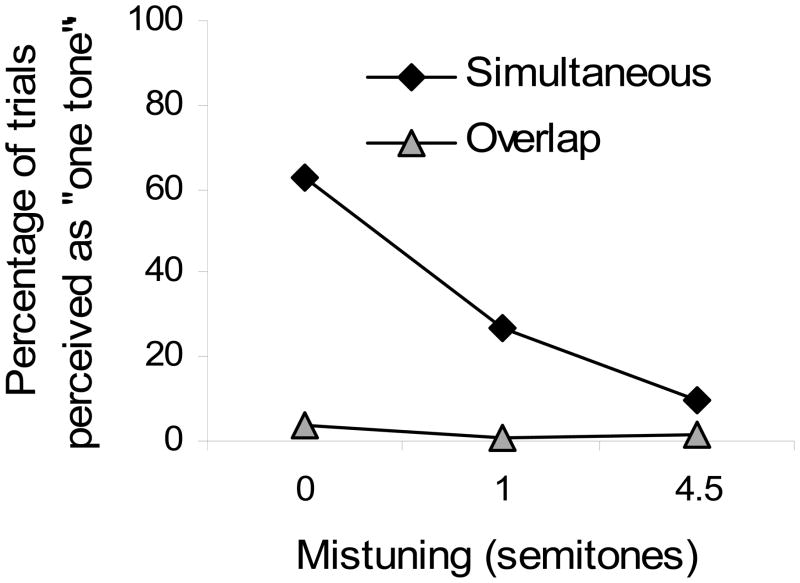
The averaged results are presented in Figure 4, with the percentage of “One tone” responses plotted as a function of the degree of mistuning. In the asynchronous Overlap conditions, listeners usually indicated that they heard two tones, regardless of the degree of mistuning. In the synchronous Simultaneous conditions, the percept depended on the degree of mistuning: for no mistuning, the majority of responses were for “One tone”, and the proportion of “One tone responses” decreased with increasing degree of mistuning. These trends were confirmed by a RMANOVA with factors of condition and amount of mistuning, which indicated that both were significant (F(1,11)=41.63, p<.001, η_p²=.79 and F(2,10)=22.21, p<.001, η_p²=.82 respectively), as was the interaction of condition and amount of mistuning F(2,10)=19.29, p<.001, η_p²=.79.

Figure 4.

Percentage of tones pairs that were perceived as “one tone”, as a function of the degree of mistuning between the lower and higher spectral regions. Diamonds represent responses from the Simultaneous condition, in which tones in the upper and lower spectral regions were gated synchronously; triangles represent responses from the Overlap condition, in which the tones were gated on and off asynchronously.

Discussion

The purpose of this experiment was to examine whether a fusion cue is a plausible candidate for a cue available in the Simultaneous condition but not available in other conditions. The data show that likelihood of identifying the stimulus as a single sound in the Simultaneous condition increased as F0 difference decreased, but was unlikely for all mistuning in the Overlap condition. Several listeners who had many years of musical experience reported that they were able to segregate the tones based on timbre, even when the two tones had the same F0. This may explain why the average proportion of “One tone” responses was not unity, even in the zero mistuning condition. Nevertheless, even in these listeners, the overall pattern of results was generally consistent with same-F0 simultaneous tones being easier to hear as fused.

Overall, the pattern of results supports the presence of a fusion cue that covaries with performance in the Simultaneous condition, but is not present in the Overlap condition or, presumably, in any of the other asynchronous conditions.

Experiment 3: Grouping with Captor Tones

The results of the previous experiments suggest that detection of F0 differences between tones played simultaneously is influenced by the perceived degree of fusion between the two tones, rather than an explicit pitch comparison. If so, it should be possible to disrupt this fusion cue by inducing perceptual segregation using cues other than gating asynchronies. One method that has been used successfully in the past involves the introduction of a sequence of tonal precursors. For instance, in a complex harmonic tone, where a single mistuned component can shift the perceived pitch of the overall complex (e.g. Moore, Glasberg, & Peters, 1985), the effect of the mistuned harmonic can be reduced or eliminated by preceding the complex with a sequence of tones at the same frequency as the mistuned harmonic (Darwin, Hukin, & al-Khatib, 1995). The sequence has the effect of “capturing” the mistuned harmonic into a separate stream from the rest of the harmonic complex, thereby reducing its contribution to the pitch of the complex. Similar manipulations have been used to alter the phonemic identity of synthetic vowels (Darwin, Pattison, & Gardner, 1989; Shinn-Cunningham, Lee, & Oxenham, 2007), and to alter thresholds in basic auditory detection tasks (Dau, Ewert, & Oxenham, 2009; Grose & Hall, 1993; Oxenham & Dau, 2001). Experiment 3 used a variant of this method to test listeners’ ability to judge F0 differences between two simultaneously presented complexes that are likely to be perceived as segregated. In this experiment, perceptual segregation was achieved via a sequence of precursors in the low spectral region, which were designed to form a perceptual stream with the target tone in the same spectral region.

We compared listeners’ F0 difference detection of tones presented simultaneously in isolation (SIM condition) – like those in Experiment 1 except with a shorter duration – to their performance when the tones were presented simultaneously following repeated presentations of the complex in the higher spectral region (SIMP condition). The repeated high-region complexes formed the tonal precursors, which were designed to form a perceptual stream with the high-region complex of the simultaneously presented target tones. This manipulation should reduce perceptual fusion between the high- and low-region target tones, causing them to be heard as two separate auditory objects, regardless of their mistuning, thereby reducing the salience of a perceptual fusion cue.

Our prediction is that, by decreasing spectral fusion, the tonal precursors will make performance in the SIMP condition poorer than performance in the SIM condition. However, according to “multiple looks” models (Green & Swets, 1966; Viemeister & Wakefield, 1991) the precursors could actually improve performance by providing listeners with more statistical information on which to base their estimate of the F0 of the high-region complex. For this reason, we included sequential conditions as controls that parallel the simultaneous conditions: one with precursors (SEQP) and one without (SEQ).

Method

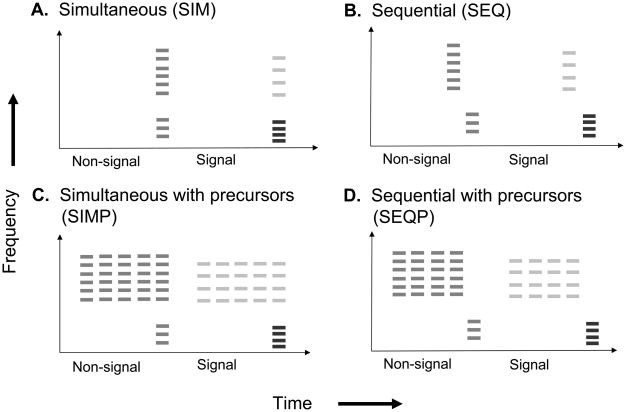
Complex tones, filtered into separate spectral regions as described for Experiment 1, were presented in each interval according to one of the four patterns shown in Figure 5. Tone durations were 100 ms including 10-ms squared-cosine ramps, and all non-simultaneous tones were separated by gaps of 50 ms. In the SIM condition, the target tones in both spectral regions were presented simultaneously. In the SEQ condition a tone in the high spectral region was followed (after a 50-ms gap) by a tone in the low spectral region. In the SIMP condition, a sequence of four precursor tones in the high spectral region was followed by the two target tones played simultaneously. In the SEQP condition, a sequence of four precursor tones in the high spectral region was followed by a tone in the low spectral region. Two intervals were presented on each trial. During one interval, all tones had the same F0. During the other interval, the F0 of the tone in the low spectral region differed from that of the tone or tones in the high spectral region by 0.5, 1, 2, or 4.5 semitones. The listener’s task was to indicate the interval in which the F0s differed. All other stimulus parameters were as in Experiment 1.

Figure 5.

A schematic of the stimuli used in Experiment 3. Participants listened to two intervals containing spectrally segregated harmonic complexes and indicated the interval in which the F0 of the high region complex differed from that of the low region complex(es). Increased spacing between lines and lighter shading indicate a higher F0. Harmonic complexes to be compared were presented simultaneously (A, C) or sequentially (B, D), with (C, D) or without (A, B) tonal precursors identical to the tone presented in the low spectral region. The diagram is not to scale.

Nineteen participants (14 female) who had not participated in Experiments 1 or 2 completed the experiment. Their ages ranged from 18 to 28 (mean age 21 yr). All participants had pure-tone thresholds of 20 dB HL or better at audiometric frequencies (from 500 to 8000 Hz). Participants were recruited through flyers and an online listing. Participants completed two sessions of approximately two hours, which included both the experiment and a brief practice session to become familiar with the task. They were compensated with cash or extra-credit points for a psychology course.

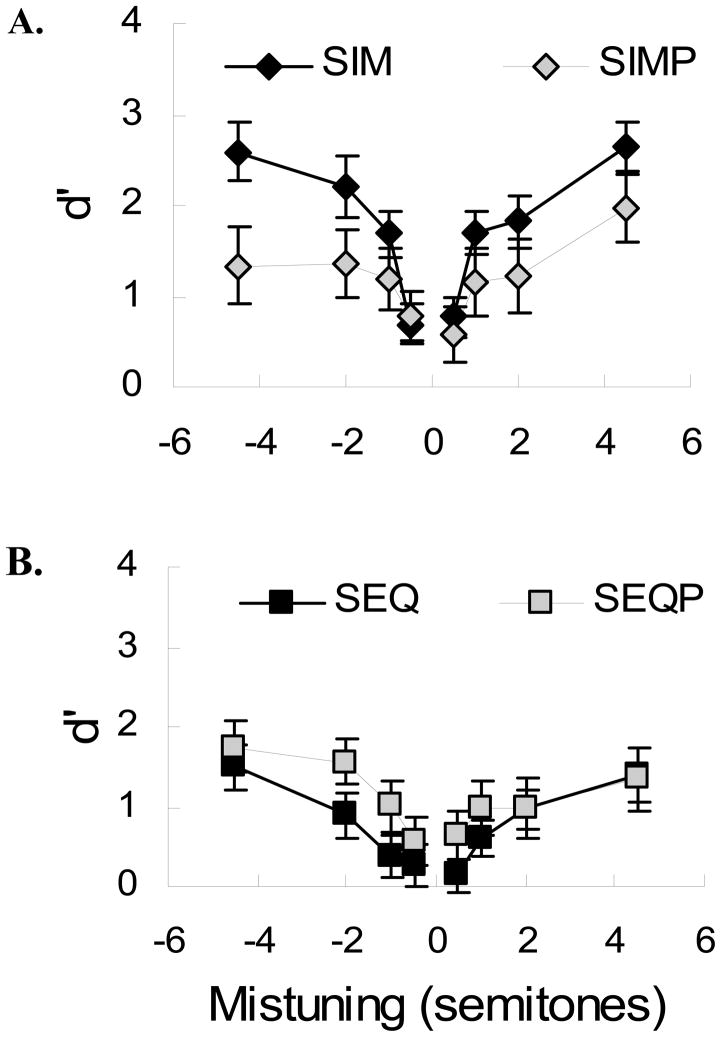
Results

Averaged results are shown in Figure 6. For each condition, d′ values were calculated from participants’ responses using the differencing strategy for 4IAX, as described in Experiment 1. A three-way RMANOVA with factors of condition, level of mistuning, and direction of mistuning showed significant effects of condition, F(3,54)=13.471, p<.001, η_p²=.43, and mistuning level, F(3,54)=30.48, p<.001, η_p²=.63, but not mistuning direction F(1,18)=.49, p=.50, η_p²=.03. The interaction between condition and mistuning level was significant F(9,162)=2.70, p=.006, η_p²=.13. All other interactions were not significant, condition × mistuning direction, F(1.02)=1.02, p=.39, η_p²=.05; mistuning direction × mistuning level, F(3,54)=.97, p=.40, η_p²=.05; condition × mistuning direction × mistuning level, F(9,162)=1.49, p=.17, η_p²=.08. Post-hoc pair-wise comparisons using Tukey’s Least Significant Difference test showed that the SEQ condition was significantly different from all other conditions (SIM p <.001, SEQP p = .024, SIMP p = .020), as was the SIM condition (SEQP p = .003, SIMP p = .011). Performance in SIMP and SEQP did not differ significantly from each other (p = .375). Performance in the SIM condition was best, followed by performance in SIMP and SEQP, and then by performance in the SEQ condition.

Figure 6.

The averaged results of Experiment 3. The top panel (A) shows performance in simultaneous F0 difference detection task either with (SIMP) or without (SIM) tonal precursors. The bottom panel (B) shows performance in sequential conditions with (SEQP) and without (SEQ) tonal precursors. Data from the top panel are indicated without markers in the bottom panel and vice versa to aid comparison across conditions. Discrimination sensitivity (d′) is shown as a function of the F0 mistuning. Performance in the two conditions with tonal precursors is not significantly different; performance in all other pairs of conditions are significantly different from each other.

Discussion

The main finding of Experiment 1 was replicated with the shorter tones used in this experiment: Participants performed more poorly on a mistuning detection task when tones in separate spectral regions were presented sequentially than when they were presented simultaneously. Performance in the two conditions with precursors was equivalent and intermediate between performance in the simultaneous and sequential conditions.

Listeners’ better performance in the SEQP relative to the SEQ condition is qualitatively consistent with the “multiple looks” idea (Green & Swets, 1966; Viemeister & Wakefield, 1991). Listeners seem able to use the precursors to generate a better estimate of the F0 of the complex in the low spectral region.

Listeners’ poorer performance in SIMP relative to SIM shows that adding tonal precursors can impair mistuning detection. Since the tonal precursors have been shown to disrupt grouping, this result is consistent with our hypothesis that disrupting grouping in a simultaneous pitch comparison task can impair performance. The performance difference supports the idea that listeners tend to detect F0 differences in simultaneously presented tones by listening for differences in perceptual fusion. This cue is absent when the complexes are heard as two separate objects, so the difference in pitch becomes more difficult to detect. The similarity in performance between SIMP and SEQP conditions supports the idea that the tonal precursors in the SIMP condition capture the final low tone into a separate stream from the high tone, which effectively forces participants to perform the condition sequentially, as in the SEQP condition.

General Discussion and Conclusions

Summary of Results

The aim of this study was to investigate how listeners’ ability to detect F0 differences (mistuning) between complex tones is affected by the relative timing of the tones. Experiment 1 showed that the performance of participants in a sequential F0 comparison task was generally poorer than in a simultaneous task with directly comparable stimuli. Fitting a logistic function to the data collected at a range of mistuning levels resulted in threshold (d′ = 1) estimates of around 1.5% and 3.5% for the simultaneously and sequentially presented tones, respectively. For the sequentially presented tones, performance often remained below ceiling even at much larger F0 separations of 4.5 semitones (~30%). Experiment 2 investigated some possible explanations for this difference, and found that disrupting the perceptual grouping of simultaneously presented complexes by introducing an onset and offset asynchrony caused performance to worsen. However, adding a silent gap between the complexes presented sequentially had no significant effect on mistuning detection. These results suggest that listeners were not making explicit F0 comparisons in the Simultaneous condition, but rather using a “fusion” cue, which was not present in the Sequential condition. This conclusion was supported by the results of Experiment 2a, which asked listeners explicitly whether they heard one or two sounds in both synchronous and asynchronous conditions, as a function of the degree of mistuning. To further test the perceptual fusion hypothesis, Experiment 3 manipulated the extent to which the simultaneous complexes were heard as a single event or source by using precursor tones to capture one of the complexes into a separate perceptual stream. The results again supported the hypothesis that listeners used the degree of perceived fusion between two simultaneous complex tones as a cue to detect mistuning.

Detrimental Influence of Timbre Differences on Sequential Pitch Comparisons

Not only was listeners’ performance in the sequential F0-comparison task poor relative to that measured in the simultaneous task, but it was also markedly poorer than expected based on studies using complexes filtered into the same spectral region and containing corresponding harmonics (e.g. Carlyon & Shackleton, 1994). The results of these studies typically show F0 difference limens (corresponding to about 70 or 80% correct) of less than 1% for tones containing resolved harmonics, as was the case here. In contrast, the participants in our study did not achieve more than about 65–73% correct on average, even when the F0 difference was as large as 4.5 semitones (approximately 30%). In terms of the “threshold” measure derived from performance in Experiment 1, our subjects achieved a d′ of 1 with a F0 difference of approximately 3.5%, which is in line with other studies that have tested F0 discrimination for tone complexes with different spectral envelopes (e.g. Micheyl & Oxenham, 2004; Moore & Glasberg, 1990). The earlier studies did not test performance at larger ΔF0s. However, three observations suggest that the poor performance at large ΔF0s was not due just to insufficient training or lack of motivation. First, the same listeners achieved high performance in the simultaneous condition, indicating that they had difficulty specifically with the sequential conditions. Second, a subset of the participants displayed near-ceiling performance in control conditions that involved comparisons between tones filtered into the same spectral region, indicating that their difficulties in the sequential case might be due largely to timbre differences. Third, a pilot study involving ten of the participants from Experiments 1 and 2 found no significant improvement in performance with continued practice listening for F0 differences with the stimuli from the Simultaneous and Sequential conditions over a period of 18 hours. Overall, it appears that for most listeners pitch comparisons between sequential sounds that have markedly different timbres are far less accurate than pitch comparisons between sounds that have the same timbre. The results of the current study suggest that this is the case even for musically experienced listeners (Experiment 1).

A Directional Asymmetry in Mistuning Detection

An asymmetry related to the direction of mistuning between the two tones was observed in Experiments 1 and 2. The results of these experiments usually showed poorer performance when the complex filtered into the higher spectral region had a higher F0 than the complex filtered into the lower spectral region, compared to the converse situation. The reason for this effect is not entirely clear. A tentative explanation is based on the “octave enlargement” or “stretched octave” phenomenon. Tones are often judged to be one octave apart when the ratio of their frequencies is slightly larger than 2, rather than exactly equal to 2. This effect has been observed not only with pure tones (Demany & Semal, 1990; Ward, 1954) but also with complex tones (Sundberg & Lindqvist, 1973), suggesting that for the harmonics in a complex tone to be perceived as having the same spacing (corresponding to the same F0s), the physical frequency spacing may have to be slightly larger at higher frequencies than at lower frequencies. As a result of this, positive mistunings (corresponding to the case where the higher spectral region contains a higher F0) may be more difficult to detect than negative mistunings. To the extent that the origin of this effect precedes the stage at which the cues and mechanisms responsible for sequential and simultaneous F0 comparisons start to diverge, this could explain why the effect was observed in both tasks. It has been suggested that the octave enlargement effect originates in neural refractoriness, an effect already observed in primary afferent fibers of the auditory nerve (McKinney & Delgutte, 1999; Ohgushi, 1983). The effect has also been explained in terms of central template models that operate on place representations (Terhardt, 1974), or on a combination of place and synchrony information (Hartmann, 1993). While these various explanations have been proposed for pure tones, it is not entirely clear whether and how neural refractoriness can account for an octave enlargement effect with complex tones. Further research is needed to clarify this issue, and to determine the origin for the small but statistically significant mistuning-detection asymmetry observed here.

Implications for Models of Pitch Perception

The results of this psychophysical study have several potentially important implications for theories and models of pitch perception. First, the results provide further evidence for, and quantitative measures of, the influence of (spectral) timbre differences on human listeners’ ability to compare the F0 (or pitch) of sequentially presented sounds. This provides an interesting test of existing pitch models, based on whether or not the model can predict such a detrimental influence of timbre differences on pitch comparisons. Models in which virtual pitch is determined independently from timbre may not be able to predict this finding at all. Models in which F0 discrimination performance is predicted based on measures of overall dissimilarity (e.g. Euclidian distance) between representations of F0 that vary depending on timbre (such as the summary autocorrelation function of Meddis and colleagues (Meddis & Hewitt, 1991; Meddis & O’Mard, 1997), may be able to predict the effect qualitatively, but it remains to be seen whether they can predict it quantitatively.

Another aspect of the present results, which existing models of pitch perception may have trouble replicating, is the surprisingly high sensitivity of human listener’s to F0 differences between simultaneously presented tones. So far, models of pitch perception have been focused on predicting the pitch or pitch salience of isolated complexes, or F0 discrimination thresholds measured using complex tones presented sequentially into the same spectral region. Some authors have developed models to account for F0-based separation of concurrent sounds, such as vowels (Assmann & Summerfield, 1990; Meddis & Hewitt, 1992). However, to our knowledge, these models have never been applied to predict performance in mistuning detection tasks involving F0 differences between groups of harmonics in different spectral regions. Therefore, it remains largely unclear whether and how these models can predict human listener’s sensitivity in such tasks.

Finally, and perhaps most importantly, the present findings indicate that human sensitivity to F0 or pitch differences depends critically upon perceptual organization processes. We found that conditions that promoted the perceptual segregation of simultaneous sounds greatly hampered listeners’ ability to detect F0 differences and mistuning. The influence of perceptual grouping mechanisms on pitch discrimination supports the view that pitch is unlikely to be determined solely by peripheral mechanisms, and that perceptual grouping and pitch mechanisms interact, perhaps at relatively central levels of analysis (e.g. Darwin et al., 1995). With rare exceptions, existing models of pitch perception do not include perceptual organization processes. They compute the pitch of incoming sounds without regard for whether or not these sounds are perceived as a single auditory object or source. These models may require substantial revisions in order to account for the present findings.