Abstract
Electron spin echo envelope modulation (ESEEM) is a technique of pulsed-electron paramagnetic resonance (EPR) spectroscopy. The analyis of ESEEM data to extract information about the nuclear and electronic structure of a disordered (powder) paramagnetic system requires accurate and efficient numerical simulations. A single coupled nucleus of known nuclear g value (gN) and spin I=1 can have up to eight adjustable parameters in the nuclear part of the spin Hamiltonian. We have developed OPTESIM, an ESEEM simulation toolbox, for automated numerical simulation of powder two- and three-pulse one-dimensional ESEEM for arbitrary number (N) and type (I, gN) of coupled nuclei, and arbitrary mutual orientations of the hyperfine tensor principal axis systems for N>1. OPTESIM is based in the Matlab environment, and includes the following features: (1) a fast algorithm for translation of the spin Hamiltonian into simulated ESEEM, (2) different optimization methods that can be hybridized to achieve an efficient coarse-to-fine grained search of the parameter space and convergence to a global minimum, (3) statistical analysis of the simulation parameters, which allows the identification of simultaneous confidence regions at specific confidence levels. OPTESIM also includes a geometry-preserving spherical averaging algorithm as default for N>1, and global optimization over multiple experimental conditions, such as the dephasing time ( ) for three-pulse ESEEM, and external magnetic field values. Application examples for simulation of 14N coupling (N=1, N=2) in biological and chemical model paramagnets are included. Automated, optimized simulations by using OPTESIM lead to a convergence on dramatically shorter time scales, relative to manual simulations.
INTRODUCTION
Electron spin echo envelope modulation (ESEEM) is a technique of pulsed-electron paramagnetic resonance (EPR) spectroscopy that reveals the energies of electron-nuclear hyperfine (hf) interactions, and, for nuclei with I≥1, nuclear quadrupole interaction (nqi) energies [1; 2]. Nuclear state mixing and a bandwidth of the microwave pulse magnetic field (B1) larger than the hf splitting afford favorable conditions for the detection of ESEEM from single or small numbers of electron-nuclear couplings. The modulation of the echo envelope is collected in the pulse time domain, and is cosine Fourier-tranformed to create an ESEEM frequency spectrum. Schematic pulse timing diagrams for the standard one-dimensional two-pulse and three-pulse ESEEM experiments are shown in Figure 1. In certain cases, qualitative information about the identity, number, and magnitude of the coupling of the coupled nuclear spin(s) can be gained from inspection of the modulation periodicities in the waveform or the line positions in the Fourier transform (FT). However, simulation of the ESEEM is required to extract the coupling parameters that give the desired detailed information about the nuclear and electronic structure of the molecular paramagnet, such as the hf tensor and electric field gradient (efg) tensor (nqi parameters). Different programs for the numerical simulation of ESEEM have been reported and used to interpret one-dimensional and two-dimensional experiments [3; 4; 5; 6; 7; 8; 9]. Although the simulations yield, in many cases, a high level of agreement with experiment, the process of matching simulation and experiment remains both subjective and time-consuming, and is the bottleneck in the interpretation of ESEEM experiments. Here, we describe an ESEEM simulation software toolbox that incorporates automated fitting with an efficient hybrid optimization approach, and provides an assessment of the statistical significance of the simulation parameters.
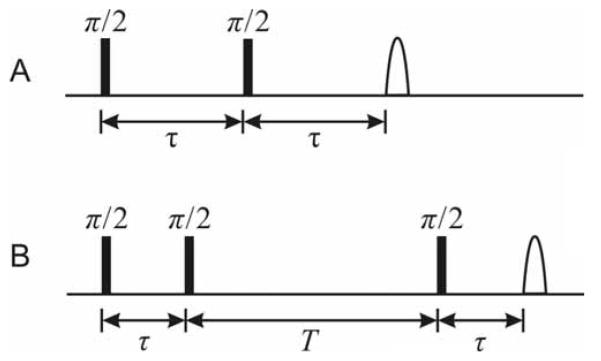
Figure 1.
Pulse timing diagrams for the two- and three-pulse ESEEM pulse sequences. A. Two-pulse sequence: π /2 — τ — π /2 — τ — detection . B. Three-pulse sequence: π /2 — τ — π /2 — T — π /2 — τ — detection.
The overall design goal of the tool box (denoted by OPTESIM, for optimization of ESEEM simulation) is to provide a modular, flexible set of routines for an automated, optimization-based simulation of diverse paramagnetic systems (arbitrary number of hf coupled nuclei with arbitrary nuclear spin; different classes of electron spins). For this purpose, a collection of functions for scripting is most appropriate. The Matlab (Mathworks, Natick, MA, USA) programming environment is chosen for the development of OPTESIM, because of the following features: (1) Matlab is generally available for academic use, (2) Matlab is easier for further development, compared to a C++ or FORTRAN environment, and (3) a number of literature numerical and optimization routines are available in Matlab. In addition, a practical consideration is that experiment control and data collection software can be developed in Matlab, which allows a seamless flow from ESEEM data acquisition to end analysis. The core calculations of the nuclear eigenvalues and eigenvectors and the time evolution of the density matrix use direct diagonalization methods [10; 11]. The optimization is achieved by using the minimization of the least-squares residuals of the match of the simulated to the experimental ESEEM, and is generally carried out in the time-domain, where distortions of the FT owing to waveform truncation are absent. Algorithms for the search of the hf, nqi, and system-specific Euler angle parameter space are as follows: genetic algorithm [12], simulated annealing [13], Nelder-Mead simplex [14], Gauss-Newton method, and Levenberg-Marquardt method [15]. A statistical assessment of the uncertainty in a parameter, with respect to other parameters, is given by the calculated simultaneous confidence region for each parameter.
We apply OPTESIM to the simulation of a system, which had been previously simulated by “manual” simulation, and to one which is too complex to efficiently simulate by “manual” simulation. In each case, a two-tier approach of genetic algorithm (coarse grained search for basin around the global minimum) followed by simplex (fine grained search for the global minimum within the basin) optimization are used. The automated, optimization simulations converge on dramatically shorter timescales, relative to manual simulations.
THEORY
Spin Hamiltonian
The stationary-state Hamiltonian for treatment of the interaction of an electron spin (S=1/2) with one nuclear spin ( I ) is formulated with a hf coupling term, a nuclear Zeeman term, and a nqi term (for I ≥ 1) , as follows:
| (1) |
where βN, , and are the nuclear magneton, electron spin operator, and nuclear spin operator, respectively, gN is the nuclear g-value, A is the hf coupling tensor, and Q is the nqi tensor [16]. The I and I’ indicate that the eigenfunctions of A and Q are, in general, different. The hf tensor has the principal components, , and is composed of an isotropic part, Aiso , and a dipolar part. In the point dipole approximation, the dipolar part is given by an axially symmetric dipolar tensor, , where Adip = (μ0 / 2h)geβegNβNreff-3 , and ge , βe , and reff are the electron g-value, Bohr magneton, and an effective distance between the electron and the nuclear spins, respectively [16]. The hf tensor Ap is rotated to the molecular frame, which is defined by a reference principal axis system (PAS) that is provisionally related to the electron g tensor PAS, by the following operation:
| (2) |
where RA is a rotation matrix, which is defined by the Euler angles, , to rotate from the electron g tensor PAS to the hf coupling tensor PAS.
The nqi tensor, Q, is defined by the nuclear quadrupole coupling constant, e2qQ/h, and the efg asymmetry parameter, η, where e, q, and Q are the elementary charge, the magnitude of the principal component of the efg tensor, and the nuclear quadrupole moment, respectively. In its PAS, the traceless nqi tensor is related to e2qQ/h and η by the following expressions:
| (3) |
| (4) |
where . In the toolbox, the orientation between the nqi tensor PAS and the hf tensor PAS is defined by the Euler angles , which consequently define a rotational matrix, RQ , and nqi tensor Q in the molecular PAS (g tensor PAS) to be expressed as follows:
| (5) |
This definition of Q by using a two-stage rotation allows an additional constraint on the mutual orientations of A and Q during numerical optimization, which adds to the flexibility in the specification of the geometry model for multiple electron-nuclear interactions.
To summarize, the general coupled electron — single nucleus system for I ≥ 1 is parameterized by using the following thirteen parameters: gN , I , Axx , Ayy , Azz , αA , βA , γA , e2qQ / h , η, αQ , βQ , and γQ (for , the five nqi-associated parameters are dropped). In practice, the coupled nucleus is assigned based on characteristic spectral features or a priori knowledge of the system, so that gN and I are fixed, which entails eleven adjustable parameters. In disordered, or powder, systems (no preferred orientation of the molecular, or g, PAS relative to B0), A, A, and A are not considered, and the number of adjustable parameters is reduced to eight. The point dipole assumption for electron-nuclear dipolar coupling reduces the number of adjustable parameters to seven. Additional nuclear couplings introduce three Euler angle parameters that describe the mutual orientations of the hf PAS, in addition to the individual nuclear coupling parameters, described above. In OPTESIM, all of the parameters can be subjected to the numerical optimization.
ESEEM Calculation
The time-domain ESEEM calculation incorporates the full density matrix diagonalization from the Mims density matrix treatment of ESEEM [10; 11]. Although the time evolution simulation of a pulsed magnetic resonance experiment is straightforward [7; 8], the explicit evaluation of the transition frequencies and intensities is computationally advantageous for optimization purposes, relative to methods that calculate the time evolution of the density matrix. Specifically, the following adapted numerical procedure [1; 2; 17], which we have used previously in ESEEM simulations [9], is found to be most efficient for constructing the two-pulse and three-pulse modulation in OPTESIM.
The Hamiltonian is first partitioned into sub-matrix representations Hα and Hβ corresponding to α (ms=1/2) and β (ms=-1/2) electron spin manifolds. Hα and Hβ are diagonalized separately with unitary matrices Mα and Mβ to obtain the eigenfrequencies, να and νβ, belonging to the α and β manifolds, respectively. The Hamiltonian, H, is transformed into H’, which corresponds to the coupled representation, as follows:
| (6) |
where M = Mα †Mβ.
The modulation frequencies and amplitudes are then calculated for specific types of experiments. For example, for the two-pulse echo envelope modulation (pulse sequence, Figure 1), the frequencies ω and amplitudes A are as follows:
| (7) |
The indices i, m, j, and k allow permutation through all elements of M and the eigenvalues.
The echo modulation amplitude E(τ) is formulated as follows [1; 2; 17]:
| (8) |
For the three-pulse echo modulation (pulse sequence, Figure 1), the frequencies ω and amplitudes A are separated into terms representing the α and β manifolds, as follows:
| (9) |
The simulated echo modulation amplitude E(τ, T) is formulated as follows [1; 2; 17]:
| (10) |
For flexibility, users can easily substitute their own time-domain ESEEM calculations into OPTESIM as Matlab functions. Therefore, experimental systems and pulse sequences other than those considered here [1; 2; 17] can be addressed by using the optimization and statistical assessment features of OPTESIM.
Powder average for disordered systems: General and geometry-preserving treatments
For a disordered, or powder, system, the ESEEM represents the average over all possible orientations of the external magnetic field vector B0, with respect to the molecular PAS [1; 2; 16; 17]. The number of orientations of B0 relative to the molecular PAS that can be evaluated is practically limited by the available computational power (time scale of the calculations) and the required accuracy. The orientation sampling vectors can be chosen as either a set of random unit vectors, or a set of evenly-distributed points on a unit sphere, or octant, if symmetry permits. Several methods have been used in the latter cases [18; 19]. In OPTESIM, a geodesic-sphere sequence generator evenly distributes vectors on a unit sphere. The generator subdivides each of the triangular faces of an icosahedron into four smaller triangles on a unit sphere in an iterative manner, yielding geodesic-sphere sequences at different levels of angular resolution. Users of OPTESIM also have the option to specify their own orientation vectors, as well as the weights of particular subsets of vectors. This approach is used for simulating orientation-selection experiments, in cases where the assumption of an isotropic g-tensor cannot be made [9; 20].
The overall envelope modulation when multiple nuclei are coupled to the electron is combined according to the product rule. Specifically, for the two-pulse sequence, the modulation is as follows [21],
| (11) |
and for the three-pulse sequence, the product is taken separately over the α and β manifolds, and the overall envelope modulation is combined, as follows [22],
| (12) |
In the case of electron spin coupling with multiple nuclei, it is computationally expedient to perform the powder, or spherical, average of individual electron—nuclear interactions prior to combination of the individual Etot (τ) , or Eα,i (τ ,T ) and Eβ,i (τ ,T) , modulation terms. This method implicitly assumes that the hf PAS of all electron—nuclear interactions are coincident. However, coincidence of all hf PAS is not generally the case, and information about the mutual orientation of the nuclei, which is contained in the order≥2 modulation product terms, is lost with this treatment. In OPTESIM, the combination rule is specified at the level of a physical model of the geometry of electron—nuclear interactions, as defined by Euler angles that specify the mutual orientation(s) of the different hf PAS. Therefore, the ESEEM is calculated and combined at each powder average orientation, and subtle structural information arising from the geometry of the multiple hf PAS can be retrieved from the overall averaged spectrum.
Optimization and statistical analysis of experimental parameters
Optimization is achieved by fitting the simulated spectrum () to the experimental one (Y) by using the minimization of the least-squares residuals, which are a function of the parameters (ϑ = [θ1,θ2,ℏ,θL]) of the Hamiltonian. The goodness of least-squares fitting for one spectrum is defined as . For a global fitting of multiple spectra with different experimental parameters, Q2 for the individual spectrum is weighted by its own noise level. The global goodness of fitting is defined as:
| (13) |
where σk2 and nk are the noise variance and number of points in spectrum k, respectively. We assume that the experimental envelope modulation is free of artifacts (for example microwave phase drift, “glitches” above the rms noise level), which is the case in our experiments [23; 24; 25], and that the noise variance of each point in the ESEEM waveform is identical (dead time points removed). In this normalized representation and with the two assumptions, the variance of the simulation error of all data points (Yk,i) is estimated as follows:
| (14) |
where is the optimized Q2 minimum at the global minimum, N is the total number of experimental points, as given by , and L is the number of independent parameters for optimization. Q2(ϑ) can be expanded at , as:
| (15) |
where are the optimal parameters when . Assuming that the terms with order >2 are negligible, and that the variances of the measurement errors follow a normal distribution, then the term:
| (16) |
follows a χ2 distribution with a freedom of L [26]. The simultaneous confidence region of parameters ϑ can be determined by the following expression:
| (17) |
The simultaneous confidence region gives an estimation of the uncertainty of a selected optimization parameter with respect to the other parameters. The probability of the simultaneous confidence region containing the true values of ϑi is determined by χ2(L) and a, as a cumulative distribution of χ2(L) from −∞ to a. For example, when L = 2 and a = 12, 22, or 32, the simultaneous confidence probability is 39.3%, 86.5%, or 98.9%.
SIMULATION OF ESEEM
The OPTESIM software consists of twenty-eight Matlab functions and eight Java classes that can be divided into the following four categories: experimental data filtering, numerical simulation, simulation parameter optimization, and distributed computation framework. These categories are incorporated into four stand-alone modules that are integrated in OPTESIM, as described below. The modules may be individually substituted by the routines of other users, if desired. Table 1 shows a code fragment example of OPTESIM.
Table 1.
A code Fragment example of OPTESIM.
| %Load experimental spectrum spectrum = filterRaw(filename, filter_options); |
| %Define a model of one deuterium and one proton with a %product rule optmodel = eseOptModel({’H2’,’H1’}, ’1*2’); |
| %Set the nulcear parameters for Nucleus 1 optmodel = changeOptModelValue(optmodel,... ’eeqQ’, 1, 0.2, ’eta’, 1, 0.1); |
| %Set the nulcear parameters for Nucleus 2 optmodel = changeOptModelValue(optmodel,... ’eeqQ’, 2, 0.2, ’eta’, 2, 0.1); |
| %Register variables for Optimization |
| %Parameter, nucleus number, index, min value, max value optmodel = registerOptModelVariable(optmodel,... ’Aiso’, 1, 1, -10, 10, ... ’r’ , 1, 2, 0, 10, ... ’Aiso’, 2, 3, -10, 10, ... ’r’ , 2, 4, 0, 10); |
| %Set initial values for %Aiso1, r1, Aiso2, r2, respectively x = [6.5, 2.5, 1.5, 2.5]; |
| %Use simplex methods for optimization options = optimset(’OutputFcn’, @esePlot, ’Display’, ’iter’); x_opted = fminsearch(@eseOptObjective, x, options); |
Experimental data filtering
Experimental data filtering allows extraction of experimental parameters from saved experimental data files and processing of the modulation amplitude waveform for simulation analysis. For two-pulse ESEEM, the extracted experimental parameters are experiment type, τ value, and B0 field. For three-pulse ESEEM, the additional experimental parameter, T, is extracted. An example data filtering routine that is compatible with our experimental control software is provided with the package. The ESEEM waveform is then processed, as follows. If necessary, baseline decay of the echo envelope, owing to spin-lattice (T1) or spin-spin (T2) relaxation processes, is removed by using an empirical decay function. This is accomplished by fitting the waveform to a user specified monoexponential, biexponential, or stretched exponential function, and then subtracting the decay function from the experimental waveform. Any points recorded within the spectrometer deadtime are removed. The deadtime portion of the waveform is reconstructed as part of the optimization during the simulation. The average noise variance (σ2) of the processed waveform (minus the deadtime fill points) is calculated.
Numerical Simulation
Numerical simulations of ESEEM are performed for one or more electron-nuclear couplings with the identity of each nucleus supplied by the user, corresponding to the parameters: gN and I. This information can often be gleened from a qualitative interpretation of the spectrum, or with the aid of multiple microwave frequency/B0 experiments. In the case of unidentified nuclei or numbers of nuclei, the most likely models can be assessed from the statistical criteria in OPTESIM for separate simulations that incorporate different types and numbers of coupled nuclei. A model for the combination of the ESEEM from multiple nuclei is also specified. In the most simple case of all nuclei coupled to the same electron spin, and a single nuclear isotope for each coupling, the envelope modulation for two-pulse and three-pulse experiments is combined according to the product rule expressions in Eq. 11 and Eq. 12, respectively. When the experimental ESEEM is known to arise from sub-populations of electron spins with different nuclear coupling(s), the “sum rule” [21; 27] for combination of the individual ESEEM is used, with a weighting factor for each population, to generate the total ESEEM. Practical cases where the sum rule and weighting are necessary are incomplete or heterogeneous isotopic substitution of a nuclear site, conformational isomers of the same paramagnetic molecule, and different paramagnetic molecules. OPTESIM allows users to specify the particular combination rule by using a numerical expression. For example, in the case of two-pulse ESEEM from a molecule with uniform isotope content at coupled nuclear site 1, and heterogenous isotopic content at coupled nuclear site 2, the combination of the individual modulation is specified by “E1*[C2,a*E2,a+C2,b*E2,b]”, where the Ei are the envelope modulation and the Ci,a/b are the normalized isotope substitution factors at site 2. The weighting can be included in the simulation as an adjustable parameter. In cases of three-pulse experiments, this combination is done by separately combining the modulation from the α and β manifolds (Eq. 12).
The calculation of the powder average ESEEM is achieved by using the following steps: (1) The user defines the nuclear parameters for each coupled nucleus and the combination rule. (2) The Hamiltonians for each electron-nuclear coupling are calculated for one orientation of the external magnetic field. (3) The modulation envelopes for each nuclear coupling are calculated based on the Hamiltonians calculated in step 2. (4) The modulation envelopes are combined to attain the overall spectrum for the one orientation. (5) Steps 2-4 are repeated until the spectra include averaging over all orientations of B0 relative to the reference PAS.
Optimization
The simulated spectrum is matched to the filtered experimental spectrum after the following transformation,
| (18) |
where and are the transformed and original simulation envelope modulation, respectively. The four real constants c1–4 are calculated by minimizing the squared residuals of the match between the transformed amplitude and the filtered experimental data. The ci are defined, as follows: c1 is the scaling factor for the simulated waveform, c3 compensates for modulation amplitude decay, and c2 and c4 are offset terms for adjusting the waveform prior to, or subsequent to, the decay operation. The scaling constants, c1, c2, and c4, in Eq. 18 are used when the target ESEEM originates from a sample in which the contributions to the ESEEM from nuclear couplings, other than the target couplings of the simulation, are not known. The minimum squared residual is set as the objective function for optimization over the adjustable parameters. For one model of number and type of nuclear couplings and method of combination, users can specify multiple experimental spectra under different experimental conditions (for example, τ value, B0 value for the same ge value) for a global optimization, with the fitting objective function defined as in Eq. 13. A standardized definition of the objective function in OPTESIM allows users to take full advantage of available Matlab optimization routines.
In our experience, owing to the large dimension of the parameter space and the rugged landscape of the objective function, gradient-based local optimization methods often fail to find the set of global optimal parameters because of the existence of many local minima, and non-gradient-based optimization methods require extensive computation power. Therefore, the computation speed becomes the bottleneck for the scale and accuracy of optimizations. One solution is to use faster C/C++ code for the core calculations that are crucial to computational speed. In our test, using a compiled C++ executable (MEX-files) for the modulation envelope calculation in Matlab resulted in a decrease of up to 1.5-fold in the time of the overall simulation. Another solution is to distribute the computation of the powder averaging to the available computational resources on a local network.
Distributed computing framework
A Java-RMI based distributed computational framework is included in OPTESIM. This framework allows users to build a distributed system of ESEEM simulation on their own PC computer hardware resources. The orientation sampling vectors for the powder average are first divided on the local computer and sent to different remote PCs according to their computational speed. The results are then collected and averaged on the local PC. A linear increase in computation speed with respect to the number of PCs can be achieved with this approach.
RESULTS
Example 1: Global simulation of ESEEM from a single 14N nucleus in an enzyme radical reaction intermediate
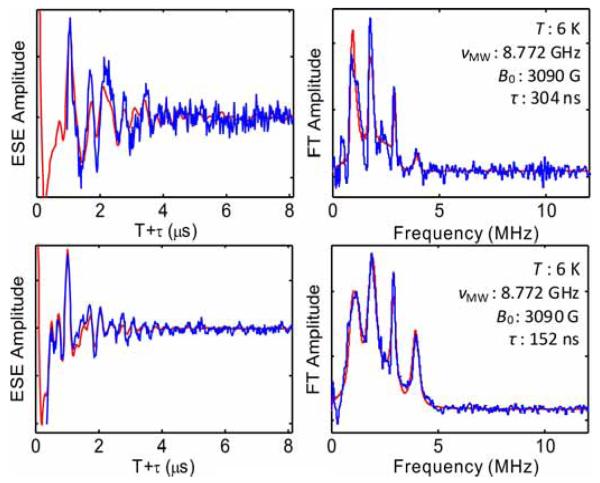
In three-pulse ESEEM studies of the cryotrapped 2-aminopropanol-generated substrate radical catalytic intermediate in the active site of coenzyme B12-dependent ethanolamine ammonia-lyase (EAL) from Salmonella typhimurium, a 14N nucleus was found to be coupled to the substrate radical [28; 29]. The narrow features in Fourier transforms of the three-pulse 14N ESEEM at 0.8-0.9, 1.7-2.0 and 2.9-3.0 MHz correspond approximately to the ν0, ν- and ν+ nqi frequencies of 14N ( electron spin manifold for Aiso>0), and the broad feature positioned around 4 MHz is the mI,=±2, or “double quantum”, feature. This spectral pattern is characteristic of the “exact cancellation” condition, in which the hf coupling and nuclear Zeeman contributions approximately cancel in one electron spin manifold [30; 31]. The coupled 14N has been assigned to a nitrogen belonging to the guanidinium group of Arg160 in the EutB subunit of EAL [24; 32]. Arg160 makes hydrogen bond contact with the substrate in the active site [24]. Multi-frequency three-pulse ESEEM spectra obtained at g=2.02 for the substrate radical were analyzed by using OPTESIM for a global optimization over the 14N nuclear parameters. Figure 2 shows the global fitting in both time and frequency domains at two different τ values. Table 1 lists the optimal parameters found for the simulation and their simultaneous trusted regions at the confidence level of 0.99. The parameter values are consistent with previously published results [24; 29]. However, the simulation with hybrid optimization converged to the parameters presented in Table 2 in approximately 1.5 hours, whereas the trial-and-error approach used in the original simulation [29] required months of intermittent effort.
Figure 2.
14N ESEEM collected from the substrate radical intermediate in ethanolamine ammonia-lyase, and Fourier transform, and simulation (red line) representing a global optimization. Top: =304 ns. Bottom: =152 ns. Simulation parameters are listed in Table 2. Conditions [24]: Microwave frequency, 8.772 GHz; magnetic field, 3090 Gauss; temperature, 6 K; microwave pulse width, 20 ns.
Table 2.
Simulation parameters for ESEEM from the coupled 14N in the substrate radical intermediate in ethanolamine ammoia-lyase. Euler angles correspond to the relative orientation of the hf and nqi PAS.
| Nuclear Parameters | Values | Simultaneous Confidence (0.99) Region |
|---|---|---|
| Aiso (MHz) | 0.933 | 0.910 – 0.958 |
| reff (Å) | 3.90 | 3.63 – 4.34 |
| e2qQ/h (MHz) | 3.075 | 3.068 – 3.084 |
| η | 0.579 | 0.568– 0.590 |
| α (deg) | 30.1 | 27.4 – 36.7 |
| β (deg) | 60.1 | 55.5 – 64.9 |
| γ (deg) | 14.7 | 6.9 – 39.0 |
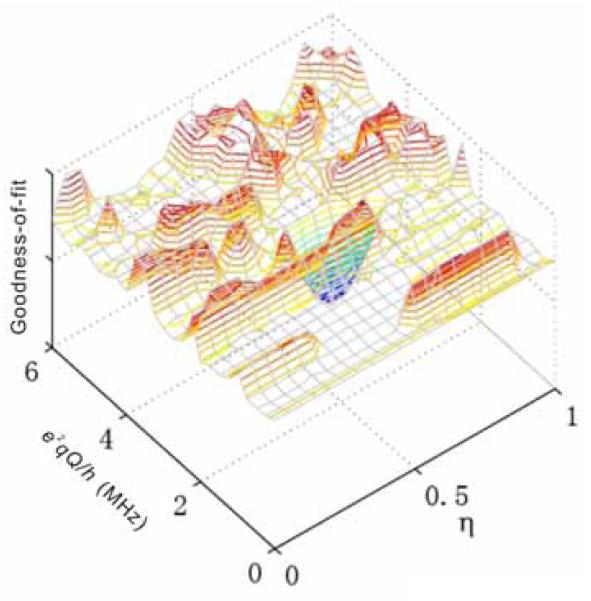
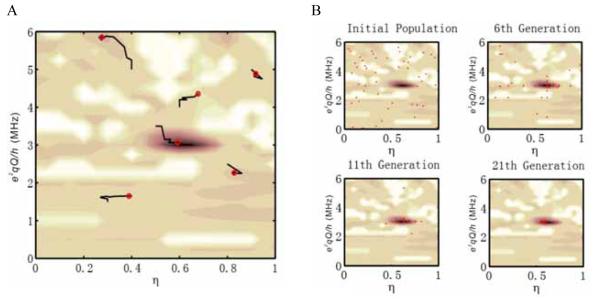
Figure 3 shows a goodness-of-fit landscape plot, which is constructed by varying the e2qQ/h and η values from 0 to 6 MHz and 0 to 1, respectively. This plot represents a simpler optimization problem over e2qQ/h and η with all other parameters fixed at their optimized values (Table 2). The roughness of the goodness-of-fit landscape prevents local optimization methods, such as conjugated gradient and Nelder-Mead simplex, from finding the global minimum with outlying starting points. Figure 4A demonstrates the failure of the Nelder-Mead simplex method with random starting points, except for the initial parameter set that is close to the global minimum. In contrast, the non-local genetic algorithm converges to the global minimum within 20 generations of a population size of 50, as shown in Figure 4B. However, a larger scale genetic algorithm with full parameter optimization requires a larger population size and generation numbers. Our experience shows that an efficient optimization of 10 parameters requires a population size of about 200 for a thorough search of the parameter space. The algorithm termination condition can be set to a specific number of stale generations [33], and the best individuals will condense at the global minimum in approximately 50 generations. With a hybrid optimization approach, the best individual generated by the genetic algorithm serves as the starting point for further local optimization methods with fast convergence (for example, simplex).
Figure 3.
Goodness-of-fit landscape for the parameters e2qQ/h and η. Other simulation parameters are fixed to their optimal values, as listed in Table 2.
Figure 4.
Trajectories of the goodness-of-fit obtained by using simplex and genetic optimization algorithms. A. Trajectories of the optimization for the Nelder-Mead simplex method on e2qQ/h and η. Red circles represent the ending points of the trajectories, which correspond to local minima. The simplex method only succeeds in finding the global minimum when the starting point is close. B. Optimization trajectory for the genetic algorithm. Red dots represent individuals in a population of 50.
The statistical assessment quantifies the importance of individual simulation parameters in reproducing the ESEEM. For discrete systems (single structure), a narrow confidence region indicates that a parameter contributes significantly to the ESEEM. For example, in the case of the 14N ESEEM in Figure 2, e2qQ/h and directly influence the frequency values of the narrow, large-amplidue 0, -, and + components, and Aiso influences the center frequency value of the dq component. These parameters therefore have relatively narrow simultaneous confidence regions (Table 1). The reff parameter influences the width of the dq feature, and therefore has a relatively wider confidence region. The Euler angles in Table 1 subtly modify the relative amplitudes of the 0, -, and +, and dq features, and have correspondingly wider confidence regions. The relatively narrow interval for Euler angle, , in Table 1, and wider confidence regions for and , is consistent with the choice of an axial dipolar (versus rhombic) hf tensor. If the influence of a parameter on the ESEEM is within the experimental noise, then the simultaneous confidence region would approach the full allowed range (for example, -180° to 180° for an angular parameter). The statistical assessment is useful for culling unnecessary parameters, which may reduce computation time.
Example 2: Mutual orientation of two 14N hf PAS in Cu(II)-bis-histamine complex
The Cu(II)-bis-histamine complex, Cu(II)(him)2(NO3)2, is a model for bis-trans equatorial coordination of Cu(II) by imidazole in proteins. The structure of the complex in Cu(II)-doped Zn(II)(him)2(NO3)2 crystal has been determined by X-ray crystallography [34], and superhyperfine (shf) coupling parameters for the remote 14N of imidazole have been calculated by using experimentally constrained density functional theory [35]. The Cu(II)(him)2(NO3)2 complex was synthesized as described [34], and a frozen 5 mM sample was prepared in 1:1 ethylene glycol/water glass in a 0.4 cm outer diameter EPR tube. Three-pulse ESEEM was collected at the B0 value for maximum ESE amplitude at g=2.069 in this disordered sample. In the special case of this nominally octahedral Cu(II) complex, all orientations of the g-tensor can be assumed to contribute to the ESE at this g position of the EPR spectrum[36]. Powder simulation of the ESEEM leads to determination of the mutual orientation of the two remote imidazole 14N hyperfine PAS, based on reproduction of subtle spectral features, which exemplifies the efficiency of OPTESIM.
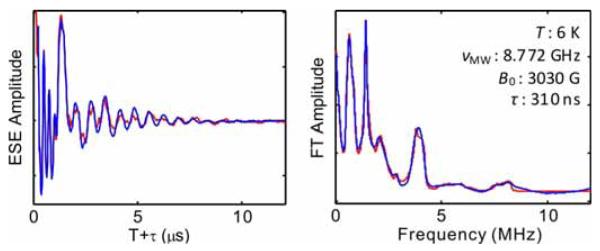
Figure 5 shows the converged simulation of three-pulse ESEEM collected from the Cu(II)-bis-histamine complex. The simulation parameters are presented in Table 3. The simulation was achieved by using a sequential application of the genetic algorithm (104 evaluations) and Nelder-Mead simplex (103 iterations) algorithm. The simulation of the experimental ESEEM spectrum involved optimization on eleven shf and nqi parameters. Eight of the parameters, including the three principal components of the remote 14N hyperfine tensor, e2qQ/h, , and the three Euler angles that relate the shf and nqi PAS, are assumed to be common to the two 14N nuclei. A significant feature of the FT of the experimental ESEEM, which is enhanced at the selected value of 310 ns, is the spectral feature around 8 MHz that arises from combination of the ΔmI=±2, or “double quantum” modulation from the two coupled 14N. The line shape of this ΔmI=±2 combination line is sensitively dependent on the mutual orientation of the two remote imidazole 14N shf PAS. This was accounted for in the simulations by varying Euler angles that relate the two remote imidazole 14N shf PAS as part of the optimization. The values of these Euler angles cause extremely subtle changes in the overall ESEEM amplitude, and the parameter space has a large dimension. Therefore, manual fitting and gradient-based optimization methods are exceptionally time-consuming and impractical.
Figure 5.
ESEEM collected from the remote 14N imidazole nuclei in the Cu(II)-bis-histamine complex and Fourier transform, and simulation (red). The simulation parameters are listed in Table 3. Conditions: Microwave frequency, 8.772 GHz; magnetic field, 3030 Gauss; temperature, 6 K; microwave pulse width, 20 ns; =310 ns.
Table 3.
Simulation parameters for ESEEM from the remote 14N imidazole nuclei in Cu(II)-bis-histamine complex. Euler angles, , , and , correspond to the relative orientation of the hf and nqi PAS, and Euler angles ’, ’, and ’, correspond to the relative orientation of the two 14N hf PAS.
| Nuclear Parameters | Values | Simultaneous Confidence (0.99) Region |
|---|---|---|
| Axx (MHz) | 2.13 | 2.10 – 2.15 |
| Ayy (MHz) | 1.81 | 1.77 – 1.84 |
| Azz (MHz) | 0.854 | 0.822 – 0.886 |
| e2qQ/h (MHz) | 1.51 | 1.50 – 1.52 |
| η | 0.668 | 0.653 – 0.683 |
| α (deg) | 7.28 | -1.35 – 16.42 |
| β (deg) | -9.34 | -11.12 – -7.33 |
| γ (deg) | -9.41 | -24.02 – 6.01 |
| α’ (deg) | 177.0 | 168.3 – 200.9 |
| β’ (deg) | 32.5 | 29.6 – 35.5 |
| γ’ (deg) | -6.7 | -17.9 – 16.6 |
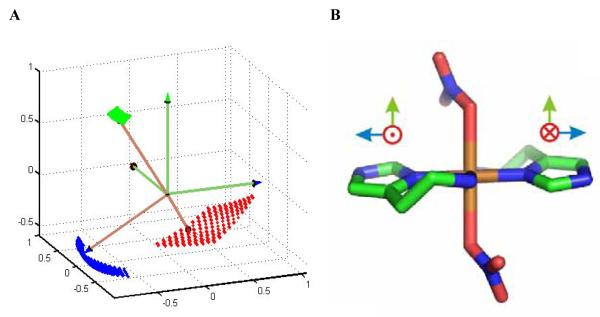
Optimization using the “hybrid” approach with a population size of 500 converged in about 10 hours on the distributed network of fourteen Pentium 4 PCs. Table 1 displays the best fit values and simultaneous confidence intervals of the simulation parameters. The shf coupling tensor, nqi parameters, and Euler angles that relate the shf and nqi PAS are in good agreement with values reported for ESEEM-detected imidazole remote 14N coupling in other Cu(II)-imidazole complexes [37; 38]. The Euler angles for the relation of the two 14N PAS in Table 3, =177°, =32.5°, and = -6.7°, indicate that the x- and y-axes are approximately opposed, and that the z-axes are approximately collinear, as depicted in Figure 6A. The relatively high symmetry of the simulated mutual orientation of the remote 14N shf tensors is consistent with the symmetry in the X-ray crystallographic structure of the Cu(II)(him)2(NO3)2 complex [34], which is shown in Figure 6B. A more detailed interpretation of the OPTESIM results for the Cu(II)-bis-histamine complex, and other Cu(II)-imidazole complexes, will be presented in a separate work.
Figure 6.
Physical model for the mutual orientation of the imidazole remote 14N hf PAS in the Cu(II)-bis-histamine complex, and X-ray crystallographic structure of Cu(II)(him)2(NO3)2.[34] A. Best-fit mutual orientation of the hf PAS of the imidazole remote 14N nuclei, obtained by using OPTESIM. The dotted surfaces represent the simultaneous confidence regions of the axes, at level 0.99. B. X-ray crystallographic structure of Cu(II)(him)2(NO3)2.[34] Proposed Cartesian axes that correspond to the directions in (A) are shown.
CONCLUSIONS
OPTESIM is a Matlab-based toolbox that presents efficient solutions to the analysis of ESEEM by using numerical simulation. Automated, optimized simulations by using the toolbox lead to convergence on dramatically shorter time scales, relative to manual simulations. The efficiency is achieved by using an implementation of the fast algorithm [1; 2; 17] for translation of the spin Hamiltonian [10; 11] into simulated ESEEM, and by the use of a hybrid, coarse-to-fine grain optimization approach. The statistical analysis of the simulation parameters allows the identification of simultaneous confidence regions at specific confident levels, which can be used to cull insignificant parameters to further speed calculations, and which supplies limits on the physical parameters (distances, angular orientations) that are used to construct molecular models from the ESEEM data. The geometry-preserving spherical averaging algorithm for N>1 allows subtle information to be extracted about the relative orientations of the hf PAS, even in powder samples. These features of OPTESIM are exemplified by the applications for simulation of 14N coupling for N=1 and N=2. OPTESIM is available for download from the following url: http://www.physics.emory.edu/optesim. The website includes a detailed description of the software, application instructions, and a tutorial.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- [1].Schweiger A, Jeschke G. Principles of pulse electron paramagnetic resonance. Oxford University Press; Oxford, UK ; New York: 2001. [Google Scholar]
- [2].Dikanov SA, Tsvetkov YD. Electron spin echo envelope modulation (ESEEM) spectroscopy. CRC Press; Boca Raton: 1992. [Google Scholar]
- [3].Keijzers CP, Reijerse EJ, Stam P, Dumont MF, Gribnau MCM. Magres - a General Program for Electron-Spin-Resonance, Endor and Eseem. Journal of the Chemical Society-Faraday Transactions I. 1987;83:3493–3503. [Google Scholar]
- [4].Poppl A, Gutjahr M, Hartmann M, Bohlmann W, Bottcher R. A study of the coordination geometry of the tetrapyridine copper(II) complex in NaY and MCM-41 by two-dimensional electron spin resonance HYSCORE spectroscopy. Journal of Physical Chemistry B. 1998;102:7752–7763. [Google Scholar]
- [5].Poppl A, Hartmann M, Bohlmann W, Bottcher R. Coordination geometry of the copper-pyridine complex in frozen solution as studied by proton and deuterium two-dimensional hyperfine sublevel correlation electron spin resonance spectroscopy. Journal of Physical Chemistry A. 1998;102:3599–3606. [Google Scholar]
- [6].Poppl A, Kevan L. A practical strategy for determination of proton hyperfine interaction parameters in paramagnetic transition metal ion complexes by two-dimensional HYSCORE electron spin resonance spectroscopy in disordered systems. Journal of Physical Chemistry. 1996;100:3387–3394. [Google Scholar]
- [7].Madi ZL, Van Doorslaer S, Schweiger A. Numerical simulation of one- and two-dimensional ESEEM experiments. Journal of Magnetic Resonance. 2002;154:181–191. doi: 10.1006/jmre.2001.2479. [DOI] [PubMed] [Google Scholar]
- [8].Shane JJ, Liesum LP, Schweiger A. Efficient simulation of ESEEM spectra using gamma. Journal of Magnetic Resonance. 1998;134:72–75. doi: 10.1006/jmre.1998.1529. [DOI] [PubMed] [Google Scholar]
- [9].Canfield JM, Warncke K. Geometry of reactant centers in the Co-II-substrate radical pair state of coenzyme B-12-dependent ethanolamine deaminase determined by using orientation-selection-ESEEM spectroscopy. Journal of Physical Chemistry B. 2002;106:8831–8841. doi: 10.1021/jp046167m. [DOI] [PubMed] [Google Scholar]
- [10].Mims WB. Amplitudes of Superhyperfine Frequencies Displayed in Electron-Spin Echo Envelope. Physical Review B. 1972;6:3543. &. [Google Scholar]
- [11].Mims WB. Envelope Modulation in Spin-Echo Experiments. Physical Review B. 1972;5:2409. &. [Google Scholar]
- [12].Goldberg DE. Genetic algorithms in search, optimization, and machine learning. Addison-Wesley Pub. Co.; Reading, Mass.: 1989. [Google Scholar]
- [13].Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by Simulated Annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- [14].Nelder JA, Mead R. A Simplex-Method for Function Minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
- [15].Levenberg K. A Method for the Solution of Certain Problems in Least Squares. Quart. Appl. Math. 1944;2:164–168. [Google Scholar]
- [16].Wertz JE, Bolton JR. Electron spin resonance; elementary theory and practical applications. McGraw-Hill; New York: 1972. [Google Scholar]
- [17].Stoll S, Schweiger A. Rapid construction of solid-state magnetic resonance powder spectra from frequencies and amplitudes as applied to ESEEM. Journal of Magnetic Resonance. 2003;163:248–256. doi: 10.1016/s1090-7807(03)00120-4. [DOI] [PubMed] [Google Scholar]
- [18].Hanson GR, Gates KE, Noble CJ, Griffin M, Mitchell A, Benson S. XSophe-Sophe-XeprView (R). A computer simulation software suite (v. 1.1.3) for the analysis of continuous wave EPR spectra. Journal of Inorganic Biochemistry. 2004;98:903–916. doi: 10.1016/j.jinorgbio.2004.02.003. [DOI] [PubMed] [Google Scholar]
- [19].Stoll S, Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. Journal of Magnetic Resonance. 2006;178:42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- [20].Hoffman BM, Martinsen J, Venters RA. General-Theory of Polycrystalline Endor Patterns - G and Hyperfine Tensors of Arbitrary Symmetry and Relative Orientation. Journal of Magnetic Resonance. 1984;59:110–123. [Google Scholar]
- [21].Rowan LG, Hahn EL, Mims WB. Electron-Spin-Echo Envelope Modulation. Physical Review. 1965;137:A61–A71. [Google Scholar]
- [22].Dikanov SA, Shubin AA, Parmon VN. Modulation effects in the electron spin echo resulting from hyperfine interaction with a nucleus of an arbitrary spin. J. Magn. Reson. 1981;42:474–487. [Google Scholar]
- [23].Canfield JM, Warncke K. Active site reactant center geometry in the Co-II-product radical pair state of coenzyme B-12-dependent ethanolamine deaminase determined by using orientation-selection electron spin-echo envelope modulation spectroscopy. Journal of Physical Chemistry B. 2005;109:3053–3064. doi: 10.1021/jp046167m. [DOI] [PubMed] [Google Scholar]
- [24].Sun L, Groover OA, Canfield JM, Warncke K. Critical role of arginine 160 of the EutB protein subunit for active site structure and radical catalysis in coenzyme B-12-dependent ethanolamine ammonia-lyase. Biochemistry. 2008;47:5523–5535. doi: 10.1021/bi702366e. [DOI] [PubMed] [Google Scholar]
- [25].Warncke K. Characterization of the product radical structure in the Co-II-product radical pair state of coenzyme B-12-dependent ethanolamine deaminase by using three-pulse H-2 ESEEM spectroscopy. Biochemistry. 2005;44:3184–3193. doi: 10.1021/bi048196t. [DOI] [PubMed] [Google Scholar]
- [26].Zhu YS. Probability and Statistics in Experimental Physics. Science Press; Beijing: 2006. [Google Scholar]
- [27].Warncke K, McCracken J. Analysis of static distributions in hydrogen hyperfine interactions in randomly oriented radicals in the solid state by using 2H electron spin echo envelope modulation spectroscopy: conformational dispersion of b-2H coupling in the model tyrosyl radical. J. Chem. Phys. 1995;103:6829–40. [Google Scholar]
- [28].Tan SL, Kopczynski MG, Bachovchin WW, Ormejohnson WH, Babior BM. Electron Spin-Echo Studies of the Composition of the Paramagnetic Intermediate Formed during the Deamination of Propanolamine by Ethanolamine Ammonia-Lyase, and Adocbl-Dependent Enzyme. Journal of Biological Chemistry. 1986;261:3483–3485. [PubMed] [Google Scholar]
- [29].Ke SC, Warncke K. Interactions of substrate and product radicals with Co-II in cobalamin and with the active site in ethanolamine deaminase, characterized by ESE-EPR and N-14 ESEEM spectroscopies. Journal of the American Chemical Society. 1999;121:9922–9927. [Google Scholar]
- [30].Mims WB, Peisach J. Nuclear Modulation Effect in Electron-Spin Echoes for Complexes of Cu2+ and Imidazole with N-14 and N-15. Journal of Chemical Physics. 1978;69:4921–4930. [Google Scholar]
- [31].Flanagan HL, Singel DJ. Analysis of N-14 Eseem Patterns of Randomly Oriented Solids. Journal of Chemical Physics. 1987;87:5606–5616. [Google Scholar]
- [32].Sun L, Warncke K. Comparative model of EutB from coenzyme B-12-dependent ethanolamine ammonia-lyase reveals a beta(8)alpha(8), TIM-barrel fold and radical catalytic site structural features. Proteins-Structure Function and Bioinformatics. 2006;64:308–319. doi: 10.1002/prot.20997. [DOI] [PubMed] [Google Scholar]
- [33].ABUHIJLEH ALATIF, WOODS C, AHMED IY. Synthesis and molecular structure of monomeric copper(II) acetates with 2-methylimidazole and 1,2-dimethylimidazole. Inorganica chimica acta. 1991;190:11–17. [Google Scholar]
- [34].Zhang C, Duan C, Hu Q, Yan D. Self-assembly in transition metal complexes: structural characterization of a copper histamine nitrate [Cu(II)(him)2(NO3)2] Journal of Chemical Crystallography. 1999;29:1153–1155. [Google Scholar]
- [35].Baute D, Arieli D, Neese F, Zimmermann H, Weckhuysen BM, Goldfarb D. Carboxylate binding in copper histidine complexes in solution and in zeolite Y: X- and W-band pulsed EPR/ENDOR combined with DFT calculations. Journal of the American Chemical Society. 2004;126:11733–11745. doi: 10.1021/ja047761c. [DOI] [PubMed] [Google Scholar]
- [36].Weltner W. Magnetic atoms and molecules. Dover Publications; New York: 1989. [Google Scholar]
- [37].Colaneri MJ, Peisach J. An Electron Spin-Echo Envelope Modulation Study of Cu(Ii)-Doped Single-Crystals of L-Histidine Hydrochloride Monohydrate. Journal of the American Chemical Society. 1992;114:5335–5341. [Google Scholar]
- [38].Colaneri MJ, Peisach J. A Single-Crystal Epr and Eseem Analysis of Cu(Ii)-Doped Bis(L-Histidinato)Cadmium Dihydrate. Journal of the American Chemical Society. 1995;117:6308–6315. [Google Scholar]