Abstract
Mechanical stresses influence the structure and function of adult and developing blood vessels. When these stresses are perturbed, the vessel wall remodels to return the stresses to homeostatic levels. Constrained mixture models have been used to predict remodeling of adult vessels in response to step changes in blood pressure, axial length and blood flow, but have not yet been applied to developing vessels. Models of developing blood vessels are complicated by continuous and simultaneous changes in the mechanical forces. Understanding developmental growth and remodeling is important for treating human diseases and designing tissue-engineered blood vessels. This study presents a constrained mixture model for postnatal development of mouse aorta with multiple step increases in pressure, length and flow. The baseline model assumes that smooth muscle cells (SMCs) in the vessel wall immediately constrict or dilate the inner radius after a perturbation to maintain the shear stress and then remodel the wall thickness to maintain the circumferential stress. The elastin, collagen and SMCs have homeostatic stretch ratios and passive material constants that do not change with developmental age. The baseline model does not predict previously published experimental data. To approximate the experimental data, it must be assumed that the SMCs dilate a constant amount, regardless of the step change in mechanical forces. It must also be assumed that the homeostatic stretch ratios and passive material constants change with age. With these alterations, the model approximates experimental data on the mechanical properties and dimensions of aorta from 3- to 30-day-old mice.
Keywords: Biomechanics, Arteries, Elastin, Collagen, Microstructure
1 Introduction
Vertebrate arteries begin as tubes of endothelial cells (ECs) that form before detectable blood flow. As flow begins, smooth muscle cells (SMCs) are recruited to surround the ECs and build the layered structure of the arterial wall. The SMCs synthesize extracellular matrix (ECM) proteins, such as elastin and collagen, that are necessary for the proper mechanical function of the large elastic arteries (Wagenseil and Mecham 2009). Total amounts of elastin and collagen gene expression (Kelleher et al. 2004) increase along with blood pressure and flow (Huang et al. 2006; Ishii et al. 2001; Wiesmann et al. 2000) through the first month of postnatal development in mice, adding mechanical resiliency to the vessel wall as the hemodynamic forces increase.
In both developing and adult vessels, it is known that mechanical stimuli influence vessel structure and function. In general, vessel lumen size depends on blood flow, vessel wall thickness depends on blood pressure and vessel length depends on axial forces (Clark 1918). When the homeostatic state is perturbed, the vessel dimensions are altered to normalize the shear, circumferential or axial stresses. Mechanical models are necessary to predict this growth and remodeling process and design treatments for human diseases where the hemodynamic forces or mechanical properties of the wall are modified. Models that include the individual constituents of the vessel wall, namely elastin, collagen and SMCs, are especially valuable because they can be related to measurable changes in the amount or organization of wall components.
One type of microstructurally based model is a constrained mixture model, where the components must deform together, and the total mixture stresses are the sum of the component stresses (Humphrey and Rajagopal 2002). Each component has an individual homeostatic stretch ratio, constitutive equation and time-varying mass fraction. Constrained mixture models have been used successfully to describe the growth and remodeling of adult arteries in response to changes in blood pressure, axial length or blood flow (Valentin and Humphrey 2009; Valentin et al. 2009; Wan et al. 2009; Alford et al. 2008; Gleason and Humphrey 2004; Gleason et al. 2004), but have not yet been applied to developing vessels. Models of developing vessels are complicated by continuous and simultaneous increases in pressure, length, and flow, along with continually changing definitions of the homeostatic state. Extending the constrained mixture model to developing vessels is important for designing treatments for genetic diseases where component amounts are altered from conception, such as supravalvular aortic stenosis (SVAS). SVAS results from a genetic mutation leading to elastin haploinsufficiency and reduced elastin protein in the vessel wall. It is characterized by narrowing of the large elastic arteries, hypertension and eventual cardiac failure (Li et al. 1997). Microstructurally based models of developing vessels are also important for understanding and recreating the growth and remodeling process to build tissue-engineered blood vessels.
This study presents a constrained mixture model for post-natal growth and remodeling of the proximal thoracic aorta in mice with multiple step changes in blood pressure, axial length and blood flow. It is assumed that the homeostatic stresses are reset with each developmental time step. Aortic dimensions increase when wall components are produced in response to mechanical perturbations as the vessel tries to return to the homeostatic stress state. The final stresses depend on the change in hemodynamic forces, the model parameters, the loaded and unloaded dimensions of the vessel and the mass fraction of each component. Comparisons are made between the model predictions and previously published data for developing mice to validate the model assumptions. Changes to the model assumptions and parameters are then made to improve the model predictions.
2 Methods
The model is based on the mixture model presented by Gleason et al. (2004) with several important modifications for developing mouse aorta. The major modification is to include simultaneous increases in pressure, length and flow and to model multiple step increases in each parameter. Additional changes are discussed in detail later. The baseline case, Case 1, retains most of the assumptions of the original model. Subsequent cases with changes to the model assumptions or parameters are determined by the results of Case 1 and are discussed at the end of the “Methods”. All new equations and most of the relevant original equations are presented here, but the reader is referred to the original papers for more detail.
2.1 Background
The developing thoracic aorta of the mouse is considered to be a constrained mixture of three components, elastin, collagen and SMCs, that must deform together. The stretch ratios for the entire mixture in the circumferential (θ) and axial (z) direction are calculated as:
| (1a) |
| (1b) |
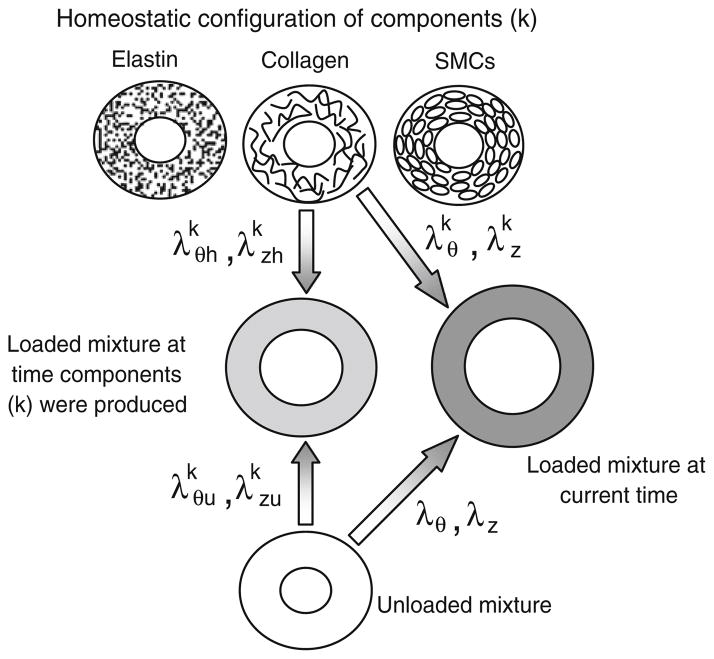
where a is the deformed inner radius of the mixture, A is the undeformed inner radius, l is the deformed length of the mixture and L is the undeformed length. Radial variations in the stretch ratio are neglected. The components have individual homeostatic or natural stretch ratios in each direction at which they are produced, and . For each time step, there are “original” components that were produced at some earlier developmental time and “new” components that are produced after the step changes in blood pressure, axial length and blood flow. Therefore, the superscript k is replaced by k = oe, oc and om or ne, nc and nm for original or new elastin, collagen and SMCs, respectively. In this model, multiple step changes in pressure, length and flow are included, so instead of a single set of new components, there is one set for each step change. Therefore, ne, nc and nm are replaced by nei, nci and nmi, where i = 1—total number of steps. In Case 1, the homeostatic stretch ratios are equal for all original and new components of each type and at each time step. The deformation state of the mixture evolves with time as growth and remodeling occur, so the current stretch ratios for the mixture, λθ and λz, may not match the stretch ratios of the mixture when different components were produced, and (Fig. 1). The current stretch ratios, and , of each component can be calculated by (Baek et al. 2006):
| (2a) |
| (2b) |
Fig. 1.
Illustration of the component and mixture stretch ratios for the constrained mixture model. Each original and new component (k) is produced at its homeostatic or natural stretch ratio ( and ). The components are produced at some earlier time in development when the mixture is stretched and from its unloaded state. At the current time, the mixture is stretched λθ and λz from its unloaded state and the components are stretched and from their homeostatic state
This definition for the component stretch ratios is consistent with Gleason et al. (2004), but uses homeostatic stretch ratios for each component instead of homeostatic unloaded dimensions. Although the homeostatic stretch ratios are constant in Case 1, the current stretch ratios of each component change with development depending on the current deformed state of the mixture and the deformed state of the mixture when each set of components was produced.
The aorta is considered a uniform, incompressible cylinder with a finite thickness, and the wall stresses are calculated by:
| (3a) |
| (3b) |
| (3c) |
where σθ and σz are the mean Cauchy stresses in the circumferential and axial directions and τ is the wall shear stress. P is the mean transmural pressure, h is the deformed wall thickness, f is the applied axial force, μ is the viscosity of blood (assumed to be 4 cP) and Q is the volumetric flow rate. The transmural distribution of stresses is not considered in this model.
The wall stresses will change as blood pressure, axial stretch and blood flow increase during the first month of post-natal development in the mouse (Huang et al. 2006; Ishii et al. 2001; Wiesmann et al. 2000). The stresses at the current pressure (Ph), deformed length (lh), flow (Qh), deformed inner radius (ah) and thickness (hh) are considered the homeostatic values for each developmental time step. To move to the next developmental time step, the pressure (P), deformed axial length (l) and flow (Q) are increased to new values:
| (4a) |
| (4b) |
| (4c) |
where εP, εl and εQ are constants for each time step determined from experimental data. Developmental changes in pressure and length will cause passive changes in the inner radius due to elastic deformation and incompressibility, respectively, which will cause subsequent alterations in shear stress. Developmental changes in flow will directly cause changes in shear stress (Eq. 3c).
In Case 1, it is assumed that the SMCs react to each of these changes independently by actively constricting or dilating the aortic wall to return the shear stress to the homeostatic values, but that they can only constrict the inner radius a maximum of 30% and dilate a maximum of 15%. These limits were chosen for the carotid artery (Gleason and Humphrey 2004; Gleason et al. 2004), but it is assumed that they also apply to the thoracic aorta as both are large elastic arteries. For example, if an increase in pressure causes an elastic deformation that increases the radius less than 30%, the SMCs can actively constrict the radius to restore the homeostatic shear stress. If an increase in flow requires a dilation of more than 15%, then the SMCs will not be able to completely restore the shear stress to the homeostatic value. When flow changes by a factor εQ, the shear stress will be normalized if the radius can change by a factor (Eq. 3c). The dilation and contraction limits are assumed to remain constant over the developmental time period, although there is evidence that arteries in young animals can contract or dilate more than adult animals in response to changes in blood flow (Langille et al. 1989). Additional experimental data are needed for better estimates of the SMC response to normalize shear stress in the developing aorta.
Although the vasoconstriction or vasodilation responses to each perturbation (flow, pressure and length) are considered independently, all of the active SMC responses are assumed to occur instantaneously compared to the longer time course of component remodeling. After this instantaneous response, component turnover begins as original components are degraded and new components are produced over time. The loaded wall thickness is optimized during remodeling as the vessel attempts to maintain the homeostatic circumferential stress. Optimization of the axial stress is not included in this study, but axial stress changes as the vessel dimensions are remodeled.
2.2 Constitutive equations
The total mean Cauchy stress on the aortic wall in each direction is the sum of the stresses in each component (σk) multiplied by the mass fraction (φk) of each component at time, s:
| (5a) |
| (5b) |
Note that the total mean stresses are functions of the mixture stretch ratios as defined by Eq. 1, while the component stresses are functions of the component stretch ratios as defined by Eq. 2. The total mean stresses are also defined by Eq. 3a and b and must equal zero in the equilibrium state with no applied loads (P = 0 and f = 0). Hence, when the mixture is in the unloaded state, the sum of the component stresses must equal zero, but the stress in each individual component is not necessarily zero.
The component stresses are related to the component stretch ratios by individual constitutive equations. There are many choices of constitutive equations, but the goal of this study is to determine the general behavior of the model applied to developing arteries, not to investigate different constitutive equations; therefore, the same equations are used here as in the original papers (Gleason and Humphrey 2004; Gleason et al. 2004). The same equations apply for original and new components; therefore, each component superscript can lead by o for original or ni for each set of new components. Elastin (e) is modeled as a neo-Hookean material and collagen (c), and passive SMCs (m) are modeled as transversely isotropic materials:
| (6) |
| (7) |
| (8) |
| (9) |
where
| (10) |
| (11) |
where
| (12) |
| (13) |
where bi (i = 1, …, 7) are material constants. SMCs also have an active stress component in the circumferential direction, so that the total circumferential stress is the sum of the passive and active components:
| (14a) |
| (14b) |
| (15) |
where
| (16a) |
| (16b) |
where λM, λ0 are material constants, TB = basal tone constant and TP, TQ and TZ represent the activation dependence on altered pressure, flow and axial stretch, respectively. In this study, it is assumed that alterations in SMC tone are primarily driven by changes in flow; therefore, TZ ≈ TP ≈ 0. TQ can be calculated according to the constraints in Gleason et al. (2004):
| (17) |
where the SMC stretch ratios and stresses are function of the time, s, elapsed since each step change in pressure, length and flow. At time = 0, the aorta is at its homeostatic state before the step change occurs and at time = sv, the instantaneous response of vasoconstriction or vasodilation occurs. Additionally, , where ho = initial wall thickness at time = 0. Note that TQ is only applicable to original muscle. The homeostatic flow rate for new muscle is εQ Qh, so for new muscle Tact = TB. In Case 1, it is assumed that the passive and active material constants are the same for the original and all newly produced components at each time step.
2.3 Component turnover
All components are continually produced over the developmental time course (Kelleher et al. 2004). Collagen and SMCs are also degraded, but elastin is an extremely stable protein and is likely not degraded. Kinetic functions and constants are used that allow turnover of collagen and SMCs after each step change in pressure, length and flow, but only production and no removal of elastin (Gleason and Humphrey 2004; Gleason et al. 2004.
| (18) |
where gk is the production function and qk is the degradation function, and are the associated rate constants for each component, k, s is the current time elapsed since a step change in pressure, length and flow and sh is the homeostatic time at which remodeling is complete. A rate constant of 6.9 allows almost complete turnover with about 0.1% of the original component remaining; therefore, and for most wall constituents in Case 1. A rate constant of zero allows no production or degradation of a component; therefore, in all cases because of the stability of the elastin protein. The rate constants do not change with developmental age. With complete turnover, all original components are degraded at each developmental time step so even with multiple steps there is no need to track previously produced components. With no degradation of elastin and/or incomplete turnover of other components in subsequent cases, the original components are present for multiple time steps, as are the new components produced from each previous developmental step, so these mass fractions and the unloaded stretch ratios of the mixture when they were produced must be tracked.
Assuming that the mass density remains constant and that the artery is incompressible, the ratio (α) of final artery mass/initial mass at any time, s, after a step change in pressure, length and flow can be determined by:
| (19) |
where a(s), h(s) and l(s) are the deformed inner radius, thickness and length at time, s, and ao, ho, lo are the initial deformed dimensions at time = 0.
The mass fractions for each component can be written in terms of α(s), α(sh), the kinetic functions and the ratios of final mass fractions of each new component Γec = φne(sh)/φnc(sh) and Γmc = φnm(sh)/φnc(sh)):
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
Because original elastin does not degrade, qe(s) = 1, but the mass fraction of original elastin will decrease as mass is produced and α(s) increases. The mass fraction equations have been generalized for incomplete turnover, but in the case of complete turnover, qk(sh) = 0 and the equations for φnk are the same as in Gleason et al. (2004). The ratio of final artery mass/initial mass can be rewritten in terms of the mass fractions of each component and the kinetic functions:
| (26) |
2.4 Physiologic and model parameters
Reviewing the equations above, there are numerous constants and experimental measurements needed as inputs to run the model and as validation to compare the model predictions. Physiologic data required as inputs and validation of the model include the loaded and unloaded dimensions, mean arterial blood pressure, axial length, volumetric blood flow and diameter compliance for the proximal thoracic aorta in mice at various stages of postnatal development. Huang et al. (2006) present most of this data for the development of mice aged 1 to 30 days and Wiesmann et al. (2000) present blood flow data in mice aged between 3 days to 16 weeks. Because the time steps are not equal in both studies or constant throughout development, the experimental data were fit with polynomial equations to obtain data for six equal time steps from 3- to 30-day-old mice (Table 1). The experimental deformed thickness (h) is calculated from the mean pressure (P), deformed inner radius (a) and circumferential stress (σθ) in Table 1 according to Eq. 3a. The experimental unloaded radius (A) and length (L) are estimated from the stretch ratios (λθ and λz) in Table 1 according to Eq. 1. The axial stretch ratio (λz) of the proximal thoracic aorta is assumed to vary linearly from 1.02 (Wagenseil et al. 2009) to 1.10 (Wagenseil et al. 2005; Guo and Kassab 2003) over the developmental time course. The cross-sectional area compliance presented in Huang et al. (2006) is converted to diameter compliance (C) (Westerhof et al. 2004) to estimate the elastic deformation of the wall in response to a step change in pressure. The experimental shear stress (τ) is calculated from Eq. 3c using the deformed inner radius (a) and volumetric flow rate (Q) in Table 1 and assuming the viscosity (μ) of blood is 4 cP. The experimental change in pressure (εP), length (εl) and flow (εQ) for each step are calculated using Eq. 4.
Table 1.
Experimental data used as inputs or validation for the constrained mixture model of developing mouse aorta
| Age (days) | a (mm) | l (mm) | h (mm) | A (mm) | L (mm) | H (mm) | λθ | λz |
|---|---|---|---|---|---|---|---|---|
| 3.0 | 0.33 | 1.70 | 0.023 | 0.15 | 1.67 | 0.048 | 2.29 | 1.02 |
| 7.5 | 0.39 | 2.02 | 0.029 | 0.19 | 1.96 | 0.056 | 2.08 | 1.03 |
| 12.0 | 0.44 | 2.35 | 0.032 | 0.23 | 2.24 | 0.059 | 1.91 | 1.05 |
| 16.5 | 0.49 | 2.67 | 0.034 | 0.28 | 2.52 | 0.060 | 1.80 | 1.06 |
| 21.0 | 0.55 | 3.00 | 0.034 | 0.32 | 2.79 | 0.061 | 1.76 | 1.07 |
| 25.5 | 0.61 | 3.32 | 0.033 | 0.35 | 3.05 | 0.061 | 1.79 | 1.09 |
| 30.0 | 0.67 | 3.64 | 0.032 | 0.36 | 3.31 | 0.062 | 1.90 | 1.10 |
| References | (Huang et al. 2006) | (Huang et al. 2006) | (Huang et al. 2006) | (Guo and Kassab 2003; Wan et al. 2009) | ||||
| Age (days) | C (mm/mmHg) | Q (ml/min) | P (mmHg) | τ (Pa) | σθ (kPa) | εP | εl | εQ |
| 3.0 | 0.0026 | 1.1 | 41 | 2.63 | 79 | |||
| 7.5 | 0.0027 | 3.9 | 53 | 5.83 | 94 | 1.28 | 1.19 | 3.44 |
| 12.0 | 0.0028 | 6.1 | 62 | 6.09 | 113 | 1.18 | 1.16 | 1.56 |
| 16.5 | 0.0031 | 7.7 | 69 | 5.45 | 135 | 1.12 | 1.14 | 1.26 |
| 21.0 | 0.0034 | 8.8 | 74 | 4.41 | 160 | 1.07 | 1.12 | 1.13 |
| 25.5 | 0.0037 | 9.2 | 77 | 3.43 | 188 | 1.04 | 1.11 | 1.05 |
| 30.0 | 0.0041 | 9.1 | 77 | 2.57 | 219 | 1.01 | 1.10 | 0.99 |
| References | (Huang et al. 2006; Westerhof et al. 2004) | (Wiesmann et al. 2000) | (Huang et al. 2006) | (Huang et al. 2006; Wiesmann et al. 2000) | (Huang et al. 2006) | |||
Loaded inner radius (a), length (l) and thickness (h), unloaded inner radius (A), length (L) and thickness (H), circumferential (λθ) and longitudinal (λz) stretch ratios, diameter compliance (C), volumetric flow rate (Q), pressure (P), shear stress (τ), circumferential stress (σθ) and increases in pressure (εP), length (εl) and flow (εQ). The loaded and unloaded dimensions for a 3-day-old mouse aorta were input at the start of the modeling process. The final loaded and unloaded dimensions predicted by the model for each step were used as starting dimensions for subsequent steps and later compared to the dimensions in this table. The compliance and increases in pressure, length and flow were input for all steps
The experimental data in Table 1 provide the mixture stretch ratios (λθ and λz) to compare with the model predictions for each time step. The component stretch ratios ( and ) depend on the mixture stretch ratios, as well as the homeostatic stretch ratios of each component ( and ) and the stretch ratios of the mixture when each component was produced ( and ) (Fig. 1) (Eq. 2). Based on the experimental data, the starting time point of the model is chosen as 3 days old, and it is assumed that the original components were produced with the aorta in the deformed configuration at that time. Hence, and for the original components at the first developmental time step equal the starting λθ and λz at 3 days which are 2.29 and 1.02, respectively (Table 1). When the step changes in pressure, length and flow are applied, the vessel diameter decreases or increases within the vasoconstriction/vasodilation limits to normalize the shear stress and the mixture stretch ratio changes instantaneously. Production of new components starts at this time and and for the new components equal the current stretch ratios of the aorta λθ(s) and λz(s). As remodeling progresses, the unloaded mixture configuration evolves to satisfy equilibrium conditions (passive stresses equal zero when no forces are applied) (Gleason and Humphrey 2004; Gleason et al. 2004). When remodeling is complete, the mixture has a new unloaded and loaded configuration that is used as the input for subsequent steps. Although and for the new components varies with remodeling time, for computational convenience it is assumed that they are equal to and when these new components are carried through to the next remodeling step.
The homeostatic stretch ratios at which the components are produced are chosen considering the physiologic stretch in a 3-day-old mouse aorta (Table 1). It is assumed that the homeostatic stretch ratios in the circumferential and axial directions are higher than this stretch for elastin, lower than this stretch for collagen, and at this stretch for SMCs (Table 2). These choices are based on the assumption that at physiologic pressures, elastin is in compression (Fonck et al. 2007), collagen is in tension (Dobrin and Canfield 1984) and SMCs are at their preferred, homeostatic stretch. Additional experimental data are needed to improve these estimates. The collagen homeostatic stretch ratios are further revised after determining the mass fractions and material constants to satisfy equilibrium conditions. In Case 1, it is assumed that original and all newly produced components have the same homeostatic stretch ratios.
Table 2.
Constants used in the constrained mixture model for the baseline case, Case 1
| Description | Symbols | Values | |
|---|---|---|---|
| Homeostatic stretch of each original component |
|
2.96, 1.45, 1.84, 0.76, 2.29, 1.02 | |
| Homeostatic stretch of each new component |
|
2.96, 1.45, 1.84, 0.76, 2.29, 1.02 | |
| Passive material constants for original components | Elastin: , collagen: , SMCs: | 35 kPa, 10 kPa, 1.5, 0.01, 2 kPa, 50 kPa, 0.01 | |
| Passive material constants for new components | Elastin: , collagen: , SMCs: | 35 kPa, 10 kPa, 1.5, 0.01, 2 kPa, 50 kPa, 0.01 | |
| Active SMC constants | λm, λ0, Tb | 0.6, 2.8, 60 kPa | |
| Production constants |
|
6.9, 6.9, 6.9 | |
| Degradation constants |
|
0.0, 6.9, 6.9 |
From Eq. 5, the total stress in the mixture is a function of the component stretch ratios ( and ) and the mass fraction of each component (φk). The starting mass fractions of elastin, collagen and SMCs in the aortic wall of 3-day-old mice (Table 3) are estimated from data on neonatal rats from Olivetti et al. (1980) assuming that the mass fraction of each component scales linearly with the volume fraction and that 75% of the wall mass is water. It is assumed that elastin and collagen mass fractions increase throughout the developmental time period, but that the rate of increase slows as gene expression decreases (Kelleher et al. 2004). The decreasing mass fraction of SMCs is calculated from the elastin, collagen and constant water mass fractions at each step. In Gleason et al. (2004), the starting mass fractions, the production and degradation functions (gk and qk) and the final mass fraction ratios of newly produced components (Γec and Γmc) are prescribed, but the total mass fraction of each component is predicted by the model. In this model, the starting mass fractions, the production and degradation functions and the final total mass fraction of each component are prescribed, and the mass fraction ratios of newly produced components are predicted by the model. The mass fraction ratios of newly produced components for each developmental step are calculated in the model from the change in total mass fraction of each component, the mass fraction of original components remaining and the predicted change in mass of the artery wall during growth and remodeling. Additional experimental data on the changes in mass fractions for each component are needed to improve these inputs and validate the model predictions for the mass fraction ratios of newly produced components.
Table 3.
Total mass fractions (φk) and percent change (% Ch) of elastin (e), collagen (c), SMCs (m) and water (w) (Kelleher et al. 2004; Olivetti et al. 1980)
| Age (days) | φe(%) | φc (%) | φm (%) | φw(%) | % Ch elastin | % Ch collagen | % Ch SMC |
|---|---|---|---|---|---|---|---|
| 3.0 | 5.8 | 1.9 | 17.3 | 75.0 | |||
| 7.5 | 7.2 | 2.4 | 15.5 | 75.0 | 24.0 | 24.0 | −10.7 |
| 12.0 | 8.6 | 2.8 | 13.5 | 75.0 | 20.0 | 20.0 | −12.4 |
| 16.5 | 10.0 | 3.3 | 11.7 | 75.0 | 16.0 | 16.0 | −13.5 |
| 21.0 | 11.2 | 3.7 | 10.1 | 75.0 | 12.0 | 12.0 | −13.6 |
| 25.5 | 12.1 | 4.0 | 8.9 | 75.0 | 8.0 | 8.0 | −11.8 |
| 30.0 | 12.6 | 4.1 | 8.3 | 75.0 | 4.0 | 4.0 | −7.2 |
The total mass fractions were used to calculate the mass fraction ratios of newly produced components for each developmental step based on the amount of original and previously produced new components left from the previous step and the change in total mass predicted by the constrained mixture model
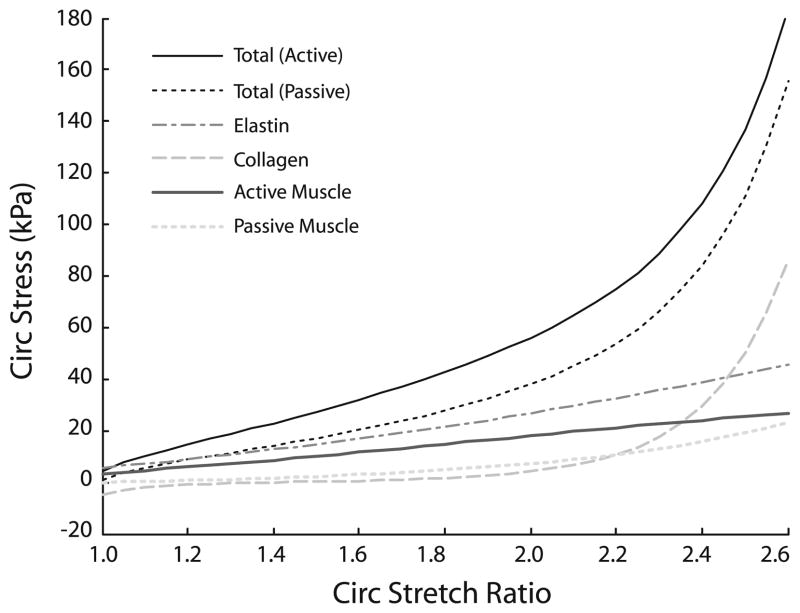
The constitutive equations for the mixture depend on the component stretch ratios and mass fractions, as well as the passive material constants (bi), and the active SMC constants (λM, λ0, and TB). With the component stretch ratios and mass fractions determined earlier, the passive and active material constants are chosen to approximate the physiologic circumferential stretch ratio, circumferential stress and pressure for 3-day-old mouse thoracic aorta and to provide the assumed stress contributions for each component (Fig. 2). It is assumed that 1) elastin and active SMCs contribute significantly to the circumferential stress at low stretch, 2) collagen contributes significantly at high stretch, 3) passive SMCs contribute minimally at all stretches, and 4) collagen becomes significantly nonlinear when the vessel is stretched about 20% beyond the physiologic value. The chosen parameters (Table 2) provide for substantially less contribution from passive and active SMCs than Gleason et al. (2004), but are consistent with limited mechanical data from mouse aorta when the SMCs are activated or killed (Faury et al. 1999). The elastin and collagen contributions are consistent with experiments performed on dog arteries when one protein is degraded (Dobrin and Canfield 1984). Axial stress is not considered, except in order of magnitude estimates, because axial stress is not presented in Huang et al. (2006). Additional experimental data on mouse arteries are needed to better quantify the contribution of each component and to include the axial behavior. In Case 1, it is assumed that the material constants are the same for original and all newly produced components.
Fig. 2.
Total stress–stretch ratio behavior and individual contributions of elastin, collagen and SMCs with the chosen material constants for a 3-day-old mouse aorta. Constants were chosen to match the physiologic stress and stretch ratio at this age (Huang et al. 2006) and to match the assumed contributions of each component as described in the text
2.5 Solution strategy
The initial starting point is that of a 3-day-old mouse thoracic aorta. The loaded and unloaded dimensions, diameter compliance, blood flow, pressure and stresses are all prescribed from the first row of Table 1. The solution steps are similar to Gleason et al. (2004), but are repeated for each developmental time step and include alterations specific to the current model. All calculations are performed with custom scripts in Matlab (Mathworks):
Prescribe step changes in pressure, deformed length and flow (εP, εl, and εQ, Table 1) from experimental data for the current step (i.e. from day 3 to day 7.5).
Calculate the mixture stretch ratios using the new inner radius after the active, instantaneous SMC response and allow component remodeling to proceed.
-
Determine the stretch ratios for original and newly produced components, and , from Eq. 2.
Use an initial guess for h(sh) (the final homeostatic deformed thickness) to determine α(sh) from Eq. 19.
Use the initial (s = 0) and final (s = sh) values of the degradation functions (qk), mass fractions (φk) and ratio of final artery mass/initial mass (α) to determine the final mass fractions ratios of the newly produced components (Γec and Γmc) from Eqs. 20 to 25.
Calculate α(s) using Eq. 26 and calculate the mass fractions for all time, s, using Eqs. 20 to 25. Remember that there will be original components, plus one set of new components for each developmental time step.
Calculate the component stresses from Eqs. 6 to 17 and the material constants in Table 2. Calculate the total mixture stress from Eq. 5.
Calculate the current wall thickness (h(s)) and axial load (f (s)) from Eq. 3a and b. Optimize h(sh) to bring the final circumferential stress as close as possible to the initial, homeostatic circumferential stress.
Solve Eq. 5 with a total passive mixture stress = 0 to satisfy the unloaded equilibrium Eq. 3a and b with P = 0 and f = 0 for the evolving unloaded dimensions of the mixture (A(s) and L(s)) as defined by Eq. 1a and b.
Calculate the unloaded thickness, H (s), using incompressibility.
Record the final loaded and unloaded dimensions of the mixture and the mass fractions of each original and newly produced component predicted by the model. Use these values to start the next developmental time step and continue the growth and remodeling process.
It is important to emphasize that in step 11, the final model predictions for the loaded and unloaded dimensions at the end of each step (i.e from day 3 to day 7.5) are used for the beginning of the next step (i.e. from day 7.5 to day 12); therefore, most of the dimensions and stresses in Table 1 for the other time steps (day 7.5–30) are not used as inputs and are solely used for comparing the model predictions to the experimental data. The only dimension input is the step change in loaded length, which is one of the stimuli for remodeling in step 1. The deformed inner radius changes to actively normalize shear stress and the deformed thickness changes to normalize circumferential stress. The undeformed dimensions change to maintain passive equilibrium as the components turnover.
For step 3, new components are produced with each developmental step. For the first step from ages 3 to 7.5 days, there are only original (oe, oc, om) and new components (ne1, nc1 and nm1). For the next step from ages 7.5 to 12 days, there are original components (oe, oc, om), plus the older new components produced in the step from ages 3 to 7.5 days (ne1, nc1 and nm1), plus the new components produced in the step from ages 7.5 to 12 days (ne2, nc2 and nm2). By the last step from ages 25.5 to 30 days, there are original components, plus five sets of older new components, plus the new components. The total starting and final mass fractions for each step are input from Table 3, but the distribution of original and new mass fractions is predicted by the model. As the vessel grows, the original and older new components that are not degraded completely are stretched farther with each step. Because collagen has a nonlinear stress response function, the stresses can quickly reach high values as the aorta grows; therefore, a breaking stress of 150 MPa (Zeugolis et al. 2008) is implemented. If the predicted stresses for any original or newly produced collagen are >150 MPa in the circumferential or axial direction, it is assumed that the fibers break and the stresses are zero. The collagen is still present and accounted for in the mass fraction, but it no longer contributes to the total tissue stress.
The major assumptions in the baseline case, Case 1, that are relevant to subsequent cases include 1) deformed inner radius is determined by active SMCs trying to maintain the starting homeostatic shear stress, 2) elastin is not degraded but collagen and SMCs are completely degraded with each developmental time step, 3) homeostatic stretch ratios do not change with development and 4) material properties do not change with development. The results from this baseline case are compared to experimental data to determine whether this constrained mixture model can predict the changes in dimensions and mechanical behavior for developing mouse aorta. The model assumptions and parameters are then changed in subsequent cases to investigate mechanisms to improve the model predictions. A summary of all cases is presented in Table 4. In Case 2, the inner radius is decoupled from the shear stress and it is assumed that the SMCs dilate a constant amount for each developmental time step. Cases 3–7 include the modification of Case 2, as well as additional changes. Case 3 adds incomplete collagen turnover. Cases 4 and 5 consider increases and decreases in the homeostatic stretch ratios, respectively. Case 6 includes an increase in the passive material properties with each step. Lastly, Case 7 has a combination of an increase in the circumferential homeostatic stretch ratio, a decrease in the axial homeostatic stretch ratio and an increase in the passive material properties with development. Physiologic explanations for each of these assumptions are included in the discussion.
Table 4.
Summary of different cases used to improve the model predictions for the dimensions and mechanical behavior of developing mouse aorta
| Case | Description | Parameters changed |
|---|---|---|
| 1 | Baseline | None |
| 2 | Assume SMCs dilate 12% regardless of flow change | a = 1.12ao for all steps |
| 3 | Incomplete collagen turnover + case 2 | , a = 1.12ao for all steps |
| 4 | Increase homeostatic stretch ratio 1% for each step + case 2 | for each step, a = 1.12ao for all steps |
| 5 | Decrease homeostatic stretch ratio 1% for each step + case 2 | for each step, a =1.12ao for all steps |
| 6 | Increase passive material constants 2% for each step + case 2 | bn = 1.02bo for each step, a = 1.12ao for all steps |
| 7 | Increase circ homeostatic stretch 3% + decrease axial homeostatic stretch 3% + increase passive material constants 8% for each step + case 2 | for each step, for each step, bn= 1.08bo for each step, a = 1.12ao for all steps |
3 Results
3.1 Inner radius and shear stress
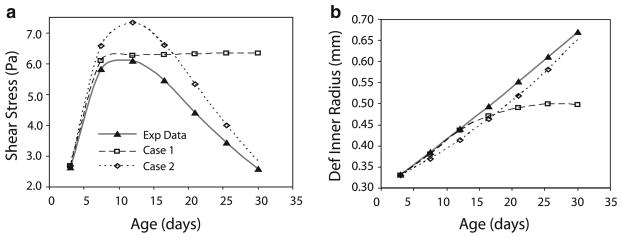
In Case 1, the SMCs instantaneously alter the inner radius in an attempt to normalize shear stress changes caused by developmental increases in blood pressure, axial length and blood flow. With the chosen limits of 30% constriction and 15% dilation, the passive changes in radius due to increases in pressure and axial length can always be normalized by the active SMCs. For the flow, the active SMCs can normalize the shear stress if .34 ≤ εQ ≤ 1.52 (Eq. 3c). According to the εQ values in Table 1 (Wiesmann et al. 2000), the SMCs can normalize the shear stress changes for all but the first two developmental time steps. The deformed inner radius and shear stress predictions for Case 1 are shown in Fig. 3. Note that the shear stress in Fig. 3a increases considerably for the first time step in Case 1, where the SMCs cannot dilate the vessel radius enough and then reaches a plateau at later values when the SMCs can accommodate the smaller flow changes. The experimentally measured blood flow reaches an asymptotic value as the mouse ages and smaller changes in inner radius are required in Case 1 to normalize the shear stress for smaller changes in flow. This is shown in Fig. 3b where the deformed inner radius for Case 1 reaches a plateau for later time points.
Fig. 3.
Comparisons of shear stresses (a) and deformed inner radius (b) between experimental data (Huang et al. 2006; Wiesmann et al. 2000) and predicted by the constrained mixture model for Cases 1 and 2 for developing mouse aorta
Experimentally, the deformed inner radius of mouse thoracic aorta increases almost linearly from days 3 to 30 (Fig. 3b) (Huang et al. 2006). Combined with the experimental blood flow data (Table 1) (Wiesmann et al. 2000), this causes the experimental shear stress to exhibit parabolic behavior during this time period (Fig. 3a). It starts around 2.5 Pa, increases to a peak of 6 Pa at 14 days and returns to 2.5 Pa at 30 days. Interestingly, the range of 1–3 Pa is the approximate shear stress in adult blood vessels across numerous mammalian species. The only way to obtain linear increases in the deformed inner radius with asymptotic increases in blood flow is to change the fundamental model assumption that the SMCs actively contract or dilate in an attempt to return to the starting shear stress at each step. In Case 2, the radius changes are decoupled from the flow rate by assuming that the SMCs dilate the deformed vessel radius 12% with each developmental time step, regardless of the actual change in blood flow. Twelve percent is the average increase in inner radius for each time step across all ages included in the model. The deformed inner radius and shear stress predictions for Case 2 are much closer to the experimental behavior (Fig. 3). Because this decoupling of flow and inner radius is required to mimic the experimental results, all subsequent cases include the assumptions of Case 2.
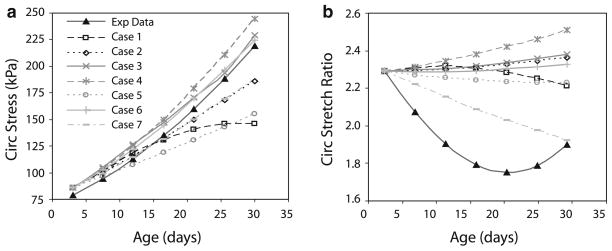
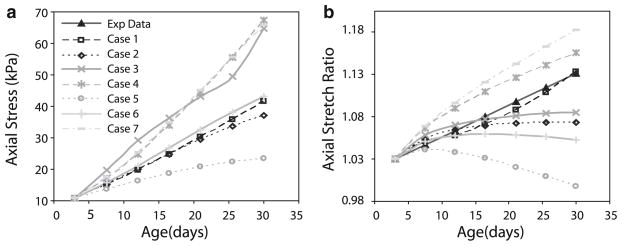
3.2 Circumferential stresses and stretch ratios
In the experimental data, the circumferential stress increases in a polynomial or exponential fashion with age (Fig. 4a) (Huang et al. 2006). In the model predictions for Case 1, the circumferential stress reaches asymptotic values at older ages. In Case 2, the circumferential stress increases linearly. The vessel wall thickness is remodeled in an attempt to normalize the circumferential stresses, but the stresses cannot be brought completely back to the homeostatic value because elastin is not degraded (Gleason et al. 2004; Gleason and Humphrey 2004). The absolute values for Case 2 can be adjusted by changing the material constants or the homeostatic stretch ratios, but overall the behavior is similar to the experimental results. The experimental data show a decrease in the circumferential stretch ratio with age for most of the developmental time period (Fig. 4b) (Huang et al. 2006). The model for Case 1 predicts a slight decrease in stretch ratio with age, but not nearly the amount seen experimentally. Case 2 predicts an increase in stretch ratio with age, which is opposite of the experimental results. Additional changes in the model assumptions or parameters are necessary to mimic the experimental results for the circumferential stretch ratio.
Fig. 4.
Comparison of circumferential stresses (a) and stretch ratios (b) between experimental data (Huang et al. 2006) and model predictions for each case as summarized in Table 4
For the circumferential stress to increase and the circumferential stretch ratio to decrease with age, the aorta must increase in stiffness during the developmental time period. Physiologically, increased stiffness may be caused by stretching of existing elastin and collagen fibers, cross-linking of the deposited elastin and collagen fibers, and phenotype changes in the SMCs as the mouse matures. In the model, stiffness can be increased by including incomplete turnover of collagen or changing the homeostatic stretch ratios or passive material constants with each developmental time step. These changes are implemented in subsequent cases to investigate which one best reproduces the experimental results. The amount of change in each parameter is chosen so that trends can be easily observed, but these changes and the physiologic basis for each one must be confirmed experimentally. A summary of the changes for each case is included in Table 4.
In Case 3, incomplete collagen turnover is included with , which leaves 10% of the original or newly produced collagen from previous steps in place at the end of remodeling. In this case, the circumferential stresses increase more than Case 2, but the circumferential stretch ratio still increases (Fig. 4). When the homeostatic stretch ratios for all components are increased 1% for each developmental step in Case 4, the stresses increase more than Case 2, but so do the stretch ratios, which is not the desired result. When all homeostatic stretch ratios are decreased 1% for each developmental step in Case 5, the stresses increase less than Case 2, and the stretch ratios decrease, but not to the extent observed experimentally. When the passive material constants for all components are increased 2% for each developmental step in Case 6, the stresses are similar to Case 2, but again the stretch ratios increase. When the circumferential homeostatic stretch ratio is increased 3%, the axial homeostatic stretch ratio is decreased 3%, and the passive material constants are increased 8% for all components at each developmental time step in Case 7, the stresses increase similarly to Case 2, but now the stretch ratios decrease like the experimental data. Therefore, Case 7, with a combination of changes tried in other cases, is the only one that can approximate the experimental data for circumferential stress and stretch ratio at different ages.
3.3 Axial stresses and stretch ratios
The axial stresses are not included in Huang et al. (2006), but the trends for different cases can still be compared. The absolute values of the stress can be altered by changing the starting material constants or homeostatic stretch ratios; therefore, the change in axial stress with developmental age is more important than the absolute values for comparing the different cases. All cases show an increase in axial stress with age (Fig. 5a). Case 5 (decreasing homeostatic stretch ratios) shows the smallest increase with age, and Case 3 (incomplete collagen turnover), Case 4 (increasing homeostatic stretch ratios) and Case 7 (combination of increases/decreases in homeostatic stretch ratios and increased passive material constants) show the largest increases with age. Note the uneven curve of Case 3, compared to the smoother curves of the other cases, because the final stress depends on whether or not older collagen fibers reach their breaking stress. This is not as apparent in the circumferential stress curve for Case 3, but still occurs.
Fig. 5.
Comparison of axial stresses (a) and stretch ratios (b) between experimental data (Huang et al. 2006) and model predictions for each case as summarized in Table 4
The axial stretch ratio is assumed to vary linearly from 1.02 to 1.10 over the developmental time period (Fig. 5b) (Wagenseil et al. 2005, 2009; Guo and Kassab 2003). Case 5 predicts a decrease in axial stretch ratio, while Case 2, Case 3 and Case 6 (increasing passive material constants) predict slight increases at young ages, with asymptotic or decreasing behavior at older ages. Only Cases 1, 4 and 7 predict increases in the axial stretch ratio that approximate the experimental data.
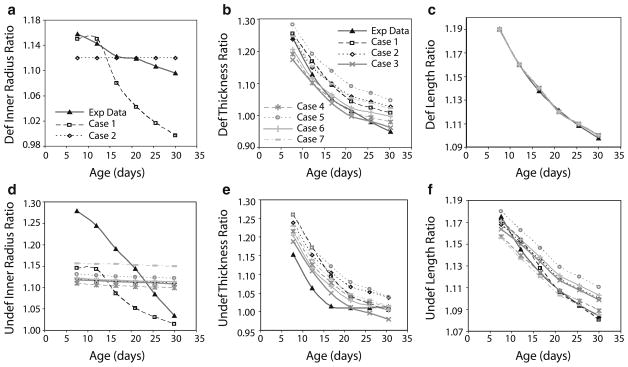
3.4 Loaded and unloaded dimensions
The ratios of final/starting loaded and unloaded dimensions at each developmental time step are compared for all cases in Fig. 6. For the deformed inner radius, only Cases 1 and 2 are plotted, because all other cases are identical to Case 2. Experimentally, the deformed radius increases less with each step as the mouse ages and the average increase for all developmental time steps is 12% (Fig. 6a). Case 1 shows much smaller increases in the deformed radius than the experimental data with a dramatic drop at the older ages. Case 2, and all subsequent cases, show a constant increase in deformed radius of 12% because that was the prescribed valued when the SMC dilation was uncoupled from the flow changes. The ratio of final/starting deformed thickness for all cases shows an exponential decay similar to the experimental data (Fig. 6b). This occurs because smaller increases in thickness are needed for smaller changes in pressure (Table 1) to normalize the circumferential stress as the mouse ages. Case 7 closely follows the experimental changes in thickness. The deformed length is prescribed for all cases; therefore, the ratio of final/starting deformed length is identical for all cases and is similar to the experimental data (Fig. 6c).
Fig. 6.
Comparison of ratios of final/starting loaded (a, b, c) and unloaded (d, e, f) dimensions for each developmental time step between experimental data (Huang et al. 2006) and model predictions for each case as summarized in Table 4
The ratio of final/starting undeformed inner radius at each developmental time step shows similar behavior to the ratio for the deformed inner radius. The behavior of Case 1 best matches the experimental data, but underestimates the increase at each age (Fig. 6d). All other cases show an almost constant ratio with age that underestimates the experimental data at young ages and overestimates the experimental data at older ages. The ratio of final/starting undeformed inner radius in Case 7 is approximately the average of the experimental data over the developmental time period. The almost constant change in undeformed inner radius for Cases 2–7 is related to the assumption that the deformed inner radius increases a constant amount for each developmental time step. The ratio of final/starting undeformed thickness shows an exponential decay with age for all cases that is similar to the experimental data (Fig. 6e). Cases 3 and 7 show the best matches to the experimental data for the undeformed thickness. The ratio of final/starting undeformed length also shows an exponential decay with age for all cases that is similar to the experimental data (Fig. 6f). Case 7 closely follows the experimental data for the undeformed length.
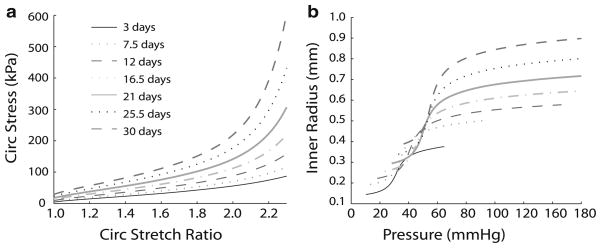
3.5 Evolving material and structural properties
Overall, the predictions for Case 7, with a combination of increasing circumferential and decreasing axial homeostatic stretch ratios and increasing passive material properties, best match the experimental data for the stresses, stretch ratios and dimensions of developing mouse aorta. The material constants, homeostatic stretch ratios, unloaded stretch ratios, mass fractions and dimensions for the start of remodeling on day 3 and predicted at the end of each developmental time step for Case 7 are used to plot the evolving stress–stretch ratio and inner radius–pressure behavior (Fig. 7). Note that the stress–stretch ratio curves shift up and become nonlinear at lower stretch ratios with age (Fig. 7a). This matches the experimentally predicted increase in physiologic stress and decrease in physiologic stretch ratio with age (Huang et al. 2006) This also provides significant material stiffening at stretch ratios just beyond the physiologic values for each age and may be a mechanism to prevent stretch-induced damage to the aorta. The radius–pressure curves shift up and to the right with age as the loaded dimensions increase (Fig. 7b). The radius–pressure curves for day 3 and day 30 are comparable to those obtained for neonatal (Wagenseil et al. 2009) and adult mouse aorta (Wagenseil et al. 2005) although the tail at low pressures is too long and the slope in the linear region is too steep. The shape of the curve can be adjusted by altering the starting material constants, homeostatic stretch ratios and vessel dimensions. The transition from the linear region (high compliance) to the horizontal region (low compliance) of the radius–pressure curve shifts to higher pressures with age and occurs near the physiologic values. This behavior prevents pressure-induced overstretch and is adjusted as the physiologic pressure increases during development.
Fig. 7.
Stress–stretch ratio (a) and inner radius–pressure (b) curves for Case 7 at each developmental time point. Case 7 best matches the experimental data and includes constant increases in the inner radius regardless of the step increases in pressure, length and flow, as well as increases in the circumferential homeostatic stretch ratios, decreases in the axial homeostatic stretch ratios and increases in the passive material constants with each step
4 Discussion
Postnatal aortic growth and development in mice is modeled by a constrained mixture model with successive step changes in blood pressure, axial length and blood flow rate. The starting dimensions for a 3-day-old mouse aorta are determined from experimental data, and postnatal development is divided into six equal time steps from 3 to 30 days old. Model parameters and the magnitude of the step changes in pressure, length and flow are estimated from experimental data. The model predictions for the loaded and unloaded dimensions of the aorta and the mass fraction ratios of newly produced elastin, collagen and SMCs at the end of each time step are used as inputs for the next time step. In the baseline model, Case 1, it is assumed that active SMCs instantaneously change the inner radius within prescribed limits to normalize the wall shear stress.
4.1 Developing arteries respond to shear differently than adult arteries
The results of Case 1 suggest that developing SMCs do not have a constant, homeostatic shear stress and that the active SMC response in the model must be revised. The experimental data for deformed inner radius (Huang et al. 2006) and blood flow (Wiesmann et al. 2000) for 3- to 30-day-old mice do not support the baseline model assumption that developing SMCs dilate just enough to normalize the shear stress at each step. In fact, the deformed inner radius and changes in blood flow must be decoupled in Case 2, and all additional cases, to reproduce the experimental results for the alterations in shear stress with developmental age. It is possible that developing SMCs grow and increase the vessel radius solely by genetic programming and changes in blood flow are irrelevant. However, years of observation on the relationships between blood flow and the radius of developing vessels show that this is probably not true (Clark 1918; Langille 1993). It is more likely that the shear stress and inner radius are coupled, but in a more complicated manner than included in the current model.
The fact that changes in flow rate and deformed inner radius cannot be treated in the simple manner used for remodeling in adult arteries, raises the intriguing possibility that developing SMCs have different shear responses than adult SMCs. It is possible that homeostatic shear stress is a constantly moving target in developing aorta, not the static value at each time point that is used in the current model. Changes in shear stress with postnatal development have been shown in rabbits (Di Stefano et al. 1998) and sheep (Langille et al. 1990). Furthermore, when blood flow is elevated in young rabbits, the artery wall is remodeled so that shear stresses match that of the control artery three months later, even though the shear stresses in the control artery have decreased during this time (Di Stefano et al. 1998). It is also possible that there is some delay between the changes in flow and the SMC response to normalize shear stress. This study only includes postnatal growth from days 3 to 30. Mice reach maturity around 90 days of age, and the vessel inner radius must reach an asymptotic value as the mice mature. When the entire developmental period from birth to maturity is considered, the blood flow and inner radius may show more similar behavior over time, with the radius reaching its maximum value later than the blood flow. In this case, the inner radius and blood flow may again be coupled, but subject to some delay that causes the radius changes to lag the flow changes. Testing these hypotheses in more sophisticated models and identifying a physiologic basis for these mechanisms will be critical for understanding how genetic programming and mechanical stimuli dictate growth and remodeling in developing blood vessels. Determining the interplay between these factors may help identify genes or proteins that can be used to encourage growth and remodeling in vitro for tissue-engineered vessels and in vivo for treating human vascular disease.
4.2 Circumferential arterial stiffness increases with developmental age
Experimentally, the circumferential and presumably the axial stresses increase with development. The circumferential stretch ratio decreases and the axial stretch ratio increases (Huang et al. 2006). Case 2 approximates the experimental deformed inner radius and the shear stresses, but cannot predict the experimental changes in wall stresses and stretch ratios. Additional cases were investigated to determine what changes are necessary to reproduce the experimental data. The best match is Case 7, where the homeostatic stretch ratio is increased in the circumferential direction and decreased in the axial direction, and the passive material constants are increased for all components with each developmental time step. Other cases with only one of these changes, or with incomplete collagen turnover, did not capture the experimental behavior. Different increases and/or decreases for individual parameters for each component were not investigated, but are certainly possible and may improve the model predictions.
One of the main goals of mathematical modeling is to provide interpretations of the experimental data. Ideally, the mathematical model would help explain the mechanical data and then microstructural evidence would support the model-based interpretation. This information could subsequently be used to manipulate the arterial microstructure to obtain desired mechanical properties. Case 7 shows that the experimental mechanical behavior can be explained by changes in the homeostatic stretch ratio and that these changes must be different in the circumferential and axial directions. These opposite changes could be related to differences in the rate of growth of the aorta, the rate of deposition of each component, the amount of components or the organization of components in each direction. For example, elastin layers have fenestrations that change in size and orientation with growth and remodeling (Wong and Langille 1996), which may affect the homeostatic stretch ratio of elastin in each direction. Additionally, collagen is arranged as helically oriented fibers in the aortic wall. If the fibers become more circumferentially oriented with development, this could explain increases in the circumferential direction and decreases in the axial direction for the collagen homeostatic stretch ratio. The current model does not include any provisions for investigating collagen fiber orientation. Future iterations could model the collagen as families of oriented fibers as introduced by Holzapfel et al. (2000) and used in several recent mixture models (Baek et al. 2006; Valentin et al. 2009; Valentin and Humphrey 2009; Wan et al. 2009). This would allow model predictions of collagen fiber orientation to be verified experimentally.
Case 7 also shows that increases in the passive material constants are necessary to predict the experimental behavior. The stiffening of individual components could be caused by increasing connections between or cross-linking of the elastin and collagen proteins and changes in the SMC phenotype with maturation. Electron micrographs of 3 days old mouse aorta show that elastin is deposited between layers of SMCs in disconnected globules. By 14 days, enough globules have been deposited to form almost complete layers of elastin (Davis 1995). Presumably, the connected sheets of elastin offer more mechanical resistance than the disconnected globules and could explain the increase in elastin stiffness with development. Expression of lysyl oxidase, a cross-linking protein, also increases during development (Kelleher et al. 2004). Lysyl oxidase expression may be stimulated by increased stress in the wall, which would help optimize the mechanical properties to withstand the increasing hemodynamic forces. Investigating lysyl oxidase amounts and the stimulus for expression would provide links between the biological, chemical and mechanical signals in developing blood vessels. Understanding these links is essential for building predictive models that integrate different signaling mechanisms.
4.3 Future experiments
Another goal of mechanical modeling is to guide future experiments. In general, there is a paucity of data for developing blood vessels, especially in mice. Huang et al. (2006) present a detailed study, but include no axial stress data, and some of their results conflict with other groups. For example, their circumferential stress values for 1.5-day and 30-day-old thoracic aorta are significantly higher than values from Wagenseil et al. (2005, 2009) for neonatal and adult mouse aorta. In addition, their mean pressure, inner deformed radius, deformed thickness and circumferential stress values are not consistent. In this study, the experimental circumferential stress is used to calculate the thickness according to Eq. 3a, but if the experimental values of deformed thicknesses are used to calculate the stress, the stress values are significantly lower. Additional data would help average out variations between studies and generate a more robust model. Additional data are also needed for better estimates of model parameters such as component amounts, component stress contributions and the amount of active SMC constriction and dilation in developing aorta.
Future experiments are necessary to test and extend the model predictions. For example, if a cross-link inhibitor is used on developing vessels, does this prevent the increase in passive material constants and can the model for Case 7 predict the experimental results? If so, can this be used to treat human diseases or alter mechanical properties in tissue-engineered vessels? If not, what additional assumptions must be changed to predict the experimental behavior? Numerous similar experiments are possible with genetically engineered mice where the amount or organization of vessel wall components has been changed. This includes mice with reduced elastin amounts (Li et al. 1998), mice with disorganized elastin fibers due to reduced amounts of associated proteins, such as fibulin-5 (Nakamura et al. 2002; Yanagisawa et al. 2002) and mice with reduced amounts of elastin and collagen cross-linking proteins, such as lysyl oxidase (Hornstra et al. 2003). The mechanisms uncovered in this iterative approach of modeling and experimentation can be used to manipulate the growth and remodeling process both in vitro and in vivo.
4.4 Model limitations and improvements
The increases in blood pressure, axial length and blood flow are most likely continuous functions, rather than the step increases included in the current model, but the step increases still provide insight into the interactions between hemodynamic forces and aortic structure and function. Most models and experimental data on adult vessel remodeling are also based on step changes, although this is probably not physiologically accurate in diseases such as hypertension. Future model improvements include continuous changes in these parameters, so that rate effects can be investigated and remodeling behavior can be predicted at any developmental time point. This approach requires continuous tracking of the vessel loaded dimensions, unloaded dimensions, homeostatic stretch ratios, unloaded stretch ratios and component mass fractions at all times. The active SMC response must also be modified. Currently, active SMCs can instantaneously constrict or dilate to provide limited alterations in diameter to normalize the shear stress. If the perturbations are small enough, for example if the developmental time step approaches zero in a continuous model, the SMCs can always return to the homeostatic shear stress and little remodeling occurs. Even with step sizes of 4.5 days in this study, the pressure, length and flow changes are small enough that the SMCs can normalize the shear stresses for all but the earliest developmental time points. One option for the SMC response in a continuous model is to include an evolving target shear stress or a delayed active SMC response. Physiologic mechanisms for these options must be investigated in parallel with the model development.
In the current model, each component has a constant turnover rate that is assumed to be the same throughout development. It could be argued that component turnover varies with developmental age and/or that the rate depends on stress or strain in the aortic wall. While the rate of turnover is constant, the total amount of each component changes with age so that elastin and collagen increase and SMCs decrease. This is consistent with gene array data in developing mice showing that elastin and collagen expression peak in the first few days after birth (Kelleher et al. 2004). Constrained mixture models have been modified to include turnover rates that are a function of stress magnitudes (Baek et al. 2006; Wan et al. 2009), but there is limited data available to determine the form of these relationships. Also, while increased stress may increase component production in adult arteries that are maintained at some low, basal production rate, it may have less effect in developing arteries with continually increasing stresses and high production rates. With continually increasing stresses in development, the rate of change of the stresses may be important for production rates. For example, when stresses are increasing quickly, production may be high and when stresses are increasing slowly, production may be low. Cardamone et al. (2010) recently found that both stress- and stress rate-mediated turnover of cells and matrix is necessary to model adaptations to dynamic alterations in flow and pressure over the cardiac cycle. Different relationships between stress, stress rate and component production rates can be investigated in future models, but experimental data are required to validate the predictions. At this stage, a constant turnover rate seems reasonable for a constrained mixture model of developing mouse aorta.
The transmural distribution of wall stresses and stretch ratios is neglected in the current model and average values are used. This approach provides information about the global changes in vessel wall dimensions and stresses. Constrained mixture models have been modified to include complete three-dimensional descriptions of the stresses and stretch ratios (Alford et al. 2008; Wan et al. 2009. The radial variations in stress and stretch ratios may have important consequences for SMC differentiation at different points across the wall thickness. The wall of large arteries is composed of the intima, media and adventitia. The intima is a thin layer of endothelial cells and basement membrane; the media is composed of circumferential layers of SMCs and elastin (called elastic laminae) with some collagen; and the adventitia is made up mostly of fibroblasts and collagen. In aorta from elastin haploinsufficient mice, the outer layers of fibroblasts that normally form the adventitial layer appear to differentiate just before birth to become elastin-producing cells that form additional elastic laminae (Wagenseil et al. 2009). A change in the radial gradient of stresses or stretch ratios due to reduced elastin levels and altered mechanical stimuli may be partly responsible for this switch in cell phenotype. Future iterations of this developmental model that include transmural wall stress and stretch ratio distributions would allow investigation of this hypothesis.
This study and most of the remodeling literature focuses on optimization of shear and circumferential stresses and neglects optimization of axial stresses. More recent work argues that axial remodeling should not be neglected (Humphrey et al. 2009). It has been shown that blood vessels grow in response to increased axial stretch, presumably to reduce the resulting axial force and normalize the axial stress (Jackson et al. 2002). Paradoxically, blood vessels will also grow and become tortuous in response to decreased axial stretch (Jackson et al. 2005). Reduced amounts of elastin or elastin-associated proteins, such as fibrillin-1, decrease the in vivo axial stretch of mouse carotid arteries (Dye et al. 2007; Wagenseil et al. 2005); therefore, the amount and organization of vessel wall constituents are important for the axial behavior and will be an important consideration for future models of developing blood vessels.
5 Conclusion
A constrained mixture model is used to predict postnatal growth and remodeling in mouse aorta. Model inputs from previously published experimental data include the loaded and unloaded dimensions of a 3-day-old mouse aorta, step changes in pressure, axial length and flow and total mass fractions of elastin, collagen and SMCs at each developmental time step. Model parameters include constant turnover rates, material properties and homeostatic stretch ratios for each component. Model predictions for the final loaded and unloaded dimensions and the mass fraction ratios of newly produced components at each step are used as the initial values for the next step to recreate the development of a 30-day-old mouse aorta. The baseline model assumes that SMCs immediately constrict or dilate the vessel inner radius within prescribed limits to maintain shear stress and then remodel the vessel wall thickness to maintain circumferential stress. The homeostatic stretch ratios and passive material properties of the components do not change with developmental age. The baseline model does not predict previously published experimental data. To approximate the experimental data, it must be assumed that the SMCs dilate a constant amount regardless of the step change in pressure, length and flow and that the homeostatic stretch ratios and passive material constants change with developmental age. These predictions can be used to interpret and guide experiments. They can also be used to test treatment options for human diseases and design protocols for growing tissue-engineered vessels.
Acknowledgments
I would like to thank Robert Mecham for helpful discussions and Ruth Okamoto and Rudolph Gleason for helpful discussions and providing example Matlab files. Funding was provided by NIH grant HL087563.
References
- Alford PW, Humphrey JD, Taber LA. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomech Model Mechanobiol. 2008;7(4):245–262. doi: 10.1007/s10237-007-0101-2. 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng. 2006;128(1):142–149. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- Cardamone L, Valentin A, Eberth JF, Humphrey JD. Modelling carotid artery adaptations to dynamic alterations in pressure and flow over the cardiac cycle. Math Med Biol. 2010 doi: 10.1093/imammb/dqq001. dqq001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark ER. Studies on the growth of blood-vessels in the tail of the frog larva—by observation and experiment on the living animal. Am J Anat. 1918;23:37–88. [Google Scholar]
- Davis EC. Elastic lamina growth in the developing mouse aorta. J Histochem Cytochem. 1995;43(11):1115–1123. doi: 10.1177/43.11.7560894. [DOI] [PubMed] [Google Scholar]
- Di Stefano I, Koopmans DR, Langille BL. Modulation of arterial growth of the rabbit carotid artery associated with experimental elevation of blood flow. J Vasc Res. 1998;35(1):1–7. doi: 10.1159/000025559. jvr35001. [DOI] [PubMed] [Google Scholar]
- Dobrin PB, Canfield TR. Elastase, collagenase, and the biaxial elastic properties of dog carotid artery. Am J Physiol. 1984;247(1 Pt 2):H124–H131. doi: 10.1152/ajpheart.1984.247.1.H124. [DOI] [PubMed] [Google Scholar]
- Dye WW, Gleason RL, Wilson E, Humphrey JD. Altered biomechanical properties of carotid arteries in two mouse models of muscular dystrophy. J Appl Physiol. 2007;103(2):664–672. doi: 10.1152/japplphysiol.00118.2007. [DOI] [PubMed] [Google Scholar]
- Faury G, Maher GM, Li DY, Keating MT, Mecham RP, Boyle WA. Relation between outer and luminal diameter in cannulated arteries. Am J Physiol. 1999;277(5 Pt 2):H1745–H1753. doi: 10.1152/ajpheart.1999.277.5.H1745. [DOI] [PubMed] [Google Scholar]
- Fonck E, Prod’hom G, Roy S, Augsburger L, Rufenacht DA, Stergiopulos N. Effect of elastin degradation on carotid wall mechanics as assessed by a constituent-based biomechanical model. Am J Physiol Heart Circ Physiol. 2004;292(6):H2754–H2763. doi: 10.1152/ajpheart.01108.2006. 01108.2006. [DOI] [PubMed] [Google Scholar]
- Gleason RL, Humphrey JD. A mixture model of arterial growth and remodeling in hypertension: altered muscle tone and tissue turnover. J Vasc Res. 2004;41(4):352–363. doi: 10.1159/000080699. [DOI] [PubMed] [Google Scholar]
- Gleason RL, Taber LA, Humphrey JD. A 2-d model of flow-induced alterations in the geometry, structure and properties of carotid arteries. J Biomech Eng. 2004;126:371–381. doi: 10.1115/1.1762899. [DOI] [PubMed] [Google Scholar]
- Guo X, Kassab GS. Variation of mechanical properties along the length of the aorta in c57bl/6 mice. Am J Physiol Heart Circ Physiol. 2003;285(6):H2614–H2622. doi: 10.1152/ajpheart.00567.2003. [DOI] [PubMed] [Google Scholar]
- Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast. 2000;61(1–3):1–48. [Google Scholar]
- Hornstra IK, Birge S, Starcher B, Bailey AJ, Mecham RP, Shapiro SD. Lysyl oxidase is required for vascular and diaphragmatic development in mice. J Biol Chem. 2003;278(16):14387–14393. doi: 10.1074/jbc.M210144200. [DOI] [PubMed] [Google Scholar]
- Huang Y, Guo X, Kassab GS. Axial nonuniformity of geometric and mechanical properties of mouse aorta is increased during postnatal growth. Am J Physiol Heart Circ Physiol. 2006;290(2):H657–H664. doi: 10.1152/ajpheart.00803.2005. [DOI] [PubMed] [Google Scholar]
- Humphrey JD, Eberth JF, Dye WW, Gleason RL. Fundamental role of axial stress in compensatory adaptations by arteries. J Biomech. 2009;42(1):1–8. doi: 10.1016/j.jbiomech.2008.11.011. S0021-9290(08)00595-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Models Methods Appl Sci. 2002;12(3):407–430. [Google Scholar]
- Ishii T, Kuwaki T, Masuda Y, Fukuda Y. Postnatal development of blood pressure and baroreflex in mice. Auton Neurosci. 2001;94 (1–2):34–41. doi: 10.1016/S1566-0702(01)00339-3. [DOI] [PubMed] [Google Scholar]
- Jackson ZS, Dajnowiec D, Gotlieb AI, Langille BL. Partial offloading of longitudinal tension induces arterial tortuosity. Arter Thromb Vasc Biol. 2005;25(5):957–962. doi: 10.1161/01.ATV.0000161277.46464.11. [DOI] [PubMed] [Google Scholar]
- Jackson ZS, Gotlieb AI, Langille BL. Wall tissue remodeling regulates longitudinal tension in arteries. Circ Res. 2002;90(8):918–925. doi: 10.1161/01.res.0000016481.87703.cc. [DOI] [PubMed] [Google Scholar]
- Kelleher CM, McLean SE, Mecham RP. Vascular extracellular matrix and aortic development. Curr Top Dev Biol. 2004;62:153–188. doi: 10.1016/S0070-2153(04)62006-0. [DOI] [PubMed] [Google Scholar]
- Langille BL. Remodeling of developing and mature arteries: endothelium, smooth muscle, and matrix. J Cardiovasc Pharmacol. 1993;21(1):S11–S17. doi: 10.1097/00005344-199321001-00003. [DOI] [PubMed] [Google Scholar]
- Langille BL, Bendeck MP, Keeley FW. Adaptations of carotid arteries of young and mature rabbits to reduced carotid blood flow. Am J Physiol. 1989;256(4 Pt 2):H931–H939. doi: 10.1152/ajpheart.1989.256.4.H931. [DOI] [PubMed] [Google Scholar]
- Langille BL, Brownlee RD, Adamson SL. Perinatal aortic growth in lambs: relation to blood flow changes at birth. Am J Physiol. 1990;259(4 Pt 2):H1247–H1253. doi: 10.1152/ajpheart.1990.259.4.H1247. [DOI] [PubMed] [Google Scholar]
- Li DY, Faury G, Taylor DG, Davis EC, Boyle WA, Mecham RP, Stenzel P, Boak B, Keating MT. Novel arterial pathology in mice and humans hemizygous for elastin. J Clin Invest. 1998;102(10):1783–1787. doi: 10.1172/JCI4487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li DY, Toland AE, Boak BB, Atkinson DL, Ensing GJ, Morris CA, Keating MT. Elastin point mutations cause an obstructive vascular disease, supravalvular aortic stenosis. Hum Mol Genet. 1997;6(7):1021–1028. doi: 10.1093/hmg/6.7.1021. [DOI] [PubMed] [Google Scholar]
- Nakamura T, Lozano PR, Ikeda Y, Iwanaga Y, Hinek A, Minamisawa S, Cheng CF, Kobuke K, Dalton N, Takada Y, Tashiro K, Ross J, Jr, Honjo T, Chien KR. Fibulin-5/dance is essential for elastogenesis in vivo. Nature. 2002;415(6868):171–175. doi: 10.1038/415171a. [DOI] [PubMed] [Google Scholar]
- Olivetti G, Anversa P, Melissari M, Loud AV. Morphometric study of early postnatal development of the thoracic aorta in the rat. Circ Res. 1980;47(3):417–424. doi: 10.1161/01.res.47.3.417. [DOI] [PubMed] [Google Scholar]
- Valentin A, Cardamone L, Baek S, Humphrey JD. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J R Soc Interface. 2009;6(32):293–306. doi: 10.1098/rsif.2008.0254. 92812083762PK762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentin A, Humphrey JD. Modeling effects of axial extension on arterial growth and remodeling. Med Biol Eng Comput. 2009;47(9):979–987. doi: 10.1007/s11517-009-0513-5. 10.1007/s11517-009-0513-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenseil JE, Ciliberto CH, Knutsen RH, Levy MA, Kovacs A, Mecham RP. Reduced vessel elasticity alters cardiovascular structure and function in newborn mice. Circ Res. 2009;104(10):1217–1224. doi: 10.1161/CIRCRESAHA.108.192054. CIRCRESAHA.108.192054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenseil JE, Mecham RP. Vascular extracellular matrix and arterial mechanics. Physiol Rev. 2009;89(3):957–989. doi: 10.1152/physrev.00041.2008. 89/3/957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenseil JE, Nerurkar NL, Knutsen RH, Okamoto RJ, Li DY, Mecham RP. Effects of elastin haploinsufficiency on the mechanical behavior of mouse arteries. Am J Physiol Heart Circ Physiol. 2005;289(3):H1209–H1217. doi: 10.1152/ajpheart.00046.2005. [DOI] [PubMed] [Google Scholar]
- Wan W, Hansen L, Gleason RL., Jr A 3-d constrained mixture model for mechanically mediated vascular growth and remodeling. Biomech Model Mechanobiol. 2009 doi: 10.1007/s10237-009-0184-z. 10.1007/s10237-009-0184-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westerhof N, Stergiopulos N, Noble M. Snapshots of hemodynamics: an aid for clinical research and graduate education. 2004. p. 42. [Google Scholar]
- Wiesmann F, Ruff J, Hiller KH, Rommel E, Haase A, Neubauer S. Developmental changes of cardiac function and mass assessed with MRI in neonatal, juvenile, and adult mice. Am J Physiol Heart Circ Physiol. 2000;278(2):H652–H657. doi: 10.1152/ajpheart.2000.278.2.H652. [DOI] [PubMed] [Google Scholar]
- Wong LC, Langille BL. Developmental remodeling of the internal elastic lamina of rabbit arteries: effect of blood flow. Circ Res. 1996;78(5):799–805. doi: 10.1161/01.res.78.5.799. [DOI] [PubMed] [Google Scholar]
- Yanagisawa H, Davis EC, Starcher BC, Ouchi T, Yanagisawa M, Richardson JA, Olson EN. Fibulin-5 is an elastin-binding protein essential for elastic fibre development in vivo. Nature. 2002;415(6868):168–171. doi: 10.1038/415168a. [DOI] [PubMed] [Google Scholar]
- Zeugolis DI, Paul RG, Attenburrow G. Factors influencing the properties of reconstituted collagen fibers prior to self-assembly: animal species and collagen extraction method. J Biomed Mater Res A. 2008;86(4):892–904. doi: 10.1002/jbm.a.31694. 10.1002/jbm.a.31694. [DOI] [PubMed] [Google Scholar]