Computational methods for identifying a layered allosteric regulatory mechanism for ALS-causing mutations of Cu-Zn superoxide dismutase 1

Abstract

The most prominent form of familial amyotrophic lateral sclerosis (fALS, Lou Gehrig’s Disease) is caused by mutations of Cu-Zn superoxide dismutase 1 (SOD1). SOD1 maintains antioxidant activity under fALS causing mutations, suggesting that the mutations introduce a new, toxic, function. There are 100+ such known mutations that are chemically diverse and spatially distributed across the structure. The common phenotype leads us to propose an allosteric regulatory mechanism hypothesis: SOD1 mutants alter the correlated dynamics of the structure and differentially signal across an inherent allosteric network, thereby driving the disease mechanism at varying rates of efficiency.

Two recently developed computational methods for identifying allosteric control sites are applied to the wild type crystal structure, 4 fALS mutant crystal structures, 20 computationally generated fALS mutants and 1 computationally generated non-fALS mutant. The ensemble of mutant structures is used to generate an ensemble of dynamics, from which two allosteric control networks are identified. One network is connected to the catalytic site and thus may be involved in the natural antioxidant function. The second allosteric control network has a locus bordering the dimer interface and thus may serve as a mechanism to modulate dimer stability. Though the toxic function of mutated SOD1 is unknown and likely due to several contributing factors, this study explains how diverse mutations give rise to a common function. This new paradigm for allostery controlled function has broad implications across allosteric systems and may lead to the identification of the key chemical activity of SOD1-linked ALS.

Introduction

ALS and SOD1

Amyotrophic lateral sclerosis (ALS) is the most common motor neuron disease [1]. Approximately 5–10% of ALS cases are due to genetically linked mutations and are termed familial ALS (fALS), while the remaining cases are of unknown cause(s), but present identical symptoms [2], suggesting a similar underlying mechanism. The most common fALS type is caused by any of the more than 100 known mutations of the enzyme Cu-Zn superoxide dismutase 1 (SOD1) [2]. All of these mutations maintain the enzyme’s natural antioxidant activity, suggesting that a new, toxic, function is introduced by mutation. This function, let alone its mechanism of action, is unknown.

There have been numerous studies of proposed disease mechanisms and treatments [3–8]. Toxic aggregation of dissociated monomers has been implicated as a driving force in disease progression. Ray et al. [6] demonstrate that small molecule docking at the dimer interface stabilizes several fALS mutants by resisting aggregation and unfolding. However, Rodriguez et al. [9] identify several SOD1 mutations that are more stable than the WT. There is no single property (e.g. dimer stability, net charge, metallation) that correlates mutation type with disease progression. It is thus assumed that ALS results from multiple contributory mechanisms [7].

The SOD1 mutations that cause ALS are unrelated, ranging widely in their chemical nature and spatial distribution within the structure. As further evidence of their diversity, patient survival times range from 1 to 17+ years, depending upon the mutation. These factors lead to our:

allosteric mechanism hypothesis

SOD1 mutants alter the correlated dynamics of the structure and differentially signal across an inherent allosteric network, thereby driving the disease mechanism at varying rates of efficiency.

The methods discussed thus far have one thing in common: they are external to SOD1 and observational, in that they identify products of the disease, but not causal components of the mechanism. In order to best understand these contributory factors, and their potentially compounding interactions, atomic level descriptions of their respective modes of action are essential. In this study we utilize computational methods to elucidate a group of atomic level interactions that support an allosterically modulated mechanism. Such a mechanism may not be universally accessible to all SOD1 mutant forms, but deriving the mechanism across a set of SOD1 mutants allows for the cohesive allosteric signal to stand out from the noise.

Allostery

Allostery is most generally described as an event at one structure location triggering a response at another (e.g. ligand binding at one location triggering a structure rearrangement that modulates the binding affinity at a secondary site). Allostery has been recognized as a regulator of protein stability [10] and a carrier of structure entropy [11]. Gunasekaran et al. [12] even hypothesize that all dynamic proteins have the potential to be controlled allosterically.

The cause and effect of allosteric communication may be readily observed, but the signal transmission mechanism is frequently not well understood. A variety of techniques have been employed, including solution NMR[13], molecular dynamics [14], Markov models [15] and network analysis metrics [16, 17]. The current study of SOD1 utilizes the “static” and “dynamic” allosteric site prediction methods recently developed by the authors [18]. Both models were validated against the well studied dihydrofolate reductase and generated allosteric control site predictions with significance values of p < 0.005.

Ensemble Representations

The ensemble representation of conformation space and structure dynamics has advanced many modeling approaches, with significant improvement coming in two related areas. First, drug design has evolved from the “lock and key” and “induced fit” paradigms to a notion of pre-existing conformation ensembles [19–22]. The structure dynamics inherently captured by conformation ensembles greatly improve binding models and have led to better drug design methods [23–25]. Second, transition state modeling [26–28] reveals intermediate structures that serve as way-points along possible transition pathways. The intermediates display structure dynamics that are not locally accessible to the stable endpoints, but may be most relevant to the biological function.

The drug design and transition state modeling methods are illustrative examples of how ensemble representations more accurately describe structure dynamics as they pertain to molecular binding interactions. The ensembles in these methods are of the traditional sense: samples in conformation space around a single structure. In the current SOD1 analysis, we take a different approach, but with a similar motivation. The dynamics of SOD1 are accessed with a mutation ensemble. Rather than sampling conformations around a single structure, we are sampling the dynamics across a family of related structures. The cumulative result is an ensemble of dynamics, distributed over an ensemble of structure variations.

Our use of mutation ensemble derived dynamics is consistent with other approaches in the literature, particulary with respect to normal mode analysis (NMA) based techniques. Van Wynsberghe and Cui [29] establish that correlated dynamics are most accurately identified from an ensemble of normal modes, not just from analyzing individual mode shapes. Petrone and Pande [30] use NMA to study allosteric structure transitions and conclude that localized residue motions are often observed, thereby necessitating a large set of NMA modes to capture the motions. Zheng et al. [31] observe the conservation of low-frequency normal modes that relate to allosteric transitions. This conservation is quantified as a robustness to sequence variation, a result which strongly supports the current SOD1 approach.

Methods

The mutation ensemble of SOD1 is assembled from crystal structures available in the protein data bank (PDB, [32]) and from computationally generated structures produced by the mutagenesis tool in PyMOL (version 1.0r0, [33]). These procedures are given in the following sections. The SOD1 structures included in this study are listed in Table 1, along with set names that are used during the analysis to reference subgroups of structures. The dimer is shown in Figure 1, with the mutation sites highlighted and key structure locations labeled.

Table 1. SOD1 Structures.

The crystal structures are listed in the top panel along with their PDB tags, crystal resolution (Å), primary literature reference, ordered pairing of chain identifiers defining the dimer and RMSD from WT (Å, taken between all common atoms). The bottom panel lists the computationally derived mutant structures, which are based on the WT crystal structure and produced with the mutagenesis wizard in PyMOL [33]. The “set names” categorize the structures into 4 groups based on their link to ALS and their method of derivation.

X-ray structures from PDB
structure	PDB	res	[ref]	dimer	RMSD	set name
WT	1HL5	1.8	[40]	BI	–	nALS-xray
A4V	1UXM	1.9	[41]	LK	1.03	yALS-xray
G37R	1AZV	1.9	[42]	BA	1.11
H46R	1OZT	2.5	[43]	MN	0.94
I113T	1UXL	1.6	[41]	GB	0.85
computationally derived from WT
mutations						set name
C6G	V14G	F20C	E21G		F45C	yALS-comp
N65S	N86S	V87A	D90A		E100G
D101G	I112T	R115G	D124G		A140G
L144S	A145G	V148G	I149T		I151T
T39I						nALS-comp

Figure 1. WT SOD1 and Mutation Sites.

SOD1 contains 153 residues and is biologically active in a homodimer form shown here, with each monomer containing a copper and zinc binding site. The bulk of the structure is a compact β-barrel and backs the active site. The residues associated with the mutations listed in Table 1, are shown with balls and sticks. Mutations with crystal structures are colored red and those that are computationally generated are colored yellow. The copper and zinc atoms are shown as dotted spheres. (Image prepared with PyMOL [33].)

The allosteric mechanism hypothesis is tested with the application of the “static” and “dynamic” allosteric control site prediction methods. The static method predicts control sites with a geometric analysis of a single conformation and reveals the structural basis for an inherent allosteric network. The dynamic method compares the harmonic motions (i.e. normal modes) between a WT and mutant; atoms that become substantially more/less involved in correlated motion are identified as allosteric control sites. These allosteric prediction methods are briefly discussed in the following sections; complete details are available in [18].

Structure Preparation

Crystal Structures

The SOD1 wild type (WT) is available in the PDB as a crystal structure of excellent resolution. Only 4 of the 100+ fALS causing SOD1 mutations are single residue mutations with complete crystal structures of similar resolution. Multiple mutations may introduce complicating secondary effects and are excluded from this analysis.

Each crystal structure contains multiple copies of the SOD1 dimer. The dimer selected for analysis is the one most central to the ensemble and is determined as follows:

1. Any dimers with missing atoms are excluded.

2. A set of RMSD values is computed for each dimer by optimally aligning it to every other dimer.

3. The average RMSD is computed for each dimer’s set of RMSD values.

4. The dimer with the minimum value is selected.

Computationally Generated Mutants

The 4 mutant SOD1 crystal structures constitute a superb structure ensemble. In an effort to (i) probe the applicability of this analysis approach to other systems that may lack such an ensemble and (ii) extend the consensus results of this analysis across even more fALS forms, an additional fALS structure set is generated with the mutagenesis tool from PyMOL. This tool uses a rotamer library and is capable of generating any possible mutation, but it only accounts for backbone rearrangement local to the mutation site. Therefore, in order to produce the highest quality set of structures the only mutations considered are those whose heavy atom topologies are equivalent to, or a subset of, the WT configuration. These permissible mutations come in two forms. A “swap” is the substitution of one atom type for another (e.g. in Asp→Leu, both δ-oxygens become carbons). A “clip” is the truncation of a WT residue into a smaller residue type (e.g. in Ile→Val, the δ-carbon is removed). This approach is applied to all applicable mutant types and produces 20 additional fALS structures: 12 “clip” and 8 “clip”+“swap”.

The NCBI Single Nucleotide Polymorphism Database [34] lists 3 missense entries for SOD1. Two of the entries are known fALS mutations: D90A (SNP tag rs80265967) and N86S (SNP tag rs11556620). The remaining entry is presumed to be a non-fALS mutant: T39I (SNP tag rs1804450). This mutation is not of the simple “clip” and “swap” variety and requires complete side chain replacement. Given the rarity of identifying a non-ALS mutant, it is included in the analysis and serves as a powerful negative control.

Analysis Techniques

Static Method

Allosteric communication is the flow of a signal across a molecular network. Any model must therefore define the molecular network and derive a function for quantifying signal transmission.

The static method defines its network such that all atom pairs within a cutoff distance are considered linked. This concept is expressed as the adjacency matrix (A) where entry A_i,j = 1 if, and only if, the distance between atoms i and j is not more than the cutoff distance. Self contact is not allowed (A_i,i = 0).

A standard metric in graph theory is degree, which is the number of connections that radiate from a node in a network. This quantity is the sum of values down the corresponding column (or row) of A. The static method generalizes this local description of contact density to a network-wide description by considering paths in the network that connect pairs of atoms. All such paths of a given length (s) are obtained by computing A^s; these values quantify the relative connectedness of each atom to the entire structure and serve as the basis for quantifying signal transmission in the static model.

Consider a structure location which is highly connected to the surrounding structure (i.e. high values down the corresponding column of A^s). Any allosteric signal that flows out of this node is distributed across its dense network of connected paths and diffuses. In contrast, a network location with relatively few radiating paths, transfers a greater magnitude of its allosteric signal down each path. This is the inverse contact path model (iCPM) and it probes the network flow of an allosteric signal. Residues are identified as control sites based on how much their iCPM values deviate from the mean of all residue iCPM values.

Dynamic Method

The dynamic method assigns the known functional differences between two structures to the differences observed in their accessible motions. This comparison is made on the foundation of elastic network based NMA [35–37]. Normal modes, which in this case are obtained with the cluster-based cNMA [38, 39] approach, provide two critical features. First, a structure’s complete set of normal modes defines a coordinate system for the motion space. That is, any structure motion can be represented as some linear combination of the normal modes. Second, through statistical mechanics, each mode’s eigenvalue is used to assign a relative significance, which indicates the importance of the mode to the overall fluctuations of the structure. As a consequence of these properties, the normal modes of one structure, along with their relative significance values, are decomposed over the normal modes of a modified structure. This weighted mapping reveals the extent to which each mode of one structure becomes more significant or less significant when mapped onto the motion space of the second structure.

Given two structures, a WT and a mutant, the dynamic method partitions the normal modes of the WT into two sets: WT+={WT modes that become relatively more significant when mapped onto the mutant} and WT−={WT modes that become relatively less significant when mapped onto the mutant}. Similarly, the mutant modes are partitioned into two sets: M+={mutant modes that become relatively more significant when mapped onto the WT} and M−={mutant modes that become relatively less significant when mapped onto the WT}. For each of these 4 sets, the dynamic method quantifies how involved each atom becomes in positively correlated motions and negative correlated motions. The residues with the largest magnitudes of correlated dynamics are identified as control sites on the allosteric network.

Control Site Identification

The static method generates iCPM data and the dynamic method generates 8 channels of correlated dynamics data. Each of these 9 raw data sets is the basis for predicting allosteric control sites. Let a candidate raw data set be given by the vector x, where each entry in the vector corresponds to a residue in the structure. The control sites are identified according to the following procedure (as established in [18]):

1. Compute the following ratio for each α-carbon: μ_i = (x_i − 〈x〉)/ 〈x〉, where 〈x〉 is the mean value of x.

2. Identify all residues with μ values at least as big as the threshold cutoff, τ.

3. Group the residues into runs of consecutive indices; each group is the top of a peak in the data.

4. Pick the residue with the largest μ value within each grouping.

This procedure is parameterized by the τ value, which defines the threshold relative to the mean. For example, a τ value of .25 corresponds to data that is 25% above the mean. As established in [18], the threshold cutoff for iCPM data is τ = 1 and the threshold cutoff for correlated dynamics data is τ = 0.45. The iCPM and correlated dynamics data are fundamentally different quantities and are not scaled on the same range; accordingly, they are subject to different τ values.

Results

Static Method

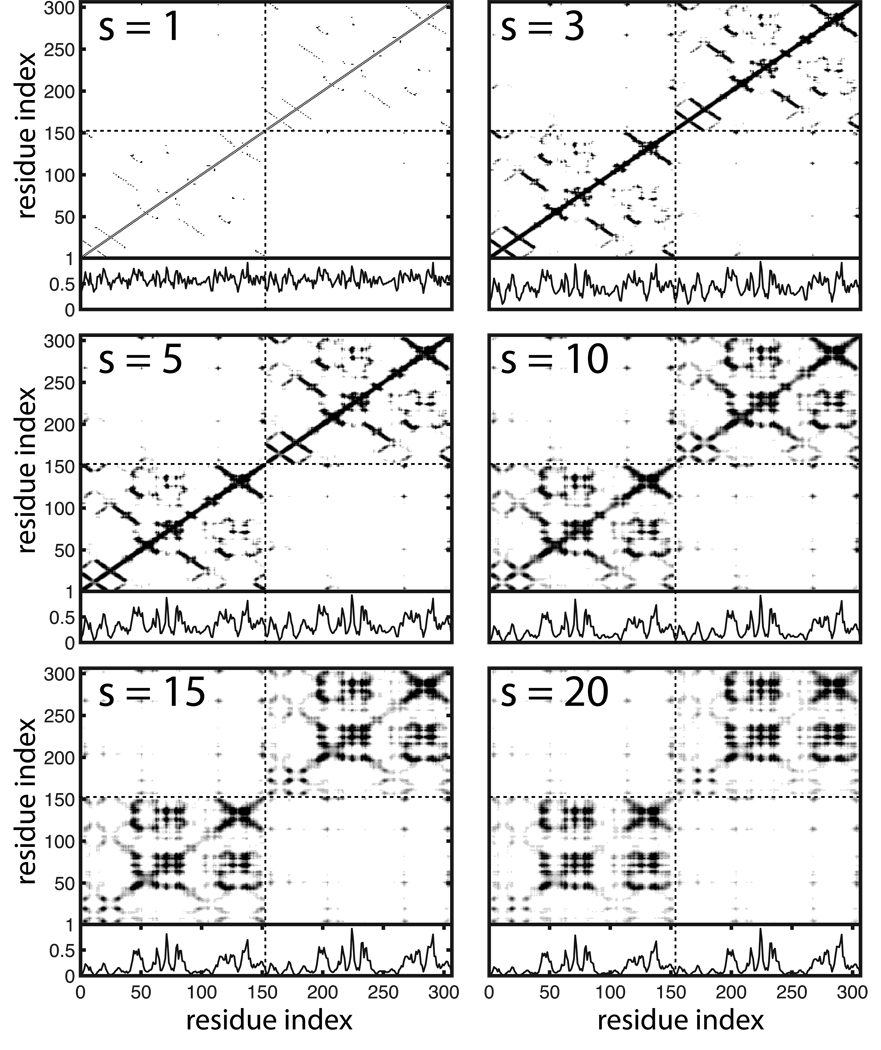
The static method is applied to all structures listed in Table 1. Figure 2 shows a dual plot series for the WT. The adjacency matrix (s=1 plot) morphs into a steady state representation of network connections (s=20 plot). The normalized degree metric shown in the bottom panel of each dual plot is the basis for computing the iCPM data. The iCPM data are computed for all of the structures in the SOD1 ensemble at a path length of s=20, and, as expected, the profiles are nearly identical: the average alignment between the WT profile and each of the other 25 structure profiles is > 0.99. Accordingly, only the WT iCPM data are presented in Figure 3.

Figure 2. Dual Plot Series for WT SOD1.

The interaction model is shown in the top panel of each dual plot and the normalized degree function is shown in the bottom panel. Dual plots are shown for random walks of length s = {1, 3, 5, 10, 15, 20}. Increasing the random walk length reveals long range network interactions that are not directly captured by the adjacency matrix (s=1). All horizontal axes are according to residue index across the dimer. The vertical axes of the top panels are also by residue index and the vertical axes of the bottom panels are degree metric values normalized on the interval [0, 1]. The dashed lines partition the monomers. The lower left and upper right quadrants of the interaction models correspond to paths between residues within the same monomer. The upper left and lower right quadrants correspond to paths that connect across the dimer interface.

Figure 3. Static Method.

The iCPM values are shown for the s=20 dual plot of Figure 2. The horizontal axis shows residue indices across the dimer, while the residue labels in the plot are given within each monomer to facilitate comparison. The control sites predicted by the τ = 1 cutoff (horizontal line) are highlighted with yellow boxes. The second tier control sites are highlighted in red. The dashed line partitions the monomers.

Residues are identified as control sites when their iCPM values are 100% larger than the mean (i.e. τ= 1, as established in [18]). This yields 5 predicted control sites in each monomer. By visual inspection, the iCPM data appears to have a secondary set of 7 control sites which do not pass the τ threshold, but do clearly stand out relative to the background data. Both tiers of predicted control sites are highlighted in Figure 3. The complete profile is color mapped onto the WT structure in Figure 4, to give a 3-dimensional view of the control sites and their relative positions. The functional significance of this network is addressed in the Discussion.

Figure 4. Structure Mapped Control Sites: Static Method.

The control sites identified by the WT iCPM (data from Figure 3) mapped onto the solvent accessible surface. Increasing iCPM values correspond to the color progression: blue → green → orange → red. Allosteric residues are found on the top groove and around the bottom cavity, both of which are adjacent to the dimer interface. In addition, these two locations are connected by an allosteric path that runs along β-strand 6 (boxed in central image). Several residues are marked by dots and labeled; these serve as reference locations along the pathway. The central image is a side view with the β-barrel of each monomer vertically oriented. The top (bottom) image is rotated about the horizontal axis to show the top (bottom) of the structure. In all views, the dimer interface is a vertical plane perpendicular to the page.

Dynamic Method

The dynamic method is applied in several stages to build up a comprehensive representation of the allosteric activity. The first stage of the analysis applies the dynamic method to each of the 4 yALS-xray structures paired against the nALS-xray structure. This analysis establishes a comparative baseline by (i) utilizing just crystal structures to avoid introducing any potential error from computationally modeled structures and (ii) enhancing the signal-to-noise ratio by averaging over several structures. The data are shown in Figure 5, where each residue that passes the threshold cutoff (τ = 0.45, as established in [18]) is identified as a control site and highlighted in yellow. As with the static analysis, there is a prominent second tier of control sites that fall below the τ threshold; these control sites are labeled and highlighted in red.

Figure 5. Dynamic Method: yALS-xray.

The average values of the dynamic method over all 4 yALS-xray structures. The control sites that pass the τ = 0.45 cutoff are highlighted in yellow. The second tier control sites are highlighted in red. The residue indices on the horizontal axis are across the dimer, while the residue labels in the plot are given within each monomer. The dashed lines partition the monomers.

The second stage of the analysis introduces computationally generated structures: the dynamic analysis is performed on the 20 yALS-comp structures paired against the nALS-xray structure. The averaged data profile (not shown) is nearly identical to that shown in Figure 5. Each of the 4 components (WT−, WT+, M− and M+) contains data for positive and negative correlations, giving 8 total data sets. Comparing each of the data sets from {yALS-xray vs nALS-xray} with the corresponding data set from {yALS-comp vs nALS-xray} produces an average alignment value >0.99. This demonstrates that computationally generated structures are virtually indistinguishable from the crystal structures under the dynamic analysis technique. The consensus control site identifications made in {yALS-xray vs nALS-xray} are also further corroborated.

The third stage of the dynamic analysis introduces a negative control by comparing the nALS-comp structure (T39I mutant) against the average profile taken across all 24 yALS structures (i.e. the 4 yALS-xray and the 20 yALS-comp). The average alignment value of this negative control with the consensus of the 24 yALS structures is 0.95. In order to isolate the functional significance of this difference, the negative control is subtracted from the consensus profile. The WT− and M+ components are nearly identical (normalized alignment > 0.99) and are thus averaged to produce a single allosteric channel. Similarly, the WT+ and M− components are also nearly identical (normalized alignment > 0.99) and are averaged to produce a single allosteric channel. This two channel allosteric profile (Figure 6) gives a cleaner representation of the control site locations than the original analysis (Figure 5).

Figure 6. Dynamic Method: yALS masked by T39I.

The averaged allosteric profiles from all 24 yALS structures, masked by the T39I negative control. The WT− and M+ components are averaged to produce the top channel and the WT+ and M− components are averaged to produce the bottom channel. Residues that pass the τ = 1 cutoff are labeled and highlighted in yellow.

Each of the channels in Figure 6, is color mapped onto the WT structure in Figure 7, to give a 3-dimensional view of the control sites and their relative positions. The functional significance of these two networks is addressed in the Discussion.

Figure 7. Structure Mapped Control Sites: Dynamic Method.

The control sites identified in the two channel plot in Figure 6, are mapped onto the WT surface. Increasing magnitudes of correlated dynamics values (data from Figure 6) correspond to the color progression: blue → green → orange → red. Left Column. The WT−/M+ channel (dominant in WT) shows circumferential bands of control sites (boxed) that, define a cross-sectional plane in each monomer that passes through the active sites. Right Column. The WT+/M− channel (dominant in yALS mutants) shows a linkage between the solvent accessible α-helix near residue Gly¹³⁰ and the dimer interface located around the central grouping of Gly¹¹⁴ and Gly¹⁵⁰. Surface transparency reveals the residues (space filled) that define the internal linkage. Structure views and labeling are as in Figure 4.

Figure 6, shows the WT−/M+ and WT+/M− channels as combined, but Figure 5 shows all channels explicitly. It should be noted that the data in Figure 5 is also suitable for a combined plot, but since it is the first plot showing data from the dynamic method, all channels are shown for completeness. The combined plot is used to highlight the connection between the 2 channels of Figure 6 and the 2 columns in Figure 7.

Discussion

The static method evaluates network flow and establishes the existence of an inherent allosteric framework in SOD1, which is observed across all 26 structures. The iCPM data in Figure 3, are not exactly mirrored between the monomers, but the predicted control sites at the τ = 1 level are exactly the same between monomers. The second tier control sites are also the same. The matching control sites, despite the structural variation between the two monomers, indicates the robust nature of the method and supports the allosteric mechanism hypothesis.

Color mapping the iCPM data of Figure 3, onto the structure in Figure 4, reveals critical insight into the underlying allosteric network. The groove in the top and the cavity in bottom of the structure are both lined with allosteric residues and are connected by a path of allosteric residues that run along β-strand 6 (residues 95–101). The groove and cavity are adjacent to the dimer interface and suggest that the allosteric activity is a regulatory mechanism for modulating dimer stability. This is consistent with the leading hypothesis in the literature involving toxic aggregation of dissociated monomers.

The multistage dynamic analysis is complex, but produces several key pieces of evidence that add to the understanding of allosteric regulation in SOD1. The T39I non-ALS mutant is used as a negative control to isolate the functionally significant allosteric activity (Figure 6). This analysis reveals that SOD1 has the capacity to operate a pair of allosteric networks, which are shown in Figure 7. Of particular significance, these networks are disjoint, which is a critical feature consistent with the observation that antioxidant and toxic functions simultaneously operate in fALS SOD1 mutants.

The WT−/M+ channel (illustrated in left column of Figure 7) corresponds to allosteric activity that is more prominent in the WT than the yALS mutants. This channel shows control sites that form a cross-sectional plane directly through the active site. The central axis of this plane is defined by the pathway of adjacent residues: Pro¹³,Asp¹¹, Arg¹⁴³, Val¹¹⁹, His⁴⁶, Phe⁴⁵, Leu⁸⁴. The WT−/M+ channel may regulate catalytic site activity and control the normal antioxidant function of SOD1.

The WT+/M− channel (illustrated in right column of Figure 7) corresponds to allosteric activity that is more prominent in the yALS mutants than the WT. This channel shows a tunnel of control sites from the solvent exposed α-helix fragment and surrounding residues to β-strand 1 and its surrounding (buried) residues on the dimer interface. The WT+/M− channel may regulate dimer interface dynamics and control dimer stability. Ray et al. [6], approached dimer stability by targeting ligand docking at the bottom cavity, which is part of the dimer interface. The WT+/M− channel indicates that dimer interface dynamics can also be controlled via the allosteric linkage to the solvent exposed locus of residues surrounding Gly¹³⁰.

The static and dynamic methods have a common goal, but are based on fundamentally different principles. There are observations to be made in comparing the results of each method.

First, the control sites of the static method (Figure 3) appear similar to the WT−/M+ channel of the dynamic method (Figure 7, left column), but yet the control sites of the static method are attributed to regulating dimer stability, while the control sites of the WT−/M+ channel of the dynamic method are attributed to antioxidant function. The critical difference is that the WT−/M+ channel of the dynamic method shows a path of allosteric residues running through the active site, while the static method shows no allosteric activity in this area.

Second, the control sites of the static method and the control sites of the WT+/M− channel of the dynamic method (Figure 7, right column) do not appear similar, but yet both are attributed to regulating dimer stability. The static method identifies allosterically active residues along the top groove and bottom cavity, while the WT+/M− channel of the dynamic method identifies internal activity at the dimer interface. It is possible that these dimer destabilizing networks may be dynamically linked. However, these networks are identified by vastly different methods and elucidating such a linkage is nontrivial. The other possibility is that two modes of dimer destabilization may be active. This is not surprising, given the spatial distribution of the known fALS mutants and the diversity of observed biophysical properties.

Third, the data of the dynamic method naturally falls into 2 groups: WT−/M+ and WT+/M−. It is rather remarkable that these groups identify disjoint allosteric networks and that each network is coherent and recognizable as a possible mechanism behind each of the two biological functions of SOD1. In contrast, the static method reveals only a single allosteric network. The static method is incredibly simplistic in design and is almost certainly insensitive to single residue mutations. It is therefore interesting to note that the static method identifies a potential dimer stabilization network, even in the WT structure. This indicates that while the fALS mutations may be required to activate the allosteric network, the SOD1 structure appears to inherently support such activity. This may explain why so many mutations are capable of triggering ALS.

In conclusion, the static and dynamic methods yield compatible and highly detailed descriptions of allosteric activity across the SOD1 structure ensemble. The following characterization is made in support of the allosteric mechanism hypothesis: Dual allosteric networks are independently involved in (1) the normal antioxidant activity of SOD1 and (2) the modulation of dimer stability. Controlling multiple biological functions (or even multiple components of a single function) via layered allosteric networks may be the unifying mechanism underlying ALS and may prove to be a feature of allosteric activity, in general.