Abstract
Computational protein structure prediction remains a challenging task in protein bioinformatics. In the recent years, the importance of template-based structure prediction is increasing due to the growing number of protein structures solved by the structural genomics projects. To capitalize the significant efforts and investments paid on the structural genomics projects, it is urgent to establish effective ways to use the solved structures as templates by developing methods for exploiting remotely related proteins that cannot be simply identified by homology. In this work, we examine the effect of employing suboptimal alignments in template-based protein structure prediction. We showed that suboptimal alignments are often more accurate than the optimal one, and such accurate suboptimal alignments can occur even at a very low rank of the alignment score. Suboptimal alignments contain a significant number of correct amino acid residue contacts. Moreover, suboptimal alignments can improve template-based models when used as input to Modeller. Finally, we employ suboptimal alignments for handling a contact potential in a probabilistic way in a threading program, SUPRB. The probabilistic contacts strategy outperforms the partly thawed approach which only uses the optimal alignment in defining residue contacts and also the reranking strategy, which uses the contact potential in reranking alignments. The comparison with existing methods in the template-recognition test shows that SUPRB is very competitive and outperform existing methods.
Introduction
Computational protein structure prediction remains a challenging task in bioinformatics and computational biophysics1-3. Methods which were developed in the past years can be roughly classified into two categories; ones which utilize structures of known proteins as a global template (template-based methods)4-8 and those which employ a coarse-grained9-11 or full atomic protein model to explore the fold space (ab initio methods). Identifying appropriate global/local templates in the database is crucially important not only for template-based structure prediction methods but also for ab initio methods (with notable exception of methods which attempt to fold a protein model using only the first principles in physics12;13), since the strategy to combine known fragment structures has been successful in several ab initio methods 14;15. In recent years, the importance of effective use of template structures is highlighted because more and more protein structures are being solved by the structural genomics projects16-19. To capitalize the significant efforts and investments paid on the structural genomics projects, it is urgent to establish effective ways to use solved structures as templates with a special emphasis on developing methods for exploiting remotely related proteins that cannot be simply identified by homology. It is also worthwhile to note the recent interesting discussions on the continuity of the protein structure space that revisit commonality among structures of different overall folds (and thus obviously do not share any ancestral relationship) 20-22 and intriguing attempt to use such structures of different fold for structure modeling23. Following these discussions, it might be able to establish a method which uses structure templates for modeling that are not conventionally considered to be similar to a query protein sequence.
Various methods have been proposed in the past for identifying and aligning remotely related templates, which include those that use sequence information extensively24;25, those that use structure-related scoring terms26;27, ones that use the hidden Markov Models28;29 and other machine-learning techniques30, and meta-server approaches 31;32.
In this work, we examine the effect of employing suboptimal alignments in template-based protein structure prediction. The algorithms for computing suboptimal alignments themselves have been developed more than a decade ago. Vingron and Argos presented a dynamic programming (DP)-based algorithm that produces suboptimal alignments each of which is constrained to contain a certain residue pair 33-35. Saqi and Sternberg's method produces alternative alignments by penalizing the path of the optimal alignment in the DP matrix36. Suboptimal alignments can also be constructed by perturbing alignment parameters37. Some other works employ thermodynamic partition functions to consider probabilities of suboptimal alignments38-41. These probabilities of suboptimal alignments can also be derived from the hidden Markov model42;43. Suboptimal alignments can be useful for biological sequence alignments because mathematically optimal alignment of two sequences does not always agree with the biologically correct alignment33;34;43;44. It was also shown that consistent regions in optimal and suboptimal alignments correspond to correctly aligned regions in many cases34. Previously, we developed a quality assessment score45 for protein structure models named the SPAD (SuboPtimal Alignment Diversity) score which considers the consistency of the optimal and suboptimal alignments46. We showed that the SPAD score has a better correlation to the root mean square deviation (RMSD) of structure models as compared with several other scores which are derived from sequence alignment properties. In our recent subsequent work, we have shown that combination of the SPAD score with several structure-related scores further improves the prediction accuracy of the quality of structure models47. Previous works on suboptimal alignments focused on applications to sequence analyses. There was an attempt to use suboptimal alignments in homology modeling48 but the current work is the first in which suboptimal alignments are thoroughly investigated and implemented in a threading algorithm.
The rest of the manuscript is organized as follows: First, we show that suboptimal alignments frequently are more correct than the optimal alignments. Moreover, we show that they contain a substantial amount of correctly aligned pairs in alignments and correct amino acid residue contacts when tertiary structure models are built based on the alignments. These results indicate the strong potential of suboptimal alignments in template-based protein structure prediction. Next, we show that employing suboptimal alignments indeed improves the accuracy of homology models of protein structures constructed by Modeller49;50, a popular homology modeling program. Finally, we design a template-based structure prediction method named SUPRB (threading with Suboptimal alignment-based PRoBabilistic residue contact information) which uses suboptimal alignment information. The main motivation of employing the suboptimal alignments is to explore a better way to handle a two-body amino acid contact potential51-53 in template-based structure prediction. Amino acid contact potentials have been shown to be effective in protein tertiary structure prediction both in template-based methods4;53;54 and ab initio methods 11;14;55. Therefore, effective use of contact potentials is one of the keys to assess structural compatibility of the target sequence to a template especially for recognizing very distantly related templates. However, contact potentials have been underused in template-based methods due to the difficulty in obtaining the optimal alignments for the contact potential by DP algorithm. An alternative choice of alignment optimization for contact potentials is by the Monte Carlo (MC) approach as proposed by Bryant and his colleagues56, however, DP has an advantage over MC in terms of less expensive computational time to cope with the growing size of a template database. To be able to handle a contact potential by DP, Skolnick and his colleagues have proposed the frozen approximation of the amino acid contacts57, which assumes that a residue position in the target protein has the same contacting residues as the equivalent position in the template structure and thus the contacting residues are not dependent on the alignment. They further proposed partly thawed and defrosted approximation in the program PROSPECTOR where interacting residue pairs are taken from the target protein using a target-template alignment generated without using a contact potential4. In this work, SUPRB goes one step further to consider interaction pairs in a probabilistic fashion by counting residue interactions in suboptimal alignments. We demonstrate that our approach, the probabilistic residue contacts, outperforms the partly thawed approximation. Performance comparison with existing threading methods shows SUPRB is very competitive with the others.
Materials and Methods
Benchmark datasets
We use the SALIGN alignment benchmark dataset58 in the analysis of suboptimal alignments and also for optimizing weighting factors for scoring terms of the threading algorithm, SUPRB. The SALIGN dataset has 200 pairwise structure-based sequence alignments. These pairs of proteins are structurally aligned and have no more than 40% sequence identity, have at least 100 aligned residues and at least 50% of the residues aligned, and at least 90% of the residues of one chain are covered in the alignment. Another structure alignment program, MAMMOTH59 is further used to ensure that at least 50% of the residues in the shorter chain are aligned. The sequence identity of the pairs ranges from 4% to 40% with an average of 16.1%. The average RMSD of the pairs is 2.73Å. This dataset was downloaded from http://salilab.org/suppmat/mamr03/.
Another dataset, the Lindahl and Elofsson's dataset (L-E dataset)60, is used for benchmarking SUPRB. The L-E dataset consists of 1130 representative proteins, each of which is assigned with a SCOP hierarchical classification of a family, a superfamily, and a fold61. Following the SCOP classification, a set of pairwise alignments are constructed in each similarity level, using a protein tertiary structure alignment program, LGA62. Aligned protein pairs in the family level set belong to the same family in SCOP; pairs in the superfamily level belong to the same superfamily but not to the same family; pairs in the fold level set belong to the same fold but not to the same superfamily. This resulted in 1076 target-template pairs for the family level, 1395 for the superfamily level, and 2761 for the fold level. The average sequence identity (and the standard deviation) of alignments are 21.3% (8.06%), 15.2% (3.3%), and 15.2% (3.8%) for the family, the superfamily, and the fold level, respectively. For each protein pair in the same structural similarity level, one protein is considered as the target and another one is considered as a template.
SUPRB threading algorithm
The novel threading algorithm employs a sequence-structure compatibility score which linearly combines five different scoring terms to evaluate fitness of a query sequence to template structures. The five terms are a sequence profile score, a secondary structure matching score, a solvent accessibility score, a main-chain angle propensity, and an amino acid contact potential. Target-template alignments are computed by the global-local dynamic programming63. A novel feature of SUPRB is that the residue contacts are handled in a probabilistic fashion by considering suboptimal alignments between a target and a template. The detailed implementation of the residue contact term and each scoring terms are described below.
Sequence profile term
A PSI-BLAST profile is generated following the method described in a Dunbrack's paper24. A query sequence is searched against the non-redundant protein sequence database36 with an E-value threshold of 0.002 for both printing and inclusion and with the maximum iteration of five passes. Low-complexity segments are masked. From the output multiple alignment, too similar sequences (mutual sequence identity ≥ 98%) and too distant sequences (sequence identity to the target ≤ 15%) are removed. The remaining sequences are weighed by the position-specific independent counts (PSIC) scheme64. Sequence i at profile position m with amino acid type a(sm) is weighted with
| (Eq. 1) |
Nm the total count of sequences in the profile which have the same amino acid type, a(sm), as at the column m. is called the effective count of the amino acid type of a(sm) at position m, determined by
| (Eq. 2) |
is the average number of different amino acid type per column in sequences in the profile which have the same amino acid type as sm. Note that the PSIC weighting scheme is different from the Henikoff weighting method65, which is used in PSI-BLAST. The Henikoff weighting assigns the same weights to positions in a sequence that form a same subset of sequences24. Here a subset of sequences in a profile is the set of sequences which have a residue at a particular position (i.e. not a gap) of a profile. In contrast, PSIC, assigns lower weights if many sequences have the same amino acid at a particular position. It was shown in that PSIC performed better than the Henikoff weighting in terms of the alignment accuracy and database search sensitivity and specificity 24.
Based on the weight, Wsm, (Eq. 1), the observed frequency of amino acid type u at column m in the profile, , is
| (Eq. 3) |
The pseudo-count, , for column m and amino acid type u, is computed as66
| (Eq. 4) |
Pu is the background frequency of amino acid type u, is the observed frequency of amino acid type v at column m (Eq. 3). Suv is the BLOSUM62 score between amino acid types u and v. The observed frequency and the pseudo-counts is combined to the estimated frequency of column m and amino acid type u, :
| (Eq. 5) |
is the effective count of amino acid type a at column m.
The profile term Sprofile follows COMPASS scoring scheme67. The score between position (column) i in the target profile, a, and position (column) j in the template, b, is
| (Eq. 6) |
and are the effective count of amino acid type u in column i and column j. and are called as the log-odds values of and , respectively, and calculated by the next equation:
| (Eq. 7) |
Here Pu is the background frequency of amino acid type u, counted from the L-E dataset. and come from Eq. 5. In Eq. 6, ci and cj are weighting factors, which are derived as follows:
| (Eq. 8) |
The score (Eq. 6) S′profile(ai,bj) is standardized to S′profile(ai,bj) as follows before computing alignments:
| (Eq. 9) |
where μ and σ are the mean and the standard deviation of scores, S′profile(ai,bj), for all possible (i,j) pairs between the target and the template.
Secondary structure term
The secondary structure of a target is predicted by SABLE68 and that of a template is defined by DSSP69, both of which have a three-state classification, i.e. helix, sheet, and coil (the other regions). The score for the secondary structure matching term SSS are adopted from the Dunbrack's paper24 (Table 1). This is an asymmetric matrix which provides scores for matches between predicted secondary structures in a target sequence with experimentally determined secondary structures in a template. Using Table 1, the secondary structure term for an amino acid pair (ai, bj) is
| (Eq. 10) |
where SSp(ai) is the predicted secondary structure of ai and SSt(bj) is the secondary structure of bj in the template structure, and Sec(i,j) is a score read from Table 1. Then, S′ss is normalized to Sss in the same way as Eq. 9.
Table 1.
The scoring matrix for the secondary structure term.
| Experimental structure in a template (SSt) | ||||
|---|---|---|---|---|
| Actual Helix | Sheet | Coil | ||
| Predicted structure in a target (SSp) |
Predicted Helix | 1.38 | −3.83 | −1.86 |
| Predicted Sheet | −3.40 | 1.54 | −1.21 | |
| Predicted Coil | −1.19 | −0.70 | 0.81 | |
The values are adopted from Wang & Dunbrack (2004).
Solvent accessibility term
The relative solvent accessible area (SAA) of the target is also obtained by SABLE. The absolute SAA of the template read from DSSP is normalized using Chothia's extend state accessible area70 to obtain the relative SAA. A two-state classification is applied for the relative SAA, i.e. buried (relative SAA ≤ 25%) and exposed (relative SAA > 25%).
| (Eq. 11) |
where SSABLE(ai) is the confidence score of SABLE, which ranges from 0 to 9, SAA(ai) and SAA(bj) is Boolean variables, which equals to either buried or exposed, and δ equals to 1 when SAA(ai) = SAA(bj) and 0 otherwise. S′SAA is normalized to SsAA in the same way as Eq. 9.
Main chain angle potential
A coarse-grained main-chain angle propensity of amino acids is considered, which is based on a Cα-model of proteins8. The torsion angle is defined with four consecutive amino acid (Cα) positions. The torsion angle space is divided into 10 bins (i.e. 36 degrees each) and the statistical potential is computed for each amino acid type by considering torsion angles located before and after the amino acid residue. The angles are sampled from 3704 representative protein structures. Thus the main-chain angle potential provides 10x10 values for each amino acid type. See our previous paper for details8. The main chain angle term for position i in the target aligned with position j in the template is
| (Eq. 12) |
where AA(ai) is the amino acid type of ai, τ1(bj), τ2(bj) are the bins of preceding and the succeeding torsion angle of residue bj in the template, respectively. p(α, τ1, τ2) is the probability that the amino acid type a is observed to have angles τ1 and τ2, and p(τ1,τ2) is the probability that any amino acid type is observed to have angles τ1 and τ2. The table of the score values is made available at the supplemental website, as described below. . S′angle is normalized to Sangle in the same way as Eq. 9.
Amino acid contact potential
A two-body statistical amino acid contact potential is employed. The potential is computed using the same set of representative protein structures as used for the main-chain angle potential. The quasi-chemical approximation is used for the reference state71 and the contact of a residue pair is defined as 4.5Å between any side-chain heavy atoms from the residue pair 8. The raw value is normalized to have the average of 0 and the standard deviation of 1.
For a target protein sequence A (a1, a2, ,, aLA) aligned with a template protein B (b1, b2, ,, bLB), residues that are in contact with an amino acid ai in the target A are determined based on the residue contact pattern of the template B. LA and LB are the length of the target A and the template B, respectively. To state this more precisely, let us introduce two functions, T, which represents a target-template alignment, and δ, which represents amino acid contacts in a protein structure:
Suppose residues ai and aj is the target protein A are aligned with bs and bt in the template B, respectively:
| (Eq. 13) |
The function T corresponds a residue in a target with a residue in a template which is aligned with the target residue in a given target-sequence alignment. T−1 is the inverse function of T. Let δ denotes residue contacts in a protein structure:
| (Eq. 14) |
Then the residue contact score for a target residue ai which is aligned with a template residue bj (= T(ai)), i.e. Scontact(ai, bj), is defined as
| (Eq. 15) |
Here the function AA denotes the amino acid type (e.g. Ala, Trp,,,) of the specified amino acid in the protein, and C(a, b) is the contact potential value for the amino acid pair (a, b). Hence, the contacting residues for ai are taken from the target, under the assumption that the residue contact pattern is conserved between the target and the template. Thus, the residue contacts are taken from the template B, while the types of contacting residues are taken from the target itself.
Eq. 15 provides the contact score given a target-template alignment. However, we need to design how to implement the contact potential in the DP-based threading algorithm, since the DP cannot optimize the alignment for the two-body contact potential4;5, which considers long-range interactions. We test the following two strategies, both of which take advantage of the use of suboptimal alignments:
(1) Reranking strategy
In this strategy, we first compute optimal and suboptimal alignments for a template and a target using the compatibility score excluding the amino acid contact term. Then, the alignments are reranked by the score with the contact term. The compatibility score, S(ai, bj), without the contact term used for the initial alignment is as follows for a target residue ai and a template residue bj:
| (Eq. 16) |
Sprofile(ai, bj), SSS(ai, bj), SSAA(ai, bj), and Sangle(ai, bj), are the terms for the profile, the secondary structure matching, the solvent accessibility, and the main-chain angle potential, respectively. All of these scores are rescaled to have the standard normal distribution as proposed by Wang and Dunbrack24. wprofile, wSS, wSAA, and wangle, are the weighting parameters for the corresponding scoring terms. The values for the weighting parameters range from 0 to 1 and they sum up to 1:
| (Eq. 17) |
In the reranking stage, the optimal and suboptimal target-template alignments are reranked by the compatibility score with the contact term:
| (Eq. 18) |
where 0 < wcontact < 1. To compute the Scontact term, the contacting amino acids for each residue, ai, in the target are taken from the target itself according to the pre-computed alignment (Eqns. 13 & 14). We use Eq. 18 (integrated with Eq. 15) to recompute the score of each residue ai in the target aligned with bj in the template, without changing the alignment itself. Thus, the compatibility score for each of the optimal and suboptimal alignments is updated and thus the order of the alignments changes. Finally, we choose the alignment with the best score as the new optimal alignment for the target and the template.
(2) Probabilistic handling of residue contacts
This strategy uses suboptimal alignments for considering residue contacts in a probabilistic fashion. In the first pass, optimal and suboptimal alignments are generated by Eq. 16, which does not contain the contact term. As these initial alignments provide a tertiary structure of the target protein, we can extract contacting residues for a given amino acid position from the target protein itself.
Using the set of optimal and suboptimal alignments, the contact term, Eq. 15, is modified as follows:
| (Eq. 19) |
where N is the total number of suboptimal alignments considered. A new index, n, is introduced, which specifies the rank of each suboptimal alignment. Thus, residue contacts are considered in a probabilistic way. For example, the number of times two amino acids ai and aj in the target are considered to be in contact with the probability of
| (Eq. 20) |
In the second pass of computing target-template alignments, Eq. 18 with the probabilistic contact (Eq. 19) is applied to update optimal and suboptimal alignments by DP algorithm. Since the score of aligning each residue pair in the target and the template, (ai, bj), for 1≤i≤LA and 1≤j≤LB to be used in the DP has changed by adding the probabilistic contact term from the original score (Eq. 16), the resulting optimal and suboptimal alignments will change. Now the updated optimal and suboptimal alignments change contacting residues for target residues, and thus the contact term (Eq. 19) is updated by the new optimal/suboptimal alignments at each iteration. Therefore a subsequent iteration will further change the alignments. The alignment computation is iterated until the fourth pass is completed or the optimal alignment converges. The convergence of the alignments is measured by the ALD score (0.05 or lower), which compares two alignments based on the paths in the dynamic programming matrix46.
Suboptimal alignments
The suboptimal alignments are computed with the algorithm proposed by Vingron and Argos34. The total number of 0.01*ltarget *ltemplate suboptimal alignments are computed. ltarget and ltemplate are the length of target and the template proteins, respectively. The algorithm first computes alignments in the forward direction as usual and also in the backward direction using the DP algorithm. By design, the alignment score stored at each cell in the forward DP matrix (i.e. the DP matrix used in the forward alignment) indicates the best score to align the two proteins up to that position in the two proteins. In the same way, each cell in the backward DP matrix contains the best score to align the two proteins backwards up to that position. Next, a combined matrix is computed by summing up the scores at each cell, (i,j), in the two DP matrices and then subtracting the pairwise score for aligning residue i and j. Now the score at each position (i, j) in the combined matrix is the best possible score for aligning the two proteins with the condition that residue i and j should be aligned with each other. Finally, the scores in the combined matrix are sorted in the descendent order and the whole alignment which trespass each selected position is constructed by tracing back the forward and backward alignments in the forward and backward DP matrices, respectively.
Parameter optimization and the benchmark on the testing datasets
Seven parameters (five weighting factors, an open gap penalty, and an extension gap penalty) are optimized based on the ProSup alignment dataset72. Combinations of the values of parameters are essentially explored exhaustively for most of the combinations of the parameter values with an interval of 0.1. The combination which gives the highest alignment accuracy that is computed as the total number of correctly aligned amino acid pair is chosen.
For testing SUPRB with the optimized parameters, we use two independent datasets from the training set (the ProSup set): the SALIGN dataset58 is used for examining the alignment accuracy and the Lindahl and Eloffson (L-E) dataset60 is used for testing both the alignment accuracy and the template recognition accuracy. The alignment accuracy on the SALIGN set is defined as the fraction of the correctly aligned residue pairs, which are determined by structural alignments by TM-Align73.
In the template recognition, the raw sequence-structure compatibility score, Sraw, is normalized by the length of the template and the target:
| (Eq. 21) |
Which are then ranked by the Z-score:
| (Eq. 22) |
μ is the mean and σ is the standard deviation computed for all the templates in the L-E set.
Availability of the software
The executable file of SUPRB, the main-chain angle potential, the contact potential, and the template-based models analyzed in this study are made available at our website: http://kiharalab.org/suprb). In addition, the source code for computing the suboptimal alignment diversity (SPAD) score is also made available at http://kiharalab.org/subalignment/.
Results
First we show that suboptimal solutions of target-template alignments contain significant number of correctly aligned residues and correct residue contacts. Then, we show that suboptimal alignments also improves accuracy of structure models when applied to a homology modeling program, Modeller49. Finally, we examine the performance of the SUPRB threading algorithm that employs suboptimal alignments for handling a residue contact potential.
Correctly aligned residues and contacting pairs in suboptimal alignments
The accuracy of template-based prediction depends on the amount of residue pairs from the target and the template which are correctly matched in the alignment. Previous works33;34;43;44 showed that there are often cases that a suboptimal alignment of a sequence pair have more correctly aligned residues than the optimal (i.e. top-scoring) alignments. Rather than a sequence alignment score (e.g. a BLOSUM matrix74) used in the previous works we use a sequence-structure compatibility score (Eq. 16) to align target sequences to template structures in the SALIGN dataset. We count correctly aligned residues and correct contacting pairs found in up to the top 100 scoring target-template alignments.
On average, only 54.1% of residues in the target are correctly aligned in the optimal alignment (x=1) (Fig. S1, Supplemental Material). Considering more suboptimal alignments increases the number of correctly aligned residues. When 100 suboptimal alignments are taken into account, the fraction of the correctly aligned residues reach to 67.3%, which is a 13.2 percentage point increase as compared with the optimal alignment (x=1).
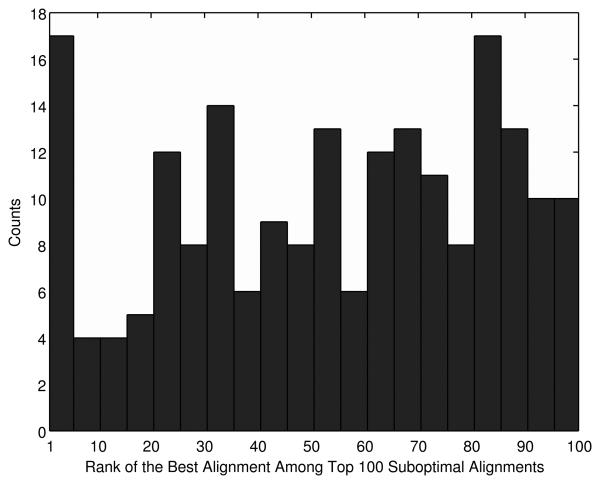
In Figure 1, we ask a different question regarding the alignment accuracy of suboptimal alignments: After all, which alignment among the top 100 scoring alignments is the most correct? To our surprise, overall, the accuracy of the suboptimal alignments seems to be irrelevant to their ranks. The highest count (17) is observed both at the rank of 1-5 but it ties with the count at the ranks of 80-85. Thus, correctly aligned residue pairs frequently occur in low ranked suboptimal alignments, and moreover, the accuracy and the rank of the alignments do not show correlation. Alignments at the rank of 1-5 tend to be relatively accurate (Fig. 1) but accumulating the top five alignments only yields a marginal gain of the accuracy of 55.7% (Fig. S1). Therefore not only the top few suboptimal alignments but also lower ranked suboptimal alignments will contribute in improving the alignment accuracy.
Figure 1.
The rank of the most correct alignments within the top 100 scoring alignments. The x axis is the rank of the most correct alignment in the top 100 and the y axis is the count of the most correct alignment occurred at that rank in the 200 target-template alignments in the SALIGN dataset. The accuracy of an alignment is measured by the fraction of correctly aligned residues in the alignment.
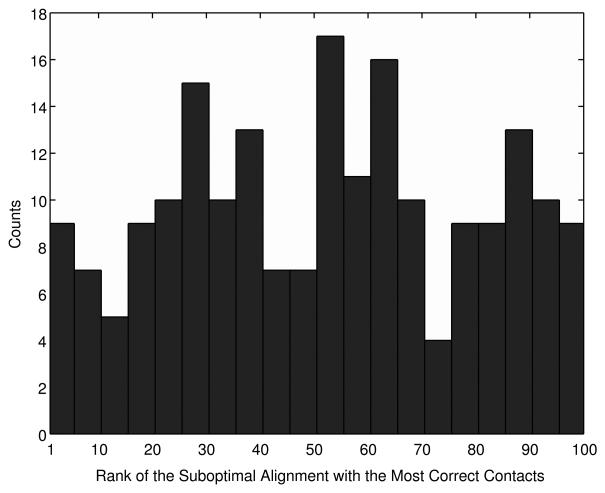
Next, we examine the accuracy of the optimal and suboptimal alignments in terms of the residue contacts. Contacting residue pairs observed in a template protein structure are transferred to a target protein based on the target-template alignment and the accuracy of the contacts in the target protein is evaluated. On average, the optimal alignment (x=1) contains 37.0% of actual contacts in target proteins and considering up to the top 100 scoring alignments increases the fraction to 49.0% (Fig. S2, Supplemental Material). Figure 2 shows the histogram of the rank of the alignment from which the largest number of correct residue contacts is transferred to the target. This histogram again illustrates that the accuracy of alignments (in terms of the contacting residue pairs) has no correlation to the rank at all. For example, suboptimal alignments at the rank of fifty or lower frequently are the best.
Figure 2.
The rank of the alignment which has the largest number of correct residue contacts. The 200 target-template alignments in the SALIGN dataset are used.
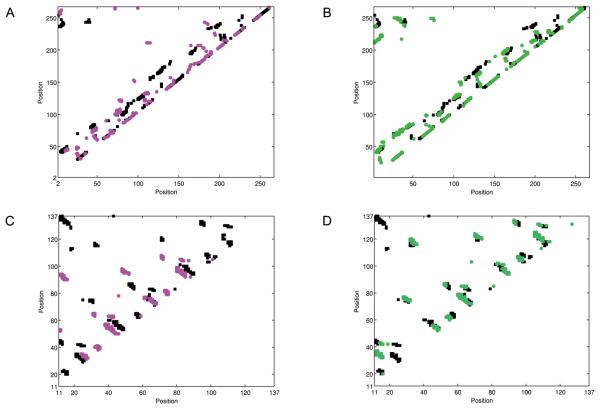
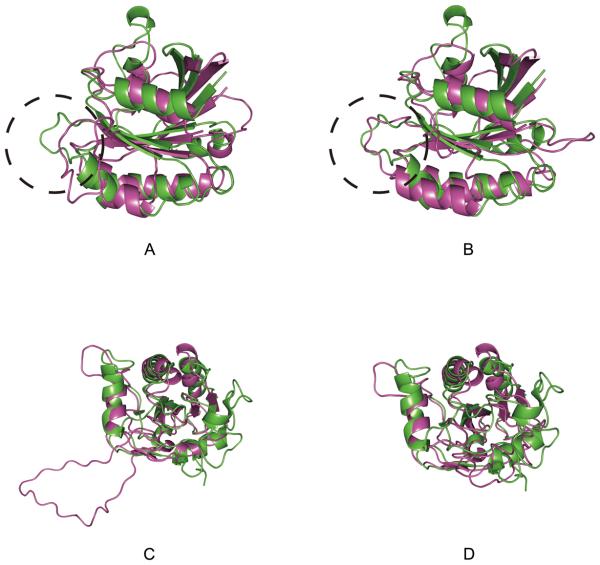
Figure 3 shows two examples that a suboptimal alignment has more correct residue contacts than in the optimal alignment. The first example is the optimal alignment and the 100th alignment between 1ad1B and 1dioA, both of which have the TIM barrel fold. The optimal alignment (Fig. 3A) only covers 11.1% of the residue contacts, while the suboptimal alignment found at the 100th (Fig. 3B) captures a larger number of correct contacts in α helices and between parallel β-strands resulting in the increase of the correct contact coverage to 30.5%. The second example is 1barA aligned with 1xyfA (β trefoil fold). The optimal alignment (Fig. 4C) has a shift in the alignment that causes a small coverage of 5.1% of the actual contacts. On the other hand, the 70th suboptimal alignment correctly captures most of the contacts between anti-parallel β-strands, resulting in the correct contact coverage of 23.2%.
Figure 3.
Residue contact maps of target proteins indicated by target-template alignments. Two contact maps are compared for a target protein, one indicated from the top-scoring alignment and another one from a sub-optimal alignment which is the most correct in terms of residue contacts. A, the contact map of the target protein, 1ad1B, indicated by the top-scoring alignment with a template, 1dioA. Black, the actual contacting residues of 1ad1B; purple, contacting residues indicated from the alignment with 1dioA. B, the contact map of 1ad1B indicated by the 100th suboptimal alignment with the 1xyfA (green). C, the contact map of 1barA; black, the actual contacting residues of 1barA; purple, contacts indicated by the top-scoring alignment with a template, 1xyfA. D, residue contacts of 1barA indicated by the 70th suboptimal alignment (green).
Figure 4.
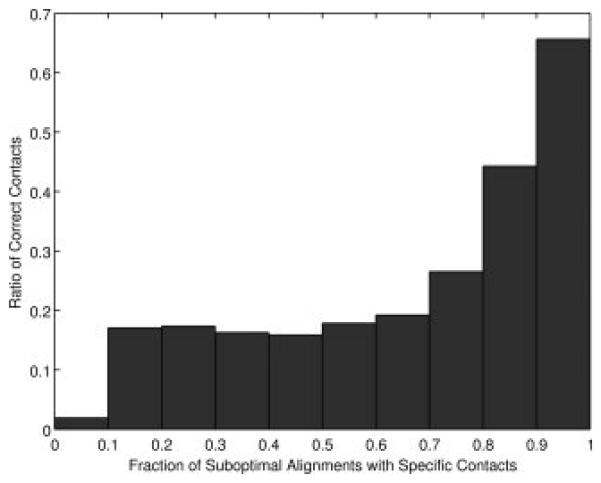
Fraction of the actual contacting residue pairs of target proteins relative to the occurrence of the contacts among the suboptimal alignments. For each target-template pairs, top 0.01xMxN alignments (M, N are the length of the target and the template, respectively) are computed and the occurrence of residue contacts among the suboptimal alignments are counted. The values are computed for each target-template pair in the SALIGN dataset and averaged.
As Figure 1 shows, the rank of individual suboptimal alignment does not tell the accuracy of residue contacts implied from the alignment. In Figure 4, we investigate if residue contacts which occur more frequently among the suboptimal alignments tend to be more accurate than less frequent ones, which turned out to be true. It is shown in Figure 4 that the number of occurrences of residue contacts in suboptimal alignments correlates well with the accuracy. 65.6% of the residue contacts which occur in more than 90% of the suboptimal alignments are correct. This value is larger than the average accuracy of the residue contacts indicated by the optimal alignments (i.e. the number of correctly predicted residue contacts among the residue contacts implied from the optimal alignments), which is 48.2%.
Using suboptimal alignments for template-based modeling
In this section we show practical usefulness of the suboptimal alignments by using them in a popular homology modeling tool, Modeller49. Conventionally, homology modeling procedure uses only the optimal alignment between a target and a template to build the final 3D coordinates model. On the other hand, several recent studies investigated the use of multiple templates to improve the model75-77. However, improving the model accuracy with multiple templates is not trivial as incorporation of additional templates can leads to deterioration of the model quality75. We compare models which are built based on the single (optimal) alignment between the target and a single template, termed SAli-ST (Single Alignment – Single Template) models, with models based on multiple alignments (optimal and suboptimal alignments), termed MAli-ST (Multiple Alignment – Single Template) models. We also examine models which are based on multiple templates, i.e. comparison between SAli-MT (Single Alignment – Multiple Template) models (i.e. the optimal alignment for each of multiple templates) and the MAli-MT models (Multiple Alignments for each of Multiple Templates). For the MAli-ST and MAli-MT models, four suboptimal alignments are added on top of the optimal alignment for each template as the input to Modeller (i.e. total of five alignments are used). For this testing, we used target proteins used in the CASP7 (Critical Assessment of Techniques for Protein Structure Prediction) 78. Five template structures for a target are selected by considering consensus among those selected by our own threading method, a prior version of SUPRB, SP426, RAPTOR_ACE79, and FOLDPRO80, of which the last four are the server predictions that are made available through the CASP7 official website (http://www.predictioncenter.org/casp7/Casp7.html). Such a consensus approach is commonly used and some of them have been successful in the past CASP experiments81;82. The alignment between a target and a template are computed with the probabilistic residue contact strategy (Eq. 19). Unaligned regions at both ends of the targets are removed if they are more than twenty residue long, since Modeller tends to generates unrealistic floppy conformation for such regions. All the models analyzed are made available at our website (http://www.kiharalab.org/suprb). The models are evaluated by the RMSD (root mean square deviation), the GDT-TS score62, and the TM-score73 to the native structure. The RMSD are computed by LGA62.
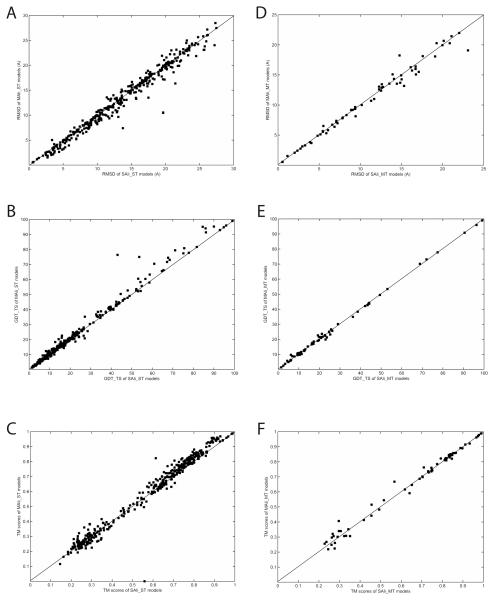
First, we examine the effect of suboptimal alignments in structure prediction with a single template by comparing the SAli-ST and the MAli-ST models (Figures 5A-C, Table 2A). Using suboptimal alignments (MAli-ST models) improves the RMSD over the SAli-ST models in 68.1% (261/383) cases. Although the average RMSD value of the MAli-ST models, 13.33Å, may not seem largely improved from that of the SAli-ST models (13.73Å), significant improvement of the MAli-ST model over the corresponding SAli-ST model, e.g. an improvement larger than 2Å, is often observed (Figure 5B). When models are evaluated by the GDT-TS and the TM-score, improvement by MAli-ST models over SAli-ST models is observed in 65.0% and 68.9% of the cases, respectively (Table 2A). Figure 5B and 5C show that improvement by Mali-ST is larger than deterioration in general both in the GDT-TS (Fig. 5B) and the TM-score (Fig. 5C).
Figure 5.
Comparison of suboptimal alignment-based models and single optimal alignment-based models. A, RMSD; B, GDT-TS score; C, TM-score of SAli-ST models and the MAli-ST models. D, RMSD, E, GDT-TS score; F, TM-score of SAli-MT models and the MAli-MT models.
Table 2.
Comparison of the single alignment and multiple alignment models for CASP7 targets. A. Models built on a single template
| SAli-ST | MAli-ST | ||
|---|---|---|---|
| RMSD | Wins/Average (Å) | 122 / 13.73 | 261 / 13.33 |
| GDT-TS | Win / Average | 134 / 19.97 | 249/ 20.81 |
| TM-Score | Win / Average | 119 / 0.570 | 264/ 0.585 |
SAli-ST: Structure models built on the optimal alignment with a single template structure; MAli-ST, models built on five (optimal and four suboptimal) alignments with the same single template structure as used in the SAli-ST models. Wins count the number of cases either SAli-ST or MAli-ST model has a smaller RMSD, a larger GDT-TS or a larger TM-score, than the other. The number of models examined is about five times more than the multiple template models in Table 5B, since here models based on each template (thus five models) for a target are examined. These tables correspond to Figure 5.
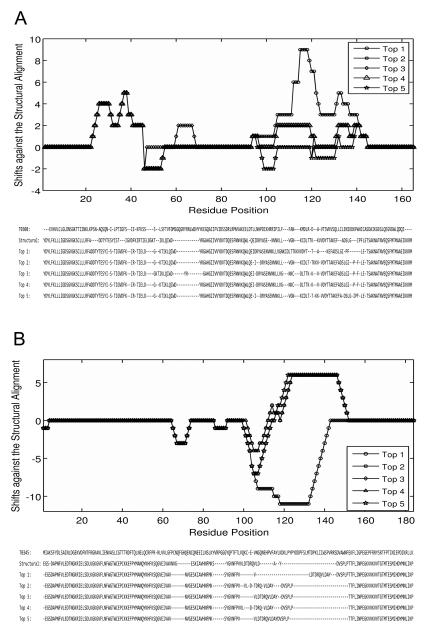
Two examples in Figure 6 illustrate how suboptimal alignments improve the RMSD in MAli-ST models. Models of two CASP7 targets, T0308 (PDB code: 2h57) and T0345 (PDB code: 2he3) are shown. In the first example, the MAli-ST model (Fig. 6A) of T0308 has an RMSD of 5.2Å while the RMSD of the SAli-ST model is of 6.9Å (Fig. 6B). Compared to the structure-based alignment between the target and the template (PDB code: 2fol), the optimal alignment has a larger shift in the region around the position 105 to 140 (Fig. 7A), which corresponds to the loop region indicated with a circle in Fig. 6A.
Figure 6.
Optimal alignment-based models and suboptimal alignment-based models of two CASP targets. Structural models are generated by Modeller. Models (shown in magenta) are superimposed to the native structure (green). A, the model of T308 based on the optimal alignment with the template structure, 2fol. The PDB code for the native structure of T308 is 2h57. B, the model of T308 which was computed based on five alternative target-template alignments. The same template, 2fol was used. C, the optimal alignment-based model of T0345. The PDB code for T0345 is 2he3. 1st9 was used as the template. D, the multiple-alignment based model for T0345.
Figure 7.
Optimal and suboptimal alignments of the two CASP7 targets and their template proteins. These alignments are used as for generating the models using Modeller shown in Figure 6. A, the shift in the target-template alignments (the top1, i.e. the optimal alignment to the top5) of T308 relative to the structural alignment (upper panel) and the actual sequence alignments (lower panel). A residue ai in the target aligned with a template residue bj+1 is considered to have a shift of +1 when it should be aligned with bj in the correct alignment. B, the alignment shifts (upper panel) and the actual sequence alignments (lower panel) for T0345.
For the second example, the MAli-ST model for T0345 (Fig. 6D) shows a large RMSD improvement from 13.8Å by the SAli-ST model (Fig. 6C) to 7.3Å. The large unstructured loop region at around residue 105-145 built by Modeller in the SAli-ST model (Fig. 6C) is due to the large alignment shift of that region in the optimal alignment (Fig. 7B). However, interestingly, suboptimal alignments have a shift to the opposite direction in that region, which cancelled out with the shift by the optimal alignment in the modeling.
We have also examined application of suboptimal alignments to structure models using multiple templates by comparing SAli-MT and MAli-MT models (Fig. 5D-F, Table 2B). We did not observe significant improvement by the MAli-MT models. The average RMSD value of the MAli-MT shows a marginal improvement over SAli-MT, however, the number of improved cases by the MAli-MT ties with deteriorated cases (32 cases each). The average GDT-TS score and the TM-score also show marginal improvement. The quality of the MAli-MT and SAli-MT models depends certainly on the quality of templates used and how the templates are combined. Investigation of a better way of integrating multiple templates and suboptimal alignments is left as a future study.
Table 2.
Comparison of the single alignment and multiple alignment models for CASP7 targets. B. Models built on multiple templates.
| SAli-MT | MAli-MT | ||
|---|---|---|---|
| RMSD | Wins/Average (Å) | 32 / 10.92 | 32 / 10.80 |
| GDT-TS | Win / Average | 23 a) / 25.16 | 38 25.40 |
| TM-Score | Win / Average | 32 / 0.644 | 32 / 0.650 |
SAli-MT: Structure models built on the optimal alignment with five template structures; MAli-ST, models built on five alignments with the same five template structures as used in the SAli-MT models. Targets were discarded when Modeller could not compute Mali-MT models.
There are three ties between SAli-MT and Mali-MT models in terms of the GDT-TS score.
Performance of SUPRB in the alignment accuracy
Finally, we examine the effect of the residue contact term for SUPRB implemented by using suboptimal alignments. This section describes results of the alignment of accuracy of SUPRB, while the template recognition accuracy is reported in the subsequent section. As described in Methods, two strategies are used to incorporate the contact term: In the reranking strategy, target-template alignments (including optimal and suboptimal alignments) computed with the local scoring terms (Eq. 16) are then reranked by the score which includes the contact term (Eq. 18). The second strategy is to handle residue contacts in a probabilistic fashion taking advantage of the suboptimal alignments (Eqns. 18 & 19).
Table 3A lists the weighting factors trained on the Prosup dataset. Terms are added one by one to the compatibility score starting from the sequence profile term. Then, the weighting factors and the opening/extending gap penalties are trained each time a new term is added to the score. It is shown that adding more terms consistently improve the alignment accuracy (considering the exact agreement): 7.8 % points, 1.9, 0.4, and 1.6 (for the reranking strategy, I in the table) or 2.1 (for the probabilistic contacts, II) improvement is observed by adding the secondary structure (SS) term, the solvent accessibility (SAA) term, the main-chain angle (Ang) term, and the residue contact (Cont) term, respectively. Particularly, it is noteworthy that adding the contact potential improves the results both by the reranking strategy (I) and the probabilistic handling of contact potential (II). Comparing the two strategies, the probabilistic contacts (II) performs better than the reranking strategy (I) (accuracy improvement: 1.6 % points and 2.1 % points for I and II), indicating that the probabilistic contacts use suboptimal alignments more effectively to capture residue contact information. We conducted the paired t-test83 to examine the statistical significance of the improvement observed at each time a new term is added. Using the p-value threshold value of 0.05, the improvements are considered to be significant for almost all the cases, except for two cases (the p-value of 0.146 for adding the angle potential when the exact matches are counted and 0.09 for adding the solvent accessibility term when matches ±4 residues are counted as correct).
Table 3A.
Weighting factors trained on the Prosup dataset.
| Weighting factor values a) | Alignment accuracy (%) b) | |||||||
|---|---|---|---|---|---|---|---|---|
| Prof | SS | SAA | Ang | Cont | Gap_o | Gap_e | Exact (±0) | ±4 residues |
| 1.0 | - | - | - | - | −4 | −0.6 | 53.2 | 71.4 |
| 0.8 | 0.2 | - | - | - | −2 | −0.2 | 61.0 (4.21×10−13) |
76.1 (2.31×10−10) |
| 0.7 | 0.2 | 0.1 | - | - | −2 | −0.2 | 62.9 (2.56×10−5) |
76.9 (0.09) |
| 0.6 | 0.1 | 0.2 | 0.1 | - | −2 | −0.2 | 63.3 (0.146) |
78.5 (0.048) |
| 0.5 | 0.2 | 0.2 | 0.1 | 0.2 | −2 | −0.2 | I c): 64.9 (1.20×10−3) II: 65.4 (2.67×10−4) |
I: 80.7 (1.8×10−3) II: 81.5 (4.8×10−4) |
Values are weighting factors for (from left to right): sequence profile, secondary structure, main-chain angle potential, solvent accessibility, residue contact potential, and the last two values are the opening and extension gap penalties. A dash (−) means that the term is not included in the combination.
The average percentage of correctly aligned residues in the top-scoring alignments. The column for ±4 residues counts a residue pair as correct when a residue in target is aligned within four residues to the correct partner in the template. In the parentheses, the p-value of the p-pair test is shown. The test evaluates the statistical significance of the average value compared to the one in the previous row.
The contact potential is used in the reranking strategy (I) or in the strategy that consider residue contacts in a probabilistic fashion (II).
The trained parameters are further tested on the SALIGN dataset (Table 3B). The scoring terms are added one by one with the weighting factors trained on the Prosup dataset (Table 3A) and the alignment accuracy is evaluated at each time. The results are essentially consistent with Table 3A, i.e. adding terms improves the accuracy, and the improvements are statistically significant in all the cases other than adding the angle potential term evaluated by the exact matches (p-value 0.098).
Table 3B.
Alignment accuracy on the SALIGN dataset.
| Scoring terms combined | Alignment accuracy (%) a) | |
|---|---|---|
| Exact (±0) | ±4 residues | |
| Sprofile | 46.5 | 67.4 |
| Sprofile, Sss | 51.3 (9.03×10−12) | 73.9 (2.73×10−12) |
| Sprofile, Sss, SSAA | 53.7 (1.49×10−7) | 77.0 (3.22×10−8) |
| Sprofile, Sss, SSAA, Sangle | 54.1 (0.098) | 77.8 (0.025) |
| Sprofile, Sss, SSAA, Sangle, Scontact | I : 55.2 (1.9×10−3) II: 55.6 (6.9×10−4) |
I: 79.2 (1.4×10−3) II: 80.7 (9.7×10−5) |
The weighting factor values and gap penalty values trained on the Prosup dataset (Table 3A) are used.
In the parentheses, the p-value of the p-pair test is shown. The test evaluates the statistical significance of the average value compared to the one in the previous row.
We further investigate the alignment accuracy in the two testing datasets, the SALIGN dataset (Table 4) and the L-E dataset (Table 5), using the parameter set optimized for the combination of all the terms (the last row in Table 3). For the probabilistic residue contact strategy, results for iterative updates of suboptimal alignments are shown. The first iteration uses alignments generated with the local scoring terms (Eq. 16) to define residue contacts, which is then recomputed by DP using the score with the probabilistic residue contacts (Eq. 18). The subsequent iteration further updates the alignments by identifying contacting residues based on the alignments of the previous pass and applying the probabilistic residue contact strategy.
Table 4.
Improvement of alignment accuracy by iterations using the probabilistic residue contacts.
| Reranking strategy |
Probabilistic handling of residue contacts | Partly Thawed a) |
||||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | |||
| Accuracy (%) |
55.15 (Partly Thawed: 0.040) |
55.07 | 55.41 (1st: 0.060) |
55.53 (2nd: 0.095) |
55.56 (3rd: 0.76) (Reranking: 0.048) (Partly Thawed: 0.0017) |
54.83 |
Benchmarked on the SALIGN dataset. The average value over all target-template alignments is shown. In the parentheses, the p-value of the paired t-test is shown. The test is performed to compare the value in the column against the one indicated before the colon in the parenthesis.
The Partly thawed approach proposed by Skolnick & Kihara (2001).
Table 5.
Improvement of alignment accuracy by iterations using the probabilistic residue contacts on the L-E dataset.
| Family | Superfamily | Fold | |
|---|---|---|---|
| Reranking Strategy | 59.63 (%) (Partly: 0.018) |
29.80 (Partly: 0.077) |
14.32 (Partly: 0.057) |
| Probabilistic contacts 1st iteration |
59.24 (Reranking: 0.018) |
29.28 (Reranking: 0.077) |
14.13 (Renranking: 0.057) |
| 2nd iteration | 59.79 (1st: 0.011) |
30.12 (1st: 0.0046) |
14.81 (1st: 0.0087) |
| 3rd iteration | 60.05 (2nd: 0.087) |
30.50 (2nd: 0.054) |
14.91 (2nd: 0.042) |
| 4th iteration | 60.12 (3rd: 0.650) (Reranking: 0.016) (Partly: 0.00072) |
30.55 (3rd: 0.470) (Reranking: 0.0038) (Partly: 0.00025) |
14.93 (3rd: 0.071) (Reranking: 0.0057) (Partly: 0.0010) |
| Partly Thawed | 59.10 | 29.45 | 14.04 |
The average accuracy for alignments at the family, the superfamily, and the fold level similarity is shown. In the parentheses, the p-value of the paired t-test is shown. The test is performed to compare the alignment accuracy with the one indicated before the colon. For example, (Reranking: x.xxx) and (Partly: x.xxx) are the p-value computed by comparing with the accuracy observed for the reranking strategy and the partly thawed approach, respectively.
The iteration of updating alignments by the probabilistic residue contacts improves the accuracy consistently from 55.07% (the 1st iteration) to 55.56% at the 4th iteration (Table 4). The reranking strategy is more accurate (55.15%) than the probabilistic contact strategy at the 1st iteration (55.07%), however, the probabilistic contact strategy overtakes the reranking strategy from the 2nd iteration. When only the optimal alignment is used, the probabilistic contact strategy converges to the “partly thawed” approach proposed by Skolnick & Kihara for a threading program PROSPECTOR4, which takes the residue contact information from the optimal sequence-profile based alignment. The comparison with the partly thawed approach (54.83%) and the probabilistic contact strategy with the 1st iteration (55.07%) (Table 4) illustrates that positive contribution of the suboptimal alignments in improvement of the accuracy. The reranking strategy (55.15%) also performs better than the partly thawed approach. Note that this comparison is intended only to show the positive effect of using suboptimal alignments but not to make performance comparison between SUPRB and PROSPECTOR, since there are many practical technical differences between the two threading methods. We decided to set the maximum number of iterations to four since the gain in the accuracy decreases monotonically resulting in a marginal improvement of 0.03% point for the 4th over the 3rd iteration. Using the p-value cutoff of 0.05, the improvement at each iteration over the previous pass does not show statistical significance (the p-value of 0.06, 0.095, and 0.76). However, the both reranking and the probabilistic contact strategy using four iterations show higher accuracy than the partly thawed approach with statistical significance. Also, the improvement by the probabilistic contact over the reranking strategy is statistically significant.
The results on the L-E dataset (Table 5) are qualitatively same as Table 4: The reranking strategy shows a higher accuracy than the probabilistic contact strategy at the 1st iteration, however, the latter makes consistent improvement by the subsequent iterative updates of residue contacts and the alignments. The results of the 4th iteration of the probabilistic contact strategy are better than the reranking strategy and the partly thawed approach with the statistical significance for all three similarity level, the family, the superfamily, and the fold.
Performance in the template recognition accuracy
Next, we examine the performance of SUPRB in terms of the template recognition accuracy in comparison with the other existing methods. The benchmark was performed on the L-E dataset. Each query protein sequence is aligned with the rest of the proteins in the L-E dataset, which are then ranked by the Z-score of the raw alignment score. Retrieved templates are evaluated in the three similarity levels between the target and templates, i.e. in the family, the superfamily, and the fold levels. In evaluating the methods for the superfamily level, template hits which belong to the same family with the query are neglected in the list, and counted if a template in the same superfamily (but not in the same family) is hit at the top1 or within top5 or not. The same is done for the evaluation at the fold level accuracy. SUPRB was run with four different scoring schemes: First, the score with the local terms without the residue contact terms (Eq. 16) was used. Then, the contact term was incorporated either by the renranking strategy (I) or by the probabilistic contacts strategy (II). In addition, we also examined another score to rank template hits, which combines the Z-score of the raw score by the probabilistic contact strategy and the SPAD score in the following fashion:
| (Eq. 23) |
As the SPAD score46 measures the consistency of the top-scoring alignment compared with the suboptimal alignments (the lower score more consistent), the Scombined score is intended to select reliable (i.e. a low SPAD score, which indicate that alignments are consistent) target-template alignments that have a high Z-score. The results by the other existing methods are taken from the paper by Liu et al.26 The results of the SP5 method are taken from the paper by Zhang et al. 6.
We first examine the performance of the four scoring schemes for SUPRB (last rows in Table 6). The two schemes with the contact potential perform better than SUPRB without contact potential except for Top1 for the fold level similarity. Interestingly, the reranking strategy shows slightly better performance than the probabilistic contacts strategy in the family level (both Top1 and Top5) and ties at Top5 for the fold level. The probabilistic contact strategy outperforms the reranking strategy for the rest of the categories (i.e. Top1 & Top5 for the superfamily and Top1 for the fold level). In the fold recognition, recognizing correct templates with a distinct Z-score is also very important. Table 7 shows that the probabilistic contacts strategy and the reranking strategy increase the Z-score of correct hits over the local score based ranking. The Scombined score applied to the probabilistic contacts strategy (the last row in Table 6) did not deteriorate the accuracy if not marginally improved it, except for one case, Top1 in the superfamily level. The improvement by the Scombined score was observed for Top5 for the superfamily and both Top1 and Top5 for the fold level similarity. The p-values calculated by the Mann-Whitney U test shows SUPRB with the probabilistic contacts strategy and the Scombined score are significantly better than SUPRB without the residue contact term except for the accuracy measured in the fold level recognition.
Table 6.
Template recognition on the Lindahl and Eloffson dataset.
| Method | Family | Superfamily | Fold | |||
|---|---|---|---|---|---|---|
| Top 1 | Top 5 | Top 1 | Top 5 | Top 1 | Top 5 | |
| PSIBLAST | 71.2 | 72.3 | 27.4 | 27.9 | 4.0 | 4.7 |
| HMMER | 67.7 | 73.5 | 20.7 | 31.3 | 4.4 | 14.6 |
| SAMT98 | 70.1 | 75.4 | 28.3 | 38.9 | 3.4 | 18.7 |
| THEADER | 49.2 | 58.9 | 10.8 | 24.7 | 14.6 | 37.7 |
| FUGUE | 82.2 | 85.8 | 41.9 | 53.2 | 12.5 | 26.8 |
| RAPTOR | 75.2 | 77.8 | 39.3 | 50.0 | 25.4 | 45.1 |
| PROSPECT II | 84.1 | 88.2 | 52.6 | 64.8 | 27.7 | 50.3 |
| SPARKS | 81.6 | 88.1 | 52.5 | 69.1 | 24.3 | 47.7 |
| SPARKS-0 | 82.9 | 90.1 | 56.5 | 72.4 | 23.1 | 43.6 |
| FOLDPro | 85.0 | 89.9 | 55.5 | 70.0 | 26.5 | 48.3 |
| SP1 | 81.3 | 87.2 | 51.8 | 65.0 | 20.2 | 35.8 |
| SP2 | 82.5 | 87.0 | 52.5 | 67.1 | 24.9 | 40.2 |
| SP2+ | 82.2 | 86.8 | 55.1 | 68.4 | 27.8 | 45.8 |
| SP3 | 81.6 | 86.8 | 55.3 | 67.7 | 28.7 | 47.4 |
| SP4 | 80.9 | 86.3 | 57.8 | 68.9 | 30.8 | 53.6 |
| SP5 a) | 82.4 (81.6) |
87.6 (87.0) |
59.8 (59.9) |
70.0 (70.2) |
37.9 (37.4) |
58.7 (58.6) |
| SUPRB No contact term |
82.9 | 89.0 | 51.4 | 66.8 | 26.8 | 51.4 |
| SUPRB reranking |
84.9 | 90.7 | 52.5 | 67.7 | 26.2 | 51.7 |
| (no cont.: 0.031) b) | (no cont.: 0.064) | (no cont: 0.120) | ||||
| SUPRB Prob. contacts |
84.5 | 90.5 | 56.9 | 69.8 | 27.4 | 51.7 |
| (no cont.: 0.035) (reranking: 0.22) |
(no cont.: 0.0078) (reranking: 0.017) |
(no cont.: 0.073) (reranking: 0.095) |
||||
| SUPRB SCombined score c) |
84.5 | 90.5 | 56.2 | 70.5 | 27.7 | 52.6 |
| (no cont: 0.035) (reranking: 0.23) (prob. Cont: 0.54) |
(no cont: 0.0068) (reranking: 0.012) (prob. Cont: 0.19) |
(no cont: 0.029) (reranking: 0.041) (prob. Cont: 0.086) |
||||
The success rate (%) of recognizing a template which belong to the same family, superfamily, or fold to the query within top1/top5 scoring templates are shown. The values for the methods other than SUPRB are taken from Liu, Zhang et al. (2007). The highest success rate for each category is highlighted in bold and the second and the third best values are underlined.
The values are for SP5f taken from Table 2 from the SP5 paper by Zhang, Liu & Zhou (2008). In the parentheses, the values for SP5,g in the table are shown.
In the parentheses, statistical significance of the ranking of correct templates is evaluated by Mann-Whitney U test. The method compared against is shown before the colon: no cont., SUPRB with no residue contact term; reranking, SUPRB with the reranking strategy; prob. Cont., SUPRB with the probabilistic contact term.
Applied to the probabilistic contacts strategy.
Table 7.
The average Z-scores of the correct hits by SUPRB.
| Family | Superfamily | Fold | ||||
|---|---|---|---|---|---|---|
| Top 1 | Top 5 | Top 1 | Top 5 | Top 1 | Top 5 | |
| SUPRB w/o contact |
9.74 | 9.41 | 5.27 | 4.45 | 3.32 | 3.03 |
| Reranking | 10.20 | 9.68 | 5.42 | 4.72 | 3.81 | 3.28 |
| Probabilistic contacts |
10.56 | 10.06 | 5.51 | 4.82 | 3.68 | 3.39 |
The template recognition results on the L-E dataset are used.
In Table 8, we examine the template ranking method we used (Eq. 21) in comparison with two other methods, a normalized score method and the one proposed for SP426 threading methods. In the normalized score method, the raw sequence-structure compatibility score for a template is first normalized the alignment length, which is then used for ranking templates. In SP4, templates are ranked by the difference between the raw alignment score and the reverse alignment score in which the alignment is made with the reversed query sequence26. If there is no structural similarity between the first and the second models, templates are reranked by the larger one of the two Z-scores, one computed for the raw alignment scores normalized by the alignment length and another one the raw scores normalized by the non-gap alignment length. Here the score from SUPRB computed with the probabilistic contact strategy is considered as the raw score, to which the two alternative methods are applied. The results (Table 8) show that both alternative methods do not work as well as Eq. 21 and the Scombined score (Eq. 23). These results may not imply general superiority of Eq. 21 and the Scombined score over them. Template ranking methods are developed based on the empirical observation of the raw score distribution of particular threading methods, and thus can be specific to each threading method.
Table 8.
Comparison with the other template ranking methods
| Family | Superfamily | Fold | ||||
|---|---|---|---|---|---|---|
| Top1 | Top5 | Top1 | Top5 | Top1 | Top5 | |
| Length normalized score |
82.1 (%) | 87.3 | 48.2 | 62.4 | 21.9 | 50.7 |
| SP4 method a) |
84.3 | 89.9 | 53.0 | 67.2 | 24.7 | 50.3 |
| SUPRB Prob. Contacts b) c) |
84.5 | 90.5 | 56.9 | 69.8 | 27.4 | 51.7 |
| SUPRB Scombined Score c), d) |
84.5 | 90.5 | 56.2 | 70.5 | 27.7 | 52.6 |
The raw target-template compatibility score by the probabilistic residue contact strategy of SUPRB is transformed in four different schemes.
Note that only the template ranking method used in SP4 is applied but not the entire SP4 threading method, to the raw compatibility score by the probabilistic residue contact strategy of SUPRB.
Eq. 21 is applied.
These values are copied from Table 6.
Eq. 23 is applied.
Finally, in comparison with the other existing methods (Table 6), SUPRB is ranked within the best 3 methods in all the cases other than Top1 for the fold level, for which the results using the Scombined score is ranked at 5th (27.7%). The head-to-head comparison between SUPRB using the Scombined score and the other methods reveals that SUPRB with Scombined score ties with SP4 and SP5 (SUPRB wins at Top1 & Top5 at the family level, Top 5 at the superfamily level, and SP4 and SP5 win in the other three cases) and are indeed the best among all. To conclude, the use of suboptimal alignments for incorporating the residue contact potential is effective also in improving the accuracy of template recognition. Moreover, SUPRB shows very competitive results in the template recognition as compared with the other existing methods.
Application to CASP8 targets
We apply SUPRB to targets of Critical Assessment of Techniques in Structure Prediction 8 (CASP8; http://predictioncenter.org/casp8) to further compare the performance of SUPRB with the other existing state-of-the-art threading methods. To this end, we selected 28 single-domain human/server targets in the template based modeling (TBM) category, since assembling structures of multiple domains is beyond the scope of this work. For this test, we prepared a template database of 10926 proteins, which are selected by the PDB-REPRDB server84 with the threshold value of 40% sequence identity and an RMSD of 6Å. For a target sequence, the template database is first scanned using SUPRB with the reranking strategy to obtain top fifty templates, which are then re-scanned using the probabilistic contact strategy. The tertiary structure of a target is built with Modeller using the five alignments between the recognized template and the target. Manual refinement is not performed.
The results are shown in Table 9 and Figure 8. The correct template is recognized as the top hit for 21 out of the 28 targets, and considering top 5 templates increases it to 22. We also compute the average GDT-TS score of the top 1 ranked model and the best among the top 5 models and compared it with all the other 72 servers participated in CASP8. The average GDT-TS score of the top 1 model by SUPRB is 58.55, which would rank at the 11th among the servers on these targets (Fig. 8). As shown in the figure, the difference of the score to higher ranked servers is small; for example, the score difference to the second server, TS429 (Pcon_multi) is 1.99. The difference to the top server (TS426, Zhang-server) is 5.07. Building an accurate tertiary structure model based on a correct template by threading needs additional key developments, which many of the top servers have implemented, such as building the structure of unaligned regions and main-chain optimization for the target sequence starting from the template structure55. Here we simply used Modeller for those tasks. Although there are differences in the servers in the types of implemented methods and their complications, the results show the competitive performance of SUPRB among the other existing methods.
Table 9.
Performance on CASP8 template-based modeling targets.
| Target | Recognized Template |
Template Correctness a) |
GDT-TS |
|---|---|---|---|
| T0389 | 2oucA | X | 71.08 |
| T0393 | 2f1kA (2gf2A) | X | 63.99 (64.78) |
| T0395 | 1surA | X | 53.78 |
| T0396 | 1jr8A | X | 88.24 |
| T0399 | 1q7fA | - | 36.57 |
| T0401 | 2pagA | X | 60.43 |
| T0407 | 2hqaA | X | 57.04 |
| T0411 | 1yt8A (1e0cA) | X | 69.28 (72.88) |
| T0415 | 1c8cA | X | 71.50 |
| T0419 | 2plrA | X | 45.65 |
| T0421 | 2plrA | X | 51.24 |
| T0425 | 1xovA | X | 56.98 |
| T0427 | 1hr6A (1bccA) | X | 50.80 (66.06) |
| T0440 | 1m65A | X | 49.64 |
| T0443 | 2abk | - | 42.05 |
| T0449 | 1snzA (2ciq) | - | 55.24 (61.82) |
| T0451 | 1s5aA (1nu3A) | X | 65.55 (67.13) |
| T0454 | 1pb6A | X | 93.27 |
| T0457 | 2qb6A | X | 52.45 |
| T0464 | 2jr6A (2hflA) | - | 45.29 (51.81) |
| T0469 | 2fhfA | X | 76.19 |
| T0474 | 1p94A | X | 83.54 |
| T0476 | 1w5sA | - | 46.84 |
| T0480 | 1dl6A | X | 68.33 |
| T0489 | 1yqyA | X | 34.64 |
| T0495 | 1gefA (2p14A) | - (X) | 30.76 (40.29) |
| T0498 | 1pgx (1mhxA) | - | 35.56 (37.78) |
| T0499 | 2i2yA (2igdA) | X | 83.48 (84.38) |
|
| |||
| Average | 58.55 (60.23) | ||
A structure model ranked at top 1 is listed. If a better model is found within top 5 ranked models, it is shown in the parentheses.
A template is considered to be correct for a target if it appears in the template list provided by the CASP8 organizers found at http://predictioncenter.org/download_area/CASP8/list_of_templates.txt.
Figure 8.
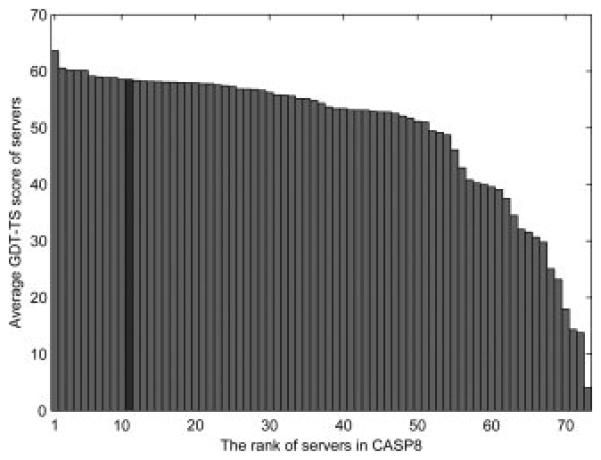
The average GDT-TS score of Top 1 models of CASP8 template-based model targets of the servers. SUPRB is shown with the dark gray bar and the other servers are shown in pale gray.
Computational time of SUPRB
The two strategies of SUPRB, the reranking strategy and the probabilistic contact strategy, obviously take more time than computing only the optimal target-template alignment using a regular dynamic programming, since they computes suboptimal alignments. Table 10 shows the execution time (user time) of SUPRB for two examples on a Linux machine with an Intel i7 2.67 Ghz processor and 12 Gb memory. For both SUPRB strategies, 0.01*ltarget *ltemplate suboptimal alignments are computed, where ltarget and ltemplate are the length of target and the template proteins, respectively. For the probabilistic contact strategy, the alignments are refined for five iterations. The SUPRB reranking strategy took 3-6 times, and the probabilistic contact strategy took ~ 10 to 30 times more the regular DP. Threading scans performed for the CASP8 targets took around 36-48 hours on a single CPU of the Linux machine.
Table 10.
Computational time of target-template alignments by SUPRB
| Target | Target length (aa) |
Template | Template length |
Regular DP (seconds) |
SUPRB I | SUPRB II |
|---|---|---|---|---|---|---|
| 1aab | 83 | 1hme | 77 | 0.25 | 0.66 | 2.70 |
| 2aky | 218 | 1gky | 186 | 1.48 | 8.83 | 43.95 |
The regular DP computes only the optimal alignment between the target and the template. Here SUPRB I and SUPRB II compute 0.01*ltarget *ltemplate suboptimal alignments, where ltarget and ltemplate are the length of target and the template proteins, respectively. SUPRB I, the reranking strategy; SUPRB II, the probabilistic residue contact strategy with 5 iterations.
Discussion
In this article, we investigated the effect of using suboptimal alignments in template-based structure prediction. Aligning two protein sequences is not trivial especially when they do not have significant sequence similarity. We showed that suboptimal alignments are often more accurate than the optimal one, and such accurate suboptimal alignments can occur even at a very low alignment score rank. Moreover, lower ranked suboptimal alignments contain a significant number of correct amino acid residue contacts. Benefits of suboptimal alignments can be immediately enjoyed by using them as input for a template-modeling tool, Modeller, by feeding a set of alternative alignments rather than a single optimal alignment between a target and a template. Finally, we employed suboptimal alignments in handling a contact potential in a probabilistic way in a threading program, SUPRB. The probabilistic contacts strategy outperforms the partly thawed approach which only uses the optimal alignment in defining residue contacts and the reranking strategy, which uses the contact potential in reranking alignments. To the best of our knowledge, this is the first time that the effect of the suboptimal alignments in structure prediction is thoroughly investigated and that the suboptimal alignments are implemented for employing a contact potential for template-based modeling. The probabilistic handling of residue contacts may also be useful to capture changes in residue contact upon protein motion. Our approach can be implemented in any DP based template-based structure prediction methods. Although we have not addressed in this manuscript, we would like to mention that suboptimal alignments are also useful in assessing the quality of template-based models, as we showed in related works45-47.
A residue contact potential is unique among the other commonly used scoring terms in threading methods in the sense that it directly represents long-range interaction85 of amino acids in the tertiary structure. Such long-range interaction is not well captured by one-body scoring terms, such as sequence-profile terms, secondary structure terms, or residue environment terms86. Hence, a residue contact potential will be a key for success in recognizing very distantly related template structures which share virtually no sequence similarity with a target protein. However, a recent trend in template-based structure prediction methods is to rely heavily on sequence-based information and occasionally on some one-body potentials but not two-body contact potentials. There are two main reasons for this trend. Firstly, sequence-information has become more and more useful as the amount of sequences in databases grows rapidly and new effective approaches have been developed for using the sequence and local structure information25. Secondly, a residue contact potential is cumbersome to handle in template recognition since the optimal alignment for a contact potential cannot be obtained with a conventional DP algorithm. In addition, one should be also noted that a residue contact pattern is not necessarily conserved even in proteins of the same family 44, thus simply copying contacting residue pairs from a template may not be the best way to use contact information.
Despite all these challenges, we believe that it is worthwhile to revisit residue contact potentials in template-based prediction, since employing sequence-structure compatibility terms rather than sequence similarity based terms is logically the only the way to find template structures with virtually no sequence similarity to a target. Such distantly related template structures are expected to be made available in an increasing pace due to the progress of experimental protein structure determinations. It is also noteworthy that the number of template structures needed for structure modeling of the entire protein space will be reduced once methods are established for detecting and utilizing very distantly related structures for target proteins16.
Recent studies have reported technical improvement in computing alignments once an appropriate template is recognized for a target protein24;87;88. However, templates should be identified in the first place for employing such advanced alignment techniques. Therefore, both techniques, i.e. distant template recognition and optimizing target-templates alignments, should be developed in a good harmony between each other to further advance our technology of template-based protein structure prediction.
Supplementary Material
Acknowledgement
The residue contact potential was provided by Yifeng D. Yang. The authors also appreciate stimulus discussion with Y. D. Yang. The authors are grateful to Rebecca Harding for proofreading the manuscript. This work is supported by grants from the National Institutes of Health (GM075004) and the National Science Foundation (DMS800568, EF0850009, IIS0915801).
Reference List
- 1.Jauch R, Yeo HC, Kolatkar PR, Clarke ND. Assessment of CASP7 structure predictions for template free targets. Proteins. 2007;69(Suppl 8):57–67. doi: 10.1002/prot.21771. [DOI] [PubMed] [Google Scholar]
- 2.Kopp J, Bordoli L, Battey JN, Kiefer F, Schwede T. Assessment of CASP7 predictions for template-based modeling targets. Proteins. 2007;69(Suppl 8):38–56. doi: 10.1002/prot.21753. [DOI] [PubMed] [Google Scholar]
- 3.Zhang Y. Progress and challenges in protein structure prediction. Curr Opin Struct Biol. 2008;18:342–348. doi: 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Skolnick J, Kihara D. Defrosting the frozen approximation: PROSPECTOR--a new approach to threading. Proteins. 2001;42:319–31. [PubMed] [Google Scholar]
- 5.Skolnick J, Kihara D, Zhang Y. Development and large scale benchmark testing of the PROSPECTOR 3.0 threading algorithm. Proteins. 2004;56:502–518. doi: 10.1002/prot.20106. [DOI] [PubMed] [Google Scholar]
- 6.Zhang W, Liu S, Zhou Y. SP5: improving protein fold recognition by using torsion angle profiles and profile-based gap penalty model. PLoS ONE. 2008;3:e2325. doi: 10.1371/journal.pone.0002325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Qu X, Swanson R, Day R, Tsai J. A guide to template based structure prediction. Curr Protein Pept Sci. 2009;10:270–285. doi: 10.2174/138920309788452182. [DOI] [PubMed] [Google Scholar]
- 8.Yang YD, Park C, Kihara D. Threading without optimizing weighting factors for scoring function. Proteins. 2008;73:581–596. doi: 10.1002/prot.22082. [DOI] [PubMed] [Google Scholar]
- 9.Kolinski A. Protein modeling and structure prediction with a reduced representation. Acta Biochim Pol. 2004;51:349–371. [PubMed] [Google Scholar]
- 10.Liwo A, Czaplewski C, Oldziej S, Scheraga HA. Computational techniques for efficient conformational sampling of proteins. Curr Opin Struct Biol. 2008;18:134–139. doi: 10.1016/j.sbi.2007.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kihara D, Lu H, Kolinski A, Skolnick J. TOUCHSTONE: an ab initio protein structure prediction method that uses threading-based tertiary restraints. Proc Natl Acad Sci U S A. 2001;98:10125–10130. doi: 10.1073/pnas.181328398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Meinke JH, Hansmann UH. Free-energy-driven folding and thermodynamics of the 67-residue protein GS-alpha3W--a large-scale Monte Carlo study. J Comput Chem. 2009;30:1642–1648. doi: 10.1002/jcc.21321. [DOI] [PubMed] [Google Scholar]
- 13.Itoh SG, Okamoto Y. Effective sampling in the configurational space of a small peptide by the multicanonical-multioverlap algorithm. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76:026705. doi: 10.1103/PhysRevE.76.026705. [DOI] [PubMed] [Google Scholar]
- 14.Das R, Baker D. Macromolecular modeling with rosetta. Annu Rev Biochem. 2008;77:363–382. doi: 10.1146/annurev.biochem.77.062906.171838. [DOI] [PubMed] [Google Scholar]
- 15.Zhou H, Skolnick J. Protein structure prediction by pro-Sp3-TASSER. Biophys J. 2009;96:2119–2127. doi: 10.1016/j.bpj.2008.12.3898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Friedberg I, Jaroszewski L, Ye Y, Godzik A. The interplay of fold recognition and experimental structure determination in structural genomics. Curr Opin Struct Biol. 2004;14:307–312. doi: 10.1016/j.sbi.2004.04.005. [DOI] [PubMed] [Google Scholar]
- 17.Baker D, Sali A. Protein structure prediction and structural genomics. Science. 2001;294:93–96. doi: 10.1126/science.1065659. [DOI] [PubMed] [Google Scholar]
- 18.Burley SK. An overview of structural genomics. Nat Struct Biol. 2000;7(Suppl):932–4. doi: 10.1038/80697. [DOI] [PubMed] [Google Scholar]
- 19.Zhang C, Kim SH. Overview of structural genomics: from structure to function. Curr Opin Chem Biol. 2003;7:28–32. doi: 10.1016/s1367-5931(02)00015-7. [DOI] [PubMed] [Google Scholar]
- 20.Skolnick J, Arakaki AK, Lee SY, Brylinski M. The continuity of protein structure space is an intrinsic property of proteins. Proc Natl Acad Sci U S A. 2009;106:15690–15695. doi: 10.1073/pnas.0907683106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kihara D, Skolnick J. The PDB is a covering set of small protein structures. J Mol Biol. 2003;334:793–802. doi: 10.1016/j.jmb.2003.10.027. [DOI] [PubMed] [Google Scholar]
- 22.Petrey D, Fischer M, Honig B. Structural relationships among proteins with different global topologies and their implications for function annotation strategies. Proc Natl Acad Sci U S A. 2009;106:17377–17382. doi: 10.1073/pnas.0907971106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Y, Skolnick J. The protein structure prediction problem could be solved using the current PDB library. Proc Natl Acad Sci U S A. 2005;102:1029–1034. doi: 10.1073/pnas.0407152101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang G, Dunbrack RL., Jr. Scoring profile-to-profile sequence alignments. Protein Sci. 2004;13:1612–1626. doi: 10.1110/ps.03601504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dunbrack RL., Jr. Sequence comparison and protein structure prediction. Curr Opin Struct Biol. 2006;16:374–384. doi: 10.1016/j.sbi.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 26.Liu S, Zhang C, Liang S, Zhou Y. Fold recognition by concurrent use of solvent accessibility and residue depth. Proteins. 2007;68:636–645. doi: 10.1002/prot.21459. [DOI] [PubMed] [Google Scholar]
- 27.Zhou H, Zhou Y. Single-body residue-level knowledge-based energy score combined with sequence-profile and secondary structure information for fold recognition. Proteins. 2004;55:1005–1013. doi: 10.1002/prot.20007. [DOI] [PubMed] [Google Scholar]
- 28.Karchin R, Cline M, Mandel-Gutfreund Y, Karplus K. Hidden Markov models that use predicted local structure for fold recognition: Alphabets of backbone geometry. Proteins. 2003;51:504–14. doi: 10.1002/prot.10369. [DOI] [PubMed] [Google Scholar]
- 29.Li SC, Bu D, Xu J, Li M. Fragment-HMM: a new approach to protein structure prediction. Protein Sci. 2008;17:1925–1934. doi: 10.1110/ps.036442.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Xu J, Jiao F, Yu L. Protein structure prediction using threading. Methods Mol Biol. 2008;413:91–121. doi: 10.1007/978-1-59745-574-9_4. [DOI] [PubMed] [Google Scholar]
- 31.Fischer D. Servers for protein structure prediction. Curr Opin Struct Biol. 2006;16:178–182. doi: 10.1016/j.sbi.2006.03.004. [DOI] [PubMed] [Google Scholar]
- 32.Ginalski K, Elofsson A, Fischer D, Rychlewski L. 3D-Jury: a simple approach to improve protein structure predictions. Bioinformatics. 2003;19:1015–1018. doi: 10.1093/bioinformatics/btg124. [DOI] [PubMed] [Google Scholar]
- 33.Mevissen HT, Vingron M. Quantifying the local reliability of a sequence alignment. Protein Eng. 1996;9:127–132. doi: 10.1093/protein/9.2.127. [DOI] [PubMed] [Google Scholar]
- 34.Vingron M, Argos P. Determination of reliable regions in protein sequence alignments. Protein Eng. 1990;3:565–569. doi: 10.1093/protein/3.7.565. [DOI] [PubMed] [Google Scholar]
- 35.Vingron M. Near-optimal sequence alignment. Curr Opin Struct Biol. 1996;6:346–352. doi: 10.1016/s0959-440x(96)80054-6. [DOI] [PubMed] [Google Scholar]
- 36.Saqi MA, Sternberg MJ. A simple method to generate non-trivial alternate alignments of protein sequences. J Mol Biol. 1991;219:727–732. doi: 10.1016/0022-2836(91)90667-u. [DOI] [PubMed] [Google Scholar]
- 37.Sommer I, Toppo S, Sander O, Lengauer T, Tosatto SC. Improving the quality of protein structure models by selecting from alignment alternatives. BMC Bioinformatics. 2006;7:364. doi: 10.1186/1471-2105-7-364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Miyazawa S. A reliable sequence alignment method based on probabilities of residue correspondences. Protein Eng. 1995;8:999–1009. doi: 10.1093/protein/8.10.999. [DOI] [PubMed] [Google Scholar]
- 39.Schlosshauer M, Ohlsson M. A novel approach to local reliability of sequence alignments. Bioinformatics. 2002;18:847–854. doi: 10.1093/bioinformatics/18.6.847. [DOI] [PubMed] [Google Scholar]
- 40.Zhang MQ, Marr TG. Alignment of molecular sequences seen as random path analysis. J Theor Biol. 1995;174:119–129. doi: 10.1006/jtbi.1995.0085. [DOI] [PubMed] [Google Scholar]
- 41.Kschischo M, Lassig M. Finite-temperature sequence alignment. Pac Symp Biocomput. 2000:624–635. doi: 10.1142/9789814447331_0060. [DOI] [PubMed] [Google Scholar]
- 42.Yu L, Smith TF. Positional statistical significance in sequence alignment. J Comput Biol. 1999;6:253–259. doi: 10.1089/cmb.1999.6.253. [DOI] [PubMed] [Google Scholar]
- 43.Cline M, Hughey R, Karplus K. Predicting reliable regions in protein sequence alignments. Bioinformatics. 2002;18:306–314. doi: 10.1093/bioinformatics/18.2.306. [DOI] [PubMed] [Google Scholar]
- 44.Godzik A. The structural alignment between two proteins: is there a unique answer? Protein Sci. 1996;5:1325–38. doi: 10.1002/pro.5560050711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kihara D, Chen H, Yang YD. Quality assessment of computational protein models. Curr Protein Pept Sci. 2009;10:216–228. doi: 10.2174/138920309788452173. [DOI] [PubMed] [Google Scholar]
- 46.Chen H, Kihara D. Estimating quality of template-based protein models by alignment stability. Proteins. 2008;71:1255–1274. doi: 10.1002/prot.21819. [DOI] [PubMed] [Google Scholar]
- 47.Yang YD, Spratt P, Chen H, Park C, Kihara D. Sub-AQUA: real-value quality assessment of protein structure models. Protein Eng Des Sel. 2010;23:617–632. doi: 10.1093/protein/gzq030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tang CL, Petrey D, Fasnacht M, Kosloff M, Alexov E, Honig B. Use of limited suboptimal alignment in homology modeling. RECOMB. 2004 poster presentation. [Google Scholar]
- 49.Eswar N, Eramian D, Webb B, Shen MY, Sali A. Protein structure modeling with MODELLER. Methods Mol Biol. 2008;426:145–159. doi: 10.1007/978-1-60327-058-8_8. [DOI] [PubMed] [Google Scholar]
- 50.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 51.Godzik A, Kolinski A, Skolnick J. Are proteins ideal mixtures of amino acids? Analysis of energy parameter sets. Protein Sci. 1995;4:2107–17. doi: 10.1002/pro.5560041016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sippl MJ. Knowledge-based potentials for proteins. Curr Opin Struct Biol. 1995;5:229–235. doi: 10.1016/0959-440x(95)80081-6. [DOI] [PubMed] [Google Scholar]
- 53.Miyazawa S, Jernigan RL. An empirical energy potential with a reference state for protein fold and sequence recognition. Proteins. 1999;36:357–69. [PubMed] [Google Scholar]
- 54.Jones DT, Taylor WR, Thornton JM. A new approach to protein fold recognition. Nature. 1992;358:86–89. doi: 10.1038/358086a0. [DOI] [PubMed] [Google Scholar]
- 55.Kolinski A, Betancourt MR, Kihara D, Rotkiewicz P, Skolnick J. Generalized comparative modeling (GENECOMP): A combination of sequence comparison, threading, and lattice modeling for protein structure prediction and refinement. Proteins. 2001;44:133–149. doi: 10.1002/prot.1080. [DOI] [PubMed] [Google Scholar]
- 56.Madej T, Gibrat JF, Bryant SH. Threading a database of protein cores. Proteins. 1995;23:356–69. doi: 10.1002/prot.340230309. [DOI] [PubMed] [Google Scholar]
- 57.Godzik A, Kolinski A, Skolnick J. Topology fingerprint approach to the inverse protein folding problem. J Mol Biol. 1992;227:227–38. doi: 10.1016/0022-2836(92)90693-e. [DOI] [PubMed] [Google Scholar]
- 58.Marti-Renom MA, Madhusudhan MS, Sali A. Alignment of protein sequences by their profiles. Protein Sci. 2004;13:1071–1087. doi: 10.1110/ps.03379804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ortiz AR, Strauss CE, Olmea O. MAMMOTH (matching molecular models obtained from theory): an automated method for model comparison. Protein Sci. 2002;11:2606–2621. doi: 10.1110/ps.0215902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lindahl E, Elofsson A. Identification of related proteins on family, superfamily and fold level. J Mol Biol. 2000;295:613–25. doi: 10.1006/jmbi.1999.3377. [DOI] [PubMed] [Google Scholar]
- 61.Andreeva A, Howorth D, Chandonia JM, Brenner SE, Hubbard TJ, Chothia C, Murzin AG. Data growth and its impact on the SCOP database: new developments. Nucleic Acids Res. 2008;36:D419–D425. doi: 10.1093/nar/gkm993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zemla A. LGA: A method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fischer D, Elofsson A, Rice DW, Eisenberg D. Assessing the performance of inverted protein folding methods by means of an extensive benchmark. Proceeding of the First Pacific Symposiumon Biocomputing. 1996:300–318. [PubMed] [Google Scholar]
- 64.Sunyaev SR, Eisenhaber F, Rodchenkov IV, Eisenhaber B, Tumanyan VG, Kuznetsov EN. PSIC: profile extraction from sequence alignments with position-specific counts of independent observations. Protein Eng. 1999;12:387–394. doi: 10.1093/protein/12.5.387. [DOI] [PubMed] [Google Scholar]
- 65.Henikoff S, Henikoff JG. Position-based sequence weights. J Mol Biol. 1994;243:574–578. doi: 10.1016/0022-2836(94)90032-9. [DOI] [PubMed] [Google Scholar]
- 66.Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sadreyev R, Grishin N. COMPASS: a tool for comparison of multiple protein alignments with assessment of statistical significance. J Mol Biol. 2003;326:317–336. doi: 10.1016/s0022-2836(02)01371-2. [DOI] [PubMed] [Google Scholar]
- 68.Adamczak R, Porollo A, Meller J. Combining prediction of secondary structure and solvent accessibility in proteins. Proteins. 2005;59:467–475. doi: 10.1002/prot.20441. [DOI] [PubMed] [Google Scholar]
- 69.Kabsch W, Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- 70.Chothia C. The nature of the accessible and buried surfaces in proteins. J Mol Biol. 1976;105:1–12. doi: 10.1016/0022-2836(76)90191-1. [DOI] [PubMed] [Google Scholar]
- 71.Skolnick J, Jaroszewski L, Kolinski A, Godzik A. Derivation and testing of pair potentials for protein folding. When is the quasichemical approximation correct? Protein Sci. 1997;6:676–88. doi: 10.1002/pro.5560060317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Domingues FS, Lackner P, Andreeva A, Sippl MJ. Structure-based evaluation of sequence comparison and fold recognition alignment accuracy. J Mol Biol. 2000;297:1003–1013. doi: 10.1006/jmbi.2000.3615. [DOI] [PubMed] [Google Scholar]
- 73.Zhang Y, Skolnick J. TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci U S A. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Chakravarty S, Godbole S, Zhang B, Berger S, Sanchez R. Systematic analysis of the effect of multiple templates on the accuracy of comparative models of protein structure. BMC Struct Biol. 2008;8:31. doi: 10.1186/1472-6807-8-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Cheng J. A multi-template combination algorithm for protein comparative modeling. BMC Struct Biol. 2008;8:18. doi: 10.1186/1472-6807-8-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Liu T, Guerquin M, Samudrala R. Improving the accuracy of template-based predictions by mixing and matching between initial models. BMC Struct Biol. 2008;8:24. doi: 10.1186/1472-6807-8-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Moult J, Fidelis K, Kryshtafovych A, Rost B, Tramontano A. Critical assessment of methods of protein structure prediction - Round VIII. Proteins. 2009;77(Suppl 9):1–4. doi: 10.1002/prot.22589. [DOI] [PubMed] [Google Scholar]
- 79.Xu J, Li M, Lin G, Kim D, Xu Y. Protein threading by linear programming. Pac Symp Biocomput. 2003:264–275. [PubMed] [Google Scholar]
- 80.Cheng J, Baldi P. A machine learning information retrieval approach to protein fold recognition. Bioinformatics. 2006;22:1456–1463. doi: 10.1093/bioinformatics/btl102. [DOI] [PubMed] [Google Scholar]
- 81.Kolinski A, Bujnicki JM. Generalized protein structure prediction based on combination of fold-recognition with de novo folding and evaluation of models. Proteins. 2005;61(Suppl 7):84–90. doi: 10.1002/prot.20723. [DOI] [PubMed] [Google Scholar]
- 82.von GM, Pas J, Wyrwicz L, Ginalski K, Rychlewski L. Application of 3D-Jury, GRDB, and Verify3D in fold recognition. Proteins. 2003;53(Suppl 6):418–423. doi: 10.1002/prot.10547. [DOI] [PubMed] [Google Scholar]
- 83.Zar JH. Biostatistical analysis. Prentice Hall; Upper Saddle River, NJ: 1999. [Google Scholar]
- 84.Noguchi T, Akiyama Y. PDB-REPRDB: a database of representative protein chains from the Protein Data Bank (PDB) in 2003. Nucleic Acids Res. 2003;31:492–493. doi: 10.1093/nar/gkg022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kihara D. The effect of long-range interactions on the secondary structure formation of proteins. Protein Sci. 2005;14:1955–1963. doi: 10.1110/ps.051479505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Luthy R, Bowie JU, Eisenberg D. Assessment of protein models with three-dimensional profiles. Nature. 1992;356:83–85. doi: 10.1038/356083a0. [DOI] [PubMed] [Google Scholar]
- 87.Joo K, Lee J, Kim I, Lee SJ, Lee J. Multiple sequence alignment by conformational space annealing. Biophys J. 2008;95:4813–4819. doi: 10.1529/biophysj.108.129684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Tan YH, Huang H, Kihara D. Statistical potential-based amino acid similarity matrices for aligning distantly related protein sequences. Proteins. 2006;64:587–600. doi: 10.1002/prot.21020. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.