Binding of non-steroidal anti-inflammatory drugs to Aβ fibril

Abstract

Non-steroidal anti-inflammatory drugs are considered as potential therapeutic agents against Alzheimer’s disease. Using REMD and atomistic implicit solvent model we studied the mechanisms of binding of naproxen and ibuprofen to the Aβ fibril derived from solid-state NMR measurements. The binding temperature of naproxen is found to be almost 40K higher than of ibuprofen implicating higher binding affinity of naproxen. The key factor, which enhances naproxen binding, is strong interactions between ligands bound to the surface of the fibril. The naphthalene ring in naproxen appears to provide a dominant contribution to ligand-ligand interactions. In contrast, ligand-fibril interactions cannot explain differences in the binding affinities of naproxen and ibuprofen. The concave fibril edge with the groove is identified as the primary binding location for both ligands. We show that confinement of the ligands to the groove facilitates ligand-ligand interactions that lowers the energy of the ligands bound to the concave edge compared to those bound to the convex edge. Our simulations appear to provide microscopic rationale for the differing binding affinities of naproxen and ibuprofen observed experimentally.

Introduction

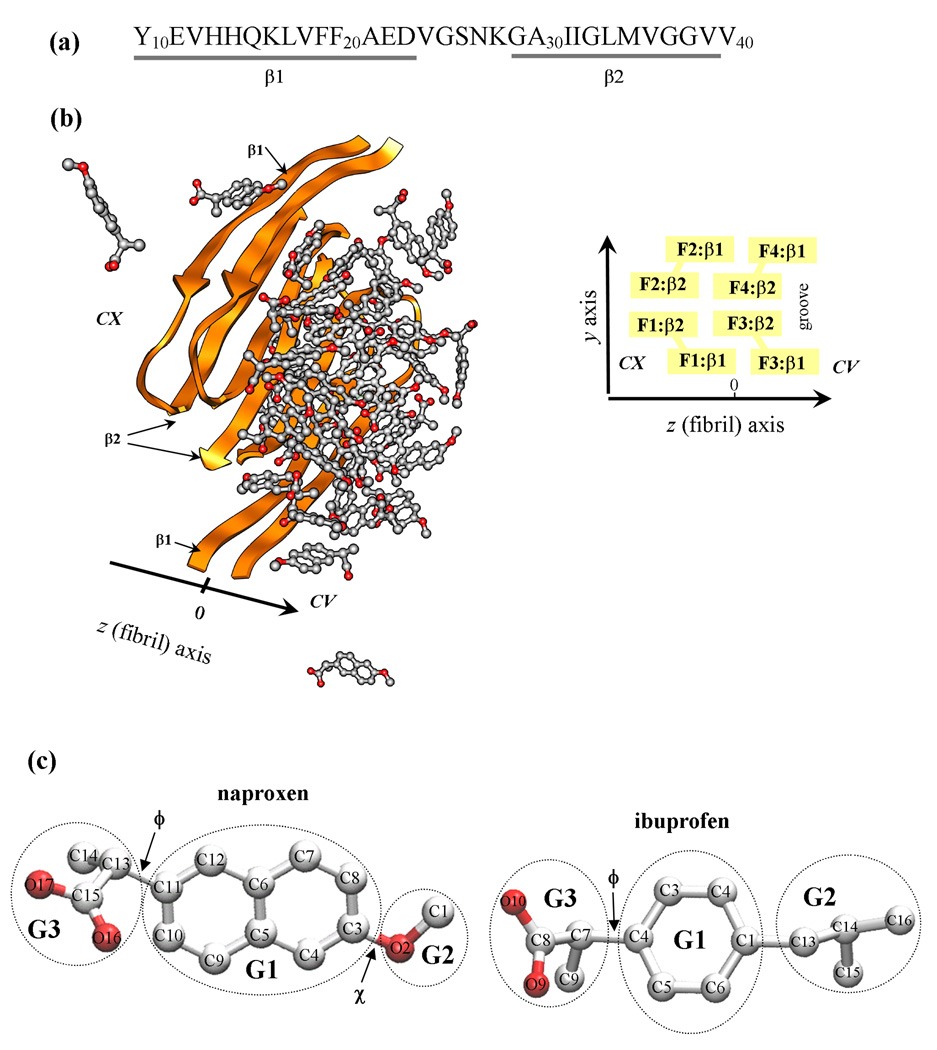
A number of age-related diseases are associated with aggregation of polypeptide chains and formation of cytotoxic amyloid fibrils^1,2. Among amyloidogenic sequences are Aβ peptides (Fig. 1a), which are the products of cellular proteolysis, and their aggregation is linked to Alzheimer’s disease (AD)³. There are many alloforms of Aβ peptides, but the most abundant are 40-mer species, Aβ_1–40. This peptide has been shown to form polymorphic amyloid fibrils depending on the preparation conditions⁴. One of them is a two-fold symmetry fibril structure derived from the solid-state NMR experiments under agitated conditions⁵ (Fig. 1b). This structure reveals that Aβ peptides are organized into parallel in-registry β-sheets laminated into four layers^5,6. Extensive β-sheet structure in Aβ_1–40 fibril is typical for all amyloid deposits independent on specific amyloidogenic sequence^6–9. Backbone hydrogen bonds and a host of side chain interactions lend considerable stability to amyloid fibrils against dissociation¹⁰.

Fig. 1.

(a) The sequence of Aβ_10–40 peptide and the allocation of the β1 and β2 β-strands formed in the fibril structure. (b) Aβ_10–40 fibril with bound naproxen molecules. Fibril protofilament is built of four stacked β-sheets formed by the β1 and β2 strands (panel (a)). A groove formed by indented β2 sheets results in the appearance of two distinct fibril edges - concave (CV) and convex (CX). The CX and CV edges are formed by the peptides F1,F2 and F3,F4, respectively. The primary binding site for naproxen and ibuprofen is the groove on the CV edge. (c) Naproxen molecule has a central hydrophobic naphthalene ring (group G1) and two polar moieties, methoxy and carboxylate groups (G2 and G3). The dihedral angles ϕ and χ are used to test parameterization of naproxen. Ibuprofen molecule has three structural moieties - hydrophobic phenyl G1 and isobutyl G2 and hydrophilic carboxylate G3 groups. The dihedral angle ϕ in ibuprofen is analogous to that in naproxen. Carbon and oxygen atoms are shown in grey and red.

Recognition of the critical role of Aβ peptides in AD has led to a search of small molecular agents controlling Aβ aggregation. One of the potential candidates is a non-steroidal anti-inflammatory drug (NSAID) naproxen¹¹. Epidemiological studies have shown that chronic prophylactic intake of naproxen moderately reduces the risk of AD^12,13. Furthermore, reexamination of the results of large-scale clinical trials suggests that under certain conditions naproxen can reduce the AD risk by 67%¹¹. However, it also appears that naproxen has no therapeutic effect in preexisting AD cases¹⁴. For example, naproxen demonstrates preventive effect against AD related alternations in brain microglia in mice models, but fails to reverse existing AD conditions¹⁵. Several in vitro experimental studies have probed the interactions between naproxen and Aβ aggregates. It has been demonstrated that naproxen binds to Aβ fibrils¹⁶. Naproxen also reduces the amount of Aβ fibrils upon its coincubation with Aβ monomers or partially dissociates preformed Aβ fibrils^16,17. Experiments have also revealed that naproxen may inhibit Aβ fibril elongation¹⁷. Finally, using short fragment of Aβ peptide Thomas et al have found that naproxen reduces β-structure content upon dissociation of amyloid fibrils¹⁸.

Although experimental studies have established the anti-aggregation action of naproxen, the molecular mechanism of its binding to Aβ fibril is largely unknown. Among the questions pertaining to naproxen binding are: (1) What is the location of naproxen binding sites in Aβ fibril? (2) What are the physicochemical factors and interactions, which control naproxen binding? (3) Does the binding mechanism of naproxen also govern binding of other NSAID ligands, such as ibuprofen? The last question is particularly interesting, because compared to naproxen ibuprofen has weaker Aβ binding affinity, yet it appears to produce stronger anti-aggregation effect^16,17.

Molecular dynamics (MD) simulations can map the process of Aβ aggregation at all-atom resolution^19,20. In recent years, MD was used to explore the mechanisms of fibril growth^21–24, to assess the energetics of fibril structures^25–27, or to investigate the assembly of amyloidogenic oligomers^28–33. However, molecular simulations of amyloidogenic peptides coincubated with ligands are still rare. Caflisch and coworkers investigated binding of tricyclic planar ligands (9,10-anthraquinone (AQ) and anthracene) to fibril forming Aβ fragments Aβ_14–20³⁴. They showed that AQ directly interferes with the formation of interstrand hydrogen bonds and thus reduces the accumulation of ordered aggregates. More recently, we used implicit solvent model to study the binding of ibuprofen to Aβ fibrils and its ability to interfere with fibril elongation^35,36. However, as of now we are not aware of computational studies probing naproxen binding to Aβ fibrils.

In this paper, we use atomistic implicit solvent model and replica exchange molecular dynamics (REMD) to answer the questions stated above. We show that naproxen as ibuprofen³⁵ binds to the edges of Aβ fibrils. Interestingly, the edge affinities are strikingly unequal that is explained by different edge surface geometries. Our simulations also suggest that the factor largely determining the binding mechanism is ligand-ligand interactions, while the energetics analysis allows us to pinpoint the naproxen and ibuprofen chemical groups involved in binding. Finally, we demonstrate that the binding of naproxen and ibuprofen to Aβ fibril is governed by the same mechanism, which is modified by the differences in the chemical structure of these ligands. We conclude the paper with the comparison of in silico and experimental data.

Materials and Methods

Simulation system

CHARMM molecular dynamics (MD) program³⁷ and atomistic force field CHARMM19 with the SASA implicit solvent model³⁸ were used for simulations of Aβ peptides, naproxen, and ibuprofen (Fig. 1). Detailed description of this model as well as its applicability and testing can be found in our previous studies^31,39. In particular, we have previously shown that CHARMM19+SASA force field reproduces well the experimental distribution of chemical shifts for C_α and C_β atoms in Aβ_1–40 monomers ³¹. Parameterization of naproxen (Fig. 1c) has been performed consistent with the CHARMM19 force field, SASA solvation parameters, and taking into account similarity of naproxen structure with amino acids (see Supplemental Materials for details). Because the naproxen pK_α value is 4.2, the polar group COO was assumed deprotonated and following SASA implicit solvent model was set neutral to prevent excessive stability of salt bridges³⁸. The complete list of naproxen force field parameters, the rationale for their selection, and testing are given in Supplemental Materials. The parameterization of ibuprofen was reported earlier³⁵.

The simulation system consists of the fibril fragment formed by four Aβ_10–40 peptides interacting with 40 ligand (naproxen or ibuprofen) molecules (Fig. 1). The N-terminal truncated Aβ_10–40 peptides were used as a model for the full-length Aβ_1–40⁴⁰. Similarities in the aggregation propensities of Aβ_1–40 and Aβ_10–40 follow from the following observations. Solid-state NMR studies have shown that both peptides form similar two-fold symmetry fibril structures^5,41. Similarities in oligomerization pathways of Aβ_1–40 and Aβ_10–40 were reported experimentally⁴² and computationally⁴⁰. It is also known that the first nine N-terminal residues in the Aβ_1–40 fibril are disordered^5,43.

The fibril structure was modeled using the coordinates of backbone atoms determined from the solid-state NMR measurements⁵. The backbones of fibril peptides (Fig. 1b) were constrained to their experimental positions using soft harmonic potentials with the constant k_c = 0.6kcal/(molŲ)²⁴. The harmonic constraints permit backbone fluctuations with the amplitude of about 0.6 Åat 360K, which are comparable with the fluctuations of atoms on the surface of folded proteins⁴⁴. Constraints were not applied to the side chains of fibril peptides. The constraints emulate the stability of amyloid fibrils, which are known to be highly resistant to dissociation⁴⁵, and eliminate the necessity to simulate large fibril systems to achieve their stability. For computational efficiency the simulation system was subject to spherical boundary condition with the radius R_s = 90Åand the force constant k_s = 10kcal/(molŲ).

The concentration ratio of Aβ peptides to ligands (i.e., the ratio of the numbers of peptides and ligands) is 1:10, which is only slightly higher than that used experimentally^16,17. (It is useful to point out that the experiments testing aggregation inhibition by organofluorine ligands showed that in order to reduce fibril load > 90% the ligand:Aβ ratio must be ≳ 10⁴⁶). The simulation system probing the binding of ibuprofen to Aβ fibril was introduced by us earlier³⁵.

Replica exchange simulations

Conformational sampling of Aβ fibril coincubated with naproxen was performed using replica exchange molecular dynamics (REMD)⁴⁷. In total, 24 replicas were distributed linearly in the temperature range from 330 to 560K with an increment of 10K. Small temperature increment provides significant overlap of energy distributions from neighboring replicas. The exchanges were attempted every 20 ps between all neighboring replicas with the average acceptance rate of 33%. Between replica exchanges the system was evolved using NVT underdamped Langevin dynamics with the damping coefficient γ = 0.15ps⁻¹ and the integration step of 2fs. Three REMD trajectories were produced resulting in a cumulative simulation time of 14.4 µs. To determine the REMD equilibration interval we monitored the system effective energy E_eff, which includes the potential and solvation energies. As a result the initial parts of REMD trajectories of the lengths up to 20 ns were excluded. Consequently, the cumulative equilibrium simulation time was reduced to ≈ 13µs. The REMD trajectories were started with random distribution of ligands in the sphere, in which they were all unbound. The convergence of REMD is discussed in Supplemental Materials. REMD simulations of Aβ fibril and ibuprofen are described elsewhere³⁵.

Computation of structural probes

The interactions between Aβ peptides and ligands and between ligands were probed by computing the numbers of contacts and hydrogen bonds (HBs), non-bonded potential energy, and accessible surface area (ASA). To assign a contact formed by naproxen, we distinguished three structural groups in the ligand (Fig. 1c): hydrophobic naphthalene ring G1 (C3–C12), hydrophilic methoxy G2 (C1–O2) and carboxylate G3 (C13–C15, O16, O17). If the distance between the centers of mass of side chain and one of the groups is less than 6.5 Å, a contact is formed. A contact between naproxen molecules occurs, if any of the G1–G3 centers of mass from different molecules are within the cut-off distance. Ligand is bound, if it forms at least one contact with Aβ side chain. Similar contact definitions were used for ibuprofen (Fig. 1c)³⁵.

The HBs between hydrophilic groups G2 or G3 in naproxen (G3 in ibuprofen) and peptide backbone NH groups were assigned according to Kabsch and Sander⁴⁸. Due to structural reasons there is an ambiguity in selecting the atoms involved in HB formed by the naproxen G2 (Fig. 1c). We checked that selecting the C1 atom in the Kabsch and Sander definition results in the HB assignments quantitatively consistent with those obtained using the definition based on HB geometry⁴⁹.

The non-bonded potential energy of interactions between the ligands and between the ligands and the fibril were computed using CHARMM INTERACTION functionality. The accessible surface areas of naproxen and ibuprofen molecules were obtained using the algorithm of Lee and Richards⁵⁰. The change in ASA due to binding is defined as the difference between the ASAs of free and bound ligands. Throughout the paper angular brackets < ‥ > imply thermodynamic averages. Unless stated otherwise, all quantities related to ligands represent the averages over all ligands. The distributions of states produced by REMD were analyzed using multiple histogram method⁵¹. Thermodynamic quantities were computed at the temperature 360K, at which Aβ peptides lock into fibril-like state during fibril growth as reported earlier^24,39.

Testing force field parameterization of naproxen

Using ab initio methods and NMR technique, Bednarek et al have performed the conformational analysis of naproxen⁵². In particular, they obtained the distributions of two dihedral angles ϕ and χ (Fig. 1c) that allowed us to test the parameterization of naproxen in CHARMM19 force field. The testing results are reported in Supplemental Materials. Testing of ibuprofen parameterization can be found in our earlier study³⁵.

Results

Binding of naproxen to Aβ fibrils

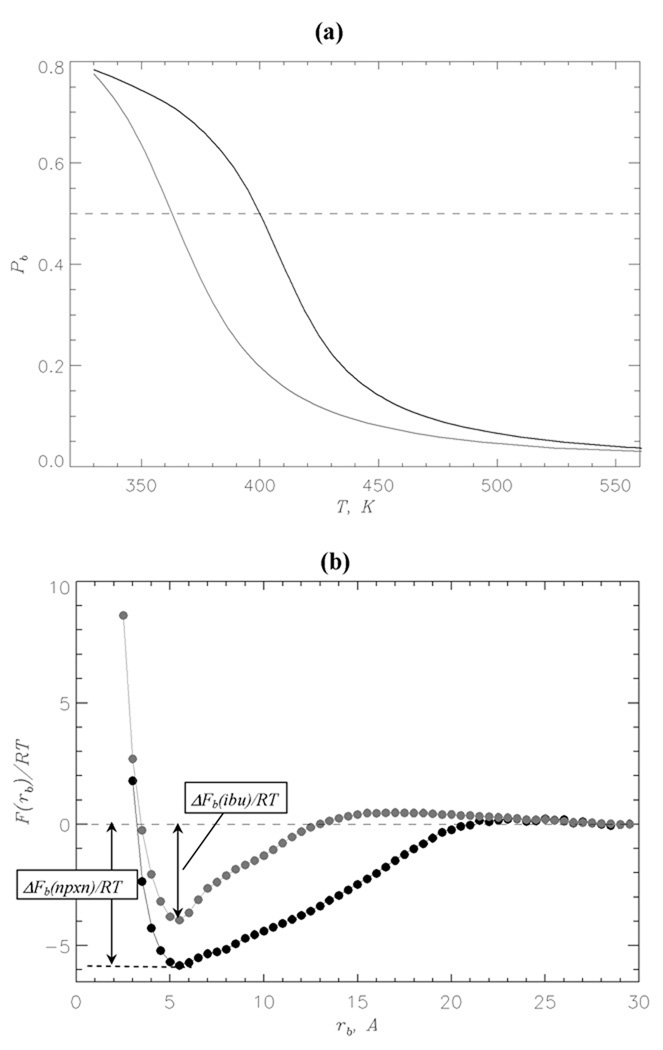
Using REMD we obtained the temperature dependence of the binding probability P_b(T) for naproxen (Fig. 2a). The midpoint of P_b(T), which occurs at 398K, is identified with the binding temperature T_b, i.e., bound naproxen states are stable (P_b > 0.5) at T < T_b. At the temperature of 360K P_b = 0.72 that implies that the average number of bound naproxen molecules is < L >= 28.8. For comparison, the binding temperature of ibuprofen is 362K and the number of bound molecules at 360K is < L >= 21.2³⁵. Therefore, according to Fig. 2a naproxen binds to Aβ fibril with higher affinity than ibuprofen.

Fig. 2.

(a) Probability P_b(T) of binding of naproxen (in black) and ibuprofen (in grey) molecules to Aβ fibril as a function of temperature. Dashed line marks P_b = 0.5. (b) Free energy of ligand molecule F(r_b) as a function of the distance r_b between ligand and the surface of Aβ fibril at 360K: naproxen (in black), ibuprofen (in grey). The binding free energy is defined as ΔF_b = F_b – F(r_b = 30Å), where F_b is obtained by integrating over the states with F(r_b) ≤ F_min + 1.0RT and F_min is the free energy minimum at small r_b. The free energies at r_b ≥ 30Å are set to zero. The figure shows that naproxen binds with higher affinity to the fibril than ibuprofen.

To further investigate naproxen interactions with the fibril we computed the free energy of ligand F(r_b) as a function of the distance r_b between ligand and the fibril surface (Fig. 2b). The plot of F(r_b) reveals a single minimum at r_b,0 ≈ 5.5Å associated with bound naproxen molecules. The binding free energy ΔF_b(nprx) is ≈ −7.6RT. The free energy minimum associated with bound ibuprofen ligands is more shallow than for naproxen and its binding free energy ΔF_b(ibu) ≈ −5.2RT (Fig. 2b). Consistent with the computations of binding temperatures the bound naproxen states are more stable than those of ibuprofen by ΔΔF_b = ΔF_b(nprx) – ΔF_b(ibu) ≈ −2.4RT.

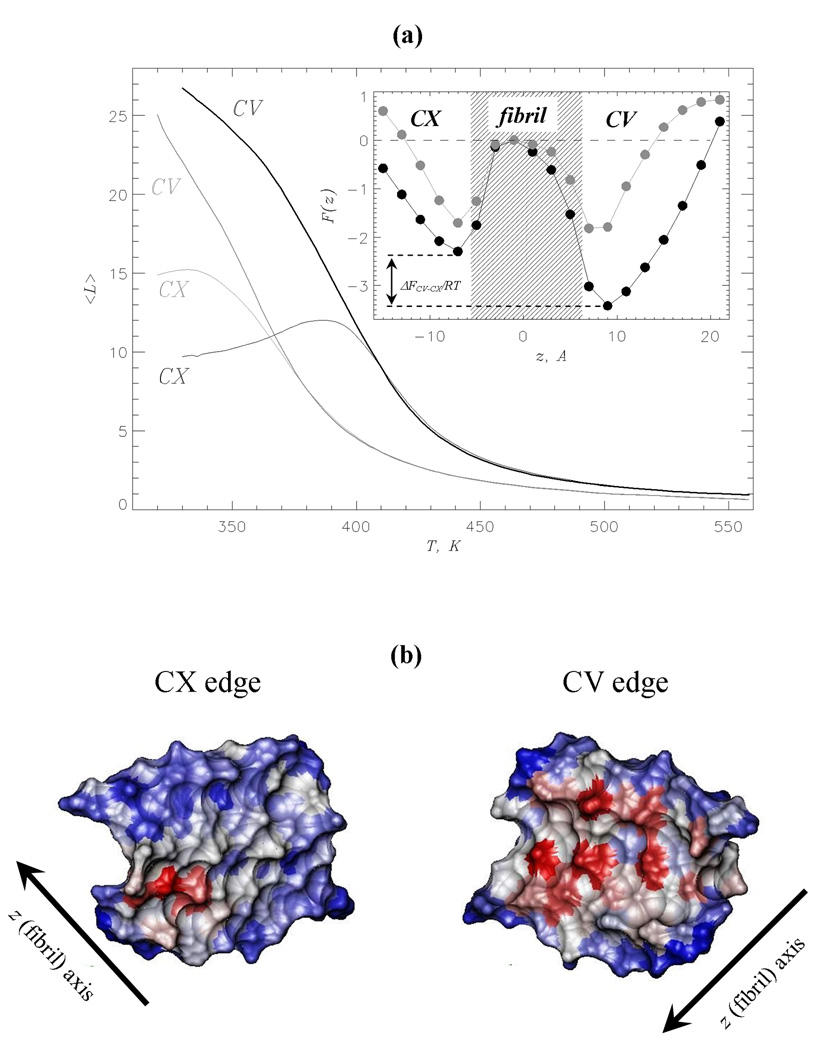
The Aβ fibril structure resolved using solid-state NMR measurements⁵ has two distinct edges, the concave (CV) with the groove and the convex (CX) with the protrusion (Fig. 1b). It is conceivable that the edges have different affinities for ligand binding. To check this possibility Fig. 3a displays the number of naproxen molecules bound to the CV and CX edges, < L_CV (T) > and < L_CX(T) >, as a function of temperature. It shows that binding of naproxen to both edges is strikingly different. Although < L_CV (T) > monotonically grows with the decrease in temperature, < L_CX(T) > reaches maximum at ≈ 390K and declines at lower temperatures. As a result at 360K the numbers of ligands bound to the CV and CX differ more than two-fold (< L_CV >≈ 22.5 vs < L_CX >≈ 10.6). For comparison, the edge affinities with respect to ibuprofen are barely distinguishable at 360K (< L_CV >≈ 13.5 and < L_CX >≈ 12.1) and only at 330K the preference for the CV binding emerges (< L_CV >≈ 22.1 and < L_CX >≈ 15.2³⁵). However, even at 330K the ibuprofen ratio < L_CV > / < L_CX > is only 1.5 compared to 2.1 for naproxen at 360K. Hence, naproxen has stronger affinity for the CV binding than ibuprofen.

Fig. 3.

(a) The numbers of ligand molecules < L > bound to the CV (thick lines) and CX (thin lines) edges vs temperature. The data for naproxen and ibuprofen³⁵ are shown (including the inset) in black and grey, respectively. Inset: The free energy of a ligand F(z) along the fibril axis z at 360K. Two free energy minima reflect ligand binding to the CV and CX fibril edges. The shaded area approximately marks the maximum extent of fibril fragment. Free energy at the fibril midpoint is set to zero. The free energy gap between the CV and CX bound states, ΔF_CV–CX = F_CV – F_CX, is computed by integrating over the states in the CV and CX minima (using the same procedure as in Fig. 2b). This figure shows that at 360K naproxen binding to CV is thermodynamically preferred, whereas ibuprofen binding to the edges is marginally different. (b) The surfaces of the CV and CX fibril edges accessible to naproxen upon binding at 360K. The surface of residue i in the peptide k is color-coded according to the number of side chain contacts < C_l(i; k) >, which it forms with naproxen: red, grey and blue correspond to large, medium, and small < C_l(i; k) > values, respectively. Accessible surface areas are computed using the probe radius of 3.3Å (naproxen radius of gyration) and visualized using VMD⁵⁹.

We also probed the formation of contacts between ligands and fibril side chains and of HBs between the ligands and the fibril backbone (see Materials and Methods). Naproxen molecules form, on an average, < C_CV >≈ 69.3 contacts with the CV edge and < C_CX >≈ 31.5 contacts with the CX. The numbers of HBs formed between naproxen and the fibril are ≈ 5.9 (CV) and ≈ 4.1 (CX). Therefore, the number of side chain contacts exceeds that of HBs about 10 fold on both fibril edges. For comparison, there are 41.4 and 37.1 contacts linking ibuprofen ligands to the fibril on the CV and CX edges at 360K, respectively. Because the corresponding numbers of HBs are 2.8 and 4.3, the ratio of the side chain contacts to HBs for ibuprofen is also ≳ 10. Thus, both ligands bind to the fibril by largely utilizing interactions with the peptide side chains rather than HBs.

Using the data above it is straightforward to compute the number of ligand-fibril contacts per one naproxen or ibuprofen molecule at 360K. A naproxen bound to the CV and CX edges forms, on an average, 3.1 and 3.0 contacts with the fibril. The respective values for ibuprofen are 3.1 on both edges. Because the numbers of interactions with the fibril per one naproxen or ibuprofen molecule are almost the same, the differences in binding affinities cannot be explained by ligand-fibril interactions (see Discussion).

Further evidence supporting the difference in binding affinities between the edges is provided by the ligand free energy F(z) computed along the fibril axis z (Fig. 1b). The inset to Fig. 3a shows that F(z) for naproxen and ibuprofen display two minima associated with the binding to the CV and CX edges. However, the naproxen free energy minima are more pronounced and of unequal depth. Indeed, the free energy gap between the CV and CX bound states, ΔF_CV–CX, is ≈ −1.1RT for naproxen, but is ≈ 0 for ibuprofen. To estimate the probabilities of binding to the edges we assume that the ligand is located on the CX edge if −15Å < z < −3Å, on the CV edge if 3Å < z < 17Å, or on the fibril side if −3Å< z < 3Å (Fig. 3a). Then the naproxen probabilities of occurrence on the CV and CX are P_CV ≈ 0.69 and P_CX ≈ 0.21, whereas for ibuprofen the difference between P_CV and P_CX is smaller (0.37 and 0.26). Only at 330K a clear preference for ibuprofen interaction with the CV edge is observed (0.57 vs 0.29, respectively³⁵). The probability for finding naproxen on the fibril side is negligibly small (P_s ≈ 0.01). Similar results were obtained for ibuprofen (P_s ≈ 0.04 at 360K).

Finally, it is useful to determine the distribution of bound naproxen ligands on the surface of Aβ fibril. Fig. 3b displays the fibril surface accessible to naproxen, which is colored according to the number of contacts each amino acid forms with the ligands. It is seen that the amino acids having large number of interactions with the ligands are located in the CV groove. To identify the amino acids constituting the naproxen binding sites, we use the following procedure³⁵. An amino acid i is included in the CV binding site, if the number of contacts with naproxen < C_l(i; k) > is no less than 70% of the maximum value on the CV edge, i.e., < C_l(i; k) >≥ 0.7 max_i,k{< C_l(i; k) >}, where k =F3,F4 (Fig. 1b). Then the naproxen binding site includes Gln15(F3), Gly29(F3), Ile31(F3), Leu34(F3), Met35(F3), Gly37(F3), Val39(F3), Glu11(F4), Gln15(F4), Leu17(F4), Phe19(F4), and Asp23(F4). The same procedure applied to the CX edge identifies four amino acids as the CX binding site - Asp23(F1), Ser26(F1), Ala30(F1), and Ile32(F1) (Fig. 3b). Interestingly, out of 16 amino acids involved in binding half are hydrophobic and 11 are also implicated in ibuprofen binding at 330K³⁵. Therefore, hydrophobic and hydrophilic residues equally contribute to naproxen binding and there is a considerable overlap between the naproxen and ibuprofen binding sites. If so, naproxen binding appears to be mainly driven by fibril surface geometry and ligand-ligand interactions rather than by specific physicochemical properties of residues (see below).

Fibril surface geometry determines binding

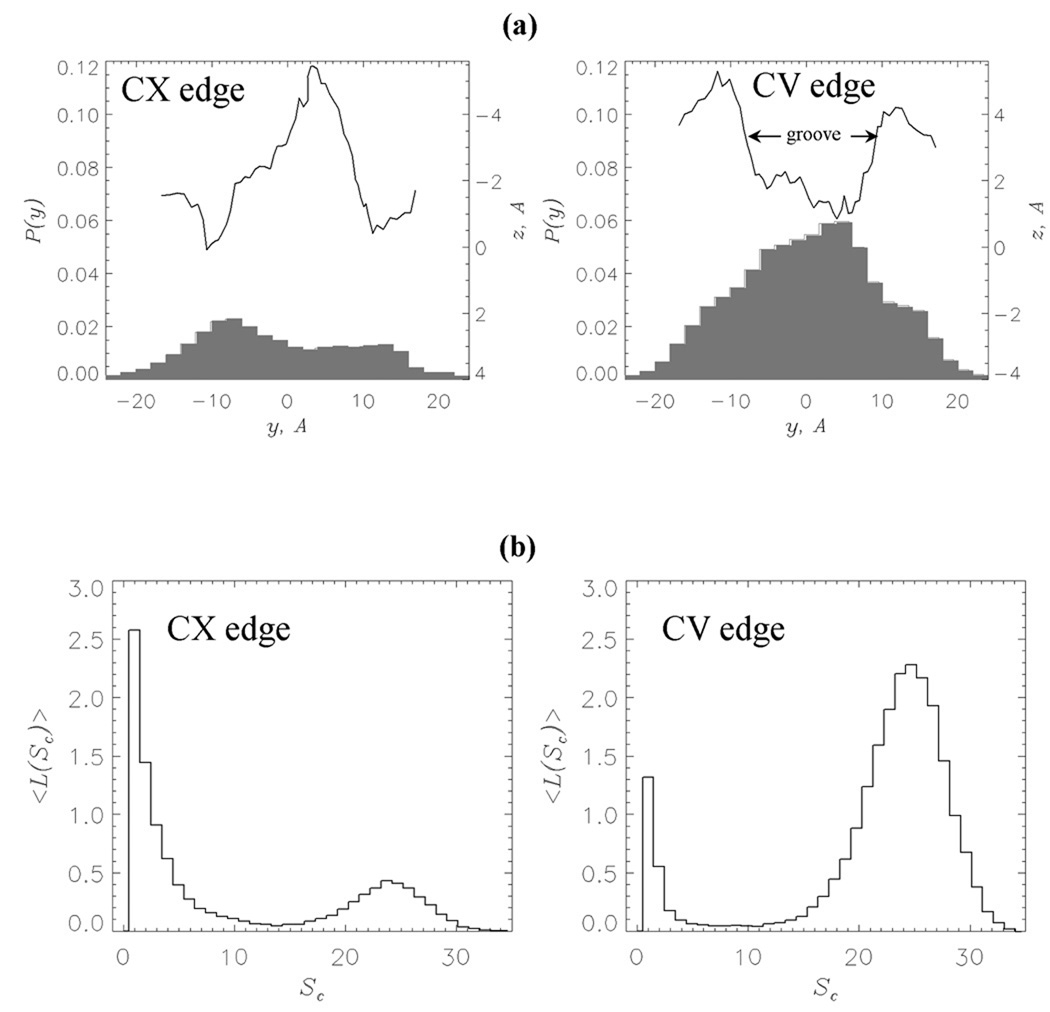
The results of REMD computations of naproxen binding suggest highly uneven distribution of ligands on the fibril surface. Specifically, most of naproxen molecules are localized on the CV edge, whereas the CX edge and the fibril sides have significantly lower affinity. To rationalize these observations, we plot in Fig. 4a the probability distributions P(y) of naproxen molecules along the y axis perpendicular to the fibril axis (Fig. 1b). On the CV edge P_CV(y) shows a pronounced maximum, whereas the probability P_CX(y) on the CX edge is low. More importantly, according to Fig. 4a the maximum in P_CV(y) on the CV edge exactly coincides with the location of the groove. In contrast, the protrusion on the CX edge matches the minimum in P_CX(y). These data indicate that naproxen ligands tend to localize in the deep indentations on the fibril surface. Similar results have been obtained in our study of ibuprofen binding³⁵.

Fig. 4.

(a) Probabilities of occurrence of naproxen molecule center of mass, P(y) (in grey), along the axis y perpendicular to the fibril axis z. The left and right panels are computed for z < 0 (CX edge) and z > 0 (CV edge), respectively (Fig. 1b). Smoothed projections of the edge surfaces on the (y, z) plane are in black. The edge surface is represented by the side chain centers of mass. (b) Distributions of the numbers of bound ligands < L(S_c) > with respect to cluster size S_c. Large peak in < L(S_c) > at S_c = 25 implicates the formation of large clusters of bound ligands localized in the groove on the CV edge (panel (a)). Both panels are obtained at 360K.

In order to establish the factors, which enhance the affinity of the CV edge, we analyzed clusters formed by bound naproxen ligands on the fibril edges. In these computations, a cluster is a set of ligands bound to the fibril edge, which does not form contacts with other bound molecules. The size of a cluster S_c is equal to the number of included ligands. Then binding to a fibril edge can be characterized by the distribution of bound ligands over clusters < L(S_c) >, where < L > is the thermally averaged number of molecules in the cluster of the size S_c. Fig. 4b shows that the distribution < L(S_c) > for the CV edge has two peaks at S_c = 1 and 25. From Fig. 4b we find that the number of naproxen molecules forming large clusters (S_c > 6) is < L_CV,l >≈ 20.2 = ϕ_CV < L_CV >, where < L_CV >≈ 22.5 is the number of ligands bound to the CV and ϕ_CV ≈ 0.90. Binding of naproxen to the CX edge results in strikingly different distribution < L(S_c) >, which, although still bimodal, is strongly biased toward small S_c. For the CX, < L_CX,l >≈ 4.4 = ϕ_CX < L_CX >, where < L_CX >= 10.6 and ϕ_CX ≈ 0.42. Therefore, about 90% of naproxen molecules bound to the CV form large clusters and according to Fig. 4a reside in the edge groove. In contrast, most (58%) of the ligands bound to the CX edge, which does not have a groove, form small or no clusters. At 360K the distribution of ibuprofen clusters on both edges is unimodal and qualitatively different from that computed for naproxen (Supplemental Material). For example, the fractions of ligands forming large clusters ϕ_CV= 0.43 and ϕ_CX = 0.25. Only at 330K the distributions < L(S_c) > for bound ibuprofen ligands become bimodal with ϕ_CV = 0.81 and ϕ_CX= 0.40 and resemble those for naproxen³⁵.

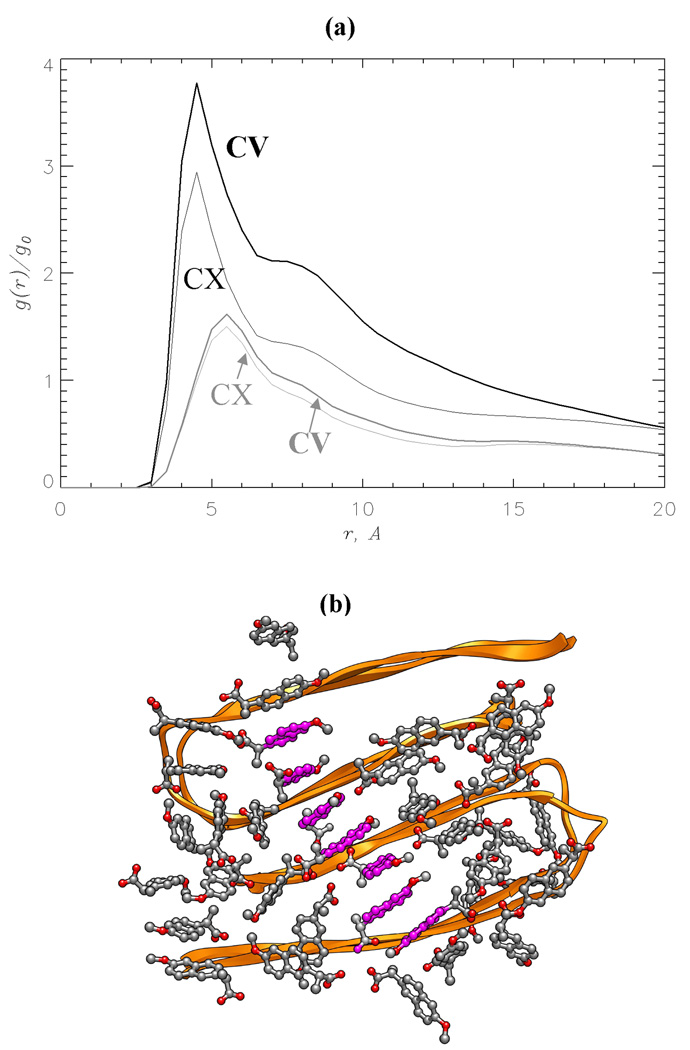
The distribution of naproxen clusters on the CV edge suggests that ligand-ligand interactions are an important factor in binding. To substantiate this conjecture we plot the radial distribution function for naproxen number density, g(r), in Fig. 5a. This function measures the local number density of ligands at the distance r from a given ligand. For naproxen g(r) peaks at 4.5Åand exceeds the bulk value g₀ four (CV edge) or three times (CX edge). In contrast, the radial distribution functions g(r) for ibuprofen have a maximum at 5.5Å, which is merely 1.5 times larger than g₀. Furthermore, ibuprofen g(r) computed for the CV and CX edges are very similar.

Fig. 5.

(a) The radial distribution functions for ligand number density, g(r): naproxen (in black), ibuprofen (in grey). The distance r is measured from the ligand center of mass. The function g(r) is normalized with the bulk value g₀. The plot reveals strong ligand-ligand interactions formed by naproxen as compared to ibuprofen. (b) The snapshot of naproxen ligands bound to Aβ fibril. Interligand interactions result in parallel alignment of naphthalene rings (shown in magenta) of the bound molecules. Both panels are obtained at 360K.

Discussion

Mechanism of ligand binding to Aβ fibril

Using REMD and atomistic implicit solvent model we have studied binding of naproxen and ibuprofen to Aβ fibril. We found that the naproxen binding temperature is almost 40K higher and its binding free energy is 2.4RT lower than of ibuprofen (Fig. 2). Our data also indicate that bound naproxen molecules are distributed highly unevenly on the fibril surface. At 360K naproxen largely binds to the concave CV edge as the ratio of the numbers of ligands bound to the CV and CX edges is < L_CV > / < L_CX >= 2.1 (Fig. 3a). At the same temperature ibuprofen has almost equal propensity for CV and CX binding (< L_CV > / < L_CX >= 1.1) and only at 330K a clear preference to bind to the CV edge emerges (< L_CV > / < L_CX >= 1.5³⁵). Consistent with these data, the binding free energy gap between the CV and CX edges is ΔF_CV–CX ≈ −1.1RT for naproxen, but it vanishes for ibuprofen (inset to Fig. 3a). This figure also suggests that the binding to the fibril sides is negligible.

What are the factors that determine the higher binding affinity of naproxen compared to ibuprofen and also selective binding of ligands to the CV edge? The probability distribution of ligands on the edges P(y) (Fig. 4a) strongly suggests that naproxen ligands concentrate in the deep groove on the CV edge and avoid protrusions on the CX edge. Furthermore, naproxen molecules confined to the CV groove exhibit cooperative binding, because about 90% of them form large clusters (ϕ_CX = 0.90, Fig. 4b). Interestingly, such propensity is muted for the ligands bound to the CX edge (ϕ_CX = 0.42). The values of ϕ_CV and ϕ_CX for ibuprofen suggest that this ligand at 360K does not have a strong preference to form large bound clusters (Fig. S3, Supplemental Materials). Consistent with the cluster analysis the radial distribution functions (Fig. 5a) are indicative of stronger naproxen-naproxen interactions compared to those occurring between ibuprofen ligands. Because the numbers of ligand-fibril contacts formed by naproxen and ibuprofen are almost identical and Figs. 4b,5a implicate the importance of ligand-ligand interactions for binding, it is likely that the higher binding propensity of naproxen originates from more favorable ligand-ligand interactions compared to ibuprofen.

To check this inference we analyzed the energetics of naproxen and ibuprofen binding at 360K (Table 1). The energies of naproxen-fibril and naproxen-naproxen interactions (without decomposing them with respect to the edges) are E_n–f ≈ −7.9kcal/mol and E_n–n ≈ −15.4kcal/mol. For comparison, at the same temperature the energies of ibuprofen-fibril and ibuprofen-ibuprofen interactions are E_i–f ≈ −8.3kcal/mol and E_i–i ≈ −5.6kcal/mol. These findings show that ibuprofen molecules form somewhat stronger interactions with the fibril than naproxen, yet have considerably weaker ligand-ligand contacts (an almost threefold difference). Hence, higher binding affinity of naproxen compared to ibuprofen cannot be explained by ligand-fibril interactions, but appears to be due to favorable ligand-ligand contacts. It is likely that a single phenyl ring in ibuprofen forms relatively weak intermolecular interactions compared to those formed between naproxen ligands with naphthalene double rings. This conjecture is checked in the next section.

TABLE I.

Ligand binding energetics

ligand	El–f, kcal/mola	El–l, kcal/molb
naproxen	−7.9	−15.4
ibuprofen	−8.3	−5.6

^aE_l–f is the energy of ligand-fibril interactions. Subscript l = n for naproxen and l = i for ibuprofen.

^bE_l–l is the energy of ligand-ligand interactions.

The analysis of energetics allows us to gain better insight into the difference in binding affinities of the edges (Table 2). Upon binding to the CX edge the average energy of naproxen-fibril interactions is E_n–f(CX) ≈ −9.3kcal/mol. The naproxen-fibril energy computed for the CV edge is E_n–f(CV) ≈ −7.3kcal/mol. At the same time, the energies of ligand-ligand interactions for naproxen bound to the CX and CV edges, E_n–n(CX) and E_n–n(CV), are −11.4 and −16.9kcal/mol, respectively. Therefore, on the CV edge the naproxen-fibril contacts are somewhat weaker, but the naproxen-naproxen interactions are considerably stronger than on the CX. As a result binding to the CV edge is energetically favorable (E(CV) – E(CX) = −3.5kcal/mol, where E(CV) and E(CX) are the potential energies of ligands on the CV and CX). For comparison, at 360K the energies of ibuprofen-fibril interactions are E_i–f(CX) ≈ −8.6kcal/mol and E_i–f (CV) ≈ −8.1kcal/mol. The energies of interactions between ibuprofen molecules bound to the CX and CV edges are E_i–i(CX) ≈ −5.2kcal/mol and E_i–i(CV) ≈ −6.0kcal/mol. Thus, for ibuprofen the difference between the ligand energies on the edges is marginal (E(CV) – E(CX) = −0.3kcal/mol) and only at 330K it becomes considerable (−2.4kcal/mol). Therefore, high affinity of the CV edge is due to strong interligand interactions induced by the confinement of bound ligands to the groove. In Supplemental Materials we report a direct test of the importance of interligand interactions, in which we switch off non-bonded interactions between naproxen molecules.

TABLE II.

Energetics of ligand binding to the CX and CV fibril edges

	CX		CV
ligand	El–f, kcal/mola	El–l, kcal/molb	El–f, kcal/mola	El–l, kcal/molb
naproxen	−9.3	−11.4	−7.3	−16.9
ibuprofen	−8.6	−5.2	−8.1	−6.0

^aE_l–f is the energy of ligand-fibril interactions. Subscript l = n for naproxen and l = i for ibuprofen.

^bE_l–l is the energy of ligand-ligand interactions.

Role of ligand chemical structure in binding

If ligand-ligand interactions are important for binding, then it is interesting to evaluate the contributions from different ligand groups (Table 3). The energy of interligand interactions contributed by the naproxen group G1 is E_n–n(CV,G1) = −9.9kcal/mol or 59% of total ligand-ligand energy E_n–n(CV). The energies attributed to G2 and G3 are −2.7 and −5.4kcal/mol or 16 and 32% of E_n–n(CV). (In these computations, G2 includes three atoms, C1, O2, and, C3.) Interligand interactions formed by the groups G1, G2, and G3 are mostly van-der-Waals interactions, whereas the contribution of electrostatic terms is ≈1% of the total ligand-ligand energy E_n–n(CV). Similar contributions of the G1–G3 are obtained for binding to the CX edge. The analysis of binding energetics is consistent with the changes in accessible surface areas (ASA) of the ligand groups. The average changes in ASA, ΔASA, for the three naproxen groups occurring upon binding to the fibril, are ΔASA(G1) = 138Å, ΔASA(G2) = 64Å, and ΔASA(G3) = 121Å. Therefore, the G1 surface area buried upon binding is the largest followed by the G3.

TABLE III.

Contributions of ligand structural groups to binding

	G1		G2		G3
ligand	El–l, kcal/mola	ΔASA, Å2b	El–l, kcal/mola	ΔASA, Å2b	El–l, kcal/mola	ΔASA, Å2b
naproxen	−9.9	138	−2.7	64	−5.4	121
ibuprofen	−2.2	61	−1.3	91	−2.5	95

^aE_l–l is the energy of ligand-ligand interactions. Subscript l = n for naproxen and l = i for ibuprofen.

^bΔASA is the change in the accessible surface area upon binding.

Similar analysis performed for ibuprofen indicates that the interligand interactions contributed by the groups G1, G2, and G3 are E_i–i(CV, G1) = −2.2kcal/mol, E_i–i(CV, G2) = −1.3kcal/mol and E_i–i(CV, G3) = −2.5kcal/mol. These energies constitute 37, 22 and 42% of the average energy of ligand-ligand interactions of the CV edge E_i–i(CV). As for naproxen G1–G3 make similar energetic contributions when bound on the CX edge. The changes in ASA for these groups due to binding are ΔASA(G1) = 61Å, ΔASA(G2) = 91Å, and ΔASA(G3) = 95Å. Therefore, the energetics and changes in ASA are in agreement that G3 makes the largest contribution to binding. This results is consistent with our previous study³⁵. More importantly, this analysis suggests that binding of naproxen and ibuprofen to the fibril is controlled by different structural groups. For naproxen, the naphthalene ring appears to make dominant contribution to ligand-ligand interactions and binding. In contrast, it is the carboxylate G3 group in ibuprofen, which is the most important for binding. The importance of naphthalene ring for binding has implications for Congo Red (CR) and thioflavin T (ThT) dyes, which are commonly used for fibril detection in the experiments and have conjugated rings. Based on our data one may suggest that the affinity of CR and ThT to fibrils is derived, at least in part, from the interactions between the conjugated rings in bound ligands.

It is possible that interactions between bound naproxen molecules order their orientation. To check this we computed the probability distribution P(cos(ϕ)) of the angles ϕ between the naphthalene rings from interacting naproxen molecules bound to the fibril (Supplemental Materials, Fig. S5). The distribution shows that the values of ϕ ≈ 0° or 180° occur about twice more frequent than other ϕ values. Therefore, parallel orientations of naproxen molecules (more precisely, of their naphthalene rings) is preferred for bound ligands (Fig. 5b). This observation is consistent with the dominant contribution of the group G1 to the naproxen-naproxen interactions. The probability distribution P(cos(ϕ)) computed for bound ibuprofen molecules reveals very weak preference for parallel orientation of ligands (data not shown) that is in line with weak ibuprofen-ibuprofen interactions.

In summary, the binding mechanisms of naproxen and ibuprofen are similar in that both ligands bind with higher affinity to the CV edge rather than to the CX. The key factor favoring binding to the CV is the occurrence of the groove, which induces ligand-ligand interactions onto the molecules confined to its volume. However, the difference in naproxen and ibuprofen binding can be traced to the difference in their chemical structure. Because ibuprofen fails to make as strong ligand-ligand interactions as naproxen, the binding affinity of ibuprofen is compromised compared to naproxen.

Comparison with experiments and simulations

Barrio and coworkers have investigated the binding of ibuprofen and naproxen to Aβ fibrils¹⁶. Because these ligands share binding sites with the molecular imaging probe ¹⁸FFDDNP⁵³, the competition curves, which probe the replacement of ¹⁸FFDDNP with naproxen or ibuprofen, can be used to measure their binding. According to the experiments half of probe molecules is replaced when the concentration of naproxen reaches 5.7 nM. The midpoints of ibuprofen competition curves occur at the concentrations at least twice larger. These findings indicate that naproxen binding affinity is higher than of ibuprofen in agreement with our data.

Common binding sites for the probe ¹⁸FFDDNP and ibuprofen or naproxen suggest several other important implications. First, it was reported that the number of probe binding sites is from 3.5 to 7.1 per 10,000 fibril peptides⁵³. Such small number of binding sites implies that ligands are bound to very few specific locations on the fibril surface that are likely to be associated with structural features rather than with the Aβ sequence. These conclusions drawn from experimental observations are in accord with our results showing that the fibril edges are the primary binding locations. Second, according to the fluorescence data bound ¹⁸FFDDNP probes tend to localize in the hydrophobic clefts on the fibril surface, but are still partially hydrated. This binding scenario is consistent with our findings identifying the groove on the CV edge as a primary binding location for naproxen and ibuprofen. Furthermore, according to our accessible surface area computations bound ligands are indeed partially exposed to water. It is also worth noting that the groove is formed by the indentation of the second β strand in Aβ sequence (29–39), which is exclusively composed of hydrophobic amino acids (Fig. 1a,b). Similar to naproxen and ibuprofen localization in the fibril hydrophobic grooves was also observed computationally for thioflavin T dye and its neutral analog BTA-1⁵⁴.

Several experimental studies have investigated the anti-aggregation effect of naproxen^16–18. It was found that naproxen can reduce the accumulation of Aβ fibrils or inhibit their elongation¹⁷. Because amyloid fibrils apparently grow via monomer addition to the edges^55–57, the arrest of their extension implicates binding of ligands to the fibril edges as it occurs in our simulations. The study of Thomas et al probed the impact of several NSAID ligands on the aggregation of Aβ peptide fragment, Aβ_25–35¹⁸. They showed that coincubation of ibuprofen and naproxen with the fibrils results in two- and six fold reduction in the β structure content, respectively. This observation support our findings, because it points to higher binding affinity of naproxen compared to ibuprofen.

In our previous simulations of Aβ fibril elongation we showed that the CV edge has about 10-fold higher affinity for binding incoming Aβ peptides than the CX edge^24,39. The simulations reported here suggest that naproxen also tends to bind to the CV edge and localize within the CV groove. If so, naproxen and Aβ peptides should directly compete for the same binding location and, consequently, naproxen is expected to interfere with the deposition of incoming Aβ peptides. This proposed mechanism of fibril growth inhibition is similar to the one observed earlier in our simulations of the growth of Aβ fibril coincubated with ibuprofen³⁶ and is also consistent with experimental results¹⁷.

An interesting question pertains to the relative anti-aggregation action and binding affinities of naproxen and ibuprofen. Experiments suggest that compared to ibuprofen naproxen has stronger binding affinity, but apparently weaker anti-aggregation effect^16,17. One potential explanation to this puzzle is the impact of ligands on the secondary structure of Aβ monomer. We have previously showed that ibuprofen binding causes minor changes in Aβ monomer conformational ensemble³⁵. However, the impact of naproxen binding can be different. Finally, it is imperative to mention two other issues. First, it will be important in the future to explore binding of NSAID ligands to other amyloid fibrils to establish universality of the binding mechanisms reported in this work. The second is the impact of NSAID on the stability of Aβ oligomers. We showed previously that ibuprofen does not form large clusters upon binding to Aβ monomers³⁵. If the same holds true for the oligomers, the mechanism of binding to relatively disordered (compared to the fibrils) Aβ oligomers may be quite different from the one observed for the fibrils.

Conclusions

Using REMD and atomistic implicit solvent model we have studied the mechanisms of binding of naproxen and ibuprofen to the Aβ fibril derived from solid-state NMR measurements. The binding temperature of naproxen is found to be almost 40K higher than of ibuprofen implicating higher binding affinity of naproxen. The key factor, which enhances naproxen binding, is strong interactions between ligands bound to the surface of the fibril. The naphthalene ring in naproxen appears to provide a dominant contribution to ligand-ligand interactions. Importantly, ligand-fibril interactions alone cannot explain differences in the binding affinities of naproxen and ibuprofen. The concave fibril edge with the groove is identified as the primary binding location of both ligands. We show that confinement of the ligands to the groove facilitates ligand-ligand interactions, thus lowering the energy of the ligands bound to the concave edge. Our simulations provide microscopic rationale for the differing binding affinities of naproxen and ibuprofen observed experimentally.