Image-based modeling of lung structure and function

Abstract

Current state-of-the-art in image-based modeling allows derivation of patient-specific models of the lung, lobes, airways, and pulmonary vascular trees. The application of traditional engineering analyses of fluid and structural mechanics to image-based subject-specific models has the potential to provide new insight into structure-function relationships in the individual via functional interpretation that complements imaging and experimental studies. Three major issues that are encountered in studies of air flow through the bronchial airways are the representation of airway geometry, the imposition of physiological boundary conditions, and the treatment of turbulence. Here we review some efforts to resolve each of these issues, with particular focus on image-based models that have been developed to simulate air flow from the mouth to the terminal bronchiole, and subjected to physiologically meaningful boundary conditions via image registration and soft tissue mechanics models.

INTRODUCTION

The lung undergoes large non-linear deformations during normal breathing. It couples several distinct subsystems, multiple scales of interest, and multiple functions of interest. The lung is typified by heterogeneity in ventilation, perfusion, and structure. While this makes this organ system more difficult to study experimentally and/or via imaging than muscle or bone, it presents exciting challenges for research into the development and application of robust and validated computational models of the lung. The application of traditional engineering analyses of fluid and structural mechanics to image-based subject-specific models has the potential to provide new insight into structure-function relationships in the individual.

One motivation for understanding the characteristics of flow within the airways is because air flow can theoretically induce physiologically significant shear on the bronchial epithelium (1) which could be important in mechanotransduction and remodeling of the airway wall when flow is abnormal. A further motivation is that the characteristics of airway flow determine particle (either noxious or therapeutic) transport and its deposition. The lungs are increasingly recognized as a potential route for delivery of systemic drugs such as insulin (2), because this avoids the hepatic metabolic pathway and may better simulate the physiological response to a food bolus. Penetration and deposition of particles within the airways depends on airway size and branching patterns, which vary between species (3) and with age. Variation in individual airway geometry therefore makes subject-specific models essential for the study of pulmonary air flow and drug delivery. Furthermore, it has been demonstrated that a strong interaction exists between lung geometry and gas properties (4, 5), which has major implications in determining gas delivery to and clearance from the lung periphery during ventilation imaging via x-ray computed tomography (CT) using xenon gas (6–8) as a contrast agent, or magnetic resonance imaging (MRI) using hyperpolarized helium gas (9–12). The ability to predict air flow and particle deposition on a subject-specific basis is therefore necessary for understanding the correlation between structure and function, for assessing individual differences in vulnerability to airborne pollutants, and to provide insights into inter-subject differences in regional lung function and underlying mechanisms of pathologic developments.

Image-based models of the lung encompass multiple spatial scales of interest: from the lung itself (and its sub-division into lobes and sub-lobar segments), to the large airways and blood vessels, and at the smallest imageable scale the alveoli and meshwork of capillaries that cover them (13, 14). Insight into structure-function relationships at these various scales of interest is enhanced by image-based models that attempt to faithfully account for structure, and that predict function based on physical laws. Image-based models of the lung have been used – amongst other purposes - to study phenomena associated with flow characteristics in the largest airways (15, 16) and in the alveolated airways (17), blood flow in the largest pulmonary vessels (18), and perfusion of the whole lung (19), as well as soft tissue deformation (20). At the alveolar level recent imaging studies are paving the way towards new models of alveolar structure that will provide insight into tissue mechanics (21–25). In addition, four-dimensional CT has also been used to simulate lung tissue motion with aims to account for respiratory motion in radiation therapy of thoracic tumors (26, 27). However, in those studies, material properties of the lung parenchymal (including tumors) were assumed homogeneous, which may limit the accuracy of the models. The goal of these studies and others is to provide a functional interpretation that complements imaging and experimental studies.

Computational or mathematical models solve equations to predict or study function. Certain classes of model may consist of a few relatively simple equations that can be solved analytically. Simulating turbulent fluid flow and pressure necessitates solving the Navier-Stokes and mass continuity equations. These are nonlinear partial differential equations that cannot be solved analytically in their generalized form. Solving these complex equations requires approximations to cope with the complexity of turbulence (this will be discussed in more detail in a later section), the use of numerical methods and parallel computing to obtain simulation results within a reasonable timeframe, and methods for defining the shape and discretization of a domain of interest in which the equations are solved. This field of research is termed `computational fluid dynamics' (CFD). CFD analysis is well established in many areas of engineering and design. Its use in physiology is considerably more difficult because biological structures are typically deformable and complex in shape. CFD is now becoming a viable tool for simulation of airflow and particle deposition in the human respiratory tract and has been pursued by a number of research groups. Three major issues encountered in airway CFD studies are: 1) the representation of airway geometry, 2) the imposition of physiological boundary conditions, and 3) the treatment of turbulence. Approaches to resolve each of these issues will be described in the following sections. A partial list of earlier CFD studies is given by Robinson et al. (28), summarizing the computational packages used, parameters tested, and success in predicting experimental data. Additionally, to the best of our knowledge, four-dimensional CT has not been applied for CFD studies.

Models that simulate air transport are usually distinct from those that consider ventilation distribution. That is, the characteristics of the local flow in a small number of image-based airways or an idealized model can be studied in detail without knowledge of where within the remainder of the vast branching structure the flow will distribute. In the following sections we will explain how these two types of model can be brought together into a single coupled model.

IMAGE-BASED MODELS OF THE AIRWAY TREE FOR CFD ANALYSIS OF AIR FLOW

The conducting airways in the mammalian lung comprise an extensive asymmetric branching structure. The complexity of the airway tree means that all computational studies of function in the conducting airways rely on at least some simplifications of the airway geometry due to constraints on computer memory and computing time. The airway tree can be simplified by assuming that it has symmetry (29) or regular asymmetry of branching (30) and/or by modeling it as a one-dimensional (1D) anatomically-based structure and integrating the governing equations for function over the (assumed) circular cross-section of the airways (31–33), or by only simulating within a subset of the tree in three-dimensional (3D) space (34, 35). Each of these simplifications can be advantageous computationally, reducing the model system to a manageable size or to the point that equations can be solved analytically. However the same simplifications can also render the models inappropriate depending on the problem of interest. For example, a single path symmetric model cannot be used to study variability of airflow delivery, and a 3D model of only a small subset of airways cannot accurately represent the pressure or flow at each of its inlet and outlet surfaces.

Imaging has previously been exploited to create anatomically-structured models of the airway tree in two main ways: 1) by conforming the model geometry to surface data of the airways that are segmented from imaging (typically CT for its quality of anatomical resolution) (15, 16, 36, 37), and 2) by tracing the centerlines of the airways to define a `one-dimensional' (1D) tree (32, 38). The first type of model will be considered here in the context of simulating fluid (air) transport via CFD. The second type of model will be introduced, and also discussed in a later section when we consider how to link models of the largest image-based airways to the deformation of the lung tissue during the breathing cycle.

3D models of the airway tree: the need for image-based geometries

The earliest studies of airway CFD used smooth cylindrical tubes merging in a single bifurcation (39), building to several bifurcations (40–43), and then more recently incorporating imaging-defined airway surface data (4, 16, 36, 37, 44, 45).

Studies based on single and double bifurcation models have been concluded insufficient for analyzing particle transport and deposition in the bronchial airways (34, 46, 47). Furthermore, several studies have demonstrated the importance of anatomically accurate geometry for valid predictions of flow and particle distribution (34, 48). Recognizing the need for a more accurate description of the airway bifurcation than is provided by symmetric models, Hegedűs et al. (49) presented a mathematical description of a morphologically realistic airway bifurcation designed for CFD study, and used their method to merge several bifurcations into multiple airway geometries. One important feature of the model was to enforce a smooth transition between the airways, and rounding at the carina. Farkas et al. (50) used the model from Hegedűs et al. (49) to piece together a model from generation 1 to generation 5 in the right upper lobe. They found that aerosol deposition is highly dependent on airway geometry, breathing parameters, and particle characteristics.

Recognizing the importance of subject-specific geometry in the prediction of airflow, several groups have constructed geometric models based on in vivo volumetric imaging (4, 16, 36, 37, 44, 45). These models are typically derived by using commercial or in-house software to create a mesh of connected triangles that covers the surface of anatomical structures (the airways) that have been segmented from volumetric imaging. The triangulated surface is then filled with a connected mesh of tetrahedral elements. Other shaped elements can also be used, but tetrahedra are most frequently employed. The quality of the resulting geometric model – that is, how well it represents the geometry of the airways and how adequate it is for computing the detail of the complex air flow – depends on the image quality, the accuracy of segmentation, the algorithms employed for meshing, and the rigor applied to testing the mesh refinement for convergence of the numerical solution. For example, poor segmentation could lead to an irregular model surface that must be `smoothed'. This can be time-consuming, and it requires subjective user input to decide which structures are real and which are erroneous.

1D models for the entire conducting airway tree and accompanying vascular trees

Anatomically-based models of the airway or pulmonary vascular trees can be derived using measurements from casts (29, 51). While models derived from these types of study have been used extensively in mathematical studies of the lung, the limitation of this approach is that the model is not subject-specific, it is not the same as the in vivo lung, and it does not have a spatial relationship with the lung tissue in which the tree is embedded. Tawhai et al. (32, 38) proposed a volume-filling branching (VFB) method for creating subject-specific imaging-based models of the airway tree that are geometrically consistent with morphometric studies (29, 30, 52, 53). The models are generated `within' the lungs/lobes, therefore the spatial relationship between the airways and the lung tissue is intrinsic. Burrowes et al. (54) later extended the method to the pulmonary arterial and venous trees, including specific definition of the supernumerary vessels that are often overlooked.

The VFB method starts with an image-based definition of the shape of the lobes and/or lungs, and the location of the central airways. The lobes are filled with a uniformly-spaced grid of seed points, where each seed point represents the location of a pulmonary acinus. The location of the seed points is defined at total lung capacity (TLC) when the lung is closest to uniformly expanded. The centerlines of the airways segmented from the imaging act as initial conditions for generation of the model. That is, branch creation is initiated from the terminal points of the initial image-based airways. The algorithm works recursively by associating the seed points with the terminal branch location to which they are closest, calculating the centre of mass of each group of seed points, splitting each group in two using the plane defined by the `parent' branch and the group's center of mass, and then creating branches that point towards the center of mass of the two point sub-sets. A generated branch is declared a terminal bronchiole if it is shorter than a user-defined limit or if it supplies only a single seed point.

This approach of combining in vivo imaging with supplemental airways has the advantage of producing a model that is specific to an imaged subject. The airway trees created with the VFB method have been shown to be morphometrically consistent with measurements from cast (29, 30, 52) and imaging (53) studies. Individual airway trees generated for human and ovine subjects have geometry appropriate to their respective species: the human airways form a relatively symmetric bifurcating tree, whereas the sheep airways branch monopodially and hence are far more asymmetric. The VFB algorithm reproduces these features in response to the shape of the lung or lobe boundary (38). This algorithm is the only method to date that produces full airway or pulmonary vascular tree models within anatomically-realistic lung shapes, and is the only method that has been used to generate non-human airway trees.

The VFB-generated model is a 1D tree with branches distributed in 3D space. This feature becomes important when considering interacting function - such as the effect of changing tissue properties on airway tethering and airway collapse – or for comparison of simulated results with spatially distributed experimental results (19). To use the model for computation, diameters must be defined throughout the entire structure. For the imaging-based (uppermost) airways the diameters are assigned directly from calculating the diameter based on image measurement of airway cross-sectional area in a plane orthogonal to the central axis. The algorithm-based airways can have diameters assigned using Horsfield or Strahler ordering weighted against a ratio of child to parent branch diameter.

The image-based 1D model has been used in various studies of lung function: inert gas mixing (31), airway thermofluid dynamics (33), ventilation distribution (55), oscillation mechanics (56, 57), and the distribution of pulmonary perfusion (19, 58). The advantage of this model for these studies is that it accounts for all airways from the trachea to the terminal bronchioles, it includes realistic heterogeneity in branch dimensions and connectivity, and the spatial connectedness to the parenchymal tissue produces realistic distributions of perfusion and ventilation with respect to the direction of gravity.

The 1D model necessarily requires 1D equations to simulate function. These are derived from generalized (3D) equations by making simplifying assumptions. The 1D equations typically `average' (integrate) the solution over the airway cross-section. Therefore the 1D model cannot provide any detail about turbulent structures in the air flow, and because it cannot properly account for turbulence there may be error in the estimation of airway resistance.

3D-1D models for seamless transition from the mouth to the terminal bronchiole

The study of airflow in the lung must ultimately be able to span from the mouth to the alveolated airways in the lung periphery. The smaller airways – beyond approximately generations 6 to 9 in the human lung – cannot usually be visualized with current clinical imaging. Lin et al. (45) presented a method for creating subject-specific 3D and 1D coupled airway mesh structures with seamless transition between the 3D and 1D scales, incorporating the desired level of geometric detail wherever it is needed in the airway tree. Subject-specific 1D models for the entire conducting airway tree (38) are converted to a high-order (cubic Hermite) 2D surface mesh of the entire domain. The parent and child branches merge at the bifurcations with a smooth, continuous surface. The uppermost airways – for which there is MDCT (multi-detector row CT) surface data - are geometry fitted (38) to enforce accurate airway surface geometry. The resulting 2D surface mesh is continuous with the surface of the VFB algorithm-based airways, which are generally assumed to have a circular cross-section. Any portion of this surface mesh can be converted to a 3D CFD-ready mesh by selecting a region of interest to study in detail. The 3D mesh is created only within those airways, and the remainder of the domain is the original 1D tree. The 3D and 1D trees are a single continuous model that has a different dimension in specified regions. An advantage of this approach is that transport can be studied in - for example – models that include successive generations, to define the conditions under which a 1D model representation will suffice.

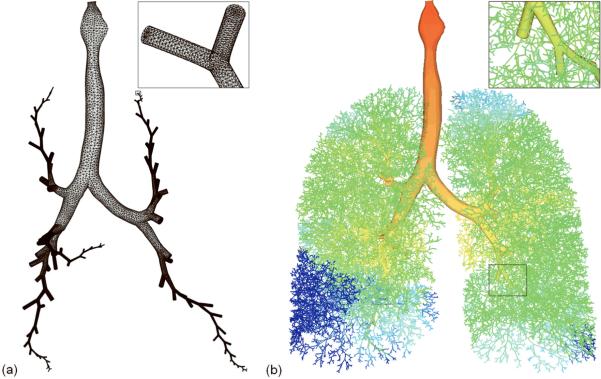
Figure 1 illustrates the creation of a subject-specific 3D-1D airway geometrical model. In Figure 1 (a), a subset of airways are isolated from the full 1D conducting airway tree for generation of a 3D geometrical model. The 3D model includes all of the central airways that were segmented from MDCT imaging for this subject, and five selected pathways (one in each of the five lobes) that extend to the terminal bronchioles up to the 25^th generation in this model). The MDCT based airways extend from generation 0 (larynx and trachea) to a maximum of generation 5; all additional airway paths in Figure 1 are from a 1D generated model. The 3D airway model allows detailed and accurate simulation of gas flow and particle transport in transition from turbulent flow in the central airways to laminar flow in the small airways in any region of interest. The remainder of the airways is supplemented by the 1D airway model as illustrated in Figure 1 (b) to bridge from the 3D airways to the lung parenchyma, allowing specification of subject-specific regional ventilation as described in the following section.

Figure 1.

(a) 3D airway mesh, consisting of central airways and 5 pathways extending up to the 25^th-generation terminal bronchioles in each of the five lobes. The insert shows the close-up view of the mesh at the terminal bronchioles. (b) 3D-1D coupled mesh and CFD computed pressure distribution (red (zero) to blue (large negative) pressure). The insert shows the continuity of the 3D and 1D meshes.

AIR FLOW AND WHOLE LUNG VENTILATION IN 3D-1D MULTI-SCALE MODELS

In the aforementioned 3D CFD studies that compute flow in a truncated domain (i.e. excluding either or both of the upper and lower airways), there is no warranty to produce physiologically-consistent regional ventilation. That is, to simulate flow through the airways a set of `boundary conditions' (BCs) must be defined so that a unique solution to the equations can be found. The BCs typically specify the pressure, flow, or velocity at the inlet and outlets of the models. Flow and pressure in the airways change during the breathing cycle and cannot be measured directly. The approach taken in earlier CFD analysis has been to specify equal pressure or flow BCs at all outlets of the model, neglecting any variation due to geometry, downstream resistance, and gravitational effects on the regional volume expansion of the lung. Both stationary and pulsatile boundary conditions have been investigated. The former yields a constant flow rate, whereas the latter adopts a breathing waveform. De Backer et al. (59) approached this problem by specifying two different pressure values at the ends of the 3D CT-resolved left and right main bronchi as an approximation of a subject-specific BC. This produced a steady inspiratory flow with different proportions distributed to the left and right lung. Other approaches to overcome the BC problem have been proposed by Lin et al. (45) and Tawhai et al. (55), using image registration and soft-tissue mechanics, respectively. Lin et al. (45) proposed a multi-scale CFD framework that utilizes 3D-1D coupled meshes (Figure 1) together with image-registration-derived regional ventilation and deformation for realistic simulation of pulmonary airflow that relates directly to an imaged subject (a subject-specific simulation). Tawhai et al. (20, 55) developed a soft-tissue-mechanics-based model for elastic deformation of the compressible lung tissue, which can be used to provide flow and/or pressure boundary conditions for a 1D tissue-embedded airway model (Figure 1(b)). The airways in Figure 1 (b) are colored by pressure. The pressure at the entrance to the model is zero, and becomes more negative (dark blue) in the peripheral airways of the dependent tissue. Because this example specified equal outlet velocities at all terminal bronchioles, the airway pressure distribution is neither uniform nor gravitationally directed.

Image registration for subject-specific boundary conditions

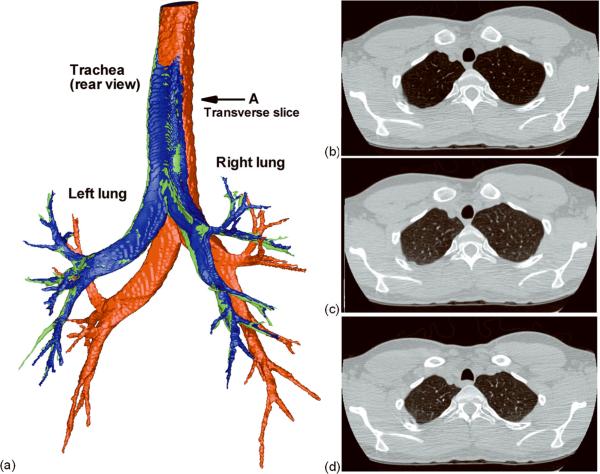
Image registration has at least two potential applications in subject-specific lung modeling: 1) estimation of regional ventilation, and 2) deformation of the airways and lobes. With respect to the first application, registration-derived estimates of regional ventilation (60–62) can be imposed via the 3D-1D coupled method to produce physiologically-consistent, subject-specific boundary conditions for CFD (45). Yin et al. (63) proposed a non-rigid image registration method to align CT lung images acquired during breath-hold at two lung volumes. This method uses the sum of squared tissue volume difference (SSTVD) as the similarity criterion to minimize the local tissue volume difference within the lungs between two images, thus preserving the tissue weight of the lungs. The mass preserving nonrigid registration method can then applied to align two CT volumetric lung images acquired at different levels of inflation to derive subject-specific regional ventilation. Such registration-derived regional ventilation is then passed to the CT-resolved airways as the flow boundary condition within a 3D-1D coupling framework, where the subject-specific 1D peripheral airway tree serves as a link between 3D central airway tree and lung parenchyma. The details can be found in Yin et al. (63). For the second application, the registration-derived displacement field can be used to deform the CFD mesh for simulation of a breathing lung. Unlike fluid-structure interaction (FSI) (64), the image-based moving-mesh CFD for compliant airways requires neither coupling with computational solid mechanics nor specifying tissue mechanical properties and tethering forces. Figure 2 (a) compares an airway that was segmented from TLC imaging with the same airway segmented from FRC imaging, and an airway that was deformed from TLC to FRC using the SSTVD-derived displacement fields. Figures 2 (b–d) show the transverse slices of the original TLC image, the transformed image from FRC to TLC, and the original FRC image. Although this subject had severe asthma, the deformed airway and transformed image agree well with the original data. This method can also be applied to each of the five lobes individually to estimate lung lobar sliding and mechanics (65).

Figure 2.

(a) Airways segmented from the original TLC image (red) and the original FRC image (green), and the deformed airway from TLC to FRC via image registration (blue). Transverse slices taken at “A”: (b) the original TLC, (c) the transformed image from FRC to TLC, and (d) the original FRC.

Soft tissue mechanics for a predictive model of ventilation distribution

The image-registration method provides subject-specific boundary conditions for the lung in the state in which it was measured. We have complemented this approach with a model for the soft tissue deformation of the lung tissue, to produce a model that is predictive of ventilation distribution in any posture and at any volume.

Tawhai et al. (20) presented a computational model for predicting the deformation of the lung tissue in response to gravitational loading. Because the lung deforms readily in response to gravity, at functional residual capacity (FRC) there is significant difference in the degree of tissue expansion and therefore tissue density in different regions of the lung. The mechanics model uses equations for large deformation theory and a constitutive law for non-linear behavior of the lung tissue (66). The geometry of the model is derived from MDCT on a subject-specific basis. Gravitational deformation is simulated by incrementally applying the gravity load while requiring that the lung remain in contact with a rigid pleural surface but that it can slide freely. The model has been validated against the regional distribution of tissue density. Tawhai et al. (20) showed that it is possible to develop differences in the gradient of tissue density between the supine and prone postures without any change in shape of the chest wall and diaphragm, and without the heart moving downwards with gravity. This contrasts with previous studies which have suggested that the heart compressing the lung tissue is a major factor in developing postural differences in density gradients.

The mechanics model can be coupled to the 3D-1D CFD model in a similar fashion to the image-registration method. In each case the volume change of a unit of tissue can be used to prescribe a BC at the end of the terminal bronchiole that ventilates that unit of tissue. This approach is satisfactory for healthy lung tissue and non-constricted airways because in that situation the expansion of the lung tissue will dominate the distribution of ventilation. However when the system is perturbed by disease (reduced elasticity of the parenchyma as in emphysema, or bronchoconstriction in asthma) the resistance of the airways becomes important and the prescription of tissue volume change as a peripheral airway BC may no longer be appropriate. Figure 1 (b) illustrates a new approach that overcomes this problem. Here the tissue mechanics model was used to define the FRC volume and elasticity of each unit of tissue (acinus) subtending the ~32,000 terminal bronchioles. The BCs were reformulated as an analytic expression for flow that is dependent on upstream resistance, acinus elasticity, and rate of change of pleural pressure. The reformulated system was coupled with the 3D-1D CFD framework (45) to give a prediction of flow distribution and pressure drop throughout the entire lung. That is, neither pressure nor flow were defined as BCs at the exits of the model, hence pressure and flow are both predicted and are both dependent on the tissue elasticity and the airway resistance. In Figure 1 (b) the model predicts a non-uniform distribution of pressures in response to a gravitational distribution of ventilation (not shown).

The link between the 3D-1D airway model geometry and the lung tissue can be exploited to counteract the disadvantage of deriving models of the lung geometry using imaging at TLC. That is, because the airways are largest and therefore most easily segmented when the lung is at TLC, most imaging data is acquired at close to this volume. Segmentation of the airway tree at FRC typically yields identification of a lesser number of airways. The disadvantage with respect to simulation studies is that at TLC the airways are wider and longer than during normal resting breathing, therefore their TLC resistance is lower and the predicted nature of the air flow and pressure drop will be inaccurate. This can be addressed for the largest airways by customizing their geometry to the FRC images, for example by geometry fitting the mesh shape. The smaller (non-segmented) model airways are embedded within the lung tissue which deforms with gravity and volume change, hence their size can be made appropriate to FRC by updating the coordinates of the mesh vertices as the lung tissue displaces. Because the CFD studies exploit 3D tetrahedralized pathways, this coordinate update serves to modify the airway mesh length and diameter under the assumption that the airway tissue behaves identically to the lung tissue. This assumption is a limitation of this approach: the largest airways do not behave identically to the lung tissue.

THE APPROPRIATENESS OF TURBULENCE MODELS FOR AIRWAY 3D CFD

Due to the constriction, expansion, curvature, and bifurcation of the upper and central airways, the air flow is characterized by transitional and turbulent behaviors, affecting gas and particle transport in several generations of the tracheobronchial tree. Flow is turbulent and/or transitional in the upper and central airways, and eventually transitions to laminar in the smaller airways. Thus, CFD models must be able to accurately capture the nature of turbulent flow and its transition to laminar flow in the lungs in a complex domain with ever-smaller airways. There are three CFD approaches for modeling turbulent flows: Direct Numerical Simulation (DNS), Large-Eddy Simulation (LES), and Reynolds-Averaged Navier-Stokes models (RANS). DNS solves the Navier-Stokes equations directly to resolve all of the turbulent eddies in the flow. LES solves the space-filtered Navier-Stokes equations to resolve large-scale energy-containing turbulent eddies, and parameterizes small-scale unresolved eddies by a subgrid-scale (SGS) model. RANS solves the Reynolds-averaged Navier-Stokes equations only for mean flow fields, and parameterizes all of the turbulent motions. Thus, in the RANS-generated velocity field, turbulent structures are completely absent. DNS is the most accurate method, but it is computationally expensive. LES that relies on a SGS turbulence model is fairly accurate, and is becoming affordable with today's computing technologies. RANS is relatively economical but inaccurate (67). Both DNS and LES are regarded as high-fidelity, high-performance CFD methods that should be executed on parallel computer clusters; however use of these methods requires a thorough understanding and knowledge of turbulence physics to properly capture the turbulent structures and interpret their physical implications. Commercially available RANS CFD software packages have been widely used to model turbulence in the human airways. However, a concern highlighted by Stapleton et al. (68) and Heenan et al. (69) is that the RANS model is inaccurate in the range of Reynolds numbers found in the oropharynx. Although it has been argued that low-Reynolds number RANS model might be adequate for transient and turbulent flows (70, 71), Varghese et al. (72) demonstrated that both low-Reynolds number RANS models and LES without the use of a proper mesh and a good SGS model poorly predict turbulent structures in eccentric stenotic flows.

Lin et al. (16) computed flow in two imaging-based models (mouth-to-airway and intra-thoracic airway) using both DNS and LES, and showed that LES is sufficient to capture the turbulent laryngeal jet at a Reynolds number of 1,700 in the trachea. The presence of turbulence was found to significantly affect airway flow patterns as well as wall shear stress, which may have pathophysiologic implications. In the intra-thoracic airway model where the upper airway was truncated, the flow became laminar. This demonstrates that imposition of proper boundary conditions when using a truncated airway model is of crucial importance to the accuracy and physiological interpretation of results. Kabilan et al. (73) examined airflow and ventilation in a CT-based ovine lung to study inter-species variability. To study the intra- and inter-subject variabilities of airflows in the human lungs, Choi et al. (15) examined the flow structures in two complete CT-based human airway models (mouth-to-airway) and three truncated airway models at the subglottis, the supraglottis, and the laryngopharynx, respectively. LES was employed in these simulations. In an inter-subject study, by comparing the turbulent laryngeal jets in the two airway models they found that the constriction ratio of the glottis with respect to the trachea and the curvature and shape of the airways can significantly affect the flows between subjects. In an intra-subject study, they found that the truncated airway models do not produce similar structures, such as mean velocities, velocity fluctuations, turbulent kinetic energy, and energy spectra, as those in the complete airway model. They further proposed an improved boundary condition for a truncated airway model to produce flow which is in better agreement with that of a complete airway model. Choi et al. (74) applied a 3D-1D coupled airway method to study flow structures and quantify mixing in the human lungs under high frequency oscillatory ventilation (HFOV). HFOV is regarded as an efficient respiratory technique to ventilate neonates and patients with acute respiratory distress syndrome. By comparing the HFOV case with the normal-breathing case and the high-frequency-normal-Reynolds-number case, they found that flow structures at flow reversal are not as effective as those at peak flow rate in mixing, but they contribute about 20% to mixing in HFOV.

AIR TRANSPORT IN THE ALVEOLATED AIR SPACES

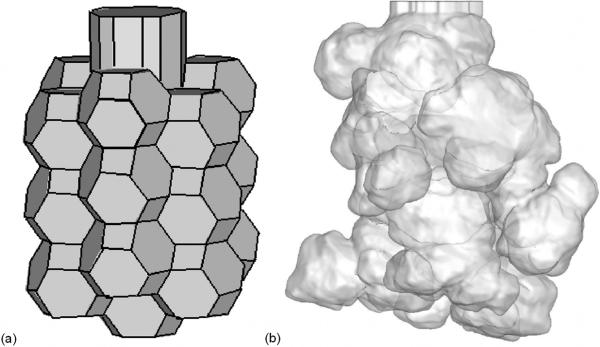
The previous sections have considered the transport of air through the bronchial (conducting) airways. The bronchial airways of the human lung bifurcate up to 28–30 times (75) before reaching the alveolated airways of the lung parenchyma, where gas exchange occurs. The lung parenchyma is sponge-like in appearance and is formed of a network of alveolated ducts and alveolar sacs. While many modeling studies make the assumption that gas transport within the pulmonary acinus occurs only by diffusion, in reality the bulk transport of gas in the alveolated airspaces is non-negligible as its summation approximates the volume of air that is inspired with each breath. Faithful portrayal of close-to-reality alveolar airspace geometry for use in silico, and solving for fluid flow using realistic breathing conditions are two crucial criteria in understanding alveolar flow phenomena (76). Several theoretical approaches have been used to model the alveolar tissue as a space-filling structure (77, 78), however these models have generally not been developed specifically for simulation of alveolar flow. Figure 3 (a) shows a model of a single alveolar sac generated using the method of Tawhai and Burrowes (14). The model is composed of truncated octahedral with a regular shape. In comparison, micro-CT imaging of the alveolated airways of the mouse lung (25, 79) show that the distribution of alveolar sacs is irregular (Figure 3 (b)).

Figure 3.

(a) Truncated octahedron geometry of an alveolar sac with 18 circumferential alveoli and one terminal alveolus. (b) Surface rendering of high resolution micro-CT image of an alveolar sac obtained by perfusion fixation from a mouse lung at 20 cmH₂O (25, 79).

Tsuda et al. (80) adopted an alveolar model of a central channel surrounded by a torus and performed CFD with rhythmic breathing by defining expansion and contraction of the model. Darquenne and Paiva (81) simulated airflow in a model of the alveolated duct based on sections of annular ring around a central channel. Sznitman et al. (82) carried out CFD simulation in the acinar tree to study the transport of nondiffusing fine inhaled particles of 1 and 3 micrometers in diameter. Kumar et al. (17) adopted the 3D truncated octahedron-based alveolar model of Tawhai and Burrowes (14). The interalveolar septa shared between two neighboring alveoli in this model have a zero thickness; CFD analysis was therefore performed with a prescribed wall motion and disregarding the tissue properties. This study found that the topological difference in the arrangement of alveolar sacs affects airflow structures, which is indicative of heterogeneous alveolar ventilation. This could be further enhanced by adopting a model structure with realistic variability in the alveolar size and shape (79), as observed by Vasilescu et al. (25).

In the above simulations of alveolar flow, the alveolar models were either assumed rigid or with prescribed wall motions. Some recent experimental studies have attempted to define the 3D alveolar structure and alveolar dynamics (21–25). These experimental studies highlight the technical difficulties in dynamic 3D imaging of the dense parenchyma and the precise definition of alveolar dynamics. At this stage this remains a challenging area of research, and the translation of dynamic imaging to image-based computational models is in its infancy.

SUMMARY AND FUTURE DIRECTIONS

The efforts described herein are building towards the ultimate goal of a `Lung Physiome', which aims to build a computational framework for understanding lung physiology and pathophysiology (see (83) for review information on the Physiome project). This is necessarily an international, multi-disciplinary, and multi-scale effort. Developing a Lung Physiome requires measurement and modeling at multiple scales of interest (organ, tissue, cell, and molecule), and – most challenging – the integration of models over multiple spatial and temporal scales, while maintaining model tractability. Pathological changes in the lung occur at the level of the cell or tissue (airway, vessel, or parenchyma), however these are subjected to the cyclic forces of breathing that are transmitted from the organ scale. Understanding the complex regional progression of lung disease that involves mechanotransduction therefore requires a computational framework that can handle multiple physical problems (e.g. air flow and tissue mechanics) and multiple spatial scales.

Image-based models for the sub-systems of the lung and their integrated function are now computationally feasible, although simulation within biological structures presents challenges over the rigid and regularly-shaped structures to which engineering analyses of fluid and structural mechanics have traditionally been applied. The lung presents its own unique challenges because of its complex structure, its delicate and highly deformable tissue, and lack of access for direct measurement of air flow and pressure.

Airway CFD is a multi-scale problem, computed in a deforming body that interacts with the surrounding tissue as the lung expands and recoils during ventilation. Predicting realistic distribution of inspired air and particulates therefore requires an organ-to-tissue link via consideration of airway-tissue coupling through FSI simulation (45) or by linking to continuum models for the tissue stress and strain (55). To model airway deformation, Lin et al. (45) proposed two approaches. The first is achieved by mapping CT images at various lung volumes via numerical optimization, which may be most suitable for the study of structure-function relationships at the organ scale. The second approach is based upon an FSI solver, which may be most appropriate for study of interplay between gas flow and airway wall/lung tissue at the local scale. The 3D-1D modeling approach proposed by Lin et al. (45) has shown promise for efficient coupling with other phenomena in the lung, for example, coupling with models of lung soft tissue mechanics (20), or distributed models of cell function (84). These types of coupled model lend themselves to studying how airflow distribution is altered by changes to the regional tissue properties in the lung: an important analysis for understanding delivery of aerosolized medicine to subjects with different pathologies. As noted by Lin et al. (45), maximum localized airway wall shear stress is increased three-fold by turbulence. This may have pathophysiologic implications for reactive inflammation and fibrosis. Linking down another scale – to interactions with the epithelial cell (85, 86) – is therefore an essential next step.