Analysis of PKR-RNA interactions by sedimentation velocity

Abstract

PKR is an interferon-induced kinase that plays a pivotal role in the innate immunity pathway for defense against viral infection. PKR is activated to undergo autophosphorylation upon binding to RNAs that contain duplex regions. Some highly structured viral RNAs do not activate and function as PKR inhibitors. In order to define the mechanisms of activation and inhibition of PKR by RNA it is necessary to characterize the stoichiometries, affinities and free energy couplings governing the assembly of the relevant complexes. We have found sedimentation velocity analytical ultracentrifugation to be particularly useful in the study of PKR-RNA interactions. Here, we describe protocols for designing and analyzing sedimentation velocity experiments that are generally applicable to studies of protein-nucleic interactions. Initially, velocity data obtained at multiple protein:RNA ratios are analyzed using the dc/dt method to define the association model and to test whether the system is kinetically limited. The sedimentation velocity data obtained at multiple loading concentrations are then globally fit to this model to determine the relevant association constants. The frictional ratios of the complexes are calculated using the fitted sedimentation coefficients to determine whether the hydrodynamic properties are physically reasonable. We demonstrate the utility of this approach using examples from our studies of PKR interactions with simple dsRNAs, the HIV TAR RNA and the VAI RNA from Adenovirus.

Introduction

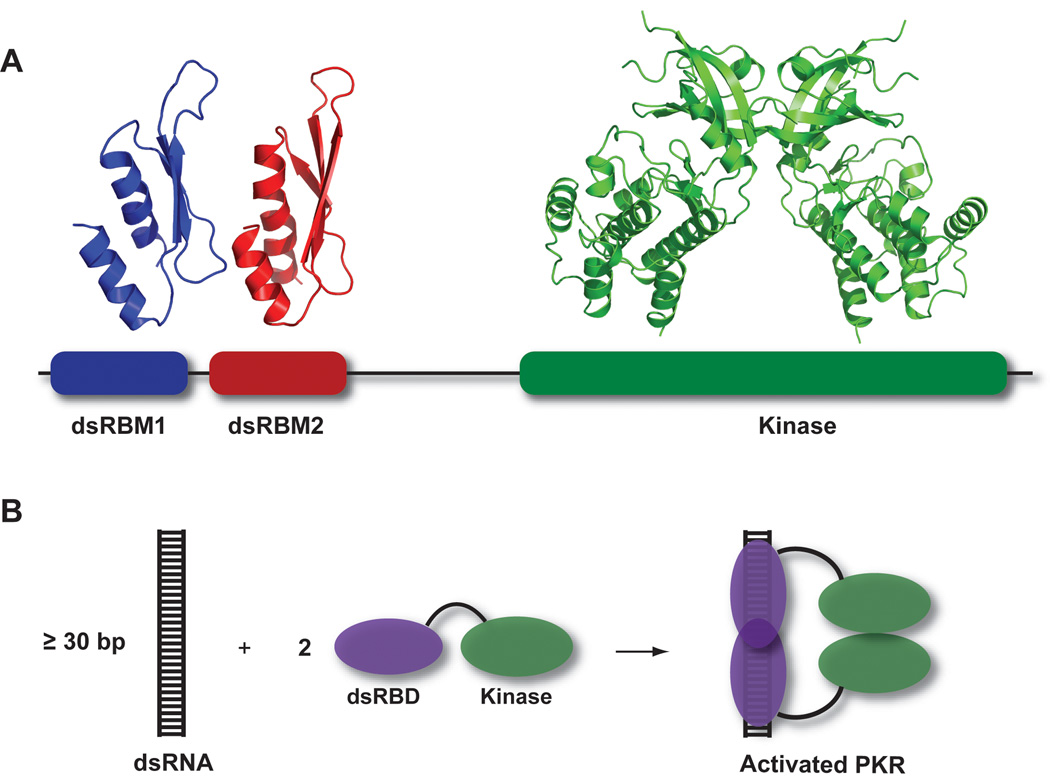
Protein kinase R (PKR) is an interferon-induced kinase that plays a key role in the innate immunity response to viral infection (Toth et al., 2006). PKR is induced in a latent form that is activated by binding dsRNA to undergo autophosphorylation and subsequently phosphorylate cellular substrates. PKR contains an N-terminal dsRNA binding domain (dsRBD), consisting of two tandem copies of the dsRNA binding motif (dsRBM) (Tian et al., 2004), and a C-terminal kinase domain, with a ~90 amino acid unstructured linker lying between these domains (Figure 1). The structures of the isolated dsRBD (Nanduri et al., 1998) and the kinase domain (Dar et al., 2005) have been solved. The linker is flexible and PKR adopts multiple compact and extended conformations in solution (VanOudenhove et al., 2009). Crystallographic and NMR studies indicate that the dsRBM binds to one face of the dsRNA helix, spanning ~ 16 basepairs (Tian et al., 2004). The interaction is not sequence-specific; however, there are some reports of selective binding of the dsRBM to specific RNA secondary structural features (Liu et al., 2000; Nagel and Ares, 2000; Spanggord and Beal, 2001; Ben-Asouli et al., 2002; Leulliot et al., 2004).

Figure 1.

Overview of PKR structure and function. A) PKR domain organization and structure. The N-terminal regulatory domain is comprised of two dsRNA binding motifs, dsRBM1 and dsRBM2 connected by an unstructured linker. Each of these motifs adopts the canonical αβββα fold in the NMR structure of dsRNA binding domain (PDB: 1QU6). In the crystal structure of a complex of the PKR kinase domain and eIF2α (PDB: 2A1A), the kinase domain has the typical bilobal structure observed in other eukaryotic protein kinases and dimerizes via the N-terminal lobe. B) Dimerization model for PKR activation by dsRNA. Binding to dsRNA induces PKR dimerization via the kinase domain, resulting in activation.

Although PKR is known to bind to dsRNAs as short as 15 bp (Schmedt et al., 1995; Bevilacqua and Cech, 1996; Ucci et al., 2007), at least 30 bp are required for activation (Manche et al., 1992; Lemaire et al., 2008). These data support an activation model where the role of the dsRNA is to bring two or more PKR monomers in close proximity to enhance dimerization via the kinase domain (Cole, 2007). Consistent with this model, HIV TAR RNA, a 23 bp hairpin with three bulges, binds a single PKR and does not activate. In contrast, a dimer of TAR binds two PKRs and activates (Heinicke et al., 2009). However, for more complex RNAs the structural features that distinguish activators of PKR from those that fail to activate are not yet well understood. Incorporation of G–I mismatches blocks PKR activation (Minks et al., 1979) but PKR is activated by RNAs containing tandem A–G mismatches and noncontiguous helices, provided the RNA adopts an overall A-form geometry (Bevilacqua et al., 1998). Some highly structured viral RNAs do not activate and function as PKR inhibitors in vivo (Langland et al., 2006).

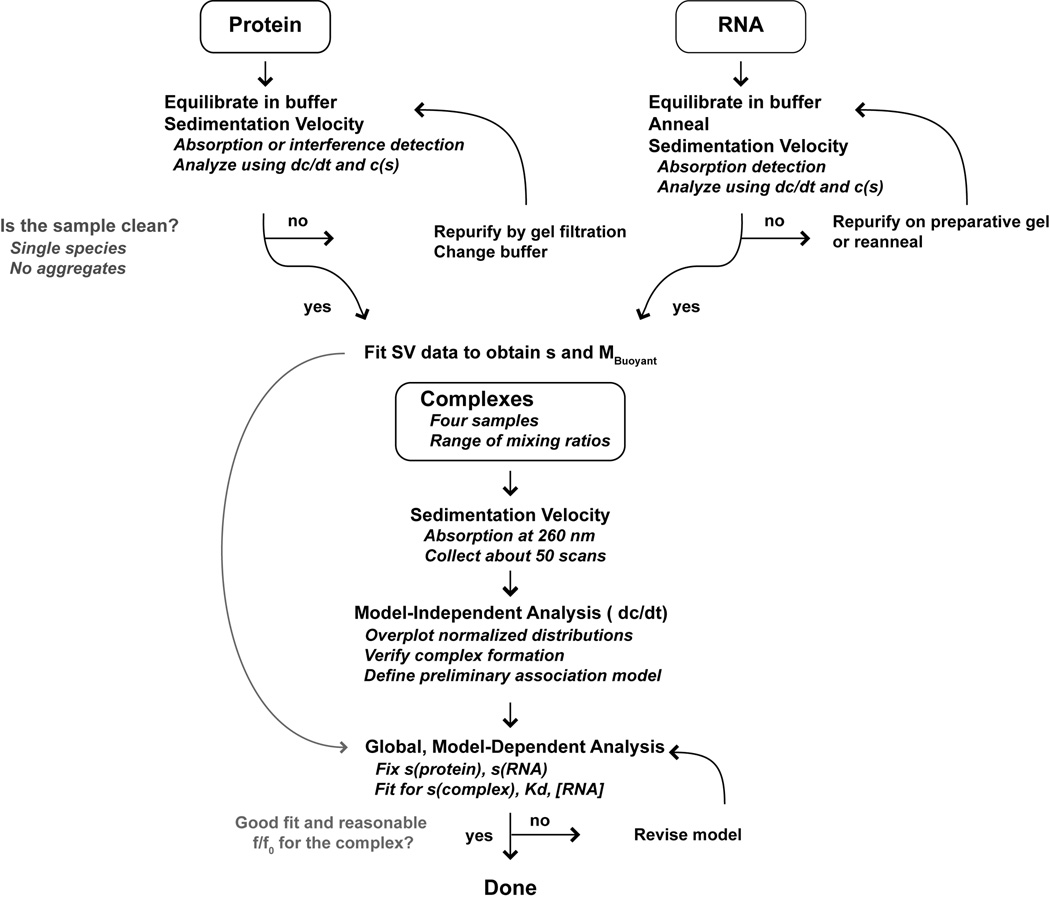
In order to define the mechanisms of activation and inhibition of PKR by RNAs it is necessary to characterize the stoichiometries, affinities and free energy couplings governing the assembly of the relevant macromolecular complexes. Protein-nucleic acid interactions are typically measured using electrophoretic mobility shift (Carey, 1991; Hellman and Fried, 2007) and nitrocellulose filter binding assays (Wong and Lohman, 1993) that are performed under non-equilibrium conditions. Although these assays can be used to accurately define binding parameters under carefully controlled conditions, nonspecific interactions generally have lower affinity and higher dissociation rates than specific interactions and are thus particularly susceptible to artifacts associated with dissociation of complexes during the measurement. Thus, analyses of nonspecific and weaker specific interactions should be performed using free solution biophysical methods. One such method, analytical ultracentrifugation (AUC), has historically played an important role in quantitative analysis of protein-nucleic acid binding reactions. Early studies utilized sedimentation velocity methods to obtain the free and bound concentrations of the reactants (Jensen and von Hippel, 1977; Draper and von Hippel, 1979; Lohman et al., 1980; Revzin and Woychik, 1981; Goodman et al., 1984) and one study suggested potential applications of equilibrium methods (Lanks and Eng, 1976). With the advent of the XL-A analytical ultracentrifuge (Giebeler, 1992) and increasing computational power it became feasible to globally analyze sedimentation equilibrium data for protein-nucleic acid systems obtained at multiple wavelengths and concentrations (Laue et al., 1993; Lewis et al., 1994; Bailey et al., 1996; Wojtuszewski et al., 2001; Daugherty and Fried, 2005). We have found these methods useful in the analysis of PKR-RNA interactions (Ucci and Cole, 2004; Ucci et al., 2007) and we have developed a software package, HeteroAnalysis, that facilitates global analysis of multiwavelength sedimentation equilibrium data (Cole, 2004). However, these analyses can be challenging. In some cases, equilibrium is not achievable due to slow precipitation of protein-RNA complexes. Global analysis of multiwavelength data requires extremely accurate extinction coefficients that are difficult to achieve due to the poor wavelength reproducibility of the XL-A. Finally, the data reduction and analysis process can be fairly tedious due to the large number of files and parameters and the necessity to carefully specify the linkages among them. Recently, we have taken advantage of “whole boundary” methods for the direct analysis of sedimentation velocity profiles of interacting systems (Stafford and Sherwood, 2004; Dam et al., 2005; Correia and Stafford, 2009; Demeler et al., 2010). These approaches work very well for characterization of PKR–RNA interactions. The measurements are fast and less affected by precipitation and the analysis is generally more straightforward than corresponding sedimentation equilibrium experiments. Below, we provide a protocol for the design and analysis of experiments to characterize protein-RNA (or protein-DNA) interactions using sedimentation velocity with absorption detection. The protocol is summarized in the flowchart in Figure 2.

Figure 2.

Experimental flowchart. For details see the text.

Reagents and Cells

Buffer used for sedimentation velocity measurements should not contain detergents and should have minimal absorbance at the wavelength of interest. Typically, we monitor RNA absorbance at 260 nm. The inclusion of a reducing agent is often required and tris(2-carboxyethyl)phosphine (TCEP) is preferred over dithiothreitol due to its lower absorbance at 260 nm. Particularly when working with highly charged macromolecules such as RNA and DNA, it is critical to include an electrolyte in the buffer to suppress the primary charge effect that slows sedimentation. Usually, 10–50 mM of monovalent salt is sufficient. The ionic strength is also a critical parameter that modulates binding affinity and may also affect solubility of the protein and the protein-nucleic acid complexes. Note that high solute concentrations can result in dynamic density and viscosity gradients that will affect sedimentation (Schuck, 2004). RNA is very susceptible to hydrolysis catalyzed by ribonucleases that are ubiquitous in the lab. For RNA work we use sterile tips and tubes and autoclaved and sterile-filtered buffers. We do not find it necessary to resort to baking glassware or using diethylpyrocarbonate-treated water. If ribonuclease contamination is a problem, it may be helpful to add a commercially available ribonuclease inhibitor to the RNA samples. The inhibitor should be kept at low concentrations so that it does contribute to the sample absorbance. RNAs have the propensity to adopt alternative secondary structures so that it may necessary to use an annealling or a snap-cooling procedure to prepare a sample with a homogeneous secondary structure. In particular, self-complementary hairpin RNAs have the propensity to form stable dimers and it may be necessary to anneal samples at low concentrations to obtain homogeneous monomers or to purify the species of interest on native gels (Heinicke et al., 2009).

Both the RNA and protein should be equilibrated in the sample buffer via dialysis, gel filtration or spin column chromatography. The contribution of buffer mismatch to the sedimentation velocity profiles is less of a concern with absorbance optics than with interference optics, but equilibration ensures that contaminating low molecular weight solutes are not carried over from the RNA or protein stocks. Standard double sector centerpieces or meniscus-matching centerpieces are used with quartz windows. The windows and centerpieces are treated with RNaseZap (Ambion, CA) and then rinsed extensively with sterile deionized water to prevent RNA degradation. It may be useful to reserve some cells exclusively for RNA experiments to ensure that the centerpieces and windows do not become contaminated with ribonucleases.

Experimental Design

It is always useful to fix as many parameters as possible in global data analysis methods. Thus, the sedimentation coefficients of the free RNA and protein should to be determined independently by analyzing each component separately. Multiple concentrations that span at least a three-fold range and encompass the concentration range to be used in the binding experiments should be run to detect potential self-association. The molecular masses of the protein and RNA are obtained from sequence. The partial specific volume (ν̄) and extinction coefficient (ε) of the protein and the buffer density (ρ) are calculated using SEDNTERP (Laue et al., 1992). There is no reliable method to calculate ν̄ for RNA oligonucleotides. Instead, this parameter can be determined indirectly from the buoyant molecular weight (M*) measured in the sedimentation velocity experiment:

$$M^{*}=M\left(1-\overline{\nu }\rho \right)$$ (1)

Typically, we collect data at a single RNA concentration chosen to provide an absorbance at 260 nm between 0.3 and 0.8, where the best sensitivity is achieved, using a broad range of protein:RNA ratios (typically from 0.5:1 to 6:1) to populate all of the species participating in the equilibrium. Of course, if the relevant binding reactions are too strong it will not be possible to resolve the K_ds with reasonable precision at the accessible reagent concentrations using the absorption optics. It can be helpful to simulate the experiment using the estimated dissociation constants with realistic noise levels to provide guidance on the optimal reagent concentrations and to determine whether it is possible to resolve the K_ds with sufficient accuracy and precision. Alternatively, fluorescence optics can be used with labeled RNAs to greatly enhance sensitivity.

Data collection

General information on how to perform sedimentation velocity experiments methods can be found in several recent reviews (Brown et al., 2008; Cole et al., 2008; Balbo et al., 2009; Stafford, 2009). As mentioned above, we typically collect absorbance data at 260 nm for analysis of protein-RNA interactions. Although data collected at additional wavelengths would be extremely useful in global analysis, particularly at 230 and 280 nm where the relative contribution of the protein is greater. The slow scan rate of the XL-A absorbance system and the poor wavelength reproducibility preclude this option. Rapid scan absorbance systems that overcome these limitations are under development (Colfen et al., 2009). Although simultaneous collection of interference and absorbance data is feasible, we have not implemented this approach because the concentrations of protein and RNA are too low in our experiments for interference. The total number of scans that one can collect per run is limited by the data collection rate of the absorbance optics on the XL-A. For our instruments, each absorbance scan requires approximately 1.5 minutes (0.003 cm / point, continuous mode). About 50 scans per cell is appropriate for reliable global data analysis, Given the slow data acquisition, a maximum of four cells is recommended, which gives a total run time of about five hours. For larger complexes, with sedimentation coefficients greater than about 5 S, one can reduce the rotor speed from the maximum (50,000 RPM for the 8 hole rotor) to slow the sedimentation rate. The rotor speed (in RPM) can be estimated using the following formula:

$$\mathit{\text{speed}}=9.7\times {10}^4\sqrt{s}$$ (2)

where s is the sedimentation coefficient of the species of interest. Alternatively, the throughput can be increased by loading sample into both sectors of the cell, recording raw intensities and analyzing pseudo-absorbance data (Kar et al., 2000).

Data analysis

Initially, velocity data are analyzed using a model-independent approach to help define the correct binding model and to determine whether the system is kinetically limited. We typically employ the time derivative method (Stafford, 1992) using the program DCDT+ (Philo, 2006) to obtain a g(s*) distribution for each sample. By inspecting an overlay of the normalized g(s*) distributions for all of the samples, one can immediately verify complex formation by the appearance of features at higher s than the free protein or RNA. The shape of the boundary will depend on the kinetics of association and dissociation. For systems that equilibrate slowly on the timescale of the sedimentation run, features will be present in the boundary corresponding to each of the species: free protein (provided the concentration is high enough to detect at 260 nm), free RNA and the protein-RNA complex. Their amplitudes but not positions will be protein-concentration dependent. In contrast, for rapidly reversible systems, complex boundary shapes are observed due to re-equilibration during sedimentation (Gilbert and Jenkins, 1959; Cann, 1970). One feature occurs at the position of one of the free components and the other feature is a reaction boundary with an apparent sedimentation coefficient lying between the faster sedimenting component and the protein-RNA complex. The sedimentation coefficient of the reaction boundary increases with increasing protein concentration. If binding is sufficiently tight, one can use the limiting sedimentation coefficient of the reaction boundary at high protein concentrations to estimate the stoichiometry of the largest complex. We use SEDNTERP (Laue et al., 1992) to calculate frictional ratios (f/f₀) based on the sedimentation coefficient, predicted mass and weight-average ῡ, assuming alternative stoichiometries for the largest protein-RNA complex. For typical protein-RNA complexes, f/f₀ lies between 1.2 and 1.6; values outside this range likely indicate an incorrect stoichiometry. Later, one can test the model more rigorously by repeating this calculation using the sedimentation coefficient of the complex obtained from global analysis (see below).

Having defined the binding model, we then globally fit the sedimentation velocity data obtained at multiple loading concentrations to determine the relevant association constants as well as the hydrodynamic properties of each complex. Several powerful software packages are available for sedimentation velocity analysis of interacting systems, including SEDPHAT (Dam et al., 2005) SEDANAL (Stafford and Sherwood, 2004; Correia and Stafford, 2009) and ULTRASCAN (Demeler et al., 2010). We find SEDANAL to be particularly convenient for analysis of PKR-RNA interactions. Association models for particular systems can be defined by the user with the model editor. It is also simple to apply constraints to the fitted parameters, such as preset limits on their allowable ranges or imposing particular relationships between parameters. As mentioned above, parameters for the free RNA and protein (sedimentation coefficient, molecular weight, density increment (1−ῡρ) and mass extinction coefficient) are fixed based on prior calculation and previous experiments. We usually find it necessary to treat the RNA loading concentrations as adjustable parameters because they often decrease upon addition of protein due to precipitation of complexes. However the protein loading concentration or alternatively, the protein:RNA ratio, should be held fixed, as the protein contribution of absorbance at 260 nm is typically too low for these parameters to be well determined from the data. Of course, the association constants and sedimentation coefficients are allowed to float during the fit. The programs for sedimentation velocity analysis of interacting systems mentioned above can be configured to fit the data assuming either rapid equilibration or kinetically-limited reactions. In all of the PKR-RNA interactions that we have examined so far, the rate of complex equilibration is fast on the timescale of sedimentation such that reaction boundaries are detected in the g(s*) distributions and good fits are obtained in global analyses assuming rapid equilibration.

As is true for all nonlinear least squares problems, a good fit is defined by the absence of systematic trends in the residuals and an overall RMS deviation consistent with the stochastic noise level. It is useful to verify that the best fit corresponds to a global minimum in the error surface by repeating the process using different initial values for the parameters being floated or using the “perturb fit and redo” feature in SEDANAL. Once the best fit has been defined, confidence intervals of the fitted parameters should be obtained based on the F-statistic, Monte-Carlo or bootstrap with replacement methods. One can also recalculate f/f₀ for the complexes, using the fitted sedimentation coefficients to determine whether the hydrodynamic properties are physically reasonable.

The parameters associated with higher order binding events are often poorly defined due to low population of the relevant species as well as strong cross-correlation between association constants and sedimentation coefficients. Inclusion of data from samples containing higher protein:RNA ratios often solves this problem by enhancing the population of the higher order complexes. One can also constrain the ratio of successive association constants or fix the sedimentation coefficient of the complexes based on a prediction of f/f₀ to reduce the number of adjustable parameters. Another problem that we have encountered is the formation of higher-order, nonspecific complexes that are not accounted for in the association model, leading to poor quality fits. SEDANAL only displays the first and last difference curve from each channel but by default it saves all of the curves in text files. We have written macros for IGOR Pro that automatically load and process these files that can be downloaded at: http://www.biotech.uconn.edu/auf/?i=aufftp. Examples of the output are shown below in Figures 3C and 4C.

Figure 3.

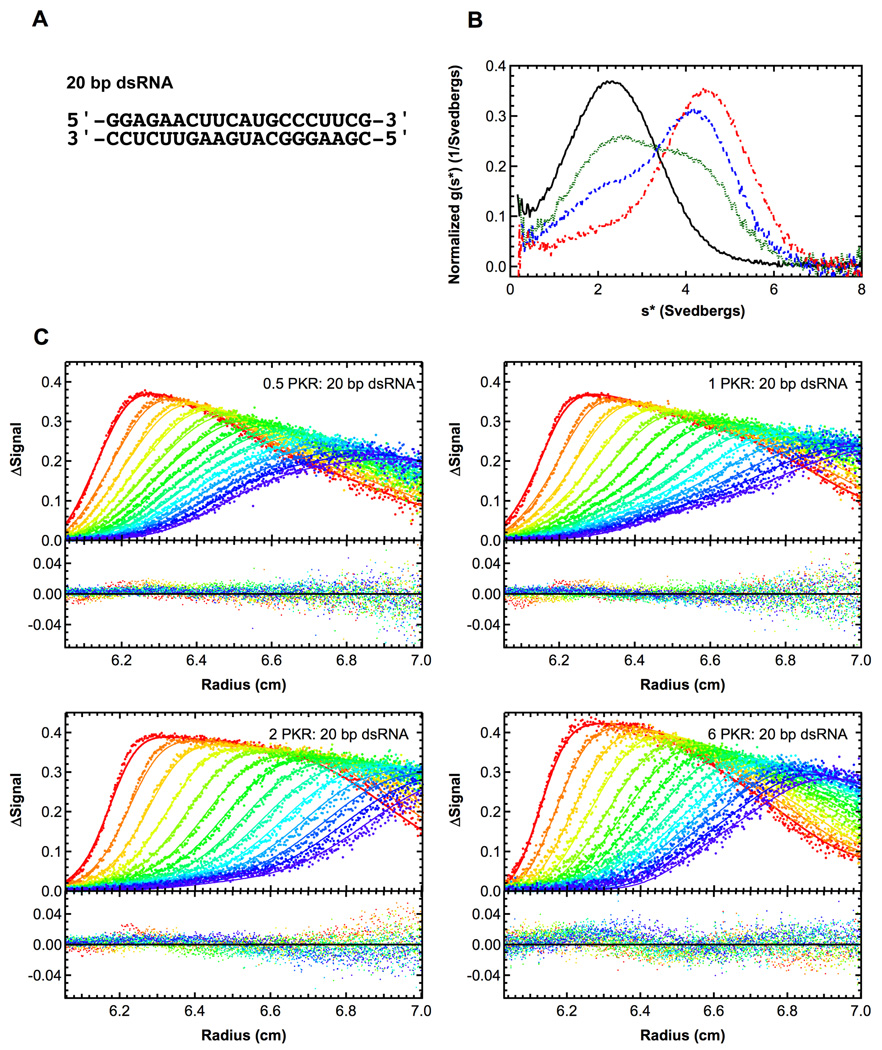
Sedimentation velocity analysis of PKR binding to a 20 bp dsRNA. A) RNA structure. B) Normalized g(s*) distributions of 1 µM dsRNA (black, solid), dsRNA + 0.5 eq. PKR (green, dot), dsRNA + 1 eq. PKR (blue, dash), dsRNA + 2 eq. PKR (red, dot-dash). The distributions are normalized by area. C) Global analysis of sedimentation velocity difference curves. The data were subtracted in pairs and four data sets at the indicated ratios of PKR: dsRNA were fit to 1:1 binding stoichiometry model. The top panels show the data (points) and fit (solid lines) and the bottom panels show the residuals (points). For clarity, only every 2^nd difference curve is shown. Conditions: rotor speed, 50,000 RPM; temperature, 20°C; wavelength, 260 nm.

Figure 4.

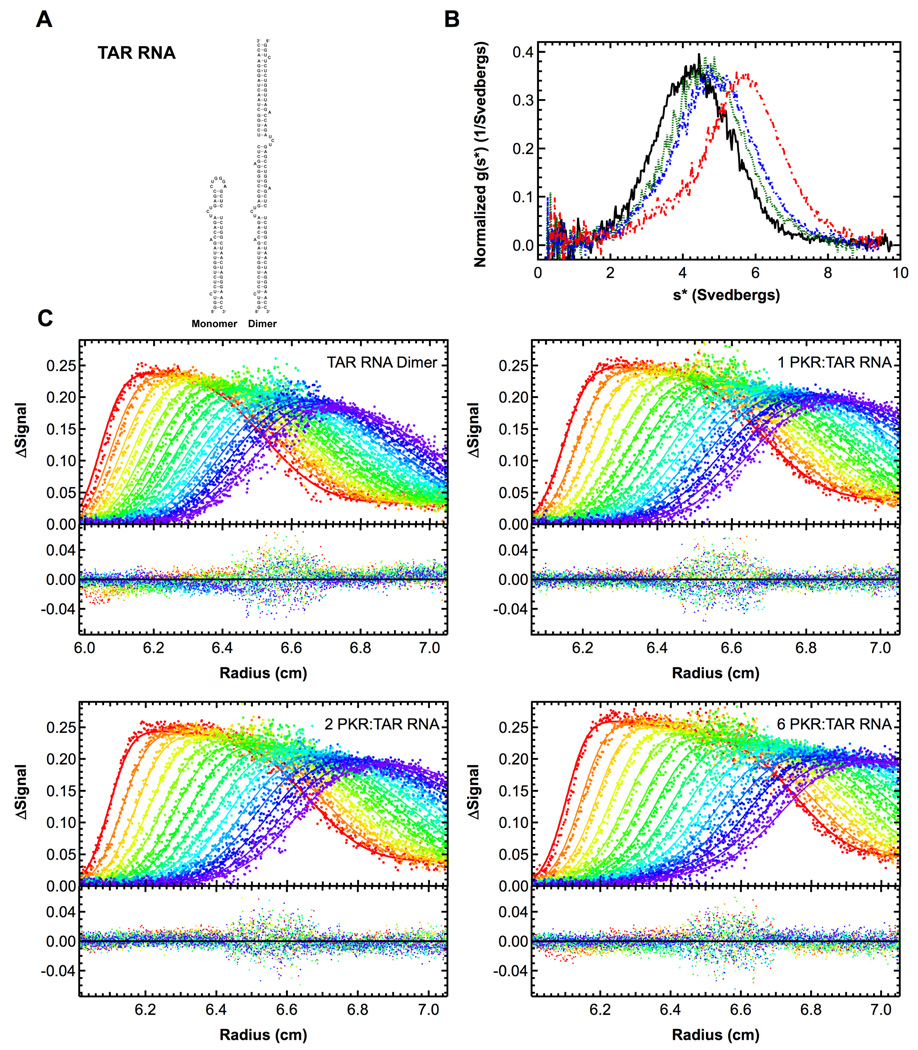
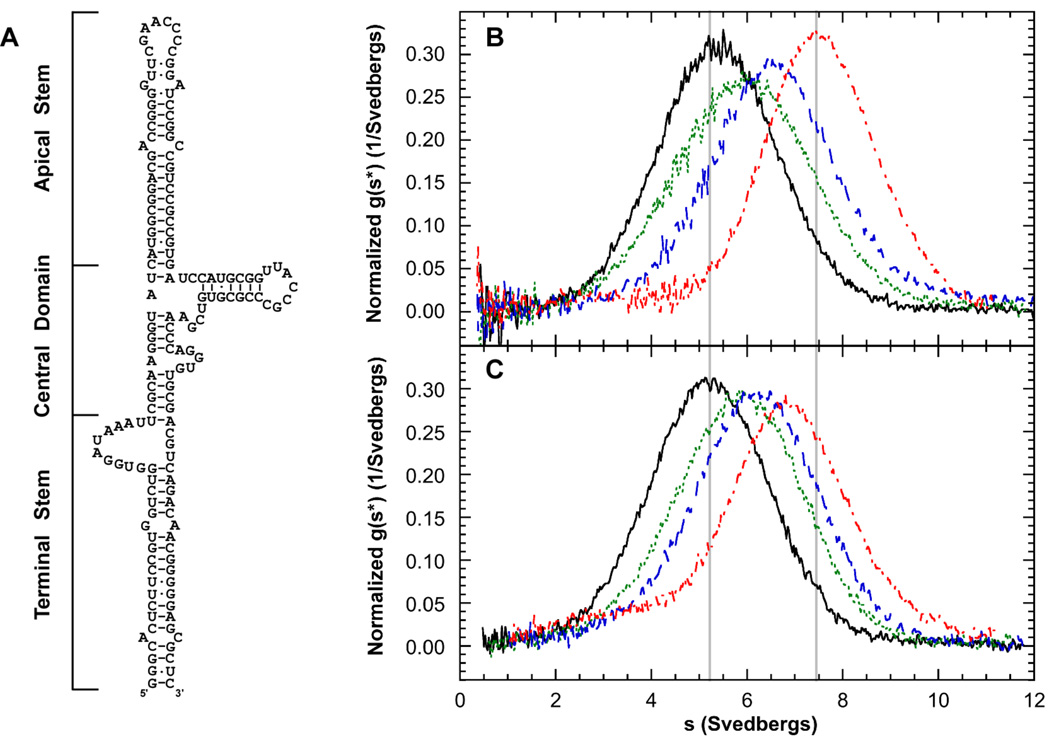
Sedimentation velocity analysis of PKR binding to HIV TAR RNA dimer. Measurements were performed in AU200 buffer at 20°C and 40,000 RPM. A) Structure of TAR monomer and dimer. B) Plot of normalized g(s*) distributions for 0.5 µM TAR dimer (black, solid), and 1 µM TAR dimer plus 1 eq. PKR (green, dot), 2 eq. PKR (blue, dash) or 6 eq. PKR (red, dot-dash). The distributions are normalized by area under the curve. C) Global analysis of the sedimentation difference curves. Scans within each dataset were subtracted in pairs to remove time-invariant background and fit to a 1:2 binding model using SEDANAL. Top panels show data points and the solid lines represent fitting results using the parameters presented in Table 1. Residuals for each fit are shown in the bottom panels. Only every 2^nd difference curve is shown for clarity. Measurements were performed in AU200 buffer at 20°C and 40,000 RPM using absorbance detection at 260 nm.

Examples

20 bp dsRNA

We have employed sedimentation velocity to define the interactions of PKR with a series of nonactivating and activating dsRNAs (Lemaire et al., 2008). Figure 3A shows a small (20 bp) nonactivating dsRNA used in these studies and figure 3B shows the normalized g(s*) distributions obtained from a titration of this RNA with PKR. In the absence of PKR, a single feature is observed near s = 2.5 S corresponding the free RNA. Upon addition of PKR, the dsRNA peak decreases in amplitude and a new feature develops which shifts to the right with increasing protein concentration. This behavior is consistent with rapidly reversible formation of an RNA-PKR complex. Assuming 1:1 binding, the limiting sedimentation coefficient of ~ 5 S corresponds to f/f₀ ~ 1.3, which is quite reasonable. Model-dependent analysis was performed in SEDANAL using the model

$$R+P\stackrel{K_{d1}}{\rightleftharpoons }\mathit{\text{RP}}$$ (3)

In this program, the sedimentation velocity scans are subtracted in pairs to remove systematic noise and the resulting difference scans are fit to Lamm equation solutions incorporating reversible association. A disadvantage of fitting difference scans is that the noise level is increased slightly. However, this method for removing systematic noise has the advantage of being model-independent, unlike the algebraic noise decomposition method used in SEDFIT and SEDPHAT (however, see (Schuck, 2010) for a contrary view). Figure 3C shows a global fit of the same data sets depicted in figure 3B to this model and Table 1 summarizes the results. The data fit well to this model with mostly random residuals and an RMS deviation close to the intrinsic noise level of the optical system. The best-fit K_d of 859 nM is fairly weak and provides an important baseline that we have used to compare dissociation constants for PKR binding to longer dsRNAs and structured RNAs (Heinicke et al., 2009; Launer-Felty et al., 2010). PKR 13 binds more strongly to longer dsRNAs. This decrease in K_d is consistent with the expected statistical effects for nonspecific protein–nucleic acid interactions where the number of binding configurations increases with the length of the dsRNA lattice (Cole, 2004).

Table 1.

PKR-RNA interaction parameters derived from sedimentation velocity analysis.

RNA	Model	Kd1 (nM)	Kd2 (nM)	s(RNA)a	s(RP)a	s(RP2)a	RMSb
20 bp	R + P ↔ RP	859 (746, 987)	--	2.52	5.14 (5.03, 5.25)	--	0.00961
TAR Dimer	R + P ↔ RP RP + P ↔ RP2	404 (257, 648)	2760 (1170,4540)	4.25	5.51 (5.02, 5.95)	7.70 (6.97, 8.60)	0.00794
A34U:U37A TAR Dimer	R + P ↔ RP RP + P ↔ RP2	331 (226, 490)	1470 (910, 2430)	4.31	5.29 (5.13, 5.47)	7.18 (6.86, 7.66)	0.00581
A34U:U37A TAR Dimer	R + P ↔ RP 2RP ↔ (RP)2	980	2.58 × 106	4.31	6.75	11.85	0.00785
VAI	R + P ↔ RP RP + P ↔ RP2	14 (3,41)	601 (359,1200)	5.34	6.78 (6.63, 7.04)	8.54 (8.30, 9.00)	0.00841
VAI + 5 mM Mg2+	R + P ↔ RP	334 (278,401)	--	5.29	7.18 (7.07, 7.29)	--	0.00691

Measurements were performed in AU 200 buffer or AU 200 buffer + Mg²⁺ at 20°C Parameters were obtained by global nonlinear least squares using SEDANAL. The values in parentheses correspond to the 95% joint confidence intervals obtained using the F-statistic to define a statistically significant increase in the variance upon adjusting each parameter from its best-fit value.

^aUncorrected sedimentation coefficient (Svedbergs).

^bRMS deviation of the fit in absorbance units.

TAR RNA dimer

The TAR RNA stem-loop has been used as a model system for studying PKR regulation by viral RNAs. However, earlier analyses have been complicated by the propensity of this RNA to form dimers (Figure 4A). We have examined PKR binding and activation by several TAR monomer and dimer constructs (Heinicke et al., 2009). For example, Figure 4B shows normalized g(s*) distributions obtained from a titration of wild-type TAR dimer with PKR. The pattern is more complex than observed for PKR binding to the 20 bp dsRNA. The maximum shifts from ~ 4.3 S for the free RNA up to ~ 5 S upon addition of 1–2 eq. PKR and then shifts more dramatically to ~ 6 S upon addition of 6 eq. of PKR. This behavior is consistent with sequential binding of two PKRs according to the model

$$\begin{array}{c}R+P\stackrel{K_{d1}}{\rightleftharpoons }\mathit{\text{RP}}\hfill \\ \mathit{\text{RP}}+P\stackrel{K_{d2}}{\rightleftharpoons }{\mathit{\text{RP}}}_2\hfill \end{array}$$ (4)

The data fit well to this model (Figure 4C) and the dissociation constants and sedimentation coefficients are shown in Table 1. This model was confirmed using a double mutant of TAR (A34U:U37A) that has an enhanced propensity to dimerize. It is interesting to note that the second PKR binds weaker than the first. This reduced affinity is not due to negative cooperativity but is a statistical effect and arises due to the reduction of the number of binding configurations upon binding of the first PKR. In both cases, the ratio K_d2:K_d1 is close to the value of 4 predicted for a simple model of a pair of noninteracting, identical sites in the TAR dimer.

An alternative model has been proposed in which binding of PKR to TAR enhances protein dimerization, resulting in formation of an (RP)₂ complex (McKenna et al., 2007a; McKenna et al., 2007b)

$$\begin{array}{c}R+P\stackrel{K_{d1}}{\rightleftharpoons }\mathit{\text{RP}}\hfill \\ 2\mathit{\text{RP}}\stackrel{K_{d2}}{\rightleftharpoons }{\left(\mathit{\text{RP}}\right)}_2\hfill \end{array}$$ (5)

This model does not fit the sedimentation velocity data for PKR binding to dimeric TAR. For example, the fit of the A34U:U37A data gives a higher RMSD relative to the sequential binding model (equation 4) and an exceptionally weak Kd₂ that is incompatible with activation data (Heinicke et al., 2009). These results highlight the capability of sedimentation velocity measurements to distinguish among closely related binding models.

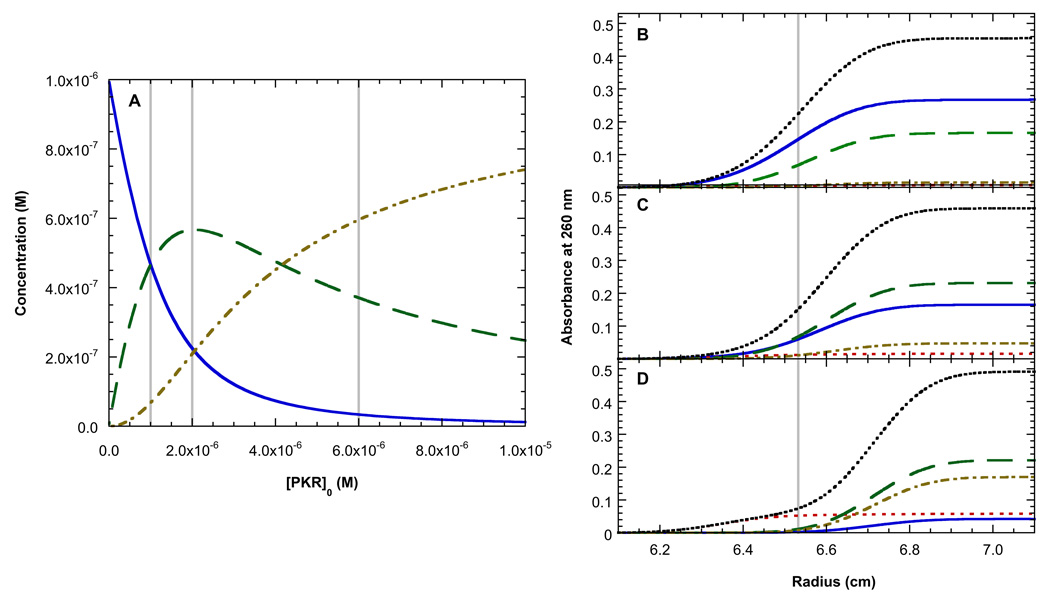
Analysis of the distribution of free RNA, protein and complexes as a function of PKR concentrations provides some insight into how we are to resolve the two binding events with good precision for the fitted parameters. Figure 5B shows the species distribution using the best-fit parameters in Table 1 with the actual PKR concentrations used for the analysis in Figure 4 (shown as gray lines). Figures 5B–C show the expected contributions of each species to the sedimentation velocity absorbance profile at the approximate midpoint of the run for each of the three RNA-protein mixtures. Reliable characterization of binding energetics requires that each of the species that participates in the equilibrium is present at measurable concentrations. At the lowest protein concentration (1 eq.), the concentrations of R, P and the RP complex are approximately equal (Figure 5A), facilitating the measurement of K_d1. However, owing to the low extinction coefficient of PKR at 260 nm, this species does not contribute much to the sedimentation velocity profile. This problem in mitigated to some extent in the global analysis in Figure 4 by fixing the protein:RNA ratios. At the two higher protein concentrations (2 eq. and 6 eq.) the RP₂ species becomes substantially populated, thereby facilitating measurement of Kd₂.

Figure 5.

Species distributions for binding of PKR to TAR RNA dimer. Concentrations were calculated based on the best fit parameters in Table 1 and the extinction coefficients of TAR and PKR at 260 nm. A) Molar concentration distributions for TAR RNA dimer (blue, solid), RP complex (green, dash) and RP₂ complex (tan, dot-dash). The vertical grey lines indicate the three PKR concentrations used in the experiment depicted in Figure 4. (B–C) Sedimentation velocity absorption profiles for TAR RNA dimer (blue, solid), PKR (red, dot), RP complex (green, dash), RP₂ complex (tan, dot-dash) and the total absorbance (black, dot) calculated for 1 eq. PKR (B), 2 eq. PKR (C) and 6 eq. PKR (D). The profile were simulated at a time corresponding to the middle of the sedimention run. The grey line indicates the midpoint of the total aborbance curve in B.

VAI

Adenovirus encodes VAI, a highly structured RNA inhibitor that binds PKR but fails to activate. VAI contains three major domains: the terminal stem, a complex central domain and an apical stem-loop (Figure 6A). We have characterized the stoichiometry and affinity of PKR binding to define the mechanism of PKR inhibition by VAI. Early enzymatic probing measurements suggested that Mg²⁺ alters VAI conformation (Clarke and Mathews, 1995), so we have characterized PKR binding in the absence and presence of divalent ion (Launer-Felty et al., 2010). Figure 6B shows that VAI has a sedimentation coefficient near 5 S and the peak shifts to the right upon binding PKR. At the highest PKR concentration (6 eq.) the main peak is located near 8.5 S with a shoulder near 3.5 S, corresponding to free PKR. Assuming a model of a single PKR binding leads to an estimate of a frictional ratio (f/f₀) of 1.28, which is much lower than the RNA alone or other PKR-RNA complexes. Thus, we fit the data to a model of sequential binding of two PKRs (Eq. 4) and the results are summarized in Table 1. The first PKR binds with quite high affinity (K_d = 14 nM) and the second binds with lower affinity (K_d = 601 nM). The uncorrected sedimentation coefficient of VAI decreases very slightly in the presence of Mg²⁺ (Table 1) but the effect is entirely due the increase in buffer density and viscosity. Thus, Mg²⁺ does not induce a large-scale change in VAI conformation. The sedimentation velocity results are supported by small angle X-ray scattering studies, where the radius of gyration (Rg) of VAI increases very slightly upon addition of Mg²⁺ (Launer-Felty et al., 2010). Although divalent ion does not induce a dramatic structural change in VAI, it does affect PKR binding. The magnitude of the shift in the g(s*) is significantly reduced (Figure 6B) and the data fit to a model of a single PKR binding with an affinity about 20-fold less than in of absence of Mg²⁺. The reduction in binding affinity is much more than the two- to three-fold expected based on nonspecific effects (Launer-Felty et al., 2010). We propose that VAI acts as an in vivo inhibitor of PKR because it binds only a single PKR under physiological conditions where divalent cation is present.

Figure 6.

Sedimentation velocity analysis of PKR binding to VAI RNA: effects of divalent ion. A) Structure of VAI. B) Normalized g(s*) distributions obtained in the absence of Mg²⁺: 0.4 µM VAI (black, solid), VAI + 1 eq. PKR (green, dot), VAI + 2 eq. PKR (blue, dash) and VAI + 6 eq. PKR (red, dot-dash). The vertical grey line on the left corresponds to the peak of the distribution for the free VAI RNA and the line on the right corresponds to the peak in the presence of 6 eq. of PKR. C) Normalized g(s*) distributions obtained in the presence of 5 mM Mg²⁺. The labeling is the same as in part B.

Conclusion

We have described protocols for designing and analyzing sedimentation velocity experiments for characterizing the stoichiometries and affinities of protein-nucleic acid interactions using several examples from our studies of the binding of PKR to RNA activators and inhibitors. Although conventional gel shift and filter binding measurements can be used to accurately define binding parameters, they are susceptible to artifacts associated with dissociation of complexes during the measurements. This can be a particular problem in the analysis of nonspecific interactions and we have emphasized free solution methods such as analytical ultracentrifugation in our PKR work. Recently we have taken advantage of efficient algorithms for fitting sedimentation velocity data to Lamm equation solutions incorporating reversible association. Although multiwavelength sedimentation equilibrium measurements work well for characterizing protein – nucleic acid interactions, the velocity experiments have several advantages: they are faster, less sensitive to formation of aggregates that often accompanies formation of protein-nucleic acid complexes and are generally easier to analyze. We have found that data collected at a single wavelength (typically, 260 nm) provides sufficient information to characterize multistep association reactions. This is fortunate, given the limitations in the current absorbance system in the XL-A. The ability to collect absorbance data more rapidly at multiple wavelengths in new instruments (Colfen et al., 2009) will certainly enhance the power of sedimentation velocity to define more complex interactions. A disadvantage of the velocity approach is the necessity to fit for the sedimentation coefficient of the complex. This complicates data analysis by requiring an additional adjustable parameters that can be strongly correlated with the dissociation constant if it is not possible to achieve high population of the complex. On the other hand, the resulting hydrodynamic information can be valuable in developing structural models of the complex.