GFT projection NMR spectroscopy for proteins in the solid state

Abstract

Recording of four-dimensional (4D) spectra for proteins in the solid state has opened new avenues to obtain virtually complete resonance assignments and three-dimensional (3D) structures of proteins. As in solution state NMR, the sampling of three indirect dimensions leads per se to long minimal measurement time. Furthermore, artifact suppression in solid state NMR relies primarily on radio-frequency pulse phase cycling. For an n-step phase cycle, the minimal measurement times of both 3D and 4D spectra are increased n times. To tackle the associated ‘sampling problem’ and to avoid sampling limited data acquisition, solid state G-Matrix Fourier Transform (SS GFT) projection NMR is introduced to rapidly acquire 3D and 4D spectral information. Specifically, (4,3)D (HA)CANCOCX and (3,2)D (HACA)NCOCX were implemented and recorded for the 6 kDa protein GB1 within about 10% of the time required for acquiring the conventional congeners with the same maximal evolution times and spectral widths in the indirect dimensions. Spectral analysis was complemented by comparative analysis of expected spectral congestion in conventional and GFT NMR experiments, demonstrating that high spectral resolution of the GFT NMR experiments enables one to efficiently obtain nearly complete resonance assignments even for large proteins.

Introduction

In recent years, solid-state NMR (SSNMR) spectroscopy has advanced as a powerful tool for comprehensive, high-resolution structural studies of proteins (McDermott et al. 2000; Castellani et al. 2002; Bockmann et al. 2003). Significant methodological developments include effective heteronuclear decoupling schemes (Bennett et al. 1995; Fung et al. 2000; Detken et al. 2002), robust, band-selective heteronuclear polarization transfer schemes employing adiabatic (Baldus et al. 1996) and SPECIFIC CP (Baldus et al. 1998) elements, broadband DARR homonuclear polarization transfer methods (Takegoshi et al. 2001; Morcombe et al. 2004) and improvements in MAS probes in terms of both B₁ homogeneity (Paulson et al. 2004) and reduction of electric field-induced sample heating (Stringer et al. 2005; Doty et al. 2006).

As a result, it is now possible to determine the three-dimensional (3D) structures of macroscopically disordered solid proteins at atomic-resolution (Franks et al. 2008; Wasmer et al. 2008) and study site-resolved dynamics using SSNMR spectroscopy (Lorieau and McDermott 2006). This has opened new avenues to study important biological systems such as membrane proteins (which constitute up to ~30% of the genomes of living organisms) and amyloid fibrils, which are otherwise very difficult to approach using the traditional structural biology tools. Moreover, SSNMR spectroscopy can provide structural information complementary to that obtained from X-ray crystallography or solution state NMR. Various multidimensional homonuclear and heteronuclear NMR experiments have been developed akin to those used in solution-state NMR spectroscopy (Hohwy et al. 1999; Hong 1999; Rienstra et al. 2000; Detken et al. 2001; Baldus 2002). The improved resolution and additional unique correlations of multidimensional experiments have been employed to assign a number of proteins in the solid state (McDermott et al. 2000; Pauli et al. 2001; Igumenova et al. 2004a, b; Marulanda et al. 2004; Franks et al. 2005; Pintacuda et al. 2007; Sperling et al. 2010). Novel 4D experiments correlating interresidue ¹³C and ¹⁵N chemical shifts to establish unique connectivities and increasing the unique correlation information of a spectrum have been demonstrated (Franks et al. 2007).

Given the unambiguous correlation information and improved resolution of high dimensional correlation experiments, spectra with very high dimensionality are attractive. However, in the “sampling-limited” NMR data acquisition regime, conventional acquisition of multidimensional data leads to use of valuable spectrometer time to sample indirect dimensions but not to achieve sufficient signal-to-noise ratios (Szyperski et al. 2002; Kim and Szyperski 2003; Szyperski and Atreya 2006); typical two-dimensional (2D), three-dimensional (3D), and four-dimensional (4D) NMR spectra need minutes, hours or days, respectively, for completion, whereas five- and six-dimensional (5D, 6D) experiments are not feasible given the time restraints. In view of the staggering increase of minimal measurement time with increasing dimensionality, which constitutes the ‘NMR sampling problem’ (Szyperski and Atreya 2006), an attractive approach is to encode the information of a high-dimensional spectrum in lower-dimensional spectra. This forms the basis of G-matrix Fourier transform (GFT) projection NMR spectroscopy (Kim and Szyperski 2003; Atreya and Szyperski 2004; Atreya et al. 2005; Eletsky et al. 2005; Liu et al. 2005; Shen et al. 2005; Szyperski and Atreya 2006; Atreya et al. 2007; Zhang et al. 2008). GFT NMR is based on joint sampling of chemical shifts in a single dimension, such that linear combinations of chemical shifts are phase-sensitively detected in a pure absorption mode and then edited into sub-spectrum by linear combination. Thereby, GFT NMR enables one to speed up NMR data collection by orders of magnitude. Importantly, the editing with the G-matrix transformation ensures that the number of peaks in each of the sub-spectra is the same as in the original high-dimensional parent spectrum. Moreover, since linear combinations of shifts are registered, the spectral width in the GFT dimension equals the sum of the spectral widths of the spectral widths of the jointly sampled shifts, resulting in increased signal dispersion.

Here, we introduce SS GFT NMR spectroscopy which meets with an urgent demand considering that artifact suppression in solid state NMR relies primarily on radio-frequency pulse phase cycling: for an n-step phase cycle, the minimal measurement times of both 3D and 4D spectra are increased n times. Specifically, we implemented SS GFT NMR experiments for rapid resonance assignment. These experiments were recorded for 56-residue protein GB1, and their utility for resonance assignment is discussed.

Materials and methods

Sample preparation and NMR spectroscopy

Protein GB1 was prepared with ¹⁵N,¹³C-labeling as a microcrystalline solid as described previously (Franks et al. 2005); an 18-mg (2.7 μmol) quantity was packed in 3.2 limited speed rotor (Varian, Inc., Fort Collins, Colorado). NMR experiments were performed on a four-channel, 500 MHz Varian Infinity Pulse Spectrometer, equipped with a Balun^{™ 1}H-¹³C-¹⁵N 3.2-mm MAS probe. The MAS rate was maintained at 11,111 ± 3 Hz, and the variable temperature unit was set to 273 K with a flow rate of 100 standard cubic feet per hour (scfh), resulting in a sample temperature of 280 ± 4 K as determined by methanol calibration (Van Geet 1968).

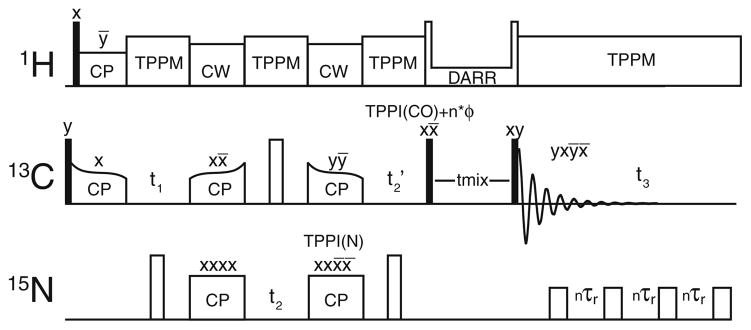
The basis for SS GFT (4,3)D (HA)CANCOCX is the three-channel correlation scheme (Fig. 1) as previously utilized for 4D CNCC spectroscopy (Franks et al. 2007). To indicate which chemical shifts are jointly sampled, the corresponding nuclei are underlined in the name of the experiments (Kim and Szyperski 2003). ¹³C Boltzmann polarization is combined with the cross polarized signal from ¹H, utilizing a short CP time to maximize signal intensity on C^α sites. Following t₁ evolution on CA[i], CA[i] to N[i], where i denotes the residue number, SPECIFIC CP (Baldus et al. 1998) transfer is achieved using conditions described below. After frequency labeling with the chemical shifts of N[i] during t₂, polarization is transferred again in band-selective manner, principally to CO[i−1]. CO chemical shifts are then jointly sampled with N[i] during t₂ but scaled with a factor κ (Kim and Szyperski 2003). Following broadband homonuclear DARR mixing, ¹³C signals are detected in the direct dimension under rotor-synchronized ¹⁵N decoupling. Throughout all chemical shift evolution and detection periods, TPPM ¹H-decoupling (Bennett et al. 1995) is applied, whereas high power continuous wave decoupling is utilized during the SPECIFIC CP transfers.

Fig. 1.

Pulse sequence used for (4,3)D HA(CA)NCOCX GFT experiments. Filled and open rectangles represent π/2 and π pulses, respectively. ¹⁵N decoupling was applied during acquisition by a π train with each pulse separated by 10 rotor periods. Efficient, band selective ¹⁵N–¹³C (N–CO) and ¹³C–¹⁵N (CA–N) polarization transfer were achieved with adiabatic SPECIFIC CP (Baldus et al. 1998), while DARR (Takegoshi et al. 2003) (RAD, Morcombe et al. 2004) was used for broadband ¹³C–¹³C mixing. Time Proportional Phase Incrementation (TPPI) (Marion and Wuthrich 1983) was applied to each pulse following time evolution periods. An additional cumulative phase was added the following t₂′ (nφ_arb) for manipulation of the spectral window (Keeler and Neuhaus 1985). Independent cosine and sine modulated subspectra are recorded by adjusting the starting point of the TPPI phases added to the second ¹⁵N CP and the ¹³C π/2 prior to mixing

The widths for high power π/2 radio-frequency (rf) pulses on ¹H, ¹³C, and ¹⁵N were 2.0, 3.0, and 5.0 μs, respectively. TPPM decoupling conditions were ${\omega }_1^{\text{H}}/2\pi =72\text{kHz}$, 16°, 7.6 μs. CA-N and N-CO SPECIFIC CP (Baldus et al. 1998) conditions were optimized using tangent ramp cross polarization (CP) was utilized for polarization transfers following the notation of Detken et al. (Detken et al. 2001) with slight modification (Franks et al. 2007):

$${\omega }_1^{\text{X}}(t)={\omega }_1^{\text{HH}}+\mid \beta \mid ·tan\left(\alpha ·\left[t-\frac{\tau }{2}\right]\right),$$ (1)

where the adiabaticity parameter is defined as

$$\alpha =\frac{2}{\tau }arctan\left(\frac{\mathrm{\Delta }}{\beta }\right).$$ (2)

Constant amplitude spin lock fields were utilized on ¹H and ¹⁵N, and tangential amplitude ramps applied to the ¹³C channel. The first (H–C) CP period was 450 μs with ${\omega }_1^{\text{H}}/2\pi =80\text{kHz}$ and ${\omega }_1^{\text{C}}/2\pi =70\text{kHz}$ (Δ/2π = 8 kHz; β/2π = −3.5 kHz), the second (CA-N) CP period was 6 ms with ${\omega }_1^{\text{C}}/2\pi \sim 17\text{kHz}$ (Δ/2π = 2 kHz; β/2π = 400 Hz) and ${\omega }_1^{\text{N}}/2\pi \sim 28\text{kHz}$. The off-resonance N-CO transfer step had a duration of 8 ms with ${\omega }_1^{\text{C}}/2\pi$ of 36.5 kHz (Δ/2π = 2 kHz; β/2π = −400 Hz) and ${\omega }_1^{\text{N}}/2\pi$ of ~28 kHz. CW decoupling with ${\omega }_1^{\text{H}}/2\pi =95\text{kHz}$ was applied during both C–N and N–C CP periods. DARR (Takegoshi et al. 2001, 2003; Morcombe et al. 2004) mixing (18 ms) was applied with the ${\omega }_1^{\text{H}}/2\pi =11\text{kHz}$ to yield ¹³C side-chain correlations.

For (4,3)D (HA)CANCOCX, the maximal evolution times were t₁(¹³CA, 32 × 135 μs) = 4.32 ms, t₂(¹⁵N, 48 × 180 μs) = 8.64 ms, t₂′(¹³CO, 48 × 90 μs; κ = 0.5) = 4.32 ms and t₃(Acquisition) = 23.04 ms (1,536 × 15 μs), while the recycle delay was set to 2 s. 4 transients per increment (corresponding to a minimal 4-step phase cycle) were acquired, yielding a total measurement time of 10.8 h.

For (3,2)D (HACA)NCOCX, frequency labeling on CA is omitted and the maximum evolution times were t₁(¹⁵N, 96 × 180 μs) = 17.28 ms, t₁′(¹³CO, 96 × 90 μs; κ = 0.5) = 8.64 ms, and t₂(Acquisition) = 23.04 ms (1,536 × 15 μs). 8 transients were acquired per FID yielding a total measurement time of 1.3 h. Chemical shifts are referenced to the external standard adamantane at 40.48 ppm. Spectra were processed in the program nmrPipe (Delaglio et al. 1995) and analyzed using the program Sparky 3.0 (Goddard and Kneller 2006).

NMR data processing

The (4,3)D experiments were processed as follows. In the direct dimension, three points were backwards linear predicted, Lorentzian–Gaussian transformations with 60 Hz net line-broadening were applied, and the time domain data multiplied with a 72° phase shifted sine-bell function, zero-filled to 2048 points, and Fourier transformed. In t₂(¹⁵N;¹³C′), a Lorentzian-Gaussian transformation with 50 Hz net line-broadening was applied, time domain data were multiplied by a 81° phase shifted sine-bell, zero filled to 256 points, and Fourier transformed. In t₃(¹³C^α), time domain data were expanded by 8 points by linear prediction, subject to a Lorentzian–Gaussian transformation with 80 Hz net line-broadening, multiplied with 81° phase shifted sine-bell function, zero-filled to 128 points and Fourier transformed.

The (3,2)D experiments were processed as follows. In the direct dimension, three points were backward linear predicted. The resulting time domain data were (1) subjected to a Lorentzian-Gaussian transformation with 60 Hz net broadening, (2) multiplied by a 72° phase shifted sine-bell function, (3) zero-filled to 4,096 points, (4) Fourier transformed, and (5) subjected to a polynomial baseline correction. The indirect dimensions were processed with Lorentzian–Gaussian transformations with 20 Hz net line-broadening, zero-filled to 1,024 points and Fourier transformed.

The (4,3)D and (3,2)D sub-spectra constituting the GFT NMR experiments were obtained by linearly combination in the frequency domain (Kim and Szyperski 2003).

Simulations

Simulations were performed in order to estimate the hypothetical spectral resolution of GFT NMR spectra for other proteins with known chemical shifts. The procedure followed those employed previously by (Tycko 1996) and (Franks et al. 2007), but with suitable adjustments for the line-widths of peaks in the GFT-dimensions, where the line-widths of jointly sampled shifts add up if non-constant time evolution periods are implemented ((Kim and Szyperski 2003); Fig. 1). As such, several proteins ranging in molecular weight from 6 to 81 kDa, were considered for calculation of the linear combinations of chemical shifts as registered in the GFT NMR experiments. In addition, the definition of spectral degeneracy (and conversely, resolution) is modified as follows. The spin system of residue i is considered ‘degenerate’ if all N, CA, CB and C′ resonance frequencies are within one line width of any other frequency j in dimension m; this is the case when the following inequality.

$$\mid {\wedge }_{i,m}-{\wedge }_{i,m}\mid \le 1{\text{w}}_m$$ (3)

is satisfied for all values of j and m, where ∧_i,m denotes the resonance frequency of interest and lw_m represents the line width.

For the GFT dimension, one then has that

$${\wedge }_{i,m}={\wedge }_{(i,\text{X})}\pm {\wedge }_{(i,\text{Y})},$$ (4)

where X and Y are the jointly sampled dimensions. The simulations were performed under a variety of assumed linewidths, in order to assess the relative benefits of enhanced digital resolution in indirect dimensions, which is available with SS GFT NMR. The directly detected line-width was assumed to be 0.5 ppm (which is typical for ¹³C resonances in uniformly ¹³C labeled solid proteins at 500 MHz).

Results and discussion

Benefits of SS GFT NMR

For both solution and state-state NMR, the benefits of increasing the dimensionality are well known. Arguably, the benefit of increased dimensionality is higher in the solid state than in solution NMR, since resolution in ¹³C-¹³C and ¹⁵N-¹³C SS 2D planes is not yet as high as typically observed in 2D ¹H-¹⁵N planes of proteins in solution. We have previously demonstrated the advantages arising from increasing the number of dimensions from three to four for several solid proteins and with various line widths (Franks et al. 2007). Nonetheless, practical limitations—including finite sampling, probe and instrument stability over long measurement times—prevent one from recording the high dimensional experiments with the desired maximal evolution times in the indirect dimensions. Hence, the use of GFT NMR spectroscopy (Kim and Szyperski 2003) to speed up the acquisition of high-dimensional spectral information in the solid state represents a valuable approach.

To guide implementation of SS GFT NMR experiments, we predicted the number of resolved spin systems in conventional and GFT spectra for protein GB1 (Table 1). For (4,3)D (HA)CANCOCX, which was recorded in 10.8 h, one obtains in agreement with the experimental results, vide infra) that 53 out of 55 spin systems are resolved: only the signals arising from E15 and E42 are not resolved in at least one of the two sub-spectra. If the 4D congener experiment is recorded within the same amount of time, maximal evolution times must be dramatically reduced and the signals of only 41 residues can be expected to be resolved. It would require more than a week to record the 4D experiment with the same maximal evolution times as the (4,3)D GFT NMR experiment; yet no additional peaks would be resolved. An even more pronounced situation is encountered when comparing (3,2)D GFT and conventional 3D experiments: the use of GFT NMR experiments recorded in 1.3 h resolves 54 of 55 possible signals, while the conventional congeners recorded with the same measurement time provides too little resolution to be practically useful. Acquisition of the conventional 3D spectrum with the same maximum evolution time as in the GFT experiment would require more than 30 times as much measurement time. Considering that, in spite of the short measurement times, the GFT spectra exhibit adequate experimental sensitivity (Table 2), we conclude that GFT NMR represents a valuable approach to avoid sampling limited data acquisition (Szyperski et al. 2002) for proteins in the solid state.

Table 1.

Number of spin systems of GB1 expected to be resolved in GFT and conventional NMR spectra recorded with either the same measurement time or maximal evolution times

Experiment type	Time (h)a	Digital resolution (ppm)b	Number of resolved peaksc
(HA)CANCOCX (4,3)D GFT	10.8	(15N) 2.3 (13CA, 13CO) 1.8	53 (50, 48, 50, 47)
(HA)CANCOCX 4D	10.8	(15N) 4.6 (13CA) 4.9 (13CO) 5.5	41
(HA)CANCOCX 4D	172.8	(15N) 2.3 (13CA, 13CO) 1.8	53
(HA)CONCACX (4,3)D GFT	10.8	(15N) 2.3 (13CA, 13CO) 1.8	53 (50, 48, 50, 39)
(HA)CONCACX 4D	10.8	(15N) 4.6 (13CA) 4.9 (13CO) 5.5	35
(HA)CONCACX 4D	172.8	(15N) 2.3 (13CA, 13CO) 1.8	53
(HACA)NCOCX (3,2)D GFT	1.3	(15N) 1.1 (13CO) 0.9	54 (40, 48, 53, 37)
(HACA)NCOCX 3D	1.3	(15N) 9.1 (13CO) 11.1	18
(HACA)NCOCX 3D	42.6	(15N) 1.1 (13CO) 0.9	54
(HACO)NCACX (3,2)D GFT	1.3	(15N) 1.1 (13CA) 0.9	52 (52, 37, 41, 28)
(HACO)NCACX 3D	1.3	(15N) 9.1 (13CA) 11.1	18
(HACO)NCACX 3D	42.6	(15N) 1.1 (13CA) 0.9	55

^aTimes were fixed to match data taken for this study

^bAcquisition linewidth was assumed to be 0.5 ppm, digital resolution values were taken from experiments performed in this study

^cNumber of CA and/or CB resonances for each amino acid residue resolved in any sub-spectrum, parentheses indicate number of sum, difference, central peak, and both sum and difference frequencies resolved in each simulated GFT experiment for GB1

Table 2.

Average signal-to-noise ratios for spectra

Experiment type	Measurement time (h)	Average signal to noise	Simulated resolved residues	Actual resolved residues
(HA)CANCOCX (4,3)D GFT	10.8
Sum		13.5	50	55
Difference		13.3	48	55
(HACA)NCOCX (3,2)D GFT	1.3
Sum		11.6	40	41
Difference		12.9	48	39
Central peaks		24.0	53	54

Comparable benefits of GFT NMR are expected when considering the hypothetical resolution expected for other proteins (Table 3), including Het-S fibrils (M_w = 5 kDa for the rigid domain), bovine pancreatic trypsin inhibitor (BPTI; M_w = 6 kDa), ubiquitin (M_w = 8.6 kDa), maltose binding protein (MBP; M_w = 42 kDa), and malate synthase G (MSG; M_w = 82 kDa). For the class of small (M_w < 10 kDa) proteins, it is expected that the (3,2)D experiments would resolve ≥80% of the spin systems in at least one sub-spectrum, and approximately half of the spin systems all sub-spectra. With the addition of another indirect dimension in the (4,3)D congeners, one expects a resolution that is either approximately the same or greater than in the conventional 3D and 4D experiment. For example, one can expect that >70% of the spin systems of MBP (42 kDa) are resolved in all (4,3)D sub-spectra, while 90% are expected to be resolved in at least one sub-spectrum. Respectively, 46 and 78% are expected to be resolved for MSG (82 kDa).

Table 3.

Predicted resolution of (3,2)D and (4,3)D SS GFT NMR compared with conventional experiments

Proteina (size)b		(4,3)D (HA)CANCOCX	(4,3)D (HA)CONCACX	(3,2)D (HACO)NCACX	(3,2)D (HACA)NCOCX
Het-Sj 45(43)	Centrald	42	43	43	42
	Sume	41	40	33	31
	Difff	42	35	31	30
	Allg	41	34	22	21
	Anyh	42	43	43	34
	Conventionali	42	42	43	42
GB1 56 (56)	Central	55	55	52	54
	Sum	55	53	37	41
	Difference	55	55	43	48
	All	51	53	28	38
	Any	55	55	49	54
	Conventional	55	55	55	55
BPTI 58 (58)	Central	53	53	47	48
	Sum	48	46	28	37
	Difference	53	44	23	30
	All	46	39	17	24
	Any	57	56	47	49
	Conventional	57	55	53	53
Ubiquitin 76 (76)	Central	71	71	69	67
	Sum	74	67	50	48
	Difference	74	71	48	52
	All	74	61	38	40
	Any	75	75	72	68
	Conventional	75	75	71	71
MBP 370 (356)	Central	282	275	144	167
	Sum	292	222	88	110
	Difference	295	202	76	112
	All	256	150	43	77
	Any	339	306	170	187
	Conventional	347	320	275	282
MSG 723 (711)	Central	413	409	162	186
	Sum	434	296	100	114
	Difference	438	282	81	137
	All	334	193	48	85
	Any	564	506	206	226
	Conventional	635	604	409	413

Previously unassigned chemical shift values were assumed to be a common (degenerate) value of 999.9 ppm. Het-S assignments are missing 10 ¹³C′ carbons

^aThe chemical shift values for each protein were derived from the following BMRB entries and references: Het-S fibrils (Siemar et al. 2005,2006) GB1 in the solid state (BMRB 15156) (Franks et al. 2005); BPTI in solution (BMRB 5358) (McDermott et al. 2000); ubiquitin in solution (BMRB 5387) (Flynn et al. 2002); maltose binding protein in solution (BMRB 4354) (Gardner et al. 1998) malate synthase G in solution (BMRB 5471) (Tugarinov et al. 2002)

^bThe size indicates the total number of residues present in the protein and, in parentheses, the number resolved with ideal resolution (0.001 ppm). Due to the absence of amide ¹H resonances in our simulations, not all residues are resolved in the simulated spectra at this limit

^c1 ppm linewidths are assumed for each evolution period, with the synchronous dimension having an additive linewidth, and 0.5 ppm in the direct dimension

^dCentral peaks are calculated assuming only X dimension (where X is the first component of the synchronously evolved (X, Y) dimension)

^eSummation peaks are calculated as Ω_X + Ω_Y

^fDifference peaks are calculated as Ω_X − Ω_Y

^gThe resonance is counted only if it is resolved in each of the summation, difference, and central peaks spectra

^hThe resonance is counted if it is resolved in one or more of the summation, difference, and central peaks spectrum

ⁱPresuming that the full grid of the XD experiment is sampled; this experiment would require an order of magnitude more time than the corresponding set of SS GFT data simulated here

^jThe simulations include amide Nitrogen, α-carbon, β-carbon, and Carbonyl only

In contrast to solution NMR, linewidths in SS NMR do not depend on the molecular weight M_w. Considering that the S/N scales with the number of protein molecules in the sample which itself scales with the inverse of M_w, it is expected that S/N ~1/M_w. Hence, we anticipate that the above prediction of resolved signals constitutes a valuable guide for practical applications of SS GFT NMR.

Implementation of GFT NMR experiments

We consider the minimum dimensionality required to assign a protein with GFT NMR as the lowest number of dimensions with which resolving nearly all (~90%) of the experimentally observed spin systems are resolved. As demonstrated above, conventional 3D or (3,2)D GFT experiments accomplish this goal. For example, even for a small protein such as GB1 with especially well resolved spectra, 2D N–C experiments are not sufficient to obtain unambiguous assignments. Rather, 3D spectra were needed to identify overlapped spin systems arising from the helix, as well as frequently occurring residue types (such as threonine). Therefore, we anticipate that for most proteins with M_w >10 kDa, at least (4,3)D experiments will be required to derive nearly complete assignments.

Hence we adapted the previously reported CANCOCX 4D sequence (Franks et al. 2007) to record (4,3)D (HA)CANCOCX (Fig. 1), where the t₂(¹⁵N) and t₃(¹³CO) evolution periods are jointly sampled. Independent cosine and sine modulated sub-spectra for GFT NMR data acquisition are formed by shifting the initial TPPI phases marked by φ₂ and φ₂′ by 0° or 90°, respectively (Fig. 1). φ₂ and φ₂′ are incremented for each t₂ time step to provide the desired modulations. The four-step phase cycle (Fig. 1) was adequate to remove artifacts caused by over the remaining ¹³C polarization from the initial broadband ¹H-¹³C cross polarization. The carrier was placed at 55 ppm, resulting in an offset of ~120 ppm for the CO region, which is much larger than the desired spectral width, in this case 44 ppm, in order to maintain rotor-synchronization for the isotropic chemical shift evolution. Thus, the CO region is folded three times. Greater flexibility in the choice of the ¹³C carrier could be afforded by utilizing TPPI (Marion and Wuthrich 1983) with phase increments different from 90° in order to adjust the spectral window (Keeler and Neuhaus 1985). The SPECIFIC CP (Baldus et al. 1998) transfers were >95% selective, i.e. <5% of the polarization before mixing was observed on an unintended nucleus. One can envision using broadband transfers along with GFT encoding given carefully considered joint sampling.

The choice of jointly sampled chemical shifts was made by considering spectral dispersion and linewidth. Correlations of inter-residue CA signals have been shown to be desirable for assignments (Seidel et al. 2004; Heise et al. 2005; Franks et al. 2007), resulting in well resolved spectra. For (4,3)D (HA)CANCOCX, the CA dimension is thus chosen to be an independently sampled dimension. The N dimension also provides critical connectivity information, so that these shifts are measured in the central peak spectrum. Since the CO dimension is used primarily to enhance resolution, the CO dimension was jointly sampled with N to measure Ω(N+CO) and Ω(N−CO) in the two sub-spectra of (4,3)D (HA)CANCOCX. Including ¹H chemical shifts is desirable, as this will encode a new information set and enhance sensitivity; however, we made no attempt to do so because both the sample and probe were not designed for such experiments (Chevelkov et al. 2006; Zhou et al. 2007a).

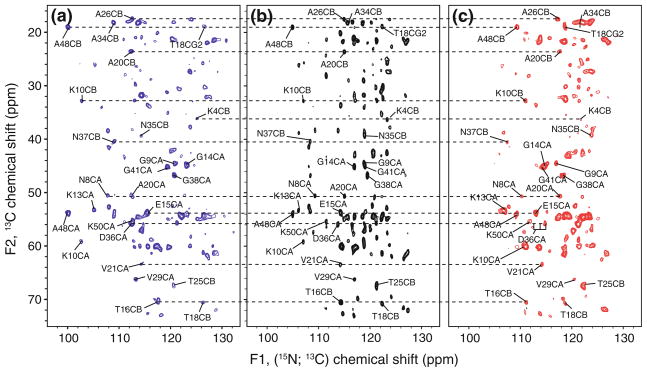
For (3,2)D (HACA)NCOCX, CA evolution is omitted. Despite its short measurement time (26.6 min), however, the central peak (HACA)NCOCX spectrum (Fig. 2b) exhibits average signal-to-noise ratios (SNR) ranging from ~10 to ~40. Peak detection is similar to 2D N(CO)CX, except that sidechains nitrogen signals of Asn (¹⁵Nδ2) and Gln (¹⁵Nε2) are not observed, since the N-CA SPECIFIC CP mixing times (~6–8 ms) chosen for the current implementation are not sufficiently long to transfer substantial polarization from Cβ to Nδ2 (in Asn) or Cγ to Nε2 (in Gln).

Fig. 2.

(3,2)D (HACA)NCOCX: subspectra comprising signals located at sums (a) and differences (b) of ¹⁵N and ¹³C′ chemcial shifts along F1 are shown on the left and right, respectively, of the central peak spectrum comprising signals at ¹⁵N chemical shifts. Positive contours above 6 times the RMS noise floor are drawn for each spectrum with contour separation factor of 1.3. The total measurement time was 87 min (t₁ 96 × 180 μs; t₁′ 96 × 90 μs). As an illustration, selected peaks are labeled and connected. Labels correspond to the destination peak with the source atom consisting of the succeeding residue’s amide ¹⁵N and a ¹³CO component as appropriate. Dashed horizontal lines were added to connect peaks from the same residue

In the two sub-spectra of (3,2)D (HACA)NCOCX, the expected improvement in resolution yields that 78% (43) of the possible (55) residues in the protein GB1 are readily identified in both sub-spectra (Fig. 2a, c). For all but one case, overlapping peaks in one sub-spectrum are resolved in the other. For example, the difference spectrum peaks of G41 and G14 are severely overlapped. However, the summation peaks are well resolved. In the case of A26 CB, the opposite is true: the summation peak is not entirely resolved, but the difference peak is resolved. In cases where ambiguity remained in the sum and difference spectra, central peaks often aided in confirming the appropriate peaks.

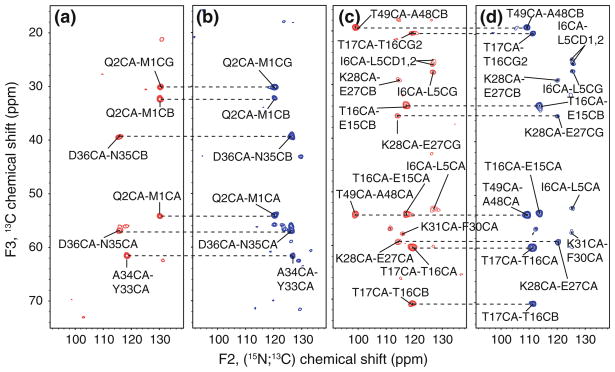
The inclusion of a third, independently sampled dimension resulted in the resolution of all possible spin systems. Among all the N, C′, CA, and CB resonances of GB1, only the Y33 CB resonance (which is near a rotational resonance condition at this MAS rate) was not observed. In addition, signals from many CG and CD signals are observed; only residues with long side chains consisting of more than 4 carbon atoms (e.g., aromatic residues and lysines) could not be completely assigned. It has been shown, however, that the use of a longer DARR mixing time would enable one to observe the missing signals (Franks et al. 2007). Two representative planes of the (4,3)D (HA)CANCOCX experiment are shown in Fig. 3, where three residues are easily identified due to the distinct peak pattern (Fig. 3a, b). The corresponding spin systems have nearly identical CA chemical shifts (within 0.1 ppm of 56.03 ppm, A34 CA = 56.1, D36 and Q2 = 55.9 pm). The mean position of the chemical shift doublet detected in the GFT dimension corresponds to the previously reported ¹⁵N chemical shifts of D36 (121.1 ppm), A34 (122.7 ppm) and Q2 (125.2 ppm). In a second, more congested plane (Fig. 3c, d), the signals of 5 residues are readily identified. The resolution introduced by the simultaneous sampling of ¹³CO is demonstrated for the T49CA-A48CB and T17CA-T16CG2 peaks. The two peaks are relatively close to one another (~2 ppm) in the difference (blue, Fig. 3d) sub-spectrum, but are separated by ~20 ppm in the sum (red, Fig. 3c) sub-spectrum.

Fig. 3.

Planes taken along F1(CA) at CA chemical of 56.0 ppm (a, b) and 60.2 ppm (c, d) from (4,3)D (HA)CANCOCX recorded for protein GB1. The CA and atoms with correlated chemical shifts are indicated. The subspectra with red contour levels comprise signals at the sum of ¹⁵N and ¹³C′ chemcial shifts, while the subspectra with blue contour lines comprise corresponding differences of shifts. Contours are cut at 6 time the RMS noise floor, with a spacing factor of 1.3. The spectra shown here were acquired in 7.2 h, inclusion of a central peaks spectrum extends the measurement time to 10.8 h (t₁ 32 × 135 μs; t₂ 48 × 180 μs; t₂′ 48 × 90 μs)

The chemical shifts derived from the GFT spectrum (Supporting Information, Table 1) agree well with the previously reported solid state NMR chemical shifts for GB1 (Franks et al. 2005). The GFT derived ¹⁵N shifts, agree to 0.2 ± 0.3 ppm with the previously reported values, with two outlying differences of 0.9 and 0.8 ppm, and a median difference of 0.1 ppm. The GFT derived chemical shifts show a 0.7 ± 2.0 ppm with liquid state NMR, while the ssNMR derived shifts are 0.6 ± 2.0 ppm from the liquid state NMR values. There was a small linear phase encoded in the ¹³C′ component of the joint ¹⁵N-¹³C′ dimension caused by an incorrect initial delay. Still, the absolute maximum difference between ssNMR and GFT derived chemical shifts is only 1.3 ppm, with an average diference of 0.0 ± 0.6 ppm, and a median difference of 0.0 ppm. As for the ¹⁵N chemical shifts, there is no significant change to the agreement with the solution NMR chemical shifts; −0.3 ± 1.1 ppm for GFT, and −0.2 ± 0.8 ppm for ssNMR. The offset caused by the phase can be compensated by simple linear regression as a function of the effective carrier offset using directly detected carbonyl peaks from the GFT experiment as calibration points. We have chosen to report the uncorrected chemical shifts obtained from the usual GFT analysis.

Conclusions

We have demonstrated the value of recording GFT NMR spectra for assigning proteins in the solid state, thereby reducing measurement times for to obtain 3D or 4D spectral information by about an order of magnitude. In a series of simulated spectra, we have demonstrated that GFT NMR is well suited for establishing highly resolved correlations in large proteins. Experimentally, we have demonstrated with GB1 that the encoded information is complete and accurate, and highly resolved spectra can be acquired in a small fraction of the time required for the conventionally sampled experiment. GFT experiments are most beneficial when data acquisition is otherwise pursued in the ‘sampling limited’ regime, as true when using micromole quantities of GB1 with current NMR instrumentation.

We anticipate that a much larger range of protein samples will come into this regime as the sensitivity of SSNMR experiments for biological solids continues to improve. Substantial sensitivity benefits have been demonstrated now by proton detection (Morcombe et al. 2005; Chevelkov et al. 2006; Zhou et al. 2007a, b), dynamic nuclear polarization (Bajaj et al. 2003), and cryogenic MAS (Doty et al. 2006). In particular, for highest magnetic field strengths (corresponding to 900 MHz ¹H resonance frequency or higher) spectral widths and thus sampling demand scale up accordingly. Recording of (4,2)D SS GFT NMR experiments may then become attractive, and for systems showing very high chemical shift degeneracy (such as membrane proteins) recording of G²FT SS NMR spectra (Atreya et al. 2005) may well become beneficial. Moreover, we expect that future implementations of SS GFT NMR experiments will profit from acquiring data in ‘clean absorption mode’ (Wu et al. 2009) to eliminate residual dispersive signal components. Taken together, we anticipate that a broad range of studies will benefit from SS GFT NMR in the future.