Comparing handrim biomechanics for treadmill and overground wheelchair propulsion

Abstract

Study design

Cross-sectional study.

Objectives

To compare handrim biomechanics recorded during overground propulsion to those recorded during propulsion on a motor-driven treadmill.

Setting

Biomechanics laboratory.

Methods

Twenty-eight manual wheelchair users propelled their own wheelchairs, at a self-selected speed, on a low-pile carpet and on a wheelchair accessible treadmill. Handrim biomechanics were recorded with an OptiPush instrumented wheelchair wheel.

Results

Across the two conditions, all handrim biomechanics were found to be similar and highly correlated (r > 0.85). Contact angle, peak force, average force, and peak axle moment differed by 1.6% or less across the two conditions. While not significant, power output and cadence tended to be slightly higher for the treadmill condition (3.5% and 3.6%, respectively), due to limitations in adjusting the treadmill grade.

Conclusion

Based on the results of this study, a motor-driven treadmill can serve as a valid surrogate for overground studies of wheelchair propulsion.

Introduction

Manual wheelchair users are at an increased risk of upper limb pain and pathology due to the repetitive loads associated with wheelchair propulsion^1–2. For this reason, wheelchair propulsion continues to be the focus of a number of research studies^3–11. While these studies share a common goal of helping to reduce the risk of injury to manual wheelchair users, the methods of reaching that goal vary, particularly with respect to the testing environment. In these studies, propulsion testing was conducted overground^3–5, on a dynamometer^6–8, or on a treadmill^9–11. Each of these testing environments offers its own advantage, though with the treadmill and the dynamometer, the edge comes at the cost of typical propulsion. Ideally, all studies of manual wheelchair propulsion would be conducted overground, as it represents the most realistic testing condition. However, overground data collection can be limiting. In order to capture a number of consecutive strokes, a sufficiently long distance is needed. This distance may not be available, or allowable, given the restrictions of the measurement equipment (motion capture, electromyography, cardio-pulmonary diagnostics, etc.). With overground testing, it is also difficult to control experimental conditions such as velocity and power output¹².

An alternative means of conducting studies of wheelchair propulsion is with a motor-driven treadmill. A treadmill provides a confined and consistent testing environment in which wheel velocity and power output can be controlled. The ability to control parameters that affect testing consistency make the treadmill useful for studying the effects of propulsion training and other interventions¹³. To appreciate the similarity of treadmill testing to overground testing, we must study the similarity of the testing results. The only comparative study involving the two conditions, conducted by Stephens and Endsberg¹⁴, examined recovery patterns during propulsion overground, on a dynamometer, and on a pair of treadmills. Since most wheelchairs are too wide to fit on a traditional exercise treadmill, the treadmill condition was created by having subjects straddle two independent treadmills running at the same speed. Data from the dynamometer and dual-treadmill conditions were combined into a single condition, making it difficult to conclude what affects if any the dual-treadmill had on recovery pattern.

The objective of this study was to compare handrim biomechanics recorded during overground propulsion (reference condition) to those recorded for the same subjects, with similar velocity and power output, during treadmill propulsion (experimental condition). We hypothesized that handrim biomechanics on a treadmill would be substantially equivalent to those found while pushing overground.

Materials and methods

Subjects

Thirty-one full-time manual wheelchair users, identified from an internal subject database and by local rehabilitation professionals, were recruited for this study. The criteria for participation included: use of a manual wheelchair as the primary mode of mobility, full function in the upper limbs with no debilitating pain, healthy enough to propel for five minutes at a time, and the use of quick-release rear axles. Prior to enrollment all subjects provided informed consent. All study documents and test procedures were approved by the Western Institutional Review Board (Olympia, WA).

Instrumentation

Data for this study were collected with an OptiPush instrumented wheelchair wheel (MAX Mobility, LLC, Antioch, TN). The OptiPush measures wheel angle and the three-dimensional forces and moments applied to the handrim during propulsion. Data are sampled at 200Hz and transmitted via Bluetooth to a laptop running the OptiPush software. The software filters forces and moments using a 4th order digital Butterworth filter with a low-pass cutoff frequency of 20Hz¹⁵. Filtered kinetics and wheel angle measurements are then used to compute propulsion variables on a stroke-by-stroke basis. Each push stroke (push and recovery phases) is defined by absolute moment about the axle (M_axle). The push phase begins when M_axle exceeds 1 Newton-meter (Nm) and the recovery phase begins when M_axle drops back within 1 Nm.

Data collection

Data for this study were obtained from a larger study of wheelchair propulsion. The methods listed here are limited to the procedures used to collect the data for this investigation.

The wheels of each subject’s wheelchair were removed and replaced by the OptiPush wheel on the right (6.0 kg for a .64 m wheel) and an inertia-compensated wheel on the left. The diameters of the wheels and handrims were chosen to match those used by the subject. Both wheels were fitted with a low-profile pneumatic tire inflated to 100 pounds per square inch. Once the wheels were attached and the OptiPush was initialized, subjects propelled their wheelchairs across a low-pile, commercial carpet with no pad (about 50 m long). Subjects were asked to select a speed that could be maintained for an extended period of time. This was done to help prevent fatigue during treadmill testing. Allowing subjects to propel at a self-selected speed also helped to prevent unwanted changes in normal propulsion technique, which may be affected by speed¹⁶. Two separate runs were made across the floor, in opposite directions, to account for any surface irregularities. Data from the first 3–4 strokes of each trial (initial acceleration phase¹⁷) and the last 3–4 strokes (deceleration phase) were disregarded. Steady-state data from each trial were combined into a single matrix from which average overground speed, power output, and the resulting handrim biomechanics were computed. Table 1 lists the equations for all variables assessed in this study.

Table 1.

Propulsion variables

Variable	Description [Units]	Equation
Speed	Mean speed during the stroke, [m/s]	(θstroke/180) ·π·D/tstroke
Cadence	Push frequency, [pushes/min]	60/tstroke
Contact Angle	Angle through which wheel rotates when hand is on handrim, [degrees]	wheel angle at recovery start − wheel angle at push start
Power Output	Power generated per stroke, [Watts]	Σ(Maxle*Δθ*π/180)/tstroke
Peak Force	Maximum total force applied to the handrim during the stroke, [Newtons]	max(Ftot), where Ftot = √(Fx2 + Fy2 + Fz2)
Average Force	Average total force applied to the handrim during the stroke, [Newtons]	mean (Ftot)
Peak Moment	Maximum moment about the axle during the stroke, [Newton-meters]	max(Maxle)

D = wheel diameter [m], θ = wheel angle [degrees], θ_stroke = angle through which the wheel rotates during the stroke [degrees], t_stroke = time to complete the stroke [s], and Δθ = point-to-point change in angle [degrees].

Subjects were then loaded onto a wheelchair accessible treadmill (Figure 1). Unlike standard treadmills, this treadmill has a wide belt (1.06 m) and a dynamic safety system. The front of the wheelchair was strapped to the frame of the treadmill using two straps that ride along linear bearings. The straps keep the wheelchair on the treadmill and prevent excessive lateral sway; however, they do not impede fore-aft movement of the wheelchair. Subjects were given several minutes to acclimate to pushing on the treadmill. During the acclimation period, the treadmill speed was set to match the subject's average overground speed and a metronome beep was provided to help the subject match treadmill cadence to overground cadence. The grade of the treadmill was increased until the subject's treadmill power output, measured on a stroke-by-stroke basis, matched the average overground power output (The average treadmill grade across all subjects was 0.81±0.28°). Once the acclimation period was complete, the treadmill was stopped and subjects were given time to rest. After a few minutes, the treadmill was restarted and subjects were asked to push their wheelchair for approximately 1 minute while OptiPush data were recorded from the right side.

Figure 1.

Photo of the treadmill test setup.

Data analysis

Seven propulsion variables, computed from data collected during the overground and treadmill trials, were compared across the two testing conditions (Table 1). These variables were selected because they are common in studies of wheelchair propulsion and have been related to upper limb health^1,2,18. For each subject, the variables were averaged across all strokes (minimum of 15 strokes) for each condition. Paired t-tests were used to analyze the differences between the mean treadmill value and the mean overground value for each variable, with the null hypothesis that the difference would equal zero. To maximize the sensitivity, no type I error correction was applied and alpha was set to 0.05. Pearson product-moment correlation coefficients were also calculated to assess the relationship between the variables calculated from each condition. For visual confirmation, scatter plots of each variable (excluding speed) were created. The plots include a line of equality (slope of 1 and intercept of 0) to evaluate the similarity of the variables. The statistical power of the study was estimated to be 77%, based on a standard deviation of 20% and a detectable change of 10%. All statistical analyses were performed using SPSS (SPSS Inc., Chicago, IL) and all plots were made using MATLAB (The MathWorks, Inc., Natick, MA).

We certify that all applicable institutional and governmental regulations concerning the ethical use of human volunteers were followed during the course of this research.

Results

Subjects

A complete set of data were obtained from twenty-eight subjects (24 men, 4 women). Data from three individuals could not be used as the protocol was not followed correctly. This reduced the projected study power to 72%. The remaining subjects ranged in age from 15 to 57 years (34.2±9.5 y) and in duration of injury from 2 to 43 years (14.5±10.4 y). Of the 28 subjects, 20 had paraplegia (T3-L1), 5 had spina bifida (T10-L5), 1 had tetraplegia (C6-7 incomplete), 1 had cerebral palsy, and 1 had a spinal lipoma.

Comparison of variables

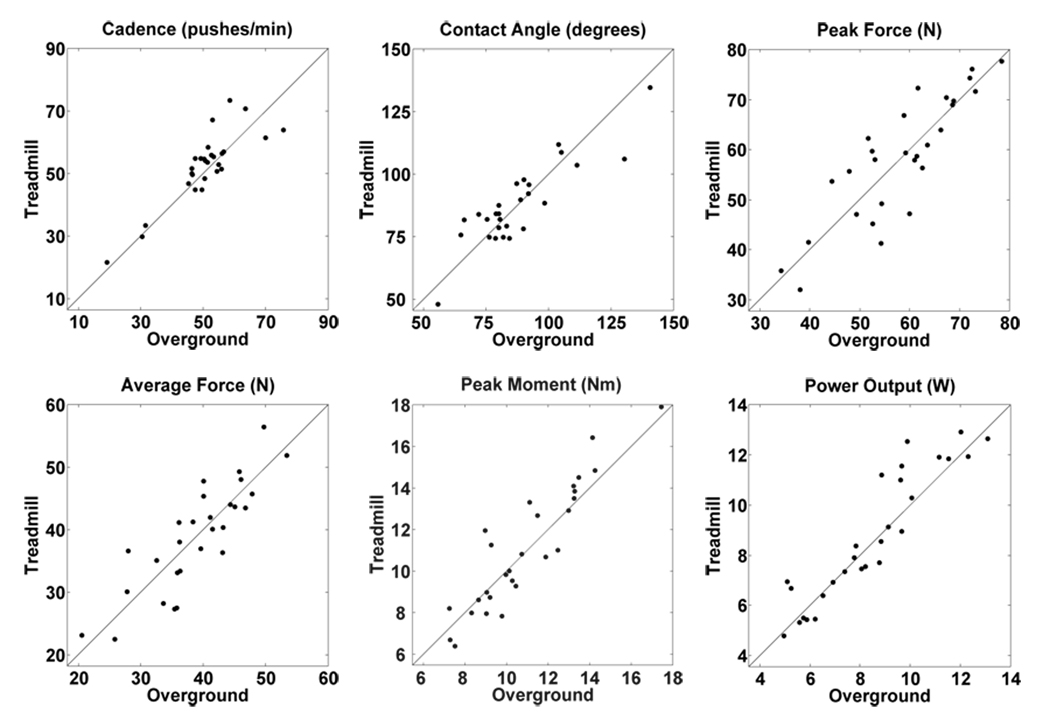
Table 2 lists the variables calculated for each condition and the percent differences between them. Most of the variables were nearly identical across the conditions with no greater than 1.6% difference between the averages. Furthermore, none of the differences were found to be statistically significant. Table 3 shows the results of the Pearson correlation analysis. As expected, the analysis produced high r-values and low p-values indicating strong correlations between the variables in each condition. The proximity of the variables to each line of equality (Figure 2) also demonstrated the congruencies between the two sets of variables.

Table 2.

Comparison of propulsion variables for each condition

Test Variable	Overground	Treadmill	% Difference	P-value
Speed (m/s)	1.09 (0.23)	1.09 (0.23)	−0.1	0.583
Power Output (W)	8.43 (2.32)	8.72 (2.59)	3.5	0.132
Cadence (pushes/min)	50.6 (10.9)	52.4 (11.1)	3.6	0.111
Contact Angle (deg)	86.6 (19.1)	86.2 (18.1)	−0.5	0.803
Peak Force (N)	58.1 (11.1)	58.4 (12.4)	0.4	0.853
Average Force (N)	38.9 (7.59)	38.9 (8.60)	−0.1	0.959
Peak Moment (Nm)	10.9 (2.47)	11.0 (2.98)	1.6	0.460

Values are mean (standard deviation).

Table 3.

Pearson correlation coefficients

Test Variable	r	P-value
Speed (m/s)	0.999	< .001
Power Output (W)	0.924	< .001
Cadence (pushes/min)	0.862	< .001
Contact Angle (deg)	0.883	< .001
Peak Force (N)	0.863	< .001
Average Force (N)	0.851	< .001
Peak Moment (Nm)	0.917	< .001

Figure 2.

Plots of the variables (top row: cadence, contact angle, peak force; bottom row: average force, peak moment, and power output). Each plot includes a line of equality (y = x) to show the proximity of the points to being equal across the treadmill and overground conditions.

Discussion

The results of this study demonstrate the strong similarities in handrim biomechanics between treadmill and overground manual wheelchair propulsion. No statistically significant differences were found between the two conditions. This does not prove equivalence; however, it does not refute it. For this comparison, the most revealing results are the descriptive statistics. Four of the 5 uncontrolled variables calculated during treadmill propulsion (contact angle, peak force, average force and peak moment) were within 2% of the values recorded during overground propulsion. In addition, every variable was highly correlated between the two conditions (r > 0.85) and tightly distributed around the line of equality for the two testing environments (Figure 2).

Compared to previous studies of wheelchair propulsion on a treadmill^9,11, the power output measured in this study was 15–65% lower. The lower power output values are attributed to a slower belt speed and/or lesser treadmill grade. Given the lower power output values, it is reasonable that the values of contact angle and cadence measured in this study were also lower than in previous studies. On the other hand, average peak force (58.4 N) was within the range of reported values (53.5 N–58.9 N) for treadmill propulsion^9,11.

While we found no significant differences between the propulsion variables, subtle differences were seen in power output, cadence, and peak moment. Power output was a controlled variable that should have been equivalent across the two conditions. Power was adjusted by increasing treadmill grade, which ranged from 0.4° to 1.7° for all subjects, until the power output measured by the OptiPush was similar to the mean power output of the overground trials. The resolution for adjusting grade was 0.1°, which limited our ability to fine tune power output on the treadmill. With greater control over treadmill grade, we are confident that power output could have been adjusted to match the overground condition.

During treadmill propulsion, cadence and peak moment were 3.6% (1.8 pushes/min) and 1.6% (0.17 Nm) higher, respectively, than during overground propulsion. The increases in both variables were likely due to the increased power output requirement of the treadmill. On average, subjects did not increase their contact angle (−0.5%) or average force (−0.1%), and made a marginal increase in peak force (0.4%). Therefore, to achieve the higher power output on the treadmill, subjects increased their strokes per minute and, to a lesser extent, the peak moment of each stroke. While the data support this conclusion, we cannot rule out the possibility that subjects altered their technique, particularly cadence, in response to pushing on a treadmill. To help subjects become comfortable on the treadmill we had them push for 2–3 minutes prior to data collection. We believe this is an important step, since most wheelchair users have never pushed on a treadmill. Additional time may have helped subjects settle into a lower cadence; however, the acclimation period was purposely limited to avoid subject fatigue.

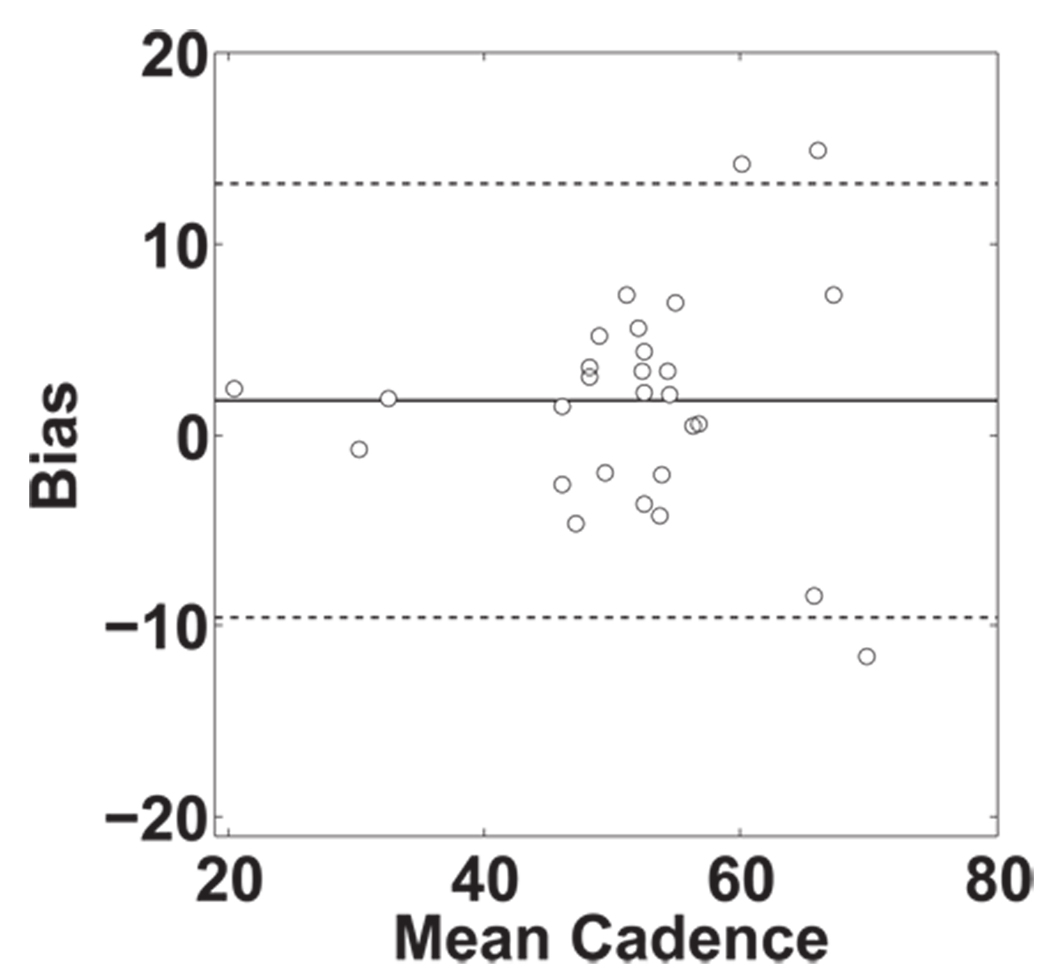
A supplementary Bland-Altman plot of cadence (Figure 3) was created to further investigate the changes in push frequency. The plot shows a slight trend in the differences between overground and treadmill cadence. Subjects who pushed more frequently experienced greater changes in cadence across the two conditions. However, given the relatively few number of data points at the extremes, it is difficult to determine if there is a definitive trend or if these subjects are outliers. The majority of the subjects pushed at a rate of about 50 strokes/min. Within this group, there was an even distribution of bias with no apparent trend. The only clear result demonstrated by the plot is a small bias (mean offset from zero) when pushing on the treadmill.

Figure 3.

Bland-Altman plot of cadence. The solid line represents the mean difference in cadence between pushing on a treadmill and pushing overground; and the dashed lines define the 95% confidence interval.

From a mechanics perspective, the two testing conditions should produce similar results. van Ingen Schenau¹⁹ provides an analysis of bipedal locomotion on both a treadmill and overground. Assuming that treadmill belt speed remains constant and air resistance is negligible, treadmill locomotion is mechanically similar to overground locomotion. The same should hold true for wheelchair propulsion. The external forces acting on a wheelchair user (gravity and ground reaction force) are the same as those acting on a bipedal walker. By selecting a coordinate system that moves with the belt¹⁹, wheelchair propulsion on a treadmill can be described with the same model used to describe overground wheelchair propulsion²⁰.

Along with biomechanics, one must consider the advantages and disadvantages of treadmill use. In addition to providing control over speed and power output, treadmills provide the means to study steady-state activity in a limited space. This makes it easier to acquire data from motion capture systems and any tethered or cumbersome devices (e.g. a cardiopulmonary monitor). Treadmills also provide unobstructed, pure pushing environments that can be used to develop upper body endurance as well as proper muscle memory and biomechanics. In this way, treadmills are beneficial to rehabilitation clinics and fitness centers that provide propulsion training and exercise services. On the other hand, treadmills can be expensive, costing over $10,000. Also, the treadmill cannot adequately represent the changes in surface, speed, and direction that occur during typical wheeling. Overground testing represents the most realistic environment for studies of wheelchair propulsion. However, based on the similarities in mechanics and the variables computed in this study, the motor-driven treadmill provides an acceptable substitute when space is limited or when steady-state propulsion is desired. Researchers and clinicians can use these data to support their own use of treadmill testing.

There were several limitations to this study. First, upper body kinematics during overground and treadmill propulsion were not collected, so we could not determine if there were differences in joint ranges of motion between the conditions. However, based on the strong similarities between the contact angle for the two conditions and the kinematic constraints on the upper extremity during the push, this seems unlikely. And second, we only studied a single power output level. Future work should include additional power output levels as well as kinematics, metabolics, and electromyography to provide a more comprehensive validation of treadmill use for studying wheelchair propulsion.

Conclusions

The motor-driven treadmill provides a controlled environment that is suitable for studying manual wheelchair propulsion. Subjects demonstrated similar handrim biomechanics to those measured during overground propulsion. The values of each propulsion variable were similar and highly correlated across the two testing conditions. To maintain comparable conditions to those overground, proper adjustments must be made to the treadmill to replicate overground speed and power output. Adequate time should also be given to help wheelchair users get accustomed to pushing on a moving belt. With these provisions, the treadmill provides a valid method of measuring wheelchair handrim biomechanics and may be an acceptable surrogate for overground studies when a controlled propulsion environment is desired.