The search for the hydrophobic force law

Abstract

After nearly 30 years of research on the hydrophobic interaction, the search for the hydrophobic force law is still continuing. Indeed, there are more questions than answers, and the experimental data are often quite different for nominally similar conditions, as well as, apparently, for nano-, micro-, and macroscopic surfaces. This has led to the conclusion that the experimentally observed force–distance relationships are either a combination of different ‘fundamental’ interactions, or that the hydrophobic force-law, if there is one, is complex – depending on numerous parameters. The only unexpectedly strong attractive force measured in all experiments so far has a range of D ≈ 100–200 Å, increasing roughly exponentially down to ~ 10–20 Å and then more steeply down to adhesive contact at D = 0 or, for power-law potentials, effectively at D ≈ 2 Å. The measured forces in this regime (100–200 Å) and especially the adhesive forces are much stronger, and have a different distance-dependence from the continuum VDW force (Lifshitz theory) for non-conducting dielectric media. We suggest a three-regime force-law for the forces observed between hydrophobic surfaces: In the first, from 100–200 Å to thousands of ångstroms, the dominating force is created by complementary electrostatic domains or patches on the apposing surfaces and/or bridging vapour cavities; a ‘pure’ but still not well-understood ‘long-range hydrophobic force’ dominates the second regime from ~ 150 to ~ 15 Å, possibly due to an enhanced Hamaker constant associated with the ‘proton-hopping’ polarizability of water; while below ~ 10–15 Å to contact there is another ‘pure short-range hydrophobic force’ related to water structuring effects associated with surface-induced changes in the orientation and/or density of water molecules and H-bonds at the water–hydrophobic interface. We present recent SFA and other experimental results, as well as a simplified model for water based on a spherically-symmetric potential that is able to capture some basic features of hydrophobic association. Such a model may be useful for theoretical studies of the HI over the broad range of scales observed in SFA experiments.

Introduction

The phenomenon of the low solubility of non-polar moieties or their strong mutual attraction in water is known as the hydrophobic interaction (HI). The HI is arguably the most important non-specific interaction in biological systems and is responsible for the creation of enclosed compartments by proteins and lipid bilayers in water, which was fundamental for the evolution of cells and therefore life. Molecular mechanisms of protein folding and adsorption are also regulated by the HI. Despite its importance, the underlying mechanisms of HI and its fundamental force law, if there is one, are still unresolved. Even though the first direct measurement of the attraction between two nominally hydrophobic surfaces was done nearly 30 years ago, the experimental and theoretical research that followed has left more puzzles than solutions. Puzzling aspects are the strength and range of the attractions measured between hydrophobic surfaces. Experiments report attractive ranges from ~ 100 to ~ 6500 Å.^1,2 The range of a few thousand ångstroms can hardly be explained by structured water alone. For rough (super)hydrophobic surfaces attractive forces are measured for separations up to 3.5 μm strongly indicating the influence of roughness.³ To solve the puzzle it is helpful to differentiate between a general HI, involving all types of forces observed in experiments, and the pure HI involving just forces unique to hydrophobic moieties (molecules, molecular groups and extended surfaces) that are still not well understood but arise from changes in the properties of water near hydrophobic surfaces. The first step in understanding the hydrophobic phenomena is to understand the ‘pure HI’ which itself may have more than one distance regime. Review of the ‘old’ data suggested that there are three regimes that could be attributed to hydrophobic interactions: one – an ‘extended long-range’ regime, extending out to many thousands of ångstroms – that is indirectly produced by hydrophobic interactions, for example, the overturning of monolayers into charged bilayer patches or domains that then interact via long-range electrostatic forces, or bridging cavities; and two – a long-range and short-range hydrophobic interaction (HI), extending out to a few hundred ångstroms – that are directly related to hydrophobic effects and which we call the pure HI. The new data with chemisorbed surfactant monolayers show that the long-range interaction appears both with physisorbed and chemisorbed surfactants, thereby showing it to be part of the pure (long-range) HI.

In addition to the lack in theory there are experimental problems creating suitable hydrophobic surfaces. Recently, it was shown that very few of the reported results are directly related to the intrinsic hydrophobicity of the surfaces in question.¹ Many seemingly contradictory or inconclusive results from studies concerning the effects of electrolyte concentration,^4-12 temperature,^13-15 and dissolved gases^7,8,10,16,17 can be attributed to surface or solution preparation techniques. To determine how various parameters affect hydrophobic interactions quantitatively, fundamental studies concerning temperature and electrolyte effects must be carried out on smooth, stable hydrophobic surfaces, such as octadecyl-tri-ethoxysilane (OTE) monolayers chemisorbed on activated mica. One of the few aspects that appear to be clear in the hydrophobic puzzle is the fact that the measured range of attraction decreases dramatically if great care is taken to eliminate electrostatic and capillary forces, for example, by rigorously deaerating the solutions. Deaeration has been found to significantly decrease the range of the extended long-range interaction between physisorbed monolayers even though cavities no longer exist while bilayer domains still exist. Does this suggest that deaeration somehow removes the long-range electrostatic interaction? Deaeration has also been found to reduce the attraction between surfactant-free oil droplets in water¹⁸ as well as the thickness of the vapour-depleted layer at hydrophobic–water interfaces¹ but not the value of the hydrocarbon–water interfacial tension.¹ Thus, the effects of deaeration on both the long- and short-range (adhesion) forces between hydrophobic surfaces in water are not currently understood.

Direct measurement of the attractive forces between two nominally hydrophobic surfaces in aqueous solution was first published nearly 30 years ago^19,20 resulting in an attractive force acting as far as 80–100 Å from contact. During this time, the range was considered extremely large and was referred to as a “long-ranged” attraction. In the following years these first measurements, the experimental situation became murkier rather than clearer with different experiments producing different magnitudes and ranges for the ‘hydrophobic force’. As experimental methods improved surface hydrophobization became more diverse, and the range of the attraction between hydrophobic surfaces was reported to be considerably longer than had been reported initially. The initially reported range of 100 Å is now considered to be part of the “short-ranged” hydrophobic interaction, with “long-range” forces extending out to separations greater than 200 Å, and even as far as 3000 Å or incredibly 6500 Å.²

The variable and surprisingly long-ranged nature of the force reported between hydrophobic surfaces used in experiments has been particularly vexing from a theoretical standpoint. It is clear from even a cursory look at the three typical types of force curves measured in these systems (e.g., Fig. 2 from ref. 1) that no simple theory could be expected to account for all of the observed behaviours. Furthermore, any credible theory must be independent of the surface preparation technique, yet different surface hydrophobization techniques have resulted in force curves that are not even qualitatively similar,^10,21 indicating that secondary factors just beyond the surface hydrophobicity contribute to the measured forces. To find a simple theory describing just the pure HI acting between all hydrophobic moieties in water, we have to find suitable conditions for experiments to avoid the secondary effects associated with hydrophobic forces. One would expect the forces associated with the pure HI to be present between all hydrophobic surfaces. Unfortunately, even the search for the pure HI has proven difficult as it is often accompanied by other forces that are difficult to avoid in typical experiments.

Fig. 2.

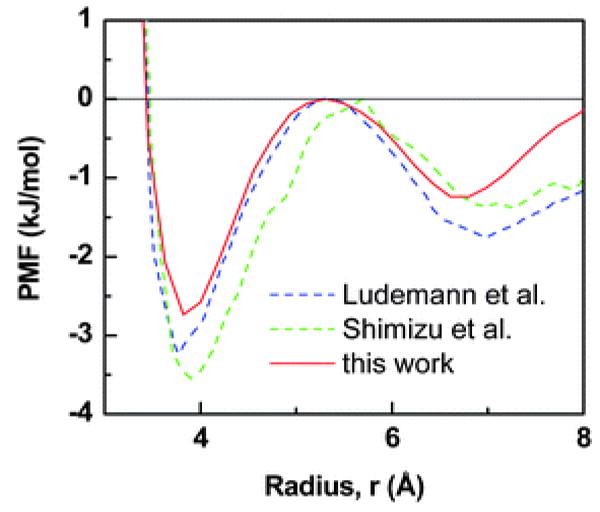
The potential of mean-force, PMF, in terms of the radial distance, r, between the pair of hydrophobes, is given above. The solid curve is obtained through our Monte Carlo simulations utilizing the spherically-symmetric water model. The dotted curves roughly depict the reported results of Ludemann et al.⁴⁶ and Shimizu et al.;⁴⁷ these two employ conventional semi-empirical force-fields for water, SPC⁴⁸ and TIP4P,⁴⁹ respectively. Our PMF has a slightly higher frequency and a moderately lower amplitude. The curves are shifted up–down so as to fix the “barrier” at zero energy.

While one major source of experimental confusion comes from the apparent dependence of the attraction on the hydrophobic surface preparation technique, another comes from the geometry of the surfaces used in the experiments, e.g., whether macroscopic and of low curvature as in surface force apparatus (SFA) experiments, or macroscopic but with nanoscopic contact of tip and surface with high curvature as in atomic force microscopy (AFM) experiments. Most experiments have studied only one type of surface under a single or limited range of solution conditions. In many cases, it has become clear that the long-range attraction observed in so many experiments or systems is not in fact due to the direct pure hydrophobic attraction at all, but to originally hydrophobic monolayers overturning into charged patchy bilayers, giving rise to a long-ranged attractive electrostatic or double-layer force,^17,22 or to bridging of pre-existing nanobubbles,^23-28 giving rise to attractive capillary forces, again depending on the technique used to hydrophobize the surfaces. For the attractive electrostatic force, lateral motion of the bilayer patches on the surfaces is required. We have seen this in our AFM imaging (the patches move and rearrange both during and between scans) as well as the finite time (seconds) the attractive force takes to build up as the two surfaces are brought together. This assumption is in agreement with the literature, which describes evidence that dynamic interactions between polarized domains of lipid layers on both surfaces may result in attraction with a great range between hydrophobized mica surfaces.²⁹

In fact, the only force present between all the hydrophobic surfaces so far studied is the “short-range” (D < 100–200 Å) force which, for biological interactions, would be considered as a long-range force. There is therefore a need to carry out unambiguous and systematic experiments of the forces between smooth, stable, hydrophobic surfaces under different solution conditions, and to closely coordinate the experiments with theoretical modeling. To date, OTE chemisorbed on activated mica has proved to be the only surface that satisfies all of the above requirements, making it a suitable surface for rigorous investigation of the hydrophobic interaction.^1,30,31,32 Knowledge that the pure HI should have a range of < 100–200 Å, and becomes particularly strong below 10 Å,³³ opens the door to several theoretical explanations that were previously dismissed by some due to their inability to explain the observed “long-range” force.

We present here recent SFA measurements done on smooth stable OTE surfaces and compare them with published measurements on different surfaces. Based on this data we would like to discuss a concept for the hydrophobic force law based on three different distance regimes. But, first, a few words about theoretical modelings of the HI, which have so far mainly focused on the shortest of the three distance regimes.

Theoretical background

Molecular simulations are frequently invoked in order to provide a better theoretical understanding of the physics underlying the HI, yet as this interaction spans multiple spatial scales, it becomes too computationally demanding to examine it with conventional fully-atomistic simulations based on semi-empirical force-fields. One possibility in overcoming this challenge might lie in multiscale simulations. Such simulations utilize simplified, coarse-grained molecular models extracted from detailed, fully-atomistic ones. Ideally, multiscale simulations employ models with a sufficient amount of information as required to describe the pertinent phenomena at the scale of interest. Such modeling strategies hold promise for examining the HI over its entire range of length scales.

Recently, Shell introduced a fundamental thermodynamic framework for multiscale simulations that can be applied to any arbitrary system of arbitrary Hamiltonian.³⁴ The key concept in this approach is the relative entropy, S_rel, given by,

$$S_{\mathit{rel}}=\sum _v{p}_v\cdot \ln \left(\frac{p_v}{{\stackrel{\sim }{p}}_v}\right)$$ (1)

where p_v denotes the probability of a particular configuration v in a detailed, fully-atomistic molecular system while p̃_v is the corresponding value in a simplified, coarse-grained molecular system. S_rel measures the extent the configurational ensemble of the simplified system reproduces the correct one in the detailed system, measured, in at least one context, by a log-likelihood.³⁴ It is bounded below by zero (indicating perfect ensemble duplication), with higher values indicating decreasing adequacy of replication. Given a reference detailed model, a novel simplified model can be optimally determined by minimizing the relative entropy.³⁴

Shell and coworkers used this approach to examine a particular spherically-symmetric model of water.³⁵ Its potential, u(r), is constructed by the superposition of a Lennard-Jones with a Gaussian, given by,

$$u(r)=4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]+B\exp \left(\frac{-{(r-r_o)}^2}{{\mathrm{\Delta }}^2}\right)$$ (2)

The usual Lennard-Jones parameters, ε and σ, define the energy and length scales of this interaction; the parameter B sets the strength of the Gaussian while r_o and Δ govern its center and spread, respectively. Consequently, Shell and coworkers evaluated the optimal values of these parameters for a grid of state points by correspondingly performing S_rel minimization.³⁵ Surprisingly, the optimized models appeared to manifest an effective hydrogen bonding interaction in the form of an energetic variation of the region in the spherically-symmetric potential corresponding with water’s nearest-neighbor distance.³⁵ Importantly, this variation in state contributes significantly in the ability of the spherically-symmetric model in reproducing aspects of waterlike behavior (e.g., water’s anomalous pairwise structure along with its unique coordination number of 4).³⁵

This coarse-grained model for water is a candidate for analyzing the multiscale nature of the HI. In this work, we do not yet intend to simulate the experiments discussed above; instead, we examine the ability of spherically-symmetric water in describing the HI on the molecular scale. Rather than examining the HI between infinite surfaces, we focus here on a simpler study, the association of a pair of methane-like hydrophobes. By this analysis, we evaluate the ability of the (optimized) spherically-symmetric model in capturing some basic features of the HI on the molecular scale, an issue which must be addressed before proceeding to use such models in the examination of the multiscale phenomena observed with the SFA.

Materials and methods

SFA measurements

The hydrophobic surfaces were prepared by a modified chemical vapor deposition based on a method by ref. 32 on back-silvered mica usually used for SFA measurements. The mica surfaces were treated with argon water plasma for 10 min at 450 mTorr. 0.5 ml OTE were placed together with mica discs into a glass Petri dish and OTE vapor was deposited during 4 h in a rough vacuum at 70 °C. The discs were rinsed with CHCl₃ and nitrogen dried before mounting to a SFA box. The SFA chamber was filled with water (Milli-Q A-10 water purification system (Millipore)). The dynamic force measurements³⁶ were done with a SFA 2000³⁷ at room temperature.

Computer simulations

Monte Carlo simulations are used to examine the ability of spherically-symmetric water in describing the HI on the molecular scale. The simulation constructs a (periodic) box with 216 water molecules; its size is chosen so that water’s density is 1.00 kg L⁻¹. One hydrophobic molecule rests at the center while another one moves along a single dimension. The corresponding potential of mean-force, a mathematical formulation of the HI, is evaluated via the multicanonical algorithm;³⁸ we perform 5 iterations to attain a sufficient flat-histogram of 50 bins. To ensure adequate statistics, 5 replicates are done. This protocol is performed for a few temperatures near ambient conditions.

We employ the spherically-symmetric water model discussed above, invoking the S_rel-optimized parameters for eqn (2).³⁵ Importantly, we examine two separate scenarios in modeling the medium: in one scenario, the potential for the water model is variable with state conditions while in the other scenario, it is constant. The parameters for the water model, along with their corresponding use in the two scenarios, are summarized in Table 1. The hydrophobes are described by methane-like molecules, expressed via a Lennard-Jones interaction.³⁹ These solutes interact with the solvent via Lorentz-Berthelot mixing rules; the parameters of these interactions, involving the hydrophobes, are summarized in Table 2.

Table 1.

The optimal parameters of the spherically-symmetric water model (as defined by eqn (2)) are given below for a range of temperatures, T, at a density of 1.00 kg L⁻¹.³⁵ Assuming infinite-dilution, these are invoked for the waterlike bath in the two different scenarios: in the variable case, the spherically-symmetric water model takes on the optimal parameters at each temperature, while in the constant case, the spherically symmetric model fixes the optimal parameters at ambient temperature (300 K)

T/K	σ/Å	ε/kJ mol−1	B/kJ mol−1	r0/Å	Δ/Å
280	2.42	22.4	25.8	2.45	1.10
300	2.43	20.4	23.3	2.46	1.09
320	2.43	19.7	22.9	2.44	1.11

Table 2.

The Lennard-Jones parameters associated with the (vacuum) interactions of the methane-like hydrophobes are given below.³⁹ Importantly, the mixing rules invoke the Lennard-Jones parameters of the fully-atomistic water model utilized in the optimization of the spherically-symmetric water model.³⁵

Hydrophobes interacting	σ/Å	ε/kJ mol−1
with themselves	3.73	1.23
with water	3.45	0.89

Results and discussion

Experimental results

The measured interactions as a function of distance are shown in Fig. 1 in a semi-log and a log plot for variously prepared hydrophobic surfaces together with data from Wood and Sharma³¹ and Meyer et al.¹

Fig. 1.

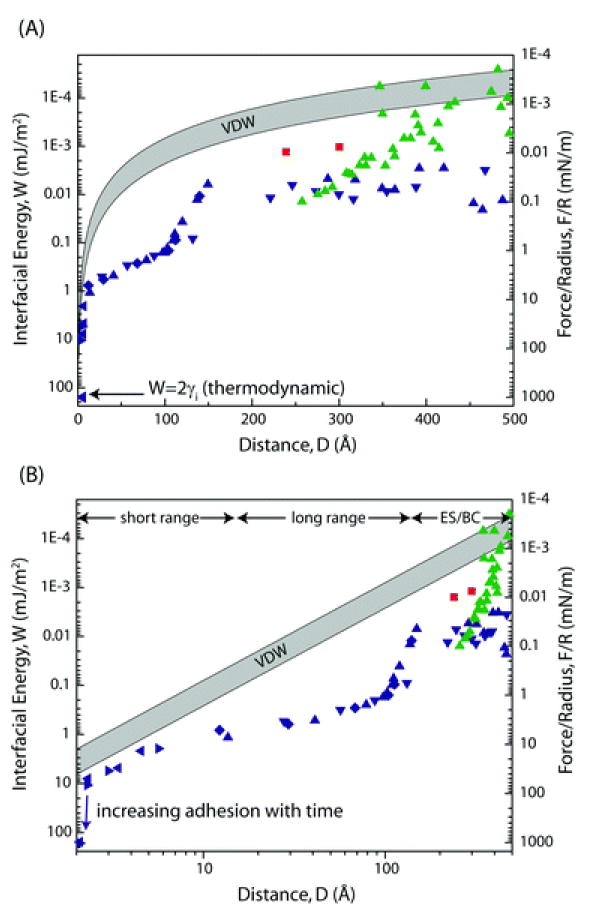
Results of experimentally measured forces between hydrophobic surfaces under different conditions presented as a semi-log (A) and a log-log (B) plot are indicated as followed: red squares: DMDOA, LB-deposited, deaerated, Wood and Sharma;³¹ green triangles: OTE, chemical vapor deposition, deaereted; all data points in blue were obtained by Meyer et al.,¹ using OTE and DODA surfaces prepared by LB-depostion. Suggested regimes are marked as the short range, long range, and ES/BC, and are discussed below. The shaded VDW force band corresponds to Hamaker constants between 3 and 10 × 10⁻²¹ J.

As shown in Fig. 1, the shape of the measured force curve can hardly be explained by one curve. It seems that there are three different regimes, first a regime up to ~ 10 Å, followed by an exponential regime up to ~ 100 Å, beyond which the forces between hydrophobic surfaces become more scattered depending on the surface and solution preparation but nevertheless are stronger than expected for van der Waals forces.

Up to now, no model exists that is capable of describing the attractive interaction between two hydrophobic surfaces for all described experimental data. The only force observed in all experiments is an attractive force below distances of 200 Å. Several reports suggest that the reported attraction above several hundred ångstroms results from different attraction forces, but not directly from HI between the surfaces.^33,40-42 Possible mechanisms for this attractive force are mainly based on local charge fluctuations created by imperfect, patchy preparation of hydrophobic surfaces resulting in attractive interaction between oppositely charged patches of the surface as well as bridging cavities.^1,42 Deaerating of water results in a dramatic decrease in the range of the attractive force.¹ There is an apparent correlation between contact angle hysteresis, indicating molecular rearrangements of the hydrophobic surface, and the existence of a force in the hundreds to thousands ångstrom range.⁴¹ These surface defects can also act as nucleation centers for bubbles. The typical Debye length of 1500 Å for pure water suggests a long range electrostatic interaction. It is worth noting that the force curve resulting from differences between experiments with and without monovalent salt, has a decay length correlating to the expected Debye length of the salt used.¹ This indicates that the observed force in this regime is not directly related to the HI and is due to imperfect hydrophobic surfaces and is mainly due to electrostatic attraction and/or bridging cavities. Therefore, we suggest the name ‘electrostatic and/or bridging cavitation’ (ES/BC) for this regime.

Ederth and Liedberg³³ observed an attractive interaction above 200 Å that was apparently the result of bridging bubbles and concluded that the pure HI has a range of <200 Å. Within this regime, the measured force distance relationship can be fitted by an exponential function from 10 Å up to 100 or 200 Ź with a decay length of 10–20 Å⁴³ but not for distances below 10 Å. Interestingly in this range the expected VDW attraction for typical hydrocarbon surfaces with Hamaker constants of 3–10 × 10⁻²¹ J is not negligible as shown in Fig. 1. Due to jump-in instabilities associated with the very strong attractive forces, and difficulties in distance resolution, experimental data for approaching surfaces below 10 Å are rare and have a large error. The maximum adhesion forces measured by Meyer, et al.¹ was determined to be F_ad/R≈500 mN m⁻¹, corresponding to an adhesion energy (based on the JKR theory) of W = 2 γ_i = 2F_ad/3πR ≈ 100 mJ m⁻², or γ_i ≈ 50 mJ m⁻² (mN m⁻¹), which is the value for hydrophobic surfaces in water. As shown by Fig. 1, the VDW attraction is not negligible in the regime below ~ 10 Å and surely plays a part in the strength of the interaction, but is clearly too weak to account for the whole of the force. Published results show that the purely attractive forces measured are greater than any conceivable van der Waals force.⁴⁴ Other explanations related to water structuring effects associated with surface-induced changes in the orientation and/or density of water molecules and H-bonds at the water–hydrophobic interface⁴⁵ may explain the existence of the unusually strong attraction in the short-range regime.

Theoretical results

Interestingly, the spherically-symmetric water bath appears to yield an effective HI that is comparable with the HI of fully-atomistic water media. For ambient conditions, Fig. 2 evaluates our computed potentials of mean-force with those utilizing fully-atomistic models for water.^46,47 On comparison, our HI has the same first-order oscillatory behavior (defined by hydration shells of water); in the spherically-symmetric case, the frequency is slightly higher and the amplitude is moderately lower. Importantly, it is encouraging that the binding energy is of the same order of magnitude.

The relation of HI with temperature is depicted in Fig. 3 for both scenarios (the water model is variable in one case and constant in the other). Importantly, the variable spherically-symmetric water attains an aspect of the HI that appears to be one of its signatures: the binding energy increases considerably with increasing temperature near ambient conditions.^46,47 Conversely, the constant spherically-symmetric water fails to describe this facet of the HI. These results reiterate observations made by Shell and coworkers: the spherically-symmetric water model must manifest a particular variation with state in the contact energy with its nearest-neighbors in order to capture waterlike properties; this allows for an effective hydrogen bonding interaction that can produce a number of signatures of water’s anomalous bulk properties.³⁵

Fig. 3.

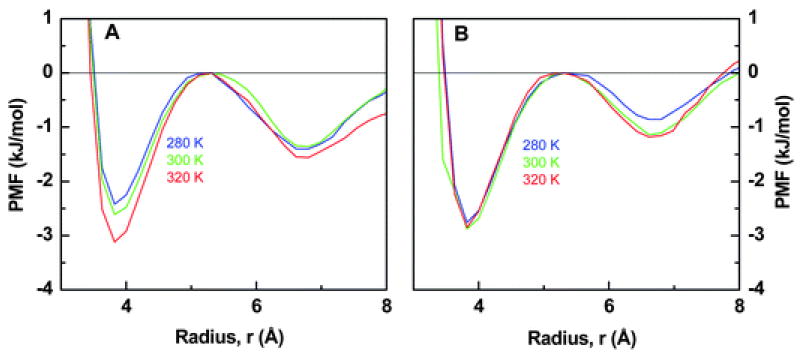
The potential of mean-force, PMF, in terms of the radial distance, r, between the pair of hydrophobes, is given above for the variable (A) and constant (B) scenarios. Each curve represents a different temperature. The variable case but not the constant case notably exhibits the following trend: with increasing temperature, the wells deepen, especially the one corresponding to binding. The curves are shifted up–down so as to fix the “barrier” at zero energy.

The approximate description of the HI with the use of spherically-symmetric water suggests that water’s molecular directionality can be effectively averaged for the “pure” HI, at least for the methane-like case study investigated here. In this simple case of the HI, the medium can be simply thought as composed of spheres, having the energy between nearest-neighbors subtly vary in state. This also suggests that it is water’s unique pairwise structure that dominates on these scales of the “pure” HI.

Conclusions

Based on this data we suggest a concept for the hydrophobic force law based on three regimes created by different forces dominating in specific distances. The longest range with an effective range of several thousand ångstroms is not a pure hydrophobic force. Instead it is based mainly on electrostatic effects due to heterogeneously charged surfaces and/or bridging effects (capillary forces) of cavities. The second force regime involved in our concept is the ‘long range’ force and although not well understood is likely a pure hydrophobic force with a range of 10–20 Å up to 100–200 Å. This force is possibly due to an enhanced Hamaker constant associated with the proton-hopping polarizability of water (cf. Grotthuss Effect) and may be important in explaining rapid protein-folding rates, faster then predicted by simple kinetic theories. Proton-hopping (the Grotthuss mechanism) rather than dipolar reorientations is the cause of the high dielectric constant (high polarizability) of liquid water and ice. Protons move over large distances and create giant dipoles. This effect on the van der Waals forces has not been considered, but may be expected to enhance the magnitude and/or range of the interaction. Since hydrophobic surfaces do not restrict the motion of water adjacent to them, we may expect that the enhanced polarizability of water at and between two hydrophobic surfaces could enhance the Lifshitz van der Waals type attraction to a magnitude and/or range that is comparable to that between conductors, i.e., by up to two orders of magnitude. This could be the origin of the long-range ‘pure’ HI, which would be very different from the short-range interaction due to water structuring effects.

The ‘short range’ force is the overwhelming force in the distance from zero (contact) up to 10 Å and is likely related to water structuring effects associated with surface-induced changes in the orientation and/or density of water molecules and H-bonds at the water–hydrophobic interface.

Finally, we show that a simplified model for water, based on a spherically-symmetric potential, is able to describe some features of the water-mediated association of molecular-sized hydrophobes (e.g., their binding energy increases with increasing temperature). Consequently, this model may eventually allow for multiscale simulations of our experiments, in turn, providing a molecular picture of the physics governing each regime of the HI. Nevertheless, other coarse-grained models for water should be examined with S_rel methodology, as it presents a powerful approach for multiscale simulations.