Abstract
During inflammation, selectin-ligand interactions provide forces for circulating leukocytes to adhere to vascular surfaces, which stretch the interacting molecules, suggesting that mechanical properties may be pertinent to their biological function. From mechanical measurements with atomic force microscopy, we analyzed the molecular characteristics of selectins complexed with ligands and antibodies. Respective stiffness of L-, E-, and P-selectins (4.2, 1.4, and 0.85 piconewton/nm) correlated inversely with the number (2, 6, and 9) of consensus repeats in the selectin structures that acted as springs in series to dominate their compliance. After reconstitution into a lipid bilayer, purified membrane P-selectin remained a dimer, capable of forming dimeric bonds with P-selectin glycoprotein ligand (PSGL)-1, endoglycan-Ig, and a dimeric form of a glycosulfopeptide modeled after the N terminus of PSGL-1. By comparison, purified membrane L- and E-selectin formed only monomeric bonds under identical conditions. Ligands and antibodies were much less stretchable than selectins. The length of endoglycan-Ig was found to be 51 ± 12 nm. These results provide a comprehensive characterization of the molecular stiffness of selectins and illustrate how mechanical measurements can be utilized for molecular analysis, e.g. evaluating the multimericity of selectins and determining the molecular length of endoglycan.
Keywords: Adhesion, Antibodies, Atomic Force Microscopy, Glycoprotein, Inflammation, Consensus Repeat, Dead Zone, Endoglycan, Selectins, Stiffness
Introduction
The physical properties of biomolecules can be exploited as tools for their analysis. For instance, electrophoresis that separates proteins according to mass and charge can be exploited to analyze molecular identity and abundance. Physical properties of many biomolecules also have critical roles in their functions. As an example, bending rigidities of actin and microtubule enable these cytoskeletal proteins to provide mechanical support to the cell. Adhesion molecules are also subjected to forces because they anchor cells to other cells or to the extracellular matrix. Mechanical properties and their relevance to biological function of DNA and muscle proteins (e.g. titin and ubiquitin) have been extensively documented (1–8). However, limited studies exist on the mechanical characterization of adhesion molecules and on the utilization of such mechanical measurements for molecular analysis. Here, we employ atomic force microscopy (AFM)4 to measure mechanical properties of molecular complexes of selectins and their ligands or monoclonal antibodies (mAbs) and use mechanical measurements to address biological issues involving these molecules.
Each of the three selectins consists of an N-terminal lectin domain, an epidermal growth factor (EGF)-like domain, 2, 6, or 9 (for L-, E- or P-selectin, respectively) short consensus repeats (CRs), a transmembrane domain, and a short cytoplasmic tail (Fig. 1A). During inflammation, selectin-ligand interactions mediate tethering and rolling of circulating leukocytes on vascular surfaces under a mechanically stressful milieu (9). These molecular complexes are subjected to physical forces that may cause deformations and/or induce conformational changes, suggesting that mechanical properties may be relevant to their adhesive function. However, very little is known about these properties and their potential relation to function.
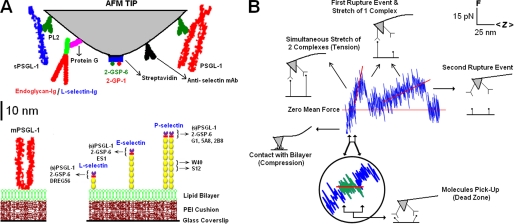
FIGURE 1.
Experimental setup and molecular stiffness measurement. A, AFM functionalization. The depiction represents a composite of all molecules adsorbed/captured on the cantilever tips and reconstituted in bilayers in different experiments. PSGL-1 and sPSGL-1, captured by PL2 in the middle, are respectively depicted as dimer and monomer. Endoglycan and L-selectin-Ig are shown as an Ig chimera captured by protein G. Biotinylated 2-GSP-6 and its nonfunctional analog 2-GP-1 are depicted as green and red dots, respectively, captured by streptavidin (blue). P-selectin is shown as a dimer, and E- and L-selectins are shown as monomers. Binding epitopes of the various ligands and anti-selectin mAbs are indicated. Bilayer-incorporated mPSGL-1 is shown as a dimer. B, representative force-distance curve with two peaks. Interpretations of different regions on the curve are shown in the schematics and explained here as follows: compressive region, gradual reduction in contact force as the cantilever retracts; dead zone, picking up and aligning the molecules; ascending segments, stretching two or one molecular complex(es); sudden drop in force, unbinding of a single molecular bond. In this case, slopes of the tensile force built-up segments prior to the breaks (red trend lines) represent stiffness of two and one molecular complex. Inset, magnification of a portion of the force-distance curve encompassing the dead zone regime (green), wherein the increase in distance with no discernible increase in force is evident.
We have previously used AFM for mechanical measurements of L- and P-selectin (10). Here, we expand the previous study by systematically characterizing the dead zone and stiffness of all three selectins complexed with different ligands and mAbs. More importantly, we present clear illustrations of how these mechanical measurements can be used to test hypotheses regarding the following issues. First, we show convincing evidence for single bond measurement and the ability to distinguish unbinding of multiple bonds in parallel versus unfolding of multiple domains in series. Second, we demonstrate that after reconstitution into a lipid bilayer, purified membrane P-selectin remained a dimer, capable of forming dimeric bonds with P-selectin glycoprotein ligand (PSGL)-1, endoglycan-Ig, and a dimeric form of a glycosulfopeptide modeled after the N terminus of PSGL-1. By comparison, purified membrane L- and E-selectins formed only monomeric bonds under identical conditions. Third, we dissect the compliance contributions from different structural components of the interacting molecules and identify the major load-bearing constituent(s). Analyses revealed that selectins contributed to bulk of the complex compliance that could be attributed to their CRs. Finally, we provide an example of measurement of molecular dimension. Our approach may be applied to study single molecule mechanical properties of other systems, such as integrin-ligand complexes.
EXPERIMENTAL PROCEDURES
Proteins and Antibodies
Human E- and L-selectin were generous gifts from M. B. Lawrence (University of Virginia, Charlottesville, VA) (11, 12). Endoglycan-Ig was a generous gift from S. D. Rosen (University of California, San Francisco) (12). P-selectin was purified from human platelets, and dimeric native PSGL-1 and monomeric recombinant soluble sPSGL-1 were purified, respectively, from human neutrophils and supernatant of Chinese hamster ovary cells transfected with sPSGL-1 (13). Membrane PSGL-1 (mPSGL-1) was a generous gift from M. Long (Chinese Academy of Sciences, Beijing, China). The following mAbs have been reported: anti-PSGL-1 nonblocking mAb PL2 (12, 14); anti-P-selectin blocking mAbs G1 (14), 5A8, 2B8, S12, and W40 (15); anti-E-selectin blocking mAb ES1 (16); and anti-L-selectin blocking mAb DREG-56 (12). Biotinylated functional 2-glycosulfopeptide-6 (2-GSP-6) and nonfunctional 2-glycopeptide-1 (2-GP-1) have also been described (17).
AFM System and Cantilever Calibration
Our AFM system has been designed, built, and calibrated in-house based on a design provided by Vincent Moy (University of Florida, Miami). It consists of a piezo translator (Poly Physik Instruments, Boston) on which a cantilever is directly mounted. A laser beam bounce technique is employed to continually monitor cantilever deflection. Our AFM uses commercial cantilevers (ThermoMicroscopes, Sunnyvale, CA; currently Veeco, Santa Barbara, CA) calibrated in situ during each experiment using the method of thermal fluctuations (18, 19).
Preparation of Selectin or PSGL-1 Bilayers and Functionalization of AFM Cantilever Tips
Coverslips with a diameter of 40 mm (Bioptechs, Butler, PA) were cleaned with a solution of 70% 12 n sulfuric acid and 30% hydrogen peroxide (by volume) at 100 °C for 45 min, rinsed extensively with deionized water (Labconco, Kansas City, MO), and stored under dust-free conditions for future use. The formation of selectin- or PSGL-1-incorporated lipid vesicle solutions has been described (20). During each experiment, bilayers were formed using the method of vesicle fusion (12, 14). The coverslips were initially coated with a 100 ppm polyethyleneimine solution (Fisher) to accommodate the occasional inversely oriented selectins or PSGL-1, which proved to be a key factor in reducing nonspecific adhesion. A 5 μl drop of the lipid vesicle solution was placed on the surface of the coverslip, incubated for 15–20 min under damp conditions, and covered with 10 ml of Hanks' balanced salt solution or Dulbecco's phosphate-buffered saline solution (Fisher) containing Ca2+, Mg2+, and 1% bovine serum albumin (BSA). The bilayers so formed had low molecular densities, which ensured their infrequent binding (15–20%) to the countermolecule-coated AFM tips. The bilayers were used immediately in the AFM experiments (Fig. 1A).
PL2, protein G, and streptavidin were adsorbed overnight at 4 °C on different AFM cantilevers, and these were used to capture (s)PSGL-1, endoglycan-Ig or L-selectin-Ig, and biotinylated 2-GSP-6 (or 2-GP-1), respectively (Fig. 1A). This ensured a proper presentation of the molecules on the cantilever tip, while also helping control the molecular lengths during the stretch experiments. Anti-P-selectin mAbs G1, 5A8, 2B8, S12, and W40, anti-E-selectin mAb ES1, and anti-L-selectin mAb DREG56 were directly adsorbed on different cantilever tips (Fig. 1A). Unlike other mAbs, W40 and S12 interact with the 5th and the 6th CR, respectively (from the N terminus), of P-selectin (Fig. 1A). Experiments were performed by repeatedly moving the ligand or mAb-coated tips to contact the selectin bilayers (to allow binding) and retracting at 250 nm/s.
Measurement of Molecular Stiffness
Individual adhesion events with tensile force and rupture (e.g. Fig. 1B) were clearly distinguishable from contacts without adhesion in which no tensile force was observed during cantilever retraction. Molecular stiffness was directly measured from the slope of the linear ascending segment of the force-distance curve when the molecular complex was stretched (prior to bond breakage), assuming that it behaved as a linear spring (Fig. 1B). This assumption has been supported by data wherein molecular stiffness did not show strong dependence on applied force (10).
Estimation of Molecular Complex Length
The extension length of the selectin-binding site (from the AFM tip) for the various anti-selectin mAbs was assumed to be equal to the length of the mAb itself (16 nm corresponding to mouse IgG1). The lengths by which protein G and streptavidin-biotinylated 2-GSP-6 complex would extend from the AFM tip were considered to be 5 and 10 nm, respectively. Based on the extensions of the ligand/antibody-binding epitopes on the selectin (from the bilayer) and the extensions of the selectin-binding sites/antigenic epitopes on the ligand/mAb (from the AFM tip), we obtained estimates for the lengths of the portions of different molecular complexes being stretched. These values are listed in Table 1 and were used to plot Fig. 3B.
TABLE 1.
Individual molecule and combined molecular complex lengths
It should be noted that for PL2-sPSGL-1 complex, the extension length from the AFM tip is the length of PL2 (16 nm) plus half the length of sPSGL-1 (25 nm), as PL2 binds roughly near the middle of sPSGL-1. Also, the length of E-selectin-PSGL-1 complex is based only on the E-selectin-binding site at the N terminus of PSGL-1 (cf. Fig. 1A) without considering other possible sites at the PSGL-1 stalk. This assumption is supported by the data in Fig. 3B in which the dead zone lengths for E-selectin-PSGL-1 and -2-GSP-6 complexes fall in line with the rest of the monomer one-peak measurements (Fig. 3B, open symbols and top thin calibration line). Other binding sites for E-selectin on the PSGL-1 stalk would result in shorter molecular complex lengths than what we have assumed above. This might throw the open symbols corresponding to the E-selectin-PSGL-1 complex off of the monomer one-peak (top thin) calibration line (Fig. 3B). The fact that this is not the case suggests that the E-selectin-binding site on PSGL-1 N terminus dominates.
| Molecule | Extends from | Extension length |
|---|---|---|
| nm | ||
| P-selectin | Lipid bilayer | 38a |
| E-selectin | Lipid bilayer | 25 |
| L-selectin | Lipid bilayer | 9 |
| PL2 and other mAbs (G1, 5A8, 2B8, ES1, and DREG56) | AFM tip | 16a |
| sPSGL-1 | AFM tip | 50a |
| Protein G | AFM tip | 5 |
| PL2-sPSGL-1 complex | AFM tip | 41 |
| Streptavidin-biotinylated 2-GSP-6 complex | AFM tip | 10 |
| Molecular complex | Total length | |
|---|---|---|
| nm | ||
| P-selectin-sPSGL-1 | 79 | |
| P-selectin-2-GSP-6 | 48 | |
| P-selectin-2B8 | 54 | |
| E-selectin-PSGL-1 | 66 | |
| E-selectin-2-GSP-6 | 35 | |
| E-selectin-ES1 | 41 | |
| L-selectin-PSGL-1 | 50 | |
| L-selectin-2-GSP-6 | 19 | |
| L-selectin-DREG56 | 25 | |
a These entries indicate values are based on previously published results, and other entries are calculated based on published results.
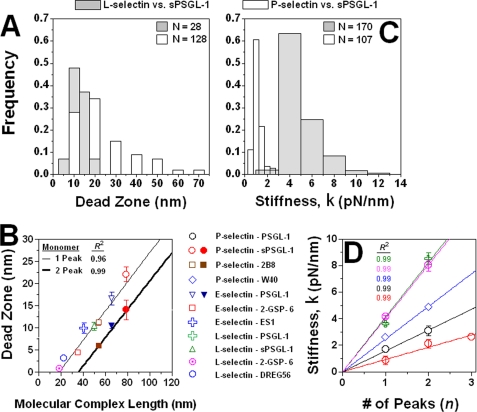
FIGURE 3.
Dead zone and stiffness measures. A and C, histograms of indicated numbers of dead zone (A) and stiffness (C) measurements for PL2-captured sPSGL-1 interacting with bilayer-anchored L-selectin (gray bars) and P-selectin (white bars) were bell-shaped. Dead zones and stiffness were measured as shown in Fig. 1B. The dead zone histogram for the longer molecular complex (i.e. P-selectin-sPSGL-1) is shifted rightward relative to that for the shorter molecular complex (i.e. L-selectin-sPSGL-1) (A). However, the stiffness histograms display the opposite trend; the peak for the L-selectin-sPSGL-1 complex is shifted rightward relative to that for the P-selectin-sPSGL-1 system (C). B, dead zone versus molecular complex length. The combined lengths of molecular complexes were calculated based on published data (see text and Table 1). Straight lines were respectively fit to data (points) measured from force-distance curves exhibiting one and two peaks. For the same molecular complex, dead zones from curves with two peaks is smaller than that from curves with one peak (color-matched filled versus open symbols). D, quantal behavior of complex stiffness. Stiffness k measured from the slope prior to the first peak of force-distance curves with n peaks is plotted versus n for the indicated molecular systems. Data (points) for the same molecular system were fit with a straight line passing through the origin. For all molecular systems studied (five shown here), the data appeared linear, k(n) = n·k(1). In other words, k(n) was an integer (n) multiple of a quantum, k(1), whose value depended on the system tested. Data in B and D are presented as mean ± S.E. of at least several tens of measurements. In some cases, error bars are smaller than sizes of symbols. Goodness-of-fits are indicated by the R2 values (color-matched in D).
RESULTS
AFM Force-distance Curves
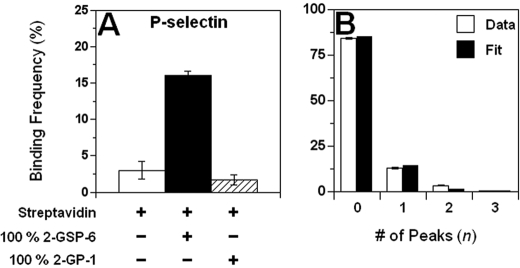
AFM cantilever tips functionalized with ligands, L-selectin-Ig, or mAbs (Fig. 1A, top) were initially driven to contact glass-supported, polyethyleneimine-cushioned lipid bilayers reconstituted with L-, E-, or P-selectin or PSGL-1 (Fig. 1A, bottom). They were then retracted to see if an adhesion event resulted. Those events with adhesion were examined to see how many force peaks were generated from the contact (e.g. a two-peak force-distance curve is shown in Fig. 1B). Finally, the stiffness of the molecular complex(es) so (and if) formed were measured (Fig. 1B). During each experiment, the bilayers were first tested using yet-to-be fully functionalized (i.e. only PL2/protein G/streptavidin-coated) or BSA-coated tips to confirm <5% nonspecific binding. Functionalization of the same tips (by incubation with ligands) or using mAbs-coated tips resulted in a 4–5-fold increase in the binding frequency, demonstrating the specificity of the interactions tested (Fig. 2A).
FIGURE 2.
Specificity controls and Poisson distribution of peak numbers. A, specific interactions between the selectin (in this case, P-selectin) and ligand (in this case, 100% 2-GSP-6) or mAb were confirmed via various treatments of the AFM cantilevers and testing them against the selectin bilayers: (nonspecific) binding was very low when AFM tips were coated with streptavidin only (open bar); functionalizing the same cantilever with ligand resulted in a dramatic increase in binding (black bar); on the contrary, incubating the streptavidin-coated AFM tip with nonfunctional 2-GP-1 did not have any effect (hatched bar). Binding frequency at each condition was calculated from 50 contacts per spot on 2–4 spots using one bilayer-tip pair and is presented as mean ± S.E. of three different bilayer-tip pairs. B, experimental (open bars) frequencies of occurrence of various numbers of peaks in force-distance curves, defined as the number of force-distance curves showing n peak(s) divided by the total number of trials, was fitted by a Poisson distribution (closed bars, average number of peaks = 0.16). Poisson distribution is expected if the peaks occur as independent events with identical probabilities, which seems reasonable for unbinding of multiple bonds in parallel but not for unfolding of multiple domains in series. Data (mean ± S.E.) have been pooled from four experiments using different bilayer-AFM tip pairs.
A force-distance curve is shown in Fig. 1B where the cantilever retraction (controlled by the piezo translator) led the force rise (measured by the photodiode), resulting in a distance increase at zero mean force termed dead zone (10). This curve displays two peaks with abrupt force drops concurrent with sudden distance increase before returning to zero mean force. The slopes of the linear ascending segments prior to the peaks correspond to the stiffness of the molecular structures being stretched at the respective times (10). The dual goals of this study are to systematically measure the dead zone and molecular stiffness of selectins complexed with several ligands and mAbs and to illustrate how these mechanical measurements can be used to analyze properties of the molecules being tested.
We hypothesized that the sawtooth pattern in the force-distance curve represented the sequential rupture of multiple selectin-ligand (or -mAb) bonds in parallel (21). This is different from the alternative hypothesis that such a pattern represented the sequential unfolding of multiple domains in series of a single protein, as was demonstrated in stretching titin (7), fibronectin and immunoglobulin (5, 8), tenascin (6), and ubiquitin (4). Our assumption is critical for the interpretation and application of the analyses of dead zone and stiffness to distinguish between the two hypotheses, which will be tested along with these analyses.
Initial evidence came from the analysis of the frequency distribution of the force peak numbers. Most force-distance curves exhibited a single peak. Occasional double peaks (Fig. 1B) and, very rarely, triple peaks were observed in the force-distance curves wherein specific interactions were allowed. However, only single peak adhesion events were observed in control experiments where specific interactions were prohibited, suggesting that the multipeak adhesion events were mediated by specific interactions between the selectins and their ligands (or mAbs). The frequency distribution of the number of force-distance curves showing 0 and 1–3 peaks followed a Poisson distribution (Fig. 2B), consistent with our hypothesis (21). For the hypothesis of sequential unfolding of multiple domains in series in a single protein to be consistent with the data in Fig. 2B, it would require the AFM tip or the bilayer to be functionalized with a protein mixture with fractions containing 1–3 unfoldable domains following the Poisson distribution, which was not the case.
Analysis of Dead Zone
Next, we show that dead zone measurements can be used to determine molecular length. To do so, we examined the dependence of the dead zone on the combined length of the interacting molecules and the number of peaks in the force-distance curve. The lengths of P-selectin (38 nm) and PSGL-1 (50 nm) were previously measured by electron microscopy (22, 23). The length of mouse IgG1 (16 nm) was estimated from crystal structures (24). The lengths of L-selectin (9 nm) and E-selectin (25 nm) were calculated by comparing their domain structures with that of P-selectin (Fig. 1A). The molecular complex lengths were calculated from the lengths of the selectin-binding site on PSGL-1 extending from the AFM tip plus the lengths the antigenic/ligand epitopes on selectins extending from the lipid bilayer (Table 1).
To enable measurement of forces comparable with the level of thermal fluctuations of the AFM cantilever, we collected data at a scan rate of 1.5 kHz and used a soft cantilever (stiffness ∼4–10 pN/nm) to obtain better force resolution. Collecting data at this rate ensured sufficient temporal resolution to allow us to zoom in on the force-distance curves to measure dead zones at nanometer resolution (Fig. 1B, inset). Regardless of the molecular identities and the nature of the interactions, the dead zone and stiffness were normally distributed (e.g. Fig. 3, A and C), with the peak position corresponding very well with the mean value. The spread in the data suggested that different molecular complexes of the same type were randomly pulled in a range of orientations (10). Furthermore, the mean dead zone increased linearly with the complex length for the dead zone measured from force-distance curves with one and two force peaks (Fig. 3B). This supports our previous interpretation that dead zones correspond to displacements of the AFM tip when molecules are being picked up and aligned along their long axes before resisting tensile forces that stretch them beyond their resting lengths (cf. Fig. 1B) (10). However, for the same molecular pair, the mean dead zones measured from force-distance curves with two peaks were smaller than those measured from curves with only one peak (Fig. 3B, color-matched open symbols versus closed symbols), resulting in a parallel downward shift of the dead zone versus molecular length plot for the two-peak case relative to that for the one-peak case. This can be explained by our hypothesis that the sawtooth pattern of the force-distance curve was caused by unbinding of multiple bonds in parallel instead of unfolding of multiple domains in series. Indeed, two spatially separated molecular complexes would have more geometrical constraints on their noncoaxial alignment than one such complex (Fig. 1B) that would predict a shorter dead zone length, which was indeed observed. Because the dead zone was obtained from a segment of the force-distance curve after formation of bonds but prior to their stretch (Fig. 1B), it should only contain information regarding how many bonds were formed in the past but not how many domains would be unfolded in the future. If the sawtooth pattern were to represent unfolding of individual domains, the dead zones measured from one- and two-peak curves would have been identical, which was not the case.
Analysis of Molecular Stiffness
Stiffness as an intrinsic property can be used to determine other aspects of a protein. To illustrate this, we analyzed the slopes of the linear ascending segments of the sawtooth pattern to examine the change in molecular structure before and after the peaks in the force-distance curves. As exemplified in Fig. 1B, the slopes prior to the first peak were twice that prior to the second peak in two-peak curves. Furthermore, the slopes prior to the first and second peaks were, respectively, three and two times that prior to the third peak in those rare three-peak events (Fig. 3D, open red symbols). These observations are shown by the linear relationship between the slope (k) prior to the first peak and the number (n) of peaks in the force-distance curves (Fig. 3D). Significantly, this multiplicity trait was not restricted to one particular system but was found in all selectin-ligand (or -mAb) systems. Because the combined stiffness of multiple springs in parallel equals the sum of the stiffness of the individual springs, these data suggest that the multiple peaks represented successive unbinding of multiple bonds in parallel. The same data also falsify the alternative hypothesis for unfolding of multiple protein domains in series. Because the combined compliance (reciprocal stiffness) of multiple springs in series equals the sum of the compliances of the individual springs, the alternative hypothesis predicts a progressive increase in slope as the domains sequentially unfold, which was not observed. On the contrary, we saw the exact opposite (Figs. 1B and 3D).
These data suggest that the slopes prior to the peaks are integer multiples of a quantal value, viz. the slope prior to the last peak (stiffness of a single binding unit) regardless of the number of peaks. For each system studied, however, it was still a question of whether this quantal unit consisted of a single bond or a cluster of bonds whose individual member dissociation could not be distinguished as distinct peaks in the AFM photodiode signals. To address this, we compared the dead zone and stiffness of monomeric and dimeric molecular complexes.
Monomeric Versus Dimeric Interactions
Electron microscopy, biochemical, and cross-linking studies have shown that PSGL-1 and P-selectin are dimers on their respective cell surfaces (22, 23, 25) and form dimeric bonds that enhance adhesion under flow (13). By comparison, the recombinant soluble sPSGL-1 is a monomer (22). Using lifetime measurements, our previous AFM studies have indicated that purified P-selectin reconstituted in lipid bilayer also supported dimeric interactions with PSGL-1 but only monomeric interactions with sPSGL-1 (14), whereas purified L-selectin reconstituted in the same way only supported monomeric interactions (12). Here, we used stiffness measurements to examine the multimericity of the interactions of selectins with different ligands. We first compared the unit stiffness of three selectins complexed with either form of PSGL-1 measured from force-distance curves with one peak. The stiffness of P-selectin-PSGL-1 complex was twice that of P-selectin-sPSGL-1 complex (Fig. 4A), indicating twice the number of springs in the former compared with the latter. By comparison, stiffness of E- and L-selectins was indifferent to the form of PSGL-1 used (Fig. 4A), indicating the same number of springs for the two forms of PSGL-1 complexed with each selectin. These data suggested that membrane P-selectin, but not membrane E- and L-selectins, supported dimeric interactions with dimeric PSGL-1 under the conditions tested.
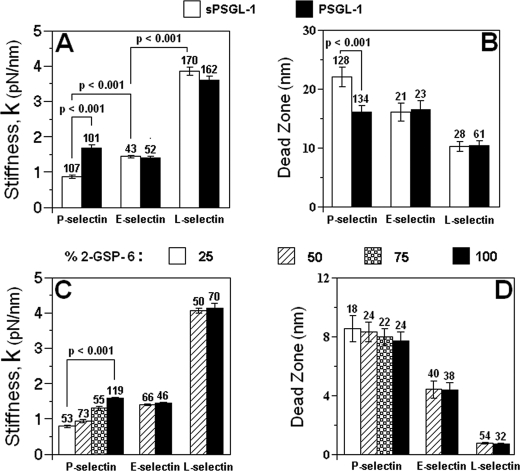
FIGURE 4.
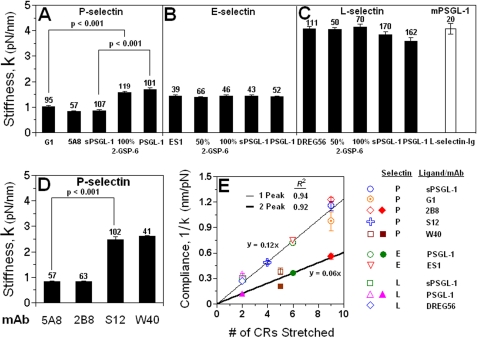
Monomeric versus dimeric interactions. Quantized stiffness (A and C) and dead zones (B and D) of three selectins are complexed with two forms of PSGL-1 (A and B) or indicated fractions of 2-GSP-6 are mixed with 2-GP-1 (C and D). Data are presented as mean ± S.E. of N measurements (indicated top each bar). Statistical analysis using ANOVA found no significant differences (p values between 0.1 and 0.9) between stiffness or dead zones of E- or L-selectin interacting with two forms of PSGL-1, whereas significant differences (p values < 0.001) were found between P-selectin-(s)PSGL-1 complexes. For the same ligand (sPSGL-1), stiffness is inversely related to length of selectin with highly significant differences (p values < 0.001) among values of three selectins complexed with sPSGL-1 (open bars in A).
Why unbinding of the two members of a dimeric bond did not produce two peaks in the force-distance curve as two monomeric bonds did (cf. Fig. 1B) might be explained by the much closer proximity of the two members of a dimeric P-selectin-PSGL-1 complex compared with two monomeric P-selectin-sPSGL-1 complexes. As a result, the sequential dissociation of the two members could not be discerned from the photodiode signals, thereby appearing as a single quantal unit. This hypothesis predicts the following: (i) for force-distance curves with the same number of peaks, the dead zone would be longer for a P-selectin-sPSGL-1 complex than a P-selectin-PSGL-1 complex, despite the same complex lengths; and (ii) the dead zone from P-selectin-PSGL-1 curves with one peak would be longer than that from P-selectin-sPSGL-1 curves with two peaks, despite that a dimeric P-selectin-PSGL-1 complex has identical stiffness as two monomeric P-selectin-sPSGL-1 complexes. The reason is that a monomeric P-selectin-sPSGL-1 complex should be less geometrically constrained when it is picked up and aligned than a dimeric P-selectin-PSGL-1 complex, which should in turn be less geometrically constrained than two monomeric P-selectin-sPSGL-1 complexes. Both predictions are validated as dead zone measures of 22.08 ± 1.69, 16.06 ± 1.17, and 14.04 ± 2.17 nm were obtained from P-selectin-sPSGL-1 one-peak, P-selectin-PSGL-1 one-peak (both Fig. 4B), and P-selectin-sPSGL-1 two-peak curves, respectively.
By comparison, the dead zones were indifferent to the form of PSGL-1 for both E- and L-selectins (Fig. 4B), in corroboration with the stiffness data (Fig. 4A) and supporting our assertion that purified E- and L-selectins could support only monomeric interactions when reconstituted into a lipid bilayer. Thus, conclusions based on two sets of related but independent measurements, stiffness and dead zone, are consistent for all three selectins.
Mixtures of Monomeric and Dimeric Ligands
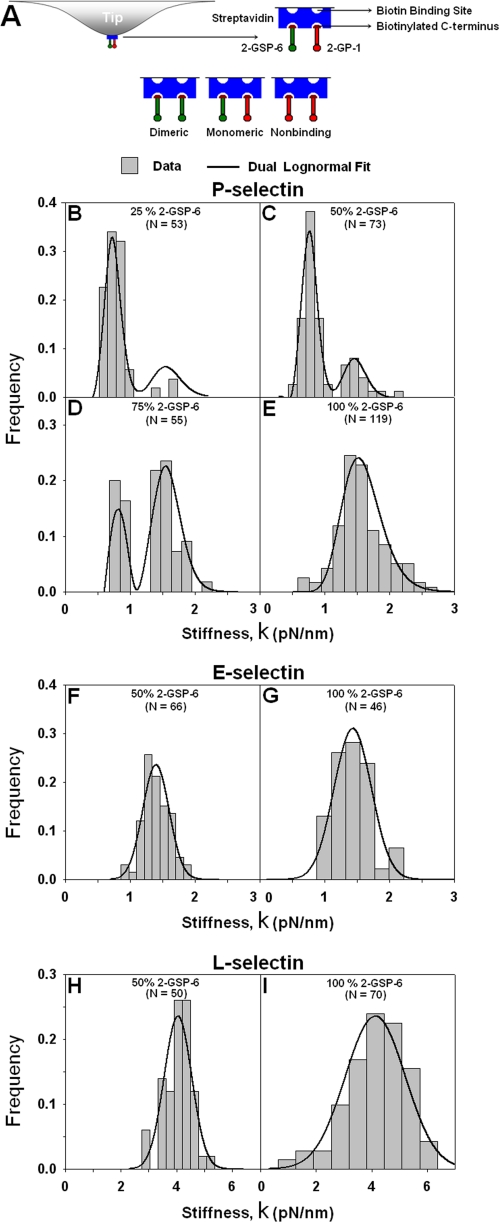
Additional experiments were performed using a glycosulfopeptide (2-GSP-6) modeled after the N terminus of PSGL-1 and its nonbinding analog, 2-GP-1, both with a single biotin at their C termini (17), which were captured in varying proportions by streptavidin pre-adsorbed on AFM tips (Figs. 1A and 5A). Streptavidin has a tetrameric quaternary structure with four biotin-binding sites, two on each side. One side should have been blocked due to adsorption on the AFM tip, leaving the other side available for binding by the biotin-tagged 2-GSP-6 or 2-GP-1. A dimeric ligand would be assembled if both exposed biotin-binding sites captured 2-GSP-6, whereas a monomeric ligand would be assembled if one site captured 2-GSP-6 and the other site captured 2-GP-1 (Fig. 5A). A nonbinding unit would result if both sites captured 2-GP-1. Monomeric and dimeric ligands with predicted fractions were thus generated by incubating streptavidin-coated AFM tips with mixture of functional 2-GSP-6 and nonfunctional 2-GP-1 at a given ratio and total concentration (Fig. 5A).
FIGURE 5.
Testing the multimericity of L-, E-, and P-selectin interactions with mixtures of monomeric and dimeric ligands. A, tetrameric streptavidin (blue) has two exposed biotin-binding sites and two blocked by adsorption on the AFM tip. Both the functional ligand 2-GSP-6 (green) and nonfunctional analog 2-GP-1 (red) have a single biotin at their C terminus and equal probability to bind to the two exposed binding sites on streptavidin. A dimeric ligand would be assembled if both sites captured 2-GSP-6; a monomeric ligand would be assembled if one site captured 2-GSP-6 and the other one captured 2-GP-1, and a nonbinding unit would result if both sites captured 2-GP-1. Incubating streptavidin-coated tips with a mixture of r × 100% 2-GSP-6 and (1 − r) × 100% 2-GP-1 would produce r2 × 100% 2-GSP-6 homodimers (dimeric ligands for selectin binding), (1 − r)2 × 100% 2-GP-1 homodimers (incapable of selectin binding), and 2r(1 − r) × 100% 2-GSP-6:2-GP-1 heterodimers (monomeric ligands for selectin binding), resulting in B1 {= 2r(1 − r)/{r2 + 2r(1 − r))} monomeric and B2 {= r2/(r2 + 2r(1 − r))} dimeric ligand fractions. Dimeric interactions are expected between dimeric selectin and dimeric ligand only. Monomeric interactions are expected if either selectin or ligand or both are monomeric. Dimensions of the AFM tip and molecules are not to scale. B–I, histograms of individual stiffness measurements from force-distance curves of a single peak of P-selectin (B–E), E-selectin (F and G), or L-selectin (H and I) interacting with 25:75 (B), 50:50 (C, F and H), 75:25 (D), and 100:0 (E, G, and I) ratios of 2-GSP-6:2-GP-1 mixtures. For P-selectin, a dual lognormal distribution was globally fit (curves) to data (bars) in all four panels (B–E) with three fitting parameters: mean of the 1st lognormal distribution, which is half of the 2nd lognormal distribution, and two standard deviations. The two lognormal distributions were normalized by NB1 and NB2, respectively, where B1 = 2r(1 − r)/(r2 + 2r(1 − r)), B2 = r2/(r2 + 2r(1 − r)), where r is the fraction of 2-GSP-6 in the mixture (0.25, 0.5, 0.75, or 1) and N is the number of measurements (indicated) in that panel. For E- or L-selectin, a single lognormal distribution was globally fit to data in two panels (F and G or H and I) with the same mean but two standard deviations, one for each panel. The curve in each panel is normalized by the number of measurements (N) in that panel.
Increasing the 2-GSP-6 fraction increased the stiffness (Fig. 4C) but decreased the dead zone (Fig. 4D) of P-selectin-2-GSP-6 complex in a dose-dependent fashion, in agreement with the predicted increase in the proportion of dimeric bonds. By comparison, neither stiffness (Fig. 4C) nor dead zone (Fig. 4D) of E- and L-selectin systems changed with 2-GSP-6 fraction, suggesting that the types of bonds formed were the same and monomeric.
The most convincing evidence came from the histogram analysis of individual stiffness measurements. For 100% 2-GSP-6, the P-selectin stiffness displayed a unimodal distribution (Fig. 5E) with the mode coinciding with the mean value (cf. Fig. 4C). With progressively decreasing proportions of 2-GSP-6, the distributions became bimodal wherein the high mode remained unchanged but a low mode emerged at half the value (Fig. 5, B–D), revealing a quantal behavior. The relative number of measurements under the two modes shifted progressively from the high value mode to the low value mode with decreasing 2-GSP-6 fraction, suggesting formation of increasing fraction of monomeric bonds at the expense of decreasing fraction of dimeric bonds. Indeed, this hypothesis was supported quantitatively by a theoretical prediction based on the experimental parameters that globally fits all four histograms very well (curves in Fig. 5, B–E). By comparison, the stiffness for E- and L-selectin exhibited only unimodal distributions (Fig. 5, F–I) with respective modes coinciding with their corresponding mean values independent of the 2-GSP-6 proportions (cf. Fig. 4C). The distribution data thus provide strong support to the mean data.
Contributions of Ligands (or mAbs) to Complex Stiffness
To delineate the relative contributions of various structural components to the molecular complex stiffness, we compared their measurements under different conditions with some elements replaced or removed. In one set of experiments, the PL2-captured (s)PSGL-1 was replaced by anti-selectin blocking mAbs that bind at or near the PSGL-1-binding site. Whereas PL2 and anti-selectin blocking mAbs recognize different antigenic epitopes, they should have similar stiffness as they are all mouse IgG1. Because selectins would be stretched the same way irrespective of whether they were pulled by PSGL-1 or mAbs, any reduction in the measured complex compliance would be the compliance of (s)PSGL-1. Surprisingly, no such reduction was detected for all three selectins (Fig. 6, A–C). These data suggested that the compliances of (s)PSGL-1 were negligible compared with those of selectins. In other words, (s)PSGL-1s were much stiffer than selectins.
FIGURE 6.
Contributions to compliance from various molecular components. A–C, lack of contribution of ligand (or mAb) to complex compliance. Stiffness measured from single-peak curves of P-selectin (A), E-selectin (B), and L-selectin (C) complexed with PL2-captured (s)PSGL-1 were compared with corresponding values measured by complexing the selectins with anti-selectin mAbs or streptavidin-captured 2-GSP-6:2-GP-1 mixtures. Statistical analyses using ANOVA found no significant differences (p values between 0.1 and 0.9) in stiffness for the same selectin complexed with either a ligand or mAb for the same form of interaction (monomeric or dimeric). The white bar in C represents data from an inverse orientation control experiment in which the stiffness of mPSGL-1 incorporated in lipid bilayer interacting with protein G-captured L-selectin-Ig on the AFM tip (cf. Fig. 1A) was measured. D, effect of selectin length on molecular stiffness. For the same P-selectin, stiffness is inversely related to the length of molecular segment stretched (cf. Fig. 1A for the antigenic epitopes of the mAbs used). Statistical analyses using ANOVA found highly significant differences (p values < 0.001) between stiffness of P-selectin complexed with blocking and capture mAbs. However, no statistical difference (p values between 0.1 and 0.9) was found between the stiffness of P-selectin complexed with two blocking mAbs, 5A8 and 2B8, or with two capture mAbs, S12 and W40. E, linear relationship between compliance and CR number. Reciprocal slopes (compliances) prior to the first peak of force-distance curves with one or two peaks were plotted against the number of CRs stretched. Two straight lines passing through the origin were fit to the one-peak and two-peak data, respectively. Slopes of the linear fits represent compliance of a single CR (0.12 nm/pN) or two CRs in parallel (0.06 nm/pN). Stiffness of a single CR equals the reciprocal of compliance (8.33 pN/nm). Data are presented as mean ± S.E. In some cases, error bars are smaller than the sizes of symbols.
In another set of experiments, PL2-captured (s)PSGL-1 was replaced by streptavidin-captured 2-GSP-6. The sPSGL-1 molecule has ∼280 amino acids, and PL2 binds near the middle of this linear mucin. By comparison, 2-GSP-6 has only 19 amino acids, and streptavidin is also much smaller than PL2. Again, these replacements did not yield any detectable reduction in the complex compliance for any of the three selectins (Fig. 6, A–C). In fact, the first mode of the stiffness distribution of P-selectin complexed with 2-GSP-6/2GP-1 mixtures (Fig. 5, B–D) coincided with the stiffness of the P-selectin-sPSGL-1 complex.
To test whether the lack of compliance contribution from the ligands was due to their method of attachment to the AFM tip, we measured the stiffness in the reverse orientation where mPSGL-1 was incorporated into the lipid bilayer, whereas L-selectin-Ig was captured on the AFM tip by protein G (Fig. 1A). The resulting stiffness value was 4.07 ± 0.21 pN/nm, comparable with the 3.6 ± 0.13 pN/nm value measured when L-selectin was incorporated in the bilayer and PSGL-1 was captured by PL2 on the AFM tip (Fig. 6C). Indeed, statistical analysis using ANOVA reports no difference between the two sets of measurements (p value = 0.19), excluding the ligand orientation as a possible cause for their lack of compliance contribution. Taken together, the data suggested that PSGL-1 and mAbs were much less stretchable than selectins and did not contribute appreciably to compliance while complexed with selectins.
Contributions of CRs to Selectin Molecular Stiffness
Although unaffected by changes in ligands (or mAbs), stiffness of the three selectins complexed with the same ligand (sPSGL-1) was different: lowest for P-selectin (0.85 pN/nm), intermediate for E-selectin (1.4 pN/nm), and highest for L-selectin (4.2 pN/nm) (Fig. 4A, open bars). A major structural difference between the three selectins is the number of CRs that determine the length of each selectin. The inverse relationship between the length of selectins and stiffness suggested that the CRs may be the major contributor to selectin compliance. To further characterize the contribution of the CRs, stiffness for P-selectin complexed with two mAbs (W40 and S12) that bind the 5th and 6th CRs from the N terminus, respectively, was measured (cf. Fig. 1A). As expected, higher stiffness (2.61 ± 0.03 and 2.49 ± 0.11 pN/nm) was observed because only part of the P-selectin molecule was stretched in these experiments (Fig. 6D).
These results are best presented by plotting molecular compliance (1/k) against the number of CRs stretched (Fig. 6E). The plots appeared linear for both single and double monomeric bonds, suggesting that the CRs were much more compliant than the lectin and EGF domains and the polyethyleneimine polymer cushion. As expected, slope of the linear fit to the single bond data was twice that of the double bond data (Fig. 6E). Taken together, the CRs behaved as springs in series with a unit stiffness of 8.33 pN/nm, obtained from the inverse of the slopes of the linear fits to the one- and two-peak monomeric bond data.
Mechanical Properties of Endoglycan
Endoglycan is a PSGL-1-like L-selectin ligand of the CD34 family of sialomucins expressed on endothelial cells (12, 26, 27). Experiments were performed using endoglycan-Ig captured by protein G adsorbed on AFM tips (Fig. 1A) to interact with P- or L-selectin bilayer. The respective stiffness measures obtained from force-distance curves with a single peak were 1.47 ± 0.04 and 4.01 ± 0.09 pN/nm. These values matched the respective values of dimeric PSGL-1 complexed with P- and L-selectins, indicating that endoglycan-Ig formed dimeric bonds with P-selectin but monomeric bonds with L-selectin and that protein G-captured endoglycan-Ig was much stiffer than selectins.
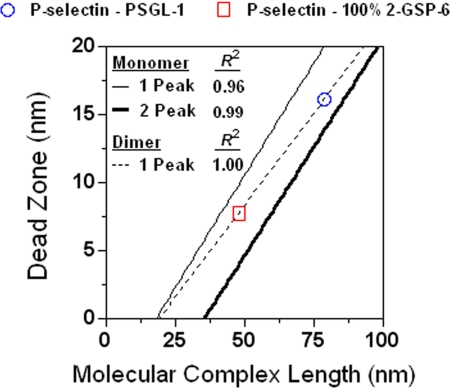
The dead zones of dimeric endoglycan-Ig-P-selectin and monomeric endoglycan-Ig-L-selectin interactions measured from force-distance curves with one peak were 23.17 ± 2.24 and 11.73 ± 0.61 nm, respectively. Using the linear relationship between dead zone and molecular complex length (Figs. 3B, top thin straight line fit, and 7) as calibration curves, the respective molecular complex lengths of 105 and 53 nm were predicted for endoglycan-Ig-P-selectin and endoglycan-Ig-L-selectin. After subtracting 38, 9, and 5 nm for P-selectin, L-selectin, and protein G, respectively, the resting length of endoglycan-Ig was computed to be 51 ± 12 nm from the selectin-binding site to the protein G-binding site.
FIGURE 7.
Dead zone versus molecular complex length for dimeric interactions. Dead zones were measured as shown in Fig. 1B. The combined lengths of molecular complexes were calculated based on published data (cf. Table 1). The thin and thick solid lines are respective fits to monomeric interaction data (not shown) from Fig. 3A measured from force-distance curves exhibiting one and two peaks. Open symbols (mean ± S.E. connected by a dotted straight line; error bars are smaller than the sizes of symbols) are dimeric interaction data measured from force-distance curves exhibiting one peak. They fall between the thin and thick solid lines. Using the thin solid and dotted lines as calibration curves, the lengths of monomeric L-selectin-endoglycan-Ig complex (53 ± 20.06 nm) and dimeric P-selectin-endoglycan-Ig complex (105 ± 27.58 nm) can be estimated from their dead zones (23.17 ± 2.24 and 11.73 ± 0.61 nm, respectively) measured from one-peak force-distance curves. Subtracting 38, 9, and 5 nm for P-selectin, L-selectin, and protein G, respectively, gave a resting length of 51 ± 12 nm for endoglycan-Ig.
DISCUSSION
In this study, we measured molecular stiffness of selectins and used mechanical measurements as a tool to address biological issues involving these molecules. The data interpretation requires that the measurements be attributed to the molecules of interest with high confidence. In single molecule AFM experiments wherein nonspecific interactions between the cantilever tip and the surface can be high, this prerequisite is often satisfied by identifying a mechanical fingerprint of the protein under study, e.g. a characteristic force-distance curve, and analyzing data that only bear this fingerprint. Such data selection also precludes variations in the protein segment being stretched due to their random adsorption on the cantilever tip and the surface tested. Here, we satisfied this prerequisite by maintaining uniformity in the stretchable protein segments (Fig. 1A) and by minimizing nonspecific binding (Fig. 2A). Importantly, we analyzed all data without pre-selection. We could not be absolutely certain whether a given force-distance curve was produced by the intended specific molecular interaction or by nonspecific adhesion. Despite this, the low nonspecific binding frequency and the absence of any pre-selection bias ensured that the total data set for each type of measurement was predominantly dominated by specific adhesion events. In addition, the distributions of the measurements (e.g. Fig. 5, B–I) were carefully examined to exclude any outliers that might represent nonspecific adhesions, which were never observed. These precautions ensured that the data and their subsequent interpretation were not adversely impacted by contamination from those rare nonspecific adhesion events. Moreover, stiffness and dead zone measurements of nonspecific interactions are not expected to change with changes in the specific molecules in ways as shown in Figs. 3–7. Thus, all of the data collectively exclude the possibility that they were results of nonspecific adhesion.
A crucial yet difficult issue in single molecule experiments is to ensure that the measured property represents that of a single pair of interacting molecules rather than multiple pairs in parallel (21). A common approach is to show that the observed events are quantized, and the frequencies of events exhibiting integer multiples of the quantal unit follow Poisson distribution with a high frequency of null events. However, these conditions are necessary but not sufficient (21). Two additional criteria must be satisfied as follows: (i) the instrument must be sufficiently sensitive to detect single molecule events so as to not wrongly identify the smallest detectable unit as a single molecule event, and (ii) at least one of the interacting molecular species must be spatially isolated into single sites (by dilution) and not be clustered so as to minimize multimeric events. As for the first criterion, it has been well established that AFM is capable of measuring single molecular interactions. The second criterion has been met using the reasoning that follows.
We have shown here that mechanical measurements can be used to distinguish between monomeric and dimeric interactions. These represent different methods from our previous work that used the lifetime versus force data (12, 14). Our methods compare dead zones and stiffness measured with alternating forms of PSGL-1 and 2-GSP-6, confirming that P-selectin and PSGL-1, which exist as dimers on their respective cell surfaces (22, 23), remained dimeric and formed dimeric bonds even after extraction and subsequent reconstitution into lipid bilayers and capture on the AFM tips, respectively. By comparison, L- and E-selectins were able to form only monomeric bonds under identical experimental conditions (Figs. 4 and 5). It remains to be determined whether L- and E-selectins are natural monomers on their respective cell surfaces.
To conclude from their inability to support dimeric interactions that E- and L-selectins existed as isolated monomeric molecules when reconstituted in the lipid bilayer (and by the same token, to conclude from its ability to support dimeric interaction that P-selectin existed as isolated dimeric molecules), we need to rule out the (only) alternative hypothesis that appeared to be consistent with our data, which is that E- and L-selectins exist as clusters of exactly two binding sites and P-selectin exists as clusters of exactly four binding sites (i.e. just two dimers). PL2 could potentially capture two monomeric sPSGL-1 or two dimeric PSGL-1 by its two Fab sites despite the fact that it was diluted as isolated molecules on the AFM tip. This scenario would match the hypothetical clustering sizes of the three bilayer-anchored selectins, thereby giving rise to the data presented here. To achieve infrequent binding, the selectins were diluted to have molecular densities of a few hundred sites/μm2, predicting tens of nanometers of average spacing between neighboring molecules if not clustered (12, 14). Electron microscopy has revealed that membrane P-selectin forms multimeric rosettes, presumably due to the hydrophobic interactions among their transmembrane segments (23), which might also be operative in the cases of E- and L-selectins. However, the size of these rosettes was nonuniform and likely depended on conditions of preparation. So there was no reason to assume that E- and L-selectin would exist as uniform clusters of just two binding sites and P-selectin would exist as uniform clusters of just four binding sites. Along related lines, streptavidin was most likely diluted to isolated single molecules on the AFM tip. Steric inhibition would prevent all four of its biotin-binding sites from being accessed by 2-GSP-6 or 2-GP-1. Hence, it is highly unlikely for a ligand constructed with a single streptavidin to form two dimeric bonds with P-selectin and at the same time one dimeric bond with E- or L-selectin.
Taken together, it is most likely that the individual peaks seen in the P-selectin-sPSGL-1 and E- and L-selectin-(s)PSGL-1 curves reflect unbinding of single monomeric bonds, whereas those seen in P-selectin-PSGL-1 curves reflect unbinding of single dimeric bonds. Also, the data showed that for P-selectin, a quantal binding unit measured in our AFM assay was a monomeric bond when it interacted with sPSGL-1 or monomeric 2-GSP-6 but a dimeric bond when it interacted with PSGL-1 or dimeric 2-GSP-6. For E- and L-selectin, the measured quantal binding units were monomeric bonds regardless of the forms of PSGL-1 or 2-GSP-6 used.
It has been suggested that the mucin-like domains of PSGL-1 could be more flexible than the folded domains of selectins, which was assumed to contribute to shear-enhanced bond formation (28). We dissected the stiffness contributions of various structural elements in the molecular system being stretched by comparing the measured stiffness with and without the elements in question (elements were either replaced or removed). This allowed us to show that PSGL-1, endoglycan-Ig, 2-GSP-6, and mAbs were much less stretchable and contributed negligibly to the complex compliance, contrary to the previous speculation (28). The selectin CRs were the major load-bearing constituents, acting as springs in series and dominating the compliance of each selectin (Fig. 6).
It is intuitive that endoglycan-Ig would form a dimeric bond with P-selectin, because it was constructed by replacing the two Fab legs of a human IgG with two endoglycan extracellular domains (12, 26, 27). But why did none of the anti-P-selectin mAbs, each of which has two Fab legs, exhibit characteristics of dimeric bonds? Also, why didn't L-selectin-Ig form dimeric bonds with mPSGL-1 (Fig. 6)? Although future studies will be required to fully address these issues, we hypothesize that fast on-rate relative to the off-rate is a key. This would allow rapid rebinding after one leg of a dimeric bond dissociates but before the other leg also dissociates. Consequently, for a dimeric bond to dissociate, the two legs have to nearly simultaneously dissociate, thereby giving rise to a solitary peak in the AFM photodiode signals.
In summary, molecular stiffness of all three selectins was systematically characterized and contrasted to those of ligands and antibodies. Mechanical property measurement was employed as a tool to address several biological issues, such as the multimericity of the interactions and molecular length. Our approach may be applied to study single molecule mechanical properties of other systems.
Acknowledgments
We thank Michael B. Lawrence, Steven D. Rosen, Richard D. Cummings, and Mian Long for valuable reagents; Jianhua Wu for help with modeling, and Wei Chen for help with curve fitting.
This work was supported, in whole or in part, by National Institutes of Health Grant AI77343.
- AFM
- atomic force microscopy
- CR
- consensus repeat
- ANOVA
- analysis of variance
- pN
- piconewton.
REFERENCES
- 1. Bryant Z., Stone M. D., Gore J., Smith S. B., Cozzarelli N. R., Bustamante C. (2003) Nature 424, 338–341 [DOI] [PubMed] [Google Scholar]
- 2. Bustamante C., Bryant Z., Smith S. B. (2003) Nature 421, 423–427 [DOI] [PubMed] [Google Scholar]
- 3. Bustamante C., Smith S. B., Liphardt J., Smith D. (2000) Curr. Opin. Struct. Biol. 10, 279–285 [DOI] [PubMed] [Google Scholar]
- 4. Carrion-Vazquez M., Li H., Lu H., Marszalek P. E., Oberhauser A. F., Fernandez J. M. (2003) Nat. Struct. Biol. 10, 738–743 [DOI] [PubMed] [Google Scholar]
- 5. Oberhauser A. F., Badilla-Fernandez C., Carrion-Vazquez M., Fernandez J. M. (2002) J. Mol. Biol. 319, 433–447 [DOI] [PubMed] [Google Scholar]
- 6. Oberhauser A. F., Marszalek P. E., Erickson H. P., Fernandez J. M. (1998) Nature 393, 181–185 [DOI] [PubMed] [Google Scholar]
- 7. Rief M., Gautel M., Oesterhelt F., Fernandez J. M., Gaub H. E. (1997) Science 276, 1109–1112 [DOI] [PubMed] [Google Scholar]
- 8. Rief M., Gautel M., Schemmel A., Gaub H. E. (1998) Biophys. J. 75, 3008–3014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. McEver R. P., Zhu C. (2010) (2010) Annu. Rev. Cell Dev. Biol. 26, 363–396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Marshall B. T., Sarangapani K. K., Wu J., Lawrence M. B., McEver R. P., Zhu C. (2006) Biophys. J. 90, 681–692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Lawrence M. B., Kansas G. S., Kunkel E. J., Ley K. (1997) J. Cell Biol. 136, 717–727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Sarangapani K. K., Yago T., Klopocki A. G., Lawrence M. B., Fieger C. B., Rosen S. D., McEver R. P., Zhu C. (2004) J. Biol. Chem. 279, 2291–2298 [DOI] [PubMed] [Google Scholar]
- 13. Ramachandran V., Yago T., Epperson T. K., Kobzdej M. M., Nollert M. U., Cummings R. D., Zhu C., McEver R. P. (2001) Proc. Natl. Acad. Sci. U.S.A. 98, 10166–10171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Marshall B. T., Long M., Piper J. W., Yago T., McEver R. P., Zhu C. (2003) Nature 423, 190–193 [DOI] [PubMed] [Google Scholar]
- 15. Mehta P., Patel K. D., Laue T. M., Erickson H. P., McEver R. P. (1997) Blood 90, 2381–2389 [PubMed] [Google Scholar]
- 16. Patel K. D., Moore K. L., Nollert M. U., McEver R. P. (1995) J. Clin. Invest. 96, 1887–1896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Yago T., Leppänen A., Qiu H., Marcus W. D., Nollert M. U., Zhu C., Cummings R. D., McEver R. P. (2002) J. Cell Biol. 158, 787–799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hutter J. L., Bechhoefer J. (1993) Rev. Sci. Instrum. 64, 1868–1873 [Google Scholar]
- 19. Wu J., Fang Y., Yang D., Zhu C. (2005) J. Biomech. Eng. 127, 1208–1215 [DOI] [PubMed] [Google Scholar]
- 20. McConnell H. M., Watts T. H., Weis R. M., Brian A. A. (1986) Biochim. Biophys. Acta 864, 95–106 [DOI] [PubMed] [Google Scholar]
- 21. Zhu C., Long M., Chesla S. E., Bongrand P. (2002) Ann. Biomed. Eng. 30, 305–314 [DOI] [PubMed] [Google Scholar]
- 22. Li F., Erickson H. P., James J. A., Moore K. L., Cummings R. D., McEver R. P. (1996) J. Biol. Chem. 271, 6342–6348 [DOI] [PubMed] [Google Scholar]
- 23. Ushiyama S., Laue T. M., Moore K. L., Erickson H. P., McEver R. P. (1993) J. Biol. Chem. 268, 15229–15237 [PubMed] [Google Scholar]
- 24. Harris L. J., Larson S. B., Hasel K. W., Day J., Greenwood A., McPherson A. (1992) Nature 360, 369–372 [DOI] [PubMed] [Google Scholar]
- 25. Barkalow F. J., Barkalow K. L., Mayadas T. N. (2000) Blood 96, 3070–3077 [PubMed] [Google Scholar]
- 26. Fieger C. B., Sassetti C. M., Rosen S. D. (2003) J. Biol. Chem. 278, 27390–27398 [DOI] [PubMed] [Google Scholar]
- 27. Sassetti C., Van Zante A., Rosen S. D. (2000) J. Biol. Chem. 275, 9001–9010 [DOI] [PubMed] [Google Scholar]
- 28. Chen S., Springer T. A. (1999) J. Cell Biol. 144, 185–200 [DOI] [PMC free article] [PubMed] [Google Scholar]