Soft Wall Ion Channel in Continuum Representation with Application to Modeling Ion Currents in α-Hemolysin

Abstract

A soft repulsion (SR) model of short range interactions between mobile ions and protein atoms is introduced in the framework of continuum representation of the protein and solvent. The Poisson-Nernst-Plank (PNP) theory of ion transport through biological channels is modified to incorporate this soft wall protein model. Two sets of SR parameters are introduced: the first is parameterized for all essential amino acid residues using all atom molecular dynamic simulations; the second is a truncated Lennard – Jones potential. We have further designed an energy based algorithm for the determination of the ion accessible volume, which is appropriate for a particular system discretization. The effects of these models of short-range interaction were tested by computing current-voltage characteristics of the α-hemolysin channel. The introduced SR potentials significantly improve prediction of channel selectivity. In addition, we studied the effect of choice of some space-dependent diffusion coefficient distributions on the predicted current-voltage properties. We conclude that the diffusion coefficient distributions largely affect total currents and have little effect on rectifications, selectivity or reversal potential. The PNP-SR algorithm is implemented in a new efficient parallel Poisson, Poisson-Boltzman and PNP equation solver, also incorporated in a graphical molecular modeling package HARLEM.

INTRODUCTION

Biological ion channels are integral membrane proteins that facilitate ion flow across the lipid bilayer by forming water-filled pores. Such ion flow generates an electrical current driven by a potential difference across the membrane. Current-voltage (I–V) characteristics of protein channels are commonly used in biology and pharmacology to characterize their specific functional properties. Because of the importance of structure-function relationships in ion channel proteins, theoretical methods for modeling ion currents through protein channels have enjoyed rapid progress.^1–4 While the most direct approach to ion currents modeling is by an all atom non-equilibrium molecular dynamics (NEMD),^5,6 such an approach remains computationally impractical given that modeling of ion flow under physiological conditions requires simulations on a microsecond time-scale. Other existing methods of ion current prediction sacrifice the atomistic representation of a system in favor of computational efficiency. These methods include Brownian dynamics (BD),^7–10 dynamic lattice Monte Carlo (DLMC)^11,12 and Poisson-Nernst-Planck (PNP) theory.^9,13–18 All three approaches share a number of common approximations, e.g. a solvent and a membrane are treated implicitly, while the protein may be represented in atomistic detail (albeit most often as a rigid body). The main difference between these coarse-grained methods of modeling is in the representation of the mobile ions. Ions are modeled as explicit particles in BD and DLMC (hence, they are semi-continuum approaches), while in PNP they are represented by their position dependent average concentrations (a continuum approach). Due to this additional approximation, PNP remains the most computationally efficient method for modeling ion permeation. For this reason we employ in this paper a generalized version of PNP, potential of mean force PNP (PMFPNP),¹⁴ which has been shown to be as accurate as BD and DLMC in narrow channels, where the original PNP is inapplicable.^11,19

Both semi-continuum and continuum approaches (e.g. BD and PMFPNP) require a priori determination of the protein boundary and the ion accessible volume (IAV) of a channel. From an atomistic view IAV is naturally established largely by short-range interactions between permeating ions and protein atoms lining the channel lumen. Therefore, in semi-continuum and continuum approaches the IAV boundary serves as an approximation of such interactions. Unfortunately, predicted currents strongly depend on the choice of IAV¹⁶. Thus, too crude an approximation of the short range interactions between permeating ions and a protein in semi-continuum and continuum models may lead to poor prediction of the I–V characteristics of the channel. Yet, in most studies reported to date, short-range protein – ion interactions have been modeled by permitting mobile ions to move only within a predetermined IAV and by forbidding them to penetrate elsewhere. Such a model is physically equivalent to hard wall repulsion (HR). An impermeable surface of the channel is typically constructed using ion exclusion radii (IER) of the protein atoms, which may be chosen as i) van der Waals (vdw) radii of the protein atoms,^13,20 ii) a sum of a vdw radius of a protein atom and a radius of a permeating ion,²¹ or iii) radii calculated from an MD simulation.^16,22 The vdw radii of atoms are usually taken from either an existing continuum electrostatics force field¹³ or a molecular mechanics force field;²¹ however, neither was designed for the calculation of the IAV of an ion channel.

Regardless of the choice of ion exclusion radii used in constructing the channel wall, the main deficiency of the HR model is that it remains rigid in the course of ion current modeling. In reality, however, the closest distance between a protein atom and a mobile ion may depend on the ion interaction with neighboring atoms and on an externally applied electric field. Therefore, representation of the channel lumen in the continuum and semi-continuum models requires greater accuracy and flexibility than is possible with the HR model.

In this work we introduce a soft repulsion (SR) model of the short range interactions between permeating ions and protein atoms lining channel lumen, which is included in a modified PMFPNP theory for an improved representation of the ion accessible volume of a channel and the short-range ion-protein interactions. The soft repulsion energy term also allows for the IAV self-adjustment in the presence of mobile ions of different kinds and in the presence of different applied potentials. The soft repulsion energy term introduced here is parameterized for all atoms of each amino acid using MD simulations in explicit water. (We will hereafter refer to this parameter-set as SR-MD). In addition, an alternative form of soft repulsion is introduced. This alternative form utilizes a truncated Lennard-Jones potential (LJ) with parameters taken from the Cornell et al. force field²³ (we will hereafter refer to this potential-set as SR-LJ). Since at short distances atom-atom interactions are dominated by van der Waals repulsion and the LJ parameters for such interactions are widely available, SP-LJ seems an appealing option. The SR-LJ parameter set, however, did not perform as well as SR-MD, perhaps due to unaccounted solvent effects.

Both BD and PMFPNP methods also depend on the choice of an ion diffusion coefficient, which, in general, is an inhomogeneous function in space. Although diffusion coefficients of ions exhibit complicated forms in the vicinity of proteins,²⁴ most recent reports on modeling channel conductance neglect the three-dimensional dependence of the diffusion coefficient on an ion position in the channel and assign either a single constant value of the diffusion constant for the whole pore,^12,16,25 or a few constant values for distinct pore regions.⁹ Recently we have tested several accurate approaches for the estimation of diffusion coefficients in channels.²⁶ Our study showed that methods utilizing the mean square displacement yield diffusion coefficients with poor precision and accuracy in the confined environment of the channel. Therefore, more accurate methods are needed for accurate calculation of three dimensional diffusion coefficient distributions in ion channels from first principles. However, before embarking on a computationally expensive route for evaluating diffusion coefficients with high precision at great computational expense we evaluate in this work how sensitive the predicted I–V properties are to the choice of a diffusion coefficient distribution. For this purpose we chose several model diffusion coefficient distributions: the distance-dependent diffusion coefficients calculated from MD simulations of ions in the vicinity of proteins and DNA²⁴, using a hydrodynamic approximation⁹ and a novel superposition of the two latter methods that takes into account both microscopic boundary effects and hydrodynamics in narrow tubes.

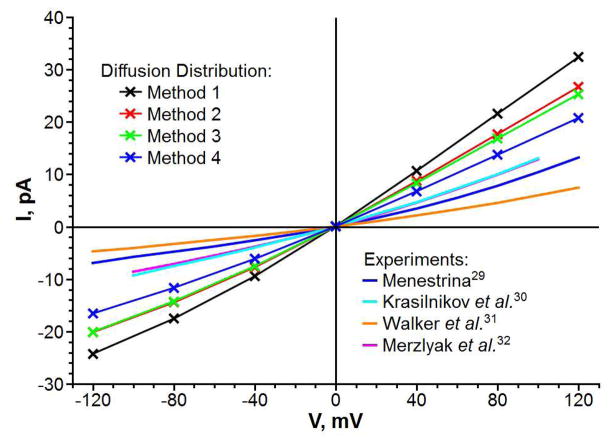
The model protein channel system in this work is α-hemolysin (AHL), a large protein toxin from Staphylococcus aureus,²⁷ which forms a heptameric complex with a relatively wide pore. AHL has been extensively studied, both theoretically^5,9,28 and experimentally.^29–33 Yet, an accurate prediction of its current conducting properties remains elusive. The improved theoretical model introduced in this work allows us to better model physical determinants that influence channel conductance, ion selectivity, and reversal potentials. The latter two properties are notoriously difficult to accurately predict in such a weakly selective channel as AHL.

This article is organized as follows. In the Methods section we first describe the PMFPNP method and its relation to the original PNP theory. Next, an extension of the PNP theory that incorporates a soft repulsion potential (PNP-SR) is introduced, followed by discussion of the SR parameters. The Poisson-Boltzmann equation with soft repulsion potential (PB-SR) is also introduced, as it serves as an essential component for IAV determination. An IAV determination protocol description follows. Finally, the diffusion coefficient setting methods are described, as well as a protocol for calculation of AHL I-V properties. In the Results section we report on the calculated I–V properties of the AHL channel using three methods: the original PNP theory (PNP-HR), PNP-SR with parameterization from MD simulations (PNP-SR-MD), and PNP-SR with truncated LJ potential (PNP-SR-LJ). In the Discussions section, predictions by PNP-HR, PNP-SR-MD and PNP-SR-LJ are compared and their differences are analyzed. The Conclusions section summarizes the main outcomes of this work. Appendix 1 describes parameterization of SR-MD potential. Appendix 2 describes technical issues of solving the PNP-SR equations numerically, such as the algorithm, pre-conditioning and precision. It also describes the new efficient parallelized PNP solver.

METHODS

A soft repulsion potential for short range ion-protein interactions is introduced in this work in the framework of the PMFPNP theory. The PNP theory has been, however, widely criticized in the literature, and hence we start this section with a short introduction to the problem. The original PNP theory neglects the finite size of ions and consequently the dielectric self-energy (DSE) of an ion. This is a severe deficiency for narrow channels modeling.^11,34,35 However, a generalization of the theory developed independently by us (termed DSE-PNP)³⁴ and others³⁶ remedies this problem. It has been shown that DSE-PNP yields results comparable to BD.³⁴ Moreover, further generalization of DSE-PNP as developed in PMFPNP is applicable in conjunction with equilibrium all atom simulations. This allows PMFPNP to accurately and efficiently estimate ion currents without employing adjustable parameters.¹⁴ It is also important to note that ions in PNP interact with each other on a mean field level via electrostatic field and, therefore, direct dynamic correlation of motion of the individual ions is neglected. The interaction of ions as individual particles may be important in channels that are simultaneously occupied by two or more ions forming a single file; however, no quantitative assessment of importance of this effect for the resulting currents has been reported to date. A modification of the PNP theory that partially overcomes this limitation was proposed and successfully applied using density functional theory - PNP (DFT/PNP).^37–39

PMFPNP

In continuum approximation, mobile ions are represented via fields of their average concentrations. In PMFPNP, a generalization of the PNP theory,^14,36 a flux of the mobile ions is determined by the drift-diffusion equation (Nernst-Planck (NP) equation) as follows:

$$\overline{j_i}(\mathbf{r})=-D_i(\mathbf{r})\left(\overline{\nabla }{C}_i(\mathbf{r})+\frac{1}{kT}{C}_i(\mathbf{r})\overline{\nabla }{\mathrm{\Psi }}_i(\mathbf{r})\right)$$ (1)

where i stands for a type of the mobile ions (Na⁺, K⁺, Cl⁻ etc.), r is a three dimensional (3D) position vector; k is the Boltzmann constant, T is temperature, D_i(r) is a space dependent diffusion coefficient of the i^th type of mobile ions, C_i(r) is its concentration, and Ψ_i(r) is its potential of mean force⁴⁰ or PMF. The first term in eq 1 describes free diffusion and the second one describes drift under an energy gradient. The continuity of the flux under steady state conditions requires the divergence of the flux to be zero:

$$\overline{\nabla }·\left[D_i(\mathbf{r})\left(\overline{\nabla }{C}_i(\mathbf{r})+\frac{1}{kT}{C}_i(\mathbf{r})\overline{\nabla }{\mathrm{\Psi }}_i(\mathbf{r})\right)\right]=0$$ (2)

The solution of eq 2 is a time-independent distribution of the mobile ion concentrations in the presence of the mean force (−Δ̄Ψ(r)).

In the PMFPNP approach PMF entering eq 1 can be divided into two terms: a single ion potential (SIP) and ion-ion interactions. SIP is more generally a single ion PMF, which accounts for a mobile ion interaction with the protein, the membrane and the solvent. SIP can be calculated from equilibrium all atom MD simulation, in which case SIP will include the effects of protein flexibility and the dielectric self-energy of an ion, as well as the effects of solvent and membrane relaxation. The ion-ion interactions are treated on the mean field level and are calculated using a corresponding Poisson equation (see below).

The original PNP theory can be recovered from PMFPNP when several additional approximations are made: the protein is treated as a rigid body, DSE of a mobile ion is neglected and short range interaction of the protein atoms with the mobile ions is approximated as a hard wall potential. With these approximations the PMF corresponding to the PNP theory can be written as:

$${\mathrm{\Psi }}_i(\mathbf{r})=q_i\varphi (\mathbf{r})+W_i^{HR}(\mathbf{r})$$ (3)

where q_i is the charge of the i^th type of mobile ions; ϕ(r) is electrostatic potential originating from the protein atom charges, other mobile ions and external potential; and $W_i^{HR}(\mathbf{r})$ is the HR between ions and the protein. HR is typically modeled by setting the diffusion coefficient to zero in the regions of space that have been pre-determined to be inaccessible to mobile ions, i.e. inside the protein and the membrane.

The electrostatic potential in eq 3 is computed using the Poisson equation:

$$\overline{\nabla }\epsilon (\mathbf{r})\overline{\nabla }\varphi (\mathbf{r})=-4\pi \left({\rho }_{\mathit{static}}(\mathbf{r})+\sum _{i=1}^{N_{\mathit{ions}}}{q}_i{C}_i(\mathbf{r})\right)$$ (4)

where ε(r) is the position dependent dielectric constant which is usually a piece-wise constant function with distinct values in the protein interior, the membrane and the solvent; and ρ_static(r) is the charge density on the protein atoms.

The Poisson and Nernst-Planck equations (eqs 2 and 4) are solved self-consistently subject to the Dirichlet boundary conditions. In this paper, boundary conditions for the ion concentrations are set to their respective bulk values at all points of the boundary accessible to ions. The electrostatic potential is set to zero at the boundaries of the cis-compartment (as shown in Figure 1) and to the value of an applied potential at the boundaries of the trans-compartment. The potential at the boundaries of the membrane region is set as a linear interpolation between its values in the cis- and trans- compartments. Numerically, the Poisson and Nernst-Planck equations are solved iteratively using a finite difference (FD) scheme with successive over-relaxation method. For more detail on numerical methods refer to our previous work¹³ and Appendix 2.

Figure 1.

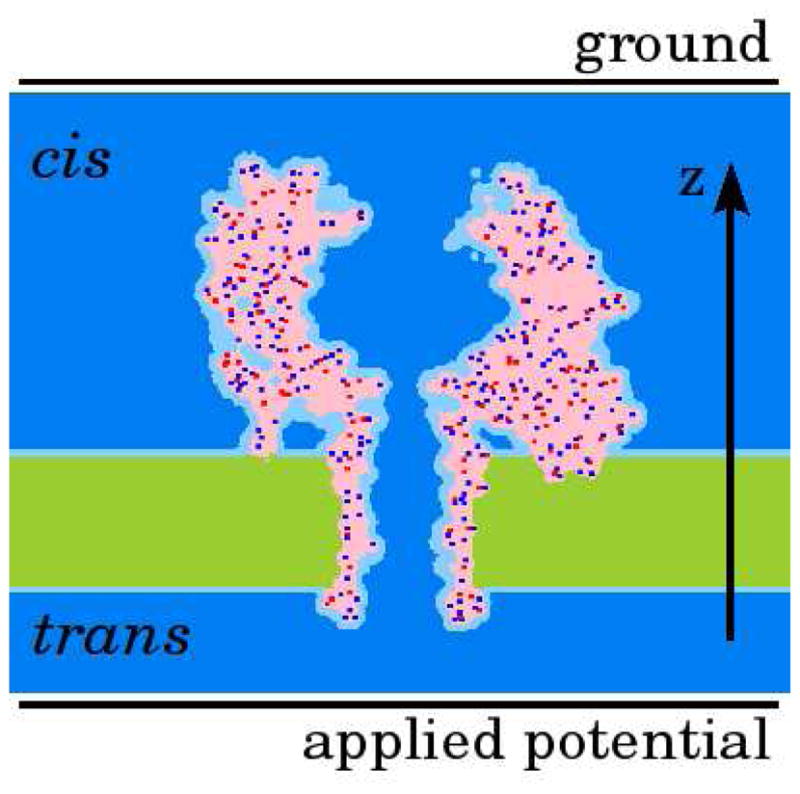
The representation of a bio-channel in PNP theory. Shown is a central slice through the YZ plane of the AHL channel. The light and dark blue together represent the solvent, characterized by the high dielectric media; green represents the low dielectric media of the membrane; pink represents low dielectric media. Protein is shown mainly in pink. Red and blue dots show negative and positive partial charges of the protein atoms; dark blue shows the ion accessible volume. Cis- and trans- compartments are located above and below the membrane respectively.

Poisson-Nernst-Planck Theory with Soft Repulsion (PNP-SR)

In this section we introduce a modified PNP theory that incorporates a soft wall ion channel. In PNP-SR short range interactions of the protein atoms with the mobile ions are approximated by a soft repulsion (SR) potential. The resulting approximate PMF is given by (compare with eq 3 of the PNP-HR):

$${\mathrm{\Psi }}_i(\mathbf{r})=q_i\varphi (\mathbf{r})+W_i^{SR}(\mathbf{r})$$ (5)

where $W_i^{SR}(\mathbf{r})$ is a 3D repulsive potential between an ion of type i and a protein. In the model implemented in this work the repulsive potential is pair-wise additive. The contribution of SR to PMF is calculated by placing a probe ion in each possible position and computing the total repulsion between protein atoms and the probe ion at each position. Thus, the 3D repulsive potential is:

$$W_i^{SR}(\mathbf{r})=\sum _l{W}_{il}^{SR}(\mathbf{r})$$ (6)

where $W_{il}^{SR}(\mathbf{r})$ is a pair-wise potential between the l^th protein atom and the ion probe of type i^th at position r. The summation includes all protein atoms.

In this work we introduce and test two alternative forms of defining and parameterizing the soft repulsion energy term. The first approach (further termed SR-MD) employs atomistic MD simulations to obtain a radial distribution function (RDF) of ions in the vicinity of a single amino acid in solution. A single ion PMF is directly related to this RDF. In SR-MD the RDF is split into long-range attractive and short range repulsive terms. The latter is fitted with the analytic potential function (SR-MD) of the following form:

$$W_{il}^{SR-MD}(\mathbf{r})=\{\begin{array}{cc}\left({\left(\frac{A_{il}}{\mid {\mathbf{r}}_l-\mathbf{r}\mid }\right)}^{{\eta }_{il}}-1\right)kT,& \mid {\mathbf{r}}_l-\mathbf{r}\mid <A_{il}\\ 0,& \mid {\mathbf{r}}_l-\mathbf{r}\mid \ge A_{il}\end{array}$$ (7)

where A_il and η_il are fitting parameters and r_l is a position of the l^th protein atom. The proposed function has only two fitting parameters, levels off to zero at distance A_il, and closely fits the repulsive part of the RDF (See Figure S1 in the Supporting Information). Such MD based W^SR accounts for direct ion-protein interactions and non-polar interactions with the solvent. A detailed description of the SR parameterization is given in Appendix 1.

An alternative approach to modeling W^SR is to use a truncated form of the Lennard-Jones potential from a molecular mechanics force field in the following form:

$$W_{il}^{SR-LJ}(\mathbf{r})=\{\begin{array}{cc}\frac{A_{il}}{{\mid {\mathbf{r}}_l-\mathbf{r}\mid }^{12}}-\frac{B_{il}}{{\mid {\mathbf{r}}_l-\mathbf{r}\mid }^6},& \mid {\mathbf{r}}_l-\mathbf{r}\mid <{(A_{il}/B_{il})}^{1/6}\\ 0,& \mid {\mathbf{r}}_l-\mathbf{r}\mid \ge {(A_{il}/B_{il})}^{1/6}\end{array}$$ (8)

where A_il and B_il are Lennard-Jones parameters for interaction between the i^th type of mobile ions with the l^th atom of the protein. Here, the parameters are taken from the Cornell et al. force field.²³ The Lennard-Jones potential was truncated for simplicity of superposition with the electrostatic potential. We will further refer to this alternative form as SR-LJ. The benefit of SR-LJ is that it does not require expensive MD simulations; however it does not account for the non-polar interactions with the solvent.

Implementation issues for PNP-SR

In principle, in the formulation of PNP-SR there is no need to explicitly determine IAV because the resulting PMF prevents ions from visiting regions of space with high energy. However, because the numerical solver of the PNP equations (described in detail in Appendix 2) is highly sensitive to the gradients of PMF, the direct usage of PMF has limitations. Fortunately, the majority of high energy gradients occur in the regions of space rarely visited by ions. Therefore, without loss of accuracy ions can be prohibited from penetrating such regions of space, which also results in improving the numerical stability of the solver. IAV in this case depends on grid spacing: on finer grids IAV includes regions of space (typically adjacent to channel atoms) that have a low population of mobile ions, while on coarser grids, such regions of space are excluded. Thus, the accuracy of the model depends on grid spacing, which is not unlike its dependency in a typical finite difference method. Hence, the dependency of the precision of IAV determination on grid spacing is similar to that for the numeric FD solver: higher precision is achieved with finer grids.

To determine the IAV we have utilized the relation of the Poisson-Boltzmann (PB) equation to the PNP theory equations. The proposed procedure considers the gradients of both the short-range repulsive and electrostatic terms of PMF as well as the gradients of concentrations. The PB equation with soft repulsion will be introduced before describing this procedure.

Poisson-Boltzmann Equation with Soft Repulsion

PNP equations reduce to an equivalent Poisson-Boltzmann equation in the absence of a flux, i.e. in the absence of applied voltage and with symmetric salt bath concentrations on the cis- and trans- compartments. Thus, solving the PB equation prior to PNP can serve as a pre-processing step that provides a good initial guess for PNP equations. Such preprocessing also significantly improves the stability of the PNP solver and speeds up convergence. A soft repulsion potential is incorporated into the PB equation in the same manner as described above for PNP equations. The modified Poisson-Boltzmann equation with soft repulsion is given by:

$$\overline{\nabla }\epsilon (\mathbf{r})\overline{\nabla }\varphi (\mathbf{r})=-4\pi \left({\rho }_{\mathit{static}}(\mathbf{r})+\sum _{i=1}^{N_{\mathit{ions}}}{q}_i{C}_i^{\mathit{Bulk}}{\lambda }_i(\mathbf{r})exp\left(-\frac{q_i\varphi (\mathbf{r})+W_i^{SR}(\mathbf{r})}{kT}\right)\right)$$ (9)

where ε(r), ϕ(r), ρ_static(r), q_i are the same as in eq 4; $C_i^{\mathit{Bulk}}$ is bulk concentration of mobile ions of i^th type; and λ_i(r) is a function that describes IAV (it equals one if r belongs to IAV and zero otherwise). The parameter λ_i(r) is introduced here for convenience. It is used to define regions of space, which are a priori unoccupied by ions (e.g. within the molecule surface of the protein). $W_i^{SR}(\mathbf{r})$ is used everywhere else. A space-dependent concentration of mobile ions can then be computed from the electrostatic potential from eq 9:

$$C_i(\mathbf{r})=C_i^{\mathit{Bulk}}{\lambda }_i(\mathbf{r})exp\left(-\frac{q_i\varphi (\mathbf{r})+W_i^{SR}(\mathbf{r})}{kT}\right)$$ (10)

Note that the SR potential enters eq 9 without any differential operators. Therefore, PB-SR is significantly more stable in the presence of high gradients of SR than the NP equation. This property is utilized in our algorithm for determining IAV for PNP-SR.

Determination of the Ion Accessible Volume of the Channel

As stressed above, the PNP numerical solver is highly unstable in the presence of high gradients of PMF. In part, these gradients are introduced to PMF by the SR potential, which increases steeply as an ion approaches protein atoms (channel wall). However, a high PMF value at a particular point of space is a reliable indicator that this region will rarely be visited by ions (with probability proportional to exp(−PMF(r)/RT)), thus ions can be excluded from such regions of space without sacrificing the accuracy of the final solution. To apply these ideas to numerical determination of IAV the following iterative procedure is used:

1. An initial guess for IAV is set such that all space is accessible to the mobile ions except for the solvent excluded volume, where. λ_i(r) and the diffusion coefficient are set to zero.

2. PB-SR (eq 9) is solved and the distribution of ion concentrations at equilibrium is determined using eq 10.

3. One iteration is completed with the Nernst-Planck equation solver using same conditions as for PB-SR in step 2 and using the solution of eq 9 obtained in step 2 as the initial guess. If, for any grid position, the change in the ion concentration is larger than ΔC_cut, (a tolerance parameter described below), or the resulting concentration is less than zero, then this position is excluded from IAV. Steps 2 and 3 are repeated until convergence.

ΔC_cut is an adjustable parameter. We have empirically determined that the resulting currents are not significantly affected by the choice of ΔC_cut in the range of 0.1M to 10 M (Figure S2), therefore the choice of the ΔC_cut value is dictated mainly by algorithmic convenience.

With the IAV determined as described above the PNP-SR equations also become better tractable numerically due to increased convergence stability. (The original PNP is notoriously numerically unstable, such that specific algorithms⁴¹ of linearization were developed or under-relaxation was used in relaxation techniques to overcome this problem).¹³ In addition, the electrostatic potential and the mobile ion concentrations calculated during IAV determination serve as a good initial guess for the final PNP-SR calculations. Such preprocessing allows us to use high values for the over-relaxation parameters in both Poisson and Nernst-Planck equation solvers, a step that significantly speeds up numerical convergence of PNP.

Position Dependent Diffusion Coefficients

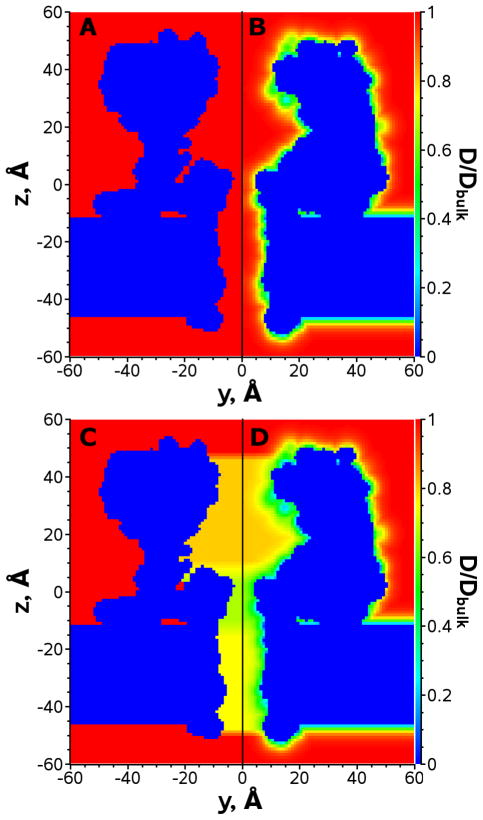
Four methods of assigning diffusion coefficients were implemented and compared. We will refer to them as methods 1–4. In method 1 the diffusion coefficients of mobile ions are set to the respective bulk value throughout IAV. The 2D slice of mobile ions diffusion coefficients in AHL pore set by this method is shown in Figure 2A.

Figure 2.

2D center cut of the 3D diffusion coefficient distribution used for numerical solution of the Nernst-Planck equation. The diffusion distributions are built using A - method 1 (for clarification of the method used see Table 1), B - method 2, C - method 3 and D - method 4. Note, only half panels are shown for compactness.

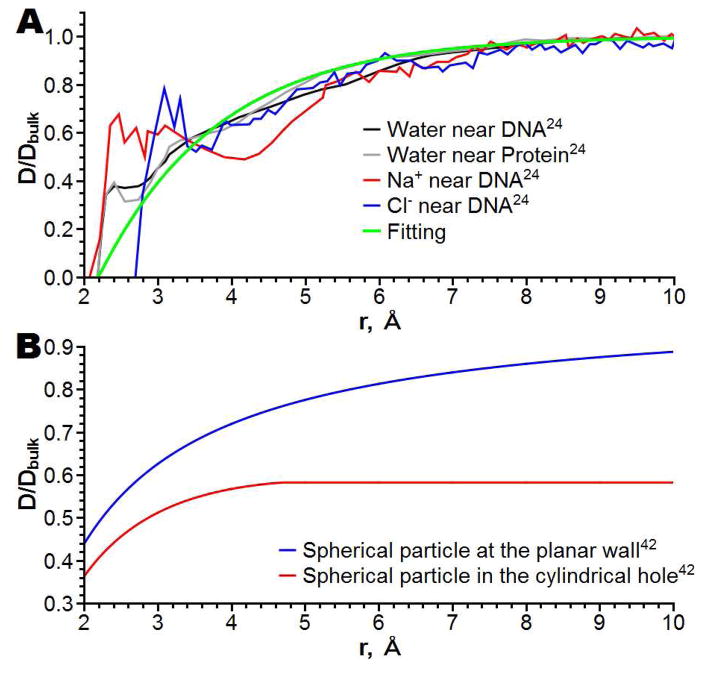
In method 2 the diffusion coefficients for ions depend on the distance to the heavy (non hydrogen) atoms of the protein lining channel pore. The distance dependence is inferred from the MD simulations of Makarov et al. ²⁴ shown in Figure 3A along with our fit using the following expression:

$$D_i(r)=D_{i,\mathit{bulk}}(1-exp(-a(r-r_0)))$$ (11)

where i is the ion type, r is the distance to the closest heavy atom, a and r₀ are fitting coefficients, which found to be 0.62 Å⁻¹ and 2.2 Å. A 2D slice of the 3D diffusion coefficient distribution around α-hemolysin using method 2 is shown in Figure 2B.

Figure 3.

(A) Normalized diffusion coefficients of ions and water molecules to its bulk value (D/D_bulk) as a function of distance r from protein’s and DNA’s heavy atoms²⁴; fitting of these diffusion coefficients by eq 11. (B) Dependence of spherical particle diffusion coefficient from the distance from molecular wall, calculated using hydrodynamic approximation;⁴² radii of spherical particle and cylindrical hole are 2 Å and 10 Å respectively.

Method 3, the hydrodynamic approximation of the diffusion coefficient, was previously used by Noskov et al.⁹ to calculate position dependent diffusion coefficients in the AHL channel. Here, their results are used without change. Briefly, in this method the diffusion coefficient in the plane perpendicular to the pore axis is set to the value of the diffusion coefficient of a spherical particle at the center of a cylindrical hole, calculated using continuous hydrodynamics. Noskov et al. ⁹ approximated this diffusion coefficient as a function of a ratio between ion radius and pore radius (β=R_ion/R_pore):

$$D_i(\beta )=\frac{D_{i,\mathit{bulk}}}{A+Bexp(\beta /C)+Dexp(\beta /E)}$$ (12)

where fitting coefficients were found to be A=0.64309, B=0.00044, C=0.06894, D=0.35647 and E=0.19409. The diffusion coefficients were first computed for a number of positions along the pore center. Then average values were computed within three distinct regions of the channel: the vestibule, the main constriction, and the trans-membrane part. These three values were further used as constant diffusion coefficients in the corresponding regions of space. A 2D slice of the diffusion coefficients calculated using method 2 is shown in Figure 2C.

Method 4 is a superposition of Methods 2 and 3. Figure 3B demonstrates the dependence of a hydrodynamic diffusion coefficient of a spherical particle on a distance to two types of walls: a plane and a cylindrical hole.⁴² As seen in this figure, the dependence of the diffusion coefficient on a distance from a plane is qualitatively similar to method 2 (Figure 3). The distance dependence in a cylindrical hole is also qualitatively similar to method 2 but its maximum value differs. Thus, in the vicinity of the channel wall the effect of the wall is prevalent (due to the local interaction of the ion with the protein atoms and slowing down of the water flow), while at larger distances the hydrodynamic flow in the cylindrical hole becomes the dominant feature. The diffusion coefficient of Method 4 is computed as follows: D₄(r)=D₂(r)*D₃(r)/D_bulk, where indexes stand for the diffusion distribution method. A 2D slice of the diffusion coefficients calculated using method 4 is shown on Figure 2D.

The mobile ions’ bulk diffusion coefficients were set to their value at infinite dilution, namely 1.957*10⁻⁵ cm² s⁻¹ for K⁺ and 2.032*10⁻⁵ cm² s⁻¹ for Cl⁻.

α-Hemolysin System Setup

Initial coordinates for AHL were taken from the protein data bank (code 7AHL).⁴³ The protein pore is aligned with the z axis and its geometric center was moved to the origin of the coordinates (for graphical representation of the system see Figure 4A). The membrane, represented as a slab with a dielectric constant equal to 2, was centered at the hydrophobic belt of AHL. The membrane thickness was set to 28 Å, which approximately corresponds to the aliphatic region of the dipalmitoylphosphatidylcholine (DPPC) bilayer. The dielectric constant of the protein was set to 4 and of the solvent to 80. A standard protonation at pH 7 was used for all ionizable residues of AHL. This agrees with the protonation assignment at pH 7 recently reported using pK_a calculations⁴⁴. The atomic charges and radii were set using Cornell et al. force field²³ for all atoms of AHL. Each atomic charge was set on the grid by distributing the charge other eight neighboring nodes of the grid.⁴⁵

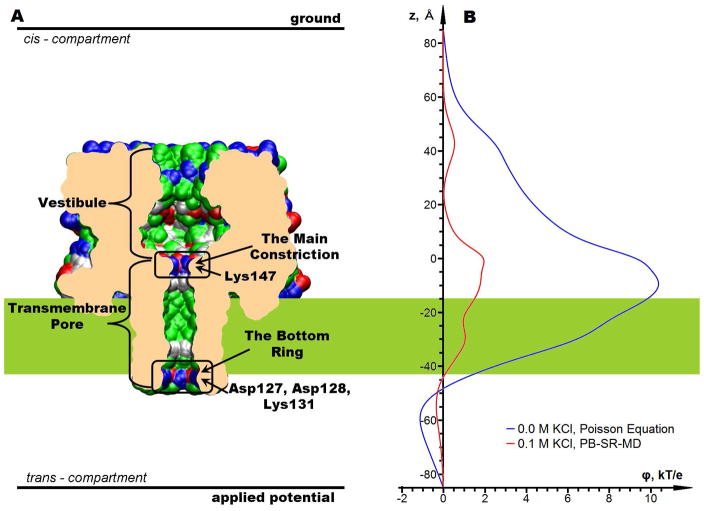
Figure 4.

(A) Central slice through the AHL channel. Molecular surface corresponds to ion accessible surface. The surface is colored according to the electrostatic characteristics of exposed residues: blue – basic, red – acetic, green – polar and white non-polar. (B) Electrostatic potential along the center of α-hemolysin pore with and without mobile ions.

The majority of the calculations reported in this paper were made on a grid of 171×171×171 with a grid scale of 1 grid node/Å. For the study of how the current depends on the grid scale, grids up to 341×341×341 with a grid scale of 2 grid nodes/Å were also used. A typical calculation consisted of 2000 iterative PNP steps, where each PNP step consisted of 20 steps of the Poisson equation solver and 20 steps of the Nernst-Planck solver. The overrelaxation parameter was 1.5 for both Poisson and Nernst-Planck solvers for the majority of the calculations. PB calculations typically consisted of 2000 iterations with the over relaxation parameter of 1.6–1.8. The total current calculated using the 171³ ų box differs by only 1% from that for a larger box of size 301³ ų (Figure S3).

RESULTS

α-Hemolysin

AHL is a large 293 residue protein toxin from Staphylococcus aureus. It forms a heptametric transmembrane channel with a relatively wide pore. The pore of the channel has two distinct regions (see Figure 4A): a vestibule and a transmembrane (TM) pore. The vestibule is the widest part of the lumen. The main constriction, which is the narrowest part of the pore, is located at the top entrance to the TM pore and is formed by Met113 and a positively charged Lys147. A second ring of charged residues exposed to the pore is formed on the opposite side of the TM pore by Asp127, Asp128 and Lys131. We will further refer to this second constriction region as the bottom ring. The total charge of this ring is negative, rendering this region cation selective. An electrostatic field distribution through the center of the channel computed using a Poisson equation is shown in Figure 4B with a blue line. This electrostatic profile is solely due to the protein, the membrane and water. It is apparent from this figure that the regions of the main constriction and the bottom ring dominate electrostatic properties of the channel. Also, the vestibule contributes to the increase in the electrostatic field in the channel lumen because of the multiple charged residues exposed in this region. However, in the presence of mobile ions the electric field in the vestibule is effectively screened by the solvent and the ions (As shown with the red curve in Figure 4B). Therefore, the contribution of the vestibule to the ion-conductance properties of the channel is expected to be minor.

Current-Voltage characteristics of α-Hemolysin

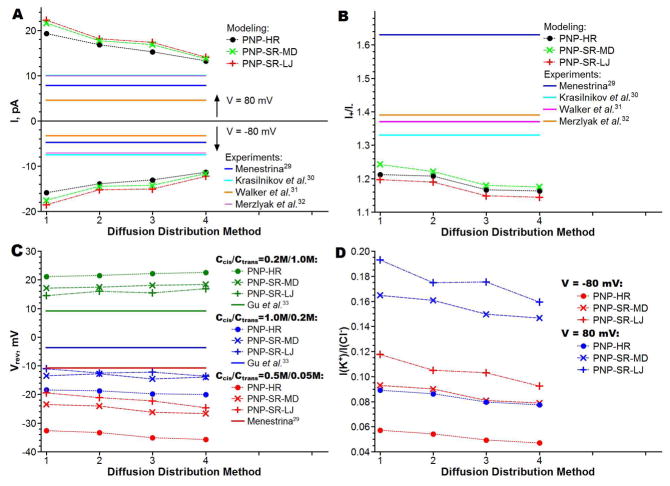
The I–V characteristics of the α-hemolysin channel were modeled in this work using a continuum-level modified PNP theory (as described in the Methods section). The modified PNP theory, termed PNP-SP, introduced a soft repulsion (SR) model for the short-range interactions between protein atoms and mobile ions. The term PNP-HR introduced in this work for consistency of notation corresponds to the original PNP theory,¹⁵ in which the ion accessible pore has a rigid wall and is determined a priori based solely on the protein structure. The influence of a diffusion constant model on predicted currents was also studied. Namely, for each model of the short-range interaction, the I–V characteristics were calculated using four different diffusion constant distributions, termed methods 1 through 4 (see the methods section and Table 1 for description). Figure 5 summarizes our results. It also shows experimental data for comparison. Complete I–V curves are shown in Figure 6 for the PNP-SR-MD calculations as well as experimental data. The calculated I–V properties of the α-hemolysin channel in 0.1M solution of KCl are compared with four experimental studies.^29–32 Note that reported conductance for this channel differs by more than 50% between experimental works. The smallest conductance is reported by Walker et al.³¹ and the largest conductance is reported by Krasilnikov et al.³⁰ As seen in Figure 5A all PNP methods overestimate channel conductance with respect to the experimental values for all diffusion constant distribution methods, and approximately to the same degree. As expected, using the diffusion constant method 4 (Table 1) (which takes into account both the hydrodynamic slowing down of the flow in the narrow tube and the protein-ion interactions at the channel wall) gives the best predicted absolute value of the current, i.e. about 30% larger than the experimental value (comparing PNP-HR to Merzlyak et al.).³² With the diffusion constant set uniformly to the bulk value (method 1) PNP overestimates currents more than twice. The results with the uniform bulk diffusion constants are shown here for reference only.

Table 1.

Diffusion constant distribution methods

Method Number	Method Description
1	Diffusion coefficients of ions are set to its bulk values throughout the space accessible by ions
2	Diffusion coefficients for ions in its accessible space are set as a function of distance from the heavy (non hydrogen) atoms of the protein. The form of dependency was calculated from the work of Makarov et al. 24
3	Hydrodynamic approximation9
4	Superposition of method 2 and 3

Figure 5.

Summary of I–V properties calculations. (A) Total currents at applied potential of 80 mV and −80 mV. (B) Rectification at applied potentials ±80 mV. (C) Reversal potentials. (D) Selectivity as a currents ratio at applied potential of 80 mV and −80 mV with symmetrical concentration (0.1 M) of mobile ions.

Figure 6.

Comparison of I–V curves predicted by PNP-SR-MD using different diffusion constant distribution methods with experimental curves.

One important property of a channel is its rectification parameter (I₊/I₋), which is defined as the ratio of the total currents at applied potentials +V and −V respectively. Unlike total currents, the rectification parameters are much more consistent among published experimental reports; therefore, we compare calculated rectification parameters with the average of the three studies.^29–32 While all predicted rectification values are smaller than the experimental values, they are systematically better than the total current prediction (Figure 5B) for all diffusion constant models. The smallest deviation from the experimental results is achieved with PNP-SR-MD, which predicts rectification at accuracy that is better than 10% of experimental value. A range of the predicted rectification values with different diffusion distributions is within 5% for all PNP calculations. Therefore, it is apparent that the choice of the diffusion constant distribution has much stronger impact on the total currents than on the current rectification.

In theoretical modeling, channel selectivity can be calculated directly as the ratio of a cation current over an anion current (I(K⁺)/I(Cl⁻)). Experimental techniques do not allow for such direct measurement of channel selectivity as a ratio of ionic currents (I(K⁺)/I(Cl⁻)). However, it is possible to evaluate channel selectivity by measuring a reversal potential, i.e. an applied potential at which there is no current through the channel exposed to the asymmetric ion concentrations in the cis-/trans- compartments (Figure 4A). The reversal potentials were calculated and compared to the experimental works for the following concentrations of KCl in cis-/trans- compartments: 0.5M/0.05M,²⁹ 1.0M/0.2M and 0.2M/1.0M.³³ The PNP-HR predicted reversal potentials significantly overestimate channel selectivity (Figure 5C). The predicted values range from 2.3 times higher than the experimental values for 0.2M/1.0M salt concentration to 5.4 times higher in the case of 1.0M/0.2M salt concentration. As also seen from Figure 5C a diffusion constant set up method has only a minor impact on this result. Both soft channel wall models (PNP-SR-MD and PNP-SR-LJ) dramatically improve prediction of the channel selectivity. On average, PNP-SR-MD predicted reversal potentials 1.3 times closer to the experimental values than PNP-HR; predictions made by PNP-SR-LJ are 1.5 times closer than PNP-HR. The selectivity (I(K⁺)/I(Cl⁻)) for the symmetric cis-/trans- salt concentrations (namely, 0.1M KCl) has a trend similar to that seen for the reversal potentials (compare Figures 5C and 5D). As with the reversal potentials the highest selectivity is predicted with the diffusion set to method 4 and the lowest one is predicted with the ion diffusion set uniformly to its bulk value (method 1), with 13% difference between them. But overall, as in the case with rectification, different diffusion distributions affect selectivity less than the total currents.

DISCUSSION

In this work we have introduced a soft repulsion model for short-range interactions between protein atoms and mobile ions within the framework of the modified PNP theory. Short-range ion-protein interactions play a determining role in forming the channel lumen accessible to mobile ions. While in PNP-HR the ion accessible volume (IAV) of a channel is set a priori and its boundary is rigid, both our SR models allow IAV to adjust in response to the local forces between the mobile ions and protein atoms. Moreover, PNP-SR-MD was specifically parameterized for this purpose for K⁺ and Cl⁻ separately (see Appendix 1 for the detailed description of this parameterization); thus, the resulting channel lumen has different boundaries for K⁺ ions and Cl⁻ ions. The soft boundary of the channel introduced in this work is determined based on whether the ion’s presence in a particular region of space is energetically favorable. Thus, determination of the protein boundary depends on both the nature of the permeating ion and the local protein group exposed to the channel. The channel boundary, which is no longer rigid, is a better model than the traditional rigid wall model and is easily extensible to the higher level of theory (for example, such treatment of the boundary is easily transferable to the BD simulations). The soft wall channels exhibit improved prediction of the AHL channel selectivity, as well as the improved numerical stability of the model.

The predicted total current and rectification are similar in PNP-HR or PNP-SR (Figures 5A and 5B) and overestimate experimental values with all choices of the diffusion coefficients. This behavior of PNP is well known and stems mainly from the neglect of the dielectric self energy (DSE) of a single ion transferring near low dielectric membrane.^11,14 Dieckmann and others⁴⁶ have found that DSE is less or equal to 2 kT in the center of a large pores. However, DSE increase dramatically upon approaching pore’s wall. Our preliminary calculations show that in AHL DSE is up to 2 kT along the center of the pore and is up to 18 kT near the pore’s wall. Therefore even for such a large pore as in AHL the neglect of DSE can still have a significant effect on total current size. While in principle the neglect of the direct ion-ion correlation inherent in PNP formulation is another possible source of this error, the simulations reported in this work were done at low salt concentration (0.1 M), a condition at which the contribution of direct ion-ion correlation is minimal. In this paper we have deliberately omitted the dielectric self energy of an ion. We also have not included the effect of protein relaxation in the presence of an ion, which has been shown to influence conductance in narrow channels.¹⁴ While the effect of both these terms is expected to be mild in AHL due to its relative width, in conjunction, we believe their neglect is mainly responsible for PNP overestimating absolute values of the total current. While the total current is affected strongly by the choice of a diffusion constant (Figures 5A and 6), the rectification of the current manifests subtle details of possible asymmetric electrostatic field distribution in the channel.

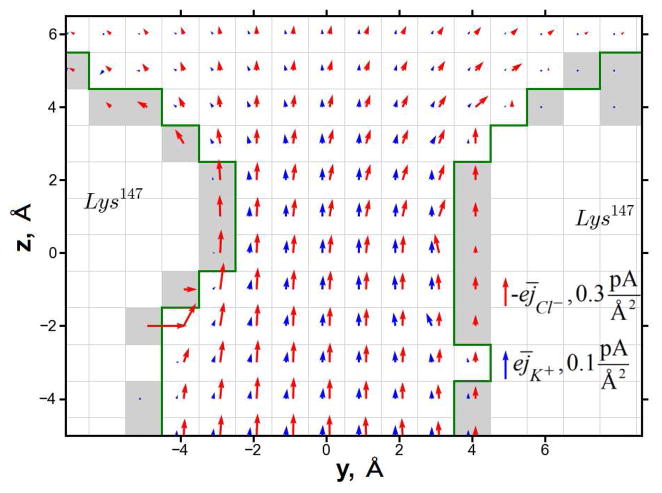
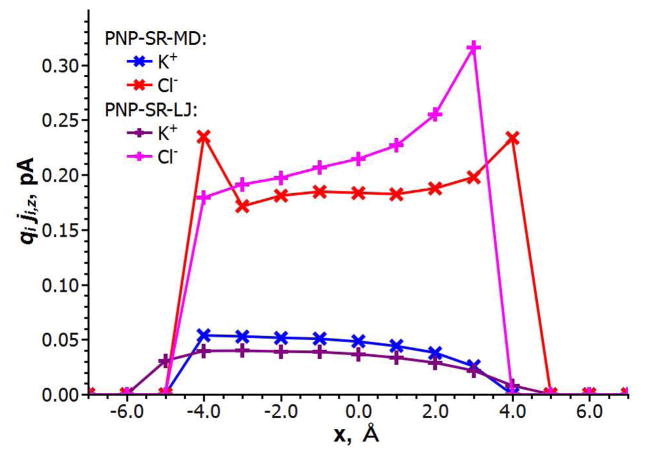
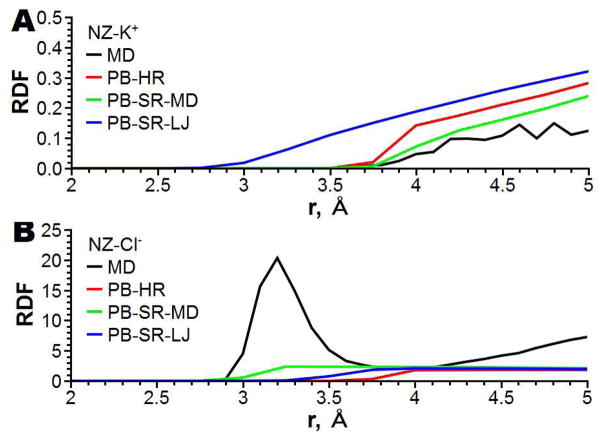
To determine which specific features of PNP-SR are responsible for the improvement of the channel selectivity prediction in comparison with PNP-HR it is instructive to look at the local distribution of the ion fluxes in the channel, especially within the main constriction region. In this region, in the PNP-SR-MD model, Cl⁻ ions pass closer to the protein wall than the K⁺ ions (as shown in Figure 7). The K⁺ flux remains mainly within the PNP-HR boundary shown as a green line in Figure 7. The PNP-SR-MD model thus results in better screening of the positively charged Lys147 exposed in the channel lumen in the area of the constriction, and, consequently, weaker ion selectivity than predicted by PNP-HR. Such screening of a positively charged residue by counter ions is in accord with the atomistic behavior of the system deduced from the molecular dynamics simulations as discussed below. In contrast, in PNP-SR-LJ Cl⁻ ions do not approach the protein wall as closely as they do in PNP-SR-MD (shown in Figure 8). At the same time the K⁺ ions pass closer to the protein wall than in either PNP-HR or PNP-SR-MD. This extra flux of cations, ironically, also manifests itself in weaker ion selectivity. The difference between apparent IAVs produced by the two PNP-SR models in the area of the main constriction can be better understood and explained by examining a radial distribution function (RDF) of ions in water near a protein residue obtained in atomistic molecular dynamics simulations. One example of such RDF, namely, the RDF of K⁺ and Cl⁻ ions in the vicinity of an isolated lysine residue in water, is shown in Figure 9. The distance at which RDF becomes significantly different from zero in the initial upswing of the first RDF peak may be taken as the closest approach of the mobile ions to the protein. As seen in Figures 9A and B SR-MD is the only continuum approximation that reproduces this feature reasonably well. (Note that by construction, all continuum models do not reproduce the fine structure of RDF due to the continuum representation of mobile ions and water molecules.) In PNP-SR-MD the K⁺ ions do not approach the N_ζ atom of the lysine closer than the atomistic RDF predicts (Figure 9A), and the Cl⁻ ions approach the N_ζ atom of the lysine significantly closer than in HR or in SR-LJ (Figure 9B). In PNP-SR-LJ, however, the K⁺ ions approach the N_ζ atom of lysine much closer than in the atomically simulated RDF (Figure 9A), resulting in an artificial flux of K⁺ along the channel wall in the main constriction region as discussed above. Thus, the steady state ion distribution in the channel obtained in PNP-SR-MD reproduces atomistic ion distribution in the channel significantly better than PNP-HR or PNP-SR-LJ.

Figure 7.

2D slice through the main constrictions of current flux as calculated by PNP-SR-MD. The current flux of K⁺ is shown by blue arrows and that of Cl⁻ by red arrows. Because the flux of K⁺ is several times smaller than Cl⁻ the current flux of K⁺ and Cl⁻ are scaled differently (see right bottom part of the figure). Green line shows the border of IAV as determine by HR; grey area highlight the difference of IAV between PNP-HR and PNP-SR-MD.

Figure 8.

Z-projection of current flux of mobile ions in the main constriction as predicted by PNP-SR-MD and PNP-SR-LJ.

Figure 9.

Comparison of radial distribution function between N_ζ atom of Lys and mobile ions (A – K⁺ and B – Cl⁻) calculated from all-atom MD simulation, PB-HR, PB-SR-MD and PB-SR-LJ.

Four different methods of setting diffusion coefficients were applied in this study. As a zero order approximation the diffusion coefficients enter the Nernst-Planck equation as scaling factors, thus it is not surprising that the absolute values of the currents scale nearly proportionally with the diffusion constants. However, a specific distribution of the inhomogeneous diffusion constants only weakly affects the rectification parameters, selectivity (I(K⁺)/I(Cl⁻)) and the reversal potentials. Thus, setting the diffusion constants such that they reproduce a combination of hydrodynamic and molecular mobility of ions in the confinement of the pore seems the best choice and significantly improves the PNP prediction of the total currents while only weakly affects other characteristics of the ion conduction, which depend more strongly on the channel wall interaction with the ions and ion PMF.

CONCLUSIONS

The proposed SR models of the short-range repulsion between protein atoms and mobile ions provides a natural approach to determine the ion accessible lumen of the channel based on energetic criterion, thus removing the need to rigidly define atomic and ionic radii (a poorly defined concept). The IAV determination procedure, developed here, takes into account the gradients of PMF as well as ion concentrations. In the α-hemolysin channel the PNP-SR significantly improved prediction of channel selectivity, a difficult property to predict in such a weakly selective channel.

Two possible methods of defining the soft repulsion energy term and its parameterization were considered, namely SR-MD and SR-LJ. SR-MD has been parameterized to faithfully reproduce the distance of closest approach of the ion to the protein residues, using the relevant radial distribution functions obtained in atomistic MD simulations of amino acids in salt solution. SR-LJ directly uses Lennard-Johns parameters of the Cornell et al. force field²³. SR-MD appears to be the best approximation of IAV possible in the scope of a continuum theory, whereas SR-LJ determines IAV incorrectly leading to additional unphysical ionic fluxes in PNP-SR-LJ. The developed SR-MD can be easily transferred to apply in other ion-conductance prediction methods, such as Brownian dynamics. The developed IAV calculation procedure can be also helpful for full PMFPNP.¹⁴

At equilibrium (in the absence of the current) PNP-SR reduces to a modified Poisson-Boltzmann equation, PB-SR. PB-SR was treated as a pre-conditioner for the ion-conductance calculations with PNP-SR. PB-SR, however, is expected to be of more general use in cases where an accurate modeling of the ion-protein interactions is desirable.

Introduction of SR and thus a better treatment of IAV in conjunction with an initial guess calculated from PB-SR results also in good stability and speed of the numerical convergence of the iterative algorithm. The algorithm for numerical solution of the PNP-SR equations converges better than PNP-HR on relatively coarse grids because it naturally avoids placing mobile ions in the regions with high energy gradients, a problem that can occur when IAV is predefined without considering PMF distribution in the channel.

In addition to introducing SR, we studied how different diffusion distribution methods affect predicted ionic currents. We found that while different diffusion distributions used in this work strongly affect the total currents, they have only minor influence on the current rectification and ionic selectivity. For these parameters the proper PMF is more important.

A new highly efficient and parallel PNP equation has been implemented. The solver works in conjunction with the graphical molecular modeling software HARLEM.^47,48

APPENDIXES

Appendix 1. Parameterization of SR-MD using MD Simulations

The total PMF of a mobile ion in the vicinity of a protein surface can be approximately split into a long range interaction term and a short range repulsion term. The short range repulsion can be further approximated as a pair-wise additive function because the closest protein atom influences this energy term the most. Short range repulsion in the vicinity of the protein atoms has a steeper shape compared to the long range interactions; using this difference we decoupled them during the parameterization. SR-MD was parameterized based on the reference RDFs between the mobile ions and the atoms of the amino acids obtained from all atom MD simulations of the amino acids in the aqueous salt solution. The SR between a protein atom and a mobile ion was approximated by eq 7. The proposed form of SR-MD has only two parameters: A_ij and η_ij. In this appendix, the parameterization of SR-MD will be described.

To compute the reference RDFs the simulations were performed for each of the 20 amino acid residues with the ACE and MTE terminal groups added to each amino acid. The simulation box was approximately 25×25×25 ų; this size allowed us to place 2–3 ions (K⁺ and Cl⁻), which roughly corresponds to 0.1 M of KCl. First, NPT simulations were conducted for 2 ns, followed by 200 ns of production run in the NVT ensemble (Total simulation time was more than 4 μs). All simulations were run using GROMACS 4.0⁴⁹ with SPC water and OPLSAA force field for the amino acids⁵⁰. The reference RDFs between each atom of the modeled residue and each kind of mobile ion were calculated with a modified version of the g_rdf routine from the GROMACS package.

SR-MD was parameterized for the best reproduction of the reference RDFs using the following procedure. First, a PMF between all residue atoms and the mobile ions was calculated from a corresponding RDF. This PMF was used to estimate initial SR-MD parameters. These initial parameters were utilized to calculate a continuum RDF between atoms of an amino acid residue and mobile ions using PB-SR-MD. Secondly, the SR-MD parameters were manually refined to achieve the best correspondence between the RDF calculated by PB-SR-MD and the reference RDF. The final parameters of SR-MD are reported in Table S1 of the Supporting Information. An example of a continuum theory RDF and a corresponding reference RDF is shown in Figure 9A for the K+ ion and in Figure 9B for Cl− ion near the N_ζ atom of the lysine residue.

Appendix 2. The Numerical PNP-SR Algorithm, its Implementation and Parallelization

In PNP theory both the Poisson equation and the Nernst-Planck equation must be solved self-consistently. As in our previous work¹³ each equation is solved using an iterative finite difference algorithm, termed successive overrelaxation (or SOR). One PNP iteration consists of several iterations over the Poisson equation solver followed by several iterations over the Nernst-Planck equation solver. We have found that 20 iterations for both solvers provide a stable and effective path to the numeric solution of the PNP equations.

In all PNP calculations an initial guess was set to a PB equation solution having the same mobile ion bulk concentrations. In the case of different concentrations in the cis- and trans- compartments, the initial guess was set using two separate PB equation solutions each of which corresponds to the mobile ion concentrations in the cis- and trans- compartments. Two solutions were merged along the membrane center. The use of the PB equation solution as a pre-processing step for the PNP equations allows for the usage of relatively high relaxation parameters in the PNP procedure itself, which greatly speeds up the convergence. Solution of a PB equation itself is much faster than PNP.

To assess an error introduced by the discretization of the model on the grid, the ion current at 80 mV was calculated for six different positions of AHL in respect to the grid (the positions were generated by the rotation of α-hemolysin along its pore axis). The calculations were done for two different grid scales: the rough grid (1 grid/Å) and the fine grid (2 grids/Å). As expected the standard deviations of currents for different positions of the protein on the grid are smaller for the finer grid. The largest standard deviation is observed for PNP-HR on the rough grid and it is only 1.4% from the average value. The difference between the average values for two grid scales is 7%, 5% and 3% for PNP-HR, PNP-SR-MD and PNP-SR-LJ methods respectively (Table S2). Therefore, discretization of a model at 1 grid/Å is sufficient to achieve an acceptable precision in solving the PNP equations. The PNP-SR-MD and PNP-SR-LJ achieve better precision on the rough grid than PNP-HR. PNP-SR-LJ is the most precise in terms of discretization on the grid; this is probably due to the fact that SR-LJ is the softest repulsion potential among models of short-range interactions utilized in this work.

Our PNP solver, which also doubles as the Poisson and PB equations solver is implemented in the C/C++ language. It is coupled to the graphical interface and scripting capabilities of the HARLEM molecular modeling package⁴⁷,⁴⁸ and thus is user-friendly, highly modular and extensible. A parallelized version of the solver was implemented using the MPI library and tested on the group cluster and computational facilities of the Pittsburgh Supercomputing Center. The parallel version of the solver allows for the calculation of the whole I–V curve within one parallel run. Because calculations of ion currents at different applied potentials are independent from each other, the network speed and latency requirements are low; thus, even a gigabit Ethernet provides good scalability for computation of a whole I–V curve. Our solver can also be executed in parallel for a single applied potential difference. However, in this case the demand for inter-process communication is high, and a gigabit Ethernet does not resolve this demand. Therefore a parallel calculation for a single applied voltage must be performed with a better network or within a single computational node. The PNP calculations reported in this paper were performed on a Beowulf type cluster with a gigabit Ethernet; each of the nodes has one dual-core CPU (Intel Pentium D830). To calculate an I–V curve consisting of 7 values of an applied potential we used 7 cluster nodes, each running two processes, for a total of 14 processes. Other parameters of the calculation were as described in the main text. The time for calculation of an initial guess was 4 minutes, redefining IAV took 11 minutes, and the parallel calculation of the I–V curve took 2.6 hours. Thus, the developed parallel PNP solver is highly efficient.