Assessment of Shear Modulus of Tissue Using Ultrasound Radiation Force Acting on a Spherical Acoustic Inhomogeneity

Abstract

An ultrasound-based method to locally assess the shear modulus of a medium is reported. The proposed approach is based on the application of an impulse acoustic radiation force to an inhomogeneity in the medium and subsequent monitoring of the spatio-temporal response. In our experimental studies, a short pulse produced by a 1.5-MHz highly focused ultrasound transducer was used to initiate the motion of a rigid sphere embedded into an elastic medium. Another 25 MHz focused ultrasound transducer operating in pulse-echo mode was used to track the displacement of the sphere. The experiments were performed in gel phantoms with varying shear modulus to demonstrate the relationship between the displacement of the sphere and shear modulus of the surrounding medium. Because the magnitude of acoustic force applied to sphere depends on the acoustic material properties and, therefore, cannot be used to assess the absolute value of shear modulus, the temporal behavior of the displacement of the sphere was analyzed. The results of this study indicate that there is a strong correlation between the shear modulus of a medium and spatio-temporal characteristics of the motion of the rigid sphere embedded in this medium.

I. Introduction

Biomechanical properties of soft tissues have been of increasing interest in medical diagnostics and surgery. Often, there is a significant correlation between a disease and local changes of biomechanical properties of tissue [1]–[3]. In addition, the biomechanical properties of tissues may be changing with age, resulting in undesirable functional changes [4]–[6].

To assess biomedical properties of tissues, several research groups are actively investigating acoustic radiation force methods. The applications of acoustic radiation force include various elasticity imaging methods [7]–[11], characterization of lesions [12], screening of muscles [13], and imaging the calcification of arteries [14]. In most cases, the shear modulus of tissue is quantified from the tissue response measured outside the region of excitation (ROE) [15]. The estimation of the shear modulus is based on the measurements of the speed of shear waves originated within and propagated away from the ROE. This approach assumes that the dispersion of the shear wave is negligible over the analyzed region and the tissue near the ROE is homogeneous. The shear wave velocity can be estimated using several methods including inversion of the Helmholtz equation [16], [17], ultrasonically tracked jitter of displacement fields associated with shear waves [18], [19], correlation-based algorithms [20], [21], and lateral time-to-peak displacement algorithm [22]. Note that the shear waves propagate orthogonally to the direction in which the acoustic radiation force is applied [22].

Alternatively, the shear modulus can be estimated directly within the ROE [7], [11], [14], [23], [24] based on the displacement measured within ROE. However, a common problem in such acoustic radiation force-based imaging techniques is that the magnitude of the force applied to any targets depends on acoustic properties of the medium because ultrasound waves attenuate unpredictably as they propagate deeper into tissue. Therefore, the reliable reconstruction of shear moduli is hampered by the fact that the amplitude of the displacement depends on the acoustic attenuation of the medium. To overcome this problem, temporal characteristics of the displacement can be used [25].

The temporal parameters of the ROE displacement in response to applied acoustic radiation force has been considered previously by Sarvazyan et al. [26]; the authors demonstrated that measurements of the time required for the displacement to reach maximum at the focal point can be used for shear modulus estimation and the rate of the displacement decrease depends on the tissue viscosity. Furthermore, Palmeri et al. [10] has applied finite element analysis to investigate time-dependent displacements of the ROE in homogeneous media characterized by different shear elastic moduli— the experiments demonstrated a correlation between shear elasticity and temporal parameters of the displacements. In this paper, we further examine the relationship between temporal characteristics of the displacement and mechanical properties of the tissue using analytical (integral-based) solution of the equation of motion and, more importantly, consider reconstruction of the mechanical properties of medium from the temporal behavior of the displacement.

The displacement of the medium can be achieved based on both absorption of ultrasound waves into media [24], [26]–[29] and reflection of ultrasound from inhomogeneities in media such as gas bubbles [30] and rigid spheres [31], [32], For example, if there is an acoustic inhomogeneity (such as a bubble or solid sphere) present in tissue, the temporal behavior of the displacement of the inhomogeneity can be indicative of the mechanical properties of a medium surrounding the inhomogeneity. Oscillations of a solid sphere placed in a viscoelastic medium were theoretically considered by Oestreicher [33]. This approach has been applied in the theoretical investigation of the behavior of the solid spheres with different diameters and densities [32], [34]. A more general approach to estimate the spatio-temporal behavior of spherical objects (solid spheres and gas bubbles) in a viscoelastic media in response to acoustic radiation force has been theoretically described by Ilinskii et al. [35]. The results of these studies [32]–[35] demonstrate that the mechanical response of gas bubbles and solid spheres under radiation force is related to the viscoelastic properties of the surrounding media and can be used to determine the local mechanical properties of the material. However, reconstruction of the elastic properties of tissue-like medium from the spatio-temporal characteristics of a sphere motion has not been fully considered.

In this paper we further investigate the inverse problem, a reconstruction of the mechanical properties of medium from the displacement of the sphere in response to applied radiation force. While both shear elasticity and viscosity can be estimated from the spatio-temporal measurements of sphere motion, this paper is primarily focused on the reconstruction of shear elasticity. Specifically, assuming that the parameters of a sphere and the duration of acoustic radiation force pulse are known, the shear modulus of the surrounding tissue is reconstructed independently of the acoustic force magnitude. The experiments were performed using a rigid sphere embedded in a soft tissue-mimicking phantom. The motion of this sphere was initiated by radiation force from an excitation ultrasound transducer. The displacement of the sphere was measured using an imaging ultrasound transducer. The local elastic properties of the surrounding material were estimated from the temporal characteristics of the sphere motion and found to be almost independent from the shear viscosity over a large range. The reconstructed values of the shear elasticity were then compared with results of direct measurements of the mechanical properties of the material. Our results suggest the unambiguous relationship between the shear modulus of the phantom material and the temporal parameters of the sphere displacement in response to the impulsive acoustic radiation force.

II. Theoretical Background

The displacement of a solid sphere or a gas bubble in response to a time-dependent acoustic radiation force has been considered previously [32]–[34]. Because most soft tissues and tissue-like materials can be considered incompressible [36] and assuming linear viscoelasticity, the equation of motion for a surrounding tissue can be written in the following form:

$$-\nabla P+\mu {\nabla }^2\overrightarrow{U}+\eta {\nabla }^2\frac{\partial \overrightarrow{U}}{\partial t}=\rho \frac{{\partial }^2\overrightarrow{U}}{\partial t^2},$$ (1)

where U⃗ is a displacement vector, μ and η are shear elasticity and viscosity, P is an internal pressure, ρ is medium density and t is time. It is assumed that the solid sphere is a non-deformable object. In the spherical system of coordinates, the displacement vector has the following components U⃗ = (U_r, U_θ, U_ϕ). Assuming that a field of the radiation force is axisymmetric, and the r-axis of the spherical system of coordinates is along the direction of acoustic radiation force, U_ϕ = 0 and boundary conditions at the surface of a sphere with a radius R in the spherical system of coordinates are

$$\begin{array}{l}{U}_r(R,\theta )=U_{0}cos\theta ,\\ U_{\theta }(R,\theta )=-U_{0}sin\theta .\end{array}$$ (2)

Here U₀ is a displacement of sphere and θ is an angle between the r-axis and displacement vector of the sphere. An applied radiation force on a displaced spherical object can be written as [37]:

$$F=-2\pi R^2\underset{0}{\overset{\pi }{\int }}({\sigma }_{rr}cos\theta -{\sigma }_{r\theta }sin\theta )sin\theta d\theta ,$$ (3)

where σ_rr and σ_rθ are stress tensor components on the surface of the object:

$$\begin{array}{l}{\sigma }_{r\theta }=\left(\mu +\eta ·\frac{\partial }{\partial t}\right)·\left(\frac{\partial U_{\theta }}{\partial r}-\frac{U_{\theta }}{r}+\frac{1}{r}\frac{\partial U_r}{\partial \theta }\right),\\ {\sigma }_{rr}=-P+2·\left(\mu +\eta \frac{\partial }{\partial t}\right)·\frac{\partial U_r}{\partial r}.\end{array}$$ (4)

The solution of (1)–(4) is described elsewhere [32]. Assume that the applied radiation force is impulsive such that the magnitude of the radiation force applied to the sphere is F₀ and its duration is t₀, the displacement of a rigid sphere in a viscoelastic media is given by:

$$U(t)=-\frac{{iF}_0}{12{\pi }^{2}R}\times \underset{-\infty }{\overset{\infty }{\int }}\frac{(e^{i\omega t_0}-1)e^{-i\omega t}}{\omega (\mu -i\omega \eta )(1-\mathit{ikR}-k^2{R}^2(1+2\beta )/9)}d\omega ,$$ (5)

where k² = (ρω²)/( μ − iωη) is a complex wave number, and β = ρ_s/ρ is a normalized density ρ_s of a solid sphere.

The integral in (5) can be evaluated numerically. Both shear viscosity and elasticity coefficients in (5) are present in explicit form and together with the parameters of the solid sphere and the surrounding medium define the spatio-temporal behavior of the sphere. A magnitude of the displacement is also proportional to a magnitude of the radiation force F₀ applied to the sphere. Generally, however, the applied force F₀ is unknown because of attenuation of ultrasound waves and the difference of the acoustic impedances of sphere and surrounding medium. Therefore, shear elasticity and viscosity may not be reliably assessed from the displacement magnitude unless the force F₀ is known. This is true regardless of the duration of the radiation force [35]. In contrast, the magnitude of applied force is not under the integral in (5), indicating that it does not affect the temporal behavior of the sphere. Therefore, shear moduli may be evaluated from the temporal characteristics of the displacement of the sphere.

Reconstruction of both shear elasticity and shear viscosity can be now posed as a minimization problem. First, the displacement of the sphere U(t) in response to the impulsive radiation force with duration of t₀ is measured. Then, assuming that the density of the surrounding tissue and the sphere’s radius and density are known, this displacement is also predicted theoretically using (5). The unknown shear elasticity μ and shear viscosity η can be estimated by minimizing the difference between the measured and calculated displacements.

III. Materials and Methods

The photograph of the experimental setup consisting of a low-frequency excitation transducer, gelatin phantom with an embedded sphere and a high-frequency imaging transducer is shown in Fig. 1. The excitation transducer was tightly attached to a plastic tank containing a phantom made of 3% gelatin (type A, Sigma-Aldrich, Inc., St. Louis, MO). The size of the phantom was 55 × 55 × 50 mm (length × width × height). The 3-mm diameter optical ball lens (Edmund Optics, Inc., Barrington, NJ), acting as a target rigid sphere, was positioned in the middle of the phantom. The density of the sphere material (LaSFN9 glass) was measured to be 4440 ± 20 kg/m³. The imaging transducer was positioned on the top of the phantom facing the excitation transducer (Fig. 1). Foci of both transducers coincided at the location of the solid sphere.

Fig. 1.

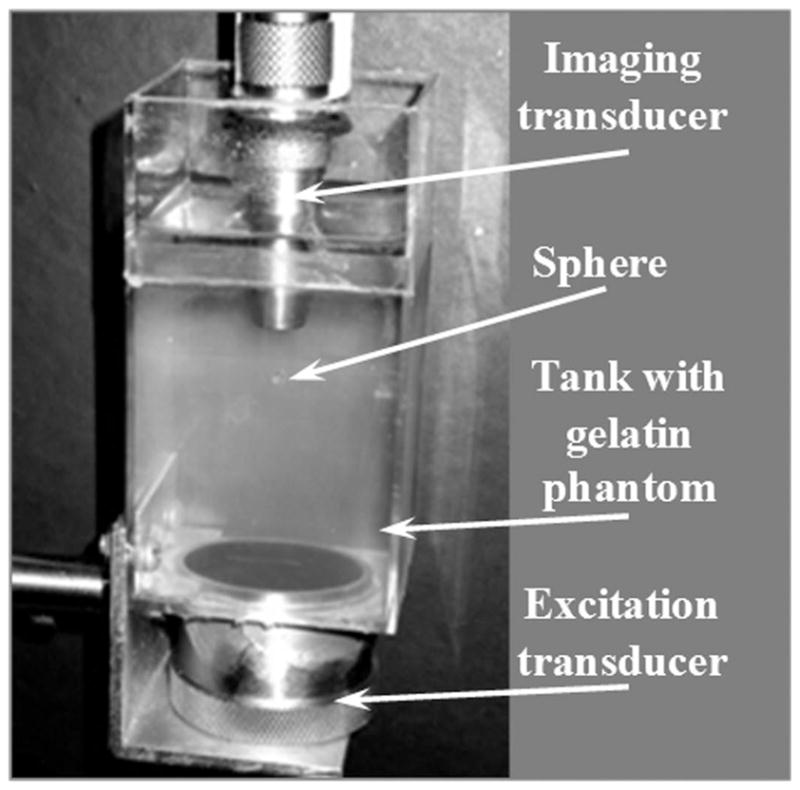
The photograph of the experimental setup. The excitation transducer was attached at the bottom of a tank while the imaging transducer was located on the top.

To generate acoustic radiation force, the 1.5-MHz single-element focused transducer (Valpey Fisher, Inc., Hopkinton, MA) was used. The transducer had a circular aperture of 38.1 mm and a focal length of 44.5 mm. This transducer was operated using a function generator (model 33250A, Agilent Technologies, Inc., Santa Clara, CA) connected to an RF power amplifier (model 240L, ENI, Inc., Rochester, NY). The function generator provided bursts of 1.5-MHz sinusoidal signals with a duration of 0.667 ms (or 1000 periods of 1.5 MHz sinusoid). The peak-to-peak amplitude of the bursts was 1 V unless specified otherwise. The RF amplifier increased the magnitude of the bursts 350 times or by 25.4 dB.

To detect the motion, the sphere was imaged using the 25-MHz single-element high-focused transducer (model V324, Panametrics, Inc., Waltham, MA) with 60% bandwidth. This transducer had the focal length of 12.7 mm and F-number of 2. This transducer, connected to a pulser-receiver (model 5910PR, Panametrics, Inc.), was operated at a pulse repetition rate of 20 kHz to allow the tracking of the sphere motion every 50 μs. The echo signals were acquired by an 8-bit 500 MS/s analog-digital acquisition card (CompuScope 8500, Gage Applied Technologies, Inc., Lockport, IL) and processed off-line.

Both the function generator and the data acquisition card were synchronized using an external trigger while the imaging transducer was operated continuously. The 500-μs delay between trigger and actual applied radiation force was provided to obtain pulse-echo signals before the sphere motion was initiated to calculate the initial position of the sphere. Displacements of the sphere in time were calculated using a phase-sensitive, cross-correlation motion tracking algorithm [38].

The values of reconstructed shear moduli were simultaneously compared with those measured directly using the phantom. A cylindrical 35-mm diameter, 17-mm high control sample of gelatin was prepared for direct uniaxial load-displacement measurement using an In-Spec 2200 benchtop portable tester (Instron, Inc., Norwood, MA). The control sample was deformed up to 10% with 0.2 mm/s speed of deformation. To evaluate the accuracy of measurements, each measurement was repeated 5 times and the sample was repositioned in the tester between the measurements.

To change a shear modulus of the phantom while maintaining the same position of foci and the sphere, the temperature of the phantom was varied in the 12 to 22°C range. The temperature of the phantom was controlled during the experiments by an electronic thermometer with an accuracy of 1°C embedded into the phantom. Measurements of both the sphere displacement and the direct measurements of shear elastic modulus were performed within the range of 12 to 22°C at 1° increments. The accuracy of the measurements of shear modulus using acoustic radiation force was evaluated over the entire temperature range, and the maximum value of standard deviation was used to analyze the error.

IV. Results and Discussion

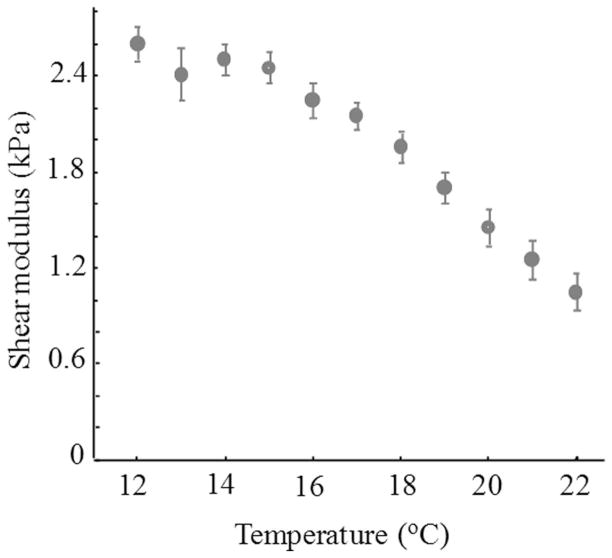
The dependence of the shear elastic modulus of 3% gelatin sample on temperature, measured using the uniaxial load-displacement test, is shown in Fig. 2. Within the 12 to 22°C range, the dependence is monotonic and shear modulus of the gelatin decreases from 2.6 to 1.0 kPa. As expected, the gelatin phantom becomes softer as the temperature rises.

Fig. 2.

The experimental dependence of the shear elastic modulus on the temperature measured with In-Spec 2200 benchtop portable tester (Instron, Inc., Norwood, MA). The error bars represent ±1 standard deviation.

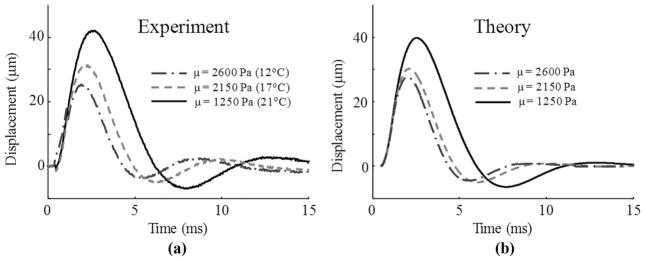
The displacements of the solid sphere in the phantom measured at 3 different temperatures (12, 17, and 21°C) are shown in Fig. 3(a). These temperatures correspond to the shear moduli 2600, 2150, and 1250 Pa, respectively. The experimental results indicate that the sphere displaces more in the softer phantom.

Fig. 3.

The experimentally measured (a) and theoretically calculated (b) displacement of the sphere embedded in phantom with the varying shear elasticity.

The average shear viscous modulus η of gelatin, evaluated using (5), was about 0.1 Pa·s with a standard deviation of 50%. Given the sensitivity of these measurements, no significant change of shear viscosity was observed within the 12 to 22°C temperature range. A similar value of shear viscosity was also reported in the literature [27] for 4% gelatin phantoms and is reasonably close to values of shear viscosity for 12% gelatin phantoms stored at room temperature [39]. Therefore, shear viscosity of 0.1 Pa·s was used in theoretical calculations and estimation of tissue elasticity. The displacements of the sphere, modeled using (5), are shown in Fig. 3(b). The density of the gelatin was taken as 1000 kg/m³.

The variations of the sphere parameters and the density of the surrounding medium with the temperature were neglected. To match the magnitudes of the experimental [Fig. 3(a)] and theoretical [Fig. 3(b)] displacements of the sphere for all values of shear moduli, the magnitude of acoustic radiation force applied to the sphere was chosen to be 5.5 mN. These calculated displacements are in good agreement with the experimental results and indicate that, as expected, the maximum displacement of the sphere is inversely proportional to the shear modulus of the phantom.

The dependence of the maximum displacement of the sphere on the shear modulus of the gelatin is presented in Fig. 4. These maximum displacements of sphere were also calculated theoretically using (5) for shear moduli within 1.0 to 2.6 kPa range and shear viscosity η = 0.1 Pa·s. The experimental measurements agree well with theoretical modeling.

Fig. 4.

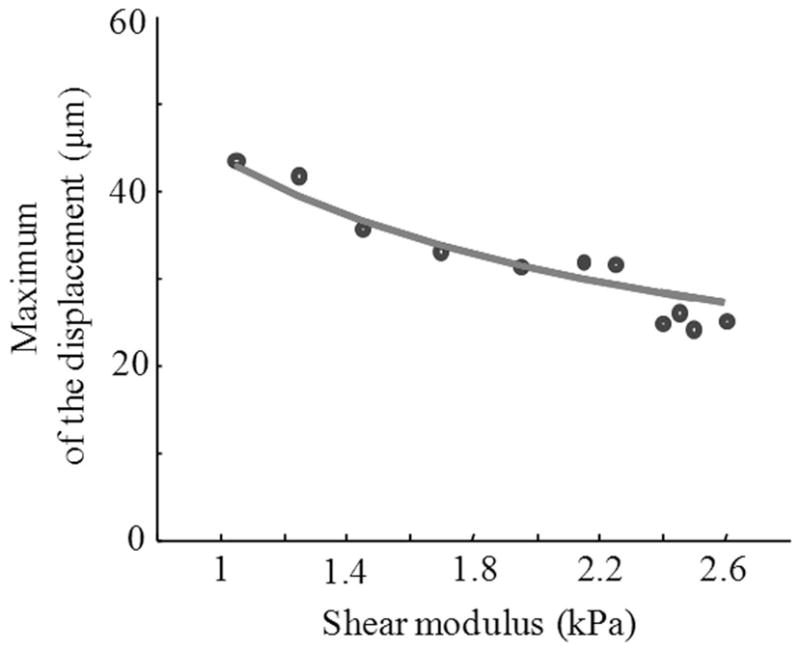
Experimental (points) and theoretical (solid line) dependences of maximum displacement of solid sphere under applied radiation force on shear modulus of surrounding tissue.

Unfortunately, to assess tissue elasticity, the measurements of the maximum displacement can be employed only if the magnitude of the acoustic radiation force applied to the sphere is known. However, the magnitude of radiation force is generally unknown because of attenuation of ultrasound waves traveling from the transducer to the acoustic inhomogeneity and the differences in acoustic impedances between tissue and the inhomogeneity [40]. Therefore, the maximum value of the displacement depends not only on the shear modulus but also on the magnitude of the radiation force applied to the sphere.

This is further demonstrated in Fig. 5, where the displacements of the sphere initiated by acoustic forces of different magnitudes are shown. The temperature of the phantom was 24°C in all measurements and the corresponding 700 Pa shear modulus, therefore, remained the same. Clearly, the maximum displacement definitely depends on the magnitude of the applied radiation force and, therefore, cannot be used to determine the shear modulus.

Fig. 5.

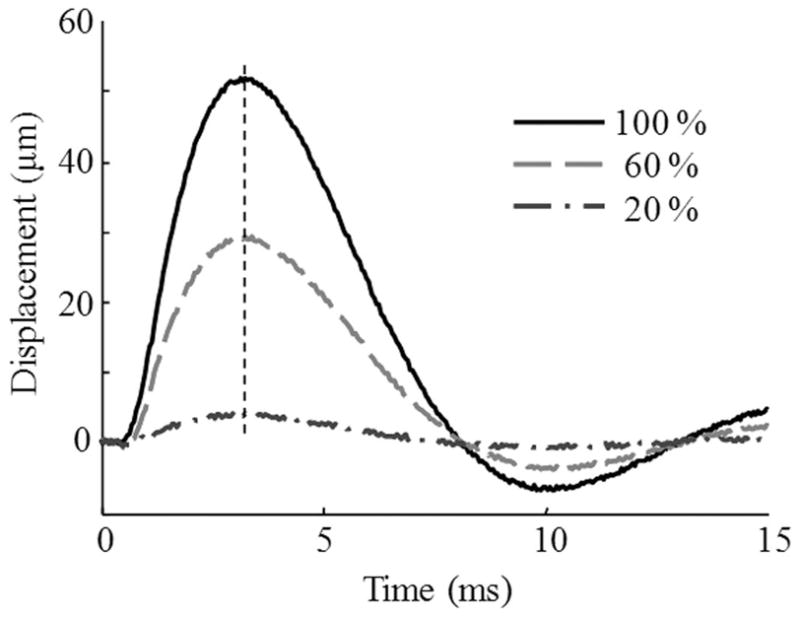
The displacements of the solid sphere in response to applied acoustic radiation forces of different magnitude. The vertical line highlights the fact that the sphere reaches its maximum displacement at exactly the same time regardless of the amplitude of applied force.

However, while the change of magnitude of an applied radiation force results in the change of the maximum value of the sphere displacement, time τ_max, defined as a time required for the sphere to reach the maximum displacement, remains the same (Fig. 5). Correspondingly, in a medium with higher shear modulus, the time τ_max is smaller (Fig. 3). Therefore, this time τ_max is unambiguously related to the shear modulus.

The relationship between the time τ_max and the shear modulus of the surrounding medium is shown in Fig. 6, where the measurements are compared with theoretical predictions. Note that the magnitude of applied radiation force does not affect the results in Fig. 6 and the dependence remains exactly the same independently of the force magnitude.

Fig. 6.

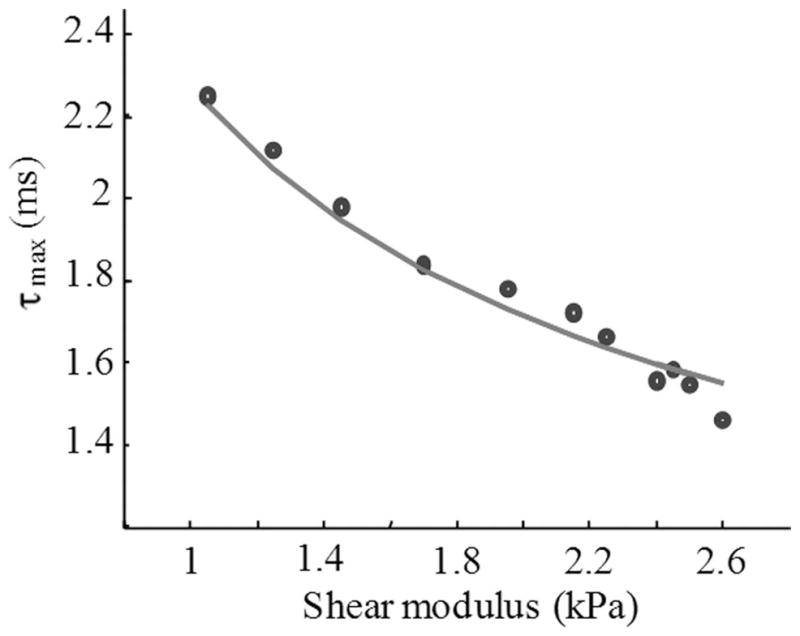
The experimental (points) and theoretical (solid line) relationship between shear modulus and the τ_max defined as a time required for the solid sphere to reach the maximum displacement.

The dependence of time τ_max on the shear modulus exhibits monotonic behavior indicating the unique relationship between these parameters. Therefore, the shear modulus of the medium surrounding the rigid sphere can be assessed using a temporal (i.e., based on measurements of time of maximum displacement τ_max) rather than a spatial (i.e., based on assessment of maximum displacement magnitude of the sphere) approach. The dependence will change with the size and the density of acoustic inhomogeneity but it will remain monotonic. For example, a bubble, induced by nano- or femtosecond laser pulse, can be such an acoustic inhomogeneity. Once the bubble reaches equilibrium, the radius of the bubble can be measured using the same imaging transducer and the ultrasound technique is described elsewhere [41], [42]. The duration of acoustic force pulse should be reasonably long to produce measurable motion of an acoustic inhomogeneity and reasonably short to avoid the inhomogeneity to reach the saturation of the displacement where the acoustic radiation force and elastic forces from the medium compensate each other. To assess the shear modulus, the measured displacement of the inhomogeneity can be approximated such that the calculated time τ_max matches the experimentally measured value [35]. Once the match is achieved, the fitting parameter—the shear modulus of the surrounding medium—will be estimated.

It is important to note that the dependence of time τ_max on the shear elastic modulus is largely independent of shear viscosity. The theoretically calculated displacements of the sphere embedded in phantom with shear elasticity of 1 kPa are shown in Fig. 7. The shear viscosity of the phantom material was set to be 0 (purely elastic phantom), 1, and 2 Pa·s, respectively. The results presented in Fig. 7 show that shear viscosity reduces the magnitude of the displacement but it does not significantly affect the time τ_max, and, therefore, the accuracy of shear elastic modulus estimation. For example, even for 10-fold increase of shear viscosity (from 0.1 to 1 Pa·s), the elasticity estimate changes only by 3%. On the contrary, once the displacement reaches the maximum (i.e., after the time τ_max), the temporal behavior of the sphere is significantly influenced by the shear viscosity. Indeed, higher shear viscosity reduces the displacement oscillations; for high shear viscosity, the displacement of the sphere becomes aperiodic. Therefore, the results presented in Fig. 7 indicate that both shear elasticity and shear viscosity can be estimated from spatio-temporal behavior of the sphere and, generally, acoustic inhomogeneity within the tissue. However, studies using sophisticated tissue-mimicking phantoms with shear viscosity close to that of soft tissues (from 0.2 to 15 Pa·s [33], [43], [44]) are required to further evaluate the simultaneous reconstruction of shear elasticity and shear viscosity of tissue.

Fig. 7.

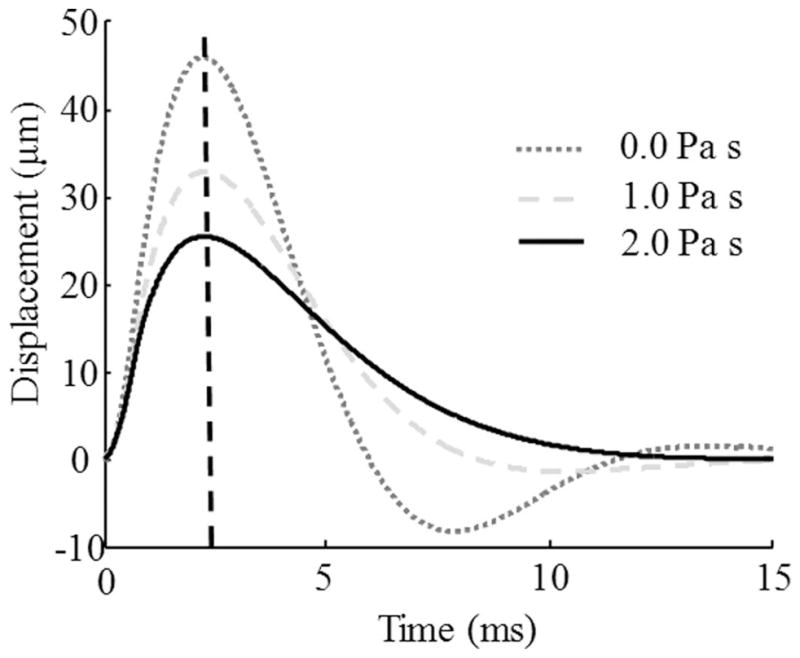
The calculated displacements of the solid sphere in response to applied acoustic radiation force. The sphere was embedded in the phantom with shear modulus of 1000 Pa. Note that the sphere reaches its maximum displacement at approximately the same time (as highlighted by vertical line) regardless of the shear viscosity of the phantom material.

A comparison of shear moduli, directly measured using the load-displacement method and assessed from the acoustic radiation force measurements, is shown in Fig. 8. The standard deviation did not exceed 5.8% in the entire data set.

Fig. 8.

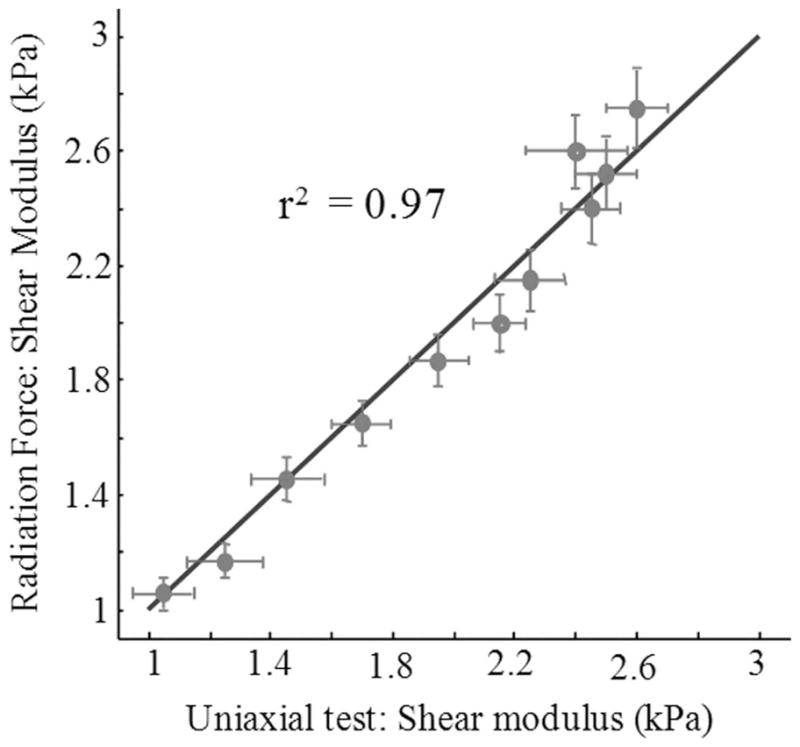
Comparison of shear moduli obtained from uniaxial test and radiation force measurements. Points represent experimental points while the solid line indicates the ideal coincident between these 2 methods. The horizontal error bars in Fig. 8 correspond to the vertical error bars in Fig. 2.

V. Conclusions

An ultrasound-based method to reconstruct the vis-coelastic properties of a medium using acoustic radiation force was developed. This method relies on the temporal measurements of the displacement of the spherical acoustical inhomogeneity such a gas bubble, and therefore, does not utilize the magnitude of the displacement, which is highly dependent on the magnitude of the applied radiation force. The phantom studies demonstrate good agreement between remote ultrasound-based measurements of shear elasticity and shear elastic modulus measured using the load-displacement method. In addition, it was found that the proposed approach is suitable for assessment of the shear elasticity almost independently from the shear viscosity. Furthermore, the developed method can be extended to assess both elasticity and viscosity of tissue independently and simultaneously.

Biographies

Andrei B. Karpiouk received his B.S, M.S., and Ph.D. degrees in laser physics from the Moscow Engineering Physics Institute (Technical University), Moscow, Russia, in 1992, 1994, and 2002, respectively.

Following his graduate work, Dr. Karpiouk was a postdoctoral fellow in the Laser Center at the University of Texas Medical Branch, Galveston, Texas from 2003 to 2004 conducting research in combined photoacoustic and ultrasound imaging for early cancer detection. From 2004 to 2008, he worked at the University of Texas at Austin, Austin, Texas as a Research Assistant where he was engaged in research of laser-tissue interaction processes and development of new methods for ultrasound-based medical imaging and sensing.

Currently, Dr. Karpiouk holds the position of Research Engineering/Scientist Associate III in the Department of Biomedical Engineering, the University of Texas at Austin, Austin, TX. His research interests are in combined medical imaging and sensing, biomedical engineering, research of laser-tissue interaction processes, measurements of biomechanical properties of soft tissues, etc. Dr. Karpiouk is an IEEE member.

Salavat R. Aglyamov received the B.S. and M.S. degrees in applied mathematics in 1991 and 1993, respectively, from Moscow State University, Moscow, Russia. He received the Ph.D. degree in biomechanics in 1999 from the Institute of Theoretical and Experimental Biophysics, Pushchino, Moscow region, Russia.

From 1993 to the present he has been working at the Institute of Mathematical Problems in Biology, Pushchino, Moscow region, Russia. From 2001 to 2002 he worked in the Biomedical Ultrasonics Lab at the University of Michigan, Ann Arbor, as a postdoctoral fellow, where he was engaged in mathematical modeling of behavior of soft biological tissue under externally applied loading.

He is currently a research associate in the Department of Biomedical Engineering at the University of Texas at Austin. His research interests are in the areas of tissue biomechanics, elasticity imaging, applied mathematics, and photoacoustics.

Yurii A. Ilinskii received the Candidate in physics and math sciences (equivalent to a Ph.D. degree) and Doctor in physics and math sciences (equivalent to Full Professor) degrees from the Physics Department of Moscow State University, Moscow, Russia, in 1962 and 1976, respectively. He is a 1975 USSR State Prize Winner for development of infrared radiation receivers.

His main research interests are nonlinear acoustics, nonlinear optics, and laser physics. In nonlinear acoustics, he was engaged in modeling of linear and nonlinear gas bubble dynamics in tissue and of interaction of gas bubbles in clouds in a liquid. He was involved in research of bubble deformation and translation in tissue in response to acoustic radiation pressure as well as in studies of nonlinear propagation and distortion of plane shear waves. In nonlinear optics, his research interests are in nonlinear effects in inhomogeneous media, infrared holography, infrared radiation receivers, nonlinear infrared spectroscopy, etc. Dr. Ilinskii has published 3 books: in 1989 with L. V. Keldysh, (in Russian), in 1993 with A. V. Andreev and V. I. Emel’yanov, and in 1994 with L. V. Keldysh. With, M. F. Hamilton and E. A. Zabolotskaya, he has also published a chapter in the book Nonlinear Acoustics in 1997.

In 1995, Yurii Ilinskii joined the department of Mechanical Engineering at the University of Texas at Austin, Austin, TX to study nonlinear acoustics and nonlinear Rayleigh wave propagation in elastic media. From 1997 through 2000, he was a Research Scientist in MacroSonix Corparation in Richmond, VA, successfully modeling an intensive acoustical field in a resonator of an arbitrary shape. From 2000 to 2003, Dr. Ilinskii moved back in the University of Texas at Austin to investigate nonlinear acoustic and thermal phenomena in thermo-acoustic engines. Currently, Dr. Ilinskii holds a Senior Research Scientist position in the Applied Research Laboratories of the University of Texas at Austin. He is involved mostly in biomedical applications based on nonlinear acoustics.

Evgenia Zabolotskaya received the degree of Candidate in Physics and Math sciences (equivalent to a Ph.D. degree) from the Physics Department of Moscow State University, Moscow, Russia, and the degree of Doctor in physics and math sciences (equivalent to Full Professor) from the General Physics Institute of the USSR Academy of Sciences, Moscow, Russia, in 1968 and 1985, respectively. In 1985 she was a 1985 USSR State Prize Winner for the contribution to nonlinear acoustics.

Her research interest is nonlinear acoustics. She was involved in modeling nonlinear gas bubble dynamics in tissue and the behavior of the bubble in response to applied radiation force. She also works in area of nonlinear propagation and distortion of plane shear waves and of nonlinear Rayleigh wave propagation along a solid elastic medium and tissue. In 1987, together with N.S. Bakhvalov and Ya. M. Zhileikin, Dr. Zabolotskaya published the book Nonlinear Theory of Sound Beams translated from Russian to English by R. T. Beyer, American Institute of Physics, New York. She is also a co-author with M. F. Hamilton and Yu. A. Ilinskii of the chapter “Dispersion” in the book Nonlinear Acoustics, published by Academic Press in 1997.

From 1991 to 1997, Evgenia Zabolotskaya worked as a Research Fellow in Mechanical Engineering of the University of Texas at Austin. Her research was related to nonlinear acoustics and nonlinear Rayleigh wave propagation in an elastic medium. In 1997, she moved in Richmond, VA to accept a Research Scientist position in MacroSonix Corporation. In 2000, Evgenia moved back to the Department of Mechanical Engineering of the University of Texas at Austin to investigate acoustical streaming in a resonator of a thermo-acoustic engine. Currently, Dr. Zabolotskaya holds a Senior Research Scientist position in the Applied Research Laboratories of the University of Texas at Austin. She is involved mostly in biomedical applications based on nonlinear acoustics.

Stanislav Y. Emelianov (M’94) received B.S. and M.S. degrees in physics and acoustics in 1986 and 1989, respectively, from the Moscow State University, Moscow, Russia, and a Ph.D. degree in physics in 1993 from the Moscow State University and the Institute of Mathematical Problems of Biology of the Russian Academy of Sciences, Push-chino, Moscow region, Russia. In 1989, he joined the Institute of Mathematical Problems of Biology, where he was engaged in both mathematical modeling of soft tissue biomechanics and experimental studies of noninvasive visualization of the mechanical properties of tissue.

Following his graduate work, he moved to the University of Michigan, Ann Arbor, as a post-Doctoral Fellow in the Bioengineering Program and in the Electrical Engineering and Computer Science Department. From 1996 to 2002, Dr. Emelianov was a research scientist at the Biomedical Ultrasonics Laboratory of the Biomedical Engineering Department at the University of Michigan, Ann Arbor.

In 2002, he joined the faculty of the Department of Biomedical Engineering at the University of Texas at Austin. His research interests are in medical imaging and therapeutics, including ultrasound, photoacoustic, elasticity, and multimodality imaging, photothermal and laser-assisted therapy, cellular/molecular imaging and therapy, functional imaging, etc.