Coding of Amplitude Modulation in Primary Auditory Cortex

Abstract

Conflicting results have led to different views about how temporal modulation is encoded in primary auditory cortex (A1). Some studies find a substantial population of neurons that change firing rate without synchronizing to temporal modulation, whereas other studies fail to see these nonsynchronized neurons. As a result, the role and scope of synchronized temporal and nonsynchronized rate codes in AM processing in A1 remains unresolved. We recorded A1 neurons' responses in awake macaques to sinusoidal AM noise. We find most (37–78%) neurons synchronize to at least one modulation frequency (MF) without exhibiting nonsynchronized responses. However, we find both exclusively nonsynchronized neurons (7–29%) and “mixed-mode” neurons (13–40%) that synchronize to at least one MF and fire nonsynchronously to at least one other. We introduce new measures for modulation encoding and temporal synchrony that can improve the analysis of how neurons encode temporal modulation. These include comparing AM responses to the responses to unmodulated sounds, and a vector strength measure that is suitable for single-trial analysis. Our data support a transformation from a temporally based population code of AM to a rate-based code as information ascends the auditory pathway. The number of mixed-mode neurons found in A1 indicates this transformation is not yet complete, and A1 neurons may carry multiplexed temporal and rate codes.

INTRODUCTION

AM, the change over time of a sound's amplitude envelope, is an important information-bearing parameter carried by communication sounds such as syllabic features in speech (Drullman et al. 1994; Füllgrabe et al. 2009; Nelken et al. 1999; Shannon et al. 1995; Steinschneider et al. 1999) and is thought to be of particular use in segregating sound sources during auditory scene analysis (Bregman 1990; Hu and Wang 2004; Yost 1991). AM also can carry important information about pitch and has been used to investigate how pitch relates to temporal as opposed to spectral aspects of the stimulus (Burns and Viemeister 1976, 1981). The sound amplitude envelope has been treated as a fundamental property of sound (Attias and Schreiner 1997, 1998; Joris et al. 2004; Smith et al. 2002), and in marmoset A1 some neurons only respond to tones if they are amplitude modulated (Liang et al. 2002), suggesting that this is a feature highly selected by the auditory system. There is a great deal known about neuronal responses to temporally modulated sounds throughout the auditory system in a number of species (e.g., Burger and Pollak 1998; Caspary et al. 2002; Creutzfeldt et al. 1980; Eggermont 1994; Frisina et al. 1990; Grothe 1994; Joris and Yin 1992; Klump et al. 2004; Kuwada and Batra 1999; Langner and Schreiner 1988; Nelson and Carney 2007; Preuss and Müller-Preuss 1990; Rose and Capranica 1985; Zheng and Escabí 2008; reviewed in Joris et al. 2004), including humans (Brugge et al. 2009). In this paper, we will resolve some outstanding issues in the processing of AM in non-human primates.

Studies using AM and other time-varying stimuli consistently suggest that the ability of cells to phase lock to high-frequency stimuli declines at successive auditory stages (Creutzfeldt et al. 1980; Joris et al. 2004; Krishna and Semple 2000; Rhode and Greenberg 1994; Schreiner and Urbas 1988). Auditory nerve fibers will phase lock to envelopes as high as 3–4 kHz, but in the cochlear nucleus, phase-locking cutoffs lie between 750 and 1,500 Hz (Rhode and Greenberg 1994; Zhao and Liang 1997). In the inferior colliculus (IC), the phase-locking limit is reduced to 500 Hz, with a majority of cells losing the ability to follow the envelope >200 Hz (Krishna and Semple 2000; Rees and Palmer 1989). Studies using AM in auditory thalamus are rare but suggest peak phase locking sensitivity <50 Hz and phase-locking limits on the order of 100 Hz (Preuss and Müller-Preuss 1990). Using click trains in the MGB, phase-locking limits were between 100 and 300 Hz with peak sensitivity between 25 and 125 Hz (Bartlett and Wang 2007; Rouiller et al. 1981).

In cortex, phase-locking cutoffs are somewhat variable. Anesthetized preparations generally yield synchronization cutoffs <50 Hz (Eggermont 1991; Gaese and Ostwald 1995; Schreiner and Urbas 1986, 1988) while awake preparations can show synchronization cutoffs up to and beyond 100 Hz (Anderson et al. 2006; Bieser and Müller-Preuss 1996; Fitzpatrick et al. 2009; Liang et al. 2002; Lu et al. 2001; Malone et al. 2007). Despite this, most cortical neurons only strongly phase lock to lower modulation frequencies with a median synchrony cutoff usually in the 10–30 Hz range (e.g., Fitzpatrick et al. 2009; Ter-Mikaelian et al. 2007). More recently at higher levels of the marmoset auditory system, starting in A1, Lu et al. (2001) report finding a population of nonphase-locking (nonsynchronized) neurons tuned for modulation frequency. These results have led to the hypothesis that the creation of distinct synchronized and nonsynchronized populations of neurons is an emergent property of A1 (Bartlett and Wang 2007; Liang et al. 2002; Lu et al. 2001) and support a transformation from a temporal code at lower levels of the auditory system to a rate-based code in higher areas. The finding of nonsynchronized neurons, however, has not been verified outside of marmosets, and a recent study in macaques fails to find a population of such neurons (Malone et al. 2007). This leads to the possibility that nonsynchronized neurons in A1 are unique to marmosets. We hypothesize that it is not species differences that lead to these differing reports but rather other experimental factors.

We examined the responses of A1 neurons, in awake macaque monkeys, to sinusoidal AM wideband noise. Modulation frequency tuning was narrower in neurons that did not exhibit any phase locking but remained broad overall. We found both synchronized and nonsynchronized neurons as well as neurons that share both characteristics. Contrary to previous studies, we did not find strong evidence that synchronized and nonsynchronized neurons comprise independent populations, and we suggest that both response types may be simultaneously present in the same neuron to a varying degree, as has been reported previously in thalamus (Bartlett and Wang 2007) and IC (Zheng and Escabí 2008).

METHODS

Overview

The general methods (surgical procedures, animal care, etc.,) were similar to those described in previous studies (O'Connor et al. 2005). A general summary of the methods follows with any differences in methods explained in more detail.

Subjects

All procedures conformed to the Public Health Service policy on experimental animal care and were approved by the UC Davis animal care and use committee. Experiments were performed on two (1 male, 1 female) adult rhesus monkeys (Macaca mulatta) weighing 6–8 kg. The monkeys sat in an acoustically “transparent” primate chair (custom made, Crist Instruments) in a double-walled, sound-attenuated, foam-lined booth (IAC: 9.5 × 10.5 × 6.5 ft) during physiological recording. They received diluted fruit juice or water during daily recording sessions and monkey chow, fruits, and supplementary water in their individual home cages. Each monkey was implanted with a head post and recording chamber for chronic access to auditory cortex. Recordings were made while the monkeys sat quietly in the primate chair in the sound booth with the head restrained with diluted juice or water given intermittently. A plastic grid (Crist Instruments) was fit into the recording chamber to guide the electrode penetrations. High-impedance tungsten microelectrodes (FHC) were driven into the cortex by a remotely controlled hydraulic microdrive (FHC) through guide tubes held by the plastic grid.

Stimulus generation and data collection

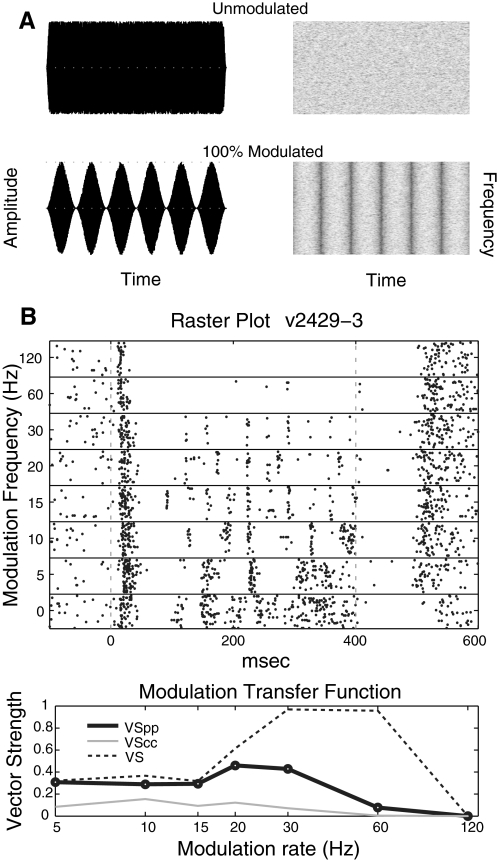
The sinusoidal AM stimuli had a “frozen” broadband noise carrier and were 400 ms in duration. Neurons at each recording site were assessed with an unmodulated noise burst and 100% modulation depth AM noise (Fig. 1A) at seven different modulation frequencies (5, 10, 15, 20, 30, 60, and 120 Hz) for a total of eight stimuli. Each stimulus was presented 50 times. For each repetition, the entire set of eight stimuli was presented in random order, without replacement, before the next repetition began.

Fig. 1.

A: AM stimuli with a noise carrier. The stimuli were created from broadband white noise bursts (top), which were also used as “unmodulated” stimuli. The amplitude of AM stimuli (bottom) is modulated by a sinusoidal envelope. In this study, all AM stimuli were 100% modulated. B: raster plot (top) and modulation transfer function (MTF, bottom) of a sample cell. Standard VS measures (MTF) indicate very strong phase locking at 30/60 Hz, whereas phase-projected VS suggests a lesser degree of synchrony. Cycle-by-cycle vector strength suggests low reliability of firing throughout. Best frequency (BF) of cell in B is 1,800 Hz.

The sound signals were generated by a digital signal processor (AT&T DSP32C) and a D/A converter (TDT Systems DA1). They then passed through a programmable attenuator (TDT Systems PA4), and a passive attenuator (Leader LAT-45). The signal was amplified (Radio Shack MPA-200) before being delivered to a speaker (Radio Shack PA-110, 10-in woofer and piezo-horn tweeter, 0.038–27 kHz) positioned at ear level 1.5 m in front of the subject.

The auditory stimuli were presented at a sampling rate of 50 kHz and were cosine ramped at onset and offset (5.0 ms rise/fall time). Stimulus intensity was adjusted to ∼65 dB SPL (<2 dB variation). Extracellular potentials were amplified and filtered (0.3–5 kHz; AM Systems 1800), sampled at 50 kHz, and stored on hard disk for later analysis. Spikes were re-sorted off-line using SPIKE2 software (CED).

Location of recording

The determination that our recordings were in A1 was based on the tonotopic gradient and latency information (maps in supplementary material)¹ obtained from physiological recording as well as postmortem histology. The frequency tuning at each recording site was assessed by using a set of pure tones with a combination of frequencies and intensities. In frequency, this set spanned a three-octave range with 1/5 octave increments around a center frequency that was estimated by hand-tuning. In intensity the set spanned 63 dB with a 7 dB increment between 15 and 78 dB SPL for a total of 150 combinations of frequency and intensity. Tone duration was 0.1 s. During data collection, the 150 tone combinations were presented in a random order and repeated at least five times. The neuronal responses to each combination were represented by the average spike counts within the first 75 ms window following stimulus onset. A two-dimensional response matrix (intensity × frequency) was obtained from these responses. The neuron's frequency tuning curve was estimated by the contour line at the mean spontaneous response (spike count in a 75 ms window before the onset of each frequency-intensity combination) plus 2 SD using Matlab's “contourc” function. The best frequency (BF) and threshold were determined from the obtained frequency tuning curve.

On termination of the experiments, electrode locations were marked at several key border points in one animal with tracking lesions (monkey Y) and in another by inserting an electrode dipped in biotinylated dextran amine (monkey V). One hour later the animal was given an overdose of sodium pentobarbital and perfused with 4% paraformaldehyde in 0.1 M phosphate buffer. In the monkey with the tracking lesions, the perfusion was poor, leading to difficulty in lesion identification. In the monkey with the biotinylated dextran markers, track reconstruction was reliable. Examination of monkey V's histology confirmed that all of the recordings took place in A1. In monkey Y, due to the bad perfusion we were forced to rely on tonotopic gradient and latency information exclusively. There was a large low frequency border between A1 and more rostral fields (most likely R), so we defined a border which conservatively estimated the extent of A1. The other recordings, which could belong to A1 or R, are excluded from the analysis. A comparison between A1 and the border area is included in the supplementary material.

Data analysis

MODULATION TRANSFER FUNCTIONS.

Modulation transfer functions (MTFs) were determined for 182 A1 neurons using both a spike rate measurement (spike count, rMTF) and a measure of temporal phase locking (phase-projected vector strength, tMTF) at each modulation frequency tested. Phase-projected vector strength (VS_PP, see next section) is a variation of vector strength that allows trial-by-trial calculations of VS without the problems contributed by low spike counts. For both rMTFs and tMTFs, the value reported at each modulation frequency is the mean of the trial-by-trial values. All calculations were made using only spikes from 70 to 400 ms poststimulus onset to exclude onset responses (the same general pattern of results holds if onsets are included). A cell was considered AM sensitive if the response to at least one modulation frequency was significantly different from the response to the unmodulated noise using either rate or temporal measures (see following text for statistical details). The best modulation frequency (BMF) of a cell was defined as the modulation frequency that resulted in the largest mean spike count or mean phase-projected vector strength (VS_PP).

VECTOR STRENGTH AND PHASE-PROJECTED VECTOR STRENGTH.

The standard, nonphase-projected formula for vector strength is

$$VS=\frac{\sqrt{{\left({\displaystyle {\sum }_{i=1}^n\cos {\theta }_i}\right)}^2+{\left({\displaystyle {\sum }_{i=1}^n\sin {\theta }_i}\right)}^2}}{n}$$ (1)

where VS is the vector strength, n is the number of spikes over all trials, and θ_i is the phase of each spike in radians, calculated by

$${\theta }_i=2\pi \frac{\left(t_i\hspace{0.17em}modulo\hspace{0.17em}p\right)}{p}$$ (2)

where t_i is the time of the spike in milliseconds relative to the onset of the stimulus and p is the modulation period of the stimulus in ms (Goldberg and Brown 1969; Mardia and Jupp 2000). One weakness of the standard VS measure is that it may give spuriously high values at low firing. This can be a problem when using single trial measurements for statistical purposes. An example of this is illustrated in Fig. 1B where at high modulation frequencies (especially 30 and 60 Hz in this example), low spike counts lead to high vector strength values (dotted line). Another shortcoming of VS is that because it is usually calculated on the summed or averaged cycle histogram to perform statistical tests, various assumptions have to be made, most of which confound firing rate with phase locking (e.g., Rayleigh test of uniform distribution) (Buunen and Rhode 1978; Mardia and Jupp 2000).

To avoid these two problems, phase-projected vector strength (VS_PP) was used. Conceptually, VS_PP compares the mean phase angle for each trial with the mean phase angle of all trials at that MF and penalizes single-trial VS values if they are not in phase with the global response. VS_PP was calculated on a trial-by-trial basis as follows

$$V{S}_{\text{PP}}=V{S}_t\hspace{0.17em}\cos \left({\phi }_t-{\phi }_c\right)$$ (3)

where VS_PP is the phase-projected vector strength per trial, VS_t is the vector strength per trial, calculated as in Eq. 1, and ϕ_t and ϕ_c are the trial-by-trial and mean phase angle in radians, calculated for each stimulus condition

$$\phi =arctan2\frac{{\displaystyle {\sum }_{i=1}^n\sin {\theta }_i}}{{\displaystyle {\sum }_{i=1}^n\cos {\theta }_i}}$$ (4)

where n is the number of spikes per trial (for ϕ_t) or across all trials (for ϕ_c) and arctan2 is a modified version of the arctangent that determines the correct quadrant of the output based on the signs of the sine and cosine inputs (Matlab, atan2). For all VS_PP calculations, a cell that fired no spikes was assigned a VS_PP of zero, but there was no minimum spike count because the condition-wide mean phase acted as an external phase reference. Whereas VS may range from 1 (all spikes occur at the same stimulus phase) to 0 (spikes times occur in any circularly symmetric pattern including random with regard to stimulus phase), VS_PP may range from 1 (all spikes in phase with the population mean phase) to –1 (all spikes 180° out of phase with population mean phase) with 0 corresponding to random or circularly symmetric phase with regard to the population mean phase. Except for the cases where there were low spike counts (e.g., Fig. 1B), the two VS measures were in good agreement. In all examples, we show both for reference, but except where otherwise noted, all statistical analysis was done using VS_PP.

To measure the reliability of a neuron to follow every cycle of modulation, we calculated cycle-by-cycle vector strength (VS_CC, Fig. 1B, gray line). This measures how reliably a neuron follows the stimulus as well as how precise the timing of firing is. This is contrasted with VS_PP, which only quantifies timing precision but not reliability. VS_CC is calculated in a similar fashion to VS_PP except it is calculated on a cycle-by-cycle basis rather than on the cycle histogram. One VS_PP value is calculated for each cycle of the stimulus, and then all these values are averaged together to arrive at VS_CC for a given trial. On any cycle where no spike is fired a value of 0 is used.

STATISTICAL TESTING.

To determine whether a neuron's response was influenced by AM, two-tailed t-tests were performed comparing the distributions of either trial-by-trial spike count (SC) or trial-by-trial VS_PP at each modulation frequency against the same measure for an unmodulated noise burst. It is important to note that this tests whether the responses can distinguish AM from its unmodulated carrier and not whether the neuron responds to AM sounds. (Note that the VS_PP measure is fundamentally tied to a modulation frequency. When we refer to the VS_PP of an unmodulated stimulus, this is a control measurement made assuming the same modulation frequency as the corresponding test stimulus—instead of a single VS_PP value for the unmodulated stimulus, the value depends on the modulation frequency of the experimental group under investigation. Control measures of VS_PP are not always 0 because some cells exhibit temporally structured firing to unmodulated stimuli.) To determine if a neuron responded to AM sounds, SC distributions were also compared against spontaneous firing (100-ms prestimulus, collected across all trials regardless of stimulus type). All t-tests were performed with P < 0.05 after Bonferroni correction for seven comparisons (1 for each modulation frequency) per cell.

We also determined whether there was significant synchronization relative to a random distribution of spikes without regard to a comparison distribution of the unmodulated sound. This was accomplished with the Rayleigh statistic (Mardia and Jupp 2000), which evaluates whether the cycle histogram (time histogram relative to each period of modulation) significantly differs from a flat distribution in time

$$RS=2n\left(V{S}_{\text{A}}^2\right)$$ (5)

where RS is the Rayleigh statistic and VS_A is a single vector strength value calculated over all trials. In all cases, we considered RS ≥17.7 to be statistically significant, which corresponds to P < 0.001 after Bonferroni correction for seven comparisons per cell (this differs from the 13.8 that is usually used when there is no multiple comparison correction).

Because Bonferroni correction controls the experiment-wide error rate (i.e., the probability that any null hypothesis is falsely rejected), it becomes very conservative for high numbers of multiple comparisons. Consequently, we used the false discovery rate (FDR) (Benjamini and Hochberg 1995) method, which for large numbers of neurons more accurately determines the number of significant neurons in a population while correcting for multiple comparisons.

JOINT DISTRIBUTION ANALYSIS.

We performed a joint distribution analysis to determine whether the rate BMF (rBMF) and temporal BMF (tBMF) were related within cells. To test the hypothesis that the rBMF and tBMF measures coincided, we designed an ad hoc Monte Carlo permutation analysis (100,000 permutations). We first determined the observed count of cells that had coincident rBMF and tBMF (o_c) and the observed count of cells where the rBMF and tBMF were adjacent (e.g., rBMF = 20, tBMF = 30, o_a) from the joint distribution o_ij. Then for each repeat, a random joint distribution ρ_ij was created by randomly pairing (without replacement) the observed rBMF and tBMF classifications, from which we determined the randomized coincident count (ρ_c) and the randomized adjacent count (ρ_a). The P value of this analysis was taken as the probability that ρ_x exceeded o_x. Because the BMFs of band-reject cells may not indicate the regions of greatest sensitivity, we restricted our analysis to cells that had both rMTFs and tMTFs classified into low-, band-, or high-pass categories (a single peak in the MTF that was significantly different from the minimum), a total of 71 cells.

BANDWIDTH ANALYSIS AND FITTING PROCEDURE.

For the bandwidth analysis, we used three different functions to fit the MTFs, a logistic (sigmoid) function (Eq. 6), a Gaussian (Eq. 7), and a log-transformed Gaussian (Eq. 8)

$$y=a+\frac{b}{1+e^{\frac{-\left(x-\mu \right)}{s}}}$$ (6)

$$y=a+be\frac{1{\left(x-\mu \right)}^2}{2s^2}$$ (7)

$$y=a+be\frac{-{\left(\text{In}\left(x\right)-\text{In}\left(\mu \right)\right)}^2}{2s^2}$$ (8)

All three functions have four free parameters determining the y offset (a), the height (b), the x center (μ), and the slope (s). Fitting was performed using Matlab's “fmincon” function. Constraints on the parameters were set as follows. Logistic: a ≥ 0; b ≥ 0; b ≤ 1.3 (max-min of data); μ ≥ 0; −33 ≤ s ≤ 33. The constraint on the height parameter prevented the fit from extrapolating too far beyond the observed data. A negative slope parameter would allow the logistic to fit a high-pass MTF rather than a low-pass MTF, but this was not observed. Gaussian: a ≥ 0; b ≤ 1.3 · (max-min of data); μ ≥ 0; 3 ≤ s ≤ 50. The slope factor restricted the full width at half height (FWHH) of the Gaussian fit to lie between ∼7 and 120 Hz. Log-transformed Gaussian: a ≥ 0; b ≤ 1.3 · (max-min of data); μ ≥ 0; s ≤ 2.36. The slope factor restricted the FWHH of the log-transformed Gaussian fit to a maximum of ∼8 octaves.

For each MTF, a fit was attempted for all three curves, and the significance of each fit was calculated. If no fit was significant at the P < 0.01 level, all fits were rejected. Otherwise, of the significant fits, the one with highest correlation coefficient value was selected. For logistic fits, a high-pass cutoff was calculated as the half-height point of the curve. For both Gaussian fits, low- and high-pass cutoffs were selected as the two half-height points on the curve, and the bandwidth was calculated as the FWHH. Low-pass cutoff and bandwidth values were rejected for any Gaussian fit where the low-pass cutoff was <0. Additionally, in cases where the MTF value at 5 Hz was either the largest value in the MTF or was within 90% of the full height of the fit, we felt that there was insufficient evidence of a reduction in response at low frequencies to justify a Gaussian fit. In these cases, we accepted the sigmoid fit when the sigmoid fit was significant at a 0.01 level regardless of the significance of the Gaussian fits. If the sigmoid fit was not significant, we calculated a high-pass cutoff (but no low-pass cutoff or bandwidth values) from the most significant Gaussian fit (P < 0.01 required). For most MTFs, there was no major difference between the Gaussian fit and the log-Gaussian fit. The general difference is in the tails—the log-Gaussian has a heavier right-hand tail while the regular Gaussian has a heavier left-hand tail. However, the log-transformed Gaussian was used because for some MTFs, the log-Gaussian fit was notably better than the Gaussian fit—generally in cases where the Gaussian fit failed to appropriately capture the floor of the MTF.

FOURIER TRANSFORM OF POPULATION SPIKE TRAIN.

To reduce low frequency noise when investigating frequency aspects of the spike train, the overall spike train (across all trials, 70 ms onset removed) was binned into 10 μs bins and convolved with a Gaussian of the same resolution with μ = 0, σ = 0.33, and a total width of 3 ms. The result of the convolution was then analyzed via FFT.

RESULTS

Dataset

Responses to the full set of modulation frequencies were determined for 182 isolated single neurons recorded from two awake macaque monkeys. Of those, 13 neither phase locked significantly (Rayleigh test with Bonferroni correction) nor yielded SCs significantly different from spontaneous or unmodulated noise (t-test with Bonferroni correction); this yielded 169 neurons that responded to at least one sound in the stimulus set. Although there was a tendency for both spike-count (rate) and phase-locked (vector strength, temporal) based response measures to prefer low modulation frequencies and for responses to span a broad range of modulation frequencies, a large variety of response properties were encountered. We also saw a mixture of synchronized and nonsynchronized response properties often observing both within an individual neuron.

The results can strongly depend on the metrics used. One difference in metrics is whether significance of phase locking is determined by the Rayleigh statistic or trial-by-trial VS_PP. The Rayleigh statistic, which has traditionally been used to test significance of phase locking, has some shortcomings that lead to high sensitivity and high false positives. Trial-by-trial VS_PP is less sensitive and so might underestimate phase locking but is less likely to result in falsely identifying phase locking (see discussion). Another important distinction is whether AM responses are compared with spontaneous activity or to the responses to unmodulated sounds. This is not a trivial distinction because a cell the firing rate of which differs from spontaneous activity is able to signal the presence of an auditory stimulus relative to no event, while a cell with a firing rate that differs from the firing rate in response to an unmodulated stimulus is able to signal the presence of modulation in that stimulus.

Synchronized and exclusively nonsynchronized neurons

PREVALENCE.

To compare across studies, we divided our cells into synchronized and exclusively nonsynchronized categories. We defined a cell to be synchronized if it exhibited significant phase locking to at least one of the tested modulation frequencies and exclusively nonsynchronized if it exhibited a significant change in firing rate without significant phase locking.

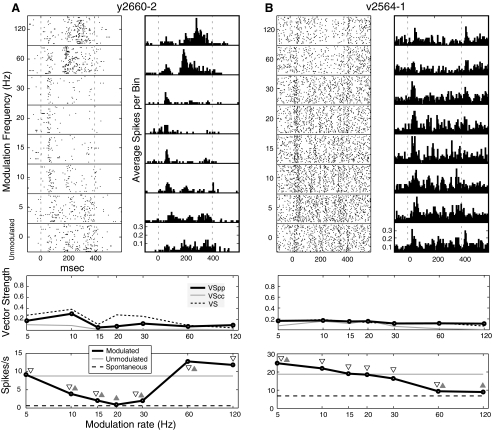
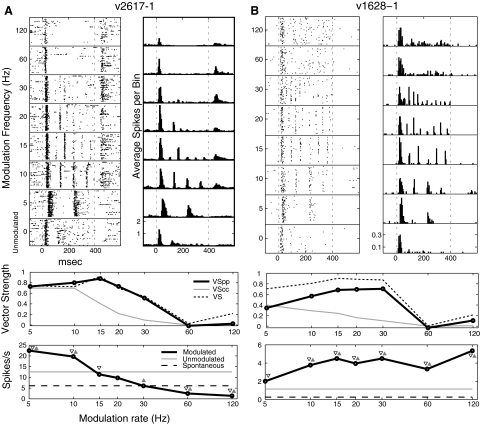
Examples of exclusively nonsynchronized neurons are shown in Fig. 2. The neuron of Fig. 2A responded to unmodulated noise with a firing rate significantly greater than the spontaneous firing rate. The response to 5 Hz modulation was similar to the response to unmodulated noise. Between 10 and 30 Hz the neuron fired at levels significantly below that evoked by the unmodulated noise. At high frequencies (60 and 120 Hz), nonsynchronized increases in activity emerge that are absent for middle frequencies, and the temporal structure of these responses appears to be different from that to unmodulated noise. The neuron of Fig. 2B shows nonsynchronized responses that were strongest at the lowest modulation frequencies and declined as modulation frequency increased. We found this pattern of declining, exclusively nonsynchronized response in 8% of our neurons (15/182). The increase in response at 5 Hz, and decreases at 60 and 120 Hz, were significantly different from that of unmodulated noise, and, except for 120 Hz, all responses were greater than the spontaneous level. Depending on whether the Rayleigh statistic or VS_PP were used to define synchrony and whether SCs were compared against spontaneous or unmodulated activity, 4–20% of A1 neurons were classified as exclusively nonsynchronized.

Fig. 2.

Nonsynchronized neurons. Top left: the spike rasters. Top right: the peristimulus time histogram (bin size = 5 ms). Middle: the temporal MTF (tMTF) shown for phase-projected vector strength (VS_PP, the primary temporal analysis for these experiments), cycle-by-cycle vector strength (VS_CC), and regular vector strength (VS, displayed for reference). Bottom: the spike rate MTF (rMTF) with both the spontaneous and unmodulated spike rates shown. Symbols indicate significant departures of the modulated firing rate from spontaneous (▿) and unmodulated (). BF of cell in A is 800 Hz and BF of cell in B is 2,800 Hz.

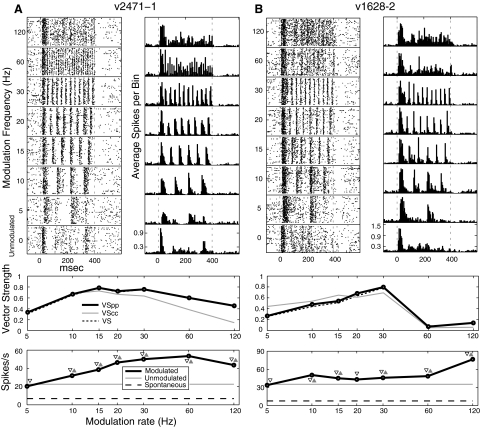
Most neurons synchronized to at least one modulation frequency. Some synchronized well to all modulation frequencies tested (Fig. 3A). In this example, cycle-by-cycle VS (VS_CC) decreases at higher modulation frequencies, indicating that the neuron fires precisely but not reliably to the modulation cycle. Other neurons phase locked to low frequencies and then had nonsynchronized responses at higher modulation frequencies (Fig. 3B).

Fig. 3.

Synchronized neurons showing high activity at high modulation frequencies. Plot details are as in Fig. 2. The cell in A phase locks well to all modulation frequencies presented. The cell in B increases its spike count at the highest modulation frequencies but loses synchrony >30 Hz. BF of cell in A is 26,000 Hz and BF of cell in B is 7,500 Hz.

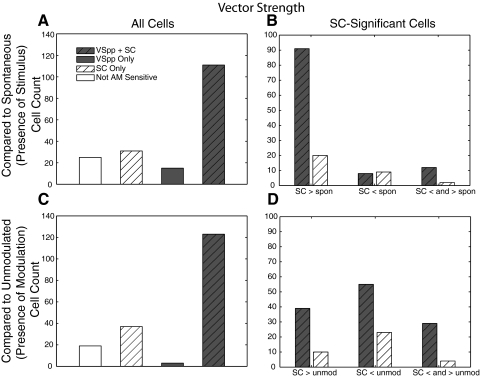
Figure 4 shows the results of the categorization when synchrony is measured by comparing VS_PP distributions between modulated sounds and the unmodulated carrier controls (see methods for an explanation of the calculation of VS_PP on unmodulated sounds) with a Bonferroni correction for multiple comparisons. When comparing SCs to spontaneous activity (Fig. 4A), 31 (17% of total) neurons were exclusively nonsynchronized—showing significant changes in SC from spontaneous activity but no significant phase locking. There were 15 (8%) exclusively synchronized neurons—showing significant phase locking but no change in firing rate from spontaneous. Another 111 (61%) neurons both changed their SC and phase locking significantly relative to spontaneous. When comparing SCs to the unmodulated noise carrier (Fig. 4C), 37 (20%) neurons were exclusively nonsynchronized, there were only 3 (2%) exclusively synchronized neurons, and 123 (68%) neurons changed both their SC and phase locking significantly relative to the unmodulated noise response.

Fig. 4.

Comparison of synchronized and nonsynchronized neurons: synchrony measured by VS_PP. In all plots, gray shading to a bar indicates cells that have significant VS_PP responses, and diagonal hatching indicates cells which have significant spike count (SC) responses. Top: SCs are compared with spontaneous firing (difference signals the presence of a stimulus). Bottom: SCs are compared with the response to an unmodulated stimulus (difference signals the presence of modulation). Left: all cells. Right: only SC-significant cells included. SC > spon: ≥1 MF greater than spontaneous, no MFs below spontaneous; SC < spon, ≥1 MF below spontaneous, no MFs greater than spontaneous; SC < and > spon, ≥1 MF below spontaneous and ≥1 MF greater than spontaneous.

Using the Rayleigh statistic to define synchrony resulted in a substantial increase in the reporting of synchrony. Relative to spontaneous and the response to the unmodulated noise carrier control, only 7 (4%) and 12 (7%) neurons were exclusively nonsynchronized using the Rayleigh statistic while the number of neurons showing synchronized responses increased to 156 (86%).

CODING WITH INCREASES AND DECREASES.

Neurons encode modulation with either increases or decreases in activity, but the manifestation of these SC-based results are different for synchronized and exclusively nonsynchronized neurons. This is at least partially because response to the unmodulated carrier tended to be greater than spontaneous, so that an apparent increase in activity relative to spontaneous for AM might actually be solely due to the response to the carrier rather than the modulation. We find that for nonsynchronized neurons both decreases and increases in activity were commonly seen whether analyzed relative to the unmodulated noise response or spontaneous activity. Synchronized neurons, on the other hand, encoded modulation with both decreases and increases in activity relative to the unmodulated noise carrier control, but they primarily increased activity relative to spontaneous for encoding an event (Fig. 4, B and D).

Relative to spontaneous, 142 neurons (78%) signaled the presence of a stimulus with a significant change in firing (t-test with Bonferroni correction for seven comparisons; Fig. 4A, SC significant). For exclusively nonsynchronized neurons, 2 increased activity at one MF and decreased at another, 20 increased activity at some MFs and never decreased, and 9 decreased at some MFs without increases (Fig. 4B, white hatched bars). The majority of the synchronized neurons showed an increase in firing rate relative to spontaneous with a much smaller number showing decreases (91 increased, 8 decreased, and 12 did both depending on MF, Fig. 4B, gray hatched bars). Therefore for nonsynchronized neurons, both decreasing and increasing codes relative to spontaneous are common, but for synchronized neurons, increases in SCs relative to spontaneous were much more likely than decreases.

When responses to AM were compared with responses to the unmodulated carrier, different results were obtained for the synchronized neurons. Unlike the coding of the presence of a stimulus where synchronized neurons were more likely to increase firing rate relative to spontaneous, when looking at modulation coding, the majority of synchronized neurons decreased firing rate relative to the unmodulated carrier (Fig. 4D, gray hatched bars, 55 neurons decreased and 39 increased, and 29 both depending on MF). Nonsynchronized neurons were also more likely to decrease relative to the unmodulated carrier (Fig. 4D, white hatched bars, 23 neurons decreased and 10 increased, and 4 both depending on MF).

A few other properties shed light on these differences. It might be that synchronized neurons have lower spontaneous rates, and a floor effect is preventing them from firing significantly below spontaneous. This is not the case; in fact both the mean and median spontaneous rates are higher for synchronized neurons (7.8 and 6.5 spike/s) than nonsynchronized neurons (5.5 and 3.6 spike/s). Another possibility is that the carrier is primarily excitatory relative to spontaneous and rarely drives the neurons below spontaneous. This appears to be the case. We found that 6/182 neurons' responses to the unmodulated carrier significantly decreased relative to spontaneous and 105/182 had significantly increased activity relative to spontaneous (t-test). This suggests that changes in activity that are observed relative to spontaneous for synchronized neurons might be more reflective of responsiveness to the carrier rather than the modulation.

CODING BOTH AN EVENT AND AM.

A single neuron's response is more informative if it is able to distinguish a modulated stimulus from both the unmodulated carrier and from no sound (spontaneous). For this to be meaningful, it must happen for the same stimulus (i.e., be measured at the same modulation frequency). A total of 116 of our neurons were capable of doing this, but very few of them (17, 46% of the exclusively nonsynchronized neurons) were exclusively nonsynchronized. For the synchronized neurons, a total of 99 neurons (79% of the synchronized neurons) had the same property. These proportions were significantly different (P = 0.001, z-test for independent proportions). This result suggests that if individual neurons in A1 are specifically encoding the presence of an AM stimulus ≤120 Hz, it is achieved chiefly through synchronized neurons.

MODULATION FREQUENCY TUNING.

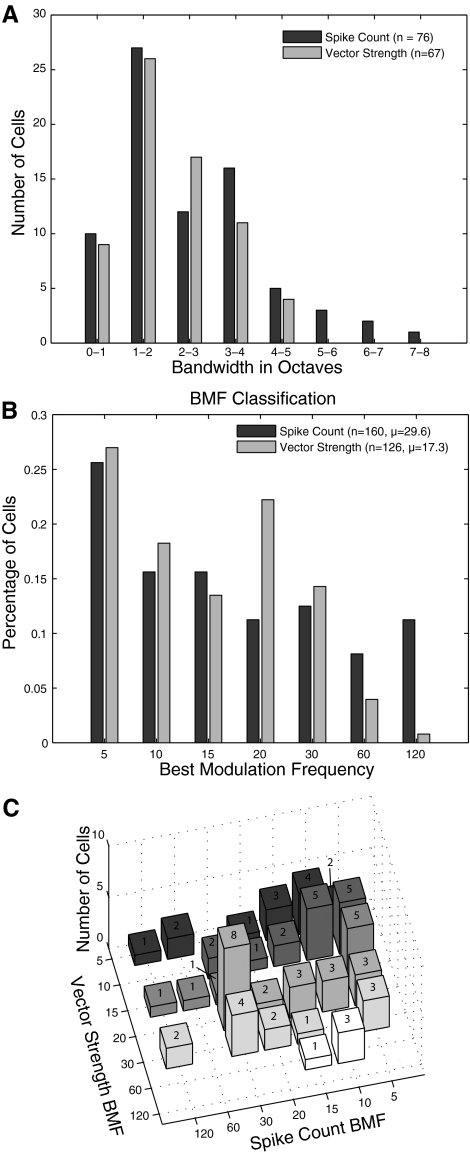
Tuning for modulation frequency tended to be broad (Fig. 5A). Because of the small number of neurons that had a significant Gaussian fit in combination with the small number of nonsynchronized neurons, statistical power for comparing bandwidth would be very low. To improve the statistical power for this analysis only, we pooled the 182 conservatively defined A1 neurons with 50 neurons on the A1/R border (these border neurons tend to have low BFs, see supplemental data for more on these neurons). Relative to the unmodulated carrier, the mean rate bandwidth of cells that were exclusively nonsynchronized was 1.59 octaves (11 cells with a defined bandwidth), while the mean rate bandwidth of synchronized cells (65 cells with a defined bandwidth) was 2.67 octaves (t-test, P = 0.03), indicating that exclusively nonsynchronized cells have narrower bandwidths. It should be noted that neither within conservatively defined A1 nor the border region did these differences reach significance, suggesting that this effect is not due solely to one of the two regions. The mean temporal bandwidth based on VS_PP was 2.13 octaves (67 cells with significant fits), which was not significantly different from the bandwidth of nonsynchronized neurons but significantly less than the rate-based code for synchronized neurons. To aid in comparison to other studies, the bandwidths measured relative to spontaneous for nonsynchronized, rate-synchronized and VS_PP-synchronized is 1.16, 2.67, and 2.13, respectively, and all comparisons are significantly different (t-test, P < 0.05).

Fig. 5.

Bandwidth and best modulation frequency for rate and temporal measures of response. A: distribution of full-width at half-height bandwidth, in octaves, for all cells in which the MTF could be well fit by a Gaussian function (see methods). For A only, 50 cells from the A1/R border area are included. B: best modulation frequencies (BMFs) for all AM-sensitive cells. C: joint distribution of rate and temporal BMFs for synchronized cells. Only cells with single-peaked MTFs for both rate and temporal measures (n = 71) included.

Relationship of temporal and rate based BMFs

For both temporal and rate measures, BMFs were more commonly found at low than at high frequencies (Fig. 5B). BMFs ≥ 60 Hz were more common for rate (31/160, 19%) than temporal measures (6/126, 5%, P = 2.8 × 10^-5 proportion test).

We asked whether rate and temporal BMFs were coincident by performing a joint distribution Monte Carlo analysis (methods). The observed joint distribution of BMF is depicted in Fig. 5C. For both coincident BMFs (e.g., rBMF = 60 Hz and tBMF = 60 Hz) and adjacent BMFs (e.g., rBMF = 30 Hz and tBMF = 20 Hz), we were unable to reject the null hypothesis of independent distribution of BMF (coincident P = 0.41, adjacent P = 0.14). This result does not support the prediction that rBMF and tBMF are closely related.

Mixed synchronized/nonsynchronized neurons

We encountered many neurons that appeared to have both synchronized and nonsynchronized responses (e.g., Fig. 3B, also Fig. 7B). As one estimate of the size of this mixed-mode population, we counted the number of cells that exhibited significant phase locking at one frequency, and a significant nonsynchronized increase in firing rate at a different modulation frequency. We looked at increases in firing rate to exclude cells the firing rate of which at some modulation frequencies is suppressed to near zero because synchrony cannot be validly measured in these cases. This method would necessarily exclude any cells with significant nonsynchronized decreases, so our estimate of the mixed-mode population may be low. Using VS_PP as our measure of phase locking, we found 82 cells (45%) that showed this pattern when firing rate was compared against spontaneous activity and 37 cells (20%) when compared against an unmodulated stimulus. A total of 32 cells (18%) had a nonsynchronized firing rate to at least one modulation frequency that was higher than that to both unmodulated noise and the spontaneous rate but also had significant phase locking to at least one different modulation frequency. Altogether, we found 87 cells (48%) with mixed-mode responses—capable of using a temporal code to signal the presence of modulation at one frequency and a nonsynchronized rate code to signal the presence of a stimulus and/or modulation at another frequency.

Fig. 7.

Synchronized neurons showing loss of phase locking at high modulation frequencies. Plot details are as in Fig. 2. The cell in A is inhibited below spontaneous at high modulation frequencies. The cell in B shows a marked drop in phase locking >30 Hz that is not accompanied by a significant change in spike count.

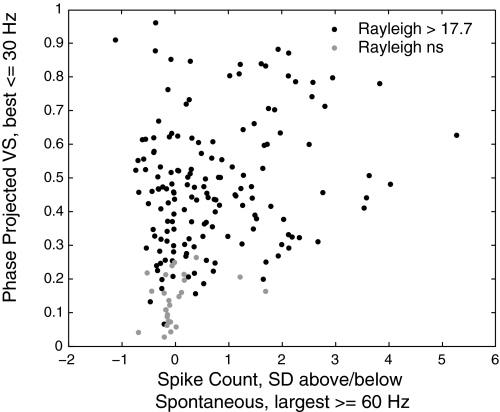
A previous study using click trains in marmosets (Lu et al. 2001) found that neurons segregated neatly into two categories based on phase locking at low modulation frequencies and SC at high modulation frequencies. This appears to differ from our finding of mixed synchronized/nonsynchronized responding neurons. To facilitate comparison with the previous study, we developed a metric similar to the one used there. In Fig. 6, we show the relationship between phase locking at low frequencies (best VS_PP ≤ 30 Hz) and a cell-normalized measure of firing rate at high frequencies (SDs above spontaneous firing rate, ≥ 60 Hz) for all 182 cells. Cells plotted in black showed significant phase locking for at least one modulation frequency (Rayleigh statistic >17.7, P < 0.001 after correction for 7 comparisons per cell), whereas those plotted in gray did not.

Fig. 6.

Scatter plot comparing temporal and rate response measures for synchronized and nonsynchronized cells. Cell spike count at high modulation frequencies (x axis) is plotted against a measure of synchrony at low modulation frequencies (best VS_PP ≤ 30 Hz, y axis). Cells with significant synchronization at low modulation frequencies (●) do not neatly segregate from cells without synchronization (○) at low modulation frequencies in terms of spike count activity at high modulation frequencies.

If our cells segregated into previously reported synchronized and nonsynchronized categories, we would expect the nonsynchronized cells (gray) to cluster in the lower right (weak phase locking at low modulation frequencies, increased firing at high modulation frequencies) and the synchronized cells (black) to cluster toward the upper left (strong phase locking at low modulation frequencies, low firing rates at high modulation frequencies) as they did in Fig. 3 from Lu et al. (2001). We do not see this pattern. In fact, only 2 of 54 cells that exhibited SCs >1 SD above spontaneous at the highest modulation frequencies did not also have significant phase locking at lower modulation frequencies.

Phase locking at high modulation frequencies

High-frequency phase-locking cutoffs decline in successive auditory stages. In Fig. 3B, we show a neuron that loses phase locking ability at high MFs but that simultaneously shows an increase in firing rate. Figure 7 plots two other cells that show a decrease in phase locking at high MFs with different rate profiles. Of the 121 neurons that showed decreased phase locking at the highest modulation frequencies, the majority (75) showed a concomitant decrease in SC (Table 1). In Fig. 7A, the neuron's firing rate is suppressed below spontaneous at 60 and 120 Hz, and the absence of firing results in a loss of phase locking. In the neuron in Fig. 7B, we see a sharp decline in phase locking between 30 and 60 Hz with no concomitant change in firing rate as if the neuron is being driven at the same rate but no longer is able to synchronize. These three modes of synchrony loss—increase of nonsynchronized activity, loss of activity, and desynchronization of activity—are suggestive of the idea that the gradual loss of synchrony at successive auditory stages is not merely due to the inability to follow a temporal envelope (e.g., due to accumulated temporal jitter in the inputs) but rather that the transformation from a temporal to a rate code may be due to multiple means of desynchronization at higher modulation frequencies.

Table 1.

Changes in phase locking and spike count measures at high modulation frequencies relative to low modulation frequencies

	VSPP
	Decrease	No Change	Increase	Total
SC decrease	75	24	1	100 (55)
SC no change	29	28	0	57 (31)
SC increase	17	8	0	25 (14)
Total	121 (66)	60 (33)	1 (1)	182 (100)

Values are in cell count. Two distributions of trial-by-trial phase-projected vector strength (VS_PP) and spike count (SC) were created for each cell, one that combined all the responses to high (≥60 Hz) modulation frequencies, and one that combined all the responses to low (≤30 Hz) modulation frequencies. The two distributions were compared using the false discovery rate method (Benjamini and Hochberg 1995) to determine how many cells exhibited an increase, decrease, or no change in each measure at high modulation frequencies relative to low modulation frequencies.

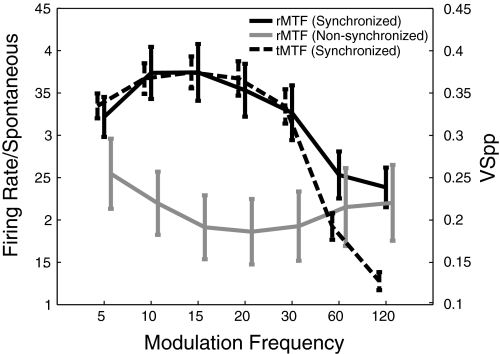
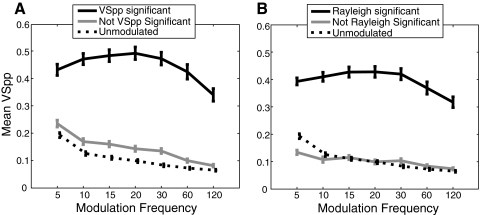
Regardless of the mode of synchrony loss, there is a large drop in the population mean vector strength (i.e., the mean of the vector strength values of each individual cell) in synchronized cells at 60 and 120 Hz. In Fig. 8, we plot the population mean rMTFs (in terms of firing rate normalized by spontaneous rate) for both synchronized (126 cells with significant phase locking as measured by VS_PP) and exclusively nonsynchronized cells (37), as well as the population mean tMTF for synchronized cells. The firing rate of synchronized cells is highly correlated with vector strength (r = 0.97), although at the higher modulation frequencies, phase locking declines more precipitously than firing rate, suggesting that there is a tendency for synchronizing cells to maintain a nonsynchronized response at modulation frequencies higher than they can reliably follow. For MFs between 10 and 30 Hz, the normalized firing rate of synchronized cells is greater than that of nonsynchronized cells (t-test, P < 0.05 in each case), but at high MFs, the normalized activity of the two populations becomes indistinguishable. It is notable that the nonsynchronized population shows the most activity at those modulation frequencies with the least synchrony (120, 60, and 5 Hz), but that relative to spontaneous the synchronized population fired more at all modulation frequencies.

Fig. 8.

Mean MTFs for synchronized and nonsynchronized cells. Left axis: mean firing rate, normalized to the spontaneous firing rate, for each cell (both rMTFs). Right axis: phase-projected vector strength (tMTF). Error bars indicate SE. MTFs are slightly offset on the x axis to improve readability.

A primary reason for the loss of population mean synchrony at high modulation frequencies is that many synchronizing cells lose synchrony as mentioned in the preceding text. Even so, we do see substantial phase-locked activity ≥60 Hz. Using VS_PP as the measure of phase locking, we found that 41 of our 182 neurons (23%) significantly phase locked to either 60 or 120 Hz stimuli: 21 cells which phase lock to 60 Hz but not 120 Hz, 7 cells that phase lock to 120 Hz but not to 60 Hz, and 13 cells that phase lock to both. If we use the more sensitive Rayleigh statistic (RS > 17.7), we find 56 cells (31%) with significant phase locking: 29 phase lock to 60 Hz, 7 phase lock to 120 Hz, and 20 phase lock to both. Figure 9 plots the population mean vector strength broken down by the presence or absence of synchrony at individual modulation frequencies. Although a drop in vector strength is present at high MFs, it is not as drastic as that seen in Fig. 8 when only cells that significantly synchronize at each MF are included, and the resulting vector strength remains substantially higher than that of the neurons that do not synchronize at the same MFs. For reference, the mean VS_PP is also shown for the unmodulated stimulus control (these values differ as a function of MF because the frequency used in the VS analysis differs at each point). It is clear from Fig. 9A that there is a small amount of synchronized activity that is not being picked up by our VS_PP measure because the not-significant VS_PP values are slightly greater than the unmodulated VS_PP control values. However, at MFs of ≥10 Hz, the RS (Fig. 9B) appears to capture all synchronous responses—the mean VS_PP of activity considered to be nonsynchronized is no different from that for the unmodulated control stimulus. However, at the lowest modulation frequency tested (5 Hz), the RS appears to overreach and produce false positives in identifying synchrony (VS_PP for unmodulated noise > VS_PP for non-Rayleigh significant).

Fig. 9.

Phase-projected vector strength values for synchronized and nonsynchronized responses. Left: significance determined by t-test of VS_PP distributions for modulated and unmodulated stimuli (P < 0.05, corrected for 7 comparisons per cell). Right: significance determined by Rayleigh statistic (RS > 17.7). All responses with significant phase locking are indicated in black. Responses without significant phase locking at a particular modulation frequency are indicated in gray (regardless of whether that cell showed phase-locked activity at another modulation frequency). VS_PP for the unmodulated response is included (dotted line). Error bars indicate SE. Unmodulated response is slightly offset on the x axis to improve readability of error bars.

The presence of synchronous firing does not indicate, however, that the cells are firing on every cycle (e.g., see Fig. 7). For the neuron of Fig. 7A, at 15 Hz there does not appear to be consistent phase locking to every cycle of modulation in the raster plots. Yet according to the tMTF (with VS and VS_PP), 15 Hz is this neuron's BMF. The high VS value at 15 Hz reflects the precision of spikes occurring within any cycle but not the reliability of firing for every cycle or every stimulus presentation. While for some cycles the response is quite reliable (see precise vertical aligning of spikes just shy of 200 ms into the stimulus), for the other cycles of modulation responses are often missing. However, when spikes are fired in these other cycles, they still are tightly vertically aligned; that is, when spikes occur, they fall in a narrow time window. To obtain high VS values precision within a cycle, rather than the ability to follow every cycle, is important. As a result, although the cell in Fig. 7A is more reliable in firing during each stimulus cycle to the 10 Hz stimulus, the number of spikes that occur at extraneous phases of the stimulus cycle results in a slight reduction in vector strength relative to the less reliable, but less noisy, firing evoked by the 15 Hz stimulus. To address this, we derived VS_CC, which requires cycle-by-cycle reliability to reach higher values (see methods). VS_CC is simply an average of the VS_PP calculated on a cycle-by-cycle basis with the assignment of 0 for any cycle with no spikes. The MTF for VS_CC is shown in light gray on the temporal MTF plot. In this example, VS_CC demonstrates a lower cutoff frequency than for vector strength proper.

Of the neurons that had significant VS_PP at 60 or 120 Hz, none had higher VS_CC than VS_PP. Furthermore, the neurons that show significance at 60 or 120 Hz show the largest drop in VS_CC relative to VS_PP (Table 2). This indicates that even the neurons that had high VS_PP values at 60 and 120 Hz had low reliability on a cycle-by-cycle basis. At 30 Hz and above fewer than half of the cycles across the synchronized population have synchronized activity (as seen by a drop of VS_CC to < ½ of VS_PP), dropping to fewer than one in six cycles (VS_CC/VS_PP <0.167) at 120 Hz, demonstrating that cycle-by-cycle reliability of firing drops off more quickly at high MFs than synchrony.

Table 2.

Change in phase locking vs. reliability as a function of modulation frequency

	No. of Cells	VSCC	VSPP	VSCC/VSPP	P
120 Hz	21	0.052	0.332	0.15	<10−13
60 Hz	35	0.103	0.424	0.24	<10−15
30 Hz	73	0.219	0.472	0.44	<10−13
20 Hz	80	0.276	0.487	0.57	<10−10
15 Hz	85	0.316	0.483	0.65	<10−7
10 Hz	85	0.358	0.477	0.75	<10−4
5 Hz	67	0.347	0.438	0.79	0.01

Average of trial-by-trial VS_PP (phase locking) and trial-by-trial cycle-by-cycle vector strength (VS_CC, reliability) for all combinations of cell and modulation frequency with significant phase locking as measured by VS_PP. The two distributions were compared using two-tailed t-tests (P < 0.05) to determine if mean reliability values were different than mean phase locking values.

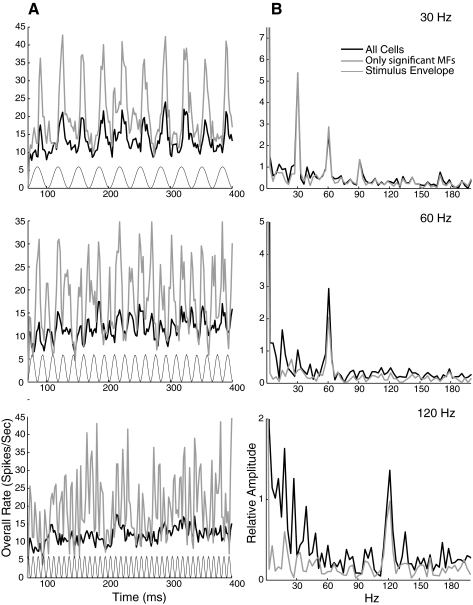
This loss of reliability while maintaining some measure of synchrony suggests that at higher modulation frequencies, a synchronized temporal code could potentially still be read out from the pooled activity of multiple synchronized neurons using volley principle coding. The volley principle hypothesizes that when one neuron misses firing in a cycle, other neurons fire on that cycle at the same phase, such that if you summed activity across neurons, every cycle could be followed. In Fig. 10, we investigate whether this could work in A1 for the higher modulation frequencies tested (30–120 Hz). Figure 10A plots a population-wide spike histogram for all cells (thick black line) and for only cells with significant synchrony at the given MF (gray line), with the representation of the stimulus envelope on the bottom for reference. Remarkably, synchronized activity is strong and coherent enough that the population spike histogram follows every envelope cycle at 60 Hz, even when nonsynchronizing cells are included. At 120 Hz this synchrony is less clear, but the FFT of the spike histogram (Fig. 10B, see methods) shows a clear peak at the stimulus modulation frequency for all three MFs, suggesting that extracting the dominant temporal frequency of the population spike train at the level of A1 can in general recover the modulation frequency of the stimulus, even when nonsynchronized cells are included.

Fig. 10.

Population phase locking at high modulation frequencies. A: spike histograms of overall response collapsed across cells (2 ms bins, 70 ms onset removed). All cells (thick black) and only cells that significantly phase locked at each MF (gray) are shown. The stimulus envelope (thin black) is provided for reference. B: Fourier transform of signals in A (see methods).

Synchrony and tonotopy

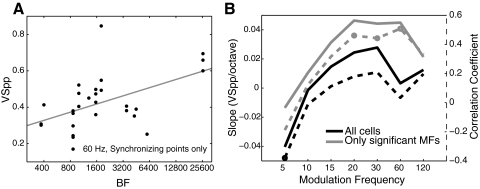
To investigate whether the degree of synchrony in a neuron is related to its BF, we performed a linear regression of the base-2 logarithm of BF with VS_PP for each modulation frequency, once using all neurons and separately using only those combinations of neuron and modulation frequency that were significantly synchronized using VS_PP. The modulation frequency with the highest overall correlation coefficient (r = 0.51) is shown as a scatter plot in Fig. 11A (60 Hz modulation, only neurons synchronizing to 60 Hz). Here we see a small but statistically significant trend (P = 0.006) for neurons with high BFs to synchronize better to 60 Hz modulation (slope of regression line = 0.045 VS_PP units octave). Figure 11B summarizes this relationship over the entire data set. When restricting the analysis to neurons that significantly phase locked at each modulation frequency, we find that neurons with higher BFs phase lock better than neurons with low BFs for a range of modulation frequencies between 20 and 60 Hz (dashed gray line). Over this range of modulation frequencies, phase-locking cells improve their phase locking by ∼0.04 VS_PP units/octave of BF. We do not see a similar trend when we look at all cells, where slopes are generally flat and correlation coefficients are near zero except for at the lowest modulation frequency tested (5 Hz), where cells with low BFs tended to phase lock better than cells with high BFs. Overall there appears to be a trend for high-BF cells to phase lock well to high MFs and for low-BF cells to phase lock better to low MFs, but it is weak enough that it is not evident in a topographic representation.

Fig. 11.

Relationship between BF and phase locking. A: scatter plot of BF against VS_PP at 60 Hz for all cells with significant phase locking at 60 Hz with regression line in gray (slope = 0.045 unit/octave). B, left axis: regression slope (solid lines) of BF against VS_PP at each tested modulation frequency for all cells (black) and only synchronizing points (gray). Right axis: correlation coefficient (dashed lines) of BF and VS_PP at each tested modulation frequency for all cells (black) and only synchronizing points (gray). Significant correlations (P < 0.05, Bonferroni corrected for 7 comparisons) are marked with circles.

DISCUSSION

Implications for neural coding of AM

CHOOSING THE CORRECT COMPARISONS.

By comparing responses to AM with responses to the unmodulated carrier, we have gained new insight into how cortex encodes temporal modulation. To evaluate how AM is encoded, it is important to choose appropriate stimuli for comparing responses. Usually, AM responses have been compared with spontaneous activity. This reveals whether the neuron can detect the presence of the sound versus no sound being present. It does not reveal whether the neuron detects the modulation.

Using synchrony measures such as VS or measuring MTFs can provide more information about modulation encoding. Because VS correlates the neural activity to the modulation frequency (known a priori), it reveals response properties linked to the modulation. MTFs by showing different responses to different MFs can also provide information about encoding MF.

In the present study, we use an additional approach by comparing AM responses to unmodulated carrier responses. This comparison tells us whether the neuron can distinguish a modulated from an unmodulated sound. This approach has been common in psychophysics (e.g., humans: Bacon and Viemeister 1985; Eddins 1999; Ewert and Dau 2004; Forrest and Green 1987; Viemeister 1979; animals: Kelly et al. 2006; Langemann and Klump 2007; O'Connor et al. 2000; Salvi et al. 1982) and to a lesser degree in modeling of neural responses (Lorenzi et al. 1995). Despite the psychophysical precedent, comparing AM to the unmodulated (or nearly unmodulated) carrier in neurophysiology is rare (Gleich and Klump 1995; Nelson and Carney 2007; Malone et al. 2007).

A novel result was obtained by comparing responsiveness to modulated and unmodulated sounds. Synchronized neurons encoded modulation with both decreases and increases in activity relative to the unmodulated noise carrier, but they primarily increased activity relative to spontaneous for encoding an event. The increase relative to spontaneous might suggest that the modulation causes increased activity. An observation of how synchronized neurons respond to the unmodulated carrier would suggest that this is incorrect. When presented by itself, the unmodulated carrier also evokes responses greater than spontaneous activity and rarely causes decreases relative to spontaneous in exclusively synchronized neurons. This suggests that the propensity for synchronized neurons to increase activity relative to spontaneous when using modulated stimuli does not reflect an effect of modulation but rather reflects how these neurons respond to the carrier. This insight would not be possible without incorporating the responses to the unmodulated carrier into the analysis.

NEURAL MULTIPLEXING IN A1.

Our data support the idea that A1 neurons are capable of carrying multiple signals with regard to AM. We reported numerous neurons with mixed-mode responses—synchronized responses at some modulation frequencies and nonsynchronized responses at others. Previously this response type has not been reported in large numbers in cortex. Inspection of earlier studies reveals that mixed-mode responses can be seen in the IC although they were not specifically pointed out (Krebs et al. 2008; Zheng and Escabí 2008). A recent study using periodic click trains in marmosets finds mixed-mode responses in thalamus but not in cortex (Bartlett and Wang 2007), which led to the conclusion that the segregation of synchronized and nonsynchronized neurons is an emergent cortical property. However, on inspecting a recent paper (Malone et al. 2007), we found data implicating mixed mode responders using AM-tones in A1 of macaques. Our data explicitly addresses this and suggests any synchrony to rate transformation should be completed further along the sensory pathway than A1.

Often mixed-mode responding neurons are nonsynchronized at higher modulation frequencies and synchronized at lower ones. This implies that the neurons carry separate signals for high and low modulation frequencies, which can be decoded by postsynaptic neurons. This leads to a picture of single A1 neurons carrying multiple signals and being involved in processing many sounds as opposed to being specialized tuned feature detectors.

In addition to carrying separate information in synchronized and nonsynchronized responses, neurons also might carry separate information more generally in temporal and rate codes. That there was no clear relationship between temporal and rate MTFs in this study argues that information about modulation frequency may be separately represented by two distinct codes. Relatively simple mechanisms can allow two different postsynaptic neurons to extract these two different types of information. The ability to represent different modulation frequencies with temporal, rate, and nonsynchronized codes suggests that at the level of A1 multiple codes are maintained, possibly to pass on to separate parallel pathways.

IMPLICATION OF BROAD MTFs ON NEURAL CODES.

The broad MTFs imply that A1 might not operate as an array of sharply tuned modulation frequency feature detectors creating a sparse MF code. Mean bandwidths overall were >2 octaves, indicating that beyond an octave on either side of the BMF, the responses are at least half as strong/synchronous. For the synchronous neurons, there are deeper implications. The broad tMTFs suggest that at any given MF, numerous neurons phase lock well. In addition it appears that many neurons are synchronously firing in phase with each other (Fig. 10). This means that the BMF might be far less of an important contributor to information about modulation than how well the population synchronizes. In such a scheme, neurons with the best phase locking, highest synchronized rate, and most coherence with the population will drive the encoding of the AM rather than necessarily those with the closest BMF to the stimulus. In other words, it might not be which neurons are firing (place code), but the frequency at which they are firing.

Quantification of phase locking and synchrony

RAYLEIGH STATISTIC.

In this study, we used VS_PP instead of the Rayleigh statistic as our preferred metric to statistically quantify phase locking. VS is a measure of effect size. The Rayleigh statistic, on the other hand, is a test statistic (i.e., a measure of statistical significance) that conveys how confident we are that a response is synchronized rather than how synchronized the response is. A cell with a low firing rate and strong synchrony can have the same Rayleigh value as a cell with a high firing rate and weak synchrony. We are more concerned with the degree of synchrony, so vector strength is a more appropriate measure.

A further potential problem with the Rayleigh statistic is its extreme sensitivity. Any temporal structure in the response, even if not locked to the modulation, can inflate the Rayleigh statistic under certain conditions. For example, onset responses are typically excluded from VS calculations because they can cause the Rayleigh statistic of an otherwise nonsynchronized response to become significant. At high MFs, this is less of a problem because the onset response is averaged over many stimulus cycles, but at lower MFs where there are fewer total cycles in the stimulus over which to average the onset response, the problem can be quite severe. Additionally, the responses to unmodulated sounds may exhibit temporal structure above and beyond simple onset responses. As an example, note the nononset temporal structure in the response to unmodulated noise in Fig. 3A. This structure may result either from sensitivity to the fine temporal structure of the stimulus or from a cell's inherent temporal pattern of firing. In our study, relatively short stimuli (400 ms) compared with some other studies could have allowed such structure to have a large influence on our Rayleigh statistic (RS) analysis. To quantify this, we calculated the RS of the responses to the unmodulated noise carrier for each modulation frequency used in our study. We found that 100/182 neurons had significant synchrony (Bonferroni corrected for 7 comparisons) in their responses to unmodulated control stimuli. Most of this effect was limited to lower modulation frequencies (5 Hz had 88 false positives, 10 Hz had 44 false positives; there was only 1 false positive at 120 Hz), and the consequences can be seen in Fig. 9B, where the mean VS_PP of non-Rayleigh-significant responses at 5 Hz is artificially lower than the mean VS_PP of the unmodulated control stimuli due to the removal of false positives from the pool of responses.

VECTOR STRENGTH.

While the RS is imperfect, limitations of measuring phase locking with VS have come to the forefront recently. As VS is calculated by creating a histogram with a period of the cycle of the modulation, it is maximal (VS = 1) if spikes occur at only one precise time in the cycle. However, if a given neuron has a broad temporal response or fires for both the rising and falling phase of AM (e.g., Malone et al. 2007), VS values will decrease dramatically. Some authors have introduced methods to try to work around these problems: Kajikawa and Hackett (2005) use an entropy-based analysis, Malone et al. (2007) calculate the correlations between modulation period histograms, and Kajikawa et al. (2008) use linear discriminant analysis. Because these focus more on general temporal coding than synchronization to the MF, these approaches were not used in this study. Another promising approach is an interspike interval analysis as performed by Imaizumi et al. (2010), but this may be more applicable to periodic click train analysis with discrete stimulus events rather than a continuous carrier.

In addition to this problem, VS does not lend itself well to trial-by-trial statistics because trials with low SCs can result in spuriously high values (for example, a trial with 1 spike will always yield a VS value of 1). To get around both the problem of low SCs and false positives with the RS, we compared the distributions of VS_PP between each modulated noise and the unmodulated carrier control. By projecting the VS of individual trials onto the population mean phase, the low SC problem goes away. The false positive problem for the Rayleigh statistic is resolved by comparing the distribution of VS_PP values evoked by modulated and unmodulated noise. By eliminating these two issues, we feel that VS_PP (rather than simply VS or RS without reference to the unmodulated response) gives us the best estimate of the number of cells that fire synchronously to our AM stimuli.

While VS (or VS_PP) provides a good metric of the temporal precision of a neuron's responses, it is not a good measure of how reliably the neuron fires to each cycle. Often in discussing results about VS, it is inadvertently implied that high VS results from the neuron accurately following the stimulus. This often leads to the misinterpretation that phase locking is limited to frequencies at which the neuron can follow the stimulus on a cycle-by-cycle basis. While it has long been known that cells can fire in proper phase while completely missing cycles (Wever 1949), this caveat is sometimes forgotten. A population of neurons can still reliably follow the modulation if different neurons fire all at the correct phase but in different cycles by a pooling principle called the volley principle. In this paper, we introduced cycle-by-cycle vector strength (VS_CC) to disentangle volley principle firing from reliable tracking of the modulation frequency. The results (Table 2, Fig. 9) indicate that at relatively low MFs, reliability (VS_CC) starts dropping off, yet a large number of neurons continue to phase lock. The population response (Fig. 10) shows synchronized activity to every cycle at 60 Hz, and the population FFT shows that even at 120 Hz, the population of neurons follows the MF. This suggests the volley principle is viable even at relatively high MFs and that across the population the synchronized neurons are generally in phase with each other.

AM sound perception

Human perception of AM sounds is complex. AM noise evokes a weak, nonspectral pitch percept that is strongest between MFs of ∼50–500 Hz (Burns and Viemeister 1976), while MFs below this typically lack pitch and are perceived as a “flutter” (Krumbholz et al. 2000), although other intermediate categories such as “roughness” are also reported (Fishman et al. 2000). The boundaries between these are subjective and difficult to define, highly variable between subjects and studies (Burns and Viemeister 1976), and the frequency range overlap for these perceptions is large. For animals, these boundaries are unavailable. In addition, spectral AM sensitivity in macaque is shifted to higher MFs than in humans (O'Connor et al. 2000), so any AM perceptual boundaries likely would not map directly to human boundaries. For these reasons, comparing responses in macaque A1 to the perception of pitch, roughness, and flutter is highly speculative. It has been suggested that in marmoset A1, exclusively nonsynchronized neurons underlie pitch perception and low MF synchronized neurons underlie flutter and that in the rostral field flutter is represented by low MF exclusively nonsynchronized neurons (Bendor and Wang 2007). Our data are somewhat at odds with this hypothesis as we see clear population-wide synchrony ≤120 Hz (the highest frequency we tested), well above the typically reported flutter/pitch boundary, and clear nonsynchronized activity at lower modulation frequencies in A1 (e.g., Figs, 2 and 10). This does not rule out the possibility that different response types underlie different perceptions, but suggests that other possibilities, such as synchronized neurons in A1 representing pitch, are viable.

Comparison to previous studies

CONTRIBUTING FACTORS TO CONFLICTING RESULTS.

A major aim of this paper is to move toward resolving the differing published results about the degree to which neurons synchronize to temporally modulated sounds in auditory cortex. We will focus on three papers that emphasize the amount of synchronized and nonsynchronized activity in A1 of awake monkeys: Lu et al. (2001) (Lu), Liang et al. (2002) (Liang), and Malone et al. (2007) (Malone). Throughout the discussion it will be important to remember that Lu reports the least synchrony and the most nonsynchronized responses while Malone reports the most synchrony and the fewest nonsynchronized responses. Experimental and analytical differences (Table 3) can lead to differing results. We believe the most relevant are the following: the stimuli, how synchronization is quantified, the recording location within the brain, biases in the sampling of neurons, the species studied, the range of modulation and durations of sounds used, and the age of the animals.

Table 3.

Comparison of AM studies, experimental and analysis parameters

	Lu et al. 2001	Liang et al. 2002	Malone et al. 2007	Yin et al. 2010, Rayleigh	Yin et al. 2010, VSPP
Stimulus	Click train	Tone AM	Tone AM	Noise AM	Noise AM
Definition of synchrony	Rayleigh>13.8 @10 Hz for BOTH first and last 450 ms	Rayleigh>13.8 @2 mod freqs	Rayleigh>13.8 @ 1 mod freq	Rayleigh>17.7 @ 1 mod freq	VSPP AM > VSPP carrier @ 1 mod freq
Frequency range, Hz	10–333	1–512	0.7–200	5–120	5–120
Duration, s	1	1	10	0.4	0.4
Onset removal, ms	100	100	None	70	70
Sound level, dB SPL	Best level	Best level	Best level	65	65
Species	Marmoset	Marmoset	Macaque	Macaque	Macaque
Cortical depth	Superficial	Superficial	All	All	All
Search stimuli	Spontaneous	Short tones	Short tones	Large battery	Large battery

Major parameters for three previous studies investigating AM in monkey cortex are compared with parameters in current study.

The definition of a synchronized response will greatly impact both the percentage of neurons that synchronize to AM and the percentage of exclusively nonsynchronized neurons. The more strictly synchronization is defined, the less likely it is that a neuron will be identified as synchronizing to AM and the more likely it is to find exclusively nonsynchronized neurons. The paper reporting the least synchronization and the largest proportion of exclusively nonsynchronized neurons (Lu) had a fairly stringent criterion requiring independent significant phase locking (RS > 13.8) for both the first and second half of a 10 Hz stimulus. The report having the most synchronization and fewest nonsynchronized responses (Malone) had the least strict criterion: RS > 13.8 for any one of nine frequencies. Our RS criterion falls somewhere between the two looking at seven modulation frequencies (with a Bonferroni correction), and our VS_PP criterion comparing modulated and unmodulated control responses is stricter than our RS criteria.

The stimuli used can have a large impact on the results. Lu (less synchrony) used broad- and narrow-band click trains. This detail is important because neurons are not only sensitive to the modulation/repetition rate but also to the amplitude envelope and duty cycle (Eggermont 1994, 2002; Heil 1997, 2001; Heil and Neubauer 2003; Krebs et al. 2008). The broad-band click trains were reported not to drive cortical cells well (Lu). The other studies, which reported more synchrony and stronger responses, used sinusoidal AM with tone (Liang, Malone) or noise carriers (present study).

In addition to the type of stimulus used, stimulus parameters can have a large impact. For example, studies extending their stimuli to lower modulation frequencies are more likely to report a high percentage of synchronization than studies that use only higher modulation frequencies. Malone had the lowest frequency tested (0.7 Hz), while Lu's range started at 10 Hz (which was the highest of all studies), and our study falls between. The highest modulation frequency can also influence the number of nonsynchronized responses seen because nonsynchronized responses are often associated with high modulation frequencies. The duration of the stimulation can also have an influence, particularly if RS is used. Shorter durations, because they have fewer cycles, are more likely to give false positive RS values (see rayleigh statistic). Longer stimuli (e.g., Malone uses 10 s stimuli) have the disadvantage that psychophysically, most temporal integration occurs over <1 s and therefore neural responses to stimuli longer than that are less comparable to psychophysical performance.

Neuronal sampling biases, the recording location within the brain, and the species and age of the subjects all might also contribute to the degree of synchrony and nonsynchronized responses. Of the studies being compared, those that targeted superficial layers of cortex (Lu, Liang) report less synchrony and more nonsynchronized responses than those that targeted all layers. However, the studies targeting superficial layers were in marmosets and those targeting all layers were in macaques. Also Lu searched for units based on spontaneous activity, Malone searched based on responses to the tonal carrier, and our study on a wide variety of sounds. Therefore the Malone study is the most likely to include neurons highly responsive to their stimuli, including low spontaneous neurons, whereas Lu is more likely to record from high spontaneous neurons that are less responsive to their stimuli. On a final note, AM sensitivity during development is influenced by age (Eggermont 1993), and a recent study by Recanzone (personal communication) has found that geriatric macaques have severely impaired phase locking to AM. Age is not a known factor for the current comparisons we are making but might be worth considering in the future.

PREVALENCE OF SYNCHRONY.

It is quite clear from this study that most A1 neurons synchronize to some modulation frequencies ≤120 Hz—69% of our cells show some synchrony as measured by phase-projected vector strength and 86% show the presence of synchrony using the more sensitive RS (with Bonferroni, Rayleigh > 17.7). Using SAM tones, Liang reports 64% of cells with Rayleigh values >13.8 for at least two modulation frequencies. Using the same criteria, 80% of our cells would be considered synchronized. Malone found ≥87% of neurons exceed a Rayleigh value of 13.8 for at least one modulation frequency. The number of synchronizing cells we found can be considered roughly similar to Malone and Liang when taking into account the different stringency in classification criteria.

In the first paper to define synchronized and nonsynchronized as two separate classes of neurons (Lu), a much smaller proportion of synchronized responses was found (36/190, 19%, Table 4). The conservative nature of Lu's quantification of synchrony seems to be one likely source of the differences between our results and theirs. Lu required neurons to have significant RS to the 10 Hz stimulus for both the first 450 ms and the last 450 ms to classify the neuron as synchronized. If we had used a longer stimulus and our neurons phase locked more weakly or stopped phase locking in the second half, by Lu's criteria these neurons would not be classified as synchronized, but by ours they would. The impact of using only one modulation frequency (10 Hz) can be further explored by reanalyzing our data. When we re-perform our analysis only using 10 Hz and Rayleigh (>13.8, P < 0.001), then the number of neurons with synchronized responses drops from 86 to 68%. A more dramatic effect is observed when we compare VS_PP values for modulated sounds versus unmodulated control sounds. Here significance goes from 69% with all frequencies and a Bonferroni correction to 42% using only 10 Hz (and no Bonferroni correction). Thus much of the difference in percentage of synchronized neurons reported could be due to neurons that synchronize to frequencies other than 10 Hz and Lu's stricter statistical criterion.

Table 4.

Comparison of AM studies, distribution of cell types

	Exclusively Nonsynchronized	Synchronized	Mixed Mode
Lu et al. (2001)	53*	19†	4†
Liang et al. (2002)	NR	64	NR
Malone et al. (2007)	2	87	16
VSPP, spike count vs. spontaneous	17	69	18
VSPP, spike count vs. unmodulated	20	69	36
Rayleigh, spike count vs. spontaneous	4	86	21
Rayleigh, spike count vs. unmodulated	7	86	44

Values are in percentage of total cells. NR, not reported.

^*Percentage of exclusively nonsynchronized neurons based on total of 94 neurons presented in the results; the 96 excluded neurons may have had nonsynchronized responses.

^†Percentage of neurons that synchronized to the click train is based on a total of 190 neurons reported in the methods; 96 of these neurons did not synchronize to 10 Hz click trains but were excluded from presentation in the results for other reasons.

We also find that the average strength of synchrony, particularly when only synchronized responses (rather than “synchronized” cells) are included (Fig. 9), only begins to drop off >60 Hz. Many (23%) of our cells exhibit significant phase locking ≥60 Hz using VS_PP. This cutoff is in line with other studies that used the RS in awake preparations [Malone, 36% phase lock >50 Hz; Liang, 25% >63.6 Hz Middlebrooks (2008), electrical stimulation SAM pulse train 42% phase lock ≥ 60 Hz; Lu, 26% >50 Hz; Ter-Mikaelian et al. (2007), ∼23% >50 Hz] but higher than studies using half height of synchronized rate [Fitzpatrick et al. (2009); 15% >64 Hz]. This is consistent with the notion that synchrony cutoff boundaries are sensitive to the measure used (Eggermont 1991) and anesthetic state (Anderson et al. 2006; Creutzfeldt et al. 1980; Fitzpatrick et al. 2009; Goldstein et al. 1959; Lu et al. 2001; Steinschneider et al. 1998; Ter-Mikaelian et al. 2007).

PROPORTION OF EXCLUSIVELY NONSYNCHRONIZED NEURONS.

There is some disagreement as to whether there are separate classes of synchronized and nonsynchronized neurons and the degree to which there is nonsynchronized activity in cortex. Lu reports a substantial number of exclusively nonsynchronized neurons (53%); Malone only finds 2%. This leads to two very different interpretations of how AM is encoded. Our data fall in between with 17% of neurons being classified as exclusively nonsynchronized when using VS_PP and comparing SCs to spontaneous.

However, in our opinion, it might be more informative to compare the nonsynchronized response to the response to the unmodulated carrier because the neurons could be responding in a sustained manner to the carrier and blind to the modulation. With this definition, we find 20% of neurons are exclusively nonsynchronized. It is possible that additional nonsynchronized responses would emerge >120 Hz in our sample, considering that ∼50% of the nonsynchronized neurons in Lu only appeared >100 Hz.

NONSYNCHRONIZED NEURONS VERSUS NONSYNCHRONIZED RESPONSES.

Previous studies (Lu, Liang) have suggested that a large majority of neurons in A1 fall into one of two well-separated classes, cells that exhibit synchronized responses to periodic stimuli and those that only exhibit nonsynchronized responses. The strongest argument for a categorical distinction between synchronized and nonsynchronized neurons in primate A1 may be found in Lu where the authors found two well-separated clusters of neurons. Synchronized neurons exhibited significant phase locking at 10 Hz and also fired more strongly <30 Hz than they did >200 Hz. Nonsynchronized neurons did not show significant phase locking ≤10 Hz and fired more strongly >200 Hz than <30 Hz. Only 9% of their neurons did not fall into one of these two categories. Notably, in the main results, it was reported that no cells fired more strongly at low modulation frequencies than at high without also showing significant phase locking at low modulation frequencies, although there is evidence for such neurons in the rostral fields of auditory cortex in a later paper (Bendor and Wang 2008).

While Lu found evidence for two classes of neurons, Malone failed to see such categories. We also do not see these distinct classes. In our data (Fig. 6), neurons with and without synchronized responses appear to lie on a continuum. There are several potential differences in our design that might account for this discrepancy. We used slightly different measures to quantify phase locking at low MFs and the relative strength of firing at high MFs. For instance, to measure phase locking, we used the largest temporal responses at modulation frequencies ≤30 Hz instead of only ≤10 Hz. Because there is often good synchrony ≤30 Hz, a 10 Hz cutoff may result in the misclassification of cells with some synchronized activity as nonsynchronized. Our analysis also included responses to 5 Hz, so neurons that only phase locked <10 Hz might also be captured in our experiments.

Another argument against two classes of neurons is the presence of mixed mode responders. We find up to 48% of neurons have synchronized responses at some modulation frequencies and nonsynchronized responses at others. Malone reports that 16% of neurons exhibited statistically significant increases in activity beyond their synchronization boundaries. These might correspond to our mixed-mode responders. Taken together the results suggest that in macaques it is probably better to talk about two types of responses (synchronized and nonsynchronized) rather than two different types of neurons, with different mixtures of these response types capable of existing within the same cell.

GRANTS

This work was funded by National Institute of Deafness and Other Communication Disorders Grants DC-02514 and T32 DC-008072.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).