Revealing the Kinematics of the Oculomotor Plant With Tertiary Eye Positions and Ocular Counterroll

Abstract

Retinal information is two-dimensional, whereas eye movements are three-dimensional. The oculomotor system solves this degrees-of-freedom problem by constraining eye positions to zero torsion (Listing's law) and determining how eye velocities change with eye position (half-angle rule). Here we test whether the oculomotor plant, in the absence of well-defined neural commands, can implement these constrains mechanically, not just in a primary position but for all eye and head orientations. We stimulated the abducens nerve at tertiary eye positions and when ocular counterroll was induced at tilted head orientations. Stimulation-induced eye velocities follow the half-angle rule, even for tertiary eye positions, and microstimulation at tilted head orientations elicits eye positions that adhere to torsionally shifted planes, similar to naturally occurring eye movements. These results support the notion that oculomotor plant can continuously apply these three-dimensional rules correctly and appropriately for all eye and head orientations that obey Listing's law, demonstrating a major role of peripheral biomechanics in motor control.

INTRODUCTION

Although incoming visual input is encoded in only two dimensions (i.e., the horizontal and vertical components on the retina), motor commands must control effectors such as the eye, head, and arm that rotate with three degrees of freedom. This third degree of freedom is often redundant since it can assume any value without changing the pointing direction of the effector (e.g., an eyeball that is spun around an axis emanating from the pupil remains pointing in the same direction). Experiments have shown that the third, torsional dimension is constrained (Helmholtz 1867; Tweed and Vilis 1987, 1990) and that these constraints are removed whenever appropriate (Crawford and Vilis 1991; Crawford et al. 1999; Misslisch et al. 1994). For eye movements, torsion is limited by Listing's law and the half-angle rule. The former states that eye positions have zero torsional components and are thus maintained in a planar range known as Listing's plane, whereas the latter holds that angular eye velocities must have nonzero torsional components such that they tilt out of Listing's plane according to the half-angle rule (Helmholtz 1867; Tweed and Vilis 1987, 1990; Tweed et al. 1990; see Klier et al. 2006, Fig. 1, A and B). These two constraints are necessarily related because, mathematically, for eye positions to lie in Listing's plane, eye velocities must tilt out of it in a position-related manner. However, is the implementation of these constraints dependent solely on neural mechanisms or is it delegated to peripheral biomechanics or a combination of both?

Fig. 1.

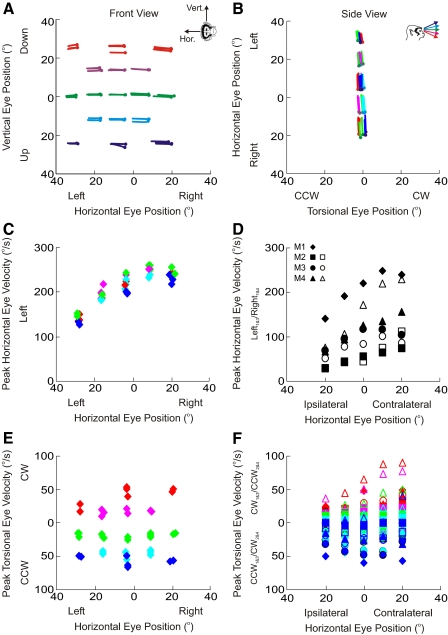
Properties of stimulation-induced eye movements. A and B: effects on eye position. Spatial plots of eye movements produced by left abducens nerve stimulation in one monkey (M1) from both front (A) and side (B) perspectives. The inset in A indicates the axes of rotation for horizontal and vertical eye movements according to the right-hand rule; the inset in B indicates color scheme for vertical eye positions (blue = 20° up; cyan = 10° up; green = center; magenta = 10° down; red = 20° down) and circles indicate initial eye position. Note that the small vertical eye-position–dependent changes in torsion seen in B are due to vergence-dependent changes in Listing's plane (Mok et al. 1992) (see methods). C and D: effects on horizontal eye velocity. Peak horizontal eye velocity for one monkey (C: data shown for each stimulation trial) and across all monkeys (D: data shown represent averages across all horizontal eye positions) is larger for contralateral than that for ipsilateral eye positions. E and F: effects on torsional eye position. Peak torsional eye velocity for one monkey (E: data shown for each stimulation trial) and across all monkeys (F: data shown represents averages across all trials at each horizontal/vertical eye position combination) has opposite signs, depending on vertical eye position. Note that to compare data across all animals, directions on the ordinate in D and F are monkey specific, depending on whether the left or right abducens nerve was stimulated. Different symbols are used to indicate the 4 monkeys (see inset in D). Three of the 4 monkeys had 2 data sets (filled and hollow symbols).

In a previous study, we showed that the half-angle rule, which helps constrain movement about the line of site, can be maintained even when the neural inputs are bypassed and stimulation is delivered directly to the abducens neurons or nerve (Klier et al. 2006). In addition, neural recordings from extraocular motoneurons have indicated that they encode the derivative of eye positions and not angular velocity, as would be necessary if they were to carry information vital to a neural implementation of the half-angle rule (Ghasia and Angelaki 2005). These results support the hypothesis that the oculomotor plant (i.e., the eye and its surrounding muscles and tissues) plays a critical role in implementing these torsional constraints.

Such a mechanical implementation of the half-angle rule has been suggested by a number of anatomical and theoretical studies (Demer 2004; Demer et al. 2000; Kono et al. 2002a; Miller 1989; Miller et al. 1993; Quaia and Optican 1998; Raphan 1998; see reviews in Angelaki and Hess 2004; Miller 2007). For example, in the most studied theory to date, the active pulley hypothesis, it is proposed that orbital pulleys, histologically identified connective tissue in the extraocular muscles, can effectively change the pulling direction of the eye muscles with changes in eye position such as to implement the three-dimensional kinematics of the eye. Indeed, visually guided eye movements such as saccades (Helmholtz 1867; Tweed and Vilis 1990), pursuit (Adeyemo and Angelaki 2005; Angelaki et al. 2003; Haslwanter et al. 1991; Tweed et al. 1992), and vergence (Van Rijn and Van den Berg 1993) obey Listing's law; other eye movements, however, such as the rotational vestibuloocular reflex (VOR) do not (Angelaki 2003; Angelaki et al. 2003; Crawford and Vilis 1991; Fetter et al. 1992).

However, the electrical stimulation studies by Klier et al. (2006) have only tested the half-angle rule with the eyes at primary and secondary positions. The picture becomes more complicated when the eye assumes tertiary positions (i.e., orientations with nonzero horizontal and vertical components) and with the introduction of ocular counterroll via whole-body tilt. The complexity arises by virtue of the introduction of a torsional component on the eye (either false [former] or real [latter]) and the ability of the plant to generate accurate three-dimensional eye movements in the presence of these added torsional components. In these situations, either 1) neural commands are needed as input to a fixed oculomotor plant, which are in turn responsible for maintaining the half-angle rule; 2) the oculomotor plant, guided by neural commands, actively changes its configuration with changes in eye position and thus the half-angle rule is still maintained (Crawford et al. 2003a,b; Demer and Clark 2005; Glasauer et al. 2001), or 3) there is a combination of these neural and mechanical changes. For example, during ocular counterrolling, gravitational cues detected by the otolith organs could be used to modify the physical position of the pulleys and realign the plant. Although evidence for such pulley reconfiguration has been observed anatomically and has been reported to be approximately half that of the induced ocular counterroll (Demer and Clark 2005; Demer et al. 2000; Kono et al. 2002a), ocular torsion was never directly measured in these studies and the effects were too small and thus hard to quantify.

In this study, by stimulating the abducens nerve while the eyes were oriented at various horizontal and vertical eye position combinations, we show for the first time that the half-angle rule is maintained at tertiary eye positions. We also characterize the stimulation-induced eye movements while statically tilting the animals in roll, either right ear down (i.e., clockwise [CW]) or left ear down (i.e., counterclockwise [CCW]). Static tilt induces an ocular counterroll that adds a torsional component to all static eye positions whose magnitude is roughly 10% of the static tilt angle (Haslwanter et al. 2002; Hess and Angelaki 1999). Characterization of these stimulation-evoked eye movements provides a snapshot of the configuration of the pulleys at the time of stimulation. We find that simulation-induced eye movements define a plane that is identical to the one defined by natural eye movements in tilted-head orientations—i.e., shifted torsionally away from Listing's plane in either the CW or CCW direction, opposite to the direction of roll tilt. These findings represent an important step toward understanding extraocular muscle mechanics, which in turn must be understood before we can grasp how the brain controls them. These results were previously presented in abstract form (Klier et al. 2009).

METHODS

Animals and setup

Four rhesus monkeys (Macaca mulatta) were chronically implanted with a delrin head ring that was attached to the skull via stainless steel or titanium screws and dental acrylic (Angelaki and Dickman 2000) to restrain the head during experiments. In a separate surgery, two scleral search coils, designed for recording three-dimensional (i.e., horizontal, vertical, and torsional) eye movements using the magnetic search coil technique (Judge 1980; Robinson 1963) were surgically implanted under the conjuctiva. The first coil was 15–17 mm in diameter and was sutured to the sclera posterior to the limbus corneae and anterior to the eye muscle insertions (Hess 1990), in a plane perpendicular to the line of sight. The second coil was about 2 mm in diameter and sutured to the sclera on the inferior surface of the globe, lateral to the inferior rectus muscle insertion (the exact orientation of this coil is less important, providing it is not coplanar with the first coil). After implantation, the larger, pericorneal coil was approximately aligned with the optic axis of the eye, thereby capable of measuring the direction of the line of sight (i.e., horizontal and vertical). The axis of the smaller coil was approximately in the plane of the larger coil, thereby measuring the torsion of the eye about the line of sight. These surgeries were performed under isoflurane anesthesia and sterile conditions and conformed to the guidelines provided by Washington University School of Medicine and the National Institutes of Health.

The monkeys sat such that their heads were in the center of three mutually orthogonal magnetic fields alternating at 60, 90, and 135 Hz (CNC Engineering, Seattle, WA) and the signals generated by the magnetic fields in the search coils were detected by three-axis phase-sensitive detectors (CNC Engineering). The magnetic field frame was mounted on a rotary motion platform (Acutronic, Pittsburgh, PA), capable of tilting the animal in roll (i.e., rotation about the nasooccipital axis). Because the magnetic fields are attached to the motion platform, the data herein reflect eye movements relative to the head. At the beginning of each experimental day, a calibration was performed in which the animals were required to fixate 13 computer-generated targets along the horizontal and vertical meridians (0, ±10, ±15, and ±20°). In addition, spontaneous eye movements were also recorded to measure Listing's plane and primary position (see Data analysis).

Experimental protocol

The abducens nucleus was identified by its characteristic burst-tonic activity during ipsilateral eye movements. Subsequently, the abducens nerve was found by searching for similar activity about 2 mm anterior, lateral and ventral to the abducens nucleus. The left abducens nerve was stimulated in monkeys M1 and M4, whereas the right abducens nerve was stimulated in monkeys M2 and M3. Note that eye movements were always recorded from the ipsilateral eye. Once identified, the following biphasic stimulation parameters were applied using a microelectrode via a bipolar stimulus isolator (FHC, Bowdoinham, ME): pulse duration = 0.2 ms, train duration = 50 ms, frequency = 500 Hz. Note that we chose these short-duration, high-frequency parameters to generate high-velocity movements with small displacements. The stimulation current, which never exceeded 50 μA (range: 9–50 μA), was determined by finding threshold current level and subsequently stimulating at 1.5-fold threshold. These are the parameters we used in a previous study (Klier et al. 2006) and they are comparable to parameters used in similar stimulation studies of the oculomotor nerve (Robinson 1968), trochlear nerve (Mays and Sparks 1983), and the abducens nucleus (Gandhi et al. 2008). Since microstimulation does not activate single neurons, but groups of neurons, we cannot speculate as to the number of orbital versus pulley or twitch versus nontwitch motoneurons that were activated. There is still debate over the existence of the former (Dimitrova et al. 2003) and there is no predicted effect on the half-angle rule with the latter (Buttner-Ennever et al. 2002, 2003).

Electrical microstimulations were applied as the monkeys fixated visual targets presented on a flat-screen monitor at a distance of 29 cm in front of them. The target array either consisted of a center target and additional targets at amplitudes of 10 and 20° in the cardinal and oblique directions, for a total of 17 targets (one animal, M1), or a 5 × 5 array of targets, each separated by 10° and spanning a 40° range both horizontally and vertically, for a total of 25 targets (three animals, M2–M4). These stimulations were applied when the animals were upright and also when they were statically tilted in roll: 45 and 90° CW (i.e., right ear down) and 45 and 90° CCW (i.e., left ear down). Fixation was determined automatically by monitoring the location of the monkeys' eyes relative to a theoretical window of 3 × 3°. On entering the fixation window the target was extinguished and the stimulation was delivered in darkness. A juice reward was given only after the stimulation-induced movement was complete. Stimulation at each target location was repeated three to five times. Stimulus presentation, juice delivery, and data acquisition were controlled with custom-written scripts in Spike2 (Cambridge Electronics Design [CED], Cambridge, UK) using a CED Power 1401 (CED). Data were antialias filtered (200 Hz, 6-pole Bessel) and then digitized by the CED at a rate of 833.33 Hz (16-bit resolution) and recorded on a computer for off-line analysis.

At each roll tilt position (including upright), eye movements were also recorded as the monkeys looked around naturally (i.e., without microstimulation). This was done by either looking around the experimental room as the experimenter encouraged the monkey to explore its entire oculomotor range (M1) or the targets in the 5 × 5 array were turned on randomly, one at a time, and the monkey was required to fixate each target, as it came on (M2–M4). These data were used to construct the natural eye-movement–defined planes at all different tilted orientations.

Data analysis

EYE POSITION ANALYSIS.

Raw eye coil signals were first calibrated (Klier et al. 2005) and converted into rotation vectors [E = tan (p/2)n, where n is the normalized axis about which the eye rotates from a chosen reference position to the current position and p is the angle of rotation about axis n]. These eye positions were first computed in magnetic field coordinates (using straight-ahead as the reference position), but then converted into Listing's coordinates (using primary position as the reference position). The transformation of data into Listing's coordinates was made using equations described previously (Haslwanter et al. 1992; Hess and Angelaki 1997a,b, 1999, 2003). Briefly, during every experimental day, a data file was collected in which the monkey made spontaneous movements in the light for a period of about 1.5 min with the head upright. According to Listing's law the computed eye position vectors are confined to a plane (Helmholtz 1867). This plane was fit using a least-squares algorithm according to the formula

$${\text{E}}_{\text{T}}=\text{a}+{\text{bE}}_{\text{V}}+{\text{cE}}_{\text{H}}$$

where E_T, E_V, and E_H are the torsional, vertical, and horizontal components of eye position E. Primary position was then determined from the plane parameters according to the equation: P = [a, c, −b]^t, where t is the transpose.

To convert data into Listing's coordinates, rotation vectors (E) corresponding to either natural or stimulation-induced eye movements were left-multiplied by the inverse of primary position P according to the formula: P⁻¹E = (P⁻¹ + E + P⁻¹ × E)/(1 − P⁻¹ ○ E), where × denotes the cross product and ○ denotes the scalar product. All eye movement data presented were processed in this way. Once the rotation vectors were converted into Listing's coordinates, we quantified how the eye-position–defined planes changed as a function of head orientation. For this, the plane equation was fit separately to naturally evoked and stimulation-evoked eye positions for each static head orientation. For stimulation trials, planes were fit only to the stimulation-induced eye movements whose onsets and offsets were determined by a velocity criteria: onset is when eye velocity exceeds 10°/s after the stimulation was delivered and offset is when eye velocity falls below 10°/s after stimulation onset. Note that whereas eye position planes were fit to visually guided and stimulation-evoked eye movements in all five static roll tilt orientations, primary position is defined only with the animal upright. Thus eye movements elicited from all roll tilt positions were converted into the same Listing's coordinates using rotation and shift values obtained from Listing's plane, as defined in the upright orientation.

For both the natural and stimulation-induced static roll tilt data, three parameters were measured for each plane fit and compared across the five different tilt angles. The “offset” parameter (a in Eq. 1) describes how the best-fit planes were shifted along the nasooccipital or torsional axis (e.g., Listing's plane with the head upright, by definition, has an offset of 0), the c parameter in Eq. 1 describes how the planes were tilted right or left (i.e., about the vertical axis), and the b parameter in Eq. 1 describes how the planes were tilted forward or backward (i.e., about the intraaural axis). Note that the “offset” value is expected to change significantly, and is therefore the value to focus on, when ocular counterroll is induced. Positive torsional offset values are expected when the animal is rotated CCW and negative values are expected when the animal is rotated CW.

Note that because the flat target screen was only 29 cm away from the monkeys' eyes, the vergence angle was about 6° (intraocular distance = 3 cm) during central target fixation and slightly decreased for targets in secondary and tertiary positions. Thus we observed the well-established pattern of eye torsion in which downward gaze causes the eyes to extort (i.e., CCW for the left eye and CW for the right eye), whereas upward gaze causes the eyes to intort (i.e., CW for the left eye and CCW for the right eye) (Mok et al. 1992) (see pattern in Fig. 1B for monkey M1 in which the left eye was recorded). This pattern was most obvious for contralateral eye positions, where the stimulation-induced eye movements were the largest.

EYE VELOCITY ANALYSIS.

To quantify the half-angle rule, Ė, the derivative of eye position, was first calculated (Ė = dE/dt), and angular eye velocity was then computed from eye velocity and eye position (Ω = 2/(Ė + E × Ė)/(1 + ⊻E⊻²). Once the components of angular velocity were computed in Listing's coordinates, plots of horizontal versus torsional eye velocity were constructed for each stimulation-induced eye movement. Linear fits (type II regression) were made to these eye velocity traces and only those fits with r² values >0.75 were included in further analysis (553 of 625, or 88%, movements were analyzed). The tilt (in degrees) of these regression lines from Listing's plane was then computed and these tilt angles were then plotted against initial vertical eye position. A second linear regression (type I regression) was subsequently fit to these data and the slope of this regression line served as our measure of the corresponding eye position dependence (i.e., half-angle rule). This analysis was conducted for the entire velocity loop (i.e., stimulation-induced and passive eye movement that returned the eye back to its starting position). As mentioned previously, the start of the velocity loop was determined by a velocity criterion, specifically when eye velocity exceeded 10°/s after the stimulation was delivered. Similarly, the end of the velocity loop was defined as the first time eye velocity decelerated under 10°/s.

RESULTS

Effects of abducens nerve stimulation at tertiary eye positions

Figure 1, A and B shows the effects of left abducens nerve stimulation on left eye position, for one animal (M1). Figure 1A shows the data from a front view, as if the observer was sitting in front of the monkey watching its eyes move, and the horizontal and vertical components of the eye movements are plotted along the abscissa and ordinate, respectively. Here eye position is illustrated as a virtual rotation about the horizontal/vertical axis according to the right-hand rule. Figure 1B shows the same data from a side view, where the narrow, torsional range of eye movements can be seen. Each trajectory reflects one stimulation-induced movement, the circles indicate initial eye positions, and each point along each trajectory indicates the evolution of the stimulation-evoked movement. Vertical eye eccentricities are color coded according to the inset of Fig. 1B. The various initial eye positions (circles) are plotted as rotation vectors in Listing's coordinates and include secondary horizontal positions (green), secondary vertical positions (centermost column), and tertiary positions (remaining circles along the diagonals).

The elicited trajectories are mainly horizontal and are directed ipsilaterally to the stimulation site (Robinson and Keller 1972; Skavenski and Robinson 1973). Notice that their amplitude, however, is larger when the animal looks to the contralateral side and smaller when the animal looks to the ipsilateral side (i.e., when initial eye position is to the left). This eye-position–dependent effect may be due to a saturation in motoneuron recruitment (i.e., all motor units are active such that electrical stimulation is less effective) and/or a physical limit on the oculomotor range (i.e., the eye can be moved only so far left when it is already looking to the left). The dependence of peak horizontal eye velocity on horizontal eye position for the same data set is demonstrated in Fig. 1C and averaged across all vertical eye positions for each animal in Fig. 1D (each animal is represented by a different symbol according to the inset in Fig. 1D). The velocities are greatest when the animal looks contralateral to the site of stimulation and smallest when the animal looks ipsilaterally. These differences in horizontal eye velocity as a function of eye position parallel the similar differences in stimulation-induced amplitude seen in Fig. 1, A and B.

Importantly, the stimulation-evoked eye velocity is not purely horizontal. As illustrated in Fig. 1E, when the animal looks down (red/magenta traces), the eyes have small CW torsional eye velocities, whereas when the animal looks up (blue/cyan traces), the eyes have small CCW torsional eye velocities. This pattern held for all animals (as illustrated in Fig. 1F; note that CW and CCW were reversed in the two animals in which we stimulated the right abducens nerve, since the expected torsional velocities are opposite in sign for the right eye). These vertical eye-position–dependent torsional eye velocities reflect what has been known as the half-angle rule. That is, depending on vertical eccentricity, eye velocity must tilt out of Listing's plane (zero torsion) to keep subsequent eye positions in Listing's plane (Tweed and Vilis 1990).

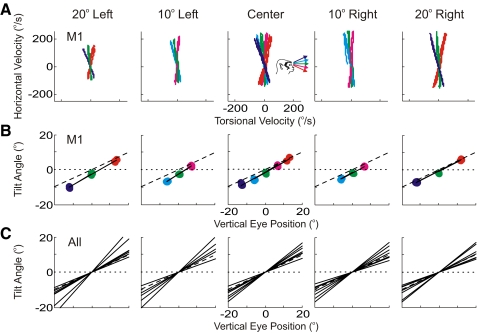
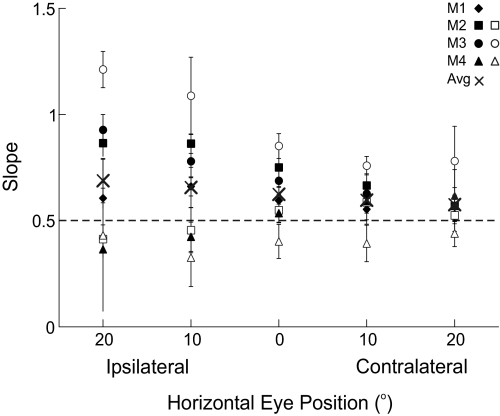
The half-angle rule was quantified for each stimulation-evoked eye movement in the following way: First, plots of stimulation-evoked horizontal eye velocity versus torsional eye velocity were made for different initial horizontal eye positions (Fig. 2A, animal M1). These loops represent changes in velocity from the start of the movement (i.e., when velocity exceeded 10°/s after stimulation onset) to the end of the movement (i.e., when velocity decreased below 10°/s after the start of the movement). The slopes of the regression lines fit to each of these loops indicate by how much angular velocity tilted out of Listing's plane for the particular horizontal/vertical initial eye position. These tilt angles were subsequently plotted as a function of vertical eye position, separately for each of the five horizontal eye positions (Fig. 2B, animal M1). The slopes of the regression lines fit to these data quantify the degree to which eye velocity tilts out of Listing's plane, thus constituting a measure of the half-angle rule. Regression lines are summarized across all horizontal eye positions, for all animals, and all days tested in Fig. 2C (also see Table 1). Note that the regression slopes are independent of horizontal eye position across all experimental days/animals [ANOVA, F(4,24) = 2.28, P = 0.09]. Since two animals were stimulated on the right and two animals were stimulated on the left, we collapsed the measures of the half-angle rule to either central fixation, ipsilateral fixation, or contralateral fixation (Fig. 3). Here one can see that measures of the half-angle rule were closest to 0.5 for contralateral eye positions and that this measure became more variable as initial eye positions became more ipsilateral, although this pattern was not significant (regression slope = 0.002, 95% confidence intervals = [−0.002, 0.008], P = 0.25). The increased variability in the half-angle rule for ipsilateral eye positions is likely explained by the fact that these movements are smaller in amplitude, have lower peak velocities, and are generally more variable (see Fig. 1).

Fig. 2.

Quantification of the half-angle rule. A: stimulation-induced velocity loops are first drawn by plotting horizontal vs. torsional eye velocity. Subsequently, these velocity loops are fit with regression lines and the angular tilt of these regression lines from a purely horizontal velocity is calculated (not shown). Inset (center) indicates color scheme for vertical eye positions (as in Fig. 1). B: tilt angles are plotted as a function of vertical eye position and the resulting slope (solid line) is the measure of the half-angle rule. The dotted line indicates a slope of 0, whereas the dashed line indicates a slope of 0.5 (i.e., the half-angle rule). A and B are corresponding data from one monkey (M1). C: the slopes from all 4 monkeys (3 of which were run twice for a total of 7 slopes) are shown. For illustrative purposes, all slopes are drawn through the origin.

Table 1.

The half-angle rule at different tertiary eye positions with the body upright

	Half-Angle Rule
Animal (Day)	20° Left	10° Left	0° (= Center)	10° Right	20° Right
M1 (1)	0.61 ± 0.05	0.66 ± 0.04	0.59 ± 0.06	0.55 ± 0.07	0.53 ± 0.05
M2 (1)	0.57 ± 0.03	0.67 ± 0.06	0.75 ± 0.09	0.86 ± 0.05	0.86 ± 0.06
M2 (2)	0.52 ± 0.07	0.59 ± 0.08	0.55 ± 0.06	0.45 ± 0.11	0.41 ± 0.07
M3 (1)	0.93 ± 0.07	0.78 ± 0.08	0.69 ± 0.06	0.63 ± 0.04	0.57 ± 0.05
M3 (2)	1.21 ± 0.09	1.09 ± 0.18	0.85 ± 0.06	0.76 ± 0.04	0.78 ± 0.16
M4 (1)	0.62 ± 0.12	0.59 ± 0.05	0.54 ± 0.04	0.42 ± 0.07	0.37 ± 0.04
M4 (2)	0.44 ± 0.06	0.39 ± 0.09	0.40 ± 0.08	0.33 ± 0.14	0.43 ± 0.36

Measures of the half-angle rule (±95% confidence intervals) (i.e., slope of regression fit to the data as in Fig. 2B), for all monkeys and days tested, at different horizontal eye positions. Values are given for each of the five horizontal eye displacements and the measures were made by taking stimulation data across the five vertical targets and each of the horizontal eye positions (except for M1 who had three vertical targets at the noncenter horizontal eye positions). Note that the left nerve was stimulated in animals M1 and M3, whereas the right nerve was stimulated in animals M2 and M4.

Fig. 3.

Measures of the half-angle rule (slope) for all animals, for each test day. The slope (type I regression; see methods) is defined by the tilt angle of eye velocity as a function of vertical eye position (see Fig. 2, B and C). Data are shown as a function of ipsilateral/contralateral eye position to compare the data across all 4 animals. Error bars indicate 95% confidence intervals. The × indicates the mean values for each horizontal eye position across all animals and the dashed line indicates a perfect half-angle rule. Values are closer to 0.5 and have less variability when horizontal eye position is contralateral to the stimulation site. This is likely explained by the fact that ipsilateral eye movements are smaller, slower, and thus more variable.

Effects of abducens nerve stimulation after static roll tilt

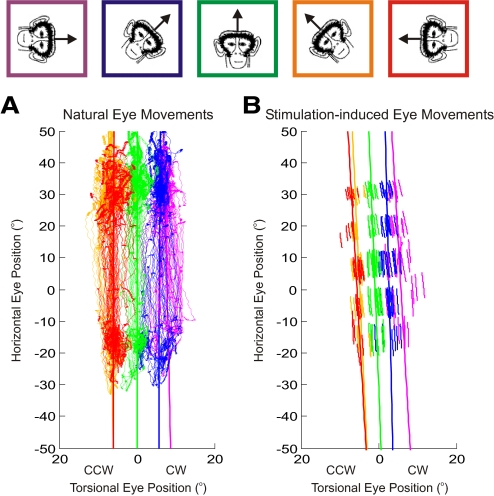
Statically tilting the monkeys induces ocular counterroll on the eyes and thus a tilt-dependent torsion is added to all eye positions (Haslwanter et al. 1992). We measured this torsion by having the animals make natural eye movements (see methods) while statically tilted in five positions, as shown for one monkey (M1) in Fig. 4A. The thin lines indicate the monkey's eye positions in Listing's coordinates, whereas the thicker near-vertical lines represent the best-fit planes to the data (both plotted in side views). Note that here the colors indicate the five static tilt positions: magenta = 90° CCW; blue = 45° CCW; green = 0° = upright; orange = 45° CW; red = 90° CW. In the upright condition (green trace), the best-fit plane is located exactly at 0° torsion since the values used to rotate the data into Listing's coordinates were taken from the natural eye movements when the animal was upright. The planes from the other tilted positions are either CW of 0° torsion (when the monkey was tilted CCW; blue and magenta traces) or CCW of 0° torsion (when the monkey was tilted CW; orange and red traces). These traces and best-fit planes served as our controls for the stimulation-induced eye movements.

Fig. 4.

Properties of eye-position–defined planes at different static roll tilt orientations of the head. A: planes defined from natural eye movements in which the monkey was encouraged to look around the entire oculomotor range. Fixations are indicated by areas of increased density. B: planes defined from stimulation-induced eye movements. Topmost panels indicate the color scheme for the 5 roll head orientations (magenta = 90° CCW; blue = 45° CCW; green = upright; orange = 45° CW; red = 90° CW). CCW, counterclockwise; CW, clockwise.

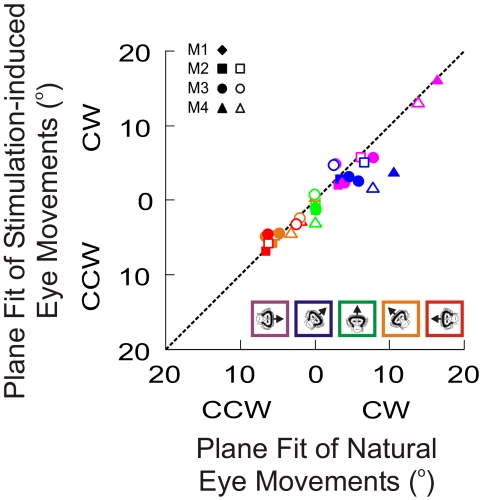
The stimulation-induced eye movements were also recorded at the five static tilt head orientations and best-fit planes were fit to them as well (Fig. 4B). On visual inspection, the stimulation-induced planes seemed to be shifted along the torsional dimension by approximately the same amount as the control, natural eye-movement–defined planes. This was quantified by comparing the respective torsional shifts of the plane fits (see methods), at each head orientation, across all animals as illustrated in Fig. 5. There was no significant difference in the torsional offsets of the two groups of planes (Wilcoxon rank-sum test, P = 0.63). The other two parameters of the plane fit (i.e., b and c in Eq. 1; data not shown) were small for both natural and stimulation-induced movements and also showed no statistically significant differences (Wilcoxon rank-sum tests, P ≫ 0.05). Thus the stimulation-evoked eye position planes are indistinguishable from those defined by natural eye movements at different static head orientations.

Fig. 5.

Torsional offset comparison of the fitted planes for stimulation-induced (ordinate) vs. natural (abscissa) eye movements for all 4 animals. Colored inset describes the roll head orientation for which each data point was collected. Different symbols are used for different animals/experiments (see inset). The dashed line indicates a slope of 1.

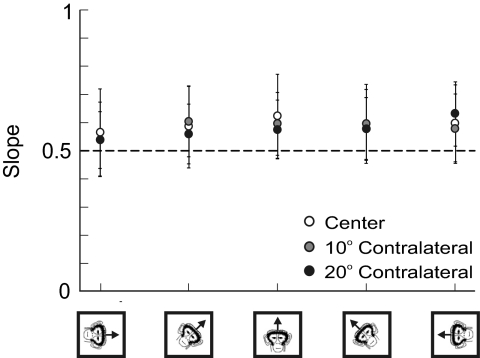
Finally, we examined the half-angle rule for the stimulation-induced eye movements at the various static tilt orientations (Fig. 6). Note that we report these values only for center (white circles), 10° contralateral (gray circles), and 20° contralateral (black circles) eye positions since ipsilateral eye positions produce variable measures of the half-angle rule due to their small amplitudes and velocities (Fig. 3). Across all animals and static tilt orientations, the average measures of the half-angle rule were 0.59 ± 0.14 for the center target, 0.58 ± 0.12 for the 10° contralateral targets, and 0.58 ± 0.11 for the 20° contralateral targets (see Table 2). There was no difference in the half-angle rule slope as a function of either horizontal eye position [ANOVA, F(2,89) = 0.63, P = 0.54] or static head orientation [ANOVA, F(4,89) = 2.12, P = 0.08].

Fig. 6.

Measures of the half-angle rule (slope) at different static roll tilt head orientations. Data (plotted only for contralateral stimulation sites) show mean (±SD) across all animals. The dashed line at 0.5 indicates a perfect half-angle rule. Data for center targets are in white, data for the 10° contralateral targets are in gray, and data for the 20° contralateral targets are in black.

Table 2.

The half-angle rule at different static tilt orientations

	Half-Angle Rule
Animal (Day)	90° CCW	45° CCW	0° (= Upright)	45° CW	90° CW
Center
M1 (1)	0.60 ± 0.04	0.60 ± 0.06	0.59 ± 0.06	0.57 ± 0.03	0.58 ± 0.04
M2 (1)	0.63 ± 0.10	0.67 ± 0.10	0.75 ± 0.09	0.73 ± 0.40	0.66 ± 0.11
M2 (2)	0.39 ± 0.09	0.46 ± 0.04	0.55 ± 0.06	0.49 ± 0.05	0.47 ± 0.04
M3 (1)	0.68 ± 0.05	0.67 ± 0.04	0.69 ± 0.06	0.70 ± 0.06	0.70 ± 0.05
M3 (2)	0.80 ± 0.08	0.82 ± 0.05	0.85 ± 0.06	0.79 ± 0.03	0.77 ± 0.06
M4 (1)	0.46 ± 0.04	0.48 ± 0.04	0.54 ± 0.04	0.50 ± 0.04	—
M4 (2)	0.40 ± 0.07	0.40 ± 0.06	0.40 ± 0.08	0.42 ± 0.02	0.41 ± 0.02
10° Contra
M1 (1)	0.54 ± 0.07	0.53 ± 0.14	0.55 ± 0.07	0.59 ± 0.04	0.59 ± 0.07
M2 (1)	0.52 ± 0.04	0.64 ± 0.06	0.67 ± 0.06	0.65 ± 0.17	0.60 ± 0.02
M2 (2)	0.43 ± 0.04	0.76 ± 0.41	0.59 ± 0.08	0.43 ± 0.14	0.48 ± 0.07
M3 (1)	0.57 ± 0.03	0.54 ± 0.06	0.63 ± 0.04	0.66 ± 0.04	0.65 ± 0.05
M3 (2)	0.73 ± 0.06	0.78 ± 0.07	0.76 ± 0.04	0.79 ± 0.05	0.76 ± 0.05
M4 (1)	0.55 ± 0.03	0.56 ± 0.07	0.59 ± 0.05	0.61 ± 0.09	—
M4 (2)	0.43 ± 0.05	0.43 ± 0.08	0.39 ± 0.09	0.44 ± 0.03	0.40 ± 0.05
20° Contra
M1 (1)	0.51 ± 0.13	0.51 ± 0.02	0.53 ± 0.05	0.56 ± 0.04	0.56 ± 0.12
M2 (1)	0.49 ± 0.03	0.49 ± 0.08	0.57 ± 0.03	0.48 ± 0.09	0.59 ± 0.02
M2 (2)	0.39 ± 0.03	0.45 ± 0.03	0.52 ± 0.07	0.49 ± 0.03	0.76 ± 0.56
M3 (1)	0.52 ± 0.04	0.55 ± 0.06	0.57 ± 0.05	0.66 ± 0.05	0.65 ± 0.03
M3 (2)	0.78 ± 0.14	0.74 ± 0.07	0.78 ± 0.16	0.77 ± 0.08	0.76 ± 0.05
M4 (1)	0.66 ± 0.09	0.68 ± 0.05	0.62 ± 0.12	0.63 ± 0.06	—
M4 (2)	0.45 ± 0.23	0.51 ± 0.08	0.44 ± 0.06	0.47 ± 0.04	0.47 ± 0.07

Mean values (±95 confidence intervals) of the half-angle rule at different static tilt orientations, shown separately for each animal and experimental session (1 or 2). Values are given at each of the five different roll orientations and the measures were made by taking stimulation data across the vertical targets at the respective horizontal eye position.

DISCUSSION

We have demonstrated that the oculomotor plant is capable of implementing the half-angle rule at different horizontal eye eccentricities, at tertiary eye positions, and even with induced ocular counterroll brought on by static roll tilt. These data provide further support for the role of the eye and its surrounding muscles and tissues in implementing three-dimensional kinematics (Klier et al. 2006). Thus we conclude that the biomechanics of the ocular plant are important for reducing the degrees of freedom problem, for saccades and for other types of eye movements driven by two-dimensional retinal signals, in a wide variety of situations.

Although our data cannot directly accept or refute any one particular theory of how the oculomotor plant implements three-dimensional kinematics, we will briefly examine how our data fall in line with the active pulley hypothesis (Demer et al. 1994, 1995; Miller 1989, 2007; Miller et al. 1993), which at present remains the most investigated theory for how the eye plant can generate the observed eye position dependence of eye velocity. Alternatives to the pulley hypothesis will also be discussed along with the role of neural signals in implementing appropriate three-dimensional rules. Finally, we will address eye movements that do not obey Listing's law or the half-angle rule.

The oculomotor plant

The pulley hypothesis has come a long way from its initial passive formulation (Miller 1989; Miller et al. 1993), in which eye muscles were free to slide through their associated pulley, which in turn was coupled to the orbital wall. This configuration allowed for limited implementation of Listing's law, making the eye rotations effectively commutative at secondary eye positions (Quaia and Optican 1998; Raphan 1998), but it could not function appropriately in tertiary eye positions (Miller 2007). The present findings clearly show that peripheral biomechanics can implement the half-angle rule even at tertiary eye orientations, a finding predicted by the active pulley hypothesis. According to this premise (Demer et al. 2000; Kono et al. 2002a), there are two distinct eye muscle types: 1) the global layer that inserts on the eye muscle tendon and moves the eye ball and 2) the orbital layer that connects to the collagen, elastin, and smooth muscle surrounding the eye and forms the oculomotor pulley (Kono et al. 2002b; Miller et al. 2003; Oh et al. 2001; Porter et al. 1995; Spencer and Porter 1998). These two muscle types have since been identified in several mammalian species (Demer 2004; Khanna and Porter 2001; Oh et al. 2001; Ruskell et al. 2005) and have been shown to have distinct patterns of innervation (Collins 1975; Demer et al. 1997, 2000).

Nonetheless, note that other studies have disputed this model in favor of those in which pulleys have only passive orbital properties (Dimitrova et al. 2003; Jampel and Shi 2006) and one in which the orbital muscle fibers do not innervate the pulleys themselves and thus they are solely dragged by virtue of their physical attachment (McClung et al. 2006). Previous models of the oculomotor plant incorporating active versus passive pulleys have found similar kinematic results irrespective of pulley motility (Quaia and Optican 1998, 2003) and so it seems that even fixed pulleys allow for changes in the axis of rotation since agonist/antagonist insertions retract/advance with changes in eye position. Moreover, some models have gone even further to claim that pulleys are not required at all (Schutte et al. 2006; van den Beden et al. 2005).

Neural inputs

Thus while the specifics of the oculomotor plant cannot be addressed by the current study, it is clear from these findings that its configuration must change for the half-angle rule to be implemented at different horizontal eccentricities. How are these changes implemented? Likely neural commands are responsible and these commands may be in the form of efference copies of eye position signals or from eye muscle proprioception (Wang et al. 2007). For example, palisade endings, which are found only in extraocular eye muscles and are present in all vertebrates, have been implicated in such a role (Eberhorn et al. 2005). Alternatively, information about eye position can arise from brain stem centers responsible for controlling eye position such as burst neurons, neural integrators, or the motoneurons themselves.

A second compelling argument for the necessity of neural signals is the preservation of appropriate ocular kinematics during static tilt. Since Listing's law and the half-angle rule are still maintained during ocular counterroll, this suggests that eye biomechanics receive information about the body's orientation relative to gravity from the otolith organs. Burst neuron firing has also been reported to be compatible with torsional shifts in the direction of ocular counterroll (Scherberger et al. 2001) and lesions of the vertical/torsional neural integrator have been shown to eliminate the shift in Listing's plane associated with ocular counterroll (Crawford et al. 2003). Our findings are consistent with the notion that rectus anatomy constitutes a half-angle gimbal that can be rotated about the torsional axis by the oblique muscles (Demer and Clark 2005).

Beyond a default strategy

It would be simple to design an eye with mechanical properties that consistently obeyed the half-angle rule—i.e., a half-angle rule gimbal whose orientation is under eye position and otolith control—and likely it is the default strategy of the plant to do so. However, not all eye movements adhere to Listing's law and the half-angle rule and thus additional neural inputs are likely required. For example, when the head is free to move and the vestibuloocular reflex (VOR) is activated, the eyes move in an equal but opposite direction to that of the head. So if the head rotates with a torsional component, the eyes must also rotate with a torsional component as well. This accumulation of torsion defies Listing's law and it has been demonstrated that the VOR obeys a quarter-angle (humans) or zero-angle (monkeys) rule instead of the half-angle rule (Angelaki 2003; Crawford and Vilis 1991; Fetter et al. 1992). For example, although some versions of the active pulley hypothesis have attempted to account for both the half-angle rule for saccades and the quarter-angle rule for the VOR (Kono et al. 2002a), none has been able to devise an acceptable pulley configuration that can satisfy both (Miller 2007; Misslisch and Tweed 2001). Thus for movements that do not exhibit a degrees of freedom problem (i.e., three-dimensional inputs and three-dimensional outputs), the default strategy must be overwritten by neural commands. How this is done remains unknown at present.

Listing's law and the half-angle rule are also temporarily, but necessarily, disobeyed during head-free gaze shifts. Since the eye has less inertia than the head, head-free gaze shifts can be broken down into two parts: the first in which the eyes move and land on the visual target and the second in which the eyes remain fixed on the target and the head catches up. Since the latter part requires that the eyes remain on target while the head continues to move, the VOR is turned on and thus the eye accumulates torsion due to the torsional components of head movement. However, since the eye-in-head obeys Listing's law, the overall torsion at the end of the gaze shift must be zero. To accomplish this, the brain generates an equal and opposite torsion during the first part of the gaze shift so that net ocular torsion is zero (Crawford et al. 1999). This intricate torsional dance must be generated at a higher neuronal level since the plant is not likely to have knowledge of the torsional components of the impending head movements. Where and how this is done also remain unknown at present.

An example that parallels this issue involves the control of torsional head movements. When the head is free to move, it obeys Donder's law—an extension of Listing's law in which torsion is allowed at various head positions (zero torsion when the head looks straight ahead, but accumulating torsion when oriented up/right, up/left, down/right, and down/left), but the same torsional values are expected for each head orientation irrespective of the trajectory the head took to reach that position. However, although there is zero torsion when looking straight ahead, one can choose to overwrite this zero torsional upright head position whenever desired by sending neural commands to the neck muscles, instructing them to bring the right ear to the right shoulder or the left ear to the left shoulder. Thus the basic default strategy of head control (i.e., Donder's law) can be overwritten by neural commands. Likely this same scenario is also true for the eyes.

Thus it appears that years of debate surrounding an extremely divisive subject have led to common ground—an intermediate strategy in which the brain circuits control an eye plant that is integral to implementing three-dimensional kinematics (Miller 2007; Smith and Crawford 1998; Tweed et al. 1994). So whereas the brain likely delivers neural commands to the eye muscles to 1) drive the plant to its correct orientations to implement the half-angle rule at tertiary eye positions and 2) control torsion for eye movements that do not obey the half-angle rule, the data in this study strongly support a default strategy for the plant such that, by realigning itself during changes in eye and head position, it can implement the half-angle rule. These findings demonstrate a remarkable ability of a motor plant to have a profound effect on an effector's kinematic constraints. Perhaps future studies will find similar constraints by neck muscles for head movements and the muscles of the limbs for arm and leg movements.

GRANTS

This study was supported by National Eye Institute Grant R01-EY-15271.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.