Transformation of Temporal Processing Across Auditory Cortex of Awake Macaques

Brian H Scott; Brian J Malone; Malcolm N Semple

doi:10.1152/jn.01120.2009

. 2010 Nov 24;105(2):712–730. doi: 10.1152/jn.01120.2009

Transformation of Temporal Processing Across Auditory Cortex of Awake Macaques

Brian H Scott ^1,^✉, Brian J Malone ¹, Malcolm N Semple ¹

PMCID: PMC3059172 PMID: 21106896

Abstract

The anatomy and connectivity of the primate auditory cortex has been modeled as a core region receiving direct thalamic input surrounded by a belt of secondary fields. The core contains multiple tonotopic fields (including the primary auditory cortex, AI, and the rostral field, R), but available data only partially address the degree to which those fields are functionally distinct. This report, based on single-unit recordings across four hemispheres in awake macaques, argues that the functional organization of auditory cortex is best understood in terms of temporal processing. Frequency tuning, response threshold, and strength of activation are similar between AI and R, validating their inclusion as a unified core, but the temporal properties of the fields clearly differ. Onset latencies to pure tones are longer in R (median, 33 ms) than in AI (20 ms); moreover, synchronization of spike discharges to dynamic modulations of stimulus amplitude and frequency, similar to those present in macaque and human vocalizations, suggest distinctly different windows of temporal integration in AI (20–30 ms) and R (100 ms). Incorporating data from the adjacent auditory belt reveals that the divergence of temporal properties within the core is in some cases greater than the temporal differences between core and belt.

INTRODUCTION

The prevailing model of auditory cortical organization in the macaque incorporates serial and parallel processing into a functional hierarchy (Kaas and Hackett 2000). Within the lateral sulcus, a central core region is the first stage of cortical processing, surrounded by a ring of secondary belt fields (Hackett et al. 1998; Jones et al. 1995; Pandya and Yeterian 1984). These hierarchical stages have been established on the basis of cytoarchitecture (Morel et al. 1993), differential thalamic projections (Hashikawa et al. 1995; Molinari et al. 1995), and selective interconnections among the cortical fields (Hackett et al. 1998). This core-belt layout, conserved to some degree across macaques, chimpanzees, and humans (Hackett et al. 2001), implies an analogous parceling of functional properties across auditory cortex.

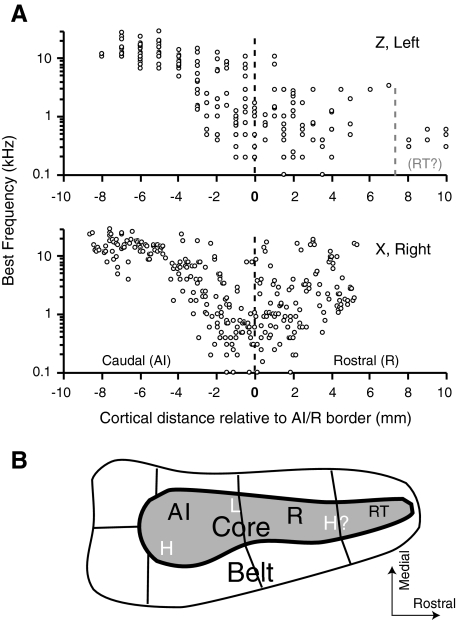
Physiologically, subdivisions of auditory cortex within the core are delimited by reversals of the tonotopic sequence—the ordered gradient of neurons' preferred frequencies across the cortical surface. Tonotopic order within the primary auditory cortex (AI) of the macaque monkey progresses from high to low frequencies moving from caudomedial to rostrolateral (Merzenich and Brugge 1973; Petkov et al. 2006). Transition into the rostral field (R) of the core is marked by a reversal as best frequencies reach their minimum and begin to rise again further rostrally, although this reversal may be incomplete. Multi-unit mapping in anesthetized macaques indicates either a partial representation favoring low frequencies (Merzenich and Brugge 1973) or a general breakdown of tonotopic order (Kosaki et al. 1997; Morel et al. 1993). In the awake macaque, Recanzone et al. (2000) produced maps of best frequency from single neurons, revealing a less precise tonotopic order within AI but demonstrating a reversal into R, as has since been confirmed (Kusmierek and Rauschecker 2009; Yin et al. 2008). The model of Hackett et al. (1998) depicts R as a core field spanning a low-frequency border with AI and a high-frequency border with a third, rostrotemporal field (RT; see Fig. 2B), yet there are few data from R to confirm its physiological properties.

Fig. 2. — The progression of BFs from high (caudal) to low (rostral) in primary auditory cortex (AI), and the reversal and degradation of that order in rostral field (R), are illustrated for the 2 most extensively sampled hemispheres. Only recordings from the core are represented, collapsed onto a single rostral-caudal axis aligned on the low-frequency border shared by AI and R (- - - at 0). For reference, a simplified diagram of the Kaas and Hackett (2000) model is shown in B with the proposed high (H) and low (L) frequency borders indicated.

The anatomical distinction between core and belt has been reported to manifest physiologically as diminished selectivity for pure tones and an emerging preference for stimuli of broader spectral bandwidth (Kusmierek and Rauschecker 2009; Rauschecker et al. 1995; Recanzone et al. 2000). Recordings from R and caudomedial belt (CM) before and after removal of AI revealed that responses to tones in R persisted in the absence of AI, whereas tone responses in CM were abolished (Rauschecker et al. 1997), implying that AI and R receive thalamic input in parallel (although not ruling out an additional serial projection from AI to R). By contrast, belt areas appear to be dependent on a serial cascade of auditory input from the primary auditory nucleus of the thalamus, via the cortical core, as suggested by the anatomy.

Evidence of parallel input bolsters the theory that AI and R share an equivalent level in the anatomical hierarchy, but it does not address the issue of how the neurons of these two fields operate in time. The onset latency of responses in R has been shown to be longer than that in AI (Kusmierek and Rauschecker 2009; Recanzone et al. 2000), but it is unclear whether R contains an identical, but delayed, version of the information in AI or represents an additional stage of temporal processing. This issue has been the topic of recent work in the marmoset, a New World primate, in which the acuity of temporal processing has been shown to diminish at more rostral stations of the core (Bendor and Wang 2007, 2008), expanding on an earlier finding in squirrel monkey (Bieser and Muller-Preuss 1996). It is not yet known whether Old World primates, including macaques and humans, share this graded temporal acuity across the auditory cortical fields. This report will explore the basic physiological properties of AI and R in the macaque and evaluate the extent to which they should be considered as a unified core. If R is engaged in temporal filtering on a longer time scale than AI, neurons there should not only possess longer onset latencies but exhibit different temporal characteristics in response to modulated stimuli.

METHODS

General methods of animal training, stimulus delivery, and physiological recording have been described previously (Malone et al. 2002, 2007; Scott et al. 2007). Subjects were two male rhesus macaques (designated animals X and Z) trained on an acoustic task but sitting passively during collection of the data presented here. All procedures were in accordance with the Society for Neuroscience guiding principles on the care and use of animals and were approved by the Institutional Animal Care and Use Committee of New York University. Animals were monitored by video as they sat in a custom chair (Crist, Hagerstown, MD) inside a double-walled anechoic room (IAC, Bronx, NY) with their heads fixed in position.

Stimuli were generated digitally (MALab software and hardware) and presented in the closed field via electrostatic speakers coupled to ear inserts. Phase and level at each ear were calibrated across frequency at the start of each session using a 1/2-in probe microphone (Brüel and Kjær 4133).

A stainless steel recording chamber 16 mm in diameter was implanted over auditory cortex in each animal using standard sterile surgical techniques. Tungsten microelectrodes (10–12 MΩ, FHC, Bowdoin, ME) were advanced with a stepping microdrive, in a vertical approach (Pfingst and O'Connor 1980). A search stimulus, optimized audiovisually for the local cortical population, was used to identify single units. Spikes from single neurons were selected using voltage/time windows, and waveforms were monitored for consistency throughout the recording; spike times were logged at a precision of 1 μs, and responses were displayed on-line using the MaLab software and event processor.

Recording sites

In animal Z, initial placement of the chamber over the left hemisphere was too far rostral to capture most of AI; after surveying the responsive area, the chamber was moved caudally to allow overlapping coverage of the full extent of auditory cortex (Fig. 3, bottom left). The two maps were co-registered using the known distance of the chamber relocation so as to align the tonotopic gradients of each map. After mapping the extent of auditory cortex available within the recording chamber over the left hemisphere in each animal, the chamber was transplanted to the right, allowing a total of four hemispheres to be sampled. In one chamber placement (animal X, right hemisphere), the angle of electrode advance was not quite vertical, so deeper sites within a track were also slightly more rostral. These recording sites were corrected for that angle to more accurately project each neuron's location onto a two-dimensional map.

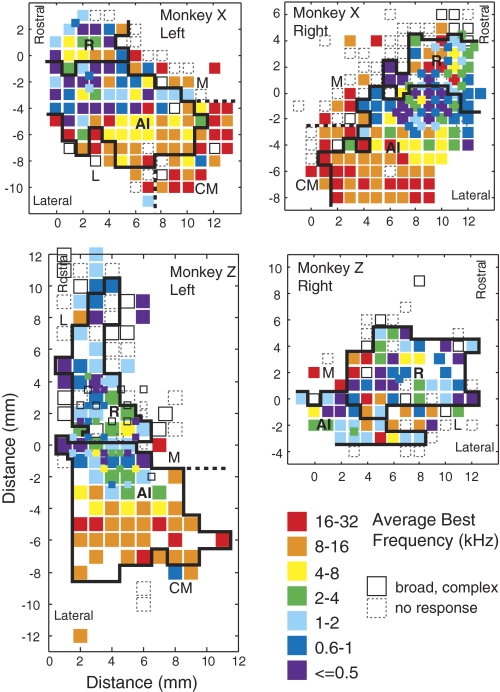
Fig. 3. — Maps of BF from the left and right hemispheres of *monkeys X* (*top*) and Z (*bottom*). Rostral is up in all panels; medial is toward the midline of the figure. Axes are in mm, relative to the AI/R border. The BFs encountered within each penetration are averaged to assign each site to an octave bin, color coded from violet (low) to red (high). Open squares, sites of auditory responsiveness but no clear BF; dashed squares, sites from which no auditory response could be evoked. Sampling was generally in a 1 mm grid, but in the right hemisphere of *animal X* and the left hemisphere of *animal Z* (*top right* and *bottom left*), the low-frequency area was sampled at a finer 0.5 mm grain—for clarity, smaller squares mark these sites. Each site was assigned to AI, R, or the belt (see text), as delineated by the heavy black lines; dashed lines separate the fields of the belt.

After completion of the physiological survey in the right hemisphere of monkey X, electrolytic lesions were placed at four points in the chamber using an electrode coated in fluorescent dye (Di I) (DiCarlo et al. 1996). Later that day, the animal was deeply anesthetized by an intravenous injection of sodium pentobarbital, then transcardially perfused. The brain was postfixed without being removed from the skull, allowing the acquisition of magnetic resonance imaging (MRI) images postmortem. The following day, the tissue was blocked and vibratome-sectioned at a thickness of 50 μm. Alternate sections were stained for Nissl substance or immunoreacted for cytochrome oxidase (CO), a metabolic enzyme previously shown to mark core auditory cortex (Hackett et al. 2001; Jones et al. 1995; Morel et al. 1993). Subsequent histology on animal Z also accords with the assignment of cortical fields described in the following text.

Basic response properties of auditory cortex

FREQUENCY TUNING.

Before quantitative data were collected, audiovisual testing was used to determine the approximate receptive field of the cell in frequency. Tones were used if they were effective; otherwise, a band-passed noise was presented, and the center frequency of that band was roved to find the appropriate range (bandwidth typically was 1/3 octave). Quantitative assessment of frequency tuning was carried out using tones in 90% of cases; the remaining data are based on the center frequency of band-passed noise (6%) or the carrier frequency of an amplitude-modulated tone (4%). These tests were performed binaurally, but if the binaural response was poor, the contra- and ipsilateral ears were tried individually. The vast majority of cells responded well to binaural stimulation (Scott et al. 2007), and 94% of all frequency tuning functions (FTFs) were constructed using diotic stimuli. Sound pressure level (in dB SPL) was also varied to ensure that a nonmonotonic or high-threshold cell was not dismissed as unresponsive. If a response appeared to be monotonic, the FTF was collected at 60 dB. In cells with strongly nonmonotonic responses, the audiovisually determined best SPL was used.

A set of frequency points was chosen individually for each unit to capture the full extent of its receptive field, and because tuning in the core can be quite sharp, extra resolution was used near the apparent best frequency (BF). Stimuli were pure tones, 100 ms long with a 5-ms cosine-squared ramp, presented every 1,000 ms for 10 trials per frequency point in blocks by frequency. The standard measure for assigning BF was maximal spike rate measured in a 100-ms window starting at tone onset. For neurons exhibiting only suppressive responses, the frequency eliciting the minimal spike rate (strongest suppression) was taken as BF. Tuning width was measured as the width at half-maximum of the linearly interpolated FTF divided by BF.

RATE-LEVEL FUNCTIONS.

Tuning for sound intensity was assessed by a rate-level function (RLF). Tones at BF were presented binaurally in blocks by SPL (from low to high). Threshold was defined as the lowest SPL at which spike rate was significantly different from spontaneous rate pooled across all SPLs by a Wilcoxon rank-sum test (P < 0.05/n, where n = number of tested SPLs). Best level (BL) was the SPL eliciting the greatest firing rate, if that firing rate was significant (by the Wilcoxon test in the preceding text) and the effect of SPL on firing rate was significant by a nonparametric one-way ANOVA (Kruskal-Wallis test, P < 0.05). The shape of the RLF was summarized by the ratio of the firing rate at BL to the firing rate at the highest SPL tested (usually 80 dB); this monotonicity index (MI) would be one for a monotonic function or zero for a fully suppressed response at high SPL (Pfingst and O'Connor 1981; Sadagopan and Wang 2008).

RESPONSE LATENCY.

Minimum latency was measured only for neurons from which a full RLF was obtained. Spikes at each SPL were binned at 1-ms resolution and convolved with a kernel to generate a smoothed spike-density function. The kernel applied was an exponential function similar in shape to an excitatory postsynaptic potential (Thompson et al. 1996) comparable with that employed by Kusmierek and Rauschecker (2009). Latency was defined as the time at which the density function exceeded mean +2 SD of the spontaneous activity. Latency was measured at each SPL in the RLF, and the shortest value taken as the minimum latency of the unit. At this same SPL, the peak of the density function (at any time between the latency and tone offset) identified the peak latency of the unit.

To ensure that latencies in this report are comparable to published data, a second procedure was applied in addition to the spike-density method described in the preceding text. The poststimulus time histogram (PSTH) method defined a driven response to a given SPL as one that exceeds mean +2 SD. All driven responses were pooled together, and spike times binned at a resolution of 2 ms. Latency was assigned as the first of three consecutive bins in which the spike rate exceeded mean +2 SD measured within each 2-ms bin (Recanzone et al. 2000). To lessen spurious results in neurons with spontaneous rates near zero, the first bin was required to contain at least two spikes and the second and third bins at least one spike (Bendor and Wang 2008). Latencies determined by these two methods differed in median by only 1 ms, and comparisons between cortical fields were not affected. All data described herein were obtained with the spike-density method.

DISCHARGE RATES AND RELIABILITY.

From each recorded cell, spontaneous discharge rate was measured using a 500-ms window over the second half of the 1,000-ms trial used to obtain the FTF; this generated one estimate at each frequency point, and these estimates were averaged. The peak discharge rate for each cell was measured over a 100-ms window positioned to include the peak of the strongest response in the FTF or RLF and represents the firing rate in response to a pure tone at optimal frequency and level. These same responses were also used to measure the variance of spike count across trials and the degree of adaptation in spike count over repeated trials (measured as the ratio of mean spike count in the last 5 trials, to mean spike count in the 1st 5 trials).

To measure the reliability of spike timing in each neuron's response across repeated presentations of a BF tone, we employed a correlation-based measure (Huetz et al. 2009; Schreiber et al. 2003). The spike train obtained from each stimulus presentation was convolved with a Gaussian filter (sigma = 10 ms, although values from 1 to 20 ms were tried with similar results). The correlation (inner product) was taken between all pairs of trials, each divided by the vector norms of the two trials. The reliability, Rcorr, is the average of all these values, and ranges from zero (no correlation) to one (highly reliable spike timing).

Amplitude- and frequency-modulated stimuli

In addition to short-duration static tones, modulations of amplitude and frequency were applied to probe the temporal filtering properties of cortical neurons. Sinusoidal AM (SAM) stimuli are defined by a tone of a given carrier frequency (f_c) modulated sinusoidally by a given modulation frequency (f_m), such that

S (t) = A [1 + m * \sin (2 π f_{m} t)] \sin (2 π f_{c} t)

where the bracketed term defines the time-varying amplitude of the stimulus (if f_c ≫ f_m). The base amplitude of the stimulus is set by A, and the depth of the modulation is determined by m (all data in this report were collected at m = 1, i.e., 100% modulation). Neurons were presented with SAM at a range of modulation frequencies (typically 0.7, 1, 2, 5, 10, 20, 50, 100, and 200 Hz) in blocks from low to high; higher frequencies were added if necessary to find the limit of discharge synchrony (described in the following text), and intermediate values could be added for greater resolution within a selected range.

Sinusoidal FM (SFM) is also defined by a sinusoidal carrier (f_c), the frequency of which is modulated at a rate determined by f_m

S (t) = A * \sin [f_{c} t - m * \sin (f_{m} t)]

As with SAM, A defines the amplitude (which remains constant within the bound of calibration error) and m defines the depth (maximum deviation of the modulated frequency from the carrier). The same carrier frequency and SPL that were used for SAM modulation transfer functions (MTFs) were used to measure SFM MTFs, to ensure the compatibility of measures derived from these functions within each cell. FM depth was manipulated on-line to maximize both discharge rate and synchrony. Modulation frequencies covered the same range (0.5–200 Hz) used for SAM.

Modulated stimuli were first presented using the neuron's BF (f_c = BF), and best level (A = peak of RLF). For cells with monotonic RLFs, or those with indeterminate best levels, A = 60 dB was used. Modulated tones, including a 0-Hz control, were presented in two long consecutive trials of 10 s separated by a 2-s interstimulus interval, using a rise time of 10 ms (cosine-squared ramp). Unless one ear obviously inhibited the response, stimuli were delivered binaurally (92% of cells). Long stimulus durations were chosen to minimize the effects of onset responses while maximizing the number of modulation periods. The SAM data collected in AI have been described previously (Malone et al. 2007, 2010).

ANALYSIS OF SAM AND SFM.

Responses to SAM and SFM were measured in terms of rate and temporal coding. Calculations of spike rate in response to SAM and SFM are based on the entire stimulus duration (10 s). To evaluate the significance of differences in average firing rate, responses were broken into 1-s epochs, and the average firing rate (across repeated trials) was calculated for each. Significance was assessed for all comparisons by a heteroschedastic t-test (P < 0.01). Calculation of spontaneous rate was based on firing rates for 1-s epochs drawn from all interstimulus intervals. Response synchronization was quantified in terms of vector strength (VS) (Goldberg and Brown 1969). To assess the statistical significance of VS, the Rayleigh statistic (2*VS²*n) was computed, and values >13.816 (Mardia 2000) were considered to be significant at P < 0.001.

The temporal filtering properties of a neuron can be summarized as a MTF, which represents some measure of a neuron's response as a function of modulation frequency. Two types of MTF were constructed from the responses of each neuron for both SAM and SFM. The rate MTF (rMTF) was defined by discharge rate as a function of modulation frequency. The peak of this function identifies the rate-based best modulation frequency (rBMF), taken to be significant if the spike rate at that modulation frequency was significantly greater than at least two other points in the function by a heteroschedastic t-test (P < 0.01) (Liang et al. 2002; Malone et al. 2007). An alternate metric computed the rBMF as the geometric mean of all frequency values at which the discharge rate was statistically indistinguishable from the peak (cf. Bendor and Wang 2008; Liang et al. 2002); similar results were obtained, so only the former rBMF is reported here. The shape of the rMTF tended to be band-pass, with maximal discharge rate at an intermediate frequency, and lower discharge rates at high and low frequencies. A rMTF was categorized as band-pass if its peak was at an intermediate frequency value, and the d′ statistic of the peak firing rate was ≥1 (Liang et al. 2002). d′ was calculated as

d' = (R_{driven} - R_{spon}) / σ_{spon}

where R_driven and R_spon are the driven and spontaneous discharge rates and σ_spon is the SD of the spontaneous rate.

Analogously, the temporal MTF (tMTF) plots synchrony (VS) against modulation frequency, and the peak of this function (if synchrony is significant) identifies the tBMF. To determine the upper limit of temporal synchrony, a point was interpolated from the tMTF by fitting a line between the Rayleigh statistic at the highest modulation frequency showing significant synchrony, and the value at the next (higher) frequency. The point where this line crossed the Rayleigh significance threshold was taken as the synchrony cutoff (Liang et al. 2002). With the carrier frequency at the neuron's BF, SFM will pass through the cell's receptive field twice per cycle, which may cause frequency doubling in the response. To avoid missing a synchronized response, VS was measured at the full modulation period and at half the modulation period; the higher of the two synchrony cutoffs was taken, and the higher VS value was used to identify the tBMF.

Statistics and pooling of data sets

Before pooling data across hemispheres or animals in the analyses in the following text, a four-way comparison was made to check that no data set was significantly different from those it was pooled with. To control for multiple tests, the Tukey-Kramer “honestly significant difference” test was used (JMP statistical software, SAS). The only manner in which the four hemispheres differed significantly was the mean BF encountered, but this can be attributed to sampling differences stemming from the placement of the recording chamber in each animal. Because relatively few neurons were sampled from belt (and not every belt region was sampled in each hemisphere), these data were pooled to provide enough statistical power for comparison with the core fields.

For continuous variables, comparisons of median values between AI and R used the nonparametric Wilcoxon rank-sum test unless otherwise stated; a two-sample Kolmogorov-Smirnov test was applied to detect changes in distribution shape as opposed to a shift in median. Fisher's exact test is used for categorical variables, taking P < 0.05 as significant. To compare properties across all five fields, nine individual Wilcoxon tests were run: AI versus each belt field, R versus each belt field, CM versus L, CM versus M, and M versus L. As each data set is used in four comparisons, significance was corrected to P < 0.01. Continuous variables were tested by least-squares regression, with effect significance indicated by the F-statistic as determined by ANOVA (JMP Software, SAS, or MATLAB, Mathworks).

RESULTS

Tonotopic organization of the core and delineation of cortical fields

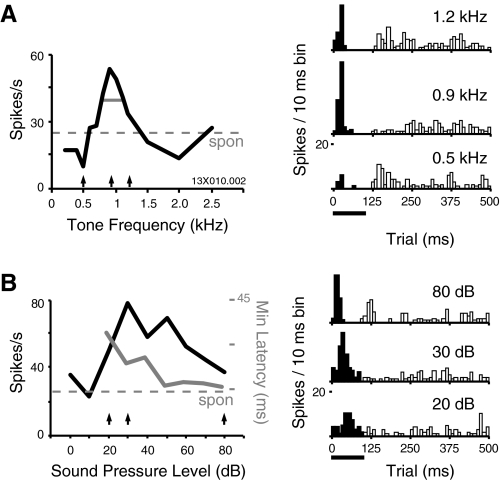
An example FTF is presented in Fig. 1A (left), along with PSTHs at three representative frequencies. The peak of the function corresponds to a strong onset excitation at 0.9 kHz, but suppression below the spontaneous rate is evident at flanking frequencies. In addition, the onset excitation is followed by suppression during the second half of the 100-ms tone presentation, and a frequency-specific excitation following tone offset; for consistency, only onset responses were used to define BF in this report.

Figure 2A presents the progression of BF values along the rostral-caudal axis in two hemispheres, both of which show a descending sequence in AI giving way to a less structured representation in R. The bottom panel, from monkey X, shows better evidence of a reversal, whereas BFs in monkey Z seem to bottom out with no clear trend toward higher BFs over a full 10 mm of tissue rostral to AI. Rostral sampling was not dense enough to conclude whether the most rostral low-frequency points (those at 8–10 mm) might correspond to field RT (Hackett et al. 1998; Morel et al. 1993; Petkov et al. 2006). Cortical distance is measured by coordinates in the recording chamber and reflects the position of the vertically oriented electrode. If the surface of the superior temporal plane descends at a 45° angle, the 8-mm length of AI, plus 6 mm of R, would correspond to ∼20 mm of cortical distance in a flattened histological section (14 mm/sin 45°). This corresponds well to the dimensions of the core defined by histological staining (Hackett et al. 1998).

Coordinates for each site in the bottom panel (right hemisphere of animal X) have been corrected for the angle and depth of the recording electrode in an attempt to compensate for the electrode approach being a few degrees off vertical. This analysis revealed that the frequency progression within individual recording tracks could be very reliable: with increasing recording depth, frequencies within AI dropped as the tip of the electrode moved slightly rostral. A reversal of that progression in more rostral penetrations marked the border between AI and R.

DEFINING THE FIELDS.

Figure 3 presents frequency maps for all four hemispheres, produced by averaging the BFs encountered within each penetration and assigning every site to an octave bin (coded by color). Borders of AI and R, determined as described in the preceding text, are overlaid on each panel. The global progression from high frequencies caudomedially to low frequencies rotrolaterally is well illustrated by the mirror-symmetric maps from monkey X (top). The bottom left map, from monkey Z, merges maps obtained from two placements of the recording chamber and provides the best evidence that the rostral field tapers to an elongated strip, as suggested by histochemistry and incorporated into the Hackett et al. (1998) model (see Fig. 2B). Folding of the gyrus, and the shift of the rostral core to the lateral bank of the circular sulcus, may explain the narrow strip of responsive tissue that is evident in this two-dimensional representation. In this survey, scant evidence was found for a second reversal of tonotopy into field RT (and in only 1 hemisphere), so further comparisons within the core will focus only on AI and R.

The total number of single units recorded in each field is presented in Table 1 subdivided by animal and hemisphere. Not every recorded cell was fully characterized, but each was quantitatively assessed for frequency tuning; responsiveness and recording stability determined how extensively a given unit was studied. In addition to the 980 single neurons in the core (n = 644 in AI, 336 in R), 34 instances of multi-unit activity were recorded. These recordings were included when constructing BF maps (Fig. 3) if single units were not available but are not reported in any population data.

Table 1.

Number of single units recorded

Animal	Field	Left Hemisphere	Right Hemisphere	Animal Total
X
	AI	194	217	411
	R	42	105	147
	M	22	40	62
	L	16	0	16
	CM	25	9	34
Z
	AI	170	63	233
	R	74	115	189
	M	15	5	20
	L	27	13	40
	CM	4	0	4
Hemisphere totals
	AI	364	280	644
	R	116	220	336
	M	37	45	82
	L	43	13	56
	CM	29	9	38

Open in a new tab

Core field totals in bold. AI, primary auditory cortex; R, rostral field; M, L, and CM, medial, lateral, and caudomedial belts, respectively.

DISTINGUISHING CORE AND BELT.

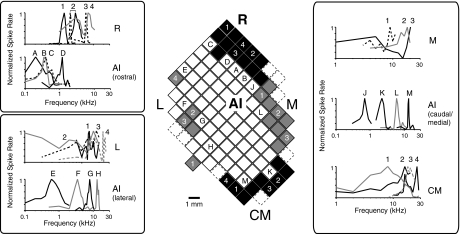
The border between core and belt was determined by a transition in the quality of frequency tuning, as illustrated in Fig. 4 (Rauschecker et al. 1997; Recanzone et al. 2000). Although a global tonotopic order is less clear in R than in AI, sharp tuning to tone frequency persists in R, validating its inclusion as part of the auditory core. Comparison of tone FTFs in core and belt, however, reveals a stark difference in tuning quality. For example, lateral AI shows sharp tuning at a range of BFs, whereas neighboring sites in the lateral belt (L) show broad, messy tuning clustering at high frequencies (Fig. 4, bottom left). Further separation of belt recordings into medial (M), lateral (L), and CM was less rigorous. No clear tonotopy could be defined in this limited survey, so these borders were drawn such that CM abutted high-frequency AI with M and L medial and lateral (respectively) to mid-to-low-frequency AI and R. The number of neurons in each field is included in Table 1, but for all belt fields, the count is far lower than in AI and R (n = 82 in M, 56 in L, 38 in CM). Sample size was not sufficient to further subdivide, so these designations do not follow the Hackett et al. (1998) model.

Comparing basic response properties within the core

DISCHARGE RATES.

In general, core auditory cortex in the awake macaque is characterized by an audible population response throughout the depth of the cortex with a particularly strong and homogeneous “hash” response in the middle layers, where the cytoarchitecture is granular and packing density is high (Cipolloni and Pandya 1991; Hackett et al. 1998; Jones et al. 1995; Pandya and Yeterian 1984). Deep to this, where the koniocortex gives way to a sparser array of large pyramidal cells, background activity is lower, and spikes are particularly large. Although individual electrode tracks were not reconstructed, the shallowest and deepest incidence of audible hash was recorded for most penetrations, allowing the assignment of a normalized cortical depth to 841 neurons. These relative estimates cannot be strictly mapped to cortical layers, but all depths were recorded with a slight bias toward the middle layers in AI, and a distribution in R that was uniform [Kolmogorov-Smirnov (K-S) test between normalized depths and a random uniform distribution; P = 0.02 in AI, P = 0.32 in R]. More importantly, the distribution did not differ significantly between AI and R (K-S test, P = 0.27), indicating that sampling bias is not likely to contribute to any observed difference between the fields.

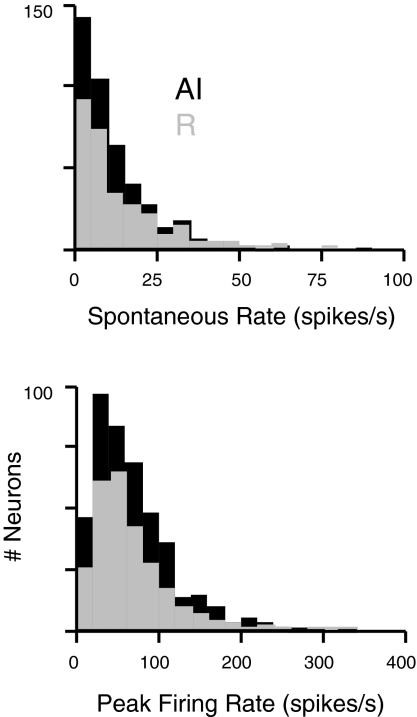
Spontaneous and driven firing rates did not differ between the fields of the core (Fig. 5). Median spontaneous rate was 8 spike/s in both fields (P = 0.67), and median peak rate was 58 spike/s in AI, R was 54 spike/s in R (P = 0.55). There was a significant effect within cells of both fields such that neurons with higher spontaneous rates tended to have higher driven rates (AI: r² = 0.29, P < 0.0001 by ANOVA; R: r² = 0.39, P < 0.0001). In responses to BF tones at best level, variance in the trial-to-trial spike count was correlated with mean spike rate in both fields (AI: r² = 0.14, P < 0.0001; R: r² = 0.30, P < 0.0001), and the ratio of variance to mean did not differ between AI and R (P = 0.12). In addition, the strength of spike rate adaptation over the course of repeated tone presentations did not differ (see methods; P = 0.85).

BFs AND TUNING WIDTH.

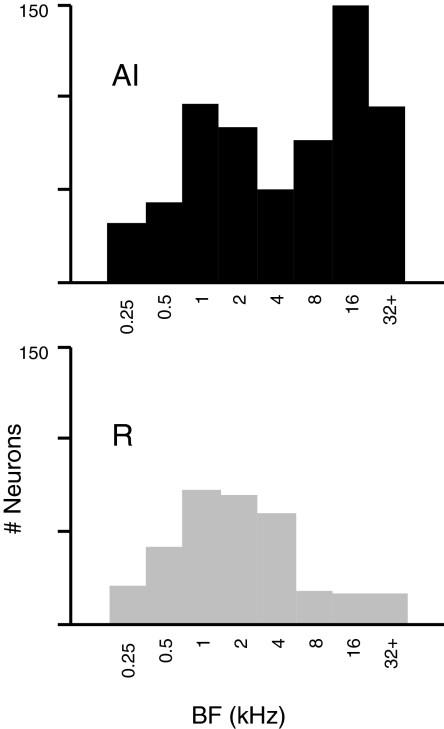
BFs of neurons encountered in AI span nearly the full range of the macaque audiogram (28 Hz to 37 kHz with peak sensitivity at 4 kHz) (Jackson et al. 1999). In contrast, the distribution in R favors low and midrange frequencies (Fig. 6, ANOVA, P < 0.0001 corrected for sample size). The skew toward high frequencies in the AI distribution may reflect a greater proportion of cortical area devoted to this frequency range, but the apparent peak at 1–2 kHz likely results from sampling low-frequency AI more densely (to maximize the yield of cells sensitive to interaural phase for other studies) (Malone et al. 2002; Scott et al. 2009). Although the full extent of the rostral core was sampled in only one hemisphere (Z, left), this tissue was tuned almost exclusively to tones ≤3 kHz. Other hemispheres showed more variation, but the spectral representation across R is compressed relative to that in AI and biased toward frequencies between 0.5 and 8 kHz. This confirms the inference from Fig. 2 that the reversed tonotopy in R, when present, is incomplete (Merzenich and Brugge 1973). The median tuning width did not differ between AI and R (P = 0.19).

Fig. 6. — The distributions of BF in AI and R emphasize different frequency ranges with a bias toward lower frequencies in R. Histograms plot BFs encountered in AI (*top*, n = 613) and R (*bottom*, n = 305); bins are octaves including BFs ≤ the bin label. Median values are the 8 kHz octave in AI, and the 2 kHz octave in R.

RATE-LEVEL FUNCTIONS.

Tones often evoked a complex mixture of excitation and suppression in neurons of the auditory core with the relative magnitude and timing of these response components varying as a function of stimulus level (e.g., Fig. 1) (see also Malone et al. 2009). The function in Fig. 1B is weakly nonmonotonic with a peak at 30 dB by the spike rate criterion used, but this belies the temporal structure obvious in the uppermost PSTH on the right, showing a sharp onset/suppression/offset response at 80 dB. The timing and magnitude of onset responses, and the shape of the RLF, are dependent on the shape and rise time of the tone onset (Heil 1997a,b; Phillips et al. 1995). Because these parameters were held constant (5 ms, cosine-squared ramp) when testing each neuron, measures derived from the RLF are valid for comparing responses across fields but should not be regarded as fixed, intrinsic characteristics of a given neuron.

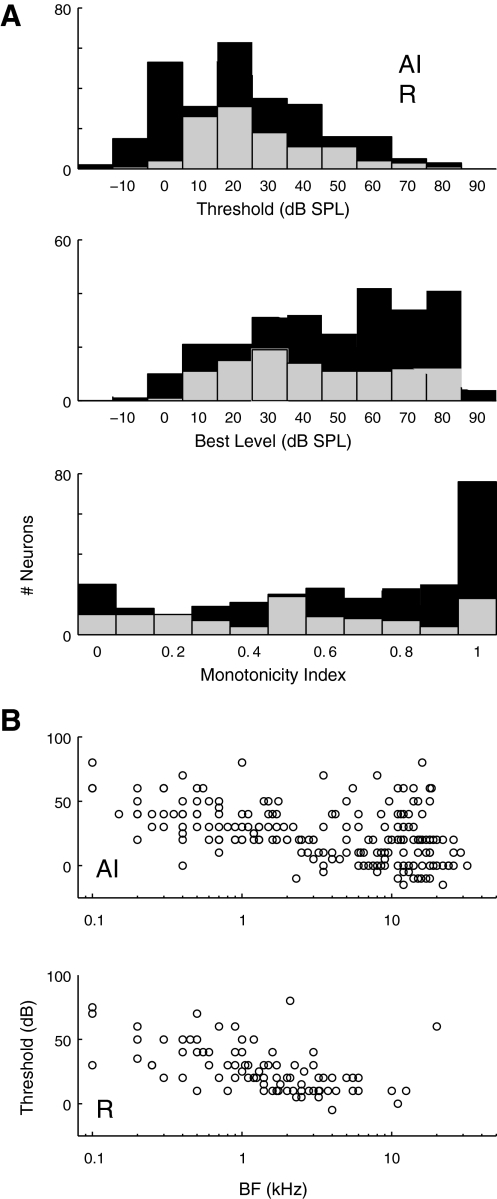
Distributions of threshold, BL, and MI are compared between AI and R in Fig. 7A. Threshold distributions in the two fields had identical medians, confirming that both fields of the core share similar sensitivity to pure-tone stimulation (Fig. 7A, AI: mean 23 dB, R: mean 27 dB, median for both fields is 20 dB; P = 0.025 by Wilcoxon rank sum, despite identical medians). Median BL in AI was marginally higher than in R (50 vs. 40 dB, P = 0.04), consistent with a greater prevalence of nonmonotonic rate-level tuning in R. Nonmonotonic RLFs were predominant in both fields with strictly monotonic functions (MI = 1) comprising just 29% (77/262) of responses in AI and 17% (18/106) in R. Strongly nonmonotonic responses (MI <0.5) were less common in AI than R (29 vs. 39%, respectively), and median MI was higher in AI than in R (0.74 vs. 0.54, P < 0.001; Fig. 7A). Threshold did not differ between monotonic and nonmonotonic functions in AI (median 20 dB for MI ≤0.5, and for MI >0.5, P = 0.54), but in R, the thresholds of monotonic functions were higher (median 20 dB for MI ≤0.5, versus 30 dB for MI >0.5, P = 0.006). At every frequency, thresholds varied widely, but the lower envelope of neural sensitivity was frequency-dependent, such that the lowest thresholds in both AI and R occurred at high BFs (Fig. 7B; P < 0.0001 by ANOVA in both fields).

It was observed that level tuning properties tended to be similar among neurons within a given electrode penetration, consistent with prior reports in anesthetized cat AI (Phillips et al. 1994). To assess quantitatively whether level tuning was randomly distributed, or clustered within penetrations, the dispersion (mean pairwise difference) between level tuning parameters (threshold, BL, and MI) was computed for every penetration yielding multiple single units with significant RLFs (101 pairs, 27 triplets, and 2 quadruplets). The median dispersion in each measurement was compared with the medians of 1,000 shuffled simulations in which values were randomly assigned among penetrations. The measured median dispersions of threshold, BL, and MI was smaller than all shuffled medians, suggesting that the apparent clustering of level tuning properties within penetrations is greater than would be expected by chance (P < 0.001). The distributions of mean tuning parameters across all penetrations did not differ from those based on the subset of penetrations with dispersion values below the minimum shuffled value (i.e., those penetrations with “significant” clustering; P > 0.7 for BL, threshold, and MI; K-S test). This indicates that clustering of level-tuning characteristics does not apply to a particular subtype of neurons (e.g., those with nonmonotonic RLFs or low thresholds) but applies generally.

RESPONSE TIMING: LATENCY AND RELIABILITY.

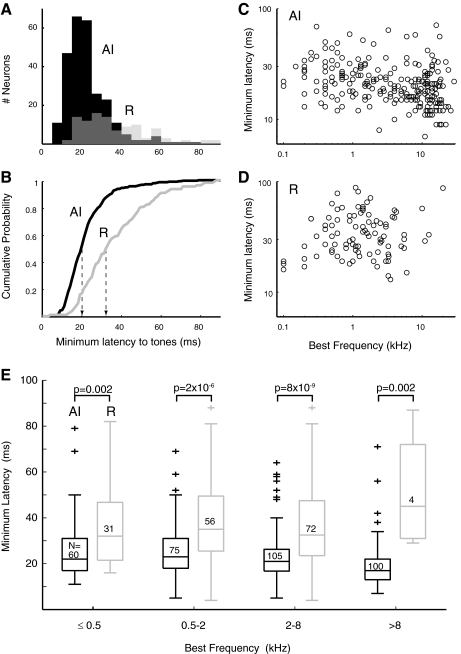
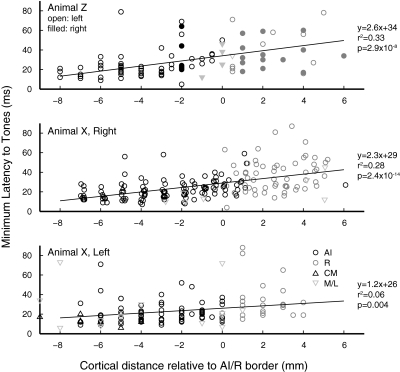
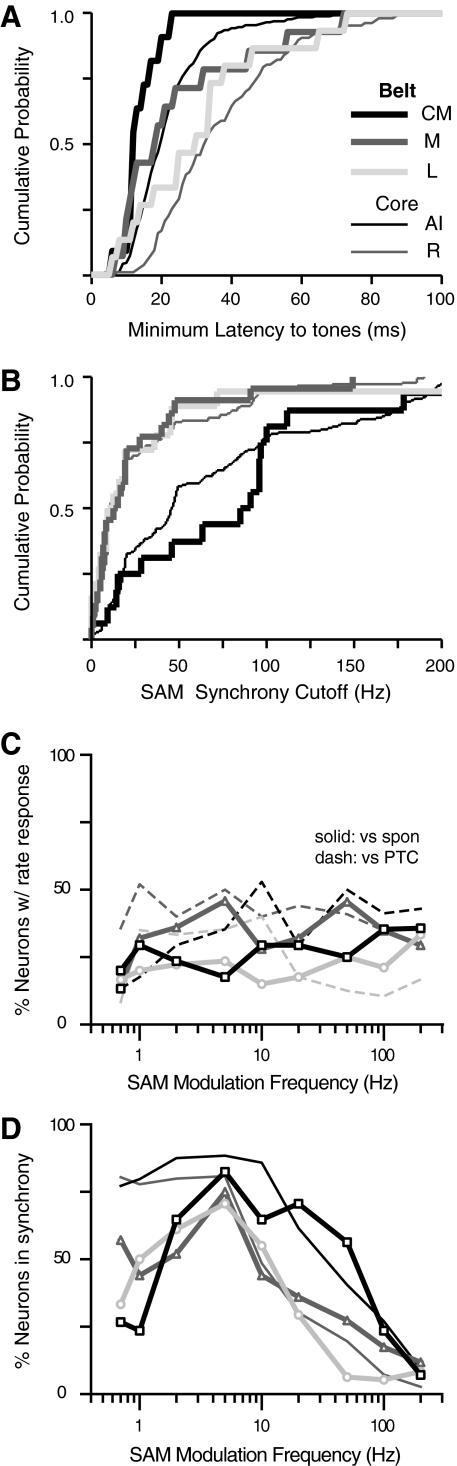
The relative timing of responses in AI and R is the aspect in which the two fields most markedly differ. Figure 8A overlays distributions of minimum latencies for neurons in AI and R, showing a skew toward short latencies in AI, and a broader distribution with a long-latency tail in R. The median latency in R is 13 ms longer than that in AI (AI: 20 ms; R: 33 ms; P = 4.2 × 10⁻¹⁷). This difference is highlighted in Fig. 8B as a shift in the cumulative distributions of minimum latency.

Fig. 8. — Minimum response latency to tones is longer in the rostral field, and short latencies are weakly correlated with higher BFs. Minimum response latencies in AI and R as overlaid histograms (A) and cumulative probability functions (B). Median latencies (indicated by - - -) are 20 ms in AI (n = 265) and 33 ms in R (n = 107), a difference of 13 ms (P = 4.2 × 10⁻¹⁷). Linear regression analysis of minimum latency against BF (C and D) confirms that latencies are shorter at higher BF in AI (P = 0.0001), but this was not significant in R. E: the difference in minimum latency between AI and R was significant across frequency. Boxes indicate median and quartiles, crosses mark outliers, sample size is indicated inside each box, and P values are from a Wilcoxon rank-sum test.

A modest contributor to this latency shift might be the difference in BFs between the two fields; in the inner ear, activation at the low-frequency apex of the cochlea lags activation of the high-frequency base by a few (∼4) milliseconds, this time being required for the traveling wave to reach the apex (Kitzes et al. 1978). Figure 8, C and D, plots the relation between latency and BF in AI and R; a weak trend exists toward shorter latencies at the highest carrier frequencies in AI, but the relative dearth of high-frequency cells in R makes the trend difficult to discern. When latencies are regressed against BF in octave bins (those used in Fig. 6), there is a weak but significant effect in AI of –1.6 ms/octave (ANOVA, P < 0.0001). The effect in R does not reach significance but shows a similar slope (−1.3 ms/octave, P < 0.06). The two BF distributions (see Fig. 6) differ in their median frequency by two octaves, which would predict a latency difference of ∼3 ms (vs. the actual difference of 13 ms). To verify that the latency difference between fields is robust, neurons with BF <0.5 kHz (near the AI/R border) were excluded; median latencies and significance were not affected (20 ms in AI, 33 ms in R, P = 7.5 × 10⁻¹⁶). Furthermore, comparison of latencies within frequency bands confirms that the latency disparity exists across all frequencies (Fig. 8E). Although the difference is stronger at higher frequencies, where AI latencies are shortest (e.g., 2–8 kHz), the effect is significant at BFs ≤500 Hz, near the AI/R border. Even among neurons with the lowest BFs encountered, ≤250 Hz, latencies in R are still significantly longer (P = 0.02).

Although the preceding analysis implies a clear transition in latency at the AI/R border, this transition occurs within a continuous latency gradient along the rostral-caudal extent of the auditory cortex (Fig. 9). Given the relationship between BF and latency within AI (Fig. 8C), an upward trend in latency would be expected to accompany the tonotopic gradient within AI; note, however, that the latencies in Fig. 9 do not appear to become shorter as the tonotopic sequence reverses in R. Linear regression of minimum latency (from all units, regardless of cortical field) against rostral-caudal position identifies a significant relationship in three of four hemispheres with an increase in latency of ∼2 ms for every mm of rostrocaudal distance.

Fig. 9. — A continuous increase in latency is evident along the rostrocaudal axis of auditory cortex. Minimum latency to tones is plotted against rostral-caudal position, relative to the BF reversal at the AI/R border. Circles mark units from core fields (AI: black, R: gray), triangles from CM, and inverted triangles from M or L. The sample size in animal Z was limited in the right hemisphere, and regresson was not significant; these points are folded into the *top panel* using filled symbols (regression in this panel includes left hemisphere data only). All units in each hemisphere, regardless of field, were included in the regression.

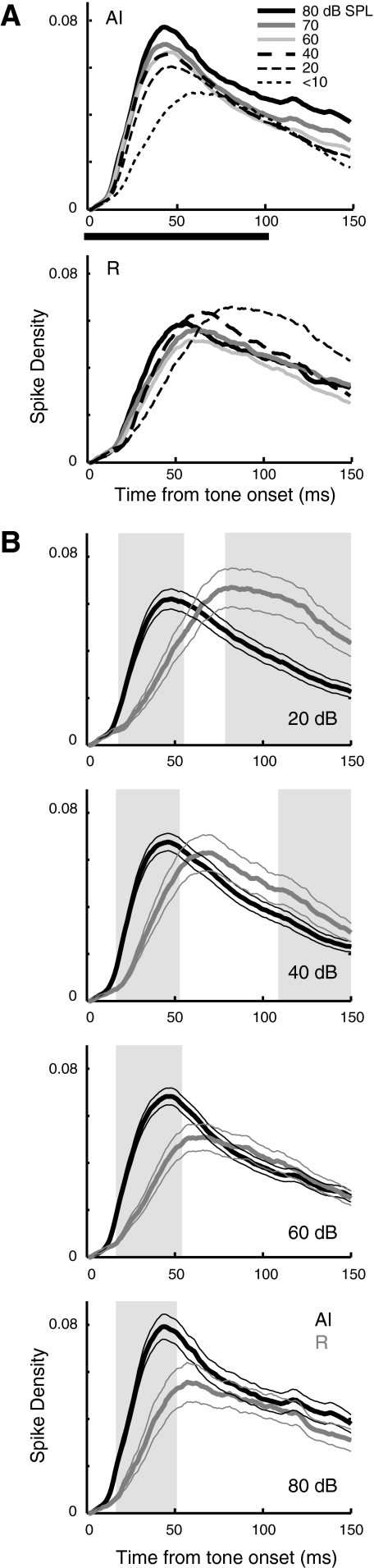
The time course of the population spiking response in each field is shown in Fig. 10, which averages the spike density functions of all significant responses at a range of SPLs. Peak response latency follows the same trend as minimum latency, being longer in R (median 42 ms in AI, 64 ms in R; P < 10^-10). In AI (Fig. 10A, top), response magnitude and the rising slope of the response are graded functions of SPL with louder tones evoking a stronger response that rises more steeply. The population response in R, by contrast, rises more slowly at any given intensity, and the magnitude of the response reflects the prevalence of nonmonotonic intensity tuning in this field (described in the preceding text). Figure 10B juxtaposes the population responses from AI and R at a range of sound intensities with shading indicating time points at which the firing rates are significantly different.

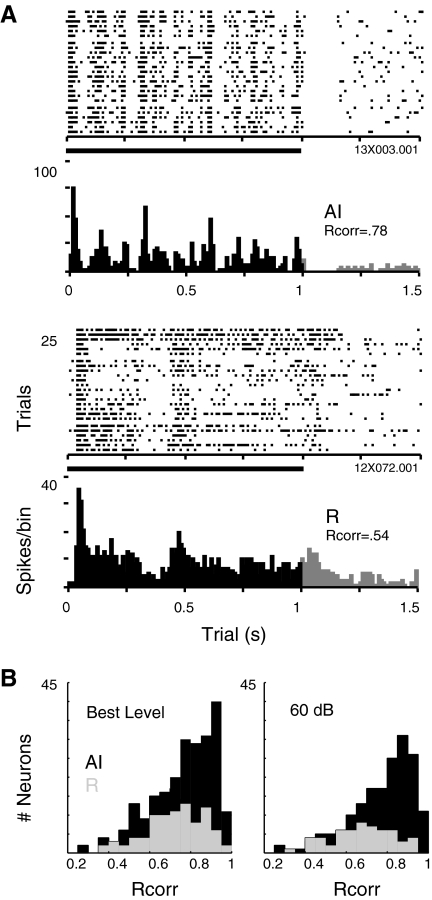
The spike rasters displayed in Fig. 11A suggest that the response of neurons in field R is not merely a delayed copy of that in AI but a qualitatively different representation. Each of these neurons is responding to a long (1 s) burst of frozen band-pass noise, optimized in center frequency, intensity, and bandwidth. The finer grain of temporal structure in AI is evident as the AI neuron reliably tracks certain features trial after trial (evident by the vertical alignment in the spike rasters), whereas discharges in R lack this structure. The difference in spike timing reliability across trials in these examples can be quantified by the Rcorr metric, which was also applied to tone responses at BF for each unit in the population. Although the variance in spike rate did not differ between the fields (see preceding text), spike timing reliability was higher in AI than in R, whether measured at the BL of each unit, or at 60 dB SPL (Fig. 11B; median Rcorr for AI and R at BL: 0.80, 0.73, P = 0.007; at 60 dB; 0.81, 0.69, P = 1.5 × 10⁻⁵). As there are no “features” within the ongoing pure tone, this difference likely reflects the reliability of the onset latency in AI.

Inline graphic — Responses to long-duration band-passed noise reveal fine temporal structure in AI and coarse structure in R. Rasters and underlying peristimulus time histograms (10-ms bins) depict the response to 1-s duration band-passed noise at the optimal center frequency and bandwidth of each cell (10-ms rise time; 25 trials of 2-s duration). Each cell was tested with multiple examples of frozen noise to confirm that the structure in each response is stimulus-specific and not an intrinsic property of the cell. In these example responses, spike timing reliability (Rcorr) was 0.78 in AI, and 0.54 in R. B: distributions of Rcorr in AI (■) and R () for pure tones presented at best level (BL, *left*, n = 229 in AI, 87 in R), and at 60 dB SPL (*right*, n = 172 in AI, 57 in R) confirm that spike timing reliability is significantly higher in AI at the population level.

AM and FM tones

MTFs.

Table 2 presents the number of cells for which MTFs were derived using SAM and SFM in AI and R plus some from the surrounding belt regions. The neural population in AI has been described previously with regard to SAM stimuli (Malone et al. 2007). Most MTFs were measured using the neuron's BF as the carrier frequency, and the distribution of carriers used resembles the distribution of BFs encountered in each field (Fig. 6). Carrier levels ranged from −10 to 90 dB SPL with a clear median at 60 dB in both fields (53% of MTFs in AI, and 40% in R, were collected at 60 dB).

Table 2.

Number of SAM and SFM MTFs from single units in four hemispheres

Animal	Field	Left Hemisphere	Right Hemisphere	Animal Total
X	AI	73 (31)	145 (108)	218 (139)
	R	16 (10)	69 (51)	85 (61)
	Belt	19 (9)	21 (20)	40 (29)
Z	AI	67 (39)	29 (19)	96 (58)
	R	19 (10)	54 (37)	73 (47)
	Belt	13 (4)	7 (6)	20 (10)
Hemisphere totals
	AI	140 (70)	174 (127)	314 (197)
	R	35 (20)	123 (88)	158 (108)
	Belt	32 (13)	28 (26)	60 (39)

Open in a new tab

Sinusoidal FM (SFM) numbers are in parentheses. SAM, sinosoidal AM; MTF, modulation transfer function.

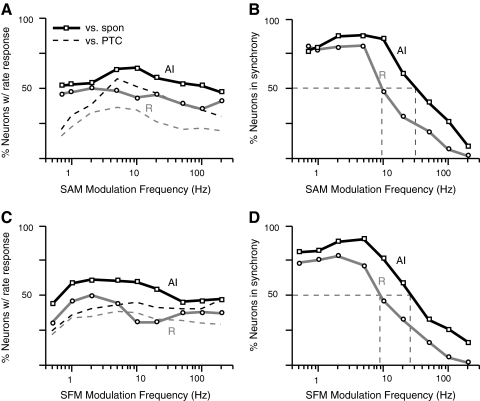
A neuron was considered to be responsive to SAM or SFM if it exhibited a significantly synchronized response to at least one modulation frequency or exhibited a significantly different firing rate from the response to the unmodulated control for at least one modulation frequency. An equal proportion of neurons in each cortical field was sensitive to SAM and SFM by this criterion (SAM: 99% in AI, 97% in R; SFM: 100% in AI, 99% in R). Cells generally were not tested with a full range of modulation frequencies if they were deemed unresponsive during initial testing, so these numbers may overestimate the prevalence of modulation responsiveness in the full cortical population. Synchrony to SAM (regardless of overall firing rate) was slightly more likely to be present in neurons within AI than in R (98% in AI, 94% in R, P = 0.02 by Fisher's exact test), and the same was true for SFM (99% in AI, 94% in R, P = 0.03). These differences are slight as the vast majority of neurons in both fields synchronize their discharges at some modulation frequency; however, the range and upper limit of frequencies at which synchrony is apparent (discussed in the following text) reinforces the temporal disparity between AI and R.

Approximately three-quarters of neurons encountered in both cortical fields displayed band-pass rMTFs (SAM, 78% in AI and 74% in R; SFM, 78% in AI and 69% in R), but the peaks of those functions tended to occur at higher modulation frequencies in AI. The median values of significant rBMFs for SAM are 10 Hz in AI and 5 Hz in R (P < 0.0001; means are 45 and 19 Hz, respectively), and for SFM are 7 Hz in AI and 4 Hz in R (P = 0.005; means of 34 and 21, respectively).

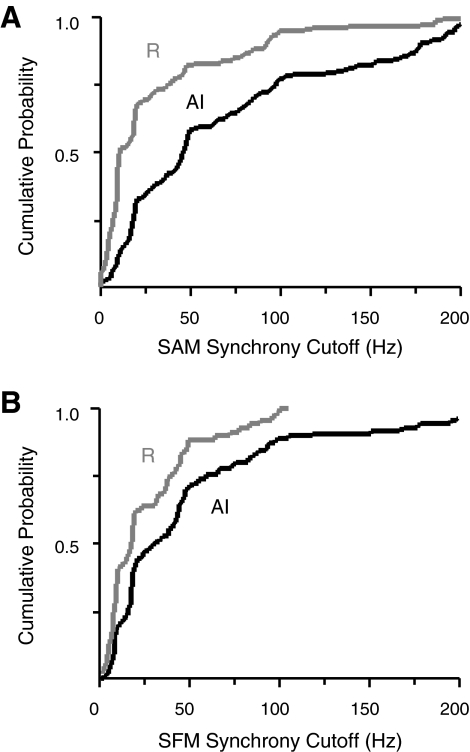
The same holds true for the peaks of tMTFs, as modulation frequencies eliciting maximal synchrony are higher in AI than in R. The median tBMFs for SAM are 5 Hz in AI compared with 2 Hz in R (P < 0.0001; means are 13 and 4.8 Hz, respectively), and for SFM, the median tBMFs are also 5 Hz in AI, 2 Hz in R (P < 0.0001; means are 18 and 7.7 Hz). The upper limit of neural synchrony showed a similar distinction between cortical fields, such that the median synchrony cutoffs for SAM are 46 Hz in AI, 10 Hz in R (P < 0.0001); for SFM, they are 31 Hz in AI, 18 Hz in R (P = 0.0003). Cumulative distributions of cutoff frequency in each field are plotted in Fig. 12 for SAM (A) and SFM (B). The temporal acuity of R is lower than that of AI for both stimuli, but the distance between the curves suggests that the disparity between AI and R is more pronounced for modulations of amplitude (Fig. 12A) than for modulations of frequency (B). These various indices of modulation responsiveness between the core fields are summarized in Table 3.

Fig. 12. — Cutoff frequencies define the limit of synchronization to modulated stimuli and reiterate the temporal disparity between the core fields. Cumulative distributions of interpolated synchrony cutoffs for SAM (A) and SFM (B) are presented for AI (black line) and R (gray line). Distributions in R rise more steeply and saturate at lower frequencies, confirming that neurons in R lose synchrony at lower modulation frequencies than neurons in AI.

Table 3.

Summary of modulation response characteristics between core fields

	AI	R	P, AI vs. R
SAM
Responsive, %	99	97	n.s.
Synchronized, %	98	94	0.02
Band-pass rMTF, %	78	74	n.s.
rBMF
Median, Hz	10	5	<0.0001
Mean, Hz	45	19
tBMF
Median, Hz	5	2	<0.0001
Mean, Hz	13	4.8
Sync cutoff, median, Hz	46	10	<0.0001
SFM
Responsive, %	100	99	n.s.
synchronized, %	99	94	0.03
bandpass rMTF, %	78	69	n.s.
rBMF
Median, Hz	7	4	0.005
Mean, Hz	34	21
tBMF
Median, Hz	5	2	<0.0001
Mean, Hz	18	8
Sync cutoff, median, Hz	31	18	0.0003

Open in a new tab

rMTF, rate MTF; rBMF and tBMF, rate-based and temporal-based, respectively, best modulation frequency.

Recent studies in the marmoset monkey have proposed a transformation in the coding of AM frequency between AI and R, such that the synchrony code for modulation frequency is replaced by spike-rate code (Bendor and Wang 2007). In the macaque data, the prevalence of rate coding (i.e., a significant rBMF—see methods) at frequencies beyond the synchrony cutoff was equal in AI and R for both SAM (16% in both fields) and SFM (13% in AI, 11% in R, P = 0.12, Fisher's exact test). Band-pass rate tuning, as defined by Liang et al. (2002), was equally prevalent in both cortical fields (SAM: 78% in AI, 74% in R, P = 0.42; SFM: 78% in AI, 69% in R, P = 0.07). Although a lack of synchronized discharges to higher rates of modulation was observed in R relative to AI, there was no concomitant increase in the prevalence of spike-rate tuning.

The difference in temporal acuity between AI and R demonstrated with SAM and SFM is consistent with the longer minimum response latencies described in the preceding text. Cutoff frequencies for SAM and SFM were inversely correlated with minimum latency to tones (ANOVA, P < 0.0001) with a slope of –1.8 Hz/ms for SAM cutoffs (for the full population, regardless of cortical field). The 13-ms difference in median latency between AI and R would predict a difference in cutoff frequencies of 23 Hz; the actual difference in the medians is 36 Hz. The slope of the effect for SFM is –1 Hz/ms, predicting a difference of 13 Hz—exactly the difference measured between AI and R. Thus is seems that the latency and SFM cutoff difference in R are manifestations of the same temporal disparity between the core fields.

Population response to dynamic stimuli

The preceding population analyses were based on summary statistics drawn from the MTF of each cell: one modulation frequency eliciting the highest spike rate or one frequency marking the upper limit of synchrony to the modulation envelope. These distributions are not illustrative of how the cortical population as a whole encodes the envelope across frequency. From all MTFs collected using either stimulus, a “population MTF” was constructed by evaluating the proportion of cells that was responding at each of the nine most commonly tested modulation frequencies. A neuron was considered to have a rate response if its discharge rate was significantly elevated or suppressed (t-test, P < 0.01) relative to the spontaneous rate of the cell, and the response at 0 Hz. Synchrony was evaluated using the Rayleigh statistic (P < 0.001) on VS (for SAM) and/or VS at 2*f_m (for SFM, to accommodate frequency doubling if present). Population MTFs are plotted in Fig. 13 for SAM and SFM and confirm the similarity in the population responses to the two types of modulation. No modulation frequency elicits a rate response in more than ∼60% of cells (A and C), and the rate response curves for SAM are almost entirely flat when measured relative to the spontaneous rate (A, solid lines). Rates relative to the unmodulated control (dashed lines) exhibit a peak at 5 Hz in AI, but both curves in R are flatter and lower overall than their AI counterparts. The SFM population rMTFs (C) look much the same: they are generally flat and weakly tuned with a slight peak at 2 Hz in R relative to the spontaneous rate but no tuning whatsoever relative to the pure tone control. Because ∼75% of individual neurons are band-pass tuned in rate (discussed in the preceding text), the lack of structure in the population MTF likely derives from heterogeneity in the peaks of these functions.

Population tMTFs (Fig. 13, B and D) were consistently low-pass in shape and reflected the diminished temporal acuity of the rostral field. At least 75% of neurons synchronized their discharges to some component of the envelope for both SAM and SFM in AI up to a modulation frequency of 10 Hz; beyond this point, synchrony declines steadily among the population. The drop occurs at lower frequencies among the population of cells in R as would be predicted from the cutoffs in the previous figure. The median point, at which only half the population retains synchrony to the envelope, is ∼30 Hz in AI, and 10 Hz in R, for both SAM and SFM (dashed lines on both panels).

Temporal properties of the auditory belt

Single neurons of the auditory belt, given their secondary position within the cortical hierarchy, would be expected to exhibit longer latencies, and more complex stimulus selectivity, than neurons of the neighboring core (Rauschecker et al. 1997; Recanzone et al. 2000). There was no difference in spontaneous rate across the core and belt fields, but peak discharge rates were lower in medial belt (M) than in either core field (P < 0.0001) and slightly lower in CM than in R (P < 0.005). The difference in peak discharge rates could reflect the metabolic difference between core and belt suggested by histochemistry and/or be a consequence of using sub-optimal tone stimuli: the response to pure tones is, by definition, less clearly tuned and reliable in the belt. Comparisons of thresholds did not reach statistical significance, but CM neurons were more likely to be monotonic, and neurons in M and L showed a greater proportion of messy RLFs than was encountered in the core. The ratio of variance to mean spike rate was lower in L than in the core (P = 0.007), and L also showed a greater degree of spike rate adaptation over repeated trials (P = 0.01), whereas other belt fields resembled the core in these respects.

Minimum latency to tone stimuli varied between fields of the belt, as illustrated by the cumulative distributions in Fig. 14A. Latency in CM is lower than in all other fields, including AI (CM median 12 ms, AI 22 ms, P = 0.001). Interestingly, latencies in R do not differ from those in L (R median 33 ms, L median 30 ms, P = 0.19) and are in fact significantly longer than those in M (M median 18.5 ms, P = 0.004), whereas M does not differ significantly from AI (P = 0.52).

Synchrony cutoff values for SAM divide the five cortical regions into two classes, as evident in Fig. 14B. Neurons in AI and CM synchronize to higher frequencies of modulation than neurons in R, L, or M. Cutoffs in AI and CM are not statistically different (AI median 46 Hz, CM median 88 Hz, P = 0.39), and both fields have significantly higher cutoffs than the other three (R median 10 Hz, L median 11 Hz, M median 12 Hz, P < 0.003 in all tests). Similar curves derived from SFM are not presented because few synchrony cutoff values (<10 per field) were collected in the belt using that stimulus.

Rate-based population MTFs from the belt fields, relative to those from the core in Fig. 13, A and B, are similarly flat and messy, suggesting no population-wide preference for modulation frequency in terms of overall spike rate (Fig. 14C). By contrast, the proportion of the neural population responding in synchrony (Fig. 14D) differs markedly between the core and belt fields in that that synchrony is rare in the belt for slow modulations <5 Hz. Above 5 Hz, the pattern suggested by the cutoff frequencies in Fig. 12B emerges with synchrony present out to higher frequencies in AI and CM and fading at lower frequencies in R, L, and M. Whereas synchrony to AM in the core fields is low-pass in character, synchrony in the belt fields is band-pass regardless of the temporal precision predicted by their onset latencies (i.e., CM resembles AI at high frequencies of modulation but resembles the other belt fields at low frequencies).

DISCUSSION

In accordance with prior anatomy and mapping studies (Hackett et al. 1998; Kosaki et al. 1997; Merzenich and Brugge 1973; Morel et al. 1993), frequency tuning formed a rough rostral-caudal gradient within AI, and identified a low-frequency border rostrally, beyond which the gradient reverses (Fig. 2A). That the reversal of the tonotopic gradient is incomplete has been suggested in a prior study of anesthetized macaque (Merzenich and Brugge 1973) and also appears to be true in awake marmoset (Bendor and Wang 2008; their Fig. 3). Although early studies were ambivalent as to whether the reversal truly defined a separate field (Jones et al. 1995), comparisons in the present study identify the rostral field as physiologically distinct in its temporal response properties. The minimum latencies of cells in R are 1.5 times longer than those in AI. Although these fields operate in parallel, in the sense that each receives direct thalamic input (Jones et al. 1995; Molinari et al. 1995; Rauschecker et al. 1995), they do not operate in synchrony. Response latencies in R lag those in AI by 13 ms on average (Fig. 8), longer than would be predicted from synaptic delay even if R received its input in serial, via AI. The difference in temporal characteristics between AI and R is also apparent in responses to modulated stimuli. Best modulation frequencies, as determined by rate, are higher in AI for both SAM and SFM, as are synchrony cutoff frequencies. In other words, both rate and synchrony codes seem to favor lower modulation frequencies in the rostral cortex.

The secondary fields of the surrounding belt, as defined by the quality of pure-tone tuning, exhibited a range of temporal response properties that were inconsistent with a straightforward model of serial processing. Sample sizes from the belt fields are small relative to those in AI and R, and in this study, the sample is biased toward recording sites adjacent to the core, yet some interesting differences between fields were evident. Neurons in area CM, adjacent to high-frequency AI, had short latencies and high limits of synchronization (Fig. 14). Latencies in field M were indistinguishable on average from those in AI and shorter than latencies in R (Kusmierek and Rauschecker 2009), again suggesting that the anatomical cascade of inputs from core to belt does not translate into sequential activation in time.

Response properties and tonotopic organization in awake cortex

Tonotopic order appears coarser in the awake preparation (Figs. 2 and 3) (Pfingst and O'Connor 1981; Recanzone et al. 2000) than is commonly seen in AI and R of anesthetized macaque (Merzenich and Brugge 1973; Morel et al. 1993) or in auditory cortex of the cat (Lee et al. 2004; Reale and Imig 1980). Within an electrode penetration, BF was typically consistent, or followed an orderly progression with depth, implying that local organization is quite precise. Therefore the apparent disorder in these maps is likely the product of experimental limitations. The vertical approach employed here allows ∼1 mm error in electrode placement (Pfingst and O'Connor 1980), and recording through the cortical depth introduces variability, as the angle of electrode travel is not normal to the cortical lamina.

Frequency tuning functions were collected at or near each cell's best level, so full frequency response areas (in frequency and SPL) are not available for most neurons. This precludes a comparison of tuning width using standard Q values (Cheung et al. 2001; Recanzone et al. 1999), although the tuning width measure employed (which is similar in concept) was consistent within the core. The width of neural tuning generally increases with SPL (Recanzone et al. 2000) and is also dependent on the rise time (Phillips et al. 1995) and spectral bandwidth (Barbour and Wang 2003) of the stimulus, whereas BF is generally invariant with these parameters. This suggests that the BFs mapped in Figs. 2 and 3, and used to delineate the fields of the core, are reliable estimates of each neuron's frequency tuning.

The level of activity described is comparable with that reported in other studies of awake primate cortex (Pfingst and O'Connor 1981). Recanzone et al. (2000) report the same level of spontaneous activity (mean 8 spike/s) in their survey of macaque cortex, and data from marmoset are similar (6 spike/s) (Bendor and Wang 2008); all three studies find no significant difference between AI and R. Peak discharge rates are higher overall than those reported previously and were not found to differ between fields; by contrast, Recanzone et al. (2000) and Bendor and Wang (2008) reported lower activation in R. Our data can replicate that result if re-analyzed using a fixed 0–100 ms window (52 spike/s in AI, 38 in R, P = 0.009) rather than a sliding window that accounts for onset latency, so the apparent difference likely reflects response timing, not magnitude.

Tuning for sound intensity

Response thresholds in AI are comparable to those reported previously in awake macaque (Pfingst and O'Connor 1981). The distributions of threshold and best level in AI and R are in accord with the results of Recanzone et al. (2000), who also report equivalent thresholds between the two fields. Threshold in that study was found to be minimal for AI cells with BFs near 1 kHz (the audiogram of the macaque has a minimum at 4 kHz), but minimal thresholds in the current study dropped steadily with increasing BF in both fields (Fig. 7B). Because that study used contralateral free-field stimuli, and this used closed-field diotic stimuli, it is possible that thresholds for low-frequency cells appear artificially high because these units are tuned to interaural phase differences other than 0° (Scott et al. 2007) or because we are bypassing the spectral filtering of the pinna (Spezio et al. 2000). Thresholds in marmoset cortex match those reported here (median of 20 dB SPL in AI and R), and best levels are similar (Bendor and Wang 2008). Nonmonotonic neurons in marmoset AI have been reported to have lower thresholds than monotonic neurons (Watkins and Barbour 2008), a finding that was not supported by our AI data although the distinction was significant in R.

Nonmonotonic tuning for tone intensity is not observed in the auditory nerve of primates (Nomoto et al. 1964) but emerges within the central auditory system and becomes more common at successively higher structures. In behaving macaque monkeys, prior studies report nonmonotonic RLFs in 51% of neurons in the inferior colliculus (IC) (Ryan and Miller 1978), and 78% in AI (Pfingst and O'Connor 1981). Using the same criterion (MI ≤ 0.9), a lower proportion of our cortical neurons had nonmonotonic RLFs: 61% in AI and 79% in R. Two factors are likely to explain this discrepancy: first, in the earlier studies, neurons were tested to a higher range of SPLs (≥90 dB SPL), such that response decreases at intensities >80 dB SPL could be observed. Second, their analysis excluded “complex” functions (e.g., a slight deviation from monotonicity in an otherwise increasing function), whereas we used only the MI ratio in our classification. If these functions are excluded from the IC data, only 35% of neurons in IC exhibited a distinct best level (Ryan and Miller 1978) consistent with an increased prevalence of nonmonotonic tuning in the cortex, relative to lower structures.

In awake marmoset AI, 64% of neurons have nonmonotonic RLFs (Sadagopan and Wang 2008); by the same criterion (MI ≤ 0.75), 50% of our AI neurons, and 68% of R neurons, have nonmonotonic RLFs. That study, like ours, reports a bimodal distribution of MI values with peaks at 1 and 0, although the peak at 0 is more prominent in the marmoset data, indicating that more neurons in marmoset cortex were fully suppressed at high intensities. Recanzone, by contrast, reports almost no MI values <0.5. In this regard, the degree of nonmonotonicity we report in awake cortex is intermediate between that found in previous studies of marmoset and macaque (compare Fig. 7A) (Recanzone et al. 2000, their Fig. 11A; Sadagopan and Wang 2008, their Fig. 2D). Our study differs from both prior studies in that rather than sampling frequency-intensity space pseudorandomly, we presented a series of tones at BF blocked by intensity. The dearth of strong suppression observed in macaque by Recanzone et al. (2000) may be attributable to their recording in the behaving state (vs. awake passive), using contralateral free-field stimulation (vs. closed-field diotic in this study, and a central speaker in the marmoset study). In comparison to the marmoset data, we cannot rule out a species difference, but the tuning of single cortical neurons to tone intensity is in general accordance between New and Old World primates.

Recanzone et al. (2000) report mean MI values of 0.83 in AI and 0.72 in R; our values are lower overall (0.67 in AI, 0.55 in R), but both studies find the MI values in R to be significantly lower, and more uniformly distributed, than those in AI. This transformation between AI and R is consistent with the greater proportion of nonmonotonic RLFs at successively higher levels of the auditory processing hierarchy. If an auditory structure contains neurons with best levels uniformly distributed across the hearing range of the animal (as is nearly true for R in our data), a given sound should activate an equivalently strong population response regardless of its intensity. The utility of such a code may be to allow a population representation of an auditory stimulus that is invariant across changes in sound level (Sadagopan and Wang 2008) as would be desirable in the recognition of a given auditory object—such as a conspecific vocalization—across a range of listening conditions.

Onset latency and temporal processing of dynamic stimuli

The most striking difference between the core fields in response to tonal stimulation was a 13-ms shift in median minimum latency between AI (20 ms) and R (33 ms). A similar disparity in latency was reported by Recanzone et al. (2000) although they report longer average latencies in both fields (32 ms in AI, 42 ms in R). That study used a standardized response area with only two trials at any one point, averaging across several frequencies and levels to measure latency; by contrast, we identified the BF of each neuron and collected 10 trials at each SPL; this would allow a shorter and less variable estimate of latency. Kusmierek and Rauschecker (2009) report a similar trend between AI and R, but their latencies are shorter overall, likely because they measured latency to several stimulus classes (including broadband noise) and reported the shortest of those. Minimum latencies in marmoset are similar to those reported here (27 ms in AI, 35 ms in R) and also significantly different between fields (Bendor and Wang 2008). The present study reinforces the initial finding of Recanzone et al. (2000) and expands on the issue of temporal processing by using dynamic stimuli. Similarity to the recent data from marmoset establish a common theme in auditory cortical processing between New and Old World primates.

As a model for the processing of complex sounds, modulations of pure-tone stimuli can mimic temporal modulations of amplitude and frequency characteristic of human speech (Ahissar et al. 2001; Zeng et al. 2005) and macaque vocalizations (Cohen et al. 2007; Ghazanfar et al. 2001). Modulations of tone amplitude (Joris et al. 2004) and frequency were used to explore the coding mechanisms and temporal limits of cortical neurons and potential disparities in the spectral and temporal response properties of AI and R. Although the MTF does not capture all the information-bearing elements of a response to SAM (Malone et al. 2007, 2010), here it has been shown to be sufficient to identify gross differences in temporal processing across fields.

Single neurons in AI and R differ in the upper limits of their ability to synchronize (Fig. 12), and, as a population, cells in R are less likely to be firing in synchrony to the envelope at most modulation frequencies (Fig. 13, B and D). This finding is similar to what recently has been reported in the auditory core fields of the awake marmoset: tBMFs are higher in AI (though the effect did not reach significance in marmoset), and synchrony cutoffs are significantly higher in AI than R in both species (Bendor and Wang 2008). The cutoff frequency, marking the upper limit of synchrony, can be taken as an index of a neuron's temporal integration window. Loosely defined, the temporal integration window is the minimum time period over which two distinct acoustic events can be resolved—for instance, two periods of sinusoidal AM producing two fluctuations in neural discharge rate. The median synchrony cutoff frequencies for single neurons in AI and R (46 and 10 Hz; Fig. 12A) correspond to temporal resolutions of 22 and 100 ms; similar estimates can be derived from the population MTFs (30 and 10 Hz; Fig. 13B), which suggest windows of 20–30 ms in AI and 100 ms in R.

The degradation of temporal synchrony in R, perhaps due to temporal integration of the acoustic signal, makes this field a candidate for rate-based coding of modulation frequency. Yet the prevalence of rate coding beyond the temporal cutoff did not differ between AI and R nor did the overall prevalence of band-pass rate tuning. The peaks of those band-pass functions tended to fall at higher modulation frequencies in AI than in R (median SAM rBMF: 10 Hz in AI, 5 Hz in R), a trend that was also reported between AI and R of marmoset, although in that species rBMFs were higher, and the difference between fields did not reach significance (median SAM rBMF: 44 Hz in AI, 27 Hz in R) (Bendor and Wang 2008). The population MTFs (Fig. 13, A and C) indicate that at any given modulation frequency, fewer cells in R show a significant rate response than in AI; this does not support the notion that responses in R reflect a transition from temporal to rate-based coding of modulation frequency (cf. (Bendor and Wang 2007; Langner and Schreiner 1988). Differences in technique may explain this disparity in part as modulation frequencies presented in this study (≤200 Hz) did not reach as high a range as those in the Wang studies, and the use of long (10 s) trials also favors sustained responses over those that adapt.

A previous analysis (Malone et al. 2007) has shown that for slow modulation frequencies, the temporal firing patterns of cells in AI encode instantaneous stimulus amplitude throughout the SAM period. Responses to SAM (and SFM) in R are qualitatively similar and show a similar (if weaker) predominance of synchrony over the low-frequency range (≤10 Hz). This suggests that common mechanisms of dynamic amplitude coding are shared between the core fields despite the difference in the upper limits of their temporal acuity. From a limited sample of SAM responses in belt (Fig. 14D), it appears that neurons of these secondary cortical fields sacrifice the representation of instantaneous amplitude at low frequencies in favor of a more restricted temporal receptive field favoring modulations of 5 Hz.

Thalamic input and correspondence to other species

Differences between AI and R may be at least partially inherited from the thalamus. In cat, the MGv shows a gradient of responsiveness orthogonal to the frequency progression, such that neurons at the anterior end of the nucleus are in more precise tonotopic order, respond with shorter latency, lock their discharges more precisely to repetitive clicks, and are more likely to have monotonic RLFs (Rodrigues-Dagaeff et al. 1989). Retrograde labeling indicates that the core fields of feline auditory cortex receive inputs that are biased in a graded manner, from anterior to posterior. Sharper tuning and shorter latencies in MGv have been confirmed in the awake guinea pig (Edeline et al. 1999), although threshold and RLF type did not differ between thalamic divisions. Physiology data in awake primate thalamus is limited, but responses to periodic stimuli suggest that cutoff frequencies are higher than those in AI (Bartlett and Wang 2007) as has also been shown in awake guinea pig (Creutzfeldt et al. 1980). These results imply a continuum of widening temporal integration windows from the thalamus, to AI, R, and RT (Bendor and Wang 2008). Although existing data do not address the mapping of temporal response properties within the primate thalamus, it is likely that the differences observed between AI and R reflect a combination of disparities in thalamic inputs and local cortical processing.

The temporal properties of CM were uncharacteristic of a secondary field: latencies were shorter than those in AI despite an apparent lack of direct input from the primary auditory nucleus of the thalamus (Jones et al. 1995; Molinari et al. 1995; Rauschecker et al. 1995). Other studies have reported latencies in CM and AI to be statistically indistinguishable (Oshurkova et al. 2008; Recanzone et al. 2000), and the earlier of those studies had a larger sample size (in CM) than that reported here; given the available data, it seems reasonable to say that CM neurons have latencies as short as, if not shorter than, those in AI. Only 10% of AI neurons in our sample had latencies as short as the median latency in CM (11 ms), so this belt field would have to receive selective inputs from the shortest-latency neurons of the core. Figure 8C shows that high-frequency neurons tend to have the shortest latencies in AI, making a feed-forward model plausible if not probable.

The peculiar characteristics of belt area CM have also been observed in multiunit data from anesthetized marmoset (Kajikawa et al. 2005): although their sample included low-frequency CM (not included in the present study), responses in CM were found to have latencies shorter than those in AI. This led Hackett and colleagues to highlight an alternate, primary-like thalamic input to field CM from the anterodorsal medial geniculate (MGad) (Kajikawa et al. 2005). The MGad resembles MGv in its cytoarchitecture and inputs, and projects to layer IV of CM in both marmoset (de la Mothe et al. 2006) and macaque (Molinari et al. 1995). However, the apparent abolition of tone responses in macaque CM after ablation of AI (Rauschecker et al. 1997) remains to be reconciled with this hypothesis. With regard to temporal processing, in both macaque and marmoset, CM is more similar to AI than to the lateral or medial belt fields.

Functional implications of cortical organization

Amplitude and frequency envelopes are used in the identification of species-specific calls by many primate species, including macaque monkeys (Cohen et al. 2007; Ghazanfar et al. 2001; Le Prell and Moody 1997), and cortex is indispensable to this task (Heffner and Heffner 1984). The fidelity of responses to SAM and SFM suggests that a neuron in AI would follow the envelope of a vocalization, or any similar sound, to the limits of its temporal precision. This may not be the case in anesthetized marmoset AI, where discharges favor amplitude transients at the expense of spectral modulations and respond to vocalizations more strongly than to similar synthesized sounds (Wang et al. 1995). This reduces the overall temporal complexity of the population response and enhances synchrony among the neural population. In awake cortex, the ability of responses to tones, SAM and SFM to predict the temporal coding of natural sounds is not yet understood.

A curious feature of the temporal disparity between AI and R is that the overlapping gradients of BF and latency (Figs. 2, 8C, and 9) appear to create a longer lag in activation for higher-frequency sounds. Figure 8E summarizes how onset latency drops with BF in AI but remains relatively constant across BF in R. The onset of a complex sound with high- and low-frequency components will generate a traveling wave of activation across AI, from the short-latency, high-BF neurons at the caudal extent, toward the longer-latency, low-BF neurons at the rostral extent. Within R, however, frequency-dependent temporal filtering may create a simultaneous activation across neurons of varying BF, facilitating the integration of frequency components into a unified auditory object.

Diminished synchrony to SAM stimuli rostral to AI in squirrel monkeys lead Bieser and Muller-Preuss (1996) to conclude that AI and the field medial to it are among “the areas where the envelope fluctuations of the monkey's calls may be encoded…” whereas “other fields have insufficient time resolution to manage such information.” The caudal core may be the highest stage at which the envelope of vocalizations is explicitly represented in neural discharge patterns; at higher cortical stations, the homology between discharge rate and stimulus envelope may erode to favor an abstract or implicit code. This representation need not be an average rate code, however, as the temporal dynamics of the response may be stimulus-selective in the absence of a clear periodicity matching that in the stimulus. It has yet to be established how responses to long-duration periodic stimuli predict responses to complex natural envelopes, within the same cells. The temporal fidelity of cortical neurons is likely to be influenced by immediate stimulus context (Dean et al. 2005; Malone et al. 2002; Ulanovsky et al. 2003), so future experiments will be needed to clarify the encoding of natural stimuli in the rostral auditory cortex.

Primary auditory neurons process acoustic features at multiple time scales (Elhilali et al. 2004; Nelken et al. 2003; Ulanovsky et al. 2003). The diversity of time scales available in AI is further elaborated in the rostral field of the core and the surrounding fields of the belt. The temporal integration windows in AI and R of the macaque correspond well with the hypothesized dual time scales at work in the analysis of human speech: a short window (20–30 ms) appropriate to detecting formant transitions and a longer window (>100 ms) on the scale of syllables and tonal contours (Boemio et al. 2005; Poeppel 2003). The caudorostral gradient of temporal properties in the core auditory fields of the awake macaque provides a basis for temporal analysis at multiple resolutions, which may be fundamental to cortical processing of complex sounds.

GRANTS

This work was supported by a W. M. Keck Foundation grant to M. N. Semple, National Institutes of Health Grants DC-05287-01 to B. H. Scott and MH-12293 to B. J. Malone, and a James Arthur Fellowship from New York University to B. H. Scott.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

ACKNOWLEDGMENTS

Present address for BJM: Keck Center for Integrative Neuroscience, 513 Parnassus Ave, San Francisco, CA 94143-0444.

REFERENCES

Ahissar E, Nagarajan S, Ahissar M, Protopapas A, Mahncke H, Merzenich MM. Speech comprehension is correlated with temporal response patterns recorded from auditory cortex. Proc Natl Acad Sci USA 98: 13367–13372, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
Barbour DL, Wang X. Auditory cortical responses elicited in awake primates by random spectrum stimuli. J Neurosci 23: 7194–7206, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Bartlett EL, Wang X. Neural representations of temporally modulated signals in the auditory thalamus of awake primates. J Neurophysiol 97: 1005–1017, 2007 [DOI] [PubMed] [Google Scholar]
Bendor D, Wang X. Differential neural coding of acoustic flutter within primate auditory cortex. Nat Neurosci 10: 763–771, 2007 [DOI] [PubMed] [Google Scholar]
Bendor D, Wang X. Neural response properties of primary, rostral, and rostrotemporal core fields in the auditory cortex of marmoset monkeys. J Neurophysiol 100: 888–906, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Bieser A, Muller-Preuss P. Auditory responsive cortex in the squirrel monkey: neural responses to amplitude-modulated sounds. Exp Brain Res Exp Hirnforsch 108: 273–284, 1996 [DOI] [PubMed] [Google Scholar]
Boemio A, Fromm S, Braun A, Poeppel D. Hierarchical and asymmetric temporal sensitivity in human auditory cortices. Nat Neurosci 8: 389–395, 2005 [DOI] [PubMed] [Google Scholar]
Cheung SW, Bedenbaugh PH, Nagarajan SS, Schreiner CE. Functional organization of squirrel monkey primary auditory cortex: responses to pure tones. J Neurophysiol 85: 1732–1749, 2001 [DOI] [PubMed] [Google Scholar]
Cipolloni PB, Pandya DN. Golgi, histochemical, and immunocytochemical analyses of the neurons of auditory-related cortices of the rhesus monkey. Exp Neurol 114: 104–122, 1991 [DOI] [PubMed] [Google Scholar]
Cohen YE, Theunissen F, Russ BE, Gill P. Acoustic features of rhesus vocalizations and their representation in the ventrolateral prefrontal cortex. J Neurophysiol 97: 1470–1484, 2007 [DOI] [PubMed] [Google Scholar]
Creutzfeldt O, Hellweg FC, Schreiner C. Thalamocortical transformation of responses to complex auditory stimuli. Exp Brain Res Exp Hirnforsch 39: 87–104, 1980 [DOI] [PubMed] [Google Scholar]
de la Mothe LA, Blumell S, Kajikawa Y, Hackett TA. Thalamic connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol 496: 72–96, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci 8: 1684–1689, 2005 [DOI] [PubMed] [Google Scholar]
DiCarlo JJ, Lane JW, Hsiao SS, Johnson KO. Marking microelectrode penetrations with fluorescent dyes. J Neurosci Methods 64: 75–81, 1996 [DOI] [PubMed] [Google Scholar]
Edeline JM, Manunta Y, Nodal FR, Bajo VM. Do auditory responses recorded from awake animals reflect the anatomical parcellation of the auditory thalamus? Hear Res 131: 135–152, 1999 [DOI] [PubMed] [Google Scholar]
Elhilali M, Fritz JB, Klein DJ, Simon JZ, Shamma SA. Dynamics of precise spike timing in primary auditory cortex. J Neurosci 24: 1159–1172, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ghazanfar AA, Smith-Rohrberg D, Hauser MD. The role of temporal cues in rhesus monkey vocal recognition: orienting asymmetries to reversed calls. Brain Behav Evol 58: 163–172, 2001 [DOI] [PubMed] [Google Scholar]
Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol 32: 613–636, 1969 [DOI] [PubMed] [Google Scholar]
Hackett TA, Preuss TM, Kaas JH. Architectonic identification of the core region in auditory cortex of macaques, chimpanzees, and humans. J Comp Neurol 441: 197–222, 2001 [DOI] [PubMed] [Google Scholar]
Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol 394: 475–495, 1998 [DOI] [PubMed] [Google Scholar]
Hashikawa T, Molinari M, Rausell E, Jones EG. Patchy and laminar terminations of medial geniculate axons in monkey auditory cortex. J Comp Neurol 362: 195–208, 1995 [DOI] [PubMed] [Google Scholar]
Heffner HE, Heffner RS. Temporal lobe lesions and perception of species-specific vocalizations by macaques. Science 226: 75–76, 1984 [DOI] [PubMed] [Google Scholar]
Heil P. Auditory cortical onset responses revisited. I. First-spike timing. J Neurophysiol 77: 2616–2641, 1997a [DOI] [PubMed] [Google Scholar]
Heil P. Auditory cortical onset responses revisited. II. Response strength. J Neurophysiol 77: 2642–2660, 1997b [DOI] [PubMed] [Google Scholar]
Huetz C, Philibert B, Edeline JM. A spike-timing code for discriminating conspecific vocalizations in the thalamocortical system of anesthetized and awake guinea pigs. J Neurosci 29: 334–350, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Jackson LL, Heffner RS, Heffner HE. Free-field audiogram of the Japanese macaque (Macaca fuscata). J Acoust Soc Am 106: 3017–3023, 1999 [DOI] [PubMed] [Google Scholar]
Jones EG, Dell'Anna ME, Molinari M, Rausell E, Hashikawa T. Subdivisions of macaque monkey auditory cortex revealed by calcium-binding protein immunoreactivity. J Comp Neurol 362: 153–170, 1995 [DOI] [PubMed] [Google Scholar]
Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev 84: 541–577, 2004 [DOI] [PubMed] [Google Scholar]
Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci USA 97: 11793–11799, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kajikawa Y, de La Mothe L, Blumell S, Hackett TA. A comparison of neuron response properties in areas A1 and CM of the marmoset monkey auditory cortex: tones and broadband noise. J Neurophysiol 93: 22–34, 2005 [DOI] [PubMed] [Google Scholar]
Kitzes LM, Gibson MM, Rose JE, Hind JE. Initial discharge latency and threshold considerations for some neurons in cochlear nuclear complex of the cat. J Neurophysiol 41: 1165–1182, 1978 [DOI] [PubMed] [Google Scholar]
Kosaki H, Hashikawa T, He J, Jones EG. Tonotopic organization of auditory cortical fields delineated by parvalbumin immunoreactivity in macaque monkeys. J Comp Neurol 386: 304–316, 1997 [PubMed] [Google Scholar]
Kusmierek P, Rauschecker JP. Functional specialization of medial auditory belt cortex in the alert rhesus monkey. J Neurophysiol 102: 1606–1622, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Langner G, Schreiner CE. Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms. J Neurophysiol 60: 1799–1822, 1988 [DOI] [PubMed] [Google Scholar]
Le Prell CG, Moody DB. Perceptual salience of acoustic features of Japanese monkey coo calls. J Comp Psychol 111: 261–274, 1997 [DOI] [PubMed] [Google Scholar]
Lee CC, Imaizumi K, Schreiner CE, Winer JA. Concurrent tonotopic processing streams in auditory cortex. Cereb Cortex 14: 441–451, 2004 [DOI] [PubMed] [Google Scholar]
Liang L, Lu T, Wang X. Neural representations of sinusoidal amplitude and frequency modulations in the primary auditory cortex of awake primates. J Neurophysiol 87: 2237–2261, 2002 [DOI] [PubMed] [Google Scholar]
Malone BJ, Scott BH, Semple MN. Context-dependent adaptive coding of interaural phase disparity in the auditory cortex of awake macaques. J Neurosci 22: 4625–4638, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
Malone BJ, Scott BH, Semple MN. Dynamic amplitude coding in the auditory cortex of awake rhesus macaques. J Neurophysiol 98: 1451–1474, 2007 [DOI] [PubMed] [Google Scholar]
Malone BJ, Scott BH, Semple MN. Temporal codes for amplitude contrast in auditory cortex. J Neurosci 30: 767–784, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
Mardia KaJ, PE Directional Statistics. New York: Wiley, 2000 [Google Scholar]
Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res 50: 275–296, 1973 [DOI] [PubMed] [Google Scholar]
Molinari M, Dell'Anna ME, Rausell E, Leggio MG, Hashikawa T, Jones EG. Auditory thalamocortical pathways defined in monkeys by calcium-binding protein immunoreactivity. J Comp Neurol 362: 171–194, 1995 [DOI] [PubMed] [Google Scholar]
Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol 335: 437–459, 1993 [DOI] [PubMed] [Google Scholar]
Nelken I, Fishbach A, Las L, Ulanovsky N, Farkas D. Primary auditory cortex of cats: feature detection or something else? Biol Cybern 89: 397–406, 2003 [DOI] [PubMed] [Google Scholar]
Nomoto M, Suga N, Katsuki Y. Discharge pattern and inhibition of primary auditory nerve fibers in the monkey. J Neurophysiol 27: 768–787, 1964 [DOI] [PubMed] [Google Scholar]
Oshurkova E, Scheich H, Brosch M. Click train encoding in primary and non-primary auditory cortex of anesthetized macaque monkeys. Neuroscience 153: 1289–1299, 2008 [DOI] [PubMed] [Google Scholar]
Pandya DN, Yeterian EH. Proposed neural circuitry for spatial memory in the primate brain. Neuropsychologia 22: 109–122, 1984 [DOI] [PubMed] [Google Scholar]
Petkov CI, Kayser C, Augath M, Logothetis NK. Functional imaging reveals numerous fields in the monkey auditory cortex. PLoS Biol 4: e215, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
Pfingst BE, O'Connor TA. A vertical stereotaxic approach to auditory cortex in the unanesthetized monkey. J Neurosci Methods 2: 33–45, 1980 [DOI] [PubMed] [Google Scholar]
Pfingst BE, O'Connor TA. Characteristics of neurons in auditory cortex of monkeys performing a simple auditory task. J Neurophysiol 45: 16–34, 1981 [DOI] [PubMed] [Google Scholar]
Phillips DP, Semple MN, Calford MB, Kitzes LM. Level-dependent representation of stimulus frequency in cat primary auditory cortex. Exp Brain Res Exp Hirnforsch 102: 210–226, 1994 [DOI] [PubMed] [Google Scholar]
Phillips DP, Semple MN, Kitzes LM. Factors shaping the tone level sensitivity of single neurons in posterior field of cat auditory cortex. J Neurophysiol 73: 674–686, 1995 [DOI] [PubMed] [Google Scholar]
Poeppel D. The analysis of speech in different temporal integration windows: cerebral lateralization as “asymmetric sampling in time.” Speech Commun 41: 245–255, 2003 [Google Scholar]
Rauschecker JP, Tian B, Hauser M. Processing of complex sounds in the macaque nonprimary auditory cortex. Science 268: 111–114, 1995 [DOI] [PubMed] [Google Scholar]
Rauschecker JP, Tian B, Pons T, Mishkin M. Serial and parallel processing in rhesus monkey auditory cortex. J Comp Neurol 382: 89–103, 1997 [PubMed] [Google Scholar]
Reale RA, Imig TJ. Tonotopic organization in auditory cortex of the cat. J Comp Neurol 192: 265–291, 1980 [DOI] [PubMed] [Google Scholar]
Recanzone GH, Guard DC, Phan ML. Frequency and intensity response properties of single neurons in the auditory cortex of the behaving macaque monkey. J Neurophysiol 83: 2315–2331, 2000 [DOI] [PubMed] [Google Scholar]
Recanzone GH, Schreiner CE, Sutter ML, Beitel RE, Merzenich MM. Functional organization of spectral receptive fields in the primary auditory cortex of the owl monkey. J Comp Neurol 415: 460–481, 1999 [DOI] [PubMed] [Google Scholar]
Rodrigues-Dagaeff C, Simm G, De Ribaupierre Y, Villa A, De Ribaupierre F, Rouiller EM. Functional organization of the ventral division of the medial geniculate body of the cat: evidence for a rostro-caudal gradient of response properties and cortical projections. Hear Res 39: 103–125, 1989 [DOI] [PubMed] [Google Scholar]
Ryan A, Miller J. Single unit responses in the inferior colliculus of the awake and performing rhesus monkey. Exp Brain Res Exp Hirnforsch 32: 389–407, 1978 [DOI] [PubMed] [Google Scholar]
Sadagopan S, Wang X. Level invariant representation of sounds by populations of neurons in primary auditory cortex. J Neurosci 28: 3415–3426, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Schreiber S, Fellous J, Whitmer D, Tiesinga P, Sejnowski T. A new correlation-based measure of spike timing reliability. Neurocomputing 52–54: 925–931, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Scott BH, Malone BJ, Semple MN. Effect of behavioral context on representation of a spatial cue in core auditory cortex of awake macaques. J Neurosci 27: 6489–6499, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
Scott BH, Malone BJ, Semple MN. Representation of dynamic interaural phase difference in auditory cortex of awake rhesus macaques. J Neurophysiol 101: 1781–1799, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Spezio ML, Keller CH, Marrocco RT, Takahashi TT. Head-related transfer functions of the Rhesus monkey. Hear Res 144: 73–88, 2000 [DOI] [PubMed] [Google Scholar]
Thompson KG, Hanes DP, Bichot NP, Schall JD. Perceptual and motor processing stages identified in the activity of macaque frontal eye field neurons during visual search. J Neurophysiol 76: 4040–4055, 1996 [DOI] [PubMed] [Google Scholar]
Ulanovsky N, Las L, Nelken I. Processing of low-probability sounds by cortical neurons. Nat Neurosci 6: 391–398, 2003 [DOI] [PubMed] [Google Scholar]
Wang X, Merzenich MM, Beitel R, Schreiner CE. Representation of a species-specific vocalization in the primary auditory cortex of the common marmoset: temporal and spectral characteristics. J Neurophysiol 74: 2685–2706, 1995 [DOI] [PubMed] [Google Scholar]
Watkins PV, Barbour DL. Specialized neuronal adaptation for preserving input sensitivity. Nat Neurosci 11: 1259–1261, 2008 [DOI] [PubMed] [Google Scholar]
Yin P, Mishkin M, Sutter ML, Fritz JB. Early stages of melody processing: stimulus-sequence and task-dependent neuronal activity in monkey auditory cortical fields A1 and R. J Neurophysiol 100: 3009–3029, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zeng FG, Nie K, Stickney GS, Kong YY, Vongphoe M, Bhargave A, Wei C, Cao K. Speech recognition with amplitude and frequency modulations. Proc Natl Acad Sci USA 102: 2293–2298, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B1] Ahissar E, Nagarajan S, Ahissar M, Protopapas A, Mahncke H, Merzenich MM. Speech comprehension is correlated with temporal response patterns recorded from auditory cortex. Proc Natl Acad Sci USA 98: 13367–13372, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B2] Barbour DL, Wang X. Auditory cortical responses elicited in awake primates by random spectrum stimuli. J Neurosci 23: 7194–7206, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] Bartlett EL, Wang X. Neural representations of temporally modulated signals in the auditory thalamus of awake primates. J Neurophysiol 97: 1005–1017, 2007 [DOI] [PubMed] [Google Scholar]

[B4] Bendor D, Wang X. Differential neural coding of acoustic flutter within primate auditory cortex. Nat Neurosci 10: 763–771, 2007 [DOI] [PubMed] [Google Scholar]

[B5] Bendor D, Wang X. Neural response properties of primary, rostral, and rostrotemporal core fields in the auditory cortex of marmoset monkeys. J Neurophysiol 100: 888–906, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] Bieser A, Muller-Preuss P. Auditory responsive cortex in the squirrel monkey: neural responses to amplitude-modulated sounds. Exp Brain Res Exp Hirnforsch 108: 273–284, 1996 [DOI] [PubMed] [Google Scholar]

[B7] Boemio A, Fromm S, Braun A, Poeppel D. Hierarchical and asymmetric temporal sensitivity in human auditory cortices. Nat Neurosci 8: 389–395, 2005 [DOI] [PubMed] [Google Scholar]

[B8] Cheung SW, Bedenbaugh PH, Nagarajan SS, Schreiner CE. Functional organization of squirrel monkey primary auditory cortex: responses to pure tones. J Neurophysiol 85: 1732–1749, 2001 [DOI] [PubMed] [Google Scholar]

[B9] Cipolloni PB, Pandya DN. Golgi, histochemical, and immunocytochemical analyses of the neurons of auditory-related cortices of the rhesus monkey. Exp Neurol 114: 104–122, 1991 [DOI] [PubMed] [Google Scholar]

[B10] Cohen YE, Theunissen F, Russ BE, Gill P. Acoustic features of rhesus vocalizations and their representation in the ventrolateral prefrontal cortex. J Neurophysiol 97: 1470–1484, 2007 [DOI] [PubMed] [Google Scholar]

[B11] Creutzfeldt O, Hellweg FC, Schreiner C. Thalamocortical transformation of responses to complex auditory stimuli. Exp Brain Res Exp Hirnforsch 39: 87–104, 1980 [DOI] [PubMed] [Google Scholar]

[B12] de la Mothe LA, Blumell S, Kajikawa Y, Hackett TA. Thalamic connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol 496: 72–96, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B13] Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci 8: 1684–1689, 2005 [DOI] [PubMed] [Google Scholar]

[B14] DiCarlo JJ, Lane JW, Hsiao SS, Johnson KO. Marking microelectrode penetrations with fluorescent dyes. J Neurosci Methods 64: 75–81, 1996 [DOI] [PubMed] [Google Scholar]

[B15] Edeline JM, Manunta Y, Nodal FR, Bajo VM. Do auditory responses recorded from awake animals reflect the anatomical parcellation of the auditory thalamus? Hear Res 131: 135–152, 1999 [DOI] [PubMed] [Google Scholar]

[B16] Elhilali M, Fritz JB, Klein DJ, Simon JZ, Shamma SA. Dynamics of precise spike timing in primary auditory cortex. J Neurosci 24: 1159–1172, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] Ghazanfar AA, Smith-Rohrberg D, Hauser MD. The role of temporal cues in rhesus monkey vocal recognition: orienting asymmetries to reversed calls. Brain Behav Evol 58: 163–172, 2001 [DOI] [PubMed] [Google Scholar]

[B18] Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J Neurophysiol 32: 613–636, 1969 [DOI] [PubMed] [Google Scholar]

[B19] Hackett TA, Preuss TM, Kaas JH. Architectonic identification of the core region in auditory cortex of macaques, chimpanzees, and humans. J Comp Neurol 441: 197–222, 2001 [DOI] [PubMed] [Google Scholar]

[B20] Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol 394: 475–495, 1998 [DOI] [PubMed] [Google Scholar]

[B21] Hashikawa T, Molinari M, Rausell E, Jones EG. Patchy and laminar terminations of medial geniculate axons in monkey auditory cortex. J Comp Neurol 362: 195–208, 1995 [DOI] [PubMed] [Google Scholar]

[B22] Heffner HE, Heffner RS. Temporal lobe lesions and perception of species-specific vocalizations by macaques. Science 226: 75–76, 1984 [DOI] [PubMed] [Google Scholar]

[B23] Heil P. Auditory cortical onset responses revisited. I. First-spike timing. J Neurophysiol 77: 2616–2641, 1997a [DOI] [PubMed] [Google Scholar]

[B24] Heil P. Auditory cortical onset responses revisited. II. Response strength. J Neurophysiol 77: 2642–2660, 1997b [DOI] [PubMed] [Google Scholar]

[B25] Huetz C, Philibert B, Edeline JM. A spike-timing code for discriminating conspecific vocalizations in the thalamocortical system of anesthetized and awake guinea pigs. J Neurosci 29: 334–350, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] Jackson LL, Heffner RS, Heffner HE. Free-field audiogram of the Japanese macaque (Macaca fuscata). J Acoust Soc Am 106: 3017–3023, 1999 [DOI] [PubMed] [Google Scholar]

[B27] Jones EG, Dell'Anna ME, Molinari M, Rausell E, Hashikawa T. Subdivisions of macaque monkey auditory cortex revealed by calcium-binding protein immunoreactivity. J Comp Neurol 362: 153–170, 1995 [DOI] [PubMed] [Google Scholar]

[B28] Joris PX, Schreiner CE, Rees A. Neural processing of amplitude-modulated sounds. Physiol Rev 84: 541–577, 2004 [DOI] [PubMed] [Google Scholar]

[B29] Kaas JH, Hackett TA. Subdivisions of auditory cortex and processing streams in primates. Proc Natl Acad Sci USA 97: 11793–11799, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B30] Kajikawa Y, de La Mothe L, Blumell S, Hackett TA. A comparison of neuron response properties in areas A1 and CM of the marmoset monkey auditory cortex: tones and broadband noise. J Neurophysiol 93: 22–34, 2005 [DOI] [PubMed] [Google Scholar]

[B31] Kitzes LM, Gibson MM, Rose JE, Hind JE. Initial discharge latency and threshold considerations for some neurons in cochlear nuclear complex of the cat. J Neurophysiol 41: 1165–1182, 1978 [DOI] [PubMed] [Google Scholar]

[B32] Kosaki H, Hashikawa T, He J, Jones EG. Tonotopic organization of auditory cortical fields delineated by parvalbumin immunoreactivity in macaque monkeys. J Comp Neurol 386: 304–316, 1997 [PubMed] [Google Scholar]

[B33] Kusmierek P, Rauschecker JP. Functional specialization of medial auditory belt cortex in the alert rhesus monkey. J Neurophysiol 102: 1606–1622, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B34] Langner G, Schreiner CE. Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms. J Neurophysiol 60: 1799–1822, 1988 [DOI] [PubMed] [Google Scholar]

[B35] Le Prell CG, Moody DB. Perceptual salience of acoustic features of Japanese monkey coo calls. J Comp Psychol 111: 261–274, 1997 [DOI] [PubMed] [Google Scholar]

[B36] Lee CC, Imaizumi K, Schreiner CE, Winer JA. Concurrent tonotopic processing streams in auditory cortex. Cereb Cortex 14: 441–451, 2004 [DOI] [PubMed] [Google Scholar]

[B37] Liang L, Lu T, Wang X. Neural representations of sinusoidal amplitude and frequency modulations in the primary auditory cortex of awake primates. J Neurophysiol 87: 2237–2261, 2002 [DOI] [PubMed] [Google Scholar]

[B38] Malone BJ, Scott BH, Semple MN. Context-dependent adaptive coding of interaural phase disparity in the auditory cortex of awake macaques. J Neurosci 22: 4625–4638, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B39] Malone BJ, Scott BH, Semple MN. Dynamic amplitude coding in the auditory cortex of awake rhesus macaques. J Neurophysiol 98: 1451–1474, 2007 [DOI] [PubMed] [Google Scholar]

[B40] Malone BJ, Scott BH, Semple MN. Temporal codes for amplitude contrast in auditory cortex. J Neurosci 30: 767–784, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B41] Mardia KaJ, PE Directional Statistics. New York: Wiley, 2000 [Google Scholar]

[B42] Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res 50: 275–296, 1973 [DOI] [PubMed] [Google Scholar]

[B43] Molinari M, Dell'Anna ME, Rausell E, Leggio MG, Hashikawa T, Jones EG. Auditory thalamocortical pathways defined in monkeys by calcium-binding protein immunoreactivity. J Comp Neurol 362: 171–194, 1995 [DOI] [PubMed] [Google Scholar]

[B44] Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol 335: 437–459, 1993 [DOI] [PubMed] [Google Scholar]

[B45] Nelken I, Fishbach A, Las L, Ulanovsky N, Farkas D. Primary auditory cortex of cats: feature detection or something else? Biol Cybern 89: 397–406, 2003 [DOI] [PubMed] [Google Scholar]

[B46] Nomoto M, Suga N, Katsuki Y. Discharge pattern and inhibition of primary auditory nerve fibers in the monkey. J Neurophysiol 27: 768–787, 1964 [DOI] [PubMed] [Google Scholar]

[B47] Oshurkova E, Scheich H, Brosch M. Click train encoding in primary and non-primary auditory cortex of anesthetized macaque monkeys. Neuroscience 153: 1289–1299, 2008 [DOI] [PubMed] [Google Scholar]

[B48] Pandya DN, Yeterian EH. Proposed neural circuitry for spatial memory in the primate brain. Neuropsychologia 22: 109–122, 1984 [DOI] [PubMed] [Google Scholar]

[B49] Petkov CI, Kayser C, Augath M, Logothetis NK. Functional imaging reveals numerous fields in the monkey auditory cortex. PLoS Biol 4: e215, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B50] Pfingst BE, O'Connor TA. A vertical stereotaxic approach to auditory cortex in the unanesthetized monkey. J Neurosci Methods 2: 33–45, 1980 [DOI] [PubMed] [Google Scholar]

[B51] Pfingst BE, O'Connor TA. Characteristics of neurons in auditory cortex of monkeys performing a simple auditory task. J Neurophysiol 45: 16–34, 1981 [DOI] [PubMed] [Google Scholar]

[B52] Phillips DP, Semple MN, Calford MB, Kitzes LM. Level-dependent representation of stimulus frequency in cat primary auditory cortex. Exp Brain Res Exp Hirnforsch 102: 210–226, 1994 [DOI] [PubMed] [Google Scholar]

[B53] Phillips DP, Semple MN, Kitzes LM. Factors shaping the tone level sensitivity of single neurons in posterior field of cat auditory cortex. J Neurophysiol 73: 674–686, 1995 [DOI] [PubMed] [Google Scholar]

[B54] Poeppel D. The analysis of speech in different temporal integration windows: cerebral lateralization as “asymmetric sampling in time.” Speech Commun 41: 245–255, 2003 [Google Scholar]

[B55] Rauschecker JP, Tian B, Hauser M. Processing of complex sounds in the macaque nonprimary auditory cortex. Science 268: 111–114, 1995 [DOI] [PubMed] [Google Scholar]

[B56] Rauschecker JP, Tian B, Pons T, Mishkin M. Serial and parallel processing in rhesus monkey auditory cortex. J Comp Neurol 382: 89–103, 1997 [PubMed] [Google Scholar]

[B57] Reale RA, Imig TJ. Tonotopic organization in auditory cortex of the cat. J Comp Neurol 192: 265–291, 1980 [DOI] [PubMed] [Google Scholar]

[B58] Recanzone GH, Guard DC, Phan ML. Frequency and intensity response properties of single neurons in the auditory cortex of the behaving macaque monkey. J Neurophysiol 83: 2315–2331, 2000 [DOI] [PubMed] [Google Scholar]

[B59] Recanzone GH, Schreiner CE, Sutter ML, Beitel RE, Merzenich MM. Functional organization of spectral receptive fields in the primary auditory cortex of the owl monkey. J Comp Neurol 415: 460–481, 1999 [DOI] [PubMed] [Google Scholar]

[B60] Rodrigues-Dagaeff C, Simm G, De Ribaupierre Y, Villa A, De Ribaupierre F, Rouiller EM. Functional organization of the ventral division of the medial geniculate body of the cat: evidence for a rostro-caudal gradient of response properties and cortical projections. Hear Res 39: 103–125, 1989 [DOI] [PubMed] [Google Scholar]

[B61] Ryan A, Miller J. Single unit responses in the inferior colliculus of the awake and performing rhesus monkey. Exp Brain Res Exp Hirnforsch 32: 389–407, 1978 [DOI] [PubMed] [Google Scholar]

[B62] Sadagopan S, Wang X. Level invariant representation of sounds by populations of neurons in primary auditory cortex. J Neurosci 28: 3415–3426, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B63] Schreiber S, Fellous J, Whitmer D, Tiesinga P, Sejnowski T. A new correlation-based measure of spike timing reliability. Neurocomputing 52–54: 925–931, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B64] Scott BH, Malone BJ, Semple MN. Effect of behavioral context on representation of a spatial cue in core auditory cortex of awake macaques. J Neurosci 27: 6489–6499, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B65] Scott BH, Malone BJ, Semple MN. Representation of dynamic interaural phase difference in auditory cortex of awake rhesus macaques. J Neurophysiol 101: 1781–1799, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B66] Spezio ML, Keller CH, Marrocco RT, Takahashi TT. Head-related transfer functions of the Rhesus monkey. Hear Res 144: 73–88, 2000 [DOI] [PubMed] [Google Scholar]

[B67] Thompson KG, Hanes DP, Bichot NP, Schall JD. Perceptual and motor processing stages identified in the activity of macaque frontal eye field neurons during visual search. J Neurophysiol 76: 4040–4055, 1996 [DOI] [PubMed] [Google Scholar]

[B68] Ulanovsky N, Las L, Nelken I. Processing of low-probability sounds by cortical neurons. Nat Neurosci 6: 391–398, 2003 [DOI] [PubMed] [Google Scholar]

[B69] Wang X, Merzenich MM, Beitel R, Schreiner CE. Representation of a species-specific vocalization in the primary auditory cortex of the common marmoset: temporal and spectral characteristics. J Neurophysiol 74: 2685–2706, 1995 [DOI] [PubMed] [Google Scholar]

[B70] Watkins PV, Barbour DL. Specialized neuronal adaptation for preserving input sensitivity. Nat Neurosci 11: 1259–1261, 2008 [DOI] [PubMed] [Google Scholar]

[B71] Yin P, Mishkin M, Sutter ML, Fritz JB. Early stages of melody processing: stimulus-sequence and task-dependent neuronal activity in monkey auditory cortical fields A1 and R. J Neurophysiol 100: 3009–3029, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B72] Zeng FG, Nie K, Stickney GS, Kong YY, Vongphoe M, Bhargave A, Wei C, Cao K. Speech recognition with amplitude and frequency modulations. Proc Natl Acad Sci USA 102: 2293–2298, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Transformation of Temporal Processing Across Auditory Cortex of Awake Macaques

Brian H Scott

Brian J Malone

Malcolm N Semple

Abstract

INTRODUCTION

Fig. 2.

METHODS

Recording sites

Fig. 3.

Basic response properties of auditory cortex

FREQUENCY TUNING.

RATE-LEVEL FUNCTIONS.

RESPONSE LATENCY.

DISCHARGE RATES AND RELIABILITY.

Amplitude- and frequency-modulated stimuli

ANALYSIS OF SAM AND SFM.

Statistics and pooling of data sets

RESULTS

Tonotopic organization of the core and delineation of cortical fields

Fig. 1.

DEFINING THE FIELDS.

Table 1.

DISTINGUISHING CORE AND BELT.

Fig. 4.

Comparing basic response properties within the core

DISCHARGE RATES.

Fig. 5.

BFs AND TUNING WIDTH.

Fig. 6.

RATE-LEVEL FUNCTIONS.

Fig. 7.

RESPONSE TIMING: LATENCY AND RELIABILITY.

Fig. 8.

Fig. 9.

Fig. 10.

Fig. 11.

AM and FM tones

MTFs.

Table 2.

Fig. 12.

Table 3.

Population response to dynamic stimuli

Fig. 13.

Temporal properties of the auditory belt

Fig. 14.

DISCUSSION

Response properties and tonotopic organization in awake cortex

Tuning for sound intensity

Onset latency and temporal processing of dynamic stimuli

Thalamic input and correspondence to other species

Functional implications of cortical organization

GRANTS

DISCLOSURES

ACKNOWLEDGMENTS

REFERENCES

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases