Abstract
Purkinje neurons can spike very rapidly for sustained periods. We examined the cycle of sodium channel gating during high-frequency firing of Purkinje neurons, focusing on the kinetics of sodium channel inactivation and recovery during and after spikes. To analyze sodium channel availability during spiking, we recorded the firing patterns of acutely dissociated Purkinje neurons in current clamp and used these records as command voltages in voltage-clamp experiments in the same cell, adding step depolarizations at various points to assay availability. Sodium channel availability decreased abruptly during the spike, as expected, but never reached zero. During spontaneous firing (∼40 Hz at 37°C), availability decreased from nearly 90% before the spike to about 10–20% after the spike. With fast steady firing stimulated by current injection (∼300 Hz at 37°C), the availability decreased from about 60% between spikes to roughly 15–20% after the spike. Thus even at the fastest firing rates, sodium channel inactivation is incomplete after a spike, leaving a substantial fraction of sodium channels immediately available for activation. Also, inactivation recovered quickly during the early interspike interval (time constant ∼1 ms at 37°C), but developed slowly during the depolarization of the late interspike interval, ensuring high availability until spike threshold. These features of sodium channel gating, especially the availability remaining after the spike, reduce the refractory period and facilitate rapid repetitive firing.
INTRODUCTION
Mammalian central neurons exhibit a wide range of spiking behaviors. Most cortical and hippocampal pyramidal cells show “regular spiking” behavior characterized by moderate firing rates and a strong degree of adaptation during maintained stimuli, whereas GABAergic neurons often have a “fast-spiking” phenotype, with a capability of firing steadily at high frequencies during prolonged stimulation (Connors and Gutnick 1990; Kawaguchi 1993; McCormick et al. 1985; Nowak et al. 2003). There is at least a rough correlation of spiking behavior with spike width, with fast-spiking neurons having relatively narrow spikes compared with those of regular-spiking pyramidal neurons (Connors and Gutnick 1990; Erisir et al. 1999; McCormick et al. 1985; Tateno et al. 2004; Zhou and Hablitz 1996). Perhaps most strikingly, there is a strong correlation between narrow action potentials and maximal firing frequency in cell-to-cell comparisons within populations of specific cell types, such as in the medial vestibular nucleus (Gittis et al. 2010).
During repetitive firing of action potentials, voltage-dependent sodium channels undergo a cycle of activation and inactivation during each spike followed by recovery from inactivation between spikes. The degree of inactivation and kinetics of recovery from inactivation are likely key factors in determining the refractory period and, in consequence, firing frequency. The kinetics of sodium channels during action potentials can be explored in voltage-clamp experiments using action potential waveforms as command voltages (Raman and Bean 1997). Such experiments have shown different results in different types of mammalian neurons, with complete inactivation of sodium channels during action potentials of tuberomammillary nucleus neurons (Taddese and Bean 2002), suprachiasmatic nucleus neurons (Jackson et al. 2004), mossy fiber boutons (Alle et al. 2009), and hippocampal CA1 and cortical pyramidal neurons (Carter and Bean 2009), but incomplete inactivation in several types of fast-spiking neurons, including cerebellar Purkinje neurons (Carter and Bean 2009; Raman and Bean 1997, 1999), vestibular nucleus neurons (Gittis et al. 2010), and cortical GABAergic interneurons (Carter and Bean 2009). In principle, the incomplete inactivation during action potentials in fast-spiking neurons—and resulting sodium channel availability immediately after a spike—could facilitate fast firing rates. So far, however, measurements of inactivation have been made only with spikes occurring during spontaneous firing or with minimal stimulation, not during conditions of rapid firing. With strong stimulation and repetitive fast firing, spike shape can change substantially and changes in spike shape could well affect sodium channel behavior.
Here, we used the action potential clamp technique to directly measure the time course and kinetics of sodium current over a broad range of spiking rates in cerebellar Purkinje neurons. We find that inactivation is incomplete during Purkinje neuron action potentials, even at the fastest sustainable firing frequencies, both at room temperature (23°C) and at 37°C. Because of the incomplete inactivation, substantial sodium channel availability is present immediately after a spike. The incomplete inactivation during each spike is likely critical in enabling high-frequency firing in Purkinje neurons and other fast-spiking neurons with narrow action potentials.
METHODS
Preparation of cells
Experiments were performed with cerebellar Purkinje neurons acutely dissociated from Black Swiss mice (postnatal days 14–20). Mice were anesthetized with isoflurane and the cerebellum was quickly removed into ice-cold solution consisting of (in mM): 110 NaCl, 2.5 KCl, 10 HEPES, 25 glucose, 75 sucrose, and 7.5 MgCl2 (pH adjusted to 7.4 with NaOH). The cerebellum was cut into chunks (∼1 mm3) and was treated for 10–20 min at room temperature with 3 mg/ml protease XXIII (Sigma Life Science) dissolved in a dissociation solution consisting of (in mM): 82 Na2SO4, 30 K2SO4, 5 MgCl2, 10 glucose, and 10 HEPES (pH adjusted to 7.4 with NaOH). The protease solution was then replaced by ice-cold dissociation solution containing 1 mg/ml trypsin inhibitor and 1 mg/ml bovine serum albumin and the chunks were kept on ice in this solution until immediately before use. To release individual cells, the tissue was passed through Pasteur pipettes with fire-polished tips. A drop of the suspension was placed in the recording chamber and diluted with a large volume of Tyrode's solution, consisting of (in mM): 155 NaCl, 3.5 KCl, 1.5 CaCl2, 1 MgCl2, 10 glucose, and 10 HEPES (pH adjusted to 7.4 with ∼5 mM NaOH). Purkinje neurons could be recognized by their large size and a single large dendritic stump.
Recording
Electrodes were pulled from borosilicate glass (VWR 53432–921) using a Sutter Instrument P-97 puller. Electrode resistances were 1.5–3.0 MΩ when filled with the internal pipette solution, consisting of (in mM): 140 potassium methanesulfonate, 10 NaCl, 1.8 MgCl2, 10 HEPES, 1 EGTA, 0.2 CaCl2, 14 creatine phosphate (Tris salt), 4 MgATP, and 0.3 Tris-GTP (pH adjusted to 7.36 with KOH). This solution has about 200 nM free calcium, calculated using Maxchelator (http://www.stanford.edu/∼cpatton/maxc.html). Electrodes were wrapped with Parafilm (American National Can) from the shank to near the tip to reduce pipette capacitance (to levels ranging from 6.0 to 12.5 pF), allowing optimal series resistance compensation without oscillation. Reported membrane potentials are corrected for a liquid junction potential of −8 mV between the internal solution and the Tyrode's solution in which current was zeroed before sealing onto the cell, measured using a flowing 3 M KCl reference electrode as described by Neher (1992).
Solution exchange and temperature control
Cells were lifted while a gigaseal was forming and positioned in front of a series of quartz flow pipes (250 μm ID, 350 μm OD; PolyMicro Technologies) attached with cyanoacrylate glue to an aluminum square rod (cross section: 1.5 × 0.5 cm) whose temperature is controlled using resistive heating elements and a feedback-controlled temperature controller (TC-344B; Warner Instruments). The flow pipes extend only about 1 mm from the aluminum rod, so the bulk solution near the ends of the flow pipes is quickly warmed by the large volume of the aluminum rod (which is electrically insulated with nail polish). Measured using a miniature thermocouple, the solution exiting from the flow pipes was found to be 37°C when the temperature of the aluminum rod was set to 38°C. With this apparatus, each of the 8–10 flow pipes is heated identically and continuously, so rapid (<1 s) solution changes can be made without fluctuations of temperature. Experiments were done both at room temperature (23°C) and at 37°C.
Electrophysiological methods
Recordings were made using a Multiclamp 700B amplifier (Molecular Devices) interfaced to a Digitdata 1322A A/D converter using pCLAMP 9.0 software (Molecular Devices). Data were filtered at 10 kHz with a 4-pole Bessel filter (Warner Instruments) and digitized at either 50 or 200 kHz. Analysis was done using IGOR Pro (WaveMetrics) using DataAccess (Bruxton Software) to import pCLAMP files into IGOR Pro.
Current-clamp recordings were performed after pipette capacity compensation (∼60% of the measured pipette capacitance) and bridge-balance compensation. After recording a segment of spontaneous firing without current injection, a series of 1-s current pulses of increasing magnitude was delivered. Firing frequency was quantified as the average frequency during the 1-s period. Spike width was measured at half-maximal height, with height calculated as the voltage difference between the peak of the spike and the minimum of the trough of the afterhyperpolarization after the spike. Spike threshold was defined as the point where the rate of depolarization is 4% of the maximum rate during the upstroke of the spike.
After recording action potentials in current clamp, the amplifier was switched to voltage-clamp mode and tuned for optimal capacity and series resistance compensation using the amplifier circuitry (typically, compensation for roughly 90% of a series resistance ranging from 2 to 10.5 MΩ). Because the sodium currents are very large in Purkinje neurons, we used a partially blocking concentration (30–90 nM) of tetrodotoxin (TTX) to reduce the currents and the associated errors due to residual series resistance. The reduced sodium currents were then subtracted from those recorded in the presence of a saturating concentration of TTX (1 μM).
Action potential clamp and time-lag correction
The combination of the rapid and large voltage changes during action potentials and the large sodium current density in Purkinje neurons required careful tuning of the voltage-clamp circuitry for series resistance compensation, as well as reduction of the sodium current to reduce errors arising from imperfect compensation.
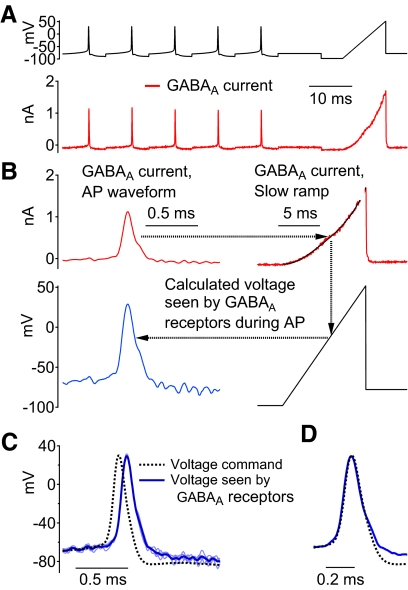
A particular concern was whether the overall system, including the partially compensated resistance of the pipette in series with the cell capacitance, allows faithful imposition of voltage using the very narrow spike waveforms of Purkinje neurons, which can have widths at half-amplitude of about 200 μs. In previous experiments (Carter and Bean 2009), we did control experiments using a second electrode to record intracellular voltage while a cell was voltage clamped with a spike waveform. These experiments showed that the action potential command voltage was accurately imposed on the cell membrane, with measured voltage at the peak of the action potential differing from the command by only about 2 mV, but with a time lag that probably reflects a delay in charging the capacitance of the cell by passing current through the series resistance of the pipette. This time lag varied from cell to cell. Because it is impractical to routinely use a second electrode to record cell voltage, we developed two methods to quantify the lag in experiments using only one electrode. Figure 1 shows the first method, which assays the voltage on the cell membrane during narrow spikes by recording current through ionotropic γ-aminobutyric acid type A (GABAA) channels and which gives a measurement of the membrane voltage as well as the time lag. A voltage command (Fig. 1A, top) was constructed from a prerecorded action potential repeated five times, followed by a slow voltage ramp. GABAA currents (Fig. 1A, bottom) were elicited by application of 5 μM muscimol (Sigma Life Science) and isolated by subtraction of currents before and after muscimol application. To better isolate GABAA current, voltage-dependent currents were minimized by using 1 μM TTX and an external solution with tetraethylammonium (TEA) replacing sodium. Figure 1B illustrates the process by which the GABAA currents during the spike waveforms were used to infer the voltage established at the cell membrane (i.e., the voltage seen by the GABAA receptors during the spike waveform). The ramp (from −98 to +52 mV over 10 ms) defines the current–voltage relationship for the muscimol-evoked current (Fig. 1B, top right); because the ramp is relatively slow, it can reasonably be assumed that the cell membrane voltage at any time during the ramp closely corresponds to the command voltage. The GABAA current recorded at each time during the action potential waveform could then be converted to the membrane voltage seen by the GABAA-receptor channels by using the ramp current–voltage relationship as a look-up table (Fig. 1B, right panels). The resulting plot of membrane voltage versus time (Fig. 1B, bottom left) was found to closely match the action potential command waveform, but with a time delay of about 80 μs (Fig. 1C shows the aligned traces). The time delay is partly due to the effect of the low-pass filter used to filter the recorded current; this filter (a 10-kHz 4-pole Bessel filter) was found to introduce a time delay of 40 μs. The results from this test fit well with experiments using a second voltage-measuring electrode in suggesting that membrane voltage can be accurately clamped during the narrow action potential voltage command but with a time delay. The procedure also provides a measurement of the time delay (in this cell, 40 μs after accounting for the effect of the filter), so that recorded currents can be accurately aligned with the command waveforms.
Fig. 1.
Measurement of action potential clamp fidelity using muscimol-evoked γ-aminobutyric acid type A (GABAA) currents. A, top: the voltage command, composed of repeated prerecorded Purkinje neuron action potentials followed by a slow (15 mV/ms) voltage ramp. Bottom: currents evoked by 5 μM muscimol recorded in the presence of 1 μM tetrodotoxin (TTX) and with tetraethylammonium (TEA) replacing external Na (obtained by subtraction of traces acquired immediately before muscimol application). B: muscimol-evoked current (red traces) during an action potential was converted to membrane voltage seen by the GABAA receptors in the cell membrane (blue trace) by comparing each point during the action potential with the current during the slow voltage ramp. To reduce noise, the ramp-evoked current was fit by a smooth curve (an empirical polynomial fit). C: membrane voltage (5 individual traces shown in light blue, average in dark blue) calculated from the muscimol-evoked current matches well with the command voltage (black dashed trace) except for a time delay. D: the same traces as in C but with the calculated membrane voltage shifted by 80 μs.
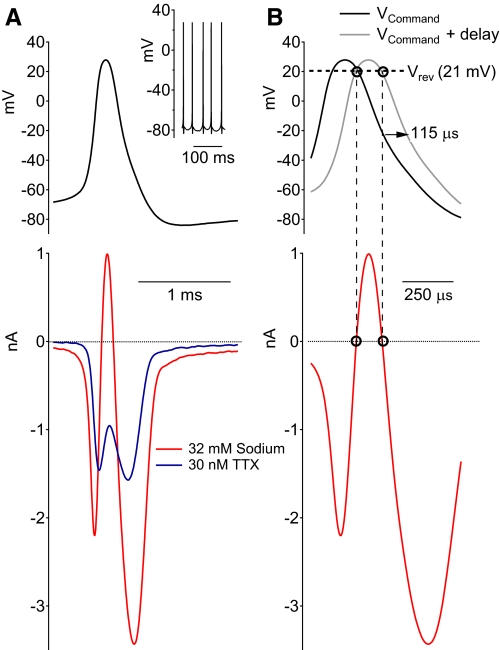
Figure 2 shows a second method to estimate the accuracy of the voltage clamp and to measure the time-lag while using only one electrode. Here, action potentials were recorded in current clamp (Fig. 2A, inset) and used as voltage command in the same cell. Sodium current was recorded under two different conditions: in the presence of a partially blocking concentration of TTX (30 nM TTX; Fig. 2A, blue trace) or after reducing the external sodium concentration from 160 to 32 mM (Fig. 2A, red trace). Reducing external sodium to 32 mM resulted in a sodium channel reversal potential of +21 mV (as measured by a series of depolarizations from a holding potential of −88 mV). Because the action potential peak (+28 mV) is depolarized relative to the altered reversal potential, the current through sodium channels becomes outward just before the peak. The time lag of the currents was measured by aligning the reversal of the sodium current during the spike waveform with the reversal potential (Fig. 2B). For the example shown in Fig. 2B, the time lag was 115 μs, or an additional delay of 75 μs after accounting for the 40 μs delay from the low-pass filter (Fig. 2B).
Fig. 2.
Measurement of time delay in cell membrane voltage using sodium channel reversal potential. A: spontaneous action potentials recorded in current clamp (inset) were used as the voltage-clamp command (top trace). Sodium currents evoked by the action potential waveform were recorded after being reduced either by partial block with 30 nM TTX (blue trace) or by reducing the extracellular concentration of sodium from 160 to 32 mM (red trace). B: using the traces recorded with 32 mM sodium, the delay in the voltage seen by the cell membrane was estimated by aligning the time of current reversal from inward to outward so that it matched the time at which the expected reversal potential of +21 mV occurred during the voltage command. The time delay in the current record for this neuron was 115 μs, of which 40 μs can be ascribed to the effect of the low-pass filter (a 10-kHz 4-pole Bessel filter) used to filter the current record.
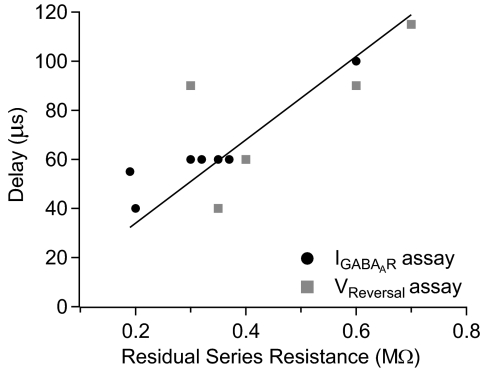
Figure 3 is a summary of time-lag measurements made using each of these procedures, plotted against the series resistance that remained after partial compensation (residual series resistance). The time lag was strongly correlated with residual series resistance (Spearman rank correlation coefficient = 0.73, P < 0.02, n = 11) and the relationship could be fit reasonably well by a straight line. Having established the relationship, we used the linear fit to estimate the time lag in cells in which it was not measured directly.
Fig. 3.
Collected results of the time delay of voltage at the cell membrane relative to command voltage. The delay was measured either by aligning muscimol-evoked currents (as in Fig. 1, black circles) or by aligning the action potential voltage command with the altered sodium reversal potential (as in Fig. 2, gray squares). The measured delays shown were corrected for the 40 μs delay arising from the low-pass Bessel filter. The delay was found to be correlated with the residual series resistance remaining after partial series resistance compensation. The solid line is the best-fit linear relationship.
Statistics and curve fitting
Collected results are presented as the mean ± SD. The nonparametric Mann–Whitney U test was used to make comparisons between two groups. The nonparametric Spearman rank-coefficient test was used to compare trends. Statistical significance was calculated from Monte Carlo simulations and reported as significant if P values were <0.05. Single exponential fits to the recovery from inactivation data were made using IGOR Pro routines.
RESULTS
Sodium currents during action potential firing
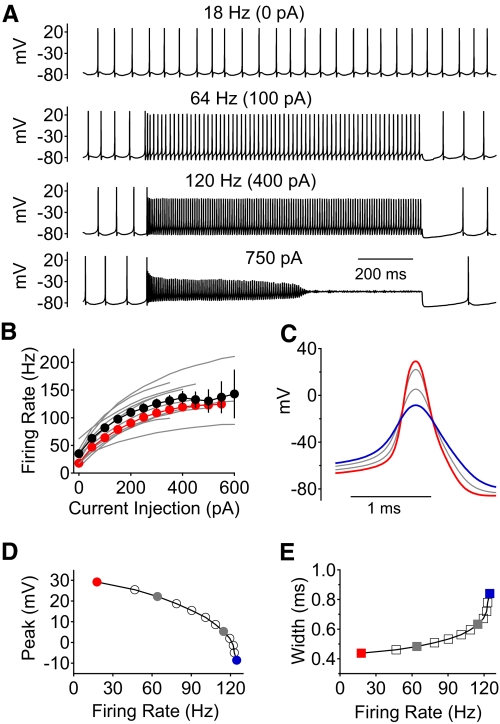
Acutely dissociated Purkinje neurons retain the capability of sustained, rapid firing when stimulated by long current injections (Khaliq et al. 2003) and thus are an ideal preparation for combining current-clamp recordings with voltage-clamp characterization of sodium channel kinetics during natural firing patterns. Figure 4A shows current-clamp recordings from a dissociated Purkinje neuron in response to long (1-s) current injections at room temperature (23°C). This neuron fired spontaneously at 18 Hz (top) in a highly regular, tonic manner. In response to injection of increasing amounts for current, the cell fired in a sustained manner over the 1-s period of current injection for current levels ≤550 pA, where the steady firing frequency was about 120 Hz. With stronger current injections, the cell fired for several hundred milliseconds before firing faded out (bottom trace). Figure 4B plots the firing frequency versus current injection (f–I curve) measured in 13 neurons. The results for the cell whose firing is shown in Fig. 4A (red symbols in Fig. 4B) were typical. On average, cells reached a maximum firing frequency (sustained for ≥1 s) of 140 ± 32 Hz (n = 13), achieved for a current injection of 546 ± 234 pA.
Fig. 4.
Spontaneous and stimulated Purkinje neuron action potential firing in response to current injection at 23°C. A: example of voltage recordings of spontaneous action potential firing (top), and firing evoked by 1 s long current injections of increasing magnitude until the neuron ceased firing during the stimulating pulse (in this case during an injection of 750 pA). B: summary of results from 13 neurons plotting the firing frequency vs. current injection; black symbols represent average ± SD and the red symbols are from the example neuron shown in A, C, D, and E. Only pulses in which firing was sustained throughout the full 1-s current injection were included in the average. C: averaged action potentials from each level of current injection for the cell in A, illustrating the change in action potential shape with firing frequency. Red trace: spontaneous action potential. Blue trace: action potential of the most rapid firing before failure. D: action potential peak voltage as a function of firing frequency. E: action potential width (measured at half the maximal amplitude) as a function of firing frequency.
As the firing rate increased with larger amounts of injected current, the action potentials changed shape. Figure 4C shows this effect for the neuron whose firing is shown in Fig. 4A. As the firing rate increased, the peak of the action potential decreased (Fig. 4D) and the width of the action potentials increased (Fig. 4E). However, even at the fastest sustained firing rates, spikes were 40–50 mV high (Fig. 4, C and D), large enough that they would be expected to propagate down the axon with a high probability if occurring in situ (Khaliq and Raman 2005). Thus the fastest firing rates that can be sustained in the dissociated cell bodies can probably also be sustained as propagating action potentials in the axons of Purkinje neurons.
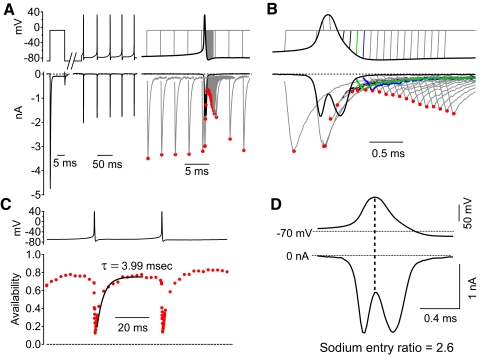
To assay sodium channel inactivation during and between action potentials, we measured sodium channel availability in voltage-clamp experiments by using a series of command waveforms constructed by inserting a voltage step to −8 mV at various times into the waveform of the firing pattern recorded from the cell. Figure 5A shows the voltage command protocol. An initial step from −88 to −8 mV determined the test pulse current with essentially full availability (as determined from inactivation curves like those in Fig. 11A). The command protocol then continued with around 150 ms of action potential firing that was previously recorded (in the same neuron), comprising, in this case, five cycles of firing. Following this, a test step to −8 mV was added to measure sodium channel availability, with the step inserted at various times before, during, and after the last action potential in the train. Peak sodium current during the test pulse (indicated by red circles in Fig. 5, A and B) provided an assay of availability during the firing cycle. To quantify availability, peak sodium current elicited by the test step was normalized to that elicited by the initial step from −88 mV (Fig. 5C). As expected, the sodium channel availability fell abruptly during the spike as channels inactivated. However, the availability never reached zero, even at its minimum immediately after the spike. In the cell whose currents are shown in Fig. 5, which was firing spontaneously at 24 Hz, the availability reached a minimum of 13% immediately after the spike. During the succeeding interspike interval (ISI), the availability increased, reaching a maximum of 78%. The time course of sodium channel recovery from inactivation after a spike could be fit fairly well with a single exponential function with a tau of 3.99 ms (Fig. 5C). The recovery is rapid compared with the duration of the ISI (∼40 ms), so that availability reaches a plateau before the middle of the ISI.
Fig. 5.
Measurement of sodium channel availability during action potential firing. A: each voltage command waveform started with a test step to −8 mV from a holding potential of −88 mV to measure full sodium channel availability, followed by about 150 ms of spontaneous action potential firing that was recorded in the same neuron and finally a voltage step to −8 mV to measure availability, added at different times during and after the last action potential in each of 80 different waveforms. The sodium current elicited by the waveforms is shown below. Currents were reduced to controllable values using subsaturating (30 nM) TTX and currents blocked by subsequent addition of 1 μM TTX were subtracted. Peak current during each step is marked by a red circle. B: sodium currents evoked by a subset of the waveforms shown on a finer timescale. Green traces show the voltage protocol and elicited current corresponding to the minimum availability, achieved shortly before the trough of the action potential. Blue traces correspond to measurements 100 μs later, when recovery from inactivation is just beginning. C: sodium channel availability was measured as peak current evoked by the second pulse to −8 mV, normalized to the current evoked by the first pulse to −8 mV from a holding potential of −88 mV, where essentially all channels are available (Fig. 11A). Availability is plotted as a function of the time during the firing cycle that the second pulse was delivered. Sodium channel availability immediately after the action potential reached a minimum of 13%. The time course of recovery of availability during the interspike interval (ISI) could be fit well by a single exponential with a time constant of 3.99 ms (black trace), with sodium channel availability reaching a maximum of 78% in between spikes. D: sodium current during the action potential waveform showed incomplete inactivation and a large amount of sodium current during the downstroke of the action potential (a sodium entry ratio of 2.59).
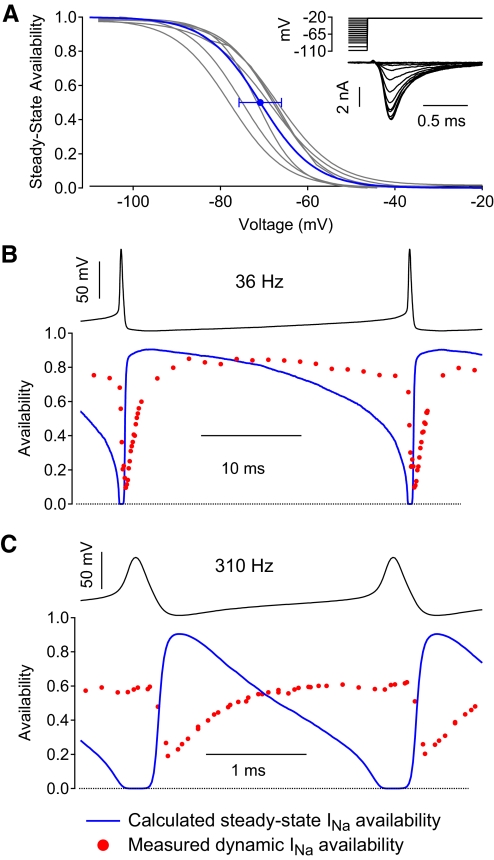
Fig. 11.
Comparison of measured instantaneous availability with predicted steady-state sodium channel availability during firing cycles. A: steady-state availability was measured as a function of voltage at 37°C using 500-ms steps to various voltages followed by a test step to −23 mV. Inset shows example sodium currents from a typical neuron; 30 nM TTX was used to reduce the magnitude of sodium currents to controllable sizes. Gray traces show inactivation curves determined in each of 6 neurons. Blue trace is the Boltzmann curve corresponding to average midpoint and average slope from the 6 neurons; error bars indicate SD of the midpoints determined in individual neurons. B: measured availability (red circles) during the firing cycle during spontaneous firing compared with the steady-state availability (blue) calculated from the average curve in A. C: same for rapid, stimulated firing. Experimental measurements of availability in B and C are from cells shown in Fig. 9, B and H.
The incomplete inactivation of the sodium current during the action potential is evident not only by the nonzero availability as assayed by test pulses, but also by the flow of substantial current during the downstroke of the action potential (Fig. 5D). In fact, more sodium current flows during the downstroke of this action potential than that during the upstroke. This can be quantified as a “sodium entry ratio,” the ratio of the total integrated sodium current during the action potential to that during the upstroke, which is the minimum necessary to form the spike (Carter and Bean 2009). In this neuron, the sodium entry ratio was 2.6.
Sodium channel availability during high-frequency stimulated firing
We next examined sodium channel availability during and between action potentials during higher-frequency stimulated firing, where the spikes are smaller and broader. We found that sodium channel inactivation was incomplete even during the fastest firing that could be achieved. Figure 6 shows measurements of sodium channel availability during the firing cycle for a single neuron at three different firing frequencies at room temperature: 14 Hz (spontaneous firing), 80 Hz (injection of 200 pA), and 107 Hz (injection of 400 pA). As the firing rate increased, the maximal availability reached during the ISI decreased, as might be expected from more frequent action potentials and the more depolarized voltages during the ISI, which had an average voltage of −79 mV during 14 Hz firing, −71 mV during 80 Hz firing, and −69 mV for 107 Hz firing. The minimum availability, reached just after the spike, also decreased with faster firing, but never reached zero.
Fig. 6.
Sodium channel availability during spontaneous and stimulated action potential firing in the same neuron. A: voltage-clamp recordings of sodium current during spontaneous firing, with availability measured using a test step to −8 mV added at various times before, during, and after a spike as in Fig. 5. B: sodium channel availability (current during second pulse normalized to current evoked by a first pulse to −88 mV) plotted as a function of the time during the firing cycle. C: sodium current during the action potential, showing incomplete inactivation during the falling phase. D–F: same analysis but using waveform of higher firing frequency evoked by steady current injection in the same neuron. G–I: same analysis but for a firing frequency near maximal for the same neuron.
The recovery of availability during the ISI could be fit reasonably well by a single exponential for all firing rates. The time constant of recovery decreased as firing became faster: the time constant was 6.1 ms for firing at 14 Hz, 2.5 ms for firing at 80 Hz, and 2.4 ms for firing at 107 Hz. The interpretation of the exponential fit for the faster firing waveforms is complicated because the membrane voltage changes relatively rapidly during the ISI. As will be shown subsequently (Fig. 11), the expected steady-state availability changes rapidly during the ISI for fast firing, so that the exponential change in dynamic availability does not represent the approach to a steady-state value.
At all firing rates, there was substantial sodium current flowing during the downstroke of the action potential, consistent with incomplete inactivation. The sodium entry ratio was 2.41 for 14 Hz spontaneous firing (Fig. 6C), 2.17 for 80 Hz firing (Fig. 6F), and 1.71 for 107 Hz firing (Fig. 6I).
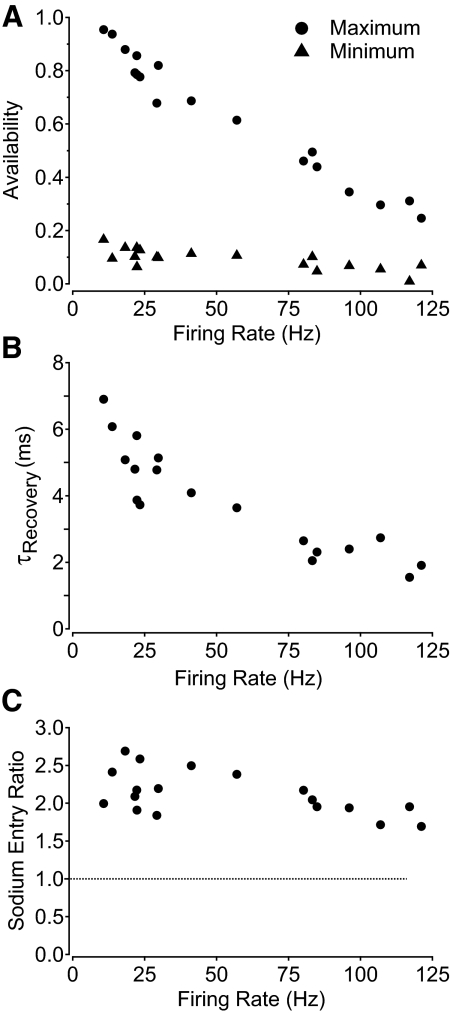
Figure 7 shows collected results for these parameters measured in eight cells over a range of 18 different firing rates. There was a high degree of consistency among cells in the values for maximal and minimal availability at a given firing frequency, with maximal availability declining from nearly 95% with the slowest spontaneous firing to roughly 25% with the fastest stimulated firing (Fig. 7A, circles). Minimum availability immediately after the spike declined from about 15% with the slowest spontaneous firing to about 7% with the fastest stimulated firing (Fig. 7A, triangles). The decrease in recovery time constant with faster firing was also a clear trend, with the time constant decreasing from about 7 ms with the slowest spontaneous firing to nearly 2 ms with the fastest stimulated firing (Fig. 7B). The sodium entry ratio also decreased with increasing firing rate (Fig. 7C), from about 2.5 at lower firing rates to nearly 1.8 at the highest firing rates.
Fig. 7.
Collected results for measurements of sodium channel availability during action potential firing at 23°C. A: maximum availability in between spikes (filled circles) and minimum availability after spikes (filled triangles) during repetitive action potential firing at different frequencies. B: kinetics of recovery of sodium channel availability from minimum to maximum during the ISI, expressed as the time constant for a single exponential fit to the recovery. C: sodium entry ratio during the action potential as a function of firing rate.
Action potential firing at physiological temperature
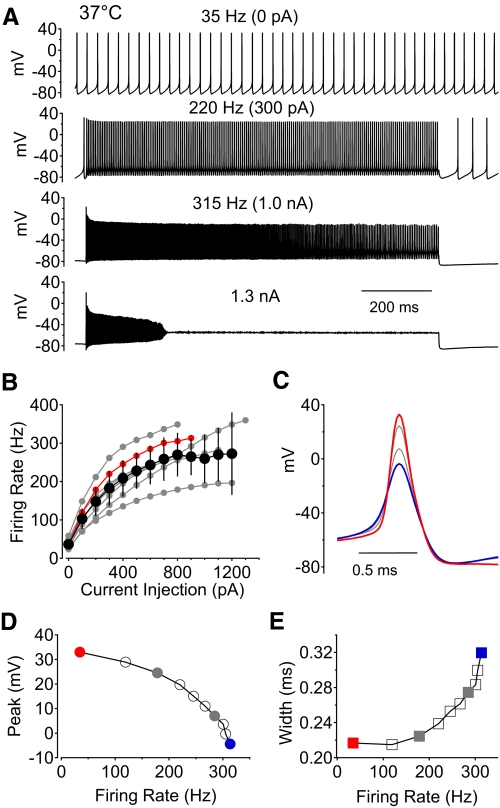
Both action potential shape and sodium channel kinetics are likely to depend significantly on temperature. We therefore did a series of experiments examining sodium channel inactivation and recovery of availability during fast firing at 37°C. Dissociated Purkinje neurons studied at 37°C fired spontaneously, as they do at room temperature. Interestingly, the frequency of spontaneous firing was not dramatically different in the population of cells studied at 37°C (36.7 ± 13.4 Hz, n = 16) compared with those studied at 23°C (34.9 ± 22.9 Hz, n = 13; P = 0.40, Mann–Whitney test). However, spontaneous action potentials at 37°C were substantially narrower (0.23 ± 0.05 ms wide at half-amplitude, n = 16) than those at 23°C (0.49 ± 0.07 ms, n = 13; P < 0.01, Mann–Whitney test). The peak voltage during the spike was slightly less positive at 37°C than that at 23°C (+24 ± 6 mV at 37°C, n = 16 vs. +27 ± 7 mV at 23°C, n = 13; P = 0.11, Mann–Whitney test). Although spontaneous firing rates were not much faster at 37°C than those at 23°C, neurons at 37°C responded to current injections with much higher frequency firing than those at room temperature (Fig. 8). Maximal firing frequency with large current injections reached an average of 309 ± 88 Hz at 37°C (n = 8) compared with 140 ± 32 Hz at 23°C (n = 13; P < 0.01, Mann–Whitney test). With increasing firing frequency, the same trends were observed as at room temperature: spike height decreased while spike width increased (Fig. 8, D and E).
Fig. 8.
Current-clamp recordings of spontaneous and stimulated firing in response to current injection at 37°C. A: voltage recordings of spontaneous action potential firing (top) and firing evoked by 1 s long current injections of increasing magnitude until the neuron ceased firing during the stimulating pulse (in this case during an injection of 1.3 nA). B: summary of results from 8 neurons plotting the firing frequency vs. current injection. Black symbols represent average ± SD; the red symbols are from the example neuron shown in A, C, D, and E. Only pulses in which firing was sustained throughout the full 1-s current injection were included in the average. C: averaged action potentials from the cell in A for each level of current injection, illustrating the change in action potential shape with firing frequency. Red trace: spontaneous action potential. Blue trace: action potential of the most rapid firing before failure. D: action potential peak voltage as a function of firing frequency. E: action potential width (measured at half the maximal amplitude) as a function of firing frequency.
Sodium current availability during firing at 37°C
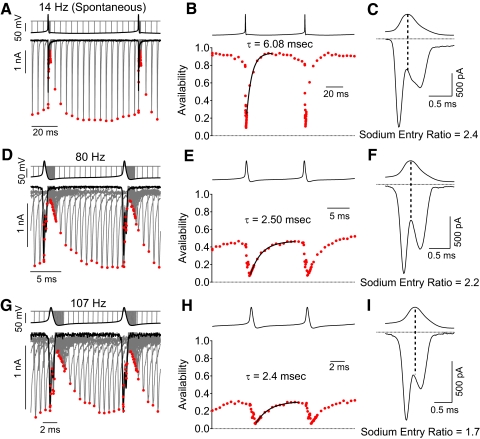
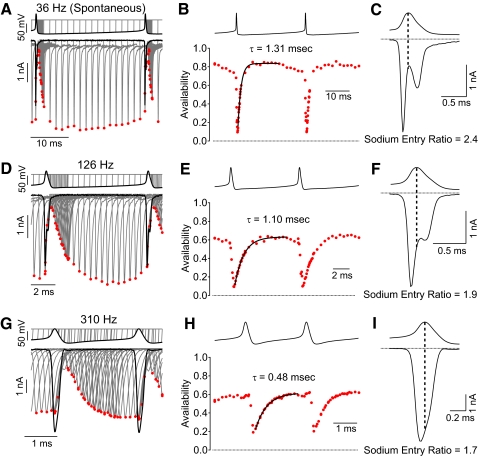
Figure 9 shows measurements of availability during the firing cycle for spontaneous and stimulated firing at 37°C. During spontaneous firing (36 Hz in this neuron, Fig. 9, A–C), sodium channel availability was high (∼80%) during most of the firing cycle. The minimum availability after the spike was 10% and channel availability recovered very rapidly after each spike (time constant of 1.3 ms, Fig. 9B) so that maximum availability was reached only 3–4 ms after the end of a spike. Consistent with incomplete inactivation during the spike, substantial sodium current flowed during the downstroke of the action potential (Fig. 9C), yielding a sodium entry ratio of 2.4.
Fig. 9.
Sodium channel availability during rapid action potential firing at 37°C. Measurements were made as in Figs. 5 and 6. A: voltage-clamp recordings of sodium current during spontaneous firing with availability measured using a test step to −8 mV added at various times during the firing cycle. B: sodium channel availability during the firing cycle. C: sodium current during the action potential, showing incomplete inactivation during the falling phase. D–F: same analysis but using waveform of higher firing frequency evoked by steady current injection in the same neuron. G–I: same analysis but for a firing frequency near maximal for a different neuron.
With faster firing at 126 Hz (Fig. 9, D–F), inactivation was still incomplete, reaching a minimum of 9%, with substantial sodium current flowing during the downstroke (sodium entry ratio of 1.9). The maximal availability between spikes was 63%, achieved with a time constant of recovery of 1.1 ms (Fig. 9E).
Figure 9, G–I shows an example of availability during maximal firing frequency with a large current injection (1,200 pA; cell different from that in Fig. 9, A–F). Inactivation during the spike was incomplete, as for slower firing. In this cell, the maximum availability between spikes was about 60% and the minimum availability after a spike was 19%. The time course of recovery was fit by an exponential with a time constant of 0.48 ms (Fig. 9H). The sodium entry ratio was 1.7 (Fig. 9I).
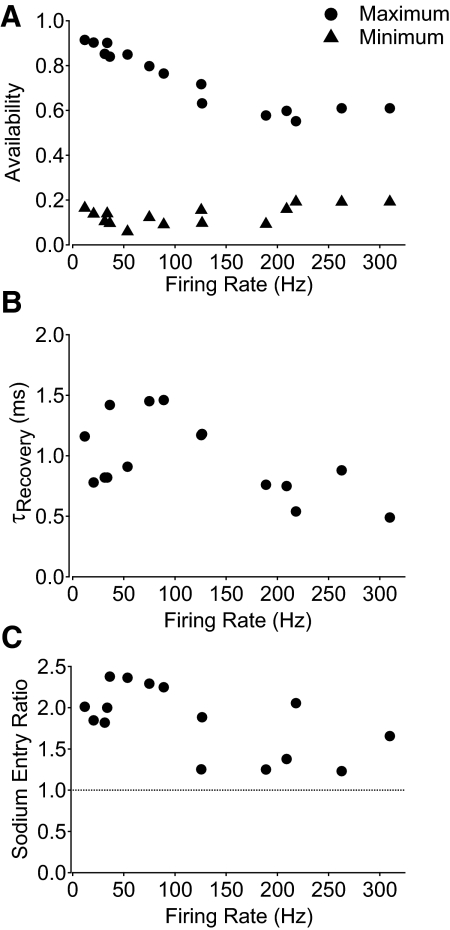
Figure 10 shows collected results for sodium channel behavior during firing at 37°C over a range of frequencies. Maximal sodium channel availability (during the ISI) showed a clear dependence on firing rate, decreasing from nearly 90% with the slowest spontaneous firing to about 60% with the fastest stimulated firing (Fig. 10A). In contrast, minimum availability (immediately after a spike) did not show obvious systematic variation with firing frequency and was between approximately 10 and 20% for all the firing rates tested. The rate of recovery from inactivation was very fast at 37°C, with time constants between 0.5 and 1.5 ms, with no clear systematic dependence on firing frequency (Fig. 10B). Measuring current flowing during the action potential showed incomplete inactivation and substantial current flow during the falling phase for all firing frequencies; the sodium entry ratio was well above 1 for all firing rates tested.
Fig. 10.
Collected results for measurements of sodium channel availability during action potential firing at 37°C. A: maximum availability between spikes (filled circles) and minimum availability after spikes (filled triangles) during repetitive action potential firing at different frequencies. B: kinetics of recovery of sodium channel availability from minimum to maximum during the ISI, expressed as the time constant for a single exponential fit to the recovery. C: sodium entry ratio during the action potential as a function of firing rate.
The maximal availability between spikes decreased from roughly 90% with spontaneous firing to about 60% with fast stimulated firing. The decrease could represent either insufficient time to recover as the ISI becomes shorter with faster firing or from the more depolarized interspike voltage resulting from current injection, which would result in decreased availability even if recovery occurred fast enough to reach steady state. To examine this point, we tested how closely the dynamic availability during the ISI approaches the expected steady-state availability. Steady-state availability was measured in six neurons using 500 ms long prepulses followed by a test pulse to −23 mV (Fig. 11A, inset). The collected values of midpoint (−70.9 ± 4.9 mV) and slope factor (6.3 ± 0.9) were used to construct an average steady-state inactivation curve (Fig. 11A, blue trace). Figure 11B shows the dynamic availability measured during spontaneous firing (from Fig. 9A) compared with the predicted steady-state availability for each point during the firing cycle. The maximum steady-state availability during the firing cycle in this neuron was nearly 90% (reached immediately after the spike, when the voltage is most negative) and steady-state availability remained >80% for the first half of the ISI. The maximal dynamic availability was roughly 85%, reached about 7–8 ms after the spike, nearly one quarter of the way into the ISI. Thus the maximal dynamic availability closely approaches the maximal steady-state availability.
For fast stimulated firing (Fig. 11C), the situation was quite different. Here, the maximal steady-state availability was also about 90%, reached immediately after the spike, but steady-state availability declined dramatically during the first half of the ISI and the dynamic availability approached steady-state availability only about halfway into the ISI, by which time steady-state availability had fallen to roughly 50%.
A striking feature of the comparison between dynamic availability and steady-state availability for fast firing is that dynamic availability is nearly constant at about 60% during the second half of the ISI, whereas steady-state availability falls rapidly from about 60% to 0% (as the membrane voltage depolarizes toward threshold). Evidently, the development of inactivation is slow enough during the approach to spike threshold that there is almost no decline of availability until spike threshold is reached. Even during spontaneous firing, when the ISI is longer and the approach to firing threshold was slower, there was very little decline in dynamic availability before spike threshold was reached. The failure of dynamic availability to decline significantly during the ISI is likely crucial in the ability of the neuron to fire repetitively.
DISCUSSION
Purkinje neurons can sustain very rapid firing (>300 Hz at 37°C) for prolonged periods, which requires repriming of the spiking machinery within about 3 ms. Our results identify three aspects of sodium channel behavior in Purkinje neurons that enable such rapid firing. First, sodium channel density is much higher than minimally necessary to generate a spike, so only partial recovery from inactivation is needed to restore spiking ability. Second, incomplete inactivation of sodium channels during the action potential leads to a fraction of channels that are immediately available after the spike. Third, recovery from inactivation is extremely rapid, occurring with a time constant of about 1 ms.
Sodium channel density
With strong stimulation at room temperature, neurons could fire at high frequency with only about 25% of the sodium channels available between spikes (Figs. 6 and 7). Consistent with this, Purkinje neurons can still fire action potentials when 60–80% of the sodium current is blocked by low concentrations of TTX (Kalume et al. 2007; Raman and Bean 1999; Swensen and Bean 2003; see also Madeja 2000). A large sodium channel density allows fast firing by requiring a smaller fraction of channels to recover from inactivation before a spike can be generated.
Although sustained firing at room temperature was possible with only about 25% maximal channel availability between spikes, interspike availability was about 60% for the fastest maintained firing at 37°C. The most rapid firing at 37°C may be limited by other factors, such as cumulative activation of calcium-activated potassium channels or failure of voltage-activated potassium channels to fully deactivate fast enough, which could prevent firing even with substantial sodium channel availability.
Incomplete inactivation of sodium channels during spikes
We found that sodium channel inactivation is incomplete during and after action potentials in Purkinje neurons at all firing frequencies, including the highest frequencies of stimulated firing. At 37°C, sodium channel availability was 10–20% immediately after the spike at all frequencies. There was no systematic variation in the minimal availability with spike frequency, even though the spike shape changes, becoming shorter and broader at higher frequencies. By itself, broadening of the spike would be expected to produce more complete inactivation. Apparently, this is compensated for by the reduction in spike peak, which would be expected to produce less complete inactivation because inactivation is slower at less depolarized voltages.
The incomplete inactivation of sodium channels during Purkinje neuron action potentials was previously noted using the waveform of the first spike in a burst of firing evoked by current injection from a negative holding potential (Raman and Bean 1997). Such bursts are generally similar to complex spikes in Purkinje neurons evoked by climbing fiber stimulation, whose generation depends largely on somatic and axonal conductances (Callaway and Ross 1997; Davie et al. 2008; Palmer et al. 2009). About 12% of the sodium channels remained available immediately after the first spike of a complex spike-like burst (Raman and Bean 1997). Thus incomplete inactivation of sodium channels likely promotes burst firing like that during complex spikes evoked by climbing fiber stimulation as well as steady high-frequency firing.
Purkinje neurons possess a steady-state “persistent” sodium current that does not inactivate even when measured with very slow voltage ramps (Kay et al. 1998; Raman and Bean 1997). This persistent current represents a component of sodium current that would not inactivate no matter how broad the spike. However, this component accounts for very little of the noninactivated sodium current following spike waveforms because the test steps following spikes in the protocols of Figs. 5, 6, and 9 elicit primarily transient sodium current, with only a very small component of persistent current (present but not easily visible in the records).
Rapid recovery from inactivation
Recovery from inactivation during the ISI was rapid, with a time constant of about 1 ms at 37°C. This is comparable to recovery kinetics of mammalian sodium channels measured near 37°C using step voltage pulse protocols: about 1 ms near −70 mV in rat node of Ranvier (Schwarz and Eikhof 1987) and about 0.5 ms near −100 mV in rat central heminodes (Leão et al. 2005). For both of these preparations, most current is likely from Nav1.6 channels (Caldwell et al. 2000; Krzemien et al. 2000; Leão et al. 2005), whereas the Purkinje neuron sodium current likely has major contributions from both Nav1.6 and Nav1.1 channels (Kalume et al. 2007; Raman et al. 1997).
For sodium current in Purkinje neurons, the kinetics of recovery from inactivation depend markedly on the voltage and duration of the prepulse that induces inactivation. Recovery is much faster after brief, large depolarizations than after long, smaller depolarizations (Raman and Bean 2001). This difference is not expected from Hodgkin–Huxley-type kinetics. The behavior in Purkinje neurons can be explained by a model in which there are two mechanisms of inactivation, one a mechanism of rapid open-channel block from which recovery is more rapid and is associated with the flow of “resurgent” current (Raman and Bean 2001). Inactivation by this mechanism is favored by brief, strong depolarizations such as action potential waveforms. The dependence on prepulse parameters highlights the importance of using natural action potential waveforms in exploring kinetics relevant to natural firing patterns.
For spontaneous firing, availability recovers within the first 25% of the ISI, when membrane voltage does not vary much and dynamic availability approaches steady-state availability (Fig. 11B). However, for rapid stimulated firing, the interspike voltage depolarizes so quickly that dynamic availability does not recover to a steady-state level of availability before steady-state availability declines again. Interestingly, there was an asymmetry in the kinetics of recovery and development of inactivation between spikes, with fast recovery during the first half of the ISI after the spike but no corresponding development during the second half of the ISI, when steady-state availability declines to nearly zero. In the Hodgkin–Huxley model, τh versus Vm is nearly symmetric around h∞ = 0.5 (Hodgkin and Huxley 1952; see Hille 2001), so one might expect roughly equivalent recovery and development phases. Sodium channels in Purkinje neurons evidently behave differently in this respect. Recovery from inactivation during the early ISI likely reflects fast recovery from the “fast blocked” state associated with resurgent current and development of inactivation during the late ISI would reflect primarily inactivation from closed states. In general, closed-state inactivation of real sodium channels is slower than expected from Hodgkin–Huxley kinetics because there is a degree of coupling of inactivation with activation that is not accounted for in the Hodgkin–Huxley model (Aldrich et al. 1983; Armstrong 1981, 2006; Bezanilla and Armstrong 1977; Goldman 1989). Our results suggest that this difference of channel behavior from the Hodgkin–Huxley model could be physiologically important for allowing rapid firing, by slowing the development of inactivation during the approach to spike threshold (i.e., minimizing inactivation occurring before channels have opened).
Temperature dependence of firing frequency
We were surprised to find little difference in the average frequency of spontaneous firing at 37°C compared with that at 23°C. This contrasts, for example, with pacemaking of cerebellar Golgi neurons, which increases from about 3 Hz at 23°C to nearly 9 Hz at 37°C (Forti et al. 2006). A mechanistic difference is that pacemaking in Golgi neurons involves the hyperpolarization activated current Ih (Forti et al. 2006), whose kinetics are strongly temperature dependent (Q10 3–4; Cao and Oertel 2005; Hart 1983; Santoro and Tibbs 1999). Purkinje neuron pacemaking does not use Ih (Nolan et al. 2003; Raman and Bean 1999), but is driven mainly by subthreshold sodium current (Raman and Bean 1999); if this is mostly a steady-state “persistent” current, kinetics may be irrelevant and temperature might have little effect.
In contrast to spontaneous firing, the maximal rate of stimulated firing was strongly temperature dependent. This suggests that firing is limited by gating kinetics of either sodium channels (e.g., recovery from inactivation) or potassium channels (e.g., deactivation).
Comparison with action potentials in other neurons
Together with previous data and modeling, our results suggest that the degree of sodium channel inactivation during the action potential varies considerably among different types of neurons. The Hodgkin and Huxley (1952) model of the squid axon action potential predicts that about 10% of the channels remain noninactivated. However, sodium channels appear to inactivate completely during the action potentials of many mammalian neurons, including tuberomammillary nucleus neurons (Taddese and Bean 2002), suprachiasmatic nucleus neurons (Jackson et al. 2004), and mossy fiber boutons (Alle et al. 2009), whereas in others, including cerebellar Purkinje neurons (Raman and Bean 1997; this study), vestibular nucleus neurons (Gittis et al. 2010), and cortical GABAergic interneurons (Carter and Bean 2009), inactivation is incomplete. The most critical factor governing the completeness of inactivation is the width of the action potential rather than differences in sodium channel kinetics (Carter and Bean 2009; Gittis et al. 2010), even though such differences do exist (Martina and Jonas 1997; Raman and Bean 1997).
Narrow action potentials and fast-spiking
Recordings across many cell types have shown a correlation of fast-spiking behavior with narrow action potentials. Our results suggest that a key link between the two characteristics is that narrow action potentials result in incomplete inactivation of sodium channels. Thus a substantial fraction of channels close during the falling phase of the spike by deactivating rather than inactivating and are immediately available for spike formation. The immediate availability results in a shorter refractory period than would follow a broader action potential producing complete inactivation of sodium channels. Our results fit well with a recent study showing that inactivation is incomplete during the narrow spikes of fast-spiking vestibular nucleus neurons and that lengthening the action potential by blocking potassium channels produces both more complete inactivation and slower spiking (Gittis et al. 2010).
Fast-spiking neurons with narrow action potentials typically have high expression of KV3 family potassium channels, which have the key property of deactivating unusually rapidly (Erisir et al. 1999; Rudy and McBain 2001; Wang et al. 1998). Experiments using dynamic clamp showed that the precise deactivation kinetics of native KV3 channels are optimized to promote fast spiking (Lien and Jonas 2003). A likely mechanism for the sensitivity to potassium channel gating kinetics is that the kinetics determine the exact shape of the falling phase of the action potential and the afterhyperpolarization, which in turn controls the completeness of inactivation and recovery kinetics of sodium channels. Thus the sensitivity of sodium channel kinetics to small changes in the voltage waveform of the falling phase of the spike may be critical in determining the fast-spiking phenotype.
GRANTS
This work was supported by the National Institute of Neurological Disorders and Stroke Grants R01-NS-36855 and F31-NS-064630/Ruth Kirschstein predoctoral fellowship to B. C. Carter.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
REFERENCES
- Aldrich RW, Corey DP, Stevens CF. A reinterpretation of mammalian sodium channel gating based on single channel recording. Nature 306: 436–441, 1983 [DOI] [PubMed] [Google Scholar]
- Alle H, Roth A, Geiger JR. Energy-efficient action potentials in hippocampal mossy fibers. Science 325: 1405–1408, 2009 [DOI] [PubMed] [Google Scholar]
- Armstrong CM. Sodium channels and gating currents. Physiol Rev 61: 644–683, 1981 [DOI] [PubMed] [Google Scholar]
- Armstrong CM. Na channel inactivation from open and closed states. Proc Natl Acad Sci USA 103: 17991–17996, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F, Armstrong CM. Inactivation of the sodium channel. I. Sodium current experiments. J Gen Physiol 70: 549–566, 1977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caldwell JH, Schaller KL, Lasher RS, Peles E, Levinson SR. Sodium channel NaV1.6 is localized at nodes of Ranvier, dendrites, and synapses. Proc Natl Acad Sci USA 97: 5616–5620, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaway JC, Ross WN. Spatial distribution of synaptically activated sodium concentration changes in cerebellar Purkinje neurons. J Neurophysiol 77: 145–152, 1997 [DOI] [PubMed] [Google Scholar]
- Cao XJ, Oertel D. Temperature affects voltage-sensitive conductances differentially in octopus cells of the mammalian cochlear nucleus. J Neurophysiol 94: 821–832, 2005 [DOI] [PubMed] [Google Scholar]
- Carter BC, Bean BP. Sodium entry during action potentials of mammalian central neurons: incomplete inactivation and reduced metabolic efficiency in fast-spiking neurons. Neuron 64: 898–909, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connors BW, Gutnick MJ. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci 13: 99–104, 1990 [DOI] [PubMed] [Google Scholar]
- Davie JT, Clark BA, Häusser M. The origin of the complex spike in cerebellar Purkinje cells. J Neurosci 28: 7599–7609, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erisir A, Lau D, Rudy B, Leonard CS. Function of specific K(+) channels in sustained high-frequency firing of fast-spiking neocortical interneurons. J Neurophysiol 82: 2476–2489, 1999 [DOI] [PubMed] [Google Scholar]
- Forti L, Cesana E, Mapelli J, D'Angelo E. Ionic mechanisms of autorhythmic firing in rat cerebellar Golgi cells. J Physiol 574: 711–729, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gittis AH, Moghadam SH, du Lac S. Mechanisms of sustained high firing rates in two classes of vestibular nucleus neurons: differential contributions of resurgent Na, Kv3, and BK currents. J Neurophysiol 104: 1625–1634, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman L. Sodium channel opening as a precursor to inactivation. A route to the inactivated state. Eur Biophys J 16: 321–325, 1989 [DOI] [PubMed] [Google Scholar]
- Hart G. The kinetics and temperature dependence of the pace-maker current If in sheep Purkinje fibres. J Physiol 337: 401–416, 1983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. Ion Channels of Excitable Membranes. Sunderland, MA: Sinauer, 2001 [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117: 500–544, 1952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson AC, Yao GL, Bean BP. Mechanism of spontaneous firing in dorsomedial suprachiasmatic nucleus neurons. J Neurosci 24: 7985–7998, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalume F, Yu FH, Westenbroek RE, Scheuer T, Catterall WA. Reduced sodium current in Purkinje neurons from Nav1.1 mutant mice: implications for ataxia in severe myoclonic epilepsy in infancy. J Neurosci 27: 11065–11074, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaguchi Y. Physiological, morphological, and histochemical characterization of three classes of interneurons in rat neostriatum. J Neurosci 13: 4908–4923, 1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay AR, Sugimori M, Llinás R. Kinetic and stochastic properties of a persistent sodium current in mature guinea pig cerebellar Purkinje cells. J Neurophysiol. 80: 1167–1179, 1998 [DOI] [PubMed] [Google Scholar]
- Khaliq ZM, Gouwens NW, Raman IM. The contribution of resurgent sodium current to high-frequency firing in Purkinje neurons: an experimental and modeling study. J Neurosci 23: 4899–4912, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaliq ZM, Raman IM. Axonal propagation of simple and complex spikes in cerebellar Purkinje neurons. J Neurosci 25: 454–463, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krzemien DM, Schaller KL, Levinson SR, Caldwell JH. Immunolocalization of sodium channel isoform NaCh6 in the nervous system. J Comp Neurol 420: 70–83, 2000 [PubMed] [Google Scholar]
- Leão RM, Kushmerick C, Pinaud R, Renden R, Li GL, Taschenberger H, Spirou G, Levinson SR, von Gersdorff H. Presynaptic Na+ channels: locus, development, and recovery from inactivation at a high-fidelity synapse. J Neurosci 25: 3724–3738, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien CC, Jonas P. Kv3 potassium conductance is necessary and kinetically optimized for high-frequency action potential generation in hippocampal interneurons. J Neurosci 23: 2058–2068, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madeja M. Do neurons have a reserve of sodium channels for the generation of action potentials? A study on acutely isolated CA1 neurons from the guinea-pig hippocampus. Eur J Neurosci 12: 1–7, 2000 [DOI] [PubMed] [Google Scholar]
- Martina M, Jonas P. Functional differences in Na+ channel gating between fast-spiking interneurones and principal neurons of rat hippocampus. J Physiol 505: 593–603, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Connors BW, Lighthall JW, Prince DA. Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. J Neurophysiol 54: 782–806, 1985 [DOI] [PubMed] [Google Scholar]
- Neher E. Correction for liquid junction potentials in patch clamp experiments. Methods Enzymol 207: 123–131, 1992 [DOI] [PubMed] [Google Scholar]
- Nolan MF, Malleret G, Lee KH, Gibbs E, Dudman JT, Santoro B, Yin D, Thompson RF, Siegelbaum SA, Kandel ER, Morozov A. The hyperpolarization-activated HCN1 channel is important for motor learning and neuronal integration by cerebellar Purkinje cells. Cell 115: 551–564, 2003 [DOI] [PubMed] [Google Scholar]
- Nowak LG, Azouz R, Sanchez-Vives MV, Gray CM, McCormick DA. Electrophysiological classes of cat primary visual cortical neurons in vivo as revealed by quantitative analyses. J Neurophysiol 89: 1541–1566, 2003 [DOI] [PubMed] [Google Scholar]
- Palmer LM, Clark BA, Gründemann J, Roth A, Stuart GJ, Häusser M. Initiation of simple and complex spikes in cerebellar Purkinje cells. J Physiol 588: 1709–1717, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Bean BP. Resurgent sodium current and action potential formation in dissociated cerebellar Purkinje neurons. J Neurosci 17: 4517–4526, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Bean BP. Ionic currents underlying spontaneous action potentials in isolated cerebellar Purkinje neurons. J Neurosci 19: 1663–1674, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Bean BP. Inactivation and recovery of sodium currents in cerebellar Purkinje neurons: evidence for two mechanisms. Biophys J 80: 729–737, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Sprunger LK, Meisler MH, Bean BP. Altered subthreshold sodium currents and disrupted firing patterns in Purkinje neurons of Scn8a mutant mice. Neuron 19: 881–891, 1997 [DOI] [PubMed] [Google Scholar]
- Rudy B, McBain CJ. Kv3 channels: voltage-gated K+ channels designed for high-frequency repetitive firing. Trends Neurosci 24: 517–526, 2001 [DOI] [PubMed] [Google Scholar]
- Santoro B, Tibbs GR. The HCN gene family: molecular basis of the hyperpolarization-activated pacemaker channels. Ann NY Acad Sci 868: 741–764, 1999 [DOI] [PubMed] [Google Scholar]
- Schwarz JR, Eikhof G. Na currents and action potentials in rat myelinated nerve fibres at 20 and 37 degrees C. Pflügers Arch 409: 569–577, 1987 [DOI] [PubMed] [Google Scholar]
- Swensen AM, Bean BP. Ionic mechanisms of burst firing in dissociated Purkinje neurons. J Neurosci 23: 9650–9663, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddese A, Bean BP. Subthreshold sodium current from rapidly inactivating sodium channels drives spontaneous firing of tuberomammillary neurons. Neuron 33: 587–600, 2002 [DOI] [PubMed] [Google Scholar]
- Tateno T, Harsch A, Robinson HPC. Threshold firing frequency–current relationships of neurons in rat somatosensory cortex: type 1 and type 2 dynamics. J Neurophysiol 92: 2283–2294, 2004 [DOI] [PubMed] [Google Scholar]
- Wang LY, Gan L, Forsythe ID, Kaczmarek LK. Contribution of the Kv3.1 potassium channel to high-frequency firing in mouse auditory neurones. J Physiol 509: 183–194, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou FM, Hablitz JJ. Layer I neurons of rat neocortex. I. Action potential and repetitive firing properties. J Neurophysiol 76: 651–667, 1996 [DOI] [PubMed] [Google Scholar]