Unified Bundling and Registration of Brain White Matter Fibers

Abstract

Magnetic resonance diffusion tensor imaging is being widely used to reconstruct brain white matter fiber tracts. To characterize structural properties of the tracts, reconstructed fibers are often grouped into bundles that correspond to coherent anatomic structures. For further group analysis of fiber bundles, it is desirable that corresponding bundles from different studies are coregistered. To address these needs simultaneously, a unified fiber bundling and registration (UFIBRE) framework is proposed in this work. The framework is based on maximizing a posteriori Bayesian probabilities using an expectation maximization algorithm. Given a set of segmented template bundles and a whole-brain target fiber set, the UFIBRE algorithm optimally bundles the target fibers and registers them with the template. The bundling component in the UFIBRE algorithm simplifies fiber-based registration into bundle-to-bundle registration, and the registration component in turn guides the bundling process to find bundles consistent with the template. Experiments with in vivo data demonstrate that the estimated bundles have an ∼80% consistency with ground truth and the root mean square error between their bundle medial axes is less than one voxel. The proposed algorithm is highly efficient, offering potential routine use for group analysis of white matter fibers.

I. Introduction

Magnetic resonance diffusion tensor imaging (DTI) is an established noninvasive technique for studying neuronal fiber pathways in vivo, particularly in the brain white matter (WM) [1], [2]. In each voxel, DTI provides a diffusion tensor (3 × 3 symmetric positive definite matrix) that describes the local Brownian motion of water molecules. Eigenvalues and eigenvectors of the tensor can be exploited to reconstruct the WM fibers [3]. To facilitate quantitative characterization of fiber pathways, WM fibers of similar geometry and location can be further grouped into fiber bundles, since they presumably belong to similar anatomical structures in the brain [4]–[9]. Comparisons of corresponding WM bundles in subjects from two or more studies can reveal brain structural differences among different patients or patient groups, or between different stages of disease progression [10]–[12]. For reliable comparisons, reconstructed fibers need to be bundled consistently across different DTI studies. Furthermore, it is desirable that fiber bundles from different studies are aligned into a common coordinate system, so that structural differences among corresponding bundles can be characterized directly.

There have been a number of fiber bundling methods proposed recently. One widely used approach is to manually place regions of interest (ROIs) within the fibers, and then group the fibers that pass through the same set of ROIs as a distinct bundle [13], [14]. In spite of its flexibility in selecting fiber bundles of interest, this method suffers from inter- and intra-operator variabilities, and is highly inefficient since ROIs have to be manually defined for each study. The bundling procedure can be automated by using computer based clustering methods that group similar fibers with minimal human intervention. To date a few algorithms of this kind have been proposed, which come with different definitions of fiber similarity and clustering approaches [4]–[9]. Ding et al. [4] defined fiber similarity as the mean Euclidean distance between corresponding segments of a pair of fibers, and used an agglomerative algorithm to merge fibers on the basis of their similarity measure. Brun et al. [5] represented a fiber as a 9-D vector that included the first- and second-order statistics of points in that fiber (centroids and covariance matrices). The Euclidean distance between fiber feature vectors was computed pairwise to create a weighted undirected graph, which was further partitioned into coherent sets using a normalized cut algorithm. Gerig et al. [6] constructed point correspondence between two fibers by mapping each point in one fiber to the closest point in the other, and employed a similar clustering method to that used by Ding et al. [4]. O'Donnell et al. [7] proposed the maximum of pointwise minimum distances between a pair of fibers as the distance measure and clustered all fibers from different subjects with a k-way normalized cut algorithm. Zhang et al. [8] defined the fiber distance as the mean of the distance between all points in a shorter fiber and their closet correspondences in another, and agglomeratively clustered fibers with mean distance below a certain threshold. Maddah et al. [9] constructed statistical bundle models based on coefficients of B-spline representation of fibers. By assuming a mixture bundle model, an expectation maximization algorithm was utilized to estimate model parameters and label fibers. These automated methods are efficient, but lack the flexibility in generating bundles that satisfy the need of specific studies, which could be otherwise achieved by manual bundling.

In addition to fiber bundling, efforts also have been made in developing registration techniques that allow corresponding fiber bundles from different studies to be aligned and compared. These techniques can be broadly categorized into three types. The first type is to align corresponding fiber bundles by registering maps of fractional anisotropy or other scalar indices of DTI data using scalar image registration algorithms [15]. Evidently, the alignment of a scalar map of DTI does not guarantee the alignment of fibers since fiber orientation information is not taken into account. The second type, which is more technically sophisticated, is to register the tensor data by utilizing the orientation information that the tensor contains [16], [17]. While being able to provide more accurate results in principle, such a registration technique has not gained anticipated popularity in the DTI community, likely owing to the complications in tensor reorientation, interpolation, and selection of appropriate tensor metrics. More recently there have been some endeavors in developing techniques for direct registration of WM fibers. For example, Leemans et al. [18] and Mayer et al. [19] each proposed an iterative scheme for estimating a rigid or affine transformation based on the alignment of individual fibers in reference data to their closest counterparts in target data. Both schemes are computationally intensive due to the process of closest-fiber finding and one-to-one fiber registration given the sheer number of fibers per volume that are typically generated by tractography. In addition, the rigid or affine transformation provides limited degrees-of-freedom for deformation, which significantly restricts the accuracy of fiber alignment. In contrast to the fiber-to-fiber registration, Ziyan et al. [20] proposed a method that aligns corresponding fiber bundles individually with an affine transformation, which is subsequently combined across bundles using a poly-affine framework. Although the computational efficiency has been substantially improved due to the bundle-to-bundle registration, it requires preclustering of fiber bundles as well as a reasonable initial affine registration.

To address the limitations in the aforementioned bundling and registration techniques, we propose a unified fiber bundling and registration (UFIBRE) algorithm. Our method starts with an initial bundling of fibers in a template fiber set, and uses an expectation maximization algorithm to jointly estimate corresponding fiber bundles in a target fiber set and the transformation from the template to the target coordinate system. The initial bundling is achieved by using the manual ROI method, which provides an opportunity to select or define any fiber bundles of interest. Our method is efficient, as only the Gaussian statistics of the bundle model is aligned and there is no need to seek the alignments of individual fibers. Such a computational efficiency permits the use of more complex transformations, such as thin plate spline transformations, to gain higher degrees of freedom for mapping template fibers to target fibers.

In the following, the problem of joint fiber bundling and registration is first formally defined; then a maximum a posteriori (MAP) framework for estimating optimal bundles and transformation is described. Qualitative and quantitative evaluations of the proposed algorithm with in vivo DTI data are also presented. To further demonstrate the utility of our algorithm, we provide an example of constructing a fiber bundle atlas for nine WM fiber bundles using in vivo DTI data. Finally, major contributions of this work are summarized, and some technical limitations are discussed so as to guide future research along this line.

II. Unified Fiber Bundling and Registration

A. Problem Definition

The goal of this work is to cluster fibers in a target fiber set and align them with a labeled template fiber set. This can be cast as an optimization problem that simultaneously seeks optimal bundles in the target fiber set and an optimal transformation from the template to the target coordinate system. Let x and y denote the template and target fiber set, respectively. Each set contains a collection of open space curves, with each curve represented by a sequence of discrete 3-D points. Let x and y be, respectively, divided into K fiber bundles, each of which contains a group of fibers that belong to a certain anatomical structure. We assume that the fibers in each bundle follow a Gaussian distribution of positions, and thus use a Gaussian mixture model to represent the fiber distribution in the whole template/target fiber set. Let μ_x and μ_y denote the means of the fiber bundles (defined as “central curves” henceafter) in x and y, respectively, σ_x and σ_y the covariance matrices, π_x and π_y the mixture proportions of each bundle Gaussian model, and T the transformation that maps (π_x, μ_x, σ_x) to (π_y, μ_y, σ_y).

Set y represents the target fibers generated tractographically from all appropriate seeds in a whole DTI data volume, while x only contains certain fibers of interest in the template dataset for a specific study. Assuming the template bundle parameters (π_x, μ_x, σ_x) are known a priori, one goal of this work is to determine the target fiber bundles that are consistent with the template. Another goal is to find an optimal transformation that maps fibers from the template to the target coordinate system. Taken together, these can be expressed as a joint estimation of the target bundle model (π_y, μ_y, σ_y) and the transformation T given (x, y, π_x, μ_x, σ_x). This can be formally defined as a Bayesian decision problem, for which an optimal solution can be obtained by a MAP approach.

B. MAP Estimation

Given (x, y, π_x, μ_x, σ_x), we find optimal (π_y, μ_y, σ_y) and T that maximize the posterior probability as follows:

$$\begin{array}{cc}\mathit{\theta }\hfill & =(\mathbf{T},{\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}})\hfill \\ \hfill & =\mathit{arg}\underset{T,{\mu }_{\mathit{y}},{\sigma }_{\mathit{y}},{\pi }_{\mathit{y}}}{\mathit{max}}p(\mathbf{T},{\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}}\mid \mathbf{x},\mathbf{y},{\mathit{\mu }}_{\mathbf{x}},{\mathit{\sigma }}_{\mathbf{x}},{\mathit{\pi }}_{\mathbf{x}})\hfill \\ \hfill & \approx \mathit{arg}\underset{T,{\mu }_{\mathit{y}},{\sigma }_{\mathit{y}},{\pi }_{\mathit{y}}}{\mathit{max}}p(\mathbf{y}\mid {\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}})\times p({\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}}\mid {\mathit{\mu }}_{\mathbf{x}},{\mathit{\sigma }}_{\mathbf{x}},{\mathit{\pi }}_{\mathbf{x}},\mathbf{T})p(\mathbf{T})\hfill \end{array}$$ (1)

where p(A∣B) denotes the conditional probability of A given B.

Assuming y is a set of independent and identically distributed fibers that are drawn from the target bundle model (π_y, μ_y, σ_y), the likelihood of y conditioned on (π_y, μ_y, σ_y) can be simplified as the product of the likelihood of each fiber as follows:

$$\begin{array}{cc}p(\mathbf{y}\mid {\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}})\hfill & =\prod _{j=1}^{M}p({\mathbf{y}}_j\mid {\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}})\hfill \\ \hfill & =\prod _{j=1}^M\sum _{k=1}^K{\pi }_{\mathbf{y},k}p({\mathbf{y}}_j\mid {\mathit{\mu }}_{\mathbf{y},\mathit{k}},{\mathit{\sigma }}_{\mathbf{y},\mathit{k}})\hfill \end{array}$$ (2)

where

$$p({\mathbf{y}}_{\mathit{j}}\mid {\mathit{\mu }}_{\mathbf{y},\mathit{k}},{\mathit{\sigma }}_{\mathbf{y},\mathit{k}})=\prod _{\mathit{i}=1}^{N_k}\frac{1}{{(2\pi )}^{3/2}{|{\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}|}^{1/2}}\times exp\left(-({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}){\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^{-1}{({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}})}^T\right).$$ (3)

Note that k, j, and i index fiber bundles, fibers in the target fiber set, and the points along each fiber, respectively; there are M fibers in y, K bundles of interest that need to be estimated, and N_k points on the central fiber μ_y,k of the kth fiber bundle. Therefore, μ_y,k,i is the coordinate of the ith point on the central fiber of the kth target bundle, and σ_y,k,i is the 3 × 3 covariance matrix of the distribution of the points corresponding to μ_y,k,i. Variable y_j,i denotes the point in the jth fiber corresponding to μ_y,k,i.

To find y_j,i, a simple approach is to resample all the fibers to a set of consecutive points such that: 1) each point has an equal distance to its neighboring points; 2) the number of points in each fiber is a constant; 3) the first and last resampled points coincide with the starting and ending points of the fibers. Resampling in such a manner allows point correspondence between y_j and μ_y,k to be naturally established. A more sophisticated method is to define the point in y_j that is closest to μ_y,k,i as y_j,i. This provides better accuracy, but it requires a correspondence finding procedure in each iteration and thus is not time efficient. Therefore, the first approach is used in the UFIBRE algorithm to obtain a fast and stable estimation of y_j,i.

It should be noted that the soundness of (3) is based on the assumption that each fiber point can be modeled as a mixture of 3-D Gaussian probability distributions and the distribution of each point is independent of other points in the same fiber.

The probability in (2) describes the likelihood of the target fibers conditioned on the Gaussian mixture model (π_y, μ_y, σ_y) (i.e. how well the target fibers data fit the model). It can be regarded as a clustering term, whose maximization would lead to optimal bundling of the fibers into K clusters on the basis of the target data only. However, maximization of such a clustering term alone can not ensure the consistency in the fiber bundles between the target and the given template, nor does it give any alignment information. To associate the target with the given template, the prior probability p(μ_y, σ_y, π_y∣μ_x, σ_x, π_x, T) has to be optimized as well.

A reasonable expression of p(μ_y, σ_y, π_y∣μ_x, σ_x, π_x, T) should be related to the similarity between the warped template model T(μ_x, σ_x, π_x) and the target model (μ_y, σ_y, π_y). There exist metrics that measure the similarity between Gaussian mixture models (e.g. Kullback Leibler divergence), whose optimization would lead to alignment of both central fibers and covariance. However, they are not used in this work due to difficulties in their optimizations. To make the optimization more tractable, only the similarity between T(μ_x) and (μ_y) is considered, i.e., only the consistency between the central fibers of the template and target bundles is sought. The mixture proportions π_y and the covariance matrices σ_y of the target bundles are determined by the clustering term [(2)]. Therefore, p(μ_y, σ_y, π_y∣μ_x, σ_x, π_x, T) can be simplified as p(μ_y∣μ_x,T).

It is further assumed that the probability distribution of errors between the central fibers of the target and template data is Gaussian, and the covariance matrices are proportional to those of the target models. Therefore, p(μ_y∣μ_x, T) is expressed as

$$p({\mathit{\mu }}_{\mathbf{y}}\mid {\mathit{\mu }}_{\mathbf{x}},\mathbf{T})=\prod _{k=1}^K\prod _{i=1}^{N_k}\frac{1}{{(2\pi )}^{3/2}{|{\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}|}^{1/2}}\times exp(-c({\mathit{\mu }}_{\mathbf{y},k,i}-\mathbf{T}({\mathit{\mu }}_{\mathbf{x},k,i})){\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^{-1}\times ({\mathit{\mu }}_{\mathbf{y},k,i}-\mathbf{T}{({\mathit{\mu }}_{\mathbf{x},k,i})}^T))$$ (4)

where |σ_y,k,i| denotes the determinant of σ_y,k,i and c is a parameter that controls the contribution of p(μ_y∣μ_x, T) to the overall objective function. Maximization of the above probability would yield a transformation T that optimally registers the central fibers of template fiber bundles with those of target fiber bundles, and also leverage the computation of (μ_y, σ_y) by giving preference to target bundles that are consistent with template bundles.

Finally, p(T) denotes the prior distribution of the transformation T. It needs to be selected such that the trade-off between the registration accuracy and the smoothness of the deformation fields is adequately balanced. The form of p(T) used in this study will be detailed in Section II-D.

Taken together, maximization of all the probabilities in (1) yields an optimal set of parameters that allow the target fibers to be bundled consistently with the given template bundles.

C. Optimization

Based on the above derivations of the posterior distribution, the MAP estimation can be expressed as maximization of the following Log probability function:

$$E(\mathbf{T},{\mathit{\mu }}_{\mathbf{y}},{\mathit{\sigma }}_{\mathbf{y}},{\mathit{\pi }}_{\mathbf{y}})=\sum _{j=1}^{M}log\left(\sum _{k=1}^K{\mathit{\pi }}_{\mathbf{y},k}\prod _{i=1}^{N_k}\frac{1}{{(2\pi )}^{3/2}{|{\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}|}^{1/2}}\times exp(-({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}){\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^{-1}{({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}})}^T)\right)-\sum _{k=1}^K\sum _{i=1}^{N_k}c\left({\mathit{\mu }}_{\mathbf{y},k,i}-\mathbf{T}({\mathit{\mu }}_{\mathbf{x},k,i})\right){\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^{-1}\times {\left({\mathit{\mu }}_{\mathbf{y},k,i}-\mathbf{T}({\mathit{\mu }}_{\mathbf{x},k,i})\right)}^T+log(p(\mathbf{T})).$$ (5)

The above function can be maximized by using the well-known expectation-maximization (EM) algorithm. Starting with an initial parameter θ, this algorithm finds the optimal parameter θ by iteratively performing an expectation step and a maximization step until convergence.

1) Expectation Step

In the expectation step of the nth iteration, the membership probability $m_{j,k}^n$ of each fiber y_j belonging to the fiber bundle (μ_y,k, σ_y,k) is estimated using the most recent estimate of parameter θⁿ⁻¹

$$m_{j,k}^n=\frac{{\pi }_{y,k}^{n-1}p\left({\mathbf{y}}_j\mid {\mathit{\mu }}_{\mathbf{y},\mathit{k}}^{\mathit{n}-1},{\mathit{\sigma }}_{\mathbf{y},\mathit{k}}^{n-1}\right)}{\sum _{k=1}^K{\pi }_{y,k}^{n-1}p\left({\mathbf{y}}_j\mid {\mathit{\mu }}_{\mathbf{y},\mathit{k}}^{\mathit{n}-1},{\mathit{\sigma }}_{\mathbf{y},\mathit{k}}^{n-1}\right)}$$ (6)

where the superscript denotes the iteration number.

2) Maximization Step

In the maximization step of the nth iteration, the parameters ( ${\mathit{\mu }}_{\mathbf{y}}^n$, ${\mathit{\sigma }}_{\mathbf{y}}^n$, Tⁿ) are optimized to minimize the objective function below

$$E_{\text{EM}}({\mathbf{T}}^n,{\mathit{\mu }}_{\mathbf{y}}^n,{\mathit{\sigma }}_{\mathbf{y}}^n)=\sum _{j=1}^M\sum _{k=1}^K{m}_{j,k}^n\sum _{i=1}^{N_k}\left(\frac{1}{2}log|{\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n|+({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n)\times {({\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n)}^{-1}{({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n)}^T\right)+\sum _{k=1}^K\sum _{i=1}^{N_k}c\left(\frac{1}{2}log|{\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n|+({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^n({\mathit{\mu }}_{\mathbf{x},k,i}))\times {({\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n)}^{-1}({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^n{({\mathit{\mu }}_{\mathbf{x},k,i}))}^T\right)+log(p({\mathbf{T}}^n))$$ (7)

where we heuristically assume that the mixture proportions in the target model are the same as in the template model (π_y = π_x).

By solving the equations $(d{E}_{\text{EM}}/d{\mathit{\mu }}_{\mathbf{y}}^n)=0$, $(d{E}_{\text{EM}}/d{\mathit{\sigma }}_{\mathbf{y}}^n)=0$, one can obtain the optimal solutions to ( ${\mathit{\mu }}_{\mathbf{y}}^n$, ${\mathit{\sigma }}_{\mathbf{y}}^n$) that minimize the above function [(7)] shown in (8a) and (8b) at the bottom of page.

$${\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n=\frac{\sum _{j=1}^M{m}_{j,k}^n{\mathbf{y}}_{j,i}+c{\mathbf{T}}^{n-1}({\mathit{\mu }}_{\mathbf{x},k,i})}{\sum _{j=1}^M{m}_{j,k}^n+c}$$ (8a)

$${\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n=\frac{\sum _{j=1}^M{m}_{j,k}^n\left({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right){\left({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right)}^T+c\left({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^{n-1}({\mu }_{\mathbf{x},k,i})\right){\left({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^{n-1}({\mathit{\mu }}_{\mathbf{x},k,i})\right)}^T}{\sum _{j=1}^M{m}_{j,k}^n+c}.$$ (8b)

Equation (8) can be rearranged as follows:

$$\begin{array}{cc}{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\hfill & =\left(\frac{\sum _{j=1}^M{m}_{j,k}^n}{\sum _{j=1}^M{m}_{j,k}^n+c}\right)\left(\frac{\sum _{j=1}^M{m}_{j,k}^n{\mathbf{y}}_{j,i}}{\sum _{j=1}^M{m}_{j,k}^n}\right)+\left(\frac{c}{\sum _{j=1}^M{m}_{j,k}^n+c}\right){\mathbf{T}}^{n-1({\mathit{\mu }}_{\mathbf{x},k,i})}\hfill \\ \hfill & =\left(1-\frac{c}{\sum _{j=1}^M{m}_{j,k}^n+c}\right)\left(\frac{\sum _{j=1}^M{m}_{j,k}^n{\mathbf{y}}_{j,i}}{\sum _{j=1}^M{m}_{j,k}^n}\right)+\left(\frac{c}{\sum _{j=1}^M{m}_{j,k}^n+c}\right){\mathbf{T}}^{n-1}({\mathit{\mu }}_{\mathbf{x},k,i}),\hfill \end{array}$$ (9a)

$${\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n=\left(1-\frac{c}{\sum _{j=1}^M{m}_{j,k}^n+c}\right)\times \left(\frac{\sum _{j=1}^M{m}_{j,k}^n\left({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right){\left({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right)}^T}{\sum _{j=1}^M{m}_{j,k}^n}\right)+\left(\frac{c}{\sum _{j=1}^M{m}_{j,k}^n+c}\right)\times \left(\right({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^{n-1}({\mu }_{\mathbf{x},k,i}))\times {({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^{n-1}({\mathit{\mu }}_{\mathbf{x},k,i}))}^T).$$ (9b)

Equation (9) is then further simplified as

$${\mathit{\mu }}_{\mathbf{y}}^n=(1-C){\mathit{\mu }}_{b/\mathbf{y}}^n+C{\mathit{\mu }}_{r/\mathbf{y}}^n$$ (10a)

$${\mathit{\sigma }}_{\mathbf{y}}^n=(1-C){\mathit{\sigma }}_{b/\mathbf{y}}^n+C{\mathit{\sigma }}_{r/\mathbf{y}}^n$$ (10b)

where

$$\begin{array}{cc}\hfill C& =\left(\frac{c}{\sum _{j=1}^M{m}_{j,k}^n+c}\right)\hfill \\ \hfill {\mathit{\mu }}_{b/\mathbf{y},\mathit{k},\mathit{i}}^n& =\left(\frac{\sum _{j=1}^M{m}_{j,k}^n{\mathbf{y}}_{j,i}}{\sum _{j=1}^M{m}_{j,k}^n}\right)\hfill \\ \hfill {\mathit{\sigma }}_{b/\mathbf{y},\mathit{k},\mathit{i}}^n& =\frac{\sum _{j=1}^M{m}_{j,k}^n\left({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right){\left({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right)}^T}{\sum _{j=1}^M{m}_{j,k}^n}\hfill \\ \hfill {\mathit{\mu }}_{\mathit{r}/\mathbf{y},\mathit{k},\mathit{i}}^n& ={\mathbf{T}}^{n-1}({\mathit{\mu }}_{\mathbf{x},k,i})\hfill \\ \hfill {\mathit{\sigma }}_{r/\mathbf{y},\mathit{k},\mathit{i}}^n& =\left({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^{n-1}({\mu }_{\mathbf{x},k,i})\right)\times {\left({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^{n-1}({\mathit{\mu }}_{\mathbf{x},k,i})\right)}^T.\hfill \end{array}$$

${\mathit{\mu }}_{\mathit{b}/\mathit{y}}^n$ and ${\mathit{\sigma }}_{\mathit{b}/\mathit{y}}^n$ denote the central fibers and covariance matrices that are obtained by maximizing the bundling term p(y∣μ_y, σ_y, π_y) alone (2). ${\mathit{\mu }}_{\mathit{r}/\mathit{y}}^n$ denote the warped template central fibers using the transformation estimated in the previous iteration. The central fibers ${\mathit{\mu }}_{\mathbf{y}}^n$ in the proposed algorithm are actually computed as a weighted sum of ${\mathit{\mu }}_{\mathit{b}/\mathit{y}}^n$ and ${\mathit{\mu }}_{\mathit{r}/\mathit{y}}^n$, with their relative weight C controlled by the parameter c (10a). The weight C is chosen to be one of the core adjustable parameters in the algorithm. The choice of C and its effect on the performance of the UFIBRE algorithm will be studied experimentally.

In principle, evaluations of the above formulas (10) for each bundle involve all the fibers in target fiber set. However, the fibers with low membership probability $m_{j,k}^m$ are excluded from the computation of μ_y,k for the sake of computational efficiency. To do so, the target fibers are first sorted in an ascending order of Mahalanobis distance to the target central fibers, which is computed as follows:

$${\mathit{\text{Dist}}}_{j,k}=\sum _{i=1}^{N_k}\left(({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n){({\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n)}^{-1}{({\mathbf{y}}_{j,i}-{\mathit{\mu }}_{\mathbf{y},\mathit{k},\mathit{i}}^n)}^T\right)$$

where Dist_j,k denotes the distance between the jth fiber and the kth bundle in the target fiber set. Assuming the number of fibers in the kth template bundle is M_k, the first M_k target fibers with smallest Dist_j,k are retained for the kth target bundle while the remaining fibers are excluded as outliers.

Lastly, the optimal Tⁿ is given by minimizing the following objective function:

$$E_{\text{EM}}(\mathbf{T})=\sum _{k=1}^K\sum _{i-1}^{N_k}c\left({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^n\left({\mathit{\mu }}_{\mathbf{x},k,i}^n\right)\right){\left({\mathit{\sigma }}_{\mathbf{y},\mathit{k},\mathit{i}}^n\right)}^{-1}\times {\left({\mathit{\mu }}_{\mathbf{y},k,i}^n-{\mathbf{T}}^n\left({\mathit{\mu }}_{\mathbf{x},k,i}^n\right)\right)}^T+log\left(p\left({\mathbf{T}}^n\right)\right).$$ (11)

D. Transformation

The above EM framework does not assume any form of transformation, i.e., transformation from rigid, affine to more complex forms may be used in this framework. Both rigid and non-rigid transformations are integrated in the UFIBRE algorithm to achieve a robust and accurate mapping between template and target datasets. Thin plate spline (TPS) is chosen as the non-rigid transformation, because it has high degrees-of-freedom and smoothness in deformation and closed-form solution for warping and parameter estimation. A unit quaternion is used to represent the rotation part of the rigid transformation, as it can lead to simple optimization.

Let v_m, δ_m, and p_m denote ${\mathit{\mu }}_{\mathbf{x},k,i}^n$, ${\mathit{\sigma }}_{\mathbf{y},k,i}^n$, and ${\mathit{\mu }}_{\mathbf{y},k,i}^n$, respectively, where $m=i+{\sum }_{j=1}^{k-1}{N}_j$, k ∈ [1, …, K], i ∈ [1, …, N_k], m ∈ [1, …, S]. With these simplified notations, (11) is rewritten as

$$E_{\text{EM}}(\mathbf{T})=\sum _{m=1}^S({\mathbf{p}}_m-\mathbf{T}({\mathbf{v}}_m)){({\mathit{\delta }}_m)}^{-1}\times {({\mathbf{p}}_m-\mathbf{T}({\mathbf{v}}_m))}^T+log(p(\mathbf{T})).$$ (12)

1) Estimation of Rigid Transformation

A rigid transformation for a point u can be expressed as

$$\mathbf{T}(u)=\mathbf{\text{Ru}}+\mathbf{t}$$ (13)

where t is a 3×1 translation vector, and R is a 3×3 rotation matrix that is subject to R^TR = I and the determinant of R is 1 (proper rotation).

The objective function in (12) is expressed as

$$E_{\text{EM}}(\mathbf{R},\mathbf{T})=\sum _{m=1}^S({\mathbf{p}}_m-{\mathbf{\text{Rv}}}_m-\mathbf{t})){({\mathit{\delta }}_m)}^{-1}{({\mathbf{p}}_m-{\mathbf{\text{Rv}}}_m-\mathbf{t})}^T$$ (14)

So far there is no existing closed-form solution for estimating R that minimizes E_EM (R, t), so an iterative algorithm [21] is used to find R. The algorithm represents the rotation matrix R with a unit quaternion for simple optimization. A rotation by angle Ω around a 3×1 unit vector l can be represented by a 4×1 unit vector q such that

$$\mathbf{q}=\left[\begin{array}{c}{q}_0\\ {\mathbf{q}}_l\end{array}\right]=\left[\begin{array}{c}cos\frac{\mathrm{\Omega }}{2}\\ sin\frac{\mathrm{\Omega }}{2}\mathbf{l}\end{array}\right].$$

The iterative algorithm [21] that finds an optimal R can be summarized as follows:

Sub-algorithm 1: estimating q that minimizes EEM (R, t)

Input: vm, δm, pm. Output: q.

1: Compute a 3×4 matrix Xm:

$${\mathbf{X}}_{\mathbf{m}}=[({\mathbf{p}}_m-{\mathbf{v}}_m),({\mathbf{p}}_m-{\mathbf{v}}_m)\times {\mathbf{I}}_{3\times 3}]$$

where the product a × A of a vector a and a matrix A is a matrix whose column vectors are the cross product of a and column vectors of A.

2: Set b = 0 and Wm = I3×3.

3: Compute a 4×4 matrix M:

$$\mathbf{M}=\sum _{m=1}^S{\mathbf{X}}_m^T{\mathbf{W}}_m{\mathbf{X}}_m.$$

4: Compute a 4×4 matrix N:

$$\mathbf{N}=\left[\begin{array}{cc}{n}_0& {\mathbf{n}}^T\\ \mathbf{n}& {\mathbf{N}}^{\prime }\end{array}\right]$$

where

$$\begin{array}{lll}{n}_0\hfill & =\hfill & \sum _{m=1}^S({\mathbf{W}}_m:{\mathit{\delta }}_m),\hfill \\ \mathbf{n}\hfill & =\hfill & 2\sum _{m=1}^S{t}_3[A[{\mathbf{W}}_m{\mathit{\delta }}_m]],\hfill \\ {\mathbf{N}}^{\prime }\hfill & =\hfill & \sum _{m=1}^S({\mathbf{W}}_m\times {\mathit{\delta }}_m).\hfill \end{array}$$

The inner product (A : B) of matrices A = (Ai,j) and B = (Bi,j) is a scalar value that is defined by Σi,j(Ai,jBi,j). The outer product A × B is a matrix whose element in the ith row and the jth column is defined as Σk,l,m,nεi,k,lεj,m,nAk,mBl,n, where εi,k,l is levi-civita symbol

$${\varepsilon }_{i,k,l}=\{\begin{array}{ll}+1,\hfill & \mathit{\text{if}}(i,k,l)\mathit{\text{is}}(1,2,3),(3,1,2),(2,3,1)\hfill \\ -1,\hfill & \mathit{\text{if}}(i,k,l)\mathit{\text{is}}(3,2,1),(1,3,2),(2,1,3)\hfill \\ 0,\hfill & \mathit{\text{otherwise}}\hfill \end{array}.$$

The matrix operator A[] is A[A] = (A − AT)/2. The matrix operator t3[] is t3[A] = [A3,2, A1,3, A2,1]T.

5: Compute the smallest eigenvalue of matrix M − bN and the corresponding normalized eigenvector q.

6: If the absolute value of the eigenvalue is close to zero, stop and return q. Otherwise, update b and Wm as follows and go to step 3,

$${\mathbf{W}}_m={(q_0^2{\delta }_m+2q_{0}S[{\mathbf{q}}_l\times {\delta }_m]+{\mathbf{q}}_l\times {\delta }_m\times {\mathbf{q}}_l)}^{-1},$$

where the matrix operator S[] is S[A] = (A + AT)/2. The outer product a × A × a of a vector a and a matrix A is a matrix whose element in the ith row and the jth column is defined as Σk,l,m,n εi,k,lεj,m,nakamAl,n.

The rotation matrix R is then computed using the resulting q

$$\mathbf{R}=\left(q_0^2-|{\mathbf{q}}_l|\right){\mathbf{I}}_{3\times 3}+2\left({\mathbf{q}}_l{\mathbf{q}}_l^T+q_0{\mathbf{q}}_l\times {\mathbf{I}}_{3\times 3}\right).$$ (15)

The translation vector t is then computed using the R

$$\mathbf{t}={\left(\sum _{m=1}^S{\mathit{\delta }}_m\right)}^{-1}\sum _{m=1}^S{\mathit{\delta }}_m({\mathbf{p}}_m-{\mathbf{\text{Rv}}}_m).$$ (16)

2) Estimation of a TPS transformation

Using {v₁, v₂, …, v_m, …} as control points, a TPS transformation for a point u can be expressed as

$$\mathbf{T}(u)=\mathbf{\text{du}}+\mathbf{w}\mathit{\varphi }(\mathbf{u})$$ (17)

where u is a column vector (u_x, u_y, u_z, 1)^T that represents the coordinate of a point; d denotes a 3 × 4 matrix that contains the affine part of TPS; ϕ(u) is an S × 1 vector whose mth component ϕ_m (u) is − ‖u − v_m‖²; w is a 3 × S coefficient matrix that transforms φ(u) to a coordinate.

The objective function in (12) is then expressed as

$$E_{\text{EM}}(\mathbf{d},\mathbf{w})=\sum _{m=1}^S({\mathbf{p}}_m-{\mathbf{\text{dv}}}_m-\mathbf{w}\mathit{\varphi }({\mathbf{v}}_m)){({\mathit{\delta }}_m)}^{-1}\times {({\mathbf{p}}_m-{\mathbf{\text{dv}}}_m-\mathbf{w}\mathit{\varphi }({\mathbf{v}}_m))}^T+\lambda P(\mathbf{d},\mathbf{w})$$ (18)

where λP(d, w) is the prior term of TPS and λ is a parameter that controls the degree-of-freedom in the TPS transformation [22]. A large λ implies a TPS with smaller freedom. In the extreme cases of λ = +∞ and λ = 0, the TPS becomes an affine and a completely free transformation, respectively.

To estimate the coefficients d and w that minimize E_EM(d, w) (18), we solve the following system of linear equations:

$$\begin{array}{c}\hfill (\mathbf{U}+S\lambda {\mathbf{W}}^{-1})\stackrel{\sim }{\mathbf{w}}+[\mathbf{V},\mathbf{V},\mathbf{V}]\stackrel{\sim }{\mathbf{d}}=\mathbf{P}\\ \hfill {\mathbf{V}}^{\mathbf{T}}\mathbf{w}=0\end{array}$$ (19)

where U is a block matrix, each 3 × 3 component of which can be represented as U_m,n = I_3×3ϕ_m(v_n). Here, I_3×3 is a 3 × 3 identity matrix. To incorporate anisotropic point localization errors, a weighting matrix W is introduced to the equations as follows [22]:

$${\mathbf{W}}^{-1}=\left[\begin{array}{ccccc}{\mathit{\delta }}_1\hfill & \hfill & \hfill & \hfill & 0\hfill \\ \hfill & \cdot \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \cdot \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \cdot \hfill & \hfill \\ 0\hfill & \hfill & \hfill & \hfill & {\mathit{\delta }}_S\hfill \end{array}\right].$$

V is a matrix composed of the coordinates of all the control points

$$\mathbf{V}=\left[\begin{array}{cccc}1\hfill & v_{1x}\hfill & v_{1y}\hfill & v_{1z}\hfill \\ \cdot \hfill & \cdot \hfill & \cdot \hfill & \cdot \hfill \\ \cdot \hfill & \cdot \hfill & \cdot \hfill & \cdot \hfill \\ \cdot \hfill & \cdot \hfill & \cdot \hfill & \cdot \hfill \\ 1\hfill & v_{Sx}\hfill & v_{Sy}\hfill & v_{Sz}\hfill \end{array}\right].$$

Similarly, P is expressed as

$$\mathbf{P}={[p_{1x}{p}_{1y}{p}_{1z}\dots p_{Sx}{p}_{Sy}{p}_{Sz}]}^T.$$

Note that in (19), d̃ and w̃ are column vectors rearranged from the coefficient matrices d and w.

3) Coarse-to-Fine Registration

Rigid registration coarsely matches template to target fibers in a stable manner due to its limited freedom. On the other hand, TPS can accurately register two sets of fibers thanks to its high degree-of-freedom, but this freedom could also result in mapping template fibers to outlier target fibers. Therefore, the UFIBRE algorithm achieves a both stable and accurate registration of fiber bundles by smoothly increasing the degree of transformation freedom, from rigid to highly nonrigid. In our implementation, a rigid transformation is used for the first seven iterations to achieve a coarse but stable alignment between fiber bundles. Our pilot experiments show that seven iterations of rigid registration are sufficient to remove intersubject differences that are caused by global rotation and translation. Following the rigid registration, a TPS transformation is used in subsequent eight iterations. To make the TPS smoothly transit from affine to highly nonrigid, we decrease λ in each iteration by a factor of ten from a starting value of 10⁴ (instead of setting λ to a constant). The value of λ = 10⁴ at the beginning yields a nearly pure affine transformation and the value of λ = 10⁻⁴ (10⁴/10⁸) in the last iteration makes the TPS a highly free transformation.

E. Outline of the UFIBRE Algorithm

Implementations of the UFIBRE algorithm are outlined as follow:

1. Rigid UFIBRE algorithm

   Input: x, y and (πx, μx, σx).

   Output: R, t.

   1: Initialize n, R, t and (πy, μy, σy) as 0, I and (πx, μx, σx).

   2: Compute membership probability $m_{j,k}^{n+1}$ using (3) and (6).

   3: Compute updated target bundle parameters $({\mathit{\mu }}_{\mathbf{y}}^{n+1},{\mathit{\sigma }}_{\mathbf{y}}^{n+1})$ using (8) and (13).

   4: Compute unit quaternion q using sub-algorithm 1.

   5: Compute updated rotation Rn+1 using (15).

   6: Compute updated rotation tn+1 using (16).

   7: If n < 7, go to step 2 and n = n + 1; otherwise stop and return Rn+1, tn+1.

2. Transform x using the resulting rigid transformation and recalculate (π_x, μ_x, σ_x)

3. Non-rigid UFIBRE algorithm

   Input: x, y and (πx, μx, σx).

   Output: d, w.

   1: Initialize λ n, d, w and (πy, μy, σy) as 104, 0, I and (πx, μx, σx).

   2: Compute membership probability $m_{j,k}^{n+1}$ using (3) and (6).

   3: Compute updated target bundle parameters $({\mathit{\mu }}_{\mathit{y}}^{n+1},{\mathit{\sigma }}_{\mathit{y}}^{n+1})$ using (8) and (11).

   4: Compute updated TPS dn+1 wn+1 by solving (19).

   5: If n < 8, go to step 2 and n = n + 1, λ = λ/10; otherwise, return dn+1, wn+1 and $({\mathit{\mu }}_{\mathit{y}}^{n+1},{\mathit{\sigma }}_{\mathit{y}}^{n+1})$.

F. 2-D Example

To illustrate the UFIBRE algorithm, we provide a simple 2-D example that graphically shows the optimization process of this algorithm. The template contained three fiber bundles, as indicated in Fig. 1(a). The target was constructed by rotating the template bundles 30° clockwise. To demonstrate the robustness of the algorithm, an outlier bundle, which did not have a correspondence in the template, was added to the target [see Fig. 1(b)]. To make the problem more challenging, the outlier bundle was deliberately positioned such that it could be easily misjudged to correspond to the third bundle in the template.

Fig. 1.

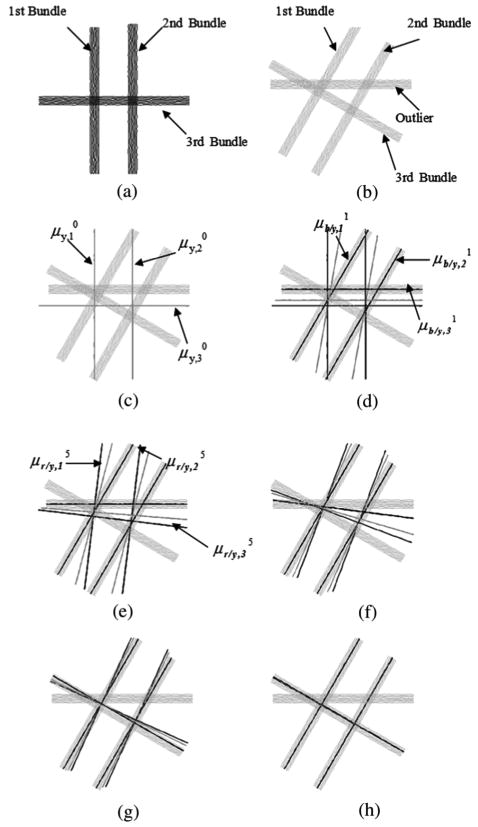
Illustrations of the optimization process of the proposed UFIBRE algorithm with a simple 2-D example. (a) Template fibers with known bundle classification. (b) Target fibers with unknown bundle classification. The target fibers (cyan), ${\mathit{\mu }}_{\mathit{b}/\mathit{y}}^n$ (blue), ${\mathit{\mu }}_{\mathit{r}/\mathit{y}}^n$ (red), and ${\mathit{\mu }}_{\mathit{y}}^n$ (green) at 0th (c), first (d), fifth (e), 12th (f), 15th (g), and 20th (h) iteration, respectively.

The UFIBRE algorithm was applied to the target as described in the preceding sections. The intermediate and final results of the optimization are illustrated in Fig. 1(c)–(h). Each of these figures shows the target fibers (cyan), ${\mathit{\mu }}_{\mathit{b}/\mathit{y}}^n$ (blue), ${\mathit{\mu }}_{\mathit{r}/\mathit{y}}^n$ (red), and ${\mathit{\mu }}_{\mathit{y}}^n$ (green). In this 2-D example, C was empirically set to 0.5, and a rigid transformation was used.

Fig. 1(c) displays the target fibers and ${\mathit{\mu }}_{\mathbf{y}}^0$, which were initialized as the unwarped template central fibers. In the first iteration, ${\mathit{\mu }}_{\mathbf{y}}^0$ was used to compute the membership probability $m_{j,k}^1$, which was then used to calculate ${\mathit{\mu }}_{\mathit{b}/\mathbf{y}}^1$. Due to the close proximity to ${\mathit{\mu }}_{\mathbf{y},3}^0$, the outlier target bundle had high membership probability of belonging to the third bundle, resulting in an incorrect ${\mathit{\mu }}_{\mathit{b}/\mathbf{y},3}^1$ as shown in Fig. 1(d). On the other hand, ${\mathit{\mu }}_{\mathit{b}/\mathbf{y},1}^1$ and ${\mathit{\mu }}_{\mathit{b}/\mathbf{y},2}^1$ were correctly determined, leading to more reasonable estimates of ${\mathit{\mu }}_{\mathbf{y},1}^1$ and ${\mathit{\mu }}_{\mathbf{y},2}^1$. In the last step of the first iteration, a rigid transformation was calculated to align the template central fibers with ${\mathit{\mu }}_{\mathbf{y}}^1$. In spite of the incorrect ${\mathit{\mu }}_{\mathit{b}/\mathbf{y},3}^1$, the template fibers were still rotated in a favorable direction as driven by the other two correct target bundles, and thus ${\mathit{\mu }}_{\mathit{r}/\mathbf{y},3}^n$ was gradually pulled toward the correct target bundle as shown in Fig. 1(d) and (e). As the weighted sum of ${\mathit{\mu }}_{\mathit{r}/y,3}^n$ and ${\mathit{\mu }}_{\mathit{b}/\mathbf{y},3}^n$, ${\mathit{\mu }}_{\mathbf{y},3}^n$ was also driven to the correct position by the movement of ${\mathit{\mu }}_{\mathit{r}/\mathbf{y},3}^n$ [Fig. 1(d)–(f)]. In the 12th iteration, ${\mathit{\mu }}_{\mathbf{y},3}^n$ had become quite close to the correct third target bundle and thus generated correct membership probability $m_{j,k}^{12}$ that led to a correct estimation of ${\mathit{\mu }}_{\mathit{b}/\mathbf{y},3}^{12}$ [Fig. 1(g)]. Finally, the warped template bundles converged to the correct target bundles as shown in Fig. 1(h). This example demonstrates that the registration process helps reduce the influence of the outlier so that the target fibers can be bundled consistently with the template.

III. Experiment and Evaluation Method

A. Imaging

The UFIBRE algorithm was implemented on in vivo DWI data obtained from eight healthy human subjects. Prior to imaging, informed consent was given by the subject according to a protocol that was approved by the local ethics committee. The data were acquired with a 3-T Philips Intera Achieva MR scanner (Best, The Netherlands) and an eight-element SENSE coil. A volume of 256 × 256 × 120 mm³ was scanned using 32 noncollinear weighting directions and a single shot, echo-planar, pulsed gradient spin echo imaging sequence with a diffusion weighting factor (i.e., b value) of 1000 s/mm². The data matrix had the size of 128 × 128 × 60, giving an isotropic resolution of 2 × 2 × 2 mm³ in the data. Three repeated scans were obtained from each subject, which were motion and distortion corrected and then averaged using Philips diffusion registration PRIDE tool (Release 0.4). Diffusion tensors were estimated from the averaged DWI data using a linear least-square fitting procedure.

B. Fiber Reconstruction

To generate the WM fibers, we employed a first order Euler integration method [23]. The voxels whose FA was greater than 0.5 were selected as seed points, from which the fibers were reconstructed by sequentially following the local principal diffusion direction at a step size of 2 mm. The fiber tracking process was terminated when voxels with FA below 0.1 were met or the angle between the principal diffusion directions of two consecutive points exceeded 45°. The above procedure yielded around 15 000 fibers for each dataset.

C. Bundle Selection

Nine WM fiber bundles of interest were manually segmented for each of the eight subjects by referring to their known anatomy. These bundles include the left and right corticospinal tracts (CST), the left and right medial lemniscus (ML), the left and right superior cerebellar peduncle (SCP), middle cerebellar peduncle (MCP) and the lower half of the splenium (SCC) and genu bundle (GCC), respectively. The bundle set from one subject was arbitrarily selected as the template fiber bundle, and Gaussian statistics (μ_x,k, σ_x,k, k = 1, …, 9) of the bundles were calculated.

D. Performance Evaluation

With the template, the proposed UFIBRE algorithms were applied to the remaining seven target fiber sets individually. The resulting bundles were compared with the manually segmented target bundles, which served as the “ground truth” in this comparison.

Since our algorithm achieves joint bundling and registration, the performance was evaluated by (1) the consistency of the estimated bundles with the ground truth, and (2) registration errors between their central fibers. Let b_k, $\overline{{\mathbf{b}}_k}$ be the estimated and the ground truth fiber bundles respectively and μ_k, $\overline{{\mathit{\mu }}_k}$ be their central fibers (k ∈ {1, … 9}). The consistency for bundle k is measured by the percent correct clustering (PCC)

$${\text{PCC}}_k=\frac{\left|\overline{{\mathbf{b}}_k}\cap {\mathbf{b}}_k\right|}{\left(\left|{\mathbf{b}}_k\right|+\left|\overline{{\mathbf{b}}_k}\right|\right)/2}\times 100\%$$ (20a)

where | ● | denotes the cardinality, i.e., the number of fibers in a bundle, and ∩ represents the intersection of two fiber bundles. The bundle registration error is measured by the root mean squared error (RMSE) between the central fibers μ_k and $\overline{{\mu }_k}$ (k ∈ {1, …, 9}), which is defined as

$${\text{RMSE}}_k=\sqrt{\sum _{i=1}^{N_k}{\left({\mathit{\mu }}_{k,i}-\overline{{\mathit{\mu }}_{k,i}}\right)}^2/N_k}.$$ (20b)

To comprehensively evaluate the proposed algorithm, we used a variety of parameter settings and tested the following aspects

1) Effect of the parameter C

To see how the weighting factor C affects the performance, we evaluated the UFIBRE algorithm with different values of C ranging from zero to one. The mean overall PCC and RMSE were presented as functions of C in order to find an optimal C that yields the best overall performance. Here the overall PCC and RMSE were calculated for each subject by averaging PCC and RMSE across the nine bundles. Their means across seven subjects were further computed for each value of C.

2) Optimal performance

To examine the performance of the algorithm with the optimal C, we reported the bundle specific mean PCC and RMSE instead of overall PCC and RMSE. To give a sense of the original differences between the template and target spaces, the RMSE between template central fibers and $\overline{{\mathit{\mu }}_k}$ were also given (“Unregistered” in Table II). With this information, one can see the effect of the UFIBRE algorithm on in vivo datasets. In addition to the quantitative evaluation, the resulting fiber bundles were also assessed visually.

TABLE II.

Statistics of RMSE for Nine Fiber Bundles Over the Seven Subjects Using the UFIBRE With C = 0.5. (Unit: Voxel)

	Un-registered		Registered
			All bundles included		MCP excluded	ML, SCP excluded
	Mean	Std	Mean	Std	Mean	Mean
CST(Left)	2.8145	0.6231	0.2315	0.2901	0.3243	0.3048
CST(Right)	4.1739	1.1585	0.6064	0.3384	0.5831	0.8357
ML(Left)	3.9206	1.3966	1.0983	0.9406	1.0961	N/A
ML(Right)	4.3691	0.3160	1.1823	1.1128	1.4149	N/A
SCP(Left)	3.3592	1.1830	1.0400	1.2057	1.1201	N/A
SCP(Right)	5.5162	1.6030	1.0033	0.7939	1.0352	N/A
MCP	4.8298	2.0292	0.2212	0.2632	N/A	0.2696
SCC	4.1748	1.2064	0.7514	0.3495	0.7621	0.7883
GCC	3.9300	1.4934	0.7465	0.3571	0.7515	0.7913

3) Effect of the number of bundles used

The above experiments were based on the use of the nine fiber bundles chosen (the left and right CST, the left and right ML, the left and right SCP, MCP, SCC, and GCC). To test the effect of the number of bundles on the performance, we excluded some bundles from the experiments. The bundle specific mean PCC and RMSE were reported for the case when ML and SCP were excluded and also for the case when MCP was excluded.

4) Consistency of factional anisotropy (FA)

To examine the consistency of diffusion parameters between the fiber bundles from the UFIBRE algorithm and those from manual segmentation, we performed group comparisons of the FA values along the nine fiber bundles studied. Let b_k,j,i and b̄_k,j,i be the ith point at the jth fiber in the kth bundle from implementation of the UFIBRE algorithm and the manual segmentation, respectively. The mean FA value along the kth bundle F_k,iF̄_k,i can then be computed for each subject as follows:

$$\begin{array}{l}{F}_{k,i}=\frac{\sum _j\mathbf{\text{FA}}({\mathbf{b}}_{k,j,i})}{\left|{\mathbf{b}}_k\right|}\\ {\overline{F}}_{k,i}=\frac{\sum _j\mathbf{\text{FA}}({\overline{\mathbf{b}}}_{k,j,i})}{\left|{\overline{\mathbf{b}}}_k\right|}\end{array}$$

where FA(a) denotes the FA value at the position a in DTI data, and | ● | denotes the cardinality. Treating F_k,i and F̄_k,i as two random variables whose values for each subject as samples from their probability distributions, we statistically compared F_k,i with F̄_k,i to see whether there are significant differences between the diffusion measurement resulting from the UFIBRE algorithm and that of manually segmented bundles. Paired t-tests were used to test the group difference along the fiber bundles, with each group containing the seven subjects studied.

5) Convergence

To analyze the convergence, the overall RMSE between the estimated central fibers ${\mathit{\mu }}_{\mathbf{y}}^n$ and manual segmentations were recorded for each of the 15 iterations.

E. Atlas Construction

The bundle correspondence and transformation information from the UFIBRE algorithm can be readily used to construct a fiber bundle atlas, which can serve as a statistical template for many purposes, such as guiding fiber tracking or bundle segmentation. To demonstrate the use of this algorithm for atlas construction, all the seven target datasets were transformed into the template coordinate system using the inverse of the transformation T previously obtained; then the corresponding bundles, which had already been estimated by the algorithm, were combined to construct a bundle atlas on the basis of the seven target and the template fiber sets. The statistics (central fiber and model covariance) of each bundle in the atlas were subsequently computed.

IV. Results

A. Performance Evaluation

1) Effect of the Parameter C

Fig. 2 shows that the UFIBRE algorithm achieves an optimal performance (maximum PCC and minimum RMSE) at C = 0.5. This indicates that the algorithm works best when the bundling term ${\mathit{\mu }}_{\mathit{b}/\mathit{y}}^n$ and registration term ${\mathit{\mu }}_{\mathit{r}/\mathit{y}}^n$ contribute equally to ${\mathit{\mu }}_{\mathit{y}}^n$ (10). Therefore, C is set to 0.5 for all the following studies.

Fig. 2.

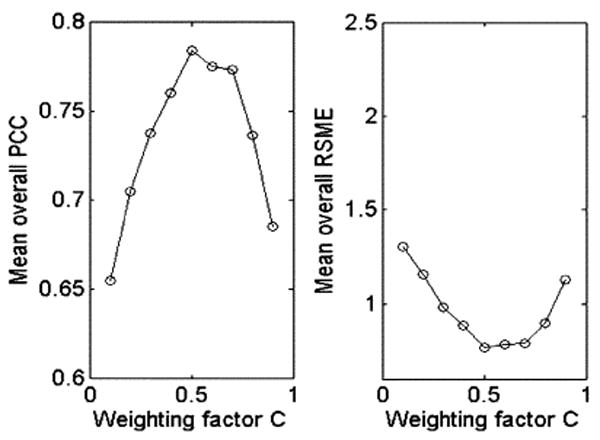
Variations of the mean overall PCC and RMSE with respect to the weighting factor C.

2) Optimal Performance

Tables I and II show the statistics of PCC and RMSE respectively for each of the fiber bundles studied. From the second and third columns in Table I, it can be seen that the estimated CST, MCP, SCC and GCC achieve an overall consistency of 85% PCC (minimum: 79%, maximum: 94% PCC) with the manually segmented bundles. From the fourth and fifth columns in Table II, it can also be seen that all the bundles give a very small average RMSE (less than 1 voxel) except the ML and SCP, whose average RMSEs are slightly greater than 1 voxel. These results indicate that our algorithm is capable of segmenting most of target bundles at a subvoxel accuracy. The relative smaller PCCs and larger average RMSEs in ML and SCP may be attributable to two factors. First, the fibers of the ML and SCP mutually overlap for a significant distance, which makes them rather difficult to distinguish for both the UFIBRE algorithm and manual segmentation. Second, there is considerable variability among the individual subjects in the course and size of the ML and SCP. Such variability contributes significantly to the difference between the template and the target data.

TABLE I.

Statistics of PCC for Nine Fiber Bundles Over the Seven Subjects Using the UFIBRE With C = 0.5

	All bundles included		MCP excluded	ML, SCP excluded
	Mean	Std	Mean	Mean
CST(Left)	0.8862	0.1091	0.8611	0.718
CST(Right)	0.7898	0.1114	0.7948	0.7175
ML(Left)	0.6936	0.2831	0.6924	N/A
ML(Right)	0.6383	0.3420	0.6049	N/A
SCP(Left)	0.6931	0.2786	0.6652	N/A
SCP(Right)	0.6553	0.2933	0.6560	N/A
MCP	0.9366	0.0718	N/A	0.9320
SCC	0.9000	0.0624	0.8968	0.8955
GCC	0.8632	0.0760	0.8593	0.8492

To demonstrate the capability of the algorithm for joint bundling and registration, estimated bundles in one of the seven target datasets were superimposed onto the template bundles, as shown in Fig. 3. In Fig. 3(a), the CST, ML, and SCP bundles of the template (red) and the target fiber (blue) set are overlaid on one coronal (top row) and sagittal (bottom row) slice of the target FA map. Note that the blue bundles, which were found by the UFIBRE algorithm, exhibit gross similarity to the manually segmented template bundles with respect to bundle structures and shapes. This indicates that our algorithm is able to bundle the target fibers in a way consistent with the template bundles. The left column of Fig. 3(a) displays the target bundles and unregistered template bundles, which shows obvious differences in the location and course between them due to differences in subject brain morphology, scan positions and orientations. The right column shows the results of registering the template bundles with the target, in which it can be seen that the postregistered template bundles overlap well with the target fibers. There is noticeable mismatch between the boundaries of the postregistered and target SCP, because the algorithm only registers their central fibers and thus does not guarantee the match of the whole bundles. Fig. 3(b) and (c), respectively, displays the MCP (b), SCC and GCC (c) bundles for template and target fibers overlaid on a transverse (top row) and sagittal (bottom row) view of the target FA map. We can also see increased similarity in the location and course for the post-registered template bundles.

Fig. 3.

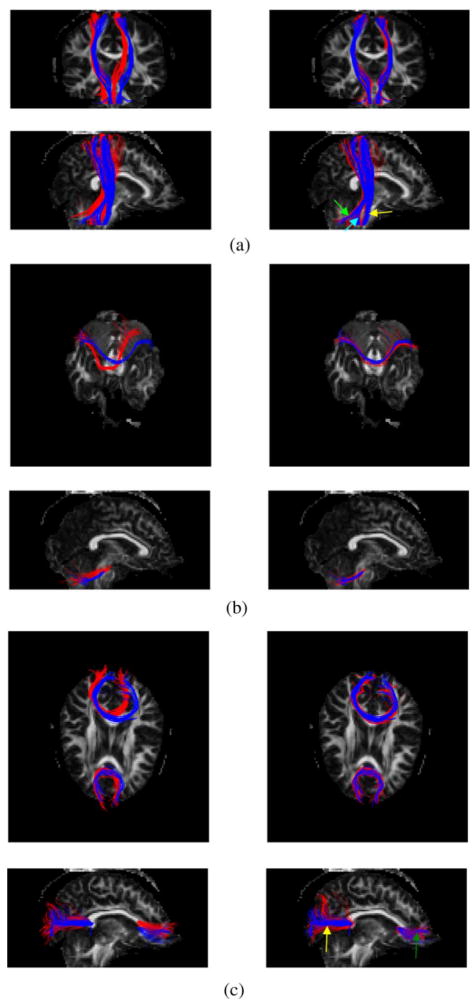
Superimposition of the template (red) and target fiber (blue) bundles on the FA map of the target data. The left column displays the unregistered template bundles with the target bundles, and the right column shows the registered and warped template bundles with the same target bundles. (a) CST (yellow arrow), ML (cyan arrow), and SCP (green arrow) bundles in coronal (top row) and sagittal (bottom row) views. (b) MCP bundle in transverse (top row) and sagittal (bottom row) views. (c) SCC (yellow arrow) and GCC (green arrow) bundles in transverse (top row) and sagittal (bottom row) views.

The estimated target bundles for a typical case were visually compared with manual segmentation in Fig. 4. In this figure, the first and third columns (red) are the fiber bundles estimated by the UFIBRE algorithm and the second and fourth columns (blue) are the bundles from manual segmentation. Note that the saggital view only displays the left CST, ML and SCP to avoid overlap with their right homologues. It can be appreciated that, for all structures, the courses and positions of the estimated target bundles are quite consistent with those from manual segmentation (blue).

Fig. 4.

Comparisons between ground truth obtained by manual segmentation (blue) and the bundles estimated by the UFIBRE algorithm (red) for one typical dataset.

3) Effect of the Number of Bundles Used

Tables I and II also show the resulting PCC and RMSE when some fiber bundles were excluded from the nine template bundle models. Comparing the third with the first column in Table I and the fifth with the third column in Table II, it can be seen that the PCCs and RMSEs with MCP excluded are very comparable to those with all the nine bundles used (with generally a slightly worse performance when MCP was excluded). With ML and SCP excluded, it can be found that the PCCs (the fourth column in Table I) and RMSEs (the sixth column in Table I) of the CST deteriorate greatly due to the fact that the ML and SCP fibers are close and similar to the CST fibers, which leads to incorrect classification of some ML and SCP fibers as CST by the algorithm. On the other hand, the performance for MCP, SCC, and GCC bundles only decreases slightly when ML and SCP were excluded. These observations indicate that including more bundles in the registration improves the performance of registering bundles in their vicinity, but the effect is very small on remote fiber bundles.

4) Consistency of Factional Anisotropy (FA)

Fig. 5 shows the group mean and standard deviation of F and F̄ together with the p-value of their paired t-tests along the nine fiber bundles studied. Comparing the first and second columns, it can be seen the curves of F's and F̄'s group mean along the bundles are quite similar. Rigorous paired t-tests between F and F̄ show that there are no statistically significant differences between them along any of the bundles (the third column) at p = 0.05 level, as all the p-values are greater than 0.2 and ∼90% of them are even greater than 0.5. Of particular notes, the ML and SCP bundles exhibit relatively smaller p-values than the other bundles; this is consistent with earlier observations that the PCC and RMSE of these two bundles are worse than others.

Fig. 5.

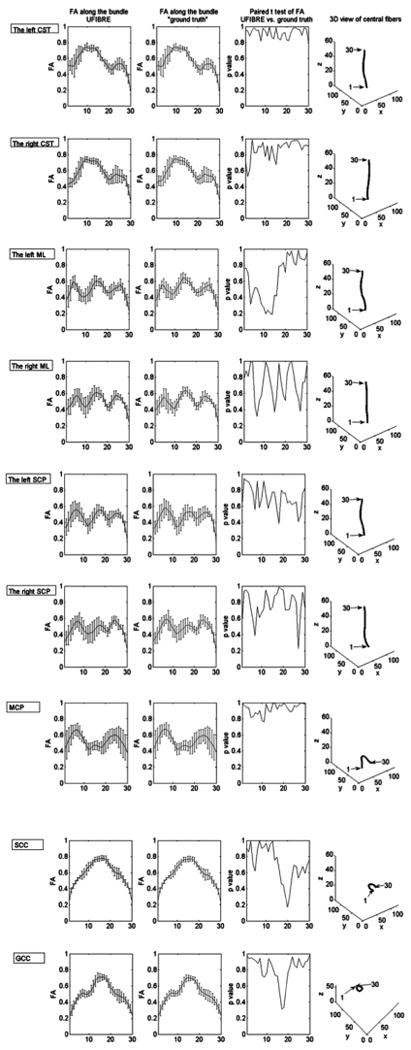
Comparisons between F and F̄ along bundles. The curve in the first column shows the group mean F with its standard deviation as error bars. Similarly the second column shows the group mean and standard deviation of F̄. The p-values of paired t-tests of F and F̄ are plotted in the third column. The last column shows the locations of the proximal and distal ends of each of the fiber bundles studied.

5) Convergence

Starting from a significantly large value (∼4 voxels), the overall RMSE stabilizes at a small value (less than 1 voxel) after 13 iterations. This indicates that 15 iterations are sufficient for the UFIBRE algorithm to achieve convergence.

6) Computational Complexity

In our experiments, there are a total of 1000 fibers approximately in the template bundles (∼100 in each of the SCP, the MCP, the ML and the CST; ∼500 in the SCC and the GCC). The number of fibers in one target dataset is usually around 15 000. Each fiber was downsampled to 30 discrete points. It takes up to 15 iterations at ∼60 s per iteration for our Matlab implementation to complete bundling and registering a whole target fiber set with the nine template bundles on an AMD Athlon 64×2 Dual-Core processor.

B. WM Fiber Atlas Construction

The atlas bundles were constructed by combining the fibers from the corresponding bundles in the eight datasets. The calculated central fibers and covariance (μ_x,k, σ_x,k, k = 1, 2,…, 9) of the atlas bundles are graphically displayed in a 3-D view in Fig. 6. At each point along the central fiber, the covariance matrix is represented by an ellipsoid. The orientations of the three axes of the ellipsoid are the same as the eigenvectors of the covariance matrix, and the lengths of the axis are equal to the square roots of the eigenvalues of the corresponding eigenvectors respectively. The ellipsoid at each central fiber point describes the distribution of all the points that belong to the same bundle and has correspondence to the central fiber point. It can be seen that the middle portion of the bundles have smaller ellipsoids or tighter distributions of points, and the ellipsoids tend to become larger towards to the ends of the bundles. In particular, the ellipsoids at the ends of some of the bundles (MCP, SCC, and GCC) sharply expanded. The compact middle portion indicates that the target bundles have been reasonably well-registered with the template. The gradually increasing covariance towards the ends is largely attributable to divergent nature of WM fiber bundles as they approach cortical regions and also partly due to accumulative errors that may occur in fiber tracking. The sudden increase of covariance at the ends suggests the tensors and thus the derived fiber tracts are less reliable near the cortical regions, where the FA is typically quite low.

Fig. 6.

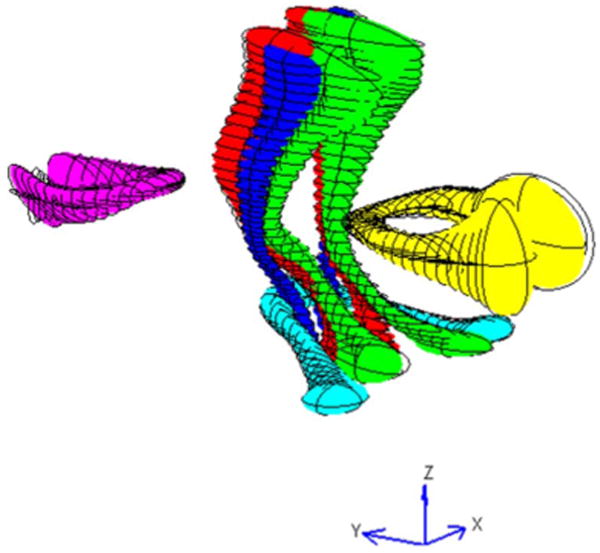
Three-dimensional view of the constructed bundle atlas from the template and seven target datasets (Red: the CST, Green: the ML, Blue: the SCP, Cyan: the MCP, Yellow: the SCC, Magenta: the GCC).

V. Discussion

We proposed in this paper a novel algorithm for joint bundling and registration of WM fibers reconstructed from DTI data. Given a set of segmented template bundles and a whole-brain target fiber set, the algorithm optimally bundles the target fibers and registers them with those in the template. Experiments with in vivo human DTI data show that, postregistration, ∼80% of fibers are correctly clustered, and the root mean square error of the bundle central fiber reaches subvoxel accuracy. The algorithm is highly efficient, converging within 15 iterations of parameter optimization at a speed of 60 s per iteration. This offers the potential of using the algorithm as a routine tool for laboratory research.

The framework we proposed has two salient and mutually beneficial features. First, the registration process guides fibers in the target to converge to bundles that are consistent with the template. This consistency is not guaranteed in conventional fiber clustering algorithms, which exclusively operate on individual datasets separately. Second, the bundling process helps simplify fiber-based registration to bundle-to-bundle registration. This avoids the process of fiber preclustering, and considerably improves the computational efficiency.

Image registration as a general image processing problem has long been the interest of many researchers. Essentially, it involves searches in a high dimensional space for transformation parameters that deform one image to optimally match another. The image registration problem, however, is ill-posed since a unique solution may not exist, and has very high computational complexity due to the high dimensional searches needed. The situation is worse for WM fiber registration, as the structures to be registered are finer and hence more complicated scenarios may occur. To approach the ill-posed, highly complex problem, it is typical to employ some regularization mechanisms and iterative optimizations, so that practically useful solutions can be obtained.

In this work, we also use regularization and iterative optimization, but further make three assumptions on fiber distributions for WM fiber registration: 1) a set of fibers in the human brain observe a Gaussian mixture model, 2) fibers in a bundle and points along the fibers are identically and independently distributed, and 3) the probability distribution of errors between the central fiber of a target and that of a template is Gaussian. These assumptions offer considerable computational benefits to parameter optimization, which renders the fiber registration problem more tractable. Although the validity of these assumptions still warrants further proof, experiments in this work demonstrate that quite appealing results can be obtained based on them. We recognize, however, more sophisticated models may better describe WM fiber distributions. For example, it was reported that a Gamma mixture distribution [9] may model the WM fiber distribution more accurately. Since parameters in the Gamma model can also be estimated by the EM algorithm, it can be in principle incorporated into our framework as well. A major drawback of using this or other more sophisticated models is disproportionally increased complication in the parameter optimization. We, therefore, note that, for fiber registration, the fiber distribution model should be chosen judiciously so that an optimal trade-off between the accuracy of model representation and the efficiency of parameter optimization is achieved.

It should be mentioned that, in this work, alignment of fiber bundles between the template and the target is only based on matching of the first order statistics (central fibers) of the bundles. The central fiber alone, however, does not carry complete information about the morphology of the fiber bundle. To align two fiber bundles more accurately, higher order statistics need to be considered. For instance, minimizing the difference in the second order statistics (covariance matrices) would provide better matching of bundle cross-sectional profiles. However, using higher order statistics may create difficulties in modeling the conditional probability, p(μ_y, σ_y, π_y∣μ_x, σ_x, π_x). A solution to this exists for the second-order statistics (i.e., using Kullback Leibler divergence), but optimization of the target bundle parameters becomes too complicated. Therefore, high order statistics are not included in this work, in order to achieve a compromise between the accuracy of bundle alignment and the efficiency of parameter optimization.

A most direct and useful application of joint bundling and registration of WM fibers is group analysis. It allows fibers from different subjects to be bundled consistently and registered into a common space, in which statistical characterization of bundle structural, architectural or geometric properties can be conveniently implemented. In addition, consistent and coregistered bundles from a group of subjects may be used to construct a parametric bundle atlas, which can be further utilized to guide other processes such as fiber tracking, bundling/labeling and registration. This application has been debuted in the present work with construction of a bundle atlas using eight human datasets.

Finally, we point out that the initial template bundles are segmented manually in this work. As mentioned earlier, this offers great flexibility in selecting or defining the bundles of interest. Notwithstanding this flexibility, the manual initial segmentation has the drawback of potentially producing subjective errors, and involving a certain amount of human labor. Manual segmentation can be avoided by using an atlas that contains well defined bundle models of interest for initialization. We have demonstrated the possibility of constructing an atlas of this kind, and plan to develop a more reliable atlas with more comprehensively defined fiber bundle models from a larger group of subjects, to enable our UFIBRE algorithm to work in a fully automated and objective fashion.

VI. Conclusion

In summary, we proposed an algorithm to automatically bundle a whole-brain fiber set and register it with a template bundle set. The resulting fiber bundles are consistent across subjects and share a common space, which facilitates further group analysis of the bundle properties. Experiments with in vivo human brain DTI data demonstrate that the algorithm we proposed is capable of bundling WM fibers in a consistent manner, and registering fiber bundles with subvoxel accuracy. Future work along this line includes development of a reliable parametric bundle atlas for fully automated implementation of this algorithm, and further applications of the automated algorithm to group analysis.