Magnifications of Single and Dual Element Accommodative Intraocular Lenses: Paraxial Optics Analysis

Abstract

Purpose

Using an analytical approach of paraxial optics, we evaluated the magnification of a model eye implanted with single-element (1E) and dual-element (2E) translating-optics accommodative intraocular lenses (AIOL) with an objective of understanding key control parameters relevant to their design. Potential clinical implications of the results arising from pseudophakic accommodation were also considered.

Methods

Lateral and angular magnifications in a pseudophakic model eye were analyzed using the matrix method of paraxial optics. The effects of key control parameters such as direction (forward or backward) and distance (0 to 2 mm) of translation, power combinations of the 2E-AIOL elements (front element power range +20.0 D to +40.0 D), and amplitudes of accommodation (0 to 4 D) were tested. Relative magnification, defined as the ratio of the retinal image size of the accommodated eye to that of unaccommodated phakic (rLM₁) or pseudophakic (rLM₂) model eyes, was computed to determine how retinal image size changes with pseudophakic accommodation.

Results

Both lateral and angular magnifications increased with increased power of the front element in 2E-AIOL and amplitude of accommodation. For a 2E-AIOL with front element power of +35 D, rLM₁ and rLM₂ increased by 17.0% and 16.3%, respectively, per millimetre of forward translation of the element, compared to the magnification at distance focus (unaccommodated). These changes correspond to a change of 9.4% and 6.5% per dioptre of accommodation, respectively. Angular magnification also increased with pseudophakic accommodation. 1E-AIOLs produced consistently less magnification than 2E-AIOLs. Relative retinal image size decreased at a rate of 0.25% with each dioptre of accommodation in the phakic model eye. The position of the image space nodal point shifted away from the retina (towards the cornea) with both phakic and pseudophakic accommodation.

Conclusion

Power of the mobile element, and amount and direction of the translation (or the achieved accommodative amplitude) are important parameters in determining the magnifications of the AIOLs. The results highlight the need for caution in the prescribing of AIOL. Aniso-accommodation or inter-ocular differences in AIOL designs (or relative to the natural lens of the contralateral eye) may introduce dynamic aniseikonia and consequent impaired binocular vision. Nevertheless, some designs, offering greater increases in magnification on accommodation, may provide enhanced near vision depending on patient needs.

Introduction

Implantation of an intraocular lens (IOL) has become standard procedure for vision correction following cataract removal. The increasing demand for perfect long-term post-operative vision has fostered a proliferation of surgical techniques of greater sophistication, and resulted in the development of novel IOL designs. Consequently, modern cataract surgery has been raised from a ‘mere’ cataract removal procedure to one of precision refractive surgery. For example, beyond the correction of sphero-cylindrical refractive error with implantation of accurately calculated power, it is now possible to customize IOL designs to control higher-order aberrations in the pseudophakic eye^1,2.

Though a standard monofocal or single-vision IOL affords near-perfect vision for a fixed (or at most, a narrow range of) viewing distance, patients may require supplementary optical devices in the form of spectacles or contact lenses for near vision to overcome the ‘induced presbyopia’ resulting from loss of accommodation following implantation of such IOLs. Multifocal IOLs and accommodative IOLs (AIOL) represent some of the current options for providing pseudophakic near vision. Though post-operative spectacle independence has been reported³, due to the simultaneous presentation of images for a range of viewing distances, multifocal IOLs inherently compromise visual performance as manifested in subjective vision complaints such as glare, halos, poor contrast and ghosting⁴. Technologies or procedures offering pseudophakic accommodation would eliminate this shortcoming. Lens refilling procedures and lens photo-modulation procedures represent promising future technologies for restoring accommodation⁵; however, several technical issues need to be addressed before such technologies can become regular clinical procedures.

AIOL is a rapidly emerging technology which is increasingly popular among researchers and clinicians⁶ and in a very short time, has become one of the preferred devices among ophthalmic surgeons attempting to restore near vision in the pseudophakic eye⁷. A wide variety of AIOL designs have been proposed. The more common designs and configurations of AIOLs are represented by the single-element (1E-AIOL) and dual-element (2E-AIOL) translating devices. Both are based on the principle of changing effective power. This change is introduced during accommodation by some suitable, albeit often complex, opto-mechanical arrangement^8–10 and results by shifting the axial position of the optical element(s) within the eye (also called translation). A translating 1E-AIOL typically consists of a single lens element positioned within the posterior chamber of the eye with special haptics designed to facilitate translation of the element (typically shifting anteriorly) during physiological accommodative effort^8,11. A 2E-AIOL is a device with a more complex opto-mechanical arrangement consisting of two lens elements coupled with elastic, flexible or spring-loaded connections⁹. The inter-element distance in this type of AIOL is altered under the effort of accommodation. A small number of 1E-AIOL designs have already obtained FDA approval^11,12 and at least one design of 2E-AIOL is currently the subject of clinical trials¹³.

Several clinical, laboratory and modelling studies have been published reporting the accommodative performances of the AIOLs¹⁴. In relation to design, magnification requires special attention as it can significantly influence optical/visual performance; which may be due to axial shifting of the optics that leads to ‘dynamic’ changes (i.e. changes associated with the action of accommodation) in the positions of the cardinal points (e.g. the nodal points) in the pseudophakic eye¹⁵. This in turn may result in dynamic changes in ocular magnification^15–16. The magnitude of such effects and their potential implications remain to be fully investigated. Several design parameters, including power of the AIOL elements, distance and direction of the translation and anatomical factors such as corneal power, anterior chamber depth and axial length may impact magnification. A theoretical study¹⁵ computed retinal image size of an eye implanted with 1E-AIOL at near focus and compared it to that obtained with near vision spectacle correction. It was concluded that the lateral magnification does not differ significantly between pseudophakic accommodation and near correction with spectacles, as the difference was less than 1%. However, the dynamic effect associated with accommodative change was not investigated. To our knowledge, magnification of 2E-AIOL is yet to be investigated.

In the present study, angular and lateral magnifications, of a model eye implanted with 1E-AIOL and 2E-AIOL were investigated. Specifically, the effects of translation of optics, and types and designs of AIOLs were evaluated using the matrix method of paraxial optics. The analytical approach employed in this study primarily aims to elucidate key control parameters relevant to the design optimisation of AIOLs and also attempts to determine potential clinical significance associated with the performance of such devices.

Methods

Matrix ray-tracing

The matrix method has been widely used in visual optics to calculate retinal image size,¹⁷ spectacle and relative spectacle magnification^18,19, and IOL power²⁰. It has also become a popular tool in ray-tracing analyses of astigmatic^21,22 and aspheric surfaces²³. This approach affords an elegant means of obtaining closed-form analytical equations to evaluate the performance of AIOLs, avoiding tedious algebraic developments²⁴. In the present study this method was used to evaluate the angular and lateral magnifications of a pseudophakic model eye.

Incident rays arriving at an optical system consisting of multiple surfaces undergo a series of refractions and translations to finally emanate from the last surface. In a matrix convention, for a rotationally symmetric optical system, refraction and transformation of a ray can be represented by a set of 2×2 refraction and translation matrices^15,25. It should be noted that while other conventions of matrical treatment are also in use^18,26, we employed that which appears to have been first applied to the study of accommodative IOLs^15,24. In that convention, input ray (ℜ) parameters on the first surface of an optical system may be represented by:

$$\Re =\left[\begin{array}{c}\hfill n·\alpha \hfill \\ \hfill h\hfill \end{array}\right]$$ (1)

where n is the refractive index of the medium of incidence, α is the angle between the ray and the optical axis, and h is the ray height on the surface. The emergent ray leaving the optical system has parameters:

$$\left[\begin{array}{c}\hfill n\prime ·\alpha \prime \hfill \\ \hfill h\prime \hfill \end{array}\right]=S.\left[\begin{array}{c}\hfill n·\alpha \hfill \\ \hfill h\hfill \end{array}\right]$$ (2)

where n′ is the refractive index of the medium in image space and S is the 2×2 matrix of the optical system given by:

$$S=\left[\begin{array}{cc}\hfill S_{11}\hfill & \hfill S_{12}\hfill \\ \hfill S_{21}\hfill & \hfill S_{22}\hfill \end{array}\right]$$ (3)

For a system containing m surfaces, where suffix 1 represents the first and m represents the last surface with dioptric powers F₁ and F_m, the system matrix S (sometimes referred to as the transformation²⁷ or transference matrix²⁶) reads:

$$S=R_m.T_{m-1}.R_{m-1}.T_{m-2}..........R_2.T_1.R_1$$ (4)

where R denotes a refraction matrix which, in general, is given by:

$$R=\left[\begin{array}{cc}\hfill 1\hfill & \hfill -F\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$$ (5)

where F is the dioptric power of the surface. Similarly, T denotes a translation matrix given by:

$$T=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill t/n\hfill & \hfill 1\hfill \end{array}\right]$$ (6)

where t/n represents the reduced distance between two consecutives surfaces.

Lateral magnification

Lateral magnification (LM) is defined as the ratio of the object size to image size²⁸. The relation between the lateral magnification and the coefficients of the matrix S of an optical system can be found by calculating the matrix that relates the ray parameters for a set of conjugate object and image points. This relation can be found by multiplying the system matrix by the translation matrices from the object plane to the optical system and from the optical system to the image plane, as follows:

$$\left[\begin{array}{c}\hfill n\prime .\alpha \prime \hfill \\ \hfill h\prime \hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill l\prime \hfill & \hfill 1\hfill \end{array}\right].\left[\begin{array}{cc}\hfill S_{11}\hfill & \hfill S_{12}\hfill \\ \hfill S_{21}\hfill & \hfill S_{22}\hfill \end{array}\right].\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill l\hfill & \hfill 1\hfill \end{array}\right].\left[\begin{array}{c}\hfill n.\alpha \hfill \\ \hfill h\hfill \end{array}\right]$$ (7)

where l and l′ as reduced object and image distances, respectively.

Expanding equation (7) we obtain

$$\left[\begin{array}{c}\hfill n\prime .\alpha \prime \hfill \\ \hfill h\prime \hfill \end{array}\right]=\left[\begin{array}{cc}\hfill S_{11}+S_{12}l\hfill & \hfill S_{12}\hfill \\ \hfill S_{21}+S_{22}l+(S_{11}+S_{12}l)l\prime \hfill & \hfill S_{22}+S_{12}l\prime \hfill \end{array}\right].\left[\begin{array}{c}\hfill n.\alpha \hfill \\ \hfill h\hfill \end{array}\right]$$ (8)

Since the object and image points are conjugate to each other, by definition, all rays passing through the object point of height h also pass through the same image point of height h′, independent of the initial value of α. In other words, h′ must be independent of ray angle. This condition can only be satisfied when the term at position S₂₁ in the system matrix equals zero, i.e.:

$$S_{21}+S_{22}l+(S_{11}+S_{12}l)l\prime =0$$

With this, the lateral magnification is obtained by:

$$\mathit{\text{LM}}=\frac{h\prime }{h}=S_{22}+S_{12}l\prime$$ (9)

Relative lateral magnification

In addition to absolute lateral magnification, relative lateral magnification, analogous to relative spectacle magnification (RSM), was calculated using two different approaches. Firstly, we calculated the relative lateral magnification (rLM₁) as the ratio of the lateral magnification of the pseudophakic eye at various levels of accommodation to the lateral magnification of the (natural) phakic model eye in the unaccommodated state. This index provides a measure of the change in lateral magnification as a function of pseudophakic accommodation with respect to the magnification of an average phakic eye focused at distance. Mathematically, it is given by:

$${\mathit{\text{rLM}}}_1=\frac{{\mathit{\text{LM}}}_a}{{\mathit{\text{LM}}}_{\mathit{\text{eye}}}}$$ (10)

where LM_eye refers to the lateral magnification of the phakic model eye in a distance focus state.

Secondly, we calculated relative lateral magnification (rLM₂) as the ratio of the lateral magnification of the pseudophakic eye at various levels of accommodation to the lateral magnification of the same (pseudophakic) eye at distance focus (unaccommodated state). This index provides a measure of change in apparent retinal image size as a function of pseudophakic accommodation in the same eye. Mathematically, it is given by:

$${\mathit{\text{rLM}}}_2=\frac{{\mathit{\text{LM}}}_a}{{\mathit{\text{LM}}}_d}$$ (11)

where LM_d and LM_a are, respectively, the lateral magnifications at distance and accommodated states of the pseudophakic eye.

Angular magnification

Various definitions for angular magnification are extant in the literature²⁹. Conventionally, angular magnification (AM) is the ratio of the image space ray angle (α′) to the object space ray angle (α) for a ray passing through conjugate points lying on the optical axis (angles shown illustrated in Figure 1). Reference rays may be the rays that pass either through the principal points³⁰ or through the centres of the entrance and exit pupils²⁹. In the present study, we used the ray passing through the centre of the entrance pupil (chief ray) as the reference for angular magnification since positions of the principal planes vary with translation of the AIOL and with the AIOL design, whereas the position of the entrance pupil (the image of the real pupil formed by the cornea) is independent of the amplitude of pseudophakic accommodation and the design of the AIOL. For a given accommodation amplitude the reference angle α, will therefore be the same for all AIOL designs.

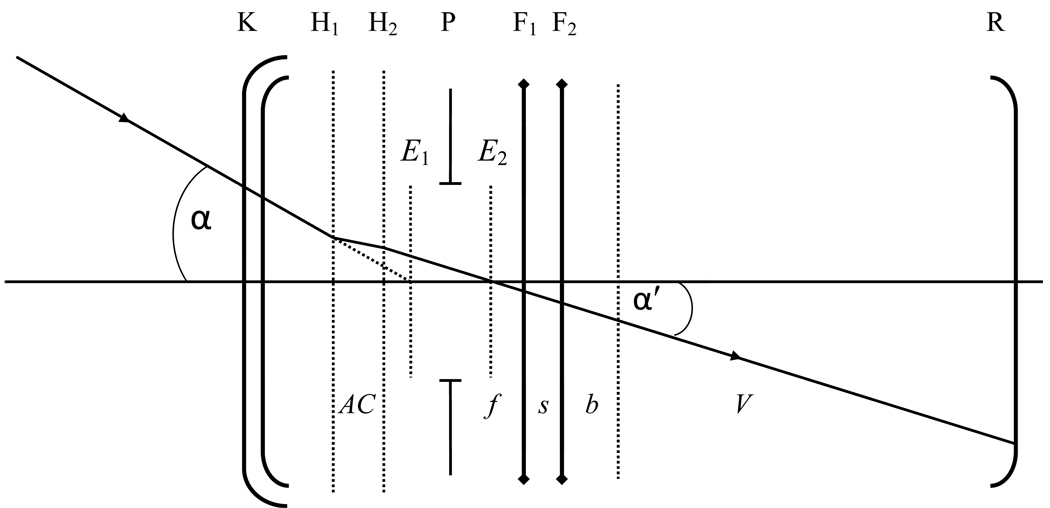
Figure 1.

Layout of the model eye with AIOL in which K refers to the cornea, H₁ and H₂ refer to the primary and secondary principal planes, P refers to the pupil, F₁ and F₂ refer to the front and rear lens elements of the AIOL respectively and R refer to the retina. The cornea was assumed to be a thin lens positioned in the plane of the anterior corneal surface. Distance AC is the anterior chamber depth, f is the space between the front element and pupil, s is the space between the two elements, b is the space between the anterior vitreous face and the rear element and V is the distance from the anterior vitreous face to the retina (the distances are exaggerated for clarity). Angle α is the incident chief ray angle at the centre of the entrance pupil E₁ and α′ is the emergent chief ray angle at the centre of the exit pupil E₂.

To find the relationship between angular magnification and the coefficients of the matrix of an optical system, we used the same method as for lateral magnification. This time, the object point is the centre of the entrance pupil and the image point is the centre of the exit pupil. Denoting x as a reduced distance of the entrance pupil from the corneal surface and x′ as the reduced distance of the exit pupil from the last surface of the AIOL, ray parameters at the exit pupil plane is given by:

$$\left[\begin{array}{c}\hfill n\prime .{\alpha }_p\prime \hfill \\ \hfill h_p\prime \hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill x\prime \hfill & \hfill 1\hfill \end{array}\right].\left[\begin{array}{cc}\hfill S_{11}\hfill & \hfill S_{12}\hfill \\ \hfill S_{21}\hfill & \hfill S_{22}\hfill \end{array}\right].\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill x\hfill & \hfill 1\hfill \end{array}\right].\left[\begin{array}{c}\hfill n.{\alpha }_p\hfill \\ \hfill h_p\hfill \end{array}\right]$$ (12)

where subscript p denotes a quantity measured in the pupil planes. For the chief ray, h_p=h_p′=0. Solving equation (12) for angular magnification (α_p′/α_p), we obtain:

$$\mathit{\text{AM}}=\frac{{\alpha }_p\prime }{{\alpha }_p}=\frac{n}{n\prime }(S_{11}+S_{22}.x)$$ (13)

where n=1 and n′=1.336 represent the refractive indices of the extraocular (air) and intraocular media.

Image nodal point position

During pseudophakic accommodation, positions of the cardinal points of the eye change due to movement of the AIOL. A change in the position of the image space (second) nodal point (N₂) with respect to the retina produces a change in retinal image size³¹. We therefore also calculated the positional change of the image nodal point. In the matrix method, the position of the image nodal point N₂ with respect to the retina R can be obtained from^15,32,33:

$$N_{2}R=-\frac{\mathit{\text{nn}}\prime }{S_{12}(S_{22}-n\prime )}$$ (14)

Computations

For computational purposes, the finite model eye of Navarro et al³⁴ was used. This model eye was chosen as it has been used previously to evaluate accommodative performance of the AIOL^16,24 and therefore provides a convenient comparative reference. The model eye parameters are given in the Appendix. The crystalline lens in the model eye was replaced with an idealized thin-lens model of a 2E-AIOL. For simplicity, the cornea was treated as a thin lens located in the plane of the anterior corneal surface. While three refraction matrices (representing the cornea, front element and rear element) and three translation matrices (representing anterior chamber, inter-element space and vitreous cavity) would have been sufficient to describe the eye, we introduced two additional translation matrices: one for translation from the front element to the fixed-position pupil (f) and another for translation from the fixed-position anterior vitreous face to the rear element of the AIOL (b) (Figure 1). This allowed the translation matrices representing the anterior chamber and the vitreous cavity to be independent of the translation of the AIOL elements. With this enhancement, the system matrix of the model pseudophakic eye from the cornea to the anterior vitreous boundary is given by:

$$S_{\mathit{\text{Eye}}}=T_b.R_{F2}.T_s.R_{F1}.T_f.T_{\mathit{\text{AC}}}.R_K$$ (15)

where T_AC, T_f, T_s and T_b are translation matrices for the anterior chamber, space between the front element and the pupil, space between the two elements and space between anterior vitreous face and rear element, respectively, and R_F2, R_F1 and R_K are the refraction matrices for the back and front elements of the AIOL and the cornea, respectively.

To evaluate the effect of power combinations of the 2E-AIOL elements, we used front element power ranging from +20 D to +40 D in 5 D steps where +20 D approximately represents a model of the 1E-AIOL. To simulate pseudophakic accommodation, two types of translation models were configured. The first configuration comprised an AIOL with a mobile front element in which the back element is maintained in a fixed position; the second configuration comprised an AIOL with a mobile back element where the front element remained fixed. Maximum translation was constrained to 2 mm in either configuration. All AIOL elements are thin-lenses in contact at their distance focus state (s = 0) implanted 2 mm behind the pupil plane.

Results

Effect of Accommodation

Both lateral and angular magnifications increased with accommodation in the pseudophakic eye whereas they decreased in the phakic model eye. For a 2E-AIOL with +35.0 D front element operating under configuration 1 (front element moving), the retinal image size increased by 25.8% at 4.0 D accommodation compared to the retinal image size of the same eye at distance focus (unaccommodated) state (or rLM₂), and by 37.5% compared to the retinal image size of the unaccommodated phakic model eye (rLM₁). Rates of increment in the apparent retinal image size in rLM₁ and rLM₂ were 9.4% and 6.5% per dioptre of accommodation, respectively (Table 1).

Table 1.

Changes in relative magnifications, angular magnification and image space nodal point (N₂) position as a function of accommodation and translation in phakic and pseudophakic model eyes. In configuration 1 of 2E-AIOL (Conf. 1), the front element moved in the forward direction and in configuration 2 (Conf. 2), the rear element moved in the backward direction for accommodation. rLM₁ is the ratio of lateral magnification of AIOL at various levels of accommodation to the magnification of the phakic model eye at distance focus (unaccommodated) state; rLM₂ is the ratio of magnifications at accommodated state to the magnification at distance focus state for the same eye; AM is angular magnification.

Change in		2E-AIOL Front Element Power				1E-AIOL	Model Eye
		+40 D	+35 D	+30 D	+25 D
rLM1 (% per D of accommodation)	Conf. 1	9.27	9.37	9.51	9.59	9.62	−0.25
	Conf. 2	21.57	27.36	39.85	81.03	-
rLM2 (% ×per D of accommodation)	Conf. 1	6.36	6.46	6.53	6.59	6.7	-
	Conf. 2	20.63	26.17	38.29	77.97	-
rLM1 (% ×per mm of translation)	Conf. 1	19.98	17.04	14.23	11.54	9.36	-
	Conf. 2	32.16	29.45	26.85	24.37	-
rLM2 (% ×per mm of translation)	Conf. 1	19.11	16.30	13.61	11.04	8.95	-
	Conf. 2	30.76	28.17	25.69	23.31	-
AM (per D of accommodation)	Conf. 1	0.013	0.013	0.014	0.015	0.016	−0.002
	Conf. 2	0.010	0.010	0.011	0.012	-
AM (per mm of translation)	Conf. 1	0.037	0.033	0.029	0.025	0.021	-
	Conf. 2	0.015	0.011	0.007	0.003	-
Forward shift of N2 (mm per D of accommodation)	Conf. 1	0.58	0.63	0.71	0.79	0.86	0.30
	Conf. 2	1.07	1.43	2.19	4.66	-

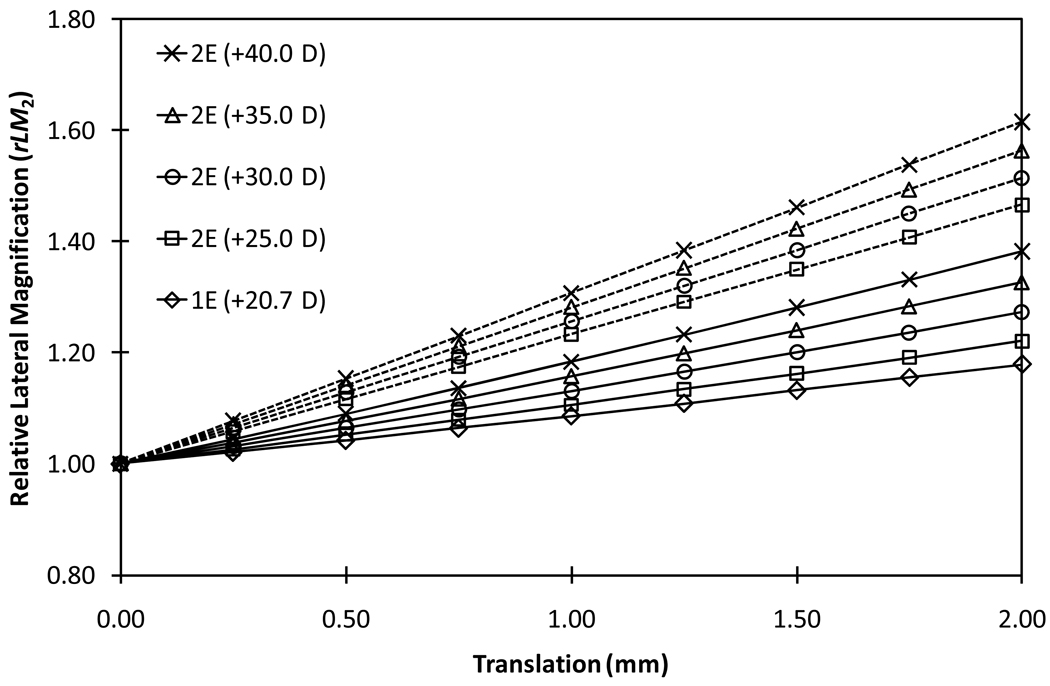
Changes in the relative lateral magnification for various models and configurations of the AIOLs as a function of pseudophakic accommodation can be seen in Figures 2 and 3. It is evident that relative lateral magnification increased at higher rates in configuration 2 (rear element moving) than in configuration 1 of the 2E-AIOL. The rate of change in magnification with accommodation increased as the power of the front element in the 2E-AIOL increase (Table 1).

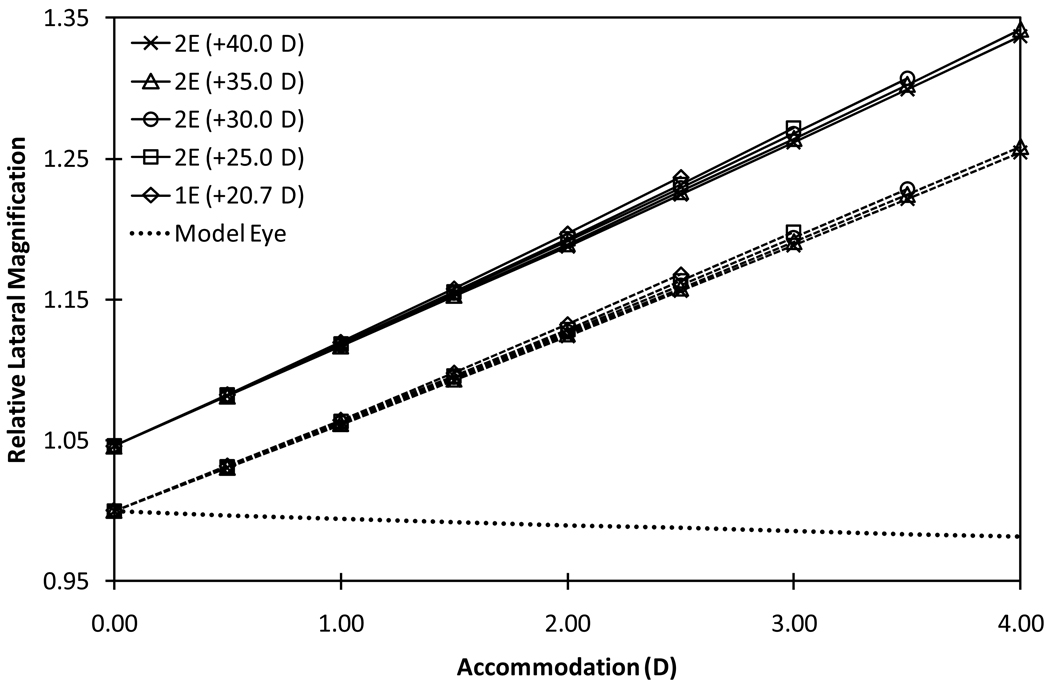
Figure 2.

Relative lateral magnifications of 1E-AIOL and configuration 1 (front-moving) of the various models of 2E-AIOL compared with that of phakic model eye. Solid plots represent rLM₁, which is the ratio of the lateral magnification of the AIOL at various levels of accommodation to the lateral magnification of the phakic model eye at distance focus (unaccommodated state) and dashed plots represent rLM₂, which is the ratio of the lateral magnification in the accommodated state to the lateral magnification at distance focus for the same pseudophakic eye. Relative magnification of the phakic model eye (dotted line) is included for comparison.

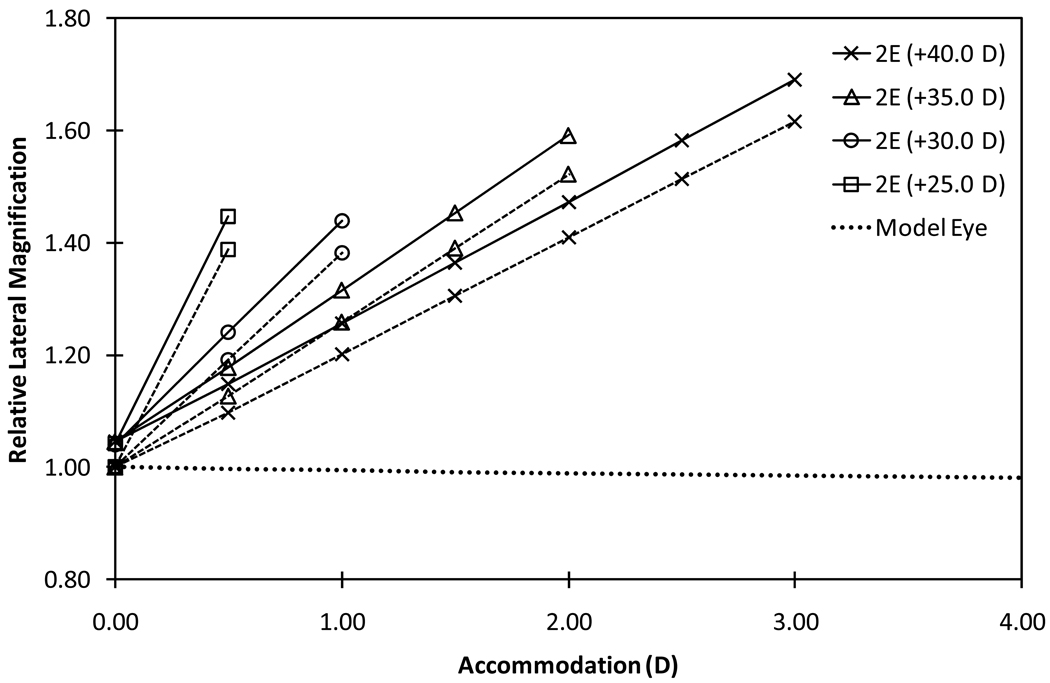
Figure 3.

Relative Lateral Magnifications of 2E-AIOLs with configuration 2 (rear-moving) compared with that of the phakic model eye magnification (dashed line). Solid plots represent rLM₁, which is the ratio of the lateral magnification of the AIOL at various levels of accommodation to the lateral magnification of the phakic model eye at distance focus (unaccommodated state) and dashed plots represent rLM₂, which is the ratio of the lateral magnification in the accommodated state to the lateral magnification at distance focus state for the same pseudophakic eye. Relative magnification of the phakic model eye (dotted line) is included for comparison.

For a 1E-AIOL with 2.5 D accommodation, which may be considered the maximum accommodation obtainable, rLM₁ and rLM₂ increased by 23.7% and 16.8%, respectively. The 1E-AIOL produced a higher rate of change in magnification with accommodation than any model of the 2E-AIOL. It should be noted that a 1E-AIOL requires translation over a longer distance than a 2E-AIOL to produce an equal amount of accommodation. The lateral and angular magnifications of the phakic model eye decreased with accommodation (Figures 2 to 4).

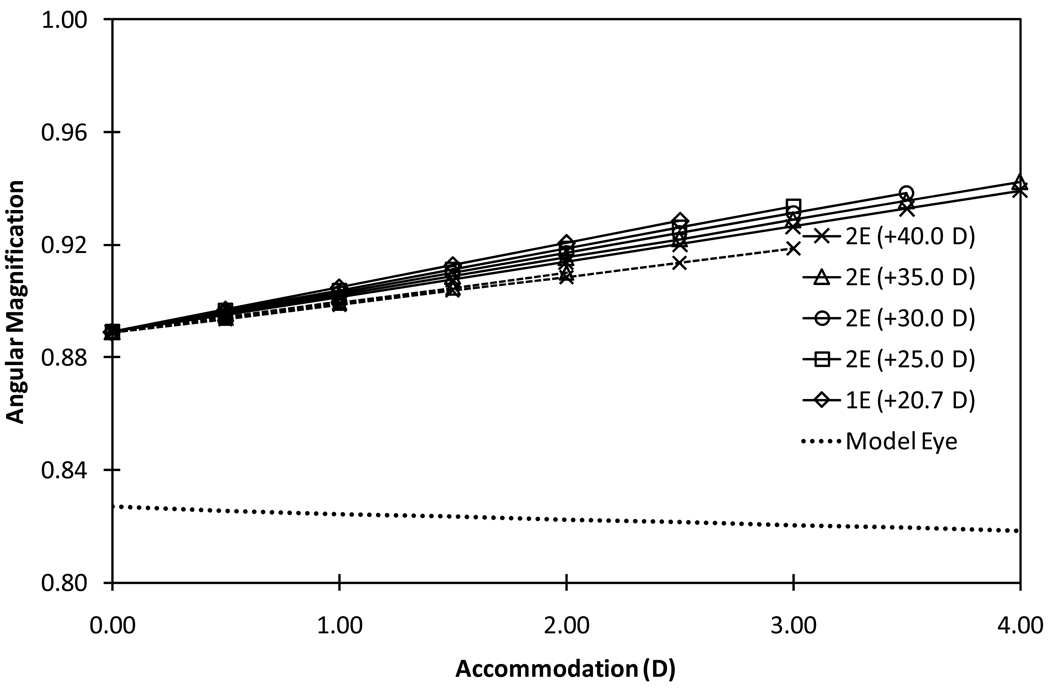
Figure 4.

Absolute values of angular magnification as a function of accommodation for various models of 2E-AIOL, 1E-AIOL and phakic model eyes magnification (dashed line). Solid lines represent configuration 1 (front-moving) and dashed lines represent configuration 2 (rear-moving). Angular magnification of the phakic model eye (dotted line) is included for comparison.

The angular magnification of the 2E-AIOL with +35 D front element operating under configuration 1 increased at a rate of 0.013/D of accommodation. The rate of change increased with decrease in the front element power of the AIOL. Slightly lesser rates of change were observed for 2E-AIOLs in configuration 2 (Figure 4). Angular magnification of the phakic model eye decreased at a rate of −0.002/D of accommodation (Table 1).

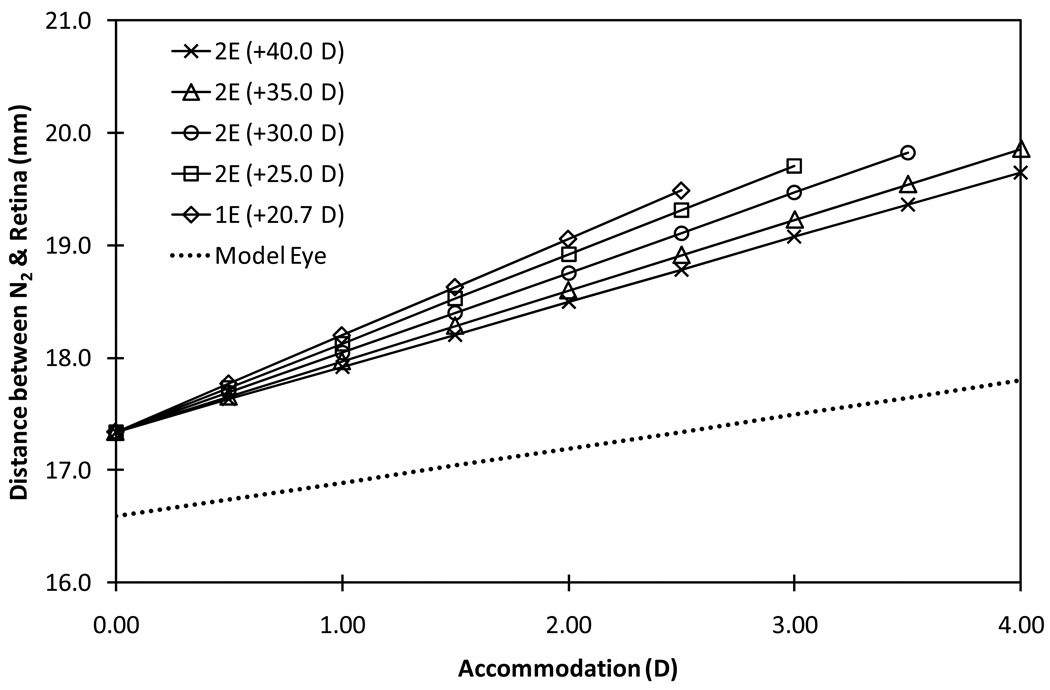
The nodal point shifted towards the cornea (moved away from the retina) with pseudophakic accommodation (Figure 5). At distance focus state, the image space nodal point (N₂) remained behind the optical system (about 17.34 mm in front of the retina); no significant differences in the position were observed between types and models of AIOLs. The nodal point shifted anteriorly at a rate ranging between 0.58 mm/D and 0.86 mm/D in configuration 1 (front element moving) depending on the power combinations of the elements; the rate of shift decreases as the power of the AIOL front element increases. In the phakic model eye, the nodal point moved away from the retina at a rate of 0.30 mm/D of accommodation.

Figure 5.

Distance between the image space nodal point (N₂) and the retina as a function of accommodation for the phakic model eye magnification (dotted line), 1E-AIOL and 2E-AIOL operating under configuration 1 (front-moving).

Effect of Translation

The rate of change in relative lateral magnifications (rLM₁ and rLM₂) ranged between 11.0% and 32.2% depending on the power of the front element and the configuration of the 2E-AIOL (Table 1). A 2E-AIOL in configuration 2 produces a higher rate of change in lateral magnification compared to a 2E-AIOL in configuration 1 (Figure 6). The rate of change in the lateral magnification per mm translation was less for a 1E-AIOL than a 2E-AIOL. The opposite was found when the change in magnification was quantified in terms of accommodation instead of translation.

Figure 6.

Relative Lateral Magnification (rLM₂) for various models of 2E-AIOL and 1E-AIOL as a function of translation of the optics. Solid lines represent configuration 1 (front-moving) and dashed lines represent configuration 2 (rear-moving). Relative Lateral Magnification is defined as the ratio of the magnification of the pseudophakic eye at various stages of translation to the magnification of the same eye at distance focus (unaccommodated state).

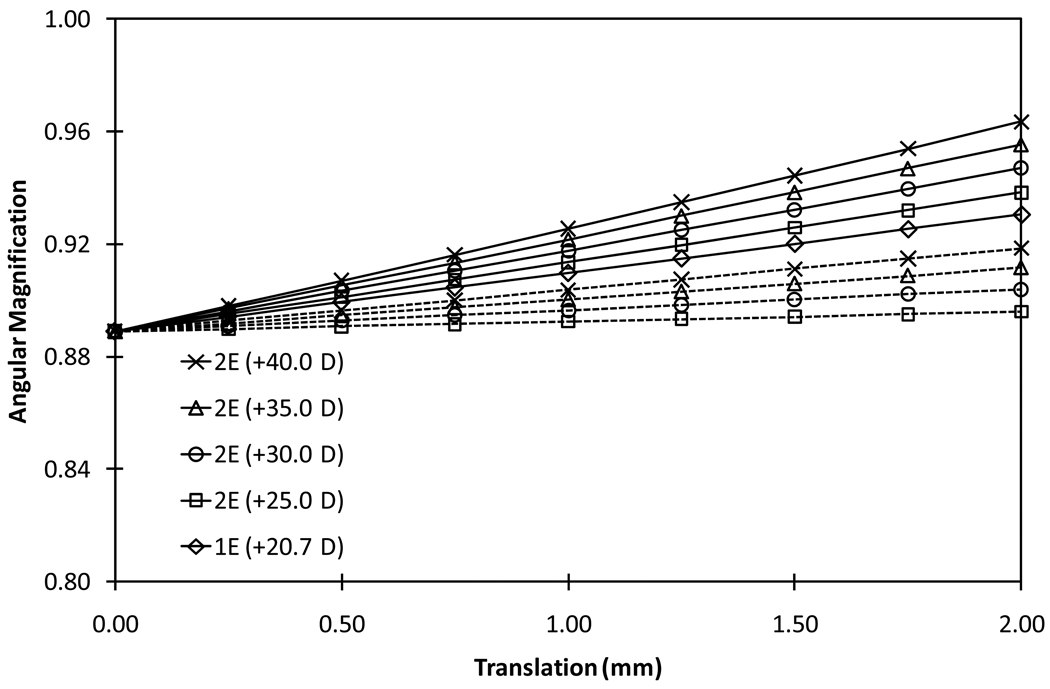
Angular magnification increased at a rate of 0.03/mm of translation for a configuration 1 (front-moving) 2E-AIOL with +35.0 D front element. The change in angular magnification was less for a configuration 2 (rear element moving) of 2E-AIOL than a configuration 1 (front element moving) 2E-AIOL (Figure 7).

Figure 7.

Absolute values of angular magnification as a function of translation of the optics for 1E-AIOL and various models of 2E-AIOL. Solid lines represent configuration 1 (front-moving) and dashed lines represent configuration 2 (rear-moving).

Discussion

In this study, changes in both angular and lateral magnification of AIOLs were considered. Lateral magnification provides a direct measure of the change in retinal image size for an object at finite distance. While interpretation of the lateral magnification is relatively straightforward, it cannot be used for a distant object (object at infinity) as lateral magnification becomes undefined. For this reason, we also evaluated angular magnification. Angular magnification is independent of the object distance and remains definable for all conjugate distances; including at a long distance (infinity) focus. In addition, angular magnification is advantageous because it can be referred to a reference input ray which is independent of the design of the AIOL. In this study, this advantage was realised by using the entrance and exit pupil planes as the reference planes to define angular magnification. Since the entrance pupil of the eye remains unchanged with accommodation and with IOL implantation, the input reference ray remains constant. A further advantage of the angular magnification is that it is independent of the axial length of the eye. Lateral magnification can be determined readily from the angular magnification given a value for the axial length.

Our results suggest that both the angular and the lateral magnifications of the eye increase proportionally with translation of the lens elements during pseudophakic accommodation. This result is in contrast to the phakic eye where magnification decreases with accommodation (Figure 3 and 4). Our results support earlier reports that phakic eye accommodation causes a decrease in apparent retinal image size³⁵; a phenomenon sometimes referred to as “accommodative micropsia”. Both a neural³⁶ and optical³⁵ cause for this effect have been proposed. A computational study demonstrated the optical minification effect of accommodation in a range of schematic eyes for which the retinal image size decreased by as much as 1.5% at 10.0 D accommodation³¹. We found a slightly higher value (2.5%).

The amount and direction of translation and powers of the lens elements are major design parameters significantly associated with magnification. These design parameters are also relevant to the accommodative performance of the AIOL. To achieve a given amount of accommodation, an AIOL with higher front element power requires less translation than an AIOL with lower front element powers^16,24. With an equal amount of translation, a higher power of the front element produces a higher amount of magnification. However, because accommodation is also proportional to the distance of translation of the optics, an AIOL with higher power of the front element will produce lesser magnification at a given accommodation amplitude.

An optical explanation for the change in magnifications in translating-optics AIOLs can be based on the relative position of the image space nodal point. Retinal image height is dependent on the distance between the retinal plane and the image space nodal point. For a given nodal ray angle, the image height increases as the nodal point to retina distance increases. In our model, the distance between the retina and the image space nodal point increased with translation of the optical element (Figure 5) which led to an increase in magnification. The rate of change in distance between the image space nodal point and the retina per millimetre of translation was greater for a 2E-AIOL with higher power of the front element. Also a higher rate was observed for a 2E-AIOL operating under configuration 2 (rear element moving) than a 2E-AIOL operating in configuration 1.

These results highlight a potential clinical issue relating to implantation of AIOL - that of dynamic aniseikonia. Dynamic aniseikonia may arise in two ways; either directly as a result of inter-ocular differences in magnification, or indirectly due to aniso-accommodation of AIOL between eyes. Clinically, when the difference in magnification between the eyes exceeds 4–5%, the two retinal images cannot be binocularly fused to provide the percept of a single image³⁷. As little as 1% imbalance in retinal image size has been reported to impair stereopsis³⁸. Assuming a nominal 2.50 D accommodation obtainable with a 2E-AIOL operating under configuration 1 and consisting of a 35.0 D front element, the relative retinal image size of the eye increases by an alarming 23.4% compared to that in the unaccommodated phakic model eye (Figure 3). Taking into account the accommodative minification of the normal phakic eye, this suggests monocular implantation of an AIOL may have a deleterious effect on binocular visual function.

Even when AIOLs are implanted binocularly, care must be taken to ensure that bilateral magnifications are matched, at least within inter-ocular tolerances, along the entire range of accommodation in order to avoid dynamic aniseikonia-induced binocular imbalance. Though the difference in magnification between various design combinations of 2E-AIOL elements powers are reasonably similar for matching accommodation levels up to 4 D, dynamic aniseikonia may arise due to differences in accommodation between the two AIOLs (i.e. aniso-accommodation). The results in this study indicate that aniso-accommodation of about 1 D would induce a retinal image size disparity of about 6% which is sufficient to severely compromise binocular vision. It must be appreciated that this scenario differs from the results of a study where 1E-AIOLs were implanted in one eye, and a conventional monofocal (non-accommodating) IOL was implanted in the other eye. When the eye implanted with the conventional IOL was corrected with near-vision spectacles and the other eye relied on the AIOL for near vision, only 1% difference in retinal image size was reported between the two eyes¹⁵. The magnification introduced by the reading spectacles apparently compensated for the difference in magnification of the two types of IOLs. It may be inferred from our results that, while the difference in magnification induced by small aniso-accommodation (<1 D) may not induce diplopia, it may be at a level sufficient to impair stereopsis.

In order to facilitate modelling, some assumptions and approximations were used in the present study. Hence, there may be aspects which have not been considered. Since the thin-lens approximation was used, magnification produced by changes in the shape-factor of lens elements could not be evaluated. However, a brief calculation shows that the effect is likely to be minimal, contributing approximately 1% (for 1 mm thick biconvex lens of 40 D lens) of the total magnification²⁸. Departure from constant magnification across the field (distortion) can be caused by implementation of specific individual or combinations of lens forms (shape factors) for the lens elements. Thus, the present results are theoretically only valid within the domain of paraxial optics approximations. However, since visual performance is typically primarily concerned with improving visual acuity, i.e. within the central retinal field, the use of paraxial approximation is reasonable.

The refractive status of the eye (myopic or hyperopic) and other ocular parameters such as corneal power and axial length, have also not been considered, but presumably have some effect on ocular magnification³⁹. For a more precise prediction of the magnification effect for different refractive errors and ocular anatomical dimensions, analyses incorporating additional parameters would be required.

In conclusion, from the optical design perspective of AIOLs, the power combination of the AIOL elements and the amount of translation are shown to be two key design parameters governing dynamic accommodation in the eye implanted with AIOL although implant position, refractive status and ocular dimensions should not be ignored. The power combination of 2E-AIOL lens elements requires special attention to avoid potential dynamic anisometropia and dynamic aniseikonia. In some cases, customised selection of designs and element combinations may be required to match their performance in a binocularly balanced manner.

Appendix

The accommodation-dependent model eye of Navarro et al⁵⁷ was used in the study as the reference phakic eye. Parameters marked with an asterisk vary with the amplitude of accommodation (i.e. are accommodation-dependent variables) which is determined from equations given following the table.

Surface	Radius	Thickness	Medium	Index
Front Cornea	7.72 mm	0.55 mm	Cornea	1.376
Back Cornea	6.50 mm	3.05 mm*	Aqueous	1.337
Pupil (stop)	-	0.00 mm	Aqueous	1.337
Lens Anterior	10.20 mm*	4.00 mm*	Aqueous	1.42*
Lens Posterior	6.00 mm*		Vitreous	1.336
Retina	-		Vitreous

Accommodation-dependent parameters:

• Anterior chamber depth:

  $$\mathit{\text{AC}}=3.05-0.05\text{log}(A+1)\mathit{\text{AC}}=3.05-0.05\text{log}(A+1)$$
• Anterior surface radius of curvature of the lens:

  $$R_1=10.2-1.75\text{log}(A+1)R_1=10.2-1.75\text{log}(A+1)$$
• Posterior surface radius of curvature of the lens:

  $$R_2=-6+0.2294\text{log}(A+1)R_2=-6+0.2294\text{log}(A+1)$$
• Crystalline lens thickness:

  $$T_L=4+0.1\text{log}(A+1)$$
• Refractive Index:

  $$n_L=1.42+9\times {10}^{-5}(10A+A^2)$$