Importance measures for epistatic interactions in case-parent trios

Summary

Ensemble methods (such as Bagging and Random Forests) take advantage of unstable base learners (such as decision trees) to improve predictions, and offer measures of variable importance useful for variable selection. LogicFS (Schwender & Ickstadt, 2008) has been proposed as such an ensemble learner for case-control studies when interactions of single nucleotide polymorphisms (SNPs) are of particular interest. LogicFS uses bootstrap samples of the data and employs the Boolean trees derived in logic regression (Ruczinski et al., 200) is base learners to create ensembles of models that allow for the quantification of the contributions of epistatic interactions to the disease risk. In this article, we propose an extension of logicFS suitable for case-parent trio data, and derive an additional importance measure that is much less influenced by linkage disequilibrium between SNPs than the measure originally used in logicFS. We illustrate the performance of the novel procedure in simulation studies and in a case study of 461 case-parent trios with autistic children.

Introduction

In association studies concerned with complex diseases, individual SNPs often only exhibit a small effect size. However, it is hypothesized that interactions of several SNPs and possibly gene-environment interactions might more strongly influence the risk of disease (Garte, 2001). Since the number of possible interactions between genetic markers and between genetic and environmental variables is vast, statistical procedures are required that can cope with this high-dimensional search space. Several methods for tackling this task have been proposed, including exhaustive searches based on multiple testing (Marchini et al., 2005; Goodman et al., 2006) and multifactor dimensionality reduction (Ritchie et al., 2001; Hahn et al., 2003; Ritchie et al., 2003), as well as machine learning methods such as Random Forests (Breiman, 2001; Lunetta et al., 2004; Bureau et al., 2005; Chen et al., 2007) and neural networks (Lucek & Ott, 1997; Ritchie et al., 2003b; North et al., 2003; Tomita et al., 2004). Besides multifactor dimensionality reduction, the restricted partition method proposed by Culverhouse et al. (2004) and logic regression introduced by Ruczinski et al. (2003) have been specifically developed for analyzing SNP data. Overviews and discussions on some of these procedure can be found in Heidema et al. (2006), McKinney et al. (2006), and Musani et al. (2007).

Logic regression has performed well in SNP association studies (Kooperberg et al., 2001; Witte & Fijal, 2001; Etzioni et al., 2004; Ruczinski et al., 2004; Andrew et al., 2008; Harth et al., 2008; Justenhoven et al., 2008; Suehiro et al., 2008), but has also been applied in other biomedical research areas such as the identification of regulatory motifs (Keles et al., 2004), HIV studies (Segal et al., 2004), DNA methylation (Feng et al., 2005), and biomarker detection (Vaidya et al., 2008). In addition, several modifications and extensions of logic regression have been proposed. Logic regression has been embedded into a Bayesian framework (Kooperberg & Ruczinski, 2005; Clark et al., 2007), and the simulated annealing algorithm employed in logic regression to search for interactions has been replaced by other probabilistic search methods such as genetic programming (Nunkesser et al., 2007) and evolutionary algorithms (Clark et al., 2005, 2008). Most recently, Li et al. (2010a) adapted logic regression, which originally has been developed for population-based association studies, to the analysis of case-parent trio data.

Similar to classification and regression trees (Breiman et al., 1984), the Boolean trees used in logic regression models are unstable, i.e. small changes in the data can lead to very different trees. Ensemble methods such as bagging (Breiman, 1996) and Random Forests (Breiman, 2001) take advantage of unstable predictors to improve predictions, and more importantly in the context of SNP association studies, offer measures of variable importance which can improve variable selection. However, none of these methods enable a direct quantification of the importance of combinations of variables. Based on this rationale, Schwender & Ickstadt (2008) proposed a procedure called logicFS (logic Feature Selection) in which a bagging version of the original logic regression is employed to identify disease-associated SNP interactions. The Boolean trees are used as base learners in this ensemble method, which allows for the quantification of the relevance of the detected SNP interactions (i.e. not only of individual SNPs) by providing an importance measure similar to one of the single variable importance measures determined in Random Forests.

In this manuscript, we adapt logicFS to case-parent trio data to stabilize the search for disease-associated interactions in such family-based data. We note that while much thought and effort has been put into the development of methods for testing candidate SNP interactions in case-parent trios (e.g. Schaid, 1999; Lunetta et al., 2000; Culverhouse et al., 2002; Cordell & Clayton, 2002; Cordell et al., 2004; Baksh et al., 2006, 2007; Kotti et al., 2007), only few methods searching directly for higher order SNP interactions in family-based data have been proposed (Martin et al., 2006; Li et al., 2010a). Moreover, we introduce a new importance measure that takes linkage disequilibrium (LD) between markers into account. The resulting approach called trioFS is then applied to simulated data, and to case-parent trios with autistic children.

Methods

Logic Regression

Logic regression introduced by Ruczinski et al. (2003) is a classification and regression procedure that adaptively searches for Boolean combinations C_k, k = 1,…,K of binary covariates (using the Boolean operators AND, OR, NOT) and incorporates these terms into a generalized linear model

$$g\left(\mathrm{E}\left(Y\right)\right)={\beta }_0+\sum _{k=1}^K{\beta }_k{C}_k,$$ (1)

where the choice of the link function g depends on the type of the response Y. If, for example, Y is binary, then g is the logit function, which is typically used for logistic regression models. The logic regression framework also includes many other forms of regression, such as linear models or Cox proportional hazard models.

To find the best logic regression model as described in equation (1), Ruczinski et al. (2003) employ a two-step procedure. First, the best scoring models of different sizes (as determined by the number of covariates used in the Boolean terms) are derived, and then model selection procedures such as permutation tests or cross-validation are used to determine the optimal model size. The search for good scoring models is carried out via simulated annealing, a stochastic search algorithm suitable for global optimization problems, and a tree-representation of the logic expressions C_k. Using a set of moves based on this tree-representation, variables and the AND- and OR-operators can be added to, removed from, or alternated in the logic expressions such that each logic expression can be reached from each other expression in a finite number of moves. In each annealing step, the new model is compared with the current logic regression model by a score function (for example, the deviance if Y is binary). If the newly proposed model is an improvement compared to the current model, it gets accepted. Otherwise, an acceptance probability based on the values of the score function for these two models is computed. This acceptance probability also considers how far the annealing has progressed, that is, it ensures that towards the end of the search newly proposed logic regression models are unlikely to get accepted if they score worse. When logic regression is applied to SNP data, each SNP S is typically split up into two binary variables S_D and S_R, coding for a dominant and a recessive effect of S, respectively. For a detailed description, see Ruczinski et al. (2003).

Recently, Li et al. (2010a) introduced an extension of logic regression enabling the analysis of case-parent trio data. As in a genotypic transmission disequilibrium test (Schaid, 1996; Cordell et al., 2004), trio logic regression uses the affected proband as a case, and the other Mendelian children (as derived from the parents’ genotypes) as matched pseudo-controls. Since there are 4^m – 1 matched pseudo-controls for each case when considering m unlinked SNPs (Cordell et al., 2004), Li et al. (2010a) restrict the analysis to the 1:3 matching typically employed when testing individual SNPs. This is achieved by randomly ordering the genotypes of the three Mendelian children at each marker, and augmenting those genotypes to generate three pseudo-controls. When SNPs are in LD, Li et al. (2010a) take the haplotype structure into account, designate a case phase for each trio, and select three random pseudo-controls under that phase scenario. As in logic regression, the genotypes are then described by two binary variables in dominant and recessive coding, and a conditional logistic likelihood is used in the search for the logic regression model that best discriminates cases and pseudo-controls.

Logic Feature Selection (logicFS)

In logicFS (Schwender & Ickstadt, 2008), logic regression is applied to several bootstrap samples drawn from the subjects in a case-control study to detect high-order SNP interactions associated with the case-control status. Thus, bagging (Breiman, 1996) with base learner logic regression is used in logicFS to stabilize the search for such interactions. To identify the interactions composing the logic expressions, and hence the logic regression models, each logic expression C_kb, b = 1,…,B, in each of the B models (or the complement of C_kb, if the respective parameter estimate ${\widehat{\beta }}_{kb}$ is negative) is transformed into a disjunctive normal form, i.e. an OR-combination of AND-combinations. Each of these AND-combinations in this disjunctive normal form represents one of the interactions.

Since some of the detected interactions will have a larger effect on the disease risk than others, Schwender & Ickstadt (2008) also propose an importance measure for quantifying the relevance of each identified interaction, which is related to one of the variable importance measures (VIM) used in Random Forests (Breiman, 2001). For each of the interactions comprised by a logic regression model, the value of the importance measure is computed by predicting the case-control status of the out-of-bag observations, i.e. the subjects that are not part of the bootstrap sample used to fit this model. This is done for both the original model as it has been found by logic regression, and a reduced model, which is derived by removing the interaction of interest from the original model and refitting the parameters in the model with the reduced logic expressions. For each iteration b = 1,…,B and each interaction P_j, j = 1,…,J, appearing in at least one of the B logic regression models, this leads to two numbers of correctly classified out-of-bag observations, denoted by N_b and $N_b^{(-j)}$ The importance of P_j is then quantified as

$$\mathrm{VIM}\left(P_j\right)=\frac{1}{B}\sum _{b:P_j\in {\mathcal{L}}_b}(N_b-{N_b}^{(-j)}),$$

where ${\mathcal{L}}_b$ is the set of all interactions comprised by the b-th logic regression model.

Logic Feature Selection for Trios (trioFS)

Similar to the analysis of data from case-control studies, applying trio logic regression to several subsets of the case-parent trio data can strengthen the identification of disease-associated SNP interactions. When randomly drawing these subsets, it is necessary to take the matching into account. Thus, we do not sample from the cases and pseudo-controls per se, but sample the case-pseudo-control status within each of the case-parent trios. Furthermore, we decided to use subsampling, i.e. to randomly draw a certain percentage of trios (typically, 63.2% of the trios, as this is the percentage of subjects expected to be in a bootstrap sample) instead of using bootstrap sampling (i.e. to randomly draw with replacement). This is foremost for computational efficiency, as sub-sampling works as good as bagging, but is computationally cheaper (Buehlmann & Yu, 2002).

In the computation of an importance measure, it would again be possible to employ the number of correct predictions of the case-(pseudo-)control status. However, since the controls are artificial, and their number is three times as large as the number of cases, we use another statistic to measure the goodness of the fitted model, namely the predictive log-likelihood ℓ_pred (Schmid & Hothorn, 2008). Thus, the parameter estimate ${\widehat{\beta }}_{1b}$ for the b-th trio logic regression model and the cases and matched pseudo-controls in the set ${\mathcal{L}}_b^{OOB}$ containing the out-of-bag observations of the b-th iteration are employed to compute the predictive log-likelihood

$${\ell }_{\text{pred}}\left({\widehat{\beta }}_{1b}\right)=\log \left(\prod _{i:i\in {\mathcal{L}}_b^{\mathrm{OOB}}}\frac{\exp \left({\widehat{\beta }}_{ib}{c}_{bi}^{\left(0\right)}\right)}{\sum _{p=0}^3{\widehat{\beta }}_{ib}{c}_{bi}^{\left(p\right)}}\right),$$

where $c_{bi}^{\left(0\right)}$ ∈ {0,1} is the value of the logic expression C_1b in the b-th model for the case in the i-th trio, and $c_{bi}^{\left(p\right)}$ (p = 1, 2, 3) are the values of C_1b for the matched pseudo-controls. This predictive log-likelihood is calculated for all B logic regression models, and the importance of an interaction P_j is calculated by removing this interaction from the models that contain P_j and computing the log-likelihood ${\ell }_{\text{pred}}\left({\widehat{\beta }}_{1b}^{(-j)}\right)$ of the respective reduced model. The importance of P_j is then given by

$${\mathrm{VIM}}_{\text{Trio}}\left(P_j\right)=-\frac{2}{B}\sum _{b:P_j\in {\mathcal{L}}_b}\left({\ell }_{\text{pred}}\left({\widehat{\beta }}_{1b}^{(-j)}\right)-{\ell }_{\text{pred}}\left({\widehat{\beta }}_{1b}\right)\right),$$

where the factor −2 is used to be in accordance with a likelihood ratio test.

A problem with importance measures such as the ones of Random Forests and logicFS, which is similar to the multicollinearity problem in linear regression, is that the importance can be lowered substantially when the corresponding SNPs are in strong LD (Lunetta et al., 2004; Nicodemus & Malley, 2009). If, for example, an interaction between the SNPs S₁, S₂, and S₃ is disease-associated, and S₁ is in strong LD with S₄, then the actual interaction will appear in some of the logic regression models, and the interaction of S₄, S₂, and S₃ is contained in other models. Hence, the actual interaction will show a reduced importance. To adjust for LD, we identify for each interaction P_j the logic regression models that contain interactions of the same number of terms as P_j, that only differ from P_j by SNPs that are in tight LD with the SNPs in P_j, where each of the replaced SNPs in P_j must have exactly one counterpart in the other interaction. If the b-th model contains such a neighbor interaction, we replace it by P_j, and refit the changed model to estimate ${\beta }_{1b}^{\ast }$. We then remove P_j from the model to compute ${\widehat{\beta }}_{1b}^{\ast (-j)}$, and the improvement

$${\mathrm{Imp}}_b^{\mathrm{LD}}\left(P_j\right)=-2\left({\ell }_{\text{pred}}\left({\widehat{\beta }}_{1b}^{\ast (-j)}\right)-{\ell }_{\text{pred}}\left({\widehat{\beta }}_{1b}^{\ast }\right)\right)$$ (2)

of the b-th model due to P_j. The adjusted importance measure is then given by

$${\mathrm{VIM}}_{\mathrm{LD}}\left(P_j\right)={\mathrm{VIM}}_{\text{Trio}}\left(P_j\right)+\frac{1}{B}\sum _{b:P_j\in {\mathcal{N}}_b}{\mathrm{Imp}}_b^{\mathrm{LD}}\left(P_j\right),$$ (3)

where ${\mathcal{N}}_b$ is the set containing all neighbor interactions of the interactions composing the b-th logic regression model.

Another problem is that an interaction might be identified by logic regression that consists of the actual disease-associated interaction and one or rarely more additional SNPs that only slightly increase the disease risk in the sample. While over-fitting is in general not a problem for the computation of the improvements as they are determined based on the out-of-bag observations, the importance of the actual interaction itself will be decreased nonetheless. This problem can be solved in a similar way as the LD problem, i.e. by replacing the extended interactions in the logic regression models, and analogous to equation (2), by calculating the improvements ${\mathrm{Imp}}_b^{\mathrm{Ext}}$ that would have been due to the actual interaction, had it been in the model instead of the extended interaction. The resulting importance measure adjusted for both LD and too large interactions is given by

$${\mathrm{VIM}}_{\mathrm{ADj}}={\mathrm{VIM}}_{\mathrm{LD}}+\frac{1}{B}\sum _{b:P_j\in {\epsilon }_b}{\mathrm{Imp}}_b^{\mathrm{Ext}}\left(P_j\right),$$ (4)

where ε_b is the set containing all interactions comprised in any of the B logic regression models that in interaction with another SNP make up one of the interactions in the b-th model. We typically restrict ε_b to interactions containing one additional variable, since we only rarely observe that an interaction intended to be disease-associated is extended by more than one interaction term in our simulation studies. However, the publicly available software also allows for the extension of more than one additional variable in the interaction terms.

To demonstrate the proposed importance measures (3) and (4) in an example, assume that trioFS with B = 5 iterations is applied to case-parent trio data, and that the disease-associated interaction P₁ consisting of the SNPs S₁, S₂, and S₃ is found in iterations 1 and 3, whereas interaction P₂ composed of S₄, S₂ and S₃ is identified in iterations 2 and 5, as S₁ and S₄ are in strong LD. In this case, ${\mathrm{Imp}}_b^{\text{Trio}}\left(P_1\right)$ will be zero for b = 2, 4, 5, and ${\mathrm{Imp}}_b^{\text{Trio}}\left(P_2\right)$ will be zero for b = 1, 3, 4, but ${\mathrm{Imp}}_b^{\mathrm{LD}}\left(P_1\right)$ will be larger than zero for b = 2, 5, and ${\mathrm{Imp}}_b^{\mathrm{LD}}\left(P_2\right)$ will be larger than zero for b = 1, 3. If we, moreover, assume that in the fourth iteration an interaction P₃ consisting of P₁ and S₅ is detected, then ${\mathrm{Imp}}_4^{\mathrm{Ext}}\left(P_1\right)\ne 0$, but ${\mathrm{Imp}}_4^{\mathrm{Ext}}\left(P_2\right)=0$ = 0, as P₃ is not an extension of P₂.

We note that while the main goal of the trioFS procedure is to generate hypothesis, not to carry out hypothesis tests per se, it is possible to define and generate permutation-based p-values for the SNP interactions based on the importance measures. In such a permutation test, the 1:3 matching has to be taken into account by randomly assigning the case status in a trio to one of the four Mendelian children derived from the parents’ genotypes. A simple approach for the p-value estimation is to apply trioFS to a sufficiently large number of permutations of the case-pseudo-control status across trios, and compare the values of the importance measures in these permutations with the observed values from the original application. However, such an approach would be computationally challenging even in small data sets. An alternative and much less time-consuming procedure, which typically leads to almost identical p-values (see the supplementary material to Schwender et al., 2010), is to employ the logic expressions found in the original analysis in all applications to the permuted case-pseudo-control status. In each iteration of this procedure, we permute the case-pseudo-control status, apply a conditional logistic regression to each of the B bootstrap samples using the respective logic expression from the original analysis as predictor, and compute the values of the importance measures based on these refitted models and the corresponding out-of-bag observations. The permutation-based p-values are then given by the fraction of the importances for an interaction determined in these iterations that are larger than or equal to the original importance.

The computation of the p-values can be further accelerated by making use of the alternative representation of the conditional likelihood proposed by Li et al. (2010b). Instead of considering all n trios in the maximization of the log-likelihood separately, one aggregates all trios showing the same value of the logic expression for the case and the same number of pseudo-controls for which the logic expression is true. Since there are only eight such case-pseudo-control combinations, and two of those do not contribute to the log-likelihood, and thus to the maximization procedure, the conditional log-likelihood can be maximized by considering six instead of n components, leading to a substantial reduction in required computing time.

Results

To illustrate the performance of trioFS, we applied the method to data from a simulation study considering different effect and sample sizes, and to a case study of parents with autistic children.

Simulation

As a first set-up, we simulated 100 data sets each consisting of genotypes for 100 unlinked SNPs, typed in 1000 case-parent trios. In each of these data sets, the SNPs S₃ and S₇ were simulated such that the chance of being a case was 3 times larger for subjects exhibiting at least one copy of the variant allele at both S₃ and S₇. Thus, a subject showing the interaction S_3D ⋀S_7D had a 3-fold increase in the chance of being a case, where the symbol ⋀ denotes the logic AND-operator. The genotypes of the other 98 SNPs were drawn under the assumption of no association with the outcome.

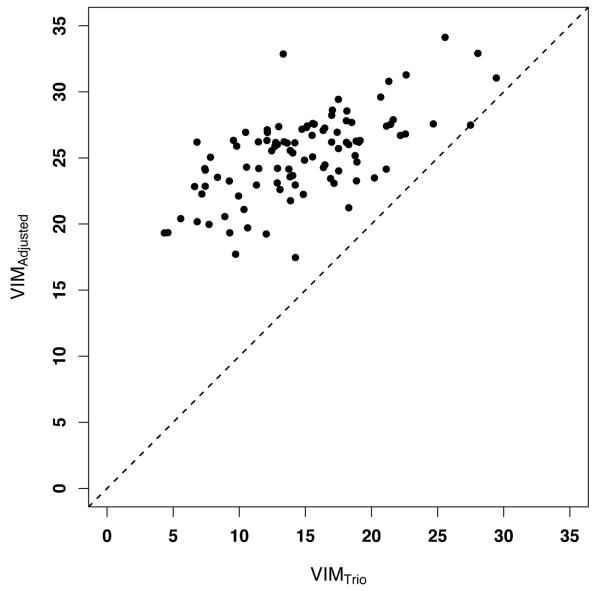
We applied trioFS with B = 20 iterations to these 100 data sets, and computed VIM_Trio, VIM_LD, and VIM_Adj. S_3D ⋀ S_7D was identified as the (usually by far) most important interaction in all applications of trioFS when considering VIM_Adj, and in all but one application when using VIM_Trio to rank the interactions. In fact, S_3D ⋀ S_7D is the only interaction that was detected in all applications. In general, S_3D⋀S_7D was considered very important by all three metrics VIM_Trio, VIM_LD, and VIM_Adj. However, with the exception of one application in which VIM_Trio = VIM_Adj, the value of VIM_Adj was typically substantially larger than the value of VIM_Trio (Figure 1). The reason for this is that although S_3D ⋀ S_7D exhibits the by far largest importance, interactions composed of S_3D⋀S_7D and one other SNP were also frequently identified in some of the iterations of trioFS, reducing the improvement due to S_3D ⋀ S_7D as quantified in equation (2) in such an iteration to zero, and thus, decreasing the overall importance of S_3D ⋀ S_7D (see Table 1 for an example output of trioFS). Adjusting for LD has no effect on VIM_Trio in this application, since all SNPs were simulated independently from each other. Thus, no pair of SNPs found in interaction with S_3D ⋀ S_7D exhibited an r²-value larger than 0.7, which was used as the defining threshold for LD in equation (3) to quantify VIM_LD (see Table 1).

Figure 1.

Scatter plot for the values of VIM_Trio and VIM_Adj for the interaction term S_3D ⋀ S_7D, derived from the applications of trioFS to 10 simulated data sets where disease risk is determined by said interaction. The values for importance measure VIM_Trio are always smaller than the corresponding values for VIM_Adj, illustrating the benefit of accounting for potentially over-fitted interactions. Since SNPs were not in linkage disequilibrium, the values for the importance measure VIM_LD are the same as the ones for VIM_Trio, and are omitted from the plot.

Table 1.

Values of VIM_Trio and the adjusted importance measures VIM_LD and VIM_Adj for the top five interactions found in the application of trioFS to one of the simulated trio data sets that resulted in the value of VIM_Trio closest to the median of the 100 VIM_Trio values. The interaction term S_3D ⋀ S_7D that specifies disease risk in this simulation is the most important finding. The other interactions also contain this term, and thus, the variable importance measure VIM_Adj that allows for this type of over-fitting is boosted. Since SNPs were not in linkage disequilibrium in this simulation, the values for the importance measures VIM_LD and VIM_Trio are identical

Interaction	VIMTrio	VIMLD	VIMAdj
S3D ⋀ S7D	14.23	14.23	22.95
$S_{3D}\wedge S_{7D}\wedge S_{40R}^C$	1.37	1.37	1.37
$S_{3D}\wedge S_{7D}\wedge S_{39R}^C$	1.18	1.18	1.18
$S_{3D}\wedge S_{7D}\wedge S_{8R}^C$	0.95	0.95	0.95
S1D ⋀ S3D ⋀ S7D	0.89	0.89	0.89

To investigate whether trioFS is also able to detect S_3D⋀ S_7D when this interaction has a smaller effect size, we simulated S₃ and S₇ such that the odds of being a case were 2.5, 2, or 1.5 times larger for subjects showing S_3D ⋀ S_7D. For each of these three odds ratio, 100 data sets were generated, each consisting of 1000 case-parent trios typed at S₃, S₇ and 98 additional independent SNPs intended to have no effect on the disease risk. Additionally, we simulated 100 data sets consisting of 500 trios for each of the four odds ratios 3, 2.5, 2, and 1.5. We then applied trioFS with B = 20 iterations to each of these data sets.

The simulation reveals that sample sizes of 1000 trios or fewer had to be considered insufficient for a study to detect interactions with odds ratios of 1.5 or smaller (Table 2).

Table 2.

Results of the applications of trioFS to the 100 data sets from each of 8 simulation scenarios in which the interaction S_3D ⋀ S_7D is intended to be disease-associated. This tables contains the numbers of applications in which this interaction is found, is identified as the most important interaction or amongst the five most important interactions, respectively, the numbers of applications in which an extension of S_3D ⋀ S_7D is identified as most important interaction or amongst the five most important interactions, respectively, and the numbers of applications in which S_3D ⋀ S_7D shows a Bonferroni corrected p-value p smaller than 0.05 or equal to zero, and an extensions exhibits a p-value p_Ext smaller than 0.05, using VIM_Adj or, in brackets, VIM_Trio as importance measure

	OR = 1.5		OR = 2.0		OR = 2.5		OR = 3.0
Trios	500	1000	500	1000	500	1000	500	1000
Found	8	33	87	100	99	100	100	100
Top 1	0 (0)	0 (0)	44 (20)	97 (72)	99 (75)	100 (96)	97 (91)	100 (99)
Top 5	1 (1)	0 (0)	54 (37)	100 (89)	99 (87)	100 (98)	100 (100)	100 (100)
Ext. Top 1	0 (0)	0 (0)	13 (20)	0 (22)	1 (24)	0 (4)	1 (7)	0 (1)
Ext. Top 5	1 (1)	1 (1)	67 (67)	98 (98)	98 (98)	99 (99)	100 (100)	99 (99)
p ≤ 0.05	0 (0)	0 (0)	0 (0)	67 (60)	59 (64)	100 (99)	99 (96)	100 (100)
p = 0	0 (0)	0 (0)	0 (0)	46 (36)	32 (37)	100 (99)	94 (92)	100 (99)
pExt ≤ 0.05	0 (0)	0 (0)	0 (0)	7 (7)	1 (1)	61 (72)	18 (47)	90 (97)

trioFS detected S_3D ⋀ S_7D only in 8 of the 100 applications to the data sets with 500 trios and 33 times in the data sets consisting of 1000 trios, where in only the former applications S_3D ⋀ S_7D ranked once under the five interactions with the largest values of either VIM_Trio or VIM_Adj. Interactions composed of S_3D ⋀ S_7D and another SNP were detected in 40 or 83 of the applications, respectively, but they were just once amongst the five top-ranking interactions in both simulation scenarios.

In all but one applications to the data sets from the simulation scenarios with odds ratios of 2.5 and 3, S_3D ⋀ S_7D was detected and ranked first when considering VIM_Adj. In a few of the analyses, S_3D ⋀ S_7D ranked not first, but typically second or third when basing this ranking on VIM_Trio, where the scenarios with the 500 trios performed worse than the scenarios with the 1000 trios. Usually, all top five interactions contained S_3D ⋀ S_7D (Table 2).

Employing VIM_Adj in the applications to the data sets from the simulation scenario with 1000 case-parent trios and an odds ratio of 2 led to the detection of S_3D ⋀ S_7D as the top-ranking interaction in 97% of the cases, whereas S_3D ⋀S_7D itself or an extension of it was found as most important interaction in 72 or 22 of the applications, respectively, if VIM_Trio was used. In the six remaining applications, three-way interactions of the SNPs with no main effect showed up as most important, but in these cases at least three of the other four top ranking SNPs were either S_3D ⋀ S_7D or an extension of it, i.e. a three-way interaction containing S_3D ⋀ S_7D. When considering the data sets consisting of 500 case-parent trios, S_3D ⋀ S_7D itself was found in 87 of the applications, and in another 12 analyses it was identified in interaction with another SNP. When the ranking is based on VIM_Trio, both S_3D ⋀ S_7D itself and extensions of it ranked first in 20 of the applications, and represented the most important interaction in 44 and 13 of the analyses, when considering VIM_Adj, respectively.

We also computed p-values based on 10,000 permutations of the case-pseudo-control status for all identified interactions, and adjusted for multiple comparisons using the Bonferroni correction. The term S_3D⋀S_7D was identified as significant in virtually all analyses based on 1000 trios, when the effect size was assumed to be 2.5 or larger (Table 2). Frequently, none of the 10,000 permuted importances were actually larger than the observed (un-permuted) importance of S_3D ⋀S_7D. The p-value was smaller than 0.05 in about 60% (VIM_Trio) or 67% (VIM_Adj) of the applications, when an odds ratio of 2 was assumed. When analyzing 500 trios, an odds ratio of 3 was necessary to systematically achieve significance. Virtually all interactions with a p-value smaller than 0.05 were either S_3D ⋀ S_7D or an extension of it. An exception is S_7D, which showed up significant in some of the applications.

To evaluate whether trioFS is also able to detect three-way interactions, S_3D ⋀ S_5D ⋀ S_7D was simulated such that it exhibits an odds ratio of 3, 2.5, or 2, and 97 SNPs were randomly drawn under the assumption of no association with the outcome. In this way, six sets consisting of 100 data sets were generated, where the data sets in three of these sets contained 500 case-parent trios, and in the other sets 1000 trios. We then applied trioFS with B = 20 iterations to all of these data sets and computed VIM_Trio and VIM_Adj.

Not surprisingly, even larger effect sizes are required to detect the higher order interaction (Table 3). Even for odds ratios of 2, neither S_3D⋀S_5D⋀S_7D nor extensions of it were identified. However, in all but one simulation scenario with odds ratio of 2.5 and 3, S_3D ⋀ S_5D ⋀ S_7D was detected by trioFS. In almost any application to the data sets with 1000 trios, this interaction ranked first when employing VIM_Adj, and it ranked first in most analyses when considering VIM_Trio. Only in a few of the applications, the value of VIM_Adj for S_3D ⋀S_5D ⋀S_7D was substantially larger than the value of VIM_Trio, as just a few extensions of S_3D⋀S_5D⋀S_7D appeared in the applications of trioFS. Instead the two-way interactions contained in S_3D ⋀ S_5D ⋀ S_7D, i.e. S_3D ⋀ S_5D, S_3D ⋀ S_7D, and S_5D⋀S_7D, showed up in almost any application of trioFS. In the settings with 500 trios, frequently at least one of these two-way interactions had a higher importance than S_3D⋀S_5D⋀S_7D, whereas the studies with 1000 trios reliably identified the three-way interaction as the most important one. This can also be summarized using the permutation-based p-values for S_3D ⋀ S_5D ⋀ S_7D, which were smaller than 0.05 in virtually any application to the 1000 trios, and zero in most of the applications. On a positive note for the smaller studies, in many instances more than just one of the two-way interactions and S_3D ⋀ S_5D ⋀ S_7D appeared amongst the top five SNPs and with a p-value smaller than 0.05, suggesting that this three-way interaction might be important for the disease risk prediction.

Table 3.

Results of the applications of trioFS to the 100 data sets from each of 8 simulation scenarios in which the interaction S_3D⋀S_5D⋀S_7D is intended to be disease-associated. This tables contains the number of applications in which this interaction is found, is identified as the most important interaction or amongst the five most important interactions, respectively, the number of applications in which one of the three two-way interactions contained in S_3D ⋀ S_5D ⋀ S_7D is identified as most important interaction or amongst the five most important interactions, respectively, and the numbers of applications in which S_3D ⋀ S_5D ⋀ S_7D shows a Bonferroni corrected p-value p smaller than 0.05 or equal to zero, and an extensions exhibits a p-value p_Ext smaller than 0.05, using VIM_Adj or, in brackets, VIM_Trio as importance measure

	OR = 2.0		OR = 2.5		OR = 3.0
Trios	500	1000	500	1000	500	1000
Found	0	0	100	99	100	100
Top 1	0 (0)	0 (0)	35 (47)	98 (89)	2 (36)	99 (100)
Top 5	0 (0)	0 (0)	79 (70)	99 (96)	89 (90)	100 (100)
Pruned Top 1	0 (0)	0 (0)	62 (44)	1 (10)	97 (63)	1 (0)
Pruned Top 5	0 (0)	0 (0)	100 (100)	99 (99)	100 (100)	98 (98)
p ≤ 0.05	0 (0)	0 (0)	37 (55)	99 (98)	46 (75)	100 (100)
p = 0	0 (0)	0 (0)	6 (10)	96 (90)	0 (3)	99 (100)
pPruned ≤ 0.05	0 (0)	0 (0)	59 (42)	45 (41)	93 (66)	7 (7)

In the final simulation set-up, we investigated the performance of trioFS and the differences between the importance measures when SNPs are in strong LD. We examined two specific settings for this simulation study, but also refer the reader to the autism case study discussed in the following section, which we believe is a particularly nice illustration of the differences between VIM_Trio and VIM_LD when SNPs are in strong LD. For each of these settings, one considering an odds ratio of 2.5 for S_3D ⋀ S_7D, the other an odds ratio of 3, we simulated 100 data sets consisting of 100 SNPs typed at 1000 trios. This time, we generated two LD-blocks of SNPs, one consisting of S₂, S₃, and S₄, and the other of S₆, S₇ and S₈. The pairwise r²-values within these blocks were larger than 0.99. The remaining 94 SNPs were randomly drawn.

Usually a minimum of three, and in most applications four of the top five interactions were composed of two SNPs, one from each of the two LD-blocks containing S₃ and S₇, with permutation-based p-values typically equal zero, but always less than 0.05 (see Table 4 for an example). The other top five interactions were always three-way interactions consisting of two SNPs from these LD-blocks and another SNP which only slightly contributed to the effect of the interaction. The term S_3D ⋀ S_7D is sometimes found as the most important interactions, however, frequently another interaction consisting of either S_2D, S_3D or S_4D, and S_6D, S_7D or S_8D ranks first.

Table 4.

The five interactions with the largest values for VIM_Trio determined in an application of trioFS to one of the simulated data sets in which S_3D ⋀ S_7D shows an odds ratio of 3. Here, S₃ is in strong LD with S₂ and S₄, and S₇ is in strong LD with S₆ and S₈. The numbers in the brackets are the Bonferroni corrected p-values corresponding to the respective importance measure

Interaction	VIMTrio	VIMLD	VIMAdj
S3D ⋀ S7D	3.69 (0.000)	9.05 (0.00)	9.05 (0.00)
S2D ⋀ S7D	2.63 (0.000)	6.61 (0.00)	9.16 (0.00)
S3D ⋀ S6D	1.79 (0.000)	6.57 (0.00)	9.80 (0.00)
S3D ⋀ S8D	0.97 (0.001)	6.56 (0.00)	7.84 (0.00)
$S_{4D}\wedge S_{6D}\wedge S_{89R}^C$	0.84 (0.043)	0.92 (0.02)	0.92 (0.02)

The identification of different two-way interactions consisting of SNPs from the two LD-blocks containing the truly associated SNPs led to a reduced value of the respective VIM_Trio. Employing VIM_LD however resulted in a substantially increased importance (see Table 4). If also three-way interactions composed of one of these two-way interactions and another SNP were found, the importance of this two-way interaction was further increased when using VIM_Adj. For example, several three-way interactions containing either S_2D ⋀ S_7D or S_3D ⋀ S_7D were identified in the analysis which led to the results presented in Table 4, but no higher-order interaction consisting of S_3D ⋀ S_7D. Thus, the importances of the former interactions, but not of the latter, were increased when using VIM_Adj.

Case Study

In this section, we consider 461 autistic children and their parents from 289 families recruited by the Autism Genetic Resource Exchange (AGRE; http://www.agre.org), a collaborative gene bank created by Cure Autism Now (CAN) and the Human Biological Data Exchange (HBD) to advance genetic research in autism spectrum disorders by consolidating large numbers of families into one collection. Genetic biomaterials and clinical data were obtained for families with at least one offspring diagnosed with an Autism Spectrum Disorder based on evaluation by the Autism Diagnostic Interview-Revised (ADI-R) and the Autism Diagnostic Observational Schedule (Geschwind et al., 2001). Cases were included if they had an ADI-R diagnosis of Autism, and data for both parents were available.

Two of the available 331 SNPs were excluded from the analysis since they were almost monomor-phic. Further, ten of the 461 trios were removed as more than 2% of the SNPs in each of these trios exhibited Mendelian errors. The haplotype-based procedure proposed by Li et al. (2010a) was used to impute the missing genotypes, and to transform the case-pseudo-control data into a format suitable for trio logic regression. We then applied trioFS with B = 20 iterations to these data.

The most important interaction detected by trioFS was a three-way interaction of rs11017112, rs7082126, and rs11017128, all showing the homozygous reference genotypes (Table 5). When considering the adjusted importance measure, a three-way interaction of the latter two SNPs and rs11017114 (also represented by the binary variable using dominant coding, i.e., the variable indicating at least one variant allele) exhibits the second largest importance. All these SNPs are from the gene Glutaredoxin 3 (GLRX3) on chromosome 10.

Table 5.

The five interactions with the largest value for VIM_Trio derived from the application of trioFS to the autism data set. For conciseness, the SNP rs-IDs are abbreviated as follows: S₁₈₀: rs11017112; S₁₈₅: rs7082126; S₁₉₂: rs11017128; S₁₈₃: rs11017114; S₁₉₃: rs4751178; S₁₄₃: rs553822; S₁₄₈: rs502862

Interaction	VIMTrio	VIMLD	VIMAdj	ORTrio	95% CI
$S_{180D}^C\wedge S_{185D}^C\wedge S_{192D}^C$	8.18	15.46	15.46	4.44	(3.26, 6.05)
$S_{182D}^C\wedge S_{185D}^C$	5.12	5.12	15.01	2.84	(2.10, 3.85)
S183D ⋀ S185D ⋀ S192D	5.06	9.94	15.17	2.58	(1.88, 3.53)
S183D ⋀ S185D ⋀ S192D ⋀ S193D	4.95	4.95	4.95	3.43	(2.45, 4.80)
$S_{143D}^C\wedge S_{148D}^C$	3.95	3.95	4.40	2.41	(1.81, 3.22)

Since the haplotype-based imputation of Li et al. (2010a) is probabilistic and data sets created by this procedure can differ, we generated ten data sets with this method and applied trioFS to each of those. All these applications led to the detection of at least one of the three-way interactions mentioned above, with a permutation-based p-value of zero throughout, where sometimes rs11017114_D was replaced by rs11017112_D, or $rs{11017112}_D^C$ by $rs{11017114}_D^C$ (and r² = 0.985 for these two SNPs). Typically, one of these three-way interactions was also identified as the most important one. Other interactions between SNPs from the same gene and/or SNPs from different genes or chromosomes were also picked up occasionally, but usually not for multiple of these data sets, hinting at spurious associations.

Since epistasis is usually defined as interactions between SNPs in different genes and/or genomic regions, we also analyzed a subset of the 329 SNPs that was previously considered elsewhere (Bowers et al., in preparation) Briefly, this subset consists of 138 independent SNPs showing pair-wise r²-values smaller than or equal to 0.2, and each glutathione-related gene is represented by the marker that has the largest estimated marginal effect size. In addition, all SNPs with a marginal p-value less than 0.1 were also included in the analysis. As before, we generated 10 case-pseudo-control data sets by applying the procedure of Li et al. (2010a) to the subset of 138 SNPs (the procedure is also applicable for “degenerate” haplotypes of size 1, i.e. individual SNPs), and analyzed these data sets with trioFS. Even though we strongly biased the selection of SNPs, the application of trioFS did not reveal interesting interactions.

Discussion

One of the main objectives in SNP association studies is the detection of interacting SNPs that explain some of the variability in the response of interest. In this manuscript, we have adapted a method suitable for finding such interactions in population-based case-control studies to case-parent trio designs. We have further proposed and motivated an adjustment of previous measures of interaction importance that corrects for linkage disequilibrium, and potentially over-fitted interactions.

Similar to importance measures from other approaches such as Random Forests, the here proposed importance measures are used to rank the interactions detected by trioFS by their importance for the disease risk, and to assess which of the found interactions are relevant risk factors. This is an appealing feature, however, should be considered a hypothesis generating rather than a hypothesis testing procedure, and ideally, interactions of interest should be validated on an independent data set if such data are available. This is obviously true for other methods as well, and the task to devise statistical methods that help to characterize interactions after discovery, and to quantify their contribution to the variation in the phenotype, is an active research area in the community (Edwards et al., 2010; Greene et al., 2010; Nicodemus et al., 2010, www.epistasis.org). We also note that for our procedure, it is possible to compute permutation-based p-values for the importances of the detected interactions, but we recommend that these p-values should be considered foremost as descriptive statistics.

The value of the proposed importance measure that adjusts for LD is computed for each neighboring interaction individually, although the SNPs forming these interactions are interchangeable. Another idea might be to jointly consider interactions that differ from each other only by SNPs in tight LD, and compute one importance for these interactions between blocks of SNPs. It is an open question whether the proposed importance measures for SNP interactions can also be used for this purpose, or if a more sophisticated measure is required.

Since not all SNPs composing a disease-associated interaction are necessarily of equal importance – some SNPs might be responsible for most of the effect, others might only lead to a marginal improvement in predicting disease risk – it might be beneficial to also develop methods to quantify how much each of the SNPs contribute individually to any particular interaction, and thus to the disease risk. Univariate testing is certainly not the ultimate solution for this problem, as some of the SNPs might not have a main effect at all, and only show an effect when interacting with other SNPs. Employing variable importance measures such as the ones of Random Forests in (trio) logic expression might lead to more reliable results, as such measures take the multivariate data structure into account.

In applications to simulated data, trioFS is almost always able to detect two- and three-way interactions even for small sample sizes when the effect sizes are large. From our experience with logic regression for population-based data and logicFS, we initially expected that trioFS should also be able to detect interactions with odds ratios considerably smaller than 2. However, in our simulations we have frequently seen “spurious” signal, i.e. interactions of null SNPs with large (estimated) odds ratios. A reason for this is due to the trio design, that is, the comparison of observed proband and the pseudo-controls. If, for example, only a single marker is considered, a trio with parents of the same homozygous genotype does not contribute to the likelihood, as all Mendelian children have the same genotype. Thus, in simulations with small data sets, large odds ratios can easily arise, although their actual significance (if assessed individually by a hypothesis test) would be low.

In an analysis of genotype data from children with autism and their parents, trioFS detects two three-way interactions each composed of SNPs from the same gene that appears to be associated with autism. After removing SNPs in LD by selecting one representative SNP for each gene, trioFS however does not identify interactions that give rise to large values of importance measures. This is not too surprising - interacting markers without main effects would not have entered this analysis, and markers with strong marginal effects might dominate and mask a potential epistatic effect.

In our computing environment, the application of trioFS to the autism data set took about 6.5 hours, where each iteration of trioFS, i.e. each application of trio logic regression, took about 19 minutes, and the computation of the importance measures a few seconds. In general, the computation time of trio logic regression depends on the number of trios and the number of iterations used in the underlying stochastic search algorithm (simulated annealing). Choosing an appropriate number of iterations typically requires some trial and error, and needs to reflect the size of the search space, i.e. should be a function of the number of markers investigated. We note that the total computing time can be cut substantially, since the applications of trio logic regression to the different subsamples of the data can be parallelized. The updated R package logicFS containing trioFS will provide the appropriate functionality for performing such parallel computations.

Nonetheless, the analysis of hundreds of thousands of SNPs would require a way too vast number of iterations, rendering an application of trio logic regression and thus of trioFS to genome-wide association studies impractical. However, we do not believe that the assessment of potential higher order interactions using hundreds of thousands of SNPs without prioritization is desirable, as the required effect sizes to detect such interactions had to be unrealistically large. Logic regression was initially developed for candidate SNP studies and can handle up to a few thousand marker, and thus, the same applies to trio logic regression and trioFS. In particular, if parallelization is employed, it might also be possible to analyze a few ten-thousand SNPs (as they might for example appear in exome sequencing) with a version of (trio) logic regression adapted to this new situation, as recent first attempts with such a modified logic regression show.

Software for trioFS will be available in an updated release of the R package logicFS. This package is freely available at http://www.bioconductor.org, the webpage of the Bioconductor project (Gentleman et al., 2004).